Simulation of the Protein-Shedding Kinetics of a Fully Vascularized Tumor

Abstract

Circulating biomarkers are of significant interest for cancer detection and treatment personalization. However, the biophysical processes that determine how proteins are shed from cancer cells or their microenvironment, diffuse through tissue, enter blood vasculature, and persist in circulation remain poorly understood. Since approaches primarily focused on experimental evaluation are incapable of measuring the shedding and persistence for every possible marker candidate, we propose an interdisciplinary computational/experimental approach that includes computational modeling of tumor tissue heterogeneity. The model implements protein production, transport, and shedding based on tumor vascularization, cell proliferation, hypoxia, and necrosis, thus quantitatively relating the tumor and circulating proteomes. The results highlight the dynamics of shedding as a function of protein diffusivity and production. Linking the simulated tumor parameters to clinical tumor and vascularization measurements could potentially enable this approach to reveal the tumor-specific conditions based on the protein detected in circulation and thus help to more accurately manage cancer diagnosis and treatment.

Introduction

Despite ongoing efforts to improve diagnosis and treatment, cancer continues to claim over eight million deaths per year worldwide.¹ Two dominant approaches have been cited² to improve outcomes: (1) earlier detection and (2) improved treatment personalization.^3,4 A focus on earlier detection stems from recent studies observing that earlier detection^5,6 can improve outcomes >30%. A focus on treatment personalization stems from the recognition that therapeutic approaches, highly effective in some patients, may have little or no benefit to other patients seemingly with the same tumor type.⁷ Consequently, tools to correctly assign patients to treatment plans are critical. Ideally, relatively cheap, highly accurate, blood bio-marker-based diagnostic tests could help diagnose disease and subsequently manage treatments.

Biomarker discovery approaches attempt to find proteins that are (1) relatively unique to the tumor, (2) indicative of its presence and likely behavior (eg, treatment response), and (3) easily quantifiable in the circulation. The underlying hypothesis of biomarker discovery approaches is that pathophysiological changes in cells or tissues are reflected through genomic alterations that influence protein expression in a disease- specific fashion. Accordingly, biomarker-discovery approaches have asserted that many potential markers are tumor-derived proteins that are shed from the tumor into circulation. Shedding for our purposes is considered as the aggregate of multiple processes, including protein secretion, extracellular domain cleavage, cell lysis, and diffusion to the circulation.

The biophysical processes governing how a protein leaves cancer cells, transits to the blood, and persists in circulation remain incompletely understood. As a purely empirical approach cannot measure shedding and persistence rates for all proteins across all tumor sizes, architectures, cell compositions, and types, we apply an interdisciplinary modeling–experimental approach as a first step toward linking biomarker expression to tumor state of viability. The ultimate goal for such an approach is to uncover fundamental biophysical processes of tumor progression, protein shedding, and protein persistence that underlie biomarker discovery, thereby accelerating biomarker development to help overcome challenges faced in cancer diagnosis and treatment.

Previous studies have advanced computational modeling to address the need for an integrated, quantitative analysis of tumor progression, typically using diffusion reaction equations describing the space and time dynamics of mass and diffusible substances (see reviews 8–18). Models using multiscale approaches (ie, linking events across subcellular, cellular, and tumoral scales),^19–32 studying vascularized tumor treatment,^33–42 and evaluating nanotherapy^37,41–52 have also been developed. Parameters in these models can be coupled with biological and clinical data, including measurements from in vitro cell culture, intravital microscopy, and histopathology. Signaling networks in cancer have been modeled,^53,54 encompassing gene,^55,56 protein,^57,58 and metabolic⁵⁹ activities. Recent work by Gambhir, Mallick, and coworkers^60–62 has helped to establish theoretical frameworks supporting cancer biomarker studies. In particular, a mathematical model relating tumor size and biomarkers secreted into circulation was developed.^60,62 Although model development has advanced, a more comprehensive understanding of biophysical processes governing protein abundance in tumors and their release into circulation by describing the complex interactions among tumor cells and their micro environment is needed. To address this and other shortcomings and to advance the study of protein biomarkers, we build upon work modeling tumor progression to develop a computational model that includes protein production and release based on tumor vascularization, cell proliferation, hypoxia, and necrosis. This system enables definition of quantitative relations linking the tumor and circulating proteomes while considering tumor structure and the associated microenvironment.

Methods

Simulation of protein shedding by vascularized tumor lesions

The mathematical model is based on Refs. ^{22, 37, 48}, and ⁶³ and is capable of representing in two spatial dimensions, viable and necrotic tumor tissues with angiogenesis-driven vas-cularization similar to that of tumor lesions and with shedding and transport of molecules throughout these tissues. The model dynamically couples a continuous tumor growth component with an angiogenesis model and accounts for blood flow, transcapillary fluid flux, interstitial fluid flow, and lymphatic drainage. This approach enables simulation of the complex interactions between tumor cells and their micro environment and the associated protein shedding and transport. Tumor growth is calculated based on the balance of cell proliferation and death. Proliferation depends on adequate cell nutrients and oxygen. Death is induced by levels of nutrients below a certain threshold. Model parameter values are calibrated to experimental data as in Refs. ^{30–32, 34, 35}, and ⁴⁸. The model and its parameters are described in the following sections.

Tumor growth

The tumor model component is based on Ref. 63, Briefly, the tumor tissue is denoted by Ω, and its boundary is denoted by Σ. In general, tumor tissue may have a proliferative region Ω_P (typically in the order of 100–200 µm around arterial vessels) in which cells have sufficient nutrients, a hypoxic region Ω_H in which nutrients and oxygen are sufficient for survival but not for proliferation, and a necrotic region Ω_N in which nutrients are insufficient for survival. The tumor growth velocity (nondimensionalized) is implemented via a generalized Darcy’s law⁶³:

$${\mathbf{v}}_c=-\mu \nabla P+{\chi }_E\nabla E$$ (1)

where m is a cell mobility representing the net effects of cell–cell and cell–matrix adhesions, P is an oncotic pressure, χ_E is a haptotaxis, and E is an extracellular matrix (ECM) density. Definitions for χ_E and E are in Ref. 63. By assuming that the cell density is constant in the proliferative region, the overall tumor growth is associated with the rate of volume change:

$$\nabla \cdot {\mathbf{v}}_c={\lambda }_p$$ (2)

where λ_p is a nondimensional net proliferation rate (see later). Here, the cell density is assumed not to exceed 70% of the total tissue, with the remainder composed of ECM. Tumor growth was simulated to Day 18 after inception, which allowed for reasonable computational cost (longer times will be explored in future work).

Angiogenesis

The vasculature model component is inspired by Ref. 64 and based on Refs. ²² and ⁶³, representing blood flow, vascular leakage, and vascular network remodeling due to wall shear stress and mechanical stresses imposed by the tumor tissue. The vasculature model is described in detail in Refs. ²² and ⁶³. The main model parameters influencing vascular flow include blood vessel pressure, vessel radii, vessel wall hydraulic conductivity, and osmotic pressure difference, with values set from previously reported experimental work.²² We simulate a simplified lung capillary organization composed of square elements, acknowledging that in reality the capillaries are heterogeneously delineated by the lung alveoli. As the tumor grows within this vascular environment, the tissue may locally experience heterogeneous access to elements diffusing from the vasculature, which may depend on tissue pressure as well as distance from the nearest vascular source.

Transport of oxygen and nutrients

The transport of nutrients (s = n) and oxygen (s = σ) is simulated from the location of the vasculature. These small molecules are supplied at rates ${\lambda }_{neo}^s$ and ${\lambda }_{pre}^s$, respectively, diffuse with a coefficient D_s, are taken up both by normal cells (with a rate ${\lambda }_{tissue}^s$) and tumor cells ( ${\lambda }_{tumor}^s$in the proliferative region and q_s in the hypoxic region), and decay (with a rate ${\lambda }_N^s$) in the necrotic regions. The formulation is⁶³

$$0=\nabla \cdot \left(D_s{\nabla }_s\right)-{\lambda }^s\left(s\right)s+{\lambda }_{ev}^s\left(\mathbf{x},t,1_{vessel},p,s,h\right)$$ (3)

$${\lambda }^s=\{\begin{array}{ll}{\lambda }_{tissue}^s\hfill & outside\mathrm{\Omega }\hfill \\ {\lambda }_{tumor}^s\hfill & in{\mathrm{\Omega }}_p\hfill \\ q_s\left(s\right)\hfill & in{\mathrm{\Omega }}_H\hfill \\ {\lambda }_N^s\hfill & in{\mathrm{\Omega }}_N\hfill \end{array}$$ (4)

where ${\overline{\lambda }}_{ev}^s$ is the constant transfer rate from both pre-existing and tumor-induced vessels, x is the position in space, t is the time, p is the tumor (solid) pressure, 1vessel is the characteristic function for vasculature (equals 1 at vessel locations and 0 otherwise), and h is the hematocrit in the vascular network related to oxygen extravasation (following Ref. 63). The extravasation is modulated by the extravascular interstitial pressure p_i scaled by the effective pressure p_e, with $k_{p_i}$ being the weight of the convective transport component of small molecules²²:

$${\lambda }_{ev}^{\sigma }={\overline{\lambda }}_{ev}^{\sigma }{1}_{vessel}\left(\mathbf{x},t\right){\left(\frac{h}{{\overline{H}}_D}-{\overline{h}}_{min}\right)}^{+}\left(1-k_{p_i}\frac{p_i}{p_e}\right)\left(1-\sigma \right)$$ (5)

Constants ${\overline{H}}_D$ and ${\overline{h}}_{min}$ represent normal and minimum blood hematocrit required for oxygen extravasation, respectively.

Production and transport of protein

Similar to the model for production, diffusion, and uptake of tumor angiogenic factors (TAFs),^22,63 which drives the angiogenesis process, the tumor cells are simulated to shed proteins ranging from very small (with size comparable to insulin, 5.7 kDa) to very large (with size comparable to titin, 3,700 kDa) when in a particular state (eg, hypoxic) and when transitioning into or out of this state. We define secreted as those proteins that are actively shed (exported or cleaved from the cell surface). Viable cells typically shed mostly secreted proteins, whereas necrosing cells tend to shed their contents as intracellular proteins. In this study, we focus on the bulk of the proteins shed from viable (proliferating or quiescent) and nonviable (necrosing) cells; in contrast, apoptotic cells will typically condense and not spill their contents into the surroundings as do the necrotic cells. Thus, in the model, the cellular states include proliferation, quiescence (hypoxia), and necrosis. ECM and vasculature creation or degradation are also assumed to trigger protein shedding by the corresponding cells.

Once shed, the proteins diffuse through the interstitial space and either decay or enter circulation into the surrounding vasculature. Assuming steady-state conditions, the overall mass balance for a protein P is

$$0=\nabla \cdot \left(D_p\nabla P\right)+{\overline{\lambda }}_{production}^P\left(1-P\right)1_{\mathrm{\Omega }}-{\overline{\lambda }}_{circulation}^P{1}_{vessel}-{\overline{\lambda }}_{decay}^{P}P$$

where D_P is the diffusivity, and ${\overline{\lambda }}_{production}^P$, ${\overline{\lambda }}_{circulation}^P$, and ${\overline{\lambda }}_{decay}^P$ are the (constant) rates of protein production, entering circulation, and decay, respectively.

For all the diffusion equations, as well as the pressure and angiogenic factors, the conditions at the boundaries are $\frac{\partial B}{\partial n}=0$ (zero Neumann condition), where B is the element at the boundary (oxygen, pressure, or protein).

A fivefold range of protein production rates was simulated, and a fivefold range of interstitial diffusivities was simulated for each production rate (Table 1). Since the effect of diffusivity is nonlinear, the values within the defined range were separated by a constant factor (3.76) to span from the lowest to the highest value. For simplicity, very small molecules were assumed to have the highest interstitial diffusivity, similar to that of insulin, while very large molecules had the lowest interstitial diffusivity, on the order of magnitude of that of larger proteins, such as titin. Protein transfer rates into the vasculature as well as decay rates were in this study assumed to be the same for all types of proteins.

Table 1.

Main model parameters and associated values.

PARAMETER	VALUE	REFERENCE
Tumor proliferation rate	1 day–1	48
Tumor necrosis threshold	0.5700	48
Tumor hypoxic threshold	0.5750	48
Oxygen diffusivity	1 (*)	63
Oxygen transfer rate from vasculature	5 (*)	63
Oxygen uptake rate by proliferating tumor cells	1.5 (*)	63
Oxygen uptake rate by hypoxic tumor cells	1.3 (*)	63
Oxygen uptake rate by tumor microenvironment	0.12 (*)	63
Oxygen decay rate	0.35 (*)	63
Protein production rate (low; medium-low; medium; medium-high; high)	0.2, 0.4, 1.0, 2.5, 5.0 (**)	Calculated
Protein diffusivities (high; medium-high; medium; medium-low; low)	0.01880; 0.00500; 0.00133; 0.00035; 0.00009 (*)	Calculated
Protein transfer rate into vasculature	0.006 (*)	Calculated
Protein decay rate	0.001 (*)	Calculated

Notes:

^*Value is rescaled by the square of the simulation system characteristic length (1 cm) and divided by the system characteristic time (one second) multiplied by the oxygen diffusivity⁸⁰ (1 × 10⁻⁵ cm²/s).

^**Values are rescaled by the model production rate of VEGF-A (VEGF-165) protein.

Model parameters

The main parameters of the model are summarized in Table 1. All other parameters are as in Ref. 22.

Experiments in vivo to obtain tumor protein data

Protein data were obtained from our previous study.⁶¹ The methods are summarized in the following sections.

Xenografts and sample collection

Epidermoid carcinoma A-431 cells (2 × 10⁹) (ATCC) were mixed 1:1 with Matrigel (BD Biosciences) and subcutaneously injected into the flanks of nude athymic BALB/c female mice (Charles River Laboratories). All animal experiments were performed as per the institutional guidelines and were approved by the Institutional Animal Care and Use Committee at Cedars-Sinai Medical Center (IACUC Number 001276). Tumor volumes were measured twice a week with a digital vernier caliper and were calculated as: π/6 × (larger diameter) × (smaller diameter). Tumor tissue and plasma were harvested after 18 days postinjection in order to avoid animal discomfort due to tumor burden. At this time, the average size of tumors was 2,500 mm³. Frozen tumor pieces from five mice were individually ground in liquid nitrogen with the aid of a ceramic mortar, and equal masses of individual tumor homogenate were pooled and suspended in RAF buffer (50 mM Tris-HCl, pH 7.4; 1% NP-40; 0.25% sodium deoxycholate; 150 mM NaCl; 1 mM EDTA, 1mM PMSF; 1 mg/ml each aprotinin, leupeptin, pepstatin; 1mM Na₃VO₄; 1 mM NaF). The homogenate was centrifuged for five minutes at 200 × g. The supernatant was sonicated on ice for two minutes and centrifuged for one hour at 12,000 × g. The supernatant (soluble fraction) was cleared through a 0.22-mm filter. Sera from five mice were pooled and depleted using two MARS-3 columns (Agilent Technologies) connected in tandem with High Performance Liquid Chromatography (HPLC). The unbound fraction was concentrated to a final concentration of 2 mg/mL. Tumor and plasma samples were labeled with C12 acrylamide as in Ref. 65.

Fractionation of plasma samples

Tumor samples were fractionated by reversed-phase chromatography using 1 mg of total protein. All samples were reduced with Dithiothreitol (DTT) (0.6 mg DTT/mg protein) and alkylated with iodoacetamide (3 mg IA/mg protein) prior to chromatography as in Ref. 66. The separation was performed in a POROS R1/10 column (4.6650 mm, Applied Biosystems) at a flow rate of 2.7 mL/min using a linear gradient of 10–80% of organic solvent over 30 minutes. The aqueous solvent was 5% acetonitrile/95% water/0.1% trifluoroacetic acid, and the organic solvent was 75% acetonitrile/15% isopropanol/10% water/0.095% trifluoroacetic acid. Fractions were collected at a rate of three fractions per minute, and 72 fractions were collected. Each fraction was individually digested in solution with trypsin (400 ng/fraction).⁶⁷ Adjacent fractions were combined based on protein chromatography features, resulting in a total of 25 fractions for mass spectrometry analysis. Plasma samples were subjected to two-dimensional fractionation based on the previously described intact protein analysis system approach.^67–70 Briefly, the sample was diluted to 10 mL with 20 mM Tris (pH 8.5) in 6% isopropanol and 4 M urea and immediately injected on an anion exchanger, Mono-Q 10/100 column (Amersham Biosciences Corp.), for the first dimension of the protein fractionation. The buffer system consisted of solvent A (20 mM Tris, pH 8.5, in 6% isopropanol and 4 M urea, pH 8.5) and solvent B (20 mM Tris in 6% isopropanol, 4 M urea, and 1 M NaCl). The separation was performed at a flow rate of 4.0 mL/min in a gradient of 0–35% solvent B for 44 minutes, 35–50% solvent B for three minutes, 50–100% solvent B for five minutes, and 100% solvent B for an additional five minutes. A total of 12 pools were collected. Each pool was then subjected to a second dimension of separation by reversed-phase chromatography. The reversed-phase fractionation was carried out on a POROS R2 column (4.6650 mm; Applied Biosystems) using trifluoroacetic acid/acetonitrile as a buffer system (solvent A: 95% H₂O, 5% acetonitrile, and 0.1% trifluoroacetic acid and solvent B: 90% acetonitrile, 10% H₂O, and 0.1% trifluoroacetic acid) at a flow rate of 2.7 mL/min. The gradient was 5% solvent A until the absorbance reached baseline (desalting step) and then 5–50% solvent B for 18 minutes, 50–80% solvent B for seven minutes, and 80–95% solvent B for two minutes. During the run, 72 900-mL fractions were collected. Each fraction was individually digested in solution with trypsin (400 ng/fraction), and the fractions were grouped into eight pools based on chromatographic features, corresponding to a total of 96 fractions for analysis from each experiment.

Protein identification and quantification

Liquid chromatography-tandem mass spectrometry (LC-MS/MS) was performed as described previously.⁶⁷ Briefly, pools of fractions were individually analyzed by LC–MS/MS in a LTQ-FTICR or LTQ-Orbitrap Mass Spectrometer (Thermo-Finnigan LLC) coupled to a nanoflow chromatography system (Eksigent) using a 25-cm column (PicoFrit 75 mm ID, New Objective) packed in-house with Magic C18 resin (Michrom BioResources) over a 90-minute linear gradient. Acquired data were automatically processed using default parameters, except where noted using the Computational Proteomics Analysis System, version 8.2.⁷¹ The tandem mass spectra were searched against version 3.44 of the human International Protein Index (IPI) (71,884 protein entries) and mouse IPI (version 3.44 with 55,078 protein entries) databases. The searches were performed with X! Tandem (version 2008.02.01). The mass tolerance for precursor ions was set to 5 ppm. The mass tolerance for fragment ions was set to 0.5 Da. A fixed modification of 71.0371 mass units was added to cysteine residues for database searching to account for the acrylamide modification, and 3.01 Da were used as variable modification to account for the heavy cysteine isotope. All identifications with a PeptideProphet⁷² probability >0.95 were submitted to ProteinProphet,⁷³ and each of the subsequent protein identifications was required to have at least two unique peptides with tryptic fragments (one missed cleavage) with allowance for variable modifications on E = −18.011, K = 6.020, M = 15.995, and Q = 217.027. In order to assign a species, at least one unique human peptide for identification as a human protein was required. One unique mouse peptide was required for identification as a mouse protein. The Q3 algorithm,⁶⁵ developed to accommodate a 3-Da mass shift in heavy and light peptides, was used to compute the ratios between the light and heavy isotopic pairs. A spectral count method⁷⁴ was used to estimate the relative abundance of proteins. More specifically, peptide spectra with the PeptideProphet probability of >0.95 or an error rate of 1% were counted for each IPI entry identified.

Comparison of human and mouse database entries

Protein sequences in human database (human IPI version 3.44) and mouse database (mouse IPI version 3.44) were computationally digested with trypsin, and a minimum of seven residues was used to match the X! Tandem default search parameter of the minimum parent fragment.

Data processing and integration

To facilitate comparisons of protein groups among samples, data were aligned by tracking all proteins that were members of a single ProteinProphet group as described by Ref. 75. This provided an analytic data set with one row for each protein group and specifically a column with values indicating the spectral count for proteins in each sample consistent with that group. The cellular location for each protein sequence was determined using the March 2008 generic GO slim from the Gene Ontology (GO) consortium (http://www.geneontology.org/GO.slims.shtml). GO slim files are reduced ontologies with significantly fewer categories than the complete GO ontology. The script map2slim (available from GO) was used to assign proteins to their nearest GO category and to identify those that are located in the extracellular or plasma membrane. Based on GO definition, the term extracellular herein refers to space outside the plasma membrane and is intended to annotate gene products that are not tightly attached to the cell surface. Therefore, proteins annotated with extracellular are basically proteins secreted into the medium. In cases that an IPI had multiple locations, the protein was considered extracellular as long as one annotation was extracellular space. The protein masses were segregated matching the nonlinear separation of diffusivities in the simulations (Table 1), ie, using a factor 3.76 to define the ranges. Accordingly, five size categories were defined: high (3,816,030–1,014,901 Da), medium-high (1,014,901–269,920 Da), medium (269,920–71,787 Da), medium-low (71,787–19,092 Da), and low (19,092–32 Da).

Results

Evolution of tumor growth in time

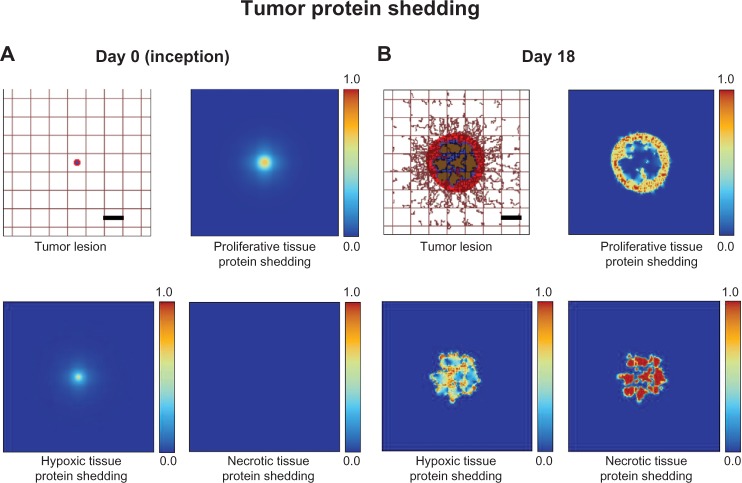
The simulated tumor begins within normal host tissue as a small avascular nodule (<100 µm) surrounded by normal (capillary) vasculature (Fig. 1A). Even though the nascent lesion is minuscule, the viable tissue is already shedding proteins produced by proliferative cells as well as a small number of hypoxic cells. Necrosis, however, is absent. As the cells proliferate and exceed the supply of oxygen in the surrounding microenvironment, hypoxia develops and triggers the release of TAFs that diffuse out of the tumor.⁶³ The surrounding capillaries uptake the TAF and start proliferating into small irregular capillaries that grow toward and into the tumor tissue. With increased access to nutrients, the lesion is able to grow larger, which in time leads to the development of hypoxia and necrosis, as the tissue geometry is distorted and the metabolic demand from the proliferative tissue exceeds the vascular supply. By Day 18, the lesion has grown to 750 µm in diameter (Fig. 1B), surrounded by numerous angiogenesis-induced capillaries. By this time, there are substantial levels of proliferative tissue-, hypoxic tissue-, and necrotic tissue-related proteins shedding into the vasculature.^22,63

Figure 1.

Visualization of protein shedding by tumor lesion at (A) inception (Day 0) and (B) on Day 18. Viable (proliferative) tumor tissue (red) encloses a hypoxic (quiescent) region (blue) without necrosis. The capillaries are modeled by the rectangular grid, with irregular sprouts generated through angiogenesis elicited by angiogenic factors from the hypoxic tissue. Shown for the two timepoints are (nondimensionalized) levels of protein shedding into vasculature for activity related to proliferative, hypoxic, and necrotic tissues. Bar, 250 µm.

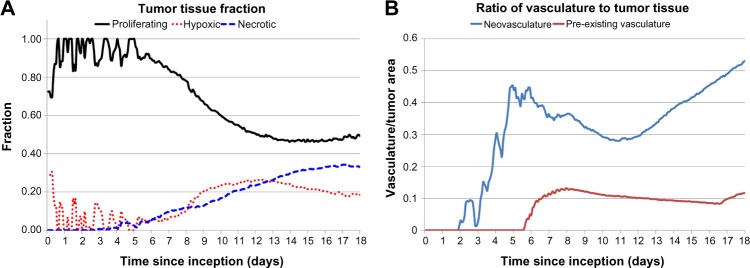
Figure 2A quantifies the fractions of proliferative, hypoxic, and necrotic tumor tissues from inception (Day 0) through Day 18, at which time 49% of the tissue is proliferative, 18% of the tissue is hypoxic, and 33% of the tissue is necrotic. After Day 6, the angiogenesis-induced supply of nutrients stabilizes the change in the tumor cell fractions, as noted by the smoother curves in Figure 2A, which is consistent with previous experimental observations showing the stabilization of tumor-induced vasculature by Day 6 after inception.⁷⁶ The ratio of neo- and pre-existing vasculature to tumor tissue during the course of growth is shown in Figure 2B. The neovascular development, in response to the tumor hypoxia, follows an oscillatory pattern with an increasing trend in time, reaching 0.5 by Day 17, whereas the pre-existing vasculature-to-tumor ratio remains fairly constant at ~0.1 after Day 6 as the growing tumor begins to co-opt the surrounding vessels. This simulates a highly vascularized lesion, with results consistent with previous modeling work.⁴⁶

Figure 2.

Analysis of tumor evolution. (A) Tumor tissue fraction indicates proportion of proliferative, hypoxic, and necrotic tissues during the growth from inception to Day 18. (B) Ratio of vasculature to tumor tissue highlights progressive angiogenic activity by the growing lesion.

Evaluation of proliferative tissue-related protein-shedding dynamics

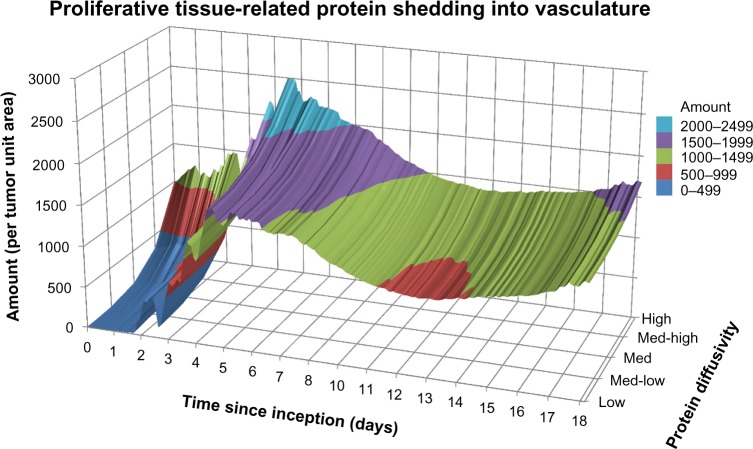
During the growth of the tumor, viable proliferative cells are simulated to secrete proteins (as defined in the Methods section), and in previous work, we have observed the extracellular domains of such proteins for viable cells.⁷⁷ In contrast, necrosing cells release their internal content into the surroundings, which includes the intracellular proteins. Figure 3 shows the amount of protein per tumor unit area released into the vasculature over the course of 18 days as a function of protein diffusivity and for a medium production rate. Following lesion inception, the initial amount entering vasculature by Day 4 is large, with the higher diffusing proteins approaching 2,200 per tumor unit area and the lower diffusing proteins being 45% less (~1,200). By Day 5, the overall amount of shedding into the vasculature reaches a maximum of ~2,500 for the higher diffusing category and ~1,600 for the lower diffusing category. As cell viability is restrained by insufficient tumor cell access to oxygen and nutrients, the amount of proteins entering the vasculature is correspondingly lowered beyond Day 5.

Figure 3.

Proliferative tissue-related protein shedding into vasculature from tumor lesion inception to Day 18 for a medium production rate.

The hypoxic conditions developed within the first five days lead to vessel creation through angiogenesis, which stabilizes the proliferation process and enables the lesion to grow in a more measured manner, as has been observed experimentally.⁷⁶ Once the vasculature is functional, the model assumes that proteins shed by the tumor can enter the circulation. The amount of proteins released into the vasculature reflects this condition by the smoother curve in Figure 3 starting on Day 6. Interestingly, a 45% decrease in protein shedding is observed during Days 5–12, reflecting a transient deterioration to vascular access by the tumor tissue. In time, this phenomenon is expected to reflect oscillations in tumor-to-vessel ratio, which have been observed in previous modeling²¹ and experimental⁷⁸ work. Simulation of proliferative tissue-related proteins with low and high production rates (not shown) evince smaller and larger amounts of protein released into the vasculature, respectively, but maintaining overall a similar profile in time as in Figure 3.

Evaluation of hypoxic tissue- and necrotic tissue-related protein-shedding dynamics

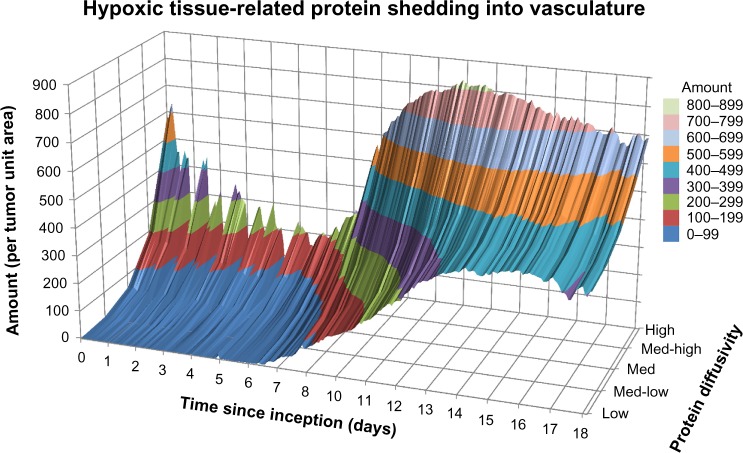
Figure 4 illustrates the release of hypoxic tissue-related proteins into vasculature as a function of their diffusivity and for a medium production rate. There is a spike of mostly high and medium-high diffusivity proteins at lesion inception on the first day, as tumor cells struggle to gain access to oxygen and nutrients from the surrounding (pre-existing) vasculature. For the next seven days, mostly high and medium-high diffusivity proteins make it to the vasculature and evince a rapidly fluctuating pattern reflecting sporadic angiogenesis. As the vasculature stabilizes after Day 7 to reach more regions of the growing tumor,⁷⁶ hypoxic tissue-related proteins of all diffusivities are shed more steadily into the vasculature, although still favoring the higher diffusing proteins by a 50% higher amount compared to the lower diffusing category.

Figure 4.

Hypoxic tissue-related protein shedding into vasculature from tumor lesion inception to Day 18 for a medium production rate.

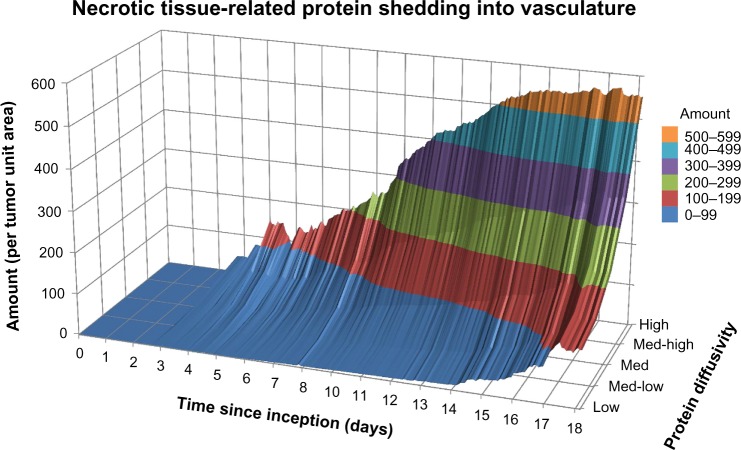
The release of nonviable cell (necrotic tissue-related) proteins for a medium production rate is shown in Figure 5. As expected, initially (Days 0–5) the overall amount is negligible since most of the cells are viable in the lesion. Within the next four days, the amount of protein shed increases by 300% as necrosis develops due to inadequate vascular access. The extent of necrosis stabilizes beyond Day 14, as the lesion becomes vascularized and the process of angiogenesis better balances with the oxygen and nutrient demand of the proliferating tumor cells, as has been observed to occur experimentally between Days 8 and 20 postlesion inception.^76,79 The exact timepoint depends on cell type and tumor conditions, and thus, Day 14 in the simulations reflects an average time. Interestingly, there is a steep disparity between the amounts of necrotic tissue-related proteins entering the vasculature based on their diffusivity (spanning a range of ~550 to ~130 proteins per tumor unit area from high to low diffusivity, respectively), in contrast to the proliferative tissue- (range of ~1,700 to ~1,300) and hypoxic (range of ~700 to ~400) tissue-related proteins.

Figure 5.

Necrotic tissue-related protein shedding into vasculature from tumor lesion inception to Day 18 for a medium production rate.

Similar to the proliferative tissue-related proteins, simulation of hypoxic tissue- and necrotic tissue-related proteins with low and high production rates (not shown) evince smaller and larger amounts of protein released into the vasculature, respectively, but maintaining overall a similar profile in time as with the medium production rate.

Assessment of stage of tumor growth based on protein shedding

The ratio of high-to-low diffusivity proteins associated with a specific cellular state may provide an indication of the stage of tumor growth as well as the extent of its vascularization. Figure 6 shows these ratios calculated for the proteins released by proliferative, hypoxic, and necrotic tissues for a medium production rate. In general, a larger ratio would indicate that the tumor tissue releasing these proteins is poorly vascularized, as the lower diffusing proteins have difficult shedding into the circulation. This hypothesis is supported by the ratio of 4.0% obtained for the necrotic tissue-related proteins compared to 1.7% for the hypoxic tissue-related proteins and 1.2% for the proliferative tissue-related proteins. The poor vascularization during the initial days after lesion inception is also reflected in the higher ratios obtained for all the cellular states, while the associated fluctuations reflect the transient instability of the incipient angiogenesis process.

Figure 6.

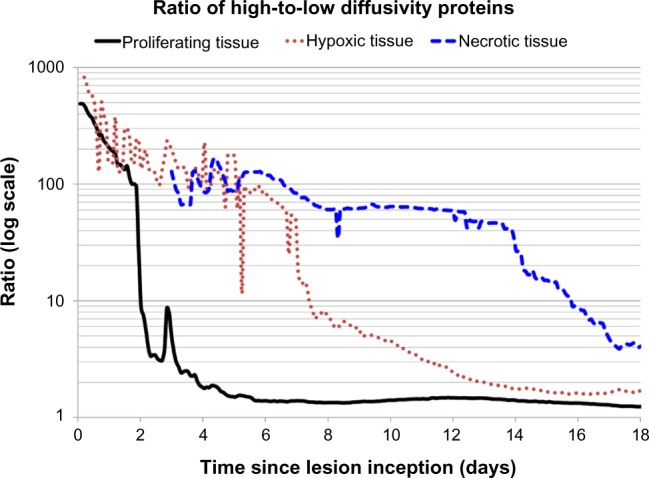
Ratio of high-to-low diffusivity proteins provides an indication of the stage of tumor growth and the extent of tumor vascularization.

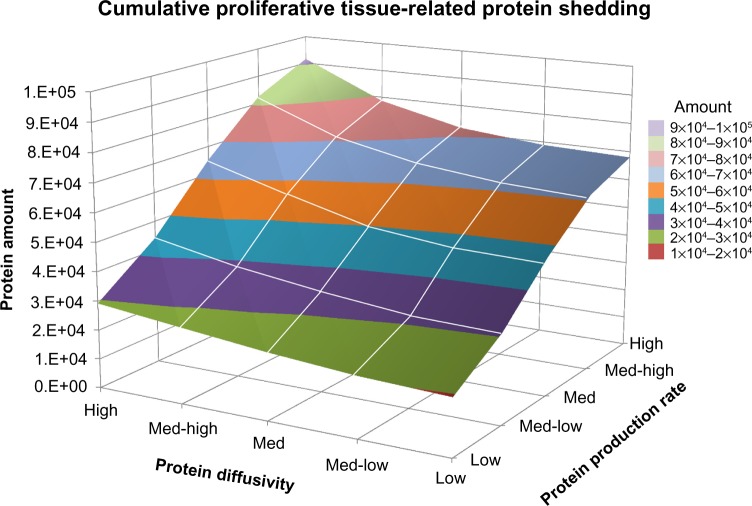
Figure 7 plots the cumulative amount of proliferative tissue-related protein shedding into vasculature from inception through Day 18, based on variation in protein diffusivity and rate of protein production. As expected, the proteins with the highest amount of release into vasculature (~100,000) have high diffusivity and a high production rate, while those with low diffusivity and a low production rate represent the smallest amount (~19,500). More interestingly, the plot highlights the three-dimensional interaction landscape among protein diffusivity (which relates to size), protein production (which relates to cellular activity), and the total amount that is released into the vasculature (which relates to the extent of tumor vascularization). Plots for the hypoxic tissue- and necrotic tissue-related proteins shedding have similar shapes (not shown).

Figure 7.

Cumulative proliferative tissue-related protein shedding from tumor lesion inception through Day 18. The graph highlights the three-dimensional interaction landscape between protein diffusivity (which relates to size), protein production (which relates to cellular activity), and the total amount that is released into the vasculature (which relates to extent of tumor vascularization).

Evaluation of protein counts from in vivo xenografts

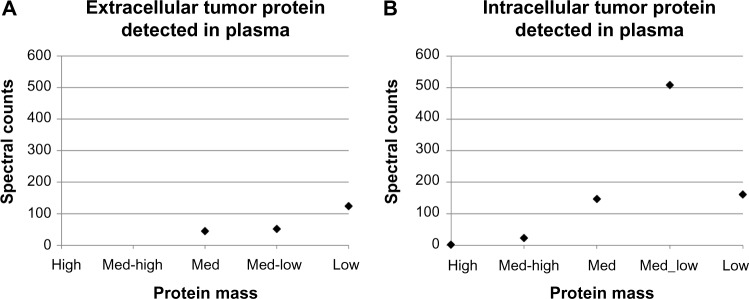
Spectral counts of human tumor derived extra- and intracellular proteins measured from plasma in circulation were obtained on Day 18 (Tables 2 and 3). As defined in the Methods section, proteins secreted to the exterior of tumor cells are labeled extracellular, while those released from the interior of the cells are called intracellular. Figure 8A shows that proteins of extracellular origin, considered proportional to cell viability, were mainly medium to low mass (ranging from 260 to 11 kDa) with the latter being most abundant. In contrast, proteins of intracellular origin (Fig. 8B), mainly reflecting cellular necrosis, spanned a wider range of mass (from 3,816 to 10 kDa) and also exhibited a wider variation in spectral counts (up to 508) than the extracellular proteins (up to 124). Assuming that protein diffusivity is inversely proportional to mass, these count variations were consistent with those simulated by the computational model on Day 18 (Fig. 3 for proliferative tissue-related proteins and Fig. 5 for necrotic tissue-related proteins). In the simulations, the proteins per tumor unit area reflect the fractions of tissue that are proliferative, hypoxic, and necrotic. Whereas the simulated tumor represents a lesion growing orthotopically, in the in vivo experiments, the tumors were xenografts, which experienced higher levels of necrosis as shown by the spectral counts. Furthermore, in looking at the human proteome, there are not nearly as large secreted proteins as there are intracellular proteins. One discrepancy was the amount of intracellular protein measured experimentally for the low-mass cases, which was much lower, and hence did not follow the exponentially increasing trend set by the other sizes (Fig. 8B). This suggests that low-mass intracellular proteins may have difficulty in shedding into circulation beyond what can merely be attributed to diffusion – an effect that would have to be further analyzed in order to account for it in the computational model.

Table 2.

Human tumor-derived extracellular (secreted) proteins measured from plasma in circulation obtained on Day 18.

GENE SYMBOL	PLASMA SPECTRAL COUNTS	TUMOR SPECTRAL COUNTS	LENGTH	MASS (DA)	SIZE CATEGORY
DMBT1	1	3	2413	260735	MED
FLG2	39	86	2391	248073	MED
GSN	1	171	782	85698	MED
CD44	4	83	742	81538	MED
GPI	4	213	558	63147	MED-LOW
ECM1	1	86	540	60674	MED-LOW
SBSN	6	125	590	60541	MED-LOW
DMKN	11	86	476	47082	MED-LOW
SERPINA1	3	14	418	46737	MED-LOW
CTSD	5	92	412	44552	MED-LOW
ANXA2	1	659	339	38659	MED-LOW
GGH	1	6	318	35964	MED-LOW
AZGP1	5	6	298	34259	MED-LOW
	2	18	275	30847	MED-LOW
SFN	10	1433	248	27774	MED-LOW
ORM2;ORM1	2	2	201	23512	MED-LOW
PYCARD	1	39	195	21627	MED-LOW
PPIA	50	174	165	18012	LOW
CALML5	25	108	146	15893	LOW
PRB4; PRH1; PRH2; PRR4	1	1	134	15097	LOW
LGALS7	12	814	136	15075	LOW
MIF	6	49	115	12476	LOW
PI3	8	70	117	12270	LOW
S100A7	12	363	101	11471	LOW
S100A8	10	731	93	10835	LOW

Table 3.

Human tumor-derived intracellular proteins measured from plasma in circulation obtained on Day 18.

GENE SYMBOL	PLASMA SPECTRAL COUNTS	TUMOR SPECTRAL COUNTS	LENGTH	MASS (DA)	SIZE CATEGORY
TTN	1	1	34350	3816030	HIGH
SYNE1	1	1	8797	1011086	HIGH
FLG	18	1809	4061	435170	MED-HIGH
TLN1	5	348	2541	269767	MED-HIGH
SFRS2IP	1	5	1463	164652	MED
SKIV2L	1	1	1246	137755	MED
XPO4	1	1	1151	130139	MED
TMF1	1	4	1093	122842	MED
DSG1	105	373	1049	113748	MED
MTHFD1	7	30	935	101559	MED
DSC1	18	148	894	99987	MED
DSC3	4	252	896	99969	MED
DPP6	1	1	865	97588	MED
TGM1	4	27	817	89787	MED
DDX21	2	5	783	87344	MED
HSD17B4	2	20	736	79686	MED
TKT	5	226	623	67878	MED-LOW
KPRP	2	6	579	64136	MED-LOW
CAT	1	43	527	59756	MED-LOW
PMPCA	1	4	525	58253	MED-LOW
CD276	1	1	534	57235	MED-LOW
TUFM	2	81	452	49542	MED-LOW
MFSD10	1	1	455	48339	MED-LOW
ENO1	215	1371	434	47169	MED-LOW
IDH1	1	34	414	46659	MED-LOW
ACAT1	5	11	427	45200	MED-LOW
SERPINB4; SERPINB3	3	223	390	44565	MED-LOW
GAPDHS	1	9	408	44501	MED-LOW
ACTBL2	1	343	376	42003	MED-LOW
CCDC86	1	6	360	40236	MED-LOW
ALDOA	38	497	364	39420	MED-LOW
ASPRV1	1	32	343	36991	MED-LOW
LDHA	19	512	332	36689	MED-LOW
CEBPB	1	1	345	36106	MED-LOW
DECR1	1	8	335	36068	MED-LOW
GAPDH	116	1111	335	36053	MED-LOW
ARG1	6	8	322	34735	MED-LOW
RALY	2	19	306	32463	MED-LOW
MARCKS	2	70	332	31555	MED-LOW
TPI1	59	286	286	30791	MED-LOW
PSMB8	2	5	276	30354	MED-LOW
CA2	5	51	260	29246	MED-LOW
NUBP2	2	9	271	28825	MED-LOW
CASP14	3	13	242	27680	MED-LOW
HSPB1	4	446	205	22783	MED-LOW
PXMP2	1	1	195	22253	MED-LOW
PRDX5	1	99	214	22086	MED-LOW
PRDX2	1	28	198	21892	MED-LOW
TMEM205	2	5	189	21198	MED-LOW
PARK7	2	101	189	19891	MED-LOW
CFL1	1	324	166	18502	LOW
FABP5; FABP5L7; FABP5L2; FABP5	46	843	135	15164	LOW
PFN1	20	151	140	15054	LOW
S100A9	50	791	114	13242	LOW
TXN	2	131	105	11737	LOW
CSTB	10	70	98	11140	LOW
CSTA	31	43	98	11006	LOW
NDUFA4	1	11	81	9370	LOW

Figure 8.

Spectral counts of human tumor-derived (A) extracellular (secreted) and (B) intracellular proteins measured from plasma in circulation obtained from live mice on Day 18. The protein mass is categorized in a range from high to low as defined in the Methods section.

Discussion

Biomarker discovery approaches assume that genomic alterations that influence disease-associated protein expression are driven by pathophysiological cell or tissue changes. However, the way these changes can influence the protein excretion from cells, diffusivity in the interstitium, and persistence in blood circulation is not well understood. In particular for cancer, the effects of tumor size, architecture, cell composition, and cell states in this regard are unclear. To complement the experimental effort and streamline the corresponding avenues of inquiry, we propose an interdisciplinary modeling–experimental approach. As a first step in this direction, we simulate the shedding into vasculature of proteins related to cell viability in a growing tumor lesion. Unlike typical observation-based biomarker studies, we employ a mechanistic tumor model that explicitly considers the biophysical processes governing the shedding and the persistence kinetics of tumor-derived circulating proteins. The spatial two-dimensionality of the simulations enables incorporation of realistic tumor-induced vasculature with corresponding gradients of diffusible substances affecting the tumor tissue. The model couples the tumor growth with the vasculature development,^22,37,48,63 including the proliferative, hypoxic, and necrotic activities of the tissue, thus providing insight into the interaction of these processes with the protein production, diffusion through the tumor interstitial space, and shedding into vasculature.

Ultimately, the goal of this interdisciplinary approach is to uncover fundamental biophysical processes of tumor progression, protein shedding, and protein persistence that characterize discovery of biomarkers, thus helping biomarker development for cancer treatment and diagnostics. We recognize that identifying biomarkers is a difficult problem that depends on many factors unrelated to shedding dynamics (eg, tissue of origin). Advancing the understanding of these dynamics, however, would help to relate the amount and fluctuations of biomarkers detected in circulation to the disease condition.

The results in this study highlight the link between protein shedding and the stage of tumor growth as well as the extent of vascularization. The proliferative tissue-, hypoxic tissue-, and necrotic tissue-related activities in time by the growing tumor are illustrated by the proteins releasing into vasculature (Figs. 3–5, respectively). These activities could potentially be correlated with different ratios of tumor tissue fractions (Fig. 2A) and vascularization (Fig. 2B) to derive tumor- specific estimation of viable, hypoxic, and necrotic tissues based on the protein detected in circulation. The ratio of high-to-low diffusivity proteins provides a further glimpse into the tumor growth stage and its vascularization. A high ratio may indicate that a particular tissue fraction is undergoing rapid increase and, further, that the vascularization may be severely impaired, since in this case, low-diffusing proteins would be expected to reach the vasculature in much smaller amounts than high-diffusing proteins. This situation seems to be the case for the necrotic tissue during Days 4–14 postinception in the simulation in this study (Fig. 6).

Although the correlation between spectral counts and protein mass for both extra- and intracellular proteins in the animal experiments on Day 18 (Fig. 8) were similar to the trends obtained from the computational model simulations (Figs. 3 and 5, respectively), the shedding of low-mass intracellular proteins did not seem to follow this trend. This could be due to a combination of factors, including an overall lower number of small intracellular proteins shed by the tumor, faster small protein degradation before the vasculature is reached, impaired diffusion, and inaccessibility to the vasculature perhaps caused by vascular deterioration. Since intracellular proteins are released upon cellular disintegration as occurs during necrosis, the surrounding microenvironment including the microvasculature would be affected by toxicity induced by the cellular debris. We further note that future experimental and computational studies should explore the relation between tumor size and viable/necrotic tumor fractions and how these parameters relate to protein production and shedding as a function of the dynamic microenvironment.

In Figures 3–5, the protein diffusivities were varied from high to low in five arbitrary increments (Table 1), while Figure 7 additionally shows variation in protein production rates varied from low to high. Future work could parcel the values for these variables in different ways than what has been illustrated here to more specifically reflect particular tumor biological data. Furthermore, for simplicity, this study initialized protein decay rates and transfer rates into vasculature to be the same for all proteins (Table 1), regardless of their diffusivities and production rates, which may not be realistic. Decay and transfer rates would depend on protein size as well as other tumor microenvironment-related variables, such as ECM density. The model could be expanded to include additional types of proteins that are secreted during tumor progression, and the parameters could be calibrated to cancer-specific values obtained from live subjects, with the ultimate goal to achieve clinically useful biomarker analysis.