Sample size calculations for stepped wedge and cluster randomised trials: a unified approach

Abstract

Objectives

To clarify and illustrate sample size calculations for the cross-sectional stepped wedge cluster randomized trial (SW-CRT) and to present a simple approach for comparing the efficiencies of competing designs within a unified framework.

Study Design and Setting

We summarize design effects for the SW-CRT, the parallel cluster randomized trial (CRT), and the parallel cluster randomized trial with before and after observations (CRT-BA), assuming cross-sectional samples are selected over time. We present new formulas that enable trialists to determine the required cluster size for a given number of clusters. We illustrate by example how to implement the presented design effects and give practical guidance on the design of stepped wedge studies.

Results

For a fixed total cluster size, the choice of study design that provides the greatest power depends on the intracluster correlation coefficient (ICC) and the cluster size. When the ICC is small, the CRT tends to be more efficient; when the ICC is large, the SW-CRT tends to be more efficient and can serve as an alternative design when the CRT is an infeasible design.

Conclusion

Our unified approach allows trialists to easily compare the efficiencies of three competing designs to inform the decision about the most efficient design in a given scenario.

1. Introduction

What is new?

• •Sample size calculations for stepped wedge cluster trials are complex and design effects have been misapplied in the literature.
• •We set out a coherent unified framework for determining the sample size for stepped wedge and parallel cluster trials.
• •We present new formula to allow trialists to determine the cluster size needed where other design parameters are fixed.

The parallel cluster randomized trial (CRT) is an established design for the evaluation of interventions delivered at the level of the cluster or where risk of contamination inhibits individual randomization [1], [2]. In the conventional parallel CRT at the beginning of the trial, half of the clusters are randomized to the intervention and half to the control. This design may be augmented by the addition of baseline measures before randomization. We refer to this design as the parallel cluster randomized trial with before and after observations (CRT-BA) [3].

The stepped wedge cluster randomized trial (SW-CRT) is a relatively new type of cluster randomized design, but rapidly increasing in popularity [4], [5], [6]. There is usually a period of baseline data collection, in which no clusters are exposed to the intervention. Subsequently, at periodic time points called “steps,” one or several clusters are randomized to cross from control to intervention, whereas the remaining clusters remain in the control condition. The study continues until all clusters have crossed to the intervention arm, and there is usually a period at the end of the study in which all clusters are exposed to the intervention [7]. The SW-CRT can be viewed an extension of the cluster trial with baseline and repeated measures, but with the addition that clusters are randomized sequentially to cross from control to intervention [8].

The Devon Active Villages study [9] was a stepped wedge trial to evaluate whether a 12-week tailored community-level physical activity intervention increased the activity levels of rural communities. A total of 128 rural villages in England were randomized to receive the intervention in one of four steps. Random samples of 50 participants, assuming that 10 would respond, were taken in each village at each of five data collection periods using a postal survey. The primary outcome of interest was the proportion of adults reporting sufficient physical activity to meet internationally recognized guidelines, whereas minutes spent in moderate-and-vigorous activity per week was analyzed as a secondary outcome. The study found no effect of the intervention on the proportions of adults meeting guidelines, but a trend toward an increase in weekly duration of activity.

The advantages and disadvantages of the SW-CRT design have been debated in the literature using ethical, practical, and logistical considerations [10], [11], [12], [13]. The SW-CRT is often considered the design of choice when it is logistically impractical to simultaneously rollout the intervention to half of the clusters; when stakeholders have a strong desire for all clusters to receive the intervention, perceiving it to be beneficial; and sometimes (although perhaps contentiously) when the intervention is believed to be more likely effective than ineffective. Because of the longitudinal nature of the SW-CRT, the design might be considered particularly suitable when there is a need to include time-varying covariates.

The consideration of statistical efficiency is another important factor when deciding between the designs. Although sample size methodology for parallel CRT designs is well established, reporting and methodological quality of the CRT design in general has been inadequate [14], whereas appropriate methodology for determining sample size needed in stepped wedge studies in particular is still in development. In the review of 12 stepped wedge studies between 1987 and 2005 [4], sample size calculations were reported in only five. It was not reported whether these sample size calculations allowed for the stepped wedge design. In another review of 25 stepped wedge studies [5], sample size calculations were clearly reported in only 8 of the 25 studies, and only 3 took into account clustering; again, it was not clear whether the stepped wedge design was accounted for.

One approach to determining the sample size needed under a cluster randomized design involves multiplying the sample size needed under an individually randomized trial by a “design effect” or variance inflation factor [15]. The design effect essentially represents the inflation over the sample size needed under individual randomization. Initial developments in sample size methodology for the SW-CRT focused on methods to determine power only [7]. Recently, a design effect for the SW-CRT was published; however, there has been some confusion over its implementation. Moreover, there has been a debate about the efficiency of this design relative to the parallel design, with some researchers claiming that the SW-CRT is more efficient [16], with others disputing this [17], [18], [19].

Hemming et al. [20] recently proposed that power calculations for the CRT and the SW-CRT be carried out using a single generic framework. Moreover, they expanded the framework to allow for designs with transition periods and multiple levels of clustering. In this article, we illustrate the application of the generic framework and present simple formulas that allow calculation of both the required number of clusters given a specified cluster size, as well as the required cluster size, given a specified number of clusters. Our specific objectives are to (1) illustrate, by example, how to implement design effects in the SW-CRT to ensure correct sample size calculations under a variety of scenarios; (2) demonstrate that the SW-CRT does not always require a smaller total sample size or smaller number of clusters than the parallel CRT; and (3) provide novel sample size methodology to allow designers to determine required cluster size in the SW-CRT, as current published design effects allow computation of the number of clusters, but not number of subjects per cluster.

2. Methods

2.1. A unified framework for designing both the stepped wedge and parallel cluster trial

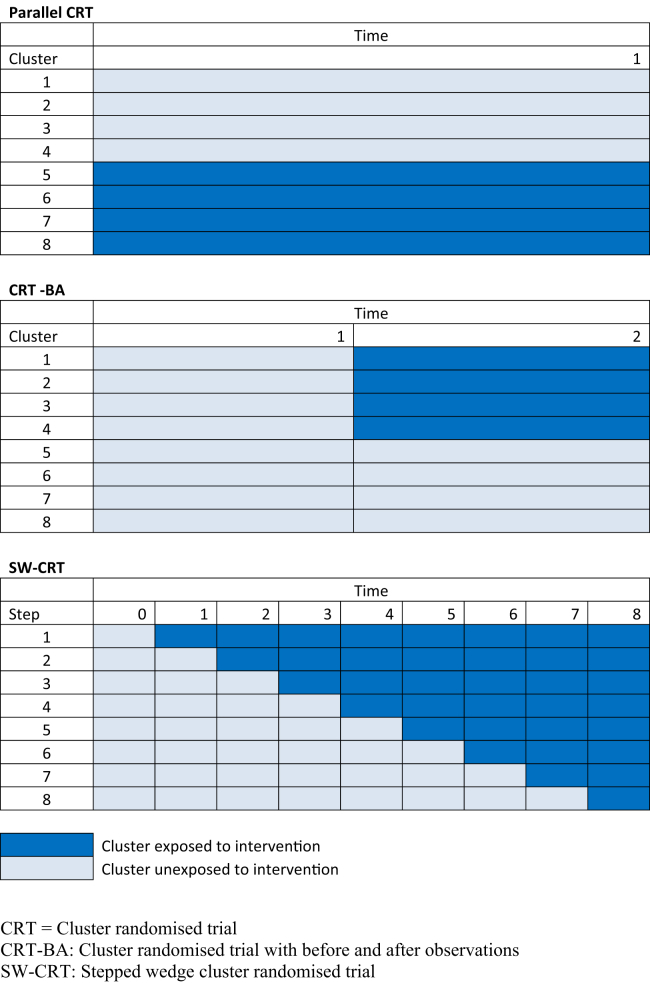
Hemming et al. [20] present a unified framework for comparing the efficiencies of the SW-CRT and the parallel CRT. We adopt a similar approach here as is illustrated schematically in Figure 1. Using this framework, the relative efficiencies of the parallel CRT design, the CRT-BA, and the SW-CRT may be more easily compared. Note that, in our framework, the total cluster sizes are fixed across the designs. In the parallel CRT design, half of the clusters are randomized to the intervention and half to the control and all clusters remain in the arm to which they had been allocated throughout the duration of the study. In studies with prospective recruitment, the width of the diagram may represent the time over which the observations are accrued (or patients recruited); otherwise, it represents the total number of observations sampled from each cluster. In the CRT-BA, the design includes a period of time in which no clusters are exposed to the intervention and then a randomization point in which half of the clusters are randomized to cross to the intervention. The period of time in which no clusters are exposed (sometimes referred to as a baseline period) might be of shorter length (or contain fewer observations) than the period of time during which half of the clusters are exposed. For simplicity in our examples, we have assumed that the cluster sizes in the before period are equal to the cluster sizes in the after period. In the SW-CRT, each cell in our diagram represents a interval during which measurements are made on different subjects in each cluster. When viewing all three designs under this unified framework, it becomes clear that all are competing designs, differing only by when the intervention is initiated in each cluster.

Fig. 1.

Schematic illustration of design of the conventional parallel CRT, the CRT-BA, and the SW-CRT (with five steps). CRT, cluster randomized trial; CRT-BA, cluster randomized trial with before and after observations; SW-CRT, stepped wedge cluster randomized trial.

Both the SW-CRT and the CRT-BA can be cross-sectional or cohort in nature. In a cross-sectional design, different participants are recruited at each step or separate cross-sectional samples are selected (e.g., from practice lists or administrative sources). In a cohort design, participants are recruited or identified at the beginning of the study and have repeated measures taken over the different steps. We only consider the cross-sectional design in this article. The cross-sectional design was used in 9 of 12 stepped wedge studies between 1987 and 2005 identified in a systematic review of this design [4].

2.2. Sample size calculations for cluster randomized studies

In this section, we summarize and compare sample size calculation formulas for the parallel CRT, the CRT-BA, and the SW-CRT. We present an appropriate design effect for each design and show how the total required sample size (i.e., the total number of measurements) under each design can be obtained by multiplication of the required sample size under individual randomization. We consider two scenarios that commonly arise in practice: in scenario A, the total available cluster size is fixed in advance of the study (equivalent across the designs) and the required number of clusters under each design must be calculated; in scenario B, the total number of available clusters is fixed in advance of the study (equivalent across the designs) and the required total cluster sizes must be determined.

We assume continuous outcomes analyzed using a generalized linear mixed model with a random effect for each cluster and additionally for the SW-CRT, a fixed effect for time representing each step [7]. Most importantly, we assume a cross-sectional design and an equal allocation rate to intervention and control. Table 1 summarizes the notation and simple algebraic relationships to be used for each design. Note that, we define the total sample size to be the total number of measurements made within the entire study. For example, under the SW-CRT design with t steps, the total study sample size is km(t + 1), that is, the number of clusters k multiplied by the number of time points t+1 and the number of observations made in each cluster per time point m. This is the intuitive definition of sample size under a cross-sectional design because it counts the number of participants (or equivalently the number of observations) within the study.

Table 1.

Notation and simple algebraic relationships

	Parallel CRT	CRT-BA	SW-CRT (with t steps)
Number of measurement times	1	2	t + 1
Sample size per cluster per measurement time	M	M/2	m = M/(t + 1)
Total sample size per clustera	M	M	M = m × (t + 1)
Total study sample size	N = M × k	N = M × k	N = m × (t + 1) × k
Total number of clustersb	k = N/M	k = N/M	k = N/[m × (t + 1)]
Number of clusters per step	Not applicable	Not applicable	g = k/t

Abbreviations: CRT, cluster randomized trial; CRT-BA, cluster randomized trial with before and after observations; SW-CRT, stepped wedge cluster randomized trial.

^aFixed under design scenario A.

^bFixed under design scenario B.

2.2.1. The parallel CRT design

First, under scenario A, we assume that the total cluster size M is fixed in advance of the trial. The common approach to sample size calculation in a parallel CRT is to compute the design effect:

$${\text{DE}}_{\text{CRT}}=1+\left(M-1\right)\rho ,$$

where M denotes the sample size per cluster (assumed equal across all clusters) and ρ is the intracluster correlation coefficient (ICC) which measures the correlation between observations within the same cluster. The total study sample size required for the CRT design is then obtained as:

$$N=N_I\times {\text{DE}}_{\text{CRT}},$$ [1]

where N_I is the total sample size required under individual randomization. Because the total sample size is the product of the number of clusters k and the cluster size M, the required number of clusters is then obtained as

$$k=\frac{N}{M}.$$

Alternatively, under scenario B, the user may start with a prespecified number of clusters (k) and wish to determine the required cluster size (M). For a fixed number of clusters, the above can simply be rearranged to determine the required sample size per cluster as:

$$M=\frac{N_I\left(1-\rho \right)}{k-N_I\rho }.$$

Of note, this design becomes prohibitive (i.e., the available number of clusters is insufficient, irrespective of their size [21]), when:

$$k<N_I\rho .$$

2.2.2. The CRT design with before and after observations

When the parallel CRT is augmented to include an equal number of measurements before and after randomization, the corresponding design effect is [3]:

$${\text{DE}}_{\text{BA}}=2\left[1+\left(\frac{M}{2}-1\right)\rho \right]\left(1-r^2\right)$$

where r represents the correlation between cluster means over the two periods:

$$r=\frac{\frac{M}{2}\rho }{1+\left(\frac{M}{2}-1\right)\rho }$$

Although r is not specifically needed, it is of interest to write the formula for the design effect in this way as it relates to the well-known result that the required sample size for a randomized controlled trial analyzed using the follow-up scores with adjustment for baseline values can be multiplied by 1 − r² where r is the correlation between the response at baseline and follow-up. Note that here, M/2 is the sample size per cluster at each measurement time. The total sample size required is then obtained as

$$N=N_I\times {\text{DE}}_{\text{BA}}$$ [2]

If the sample size per cluster M is specified, it is then straightforward to determine the required number of clusters in scenario A by dividing N by M.

In scenario B, it is necessary to determine the required total sample size per cluster, M, given a fixed number of clusters k. Given k, and knowledge of the sample size required under individual randomization, M can be determined as the positive solution to a quadratic equation. Details and derivation are provided in Appendix A at www.jclinepi.com.

2.2.3. The stepped wedge CRT design

In their seminal article on stepped wedge studies, Hussey and Hughes [7] derive a method of estimating the power available from an SW-CRT. This method involves specification of the number of steps t, number of clusters randomized per step g, the number of observations per cluster per period m, and other conventional parameters, such as the effect size and level of significance. Using the notation presented in Table 1, the total number of clusters will be k = g × t and the total sample size per cluster will be M = m × (t + 1). We do not present these formulae here [22], but assuming a mixed-effects linear regression model (fixed effect for step and random effect for cluster), relatively complex calculations allow estimation of the power available [23].

Following on from this work, a design effect for stepped wedge studies has been derived, which allows determination of number of clusters needed for a given sample size per cluster per period (m) and number of steps (t) [24]. Then, the corresponding design effect is:

$${\text{DE}}_{\text{SW}}=\left(t+1\right)\frac{1+\rho \left(tm+m-1\right)}{1+\rho \left(\frac{tm}{2}+m-1\right)}\times \frac{3\left(1-\rho \right)}{2\left(t-\frac{1}{t}\right)}$$

The total required study sample size will be:

$$N=N_I\times {\text{DE}}_{\text{SW}}$$ [3]

Under scenario A, the total number of clusters k can then be determined as:

$$k=\frac{N}{\left(t+1\right)m}$$ [4]

and the number of clusters randomized per step (g) can be determined as k divided by t. Note that, the design effect requires the number of steps to be specified in advance; in practice, this could be determined by logistical considerations, for example, the number of personnel available to implement an intervention at one time in a group of practices.

Under scenario B, a fixed number of clusters (k) and number of steps (t) are specified—and implicit in this the number of clusters randomized per step (g = k/t). It is then possible to determine the required number of observations per cluster per period (m) as the positive solution to a quadratic equation. Again, this quadratic and its solution are provided in Appendix B at www.jclinepi.com. The calculation of the total required sample size from each cluster then follows as M = m × (t + 1).

3. Results

3.1. Relative efficiencies of the three designs

Table 2 presents design effects calculated under the three designs, assuming ICCs ranging from small (0.001) to large (0.25) and total cluster sizes fixed at M = 30, 60, 150, or 300. For the SW-CRT design, results are presented for either two or five steps, implying cluster sizes per period of either m = 10 or 50. Although some have questioned whether a study with only two steps can be considered a legitimate stepped wedge design, systematic reviews of this design [4], [5] included studies ranging from 2 to 29 steps and 2 to 36 steps, respectively. Although an ICC in the region of 0.25 would be unusual for a clinical outcome measure, it might be the order of magnitude for a process measure [25], [26]. The design effects presented in this table can be used to determine the required sample size for any planned study with these design parameters, by multiplication of the required sample size under an individually randomized trial. The total number of clusters required can then be obtained by dividing by M.

Table 2.

Design effects to determine the required study sample size given a fixed sample size from each cluster (M)

M	ρ	CRT	CRT-BA		SW-CRT
Design effect	Implied r	Design effect	t	Design effect
30	0.001	1.03	0.01	2.03	2	3.03
30	0.01	1.29	0.13	2.24	2	3.22
30	0.05	2.45	0.44	2.74	2	3.58
30	0.1	3.90	0.63	2.93	2	3.63
30	0.25	8.25	0.83	2.75	2	3.23
60	0.001	1.06	0.03	2.06	5	1.92
60	0.01	1.59	0.23	2.44	5	2.20
60	0.05	3.95	0.61	3.06	5	2.61
60	0.1	6.90	0.77	3.18	5	2.65
60	0.25	15.75	0.91	2.86	5	2.33
150	0.001	1.15	0.07	2.14	2	3.13
150	0.01	2.49	0.43	2.83	2	3.72
150	0.05	8.45	0.80	3.42	2	4.05
150	0.1	15.90	0.89	3.41	2	3.94
150	0.25	38.25	0.96	2.94	2	3.34
300	0.001	1.30	0.13	2.26	5	2.07
300	0.01	3.99	0.60	3.17	5	2.70
300	0.05	15.95	0.89	3.59	5	2.93
300	0.1	30.90	0.94	3.50	5	2.83
300	0.25	75.75	0.98	2.97	5	2.39

Abbreviations: ρ, intracluster correlation coefficient; t, number of steps; CRT, cluster randomized trial; CRT-BA, cluster randomized trial with before and after observations; SW-CRT, stepped wedge cluster randomised trial.

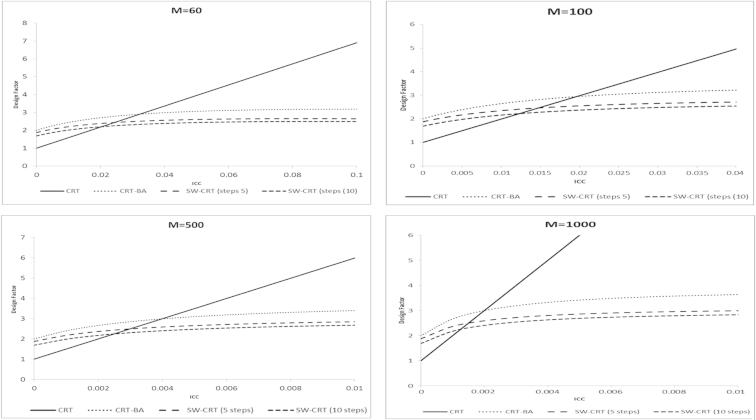
Readers can use the presented formulas to compare the relative efficiencies of these three designs in practical scenarios where there is a legitimate choice among the designs. For illustration purposes, Figure 2 compares the relative efficiencies of the three designs assuming fixed total cluster sizes of M = 60, 100, 500, and 1,000 for a range of ICC values. For the SW-CRT design, we assume either 5 or 10 steps, which implies cluster sizes per step ranging from 5 to 167. In a systematic review of 70 stepped wedge trials J. Martin, Girling A., Taljaard M., and K. Hemming, Unpublished data, 2015, the mean cluster sizes per step ranged from a minimum of 4 to a maximum of 165.

Fig. 2.

Comparative efficiency of the conventional parallel CRT, the CRT-BA, and the SW-CRT (for fixed cluster sizes). CRT, cluster randomized trial; CRT-BA, cluster randomized trial with before and after observations; SW-CRT, stepped wedge cluster randomized trial.

Design effects are presented for the SW-CRT design with 5 and 10 steps. These results demonstrate how efficiency and comparability of the different designs depends crucially on the ICC and the sample size per cluster. First, note that, all design effects for the range of ICC considered are greater than 1, indicating the loss of efficiency relative to individual randomization. However, comparing across these three study designs, design effects for the parallel CRT design tend to be lower than for the competing designs when ρ is small; thus, in such situations, the parallel CRT design may be more efficient (requiring fewer total number of observations and fewer clusters) than either the CRT-BA or the SW-CRT. On the other hand, the design effects for the SW-CRT design are lower when ρ is large; thus, in such situations, the stepped wedge design may be more efficient than the parallel CRT design. The value for ρ at which the SW-CRT becomes more efficient depends on the cluster size and may be read from the graphs. Figure 2 also shows that in the scenarios considered here (and under the assumption of equal cluster sizes in the before and after period), the CRT-BA design is always less efficient than the SW-CRT design, whereas the SW-CRT design with 10 steps tends to be more efficient than a design with 5 steps, although this will not necessarily be true in general.

3.2. Examples: implementation of sample size calculations for the SW-CRT

We now illustrate implementation of the calculations under the three designs. Because these design effects are relatively well known in the case of a parallel CRT with a fixed cluster size, we focus here on implementation for the SW-CRT where they have been much less commonly used. In addition to scenarios A and B, we consider a third scenario (C) where the study size is completely fixed and it is necessary to determine the power. For the purpose of illustration, we consider a study designed to detect a small standardized effect size of 0.2 on a continuous scale with 80% power and 5% significance. Under individual randomization, such a design would require 788 participants (394 per arm) using a two sample t-test. Although the design effects may be used, under some assumptions, in the case of dichotomous outcomes, our examples consider continuous outcomes only. For a planned clustered design, we consider both small (0.01), moderate (0.1), and large (0.25) anticipated ICCs and compare the power achievable or sample size required (both number of clusters and cluster size) among the three design choices under consideration here (the parallel CRT, the CRT-BA, and the SW-CRT). Note that, as required, all required sample sizes were rounded up to the nearest integer. Note that, all decimal places were carried in calculations to preserve accuracy.

3.2.1. Design scenario A: determining the number of clusters required given a fixed cluster size

In this scenario, the total cluster size M is specified in advance of the trial. Determining the number of clusters required for the SW-CRT design with t steps then involves the following:

• 1.Determine required sample size under individual randomization (N_I).
• 2.Calculate the cluster size per period (m) using the specified M and number of steps (t), that is, $m=\frac{M}{t+1}$.
• 3.Calculate the design effect DE_SW.
• 4.Determine the total number of clusters (k) required using Equation 4.
• 5.Determine the number of clusters randomized per step (g = k/t).

In practice, some rounding will have to take place (as the number of clusters must be a multiple of t), and so, the actual power of the design might not be at the specified level. To ensure this rounding has not had a substantial impact, the actual power of the design can be determined as per the process outlined under scenario C below. For example, if the number of clusters randomized at each step is determined to be substantially less than one, any rounding up to one cluster per step will result in an actual power much greater than that required. In such circumstances, the design constraints set may need to be modified (e.g., reducing the number of steps to ensure there are not more steps than clusters).

The required sample sizes in this example, assuming fixed M = 30 and 100, and t = 2 or 9 are presented in Table 3. Table 3 illustrates that when the ICC is large (0.25), the total sample size (and thus, the number of clusters) under the SW-CRT and the CRT-BA is reduced by a substantial amount compared to that under a parallel CRT. When the ICC is small (0.01), the parallel CRT is the most efficient study design. When the ICC is small (0.01) but the cluster size is large, then in this example, the SW-CRT is almost as efficient as the parallel CRT. When the ICC is small and the cluster size is small, then in this example, the parallel CRT is more efficient than the CRT-BA.

Table 3.

Example: design effects (DEs), total required study sizes (N), and number of clusters (k) required under each design given fixed total cluster sizes M and ICC (ρ)

Design constraints			CRT			CRT-BA			SW-CRT
M	ρ	t	DECRT	N	k	DEBA	N	k	DESW	N	k
30	0.01	2	1.29	1,017	34	2.24	1,766	59	3.22	2,538	85
30	0.25	2	8.25	6,501	217	2.75	2,167	73	3.23	2,544	85
100	0.01	9	1.99	1,569	16	2.64	2,084	21	2.16	1,702	18
100	0.25	9	25.75	20,291	203	2.92	2,298	23	2.25	1,772	18

Abbreviations: ICC, intracluster correlation coefficient; t, number of steps in the stepped wedge design; CRT, cluster randomized trial; CRT-BA, cluster randomized trial with before and after observations; SW-CRT, stepped wedge cluster randomized trial.

Example relates to a trial requiring 788 observations under individual randomization. Note that, N and k are rounded up to the nearest integer.

We illustrate the detailed calculations for a cluster size of 30 and ICC of 0.01 in Appendix C at www.jclinepi.com.

3.2.2. Design scenario B: determining the cluster size required given a fixed number of clusters

In this scenario, the number of clusters is fixed and the objective is to determine the sample size per cluster. Determining the required cluster size involves the following steps:

• 1.Determine sample size under individual randomization.
• 2.Set design constraints: the number clusters (k) and the number of steps (t). This determines the number of clusters available per step (g = k/t).
• 3.Determine the required sample size per cluster per period (m) using the formula provided in Appendix B at www.jclinepi.com. This gives the total required sample size per cluster as M = m × (t + 1).

Again, if any rounding up of the number of steps has occurred, the actual power of the design can be computed as illustrated under scenario C below.

The required total cluster sizes (M) in this example, assuming fixed k = 30 or 60, and t = 2 or 5 steps are presented in Table 4. Note that, in this case, the parallel CRT design is not feasible unless the number of clusters exceeds N_I × ρ, which gives minimum required numbers of clusters of 8 and 197 corresponding to ρ = 0.01 and 0.25, respectively. The CRT requires a reasonable cluster size (i.e., M = 36 or 15) when there are only 30 or 60 clusters available and the ICC is small. When the ICC is large (0.25), then the parallel CRT becomes infeasible irrespective of the cluster size. Under the SW-CRT design, the study does not become prohibitive with a large ICC, requiring cluster sizes of M = 90 or 30 (for k = 30 and 60 clusters, respectively). In the SW-CRT, when the ICC is large (0.25), the sample size needed actually decreases over that when the ICC is small (when the number of clusters is fixed at 30). This is in stark contrast to the parallel CRT.

Table 4.

Example: required total sample sizes per cluster (M) and total study size (N) under each design given fixed number of clusters k and ICC (ρ)

Design constraints			CRT		CRT-BA		SW-CRT
k	ρ	t	M	N	M	N	M	N
30	0.01	2	36	1,080	66	1,980	96	2,880
60	0.01	5	15	900	30	1,800	30	1,800
30	0.25	2	Infeasible (min number clusters 197)		76	2,280	90	2,700
60	0.25	5	38	2,280	30	1,800

Abbreviations: ICC, intracluster correlation coefficient; t, number of steps in the stepped wedge design; CRT, cluster randomized trial; CRT-BA, cluster randomized trial with before and after observations; SW-CRT, stepped wedge cluster randomized trial.

Example relates to a trial requiring 788 observations under individual randomization. Note that both M and N are rounded up to the nearest integer.

3.2.3. Design scenario C: determining the power given a fixed number of clusters and cluster size

In this scenario, we illustrate how power can be determined for a fixed sample size. We also use this scenario to illustrate how increasing the cluster size in an SW-CRT can increase power indefinitely, in contrast to a parallel CRT where increasing cluster size can increase power only up to a certain point determined by the ICC. We assume that the number of clusters available is limited. However, although the number of clusters is fixed, we assume M can be increased to reach the desired power. Determining power involves the following steps:

• 1.Set design constraints, including the number clusters (k), the number of steps (t), the number of clusters randomized per step (g), and the sample size per cluster per period (m).
• 2.Determine power available using the Hussey and Hughes mixed model approach [7], [22]. Note that, we have not replicated this formula here, but it has been implemented in various packages [23].

We present illustrative power calculations, assuming a total of 10 clusters available, for a small ICC (0.01) and a moderate ICC (0.1). We compare the increase in power obtained when the total sample size from each cluster increases from 100 to 300. For the SW-CRT, we assume five steps with two clusters randomized per step. We have estimated the power using the Stata function stepped wedge, which use critical values from the standard normal distribution, rather than from the t distribution, as we have in our scenarios here. The results are presented in Table 5. Under a z-test, the sample size required under individual randomization is 786. Under the parallel CRT design, when the ICC is small (0.01), the trial has close to 80% power when the cluster sizes are 300 and there is an improvement in power when increasing the cluster size from 100 to 300. However, when the ICC is moderate (0.1), there is no increase in power when the cluster size increases from 100 to 300. It is well known that increasing the cluster size in a parallel CRT has a limiting effect on the power and that beyond a certain point, determined by the ICC, no further increases in power can be achieved [27].

Table 5.

Example: effect of increasing the cluster size (M) given a fixed number of clusters (k) under the three designs

Design constraints			CRT		CRT-BA		CRT-SW
k	ρ	M	N	Power (%)	N	Power (%)	N	t	m = M/(t + 1)	Power (%)
10	0.01	100	1,000	61	1,000	49	1,020a	5	17	55
10	0.01	300	3,000	78	3,000	87	3,000	5	50	91
10	0.1	100	1,000	16	1,000	41	1,020a	5	17	49
10	0.1	300	3,000	16	3,000	83	3,000	5	50	90

Abbreviations: t, number of steps in the stepped wedge design; ρ, intracluster correlation coefficient; CRT, cluster randomized trial; CRT-BA, cluster randomized trial with before and after observations; SW-CRT, stepped wedge cluster randomized trial.

Example relates to a trial requiring 786 (z-test) observations under individual randomization.

^aTotal sample size is 1,020 due to constraints with m having to be a multiple of (t + 1).

In the SW-CRT, the power available when the total cluster size is 100 (and cluster sizes per measurement occasion are 17) is less than that of the parallel CRT when the ICC is small. However, when the cluster size is 300, the power increases substantially (from about 50% to 90%), for both the small and moderate ICC. This therefore illustrates that when the trial is limited to a small number of clusters, the SW-CRT allows levels of power to be obtained that could not be obtained in a parallel CRT, even with very large cluster sizes. The CRT-BA is never the most efficient design in this example, although the levels of power available are not much less than in the SW-CRT.

4. Discussion

When an SW-CRT design will be preferable to a parallel CRT or CRT-BA depends on many considerations—efficiency just being one consideration. Our work considers the issue of efficiency only and so does not inform general design decisions. Nonetheless, there are some observations here which are worthy of consideration. We observed that, when the total number of observations per cluster is fixed across the designs, the comparative efficiency of the designs depends on the ICC and cluster size, with the SW-CRT being more efficient (in terms of minimizing both the number of clusters and total cluster size) when the ICC was higher. We also observed that when a design is constrained by a small number of clusters, the SW-CRT, particularly when the ICC is large, offers the opportunity to achieve levels of power that might not be possible under a parallel design. Related to this, in the SW-CRT, we also observed, again when the ICC was large, that larger cluster sizes and a small number of clusters can be more efficient than a design with a large number of clusters each of small size. This is in stark contrast to the parallel design where the opposite is true [27].

In the examples considered here, the SW-CRT was more efficient when the ICC was higher. Intracluster correlations are generally higher for process outcomes than for clinical outcomes [26], [28]. Therefore, very generally, for studies in which the primary outcome is a process outcome, it is more likely that the SW design will be more efficient, whereas for studies with a clinical outcome, the parallel design may be more efficient. Whether one design or another will be more efficient should be investigated on a case-by-case basis, that is, by determining power available under the various designs based on the anticipated design characteristics. Whether in practice this design will be the most efficient of course depends on having accurate estimates of the cluster size and ICC.

There are of course other issues that we have not considered. For example, we have limited our consideration to just three designs. There are other designs, which might be even more efficient, for example, mixtures of parallel and stepped wedge studies [29], CRT-BA designs where the before and after periods are not of equal size [22], or so called dog-leg designs [30]. Other potentially efficient designs are cohort designs in which the same participants are measured repeatedly throughout the study. However, design effects for cohort stepped wedge studies have not yet been developed. Perhaps more importantly, we did not fully consider how efficiency varies by the number of steps, when the total cluster size is not fixed, nor variation in step sizes—issues that deserve further investigation. A large number of steps may not lead to the most efficient designs, and any increase in efficiency over the parallel design might wane after a certain number of steps. Our work also assumes constant cluster sizes when in practice cluster sizes commonly vary. Further work is needed to establish how variation in cluster sizes (over time and between clusters) affects power and to derive design effects that accommodate varying cluster sizes. We have also not considered the issue of estimating the ICC at the design stage, although we have illustrated that sensitivity to underestimation of the ICC at the design stage would seem to be less when designing an SW-CRT. Although we have considered only continuous outcomes in our illustrations, the design effects may be applied in the case of dichotomous outcomes. Further work is, however, required to understand the implications for power in the case of rare events or when the assumption of approximate normality is not satisfied.

There are also implications of any time needed to embed the intervention into the cluster. For example, dispersion and dissemination of a service delivery intervention may require time which must be appropriately factored in at the design stage. Where this implementation period is short, we have shown that it has little impact on power [20]. However, when the time needed to embed an intervention is substantial, observations or participants during this embedding period are neither exposed nor unexposed to the intervention and so should not be included at the design stage. In the design of a conventional parallel cluster trial, such a period occurs at the start of the trial with little consequence other than to increase the duration of the study by this period. However, under an SW-CRT, this period of time would have to be incorporated at every step and so could increase the duration of the trial substantially.

Finally, robust trial designs must give unbiased estimates of effectiveness. Whether there are any biases inherent to a stepped wedge design are yet to be elucidated. Potential sources of bias include the risk of selection bias due to lack of concealment of allocation (if individuals are recruited after the allocation is known), lack of blinding, and lack of robust assessment of outcomes, but these concerns are common to all cluster randomized controlled trials [31]. Of possible importance only in the stepped wedge design, however, is the impact of underlying temporal trends and the assumption of adequate adjustment at the analysis stage. If the stepped wedge design is being used as a form of evaluation chosen over a nonrandomized form of evaluation (such as a controlled before and after design), then these caveats require due attention and the fact that the design involves randomization should not discount the possibility of bias.

5. Conclusions

The SW-CRT offers an opportunity for robust evaluation in settings where the alternative may well have been a nonrandomized evaluation—using for example a controlled or before and after design. It also offers a potentially efficient design, and so, the SW-CRT might be viewed as an alternative competing design to the parallel CRT. Sample size calculations are known to be poorly conducted and reported when using novel designs. The framework presented here should help trialists implement these calculations correctly.