Abstract
Automatic construction of user-desired topical hierarchies over large volumes of text data is a highly desirable but challenging task. This study proposes to give users freedom to construct topical hierarchies via interactive operations such as expanding a branch and merging several branches. Existing hierarchical topic modeling techniques are inadequate for this purpose because (1) they cannot consistently preserve the topics when the hierarchy structure is modified; and (2) the slow inference prevents swift response to user requests. In this study, we propose a novel method, called STROD, that allows efficient and consistent modification of topic hierarchies, based on a recursive generative model and a scalable tensor decomposition inference algorithm with theoretical performance guarantee. Empirical evaluation shows that STROD reduces the runtime of construction by several orders of magnitude, while generating consistent and quality hierarchies.
Keywords: Topic Modeling, Ontology Learning, Interactive Data Exploration, Tensor Decomposition
1. Introduction
Constructing a topic hierarchy for large text collection, such as business documents, news articles, social media messages, and research publications, is helpful for information workers, data analysts and researchers to summarize and navigate them in multiple granularity efficiently. While existing hierarchical topic models can be used to produce such hierarchies as an exploration tool, they still require human curation (e.g., modify the structure and label the topics) to meet the quality requirement for reliable exploitation. The manual work for curation is very expensive. This work focuses on helping with the structure modification task.
The nature of this task is interactive and iterative. On one hand, people use a topic model to explore a dataset when the topics are unknown a priori. Thus it is hard to determine the best shape of the hierarchy upfront. On the other hand, as they see the results (inferred topics even with imperfect structure), people have ideas about a more desirable structure, e.g., one topic should be expanded, or multiple topics should be merged. Then they may want to modify part of the hierarchy but preserve other parts that already look good to be labeled. Some modification, such as expanding a topic, is again exploratory and needs help from the machine. It takes multiple iterations of human investigation and algorithm run to finish the construction.
To enable interactive construction of the topic hierarchy, i.e., allowing users to modify the structure on the go, the system needs to satisfy two conditions: efficiency and consistency. Efficiency is necessary for users to see results quickly and react before they lose the context. Consistency is necessary for confusion-free modification, and has two-fold meanings: when people want to modify certain parts of the hierarchy, the remaining parts should be preserved after each run (single-run consistency); and a system should output undifferentiated results given identical input in multiple runs (multi-run consistency).
Limitation of prior work
Most existing hierarchical topic modeling techniques [10, 17, 20, 14, 2] are based on the extensions of latent Dirichlet allocation (LDA), and are not designed for interactive construction of the hierarchy. First, the inference algorithms for these models are expensive, demanding hundreds or thousands of passes of data. Second, an inference algorithm generates one hierarchy for one corpus in one run of the algorithm. Running the inference algorithm with a slightly modified hierarchy structure does not guarantee preservation of topics in untouched branches. Rerunning the inference algorithm with the same input may result in very different results. Therefore, both single-run and multi-run consistency conditions are violated if we use them for interaction.
Our solution
We consider a strategy of top-down, progressive construction of a topical hierarchy, instead of inferring a complex hierarchical model all at once. Thus the construction can be done via a series of interactive operations, such as expanding a topic, collapsing a topic, merging topics and removing topics. Efficient and consistent algorithms can then be designed for each operation. Users can see the results after each operation, and decide what operation to take next. This strategy has several benefits: users can easily control the complexity of the hierarchy; users can see intermediate results and curate the hierarchy in early stages; and it is easier for curators to focus on one simple operation a time.
To support these interactive operations in an efficient and consistent manner, we resort to moment-based inference. Simply put, moment-based inference compresses the original data by collecting important statistics from the documents, e.g., term co-occurrences, and uses these statistics to infer topics. For one advantage, the inference based on the compressed information avoids the expensive, numerous passes of the data. For another advantage, the compression reduces randomness in the data by aggregation. With careful choice of the statistics and the inference method, we can uncover the topics with theoretical guarantee. Modifications to the hierarchy can be supported by manipulating the moments.
We establish a top-down hierarchy construction framework STROD based on these ideas. To the best of our knowledge, it is the first framework towards interactive topical hierarchy construction. The following summarizes our main contributions:
We propose a new hierarchical topic model such that the modification operations mentioned above can be achieved by several atomic operators to the model.
We develop a scalable tensor-based recursive orthogonal decomposition (STROD) method for efficient and consistent construction.
Our experiments demonstrate that our method is several orders of magnitude more efficient than the alternatives, while generating consistent, quality topic hierarchy that is comprehensible to users.
2. Related Work
Statistical topic modeling techniques model a document as a mixture of multiple topics, while every topic is modeled as a distribution over terms. Two important models are probabilistic latent semantic analysis (PLSA) [13] and its Bayesian extension latent Dirichlet allocation (LDA) [5]. They model the generative processes of each term from each document in a corpus, and then infer the unknown distributions that best explain the observed documents.
Hierarchical topic models follow the same generative spirit. Instead of having a pool of flat topics, these models assume an internal hierarchical structure of the topics. Different models use different generative processes to simulate this hierarchical structure, such as nested Chinese Restaurant Process [10], Pachinko Allocation [17], hierarchical Pachinko Allocation [20], recursive Chinese Restaurant Process [14], and nested Chinese Restaurant Franchise [2]. When these models are applied to constructing a topical hierarchy, the entire hierarchy is inferred all at once from the corpus.
The main inference methods for these topic models can be divided into two categories: MCMC sampling [11] and variational inference [5]. They are essentially approximation of the Maximum Likelihood (ML) principle (including its Bayesian version maximum a posterior): Find the best parameters that maximize the joint probability specified by a model. There has been a substantial amount of work on speeding up LDA inference, e.g., by leveraging sparsity [22, 30, 16] and parallelization [21, 24, 31], or online learning mechanism [1, 12, 8]. Few of these ideas have been adopted by the hierarchical topic model studies.
These inference methods have no theoretical guarantee of convergence within a bounded number of iterations, and are nondeterministic either due to the sampling or the random initialization. Recently, a new inference method for LDA has been proposed based on a method of moments, rather than ML. It is found to have provable error bound and convergence properties in theory [3].
All of the hierarchical topic models follow the bag-of-words assumption, while some other extensions of LDA have been developed to model sequential n-grams to achieve better interpretability [26, 29, 18]. No one has integrated them in a hierarchical topic model. The efficiency and consistency issues will become more challenging in an integrated model. A practical approach is to decouple the topic modeling part and the phrase mining part. Blei and Lafferty [4] have proposed to use a statistical test to find topical phrases, which is time-consuming. A much less expensive heuristic is studied in recent work [6] and shown to be effective.
There are a few alternative approaches to constructing a topical hierarchy. Pujara and Skomoroch [23] proposed to first run LDA on the entire corpus, and then split the corpus heuristically according to the results and run LDA on each split corpus individually. CATHY [28] is a recursive topical phrase mining framework for short, content-representative text. It also decouples phrase mining and topic discovery for efficiency purpose. Though it is not designed for generic text, it bears some similarity with this work such as top-down recursion and compression of documents.
After the hierarchy is constructed from a corpus, people can label these topics and derive topic distributions for each document [25]. Those are not the subject of this paper. Broadly speaking, this work is also related to: hierarchical clustering of documents [9], queries [19], keywords [28] etc.; and ontology learning [15], which mines subsumption (‘is-a’) relationships from text.
3. Problem Formulation
Given a corpus, our goal is to construct a user-desired topical hierarchy, i.e., a tree of topics, where each child topic is about a more specific theme within the parent topic.
For easy interaction, the topics need to be visualized in user-friendly forms. Unigrams are often ambiguous, especially across fine-grained topics [27]. We choose to enhance the topic representation with ranked phrases. The ranking should reflect both their popularity and discriminating power for a topic. For example, the top ranked phrases for the database topic can be: “database systems”, “query processing”, “concurrency control” …. A phrase can appear in multiple topics, though it will have various ranks in them.
Formally, the input data are a corpus of D documents. The d-th document can be segmented into a sequence of ld tokens. All the unique tokens in this corpus are indexed using a vocabulary of V terms. And wd,j ∈ [V], j = 1, …, ld represents the index of the j-th token in document d. A topic t is defined by a probability distribution over terms Φt ∈ ΔV–1, and an ordered list of phrases 𝒫t = {Pt,1, Pt,2, …}, where Pt,i is the phrase ranked at i-th position for topic t.
A topical hierarchy is defined as a tree 𝒯 in which each node is a topic. Every non-leaf topic t has Ct child topics. We assume Ct is bounded by a small number K, such as 10, because the topical hierarchy is intended for human to efficiently browse the subtopics for each topic. The number K is named the width of the tree 𝒯.
A topical hierarchy for a corpus is constructed via a series of user operations. An operation transforms one topic hierarchy 𝒯 to another 𝒯′. A top-down construction framework supports the following user operations.
Expand – for an arbitrary topic t in 𝒯, grow a subtree rooted at t.
Collapse – for an arbitrary topic t in 𝒯, remove all its descendant topics.
Split – for an arbitrary topic t in 𝒯, split it into k topics.
Remove – for an arbitrary set of topics t1, …, tn in 𝒯, delete these topics.
Merge – for an arbitrary set of topics t1, …, tn in 𝒯, merge these topics as a new topic, whose parent is the least common ancestor of them, and whose children are the union of the children of all merged topics.
Move – for an arbitrary topic t in 𝒯, move the subtree rooted at t to be under a different parent topic t′.
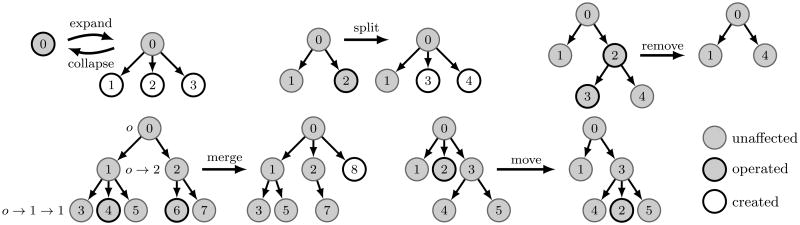
Figure 1 demonstrates these operations. In these operations, only a few topics are affected, so users can consistently modify the hierarchy and control the change.
Figure 1.
Examples of 6 user operations. A topic can be indexed by a integer (in the circle), or by the path from root
For convenience, we index a topic using the top-down path from root to this topic. The root topic is indexed as o. Every non-root topic t is recursively indexed by πt → χt, where πt is the path index of its parent topic, and χt ∈ [Ct] is the index of t among its siblings. For example, topic 2 in the ‘merge’ example of Figure 1 is indexed as o → 2, and topic 3 in the same tree is indexed as o → 1 → 1. The level ht of a topic t is defined to be its distance to the root. So root topic is in level 0, and topic o → 1 → 1 is in level 2. The height H of a tree is defined to be the maximal level over all the topics in the tree. Clearly, the total number T of topics is upper bounded by .
4. The STROD Framework
We develop a Scalable Tensor Recursive Orthogonal Decomposition (STROD) framework for interactive topical hierarchy construction. In Section 4.1, we propose a new hierarchical topic model, and introduce how the user operations can be achieved by atomic manipulations to the model. In Section 4.2, we present our tensor-based algorithms supporting these operations. Section 4.3 introduces topical phrase mining and ranking based on the inferred model parameters.
4.1 Hierarchical Topic Modeling
Generative hierarchical topic modeling assumes the documents are generated from a latent variable model, and then infers the model parameters from observed documents to recover the topics. Distinct from prior work, we do not infer a hierarchy for one corpus only once. Instead, we allow users to perform consistent modification to the hierarchy. Therefore, we need a model that is convenient for manipulation and supports all the user operations introduced in Section 3.
We first introduce our generative model when the hierarchy structure is fixed, and then discuss atomic operators to manipulate the model structure.
4.1.1 Latent Dirichlet Allocation with Topic Tree
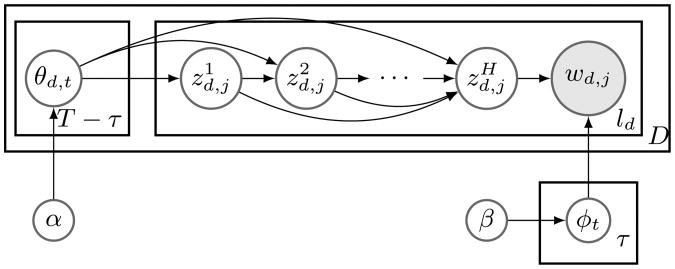
In this subsection we assume the topic hierarchy structure is fixed. Its height is H, and there are τ leaf nodes and T – τ non-leaf nodes. For ease of explanation we assume all leaf nodes are on the level of H.
Every leaf topic node t(Ct = 0) has a multinomial distribution ϕt = p(w = ·|t) over terms. Every document d paired with a non-leaf node t(Ct > 0) has a multinomial distribution θd,t = p(w = ·|d,t) over t's child topics: t → 1 through t → Ct. θd,t represents the content bias of document d towards t's subtopics. For the ‘merge’ example in Figure 1, before merge, there are 3 non-leaf topics: o, o → 1 and o → 2. So a document d is associated with 3 multinomial distributions over topics: θd,o over its 2 children, θd,o→1 over its 3 children, and θd,o→2 over its 2 children. Each multinomial distribution θd,t is generated from a Dirichlet prior (αt→1, …, αt→Ct). αt→z represents the corpus' bias towards z-th child of topic t, and .
To generate a token wd,j, we first sample a path from the root to a leaf node . The nodes along the path are sampled one by one, starting from the root. Each time one child is selected from all children of , from the multinomial . When a leaf node is reached, the token is generated from its multinomial distribution .
The whole generative process is:
For each leaf node t in 𝒯, generate its distribution over terms ϕt ∼ Dir(β);
- For each document d ∈ [D]:
- For each non-leaf node t in 𝒯, draw a multinomial distribution over its subtopics: θd,t ∼ Dir(αt→1, …, αt→Ct);
- For each token index j ∈ [ld] of document d:
- i ← 0;
- While is not a leaf node:
- i ← i + 1;
- Draw subtopic ;
- Generate token .
Its graphical representation is Figure 2. Table 1 collects the notations.
Figure 2. Latent Dirichlet Allocation with Topic Tree.
Table 1. Notations used in our model.
| Symbol | Description | |
|---|---|---|
| D | the number of documents in the corpus | |
| V | the number of unique terms in the corpus | |
| H | the height of the topical hierarchy | |
| T | the total number of topics in the hierarchy | |
| τ | the number of leaf topics in the hierarchy | |
| Ct | the number of child topics of topic t | |
| ld | the length (number of tokens) of document d | |
| πt | the parent topic of topic t | |
| χt ∈ [Cπt] | the index of topic t among its siblings | |
| wd,j ∈ [V] | the j-th token in the document d | |
|
|
the child index of the topic at level i for wd,j | |
| ϕt | topic t's multinomial distribution over terms | |
| αt | the Dirichlet hyperparameter of topic t | |
| θd,t | document d's distribution over t's child topics |
For every non-leaf topic node, we can derive a term distribution by marginalizing their children's term distributions:
| (1) |
So in our model, the term distribution ϕt for an internal node in the topic hierarchy can be calculated as a mixture of its children's term distributions. The Dirichlet prior α determines the mixing weight.
When the structure 𝒯 is fixed, we need to infer its parameters ϕ(𝒯) and ϕ(𝒯) from a given corpus. When the height of the hierarchy H = 1, our model reduces to the flat LDA model.
4.1.2 Model Structure Manipulation
The main advantage of this model is that it can be consistently manipulated to accommodate user operations.
Proposition 1. The following atomic manipulation operators are sufficient in order to compose all the user operations introduced in Section 3:
EXP(t, k). Discover k subtopics of a leaf topic t.
MER(t1, t2). Merge two topics t1 and t2 into a new topic t3 under their least common ancestor t.
MOV(t1, t2). Move the subtree rooted at topic t1 to be under t2.
The following are examples about how to use these manipulation operators to compose the user operations in Figure 1.
‘Collapse’ – applying MER(o, o → 1) three times.
‘Split’ – EXP(o → 2, 2) followed by MER(o, o → 2).
‘Remove’ – MER(o → 2, o → 2 → 1) followed by MER(o, o → 2).
Implementation of these atomic operators needs to follow the consistency requirement.
-
Single-run consistency – suppose the topical hierarchy 𝒯1 is altered into 𝒯2 after a user operation, certain nodes are not affected. For example, in the ‘merge’ operation in Figure 1, node 0,1,2,3,5,7 are not touched. The consistency condition requires that, if we restart step 2-(b) whenever we reach an affected node in step 2-(b)-ii, 𝒯1 and 𝒯2 are equivalent generative models, i.e., generate the same documents in expectation. By this definition, we have the following proposition.
Proposition 2. A single run altering 𝒯1 into 𝒯2 is consistent if and only if i) for each unaffected leaf node t, αt (𝒯1) = αt (𝒯2), ϕt (𝒯1) = ϕt (𝒯2); and ii) for each internal node .
Multi-run consistency – with identical input across multiple runs, one operator should output nearly identical (undifferentiated to human) α and ϕ.
Section 4.2 presents a moment-based method to compute these operators efficiently and consistently.
4.2 Moment-based Operation
In statistics, the ξ-th order population moment of a random variable is the expectation of its ξ-th power. In our problem, the random variable is a token wd,j in a document d. The ξ-th population moment is the expected co-occurrence of terms in ξ token positions. They are related to the model parameters α and ϕ. The method of moments collects empirical moments from the corpus, and estimate α and ϕ by fitting the empirical moments with theoretical moments. As a computational advantage, it only relies on the term co-occurrence statistics. The statistics contain important information compressed from the full data, and require only a few scans of the data to collect.
To compute our three atomic operators, we generalize the notion of population moments. We consider the population moments conditioned on a topic t. The first order conditional moment E1 (t) is a vector in ℝV . Component x is the expectation of 1w=x given that w is drawn from topic t's descendant.
| (2) |
The second order moment E2 (t) ∈ ℝV×V is a V × V tensor (hence, a matrix), storing the expectation of the co-occurrences of two terms w1 and w2 given that they are both drawn from topic t's descendants. Integrating over the document-topic distribution θ, we have:
| (3) |
The operator ⊗ denotes an outer product between tensors: if A ∈ ℝs1× … × sp, and B ∈ ℝsp+1× … ×sp+q, then A⊗B is a tensor in ℝs1× … ×sp+q, and [A⊗B]i1 … ip+q = Ai1 … ip Bip+1 …ip+q.
Likewise, we can derive the third order moment E3(t) ∈ ℝV×V×V (a V × V × V tensor) as the expectation of co-occurrences of three terms w1, w2 and w3 given that they are all drawn from topic t's descendants:
| (4) |
Equations (2)–(4) characterize the theoretical conditional moments for topic t using model parameters associated with t's children. The empirical conditional moments can be estimated from data and parameters of t's ancestors.
For topic t, we estimate the empirical ‘topical’ count of term x in document d as:
| (5) |
Recall that πt is t's parent. cd,x(t) can be recursively computed through cd,x(πt) and the boundary is cd,x(o) = cd,x, i.e., the total counts of term x in document d.
Then we can estimate empirical conditional moments using these empirical topical counts:
| (6) |
where . These enable fast estimation of empirical moments by passing data once.
The following three subsections discuss the computation of the three atomic operators EXP, MER and MOV with the method of moments.
4.2.1 EXP Operator
EXP(t, k) should find k subtopics under topic t, without changing any existing model parameters. So we need an algorithm that returns (αt→z, ϕt→z), z ∈ [k], with . By recursion, we note that only αo needs to be set by a user. It controls the degree of topical purity of documents. When αo →∞, each document is only about one leaf topic.
We employ the method of moments. In Equations (2)– (4), we replace the left hand side with the empirical conditional moments estimated from the data. The right hand side is theoretical moments with αt→z, ϕt→z, Z ∈ [k] as unknown variables. Solving these equations yields a solution of the acquired model parameters. The following theorem by Anandkumar et al. [3] suggests that we only need to use up to 3rd order moments to find the solution.
Theorem 1. Assume M2 and M3 are defined as:
| (7) |
where λz > 0, vz's are linearly independent, and ‖vz‖ = 1. When M2 and M3 are given, vz and λz in Equation (7) can be uniquely solved in polynomial time.
To write Equations (2)–(4) in this form, we define:
| (8) |
| (9) |
| (10) |
where Ω(A, a, b, c) permutes the modes of tensor A, such that Ω(A,a,b,c)i1,i2,i3 = Ai1,i2,i3. It follows that:
So they fit Equation (7) nicely, and intuitively. If we decompose M2 (t) and M3 (t), the z-th component is determined by the child's term distribution ϕt→z, and its weight is , which is equal to p(t → z|t).
M2(t) is a dense V × V matrix, and M3(t) is a dense V × V × V tensor. Direct application of the tensor decomposition algorithm in [3] is challenging due to the creation of these huge dense tensors. Therefore, we design a more scalable algorithm. The idea is to bypass the creation of M2 (t) and M3(t) and utilize the sparsity and decoupled decomposition of the moments. We go over Algorithm 1 to explain it.
Line 1.1 collects the empirical moments with one scan of the data.
Lines 1.2 to 1.6 project the large tensor M3 ∈ ℝ V×V×V into a smaller tensor T̃ ∈ ℝ k×k×k . T̃ is not only of smaller size, but also can be decomposed into an orthogonal form: . are orthonormal vectors in ℝk. This is assured by the whitening matrix W calculated in Line 1.5, which satisfies WT M2W = I. This part contains two major tricks:
- When calculating W, the straightforward computation requires spectral decomposition of M2. We avoid explicit creation of M2, but achieve the equivalent spectral decomposition. We first perform spectral decomposition for E2(t) = UΣ1UT , where U ∈ ℝV × k is the matrix of k eigenvectors, and Σ1 ∈ ℝk × k is the diagonal eigenvalue matrix. The k column vectors of U form an orthonormal basis of the column space of E2(t). E1(t)'s representation in this basis is M1 = UT E1(t). According to Equation (8), M2 can now be written as:
So a second spectral decomposition can be performed on , as . Then we have UU′Σ(UU′)T as M2's spectral decomposition. The space requirement is reduced from V2 to m = ‖E2(t)‖0 ≪ V2 , because only term pairs ever cooccurring in one document contribute to non-zero elements of E2(t). The time for spectral decomposition is reduced from 𝒪(V2 K) to 𝒪(mK). - The straightforward computation of the tensor product T̃ = M3(t)(W, W, W) using explicit M3(t) and W requires 𝒪(V3) space and 𝒪(V3 K+Ll̄2) time, where l̄2 is the maximal document length. We decouple M3(t) as a summation of multiple tensors, such that the product between each tensor and W is in a decomposable form: either (v ⊗v ⊗v)(W, W, W) or (v ⊗ B)(W, W, W), which can be computed as easily as (WT v)⊗3 or (WT v) ⊗) (WT BW).
(11)
where and is the x-th column of WT. U2(W,W,W) and U3(W, W, W) can be obtained by permuting U1(W, W, W)'s modes. The renovated procedure needs only one pass of data in O(LK2) time.
Lines 1.7 to 1.14 perform orthogonal decomposition of T̃ via a power iteration method. The orthonormal eigenpairs are found one by one. To find one such pair, the algorithm randomly starts with a unit-norm vector v, runs power iteration (Line 1.11) for n times, and records the candidate eigenpair. This process further repeats by N times, starting from various unit-norm vectors. Line 1.12 picks the eigenpair with the largest eigenvalue. After an eigenpair is found, the tensor T̃ is deflated by the found component (Line 1.14), and the same power iteration is applied to it to find the next eigenpair. After all the k orthonormal eigenpairs are found, they can be used to uniquely determine the k target components (αt→z,ϕt→z) (Line 1.13).
Line 1.15 computes the empirical topical counts for the k inferred child topics. It requires one scan of the data.
The decomposition by Algorithm 1 is fast and unique with sufficient data.
Theorem 2. Assume M2 and M3 are defined as in Equation (7), λz > 0, and vz 's are linearly independent with unit-norm, then Algorithm 1 finds exactly the same set of with high probability. The power iteration step of Line 1.11 converges in a quadratic rate.
Algorithm 1. EXP(t, k).
It satisfies single-run consistency. Multi-run consistency is guaranteed if the empirical moments are close to theoretical moments. We empirically evaluate it in Section 5.
The overall time complexity for EXP is 𝒪(LK2 + Km + NnK4), which can be regarded linear to the data size since N and n can be as small constants as 10 to 30, and K is a small number like 10 to 50 due to our assumption of human manageable tree width. It requires only three scans of data.
4.2.2 MER Operator
Algorithm 2. MER(t1, t2).
To merge two topics t1 and t2, we need to find their least common ancestor t (Line 2.1), subtract the topical counts c(t′) and the Dirichlet prior αt′ for any other topic t′ in the path between t1 and t2 (Lines 2.2–2.11), and then create a new node t3 to sum up the topical counts and Dirichlet prior of t1 and t2 (Lines 2.14–2.16) with one exception: when t1 is t2's direct ancestor or direct descendant, we can just use t as the merged topic node (Line 2.12). We then move the children of t1 and t2 to be under the merged topic node (Lines 2.17–2.18). Last, we remove t1 and t2 and add t3 to the topical hierarchy (Line 2.19). The complexity for MER is 𝒪(LH).
4.2.3 MOV Operator
Algorithm 3. MOV(t1, t2).
To move the subtree rooted at t1 to be under t2, we first subtract topical counts and Dirichlet prior from every ancestor of t1 (Lines 3.1–3.5), and then add them to every ancestor of t2, including t2 itself (Lines 3.6–3.10). Finally, we set the parent of t1 to be t2. The complexity for MOV is 𝒪(LH).
The implementation of MER and MOV using Algorithms 2 and 3 satisfy both multi-run and single-run consistency requirement.
4.3 Phrase Mining and Ranking
After the term distribution in each topic is inferred, we can then mine and rank topical phrases within each topic. The phrase mining and ranking in STROD adapt CATHY [27] to generic text. Here we briefly present the process.
In this work, a phrase is defined as a frequent consecutive sequence of terms of arbitrary lengths. To filter out incomplete phrases (e.g., ‘vector machine’ instead of ‘support vector machine’) and frequently co-occurred terms that do not make up a meaningful phrase (e.g., ‘often use’), we use a statistical test to select quality phrases [7], and record the count cd,P of each phrase P in each document d.
After the phrases of mixed lengths are mined, they are ranked with regard to the representativeness of each topic in the hierarchy, based on two factors: popularity and discriminativeness. A phrase is popular for a topic if it appears frequently in documents containing that topic (e.g., ‘information retrieval’ has better popularity than ‘cross-language information retrieval’ in the Information Retrieval topic). A phrase is discriminative of a topic if it is frequent only in the documents about that topic but not in those about other topics (e.g., ‘query processing’ is more discriminative than ‘query’ in the database topic).
We use the topical term distributions inferred from our model to estimate the ‘topical count’ cd,P (t) of each phrase P in each document d, in a similar way as we estimate the topical count of terms in Equation (5):
Let the conditional probability p(P|t) be the probability of “randomly choose a document and a phrase that is about topic t, the phrase is P.” It can be estimated as . The popularity of a phrase P in a topic t can be quantified by p(P|t). The discriminativeness can be measured by the log ratio between the probability p(P|t) conditioned on topic t and the probability p(P|πt) conditioned on its parent topic .
A good ranking function to combine these two factors is their product:
| (12) |
which has an information-theoretic sense: the pointwise KL-divergence between the two probabilities [27]. Finally, we use rt(P) to rank phrases in topic t in the descending order.
5. Experiments
In this section we first introduce the datasets and the methods used for comparison, and then describe our evaluation on efficiency, consistency, and quality.
Datasets
Our performance study is on four datasets:
DBLP title: A set of titles of recently published papers in DBLP (www.dblp.org). The set has 1.9M titles, 152K unique terms, and 11M tokens.
CS abstract: A dataset of computer science paper abstracts from Arnetminer (www.arnetminer.org). The set has 529K papers, 186K unique terms, and 39M tokens.
TREC AP news: A TREC news dataset (1998). It has 106K full articles, 170K unique terms, and 19M tokens.
Pubmed abstract: A dataset of life sciences and biomedical topic. We crawled 1.5M abstracts from Jan. 2012 to Sep. 2013 on Pubmed (www.ncbi.nlm.nih.gov/pubmed). The dataset has 98K unique terms and 169M tokens.
We remove English stopwords from all the documents.
Methods for comparison
We mainly evaluate EXP because it dominates the runtime, and its consistency in real-world data is subject to empirical evaluation. We compare the following topical hierarchy construction methods.
hPAM – parametric hierarchical topic model. The hierarchical Pachinko Allocation Model [20] is a state-of-the-art parametric hierarchical topic modeling approach. hPAM outputs a specified number of supertopics and subtopics, as well as the associations between them.
nCRP – nonparametric hierarchical topic model. We choose nCRP to represent this category for its relative efficiency. It outputs a tree with a specified height. The number of topics cannot be set exactly. We tune its hyperparameter to generate an approximately identical number of topics as other methods.
splitLDA – recursively applying LDA, as discussed in Section 2. This heuristic method is more efficienct than the above two methods. We implement splitLDA on top of an efficient single-machine LDA inference algorithm [30].
CATHY – recursively clustering term co-occurrence networks. CATHY [27] uses a term co-occurrence network to compress short documents and performs topic discovery through an EM algorithm.
STROD and its variations RTOD, RTOD2, RTOD3 – recursively applying our EXP operator to expand the tree. We implement several variations to analyze our scalability improvement techniques: (i) RTOD: recursive tensor orthogonal decomposition without scalability improvement [3]; (ii) RTOD2: RTOD plus the efficient computation of whitening matrix by avoiding creation of M2; (iii) RTOD3: RTOD plus the efficient computation of tensor product by avoiding creation of M3; and (iv) STROD: Algorithm 1 with the full scale-up technique.
5.1 Efficiency
The first evaluation assesses the efficiency of different algorithms when constructing a topical hierarchy with the same depth and width.
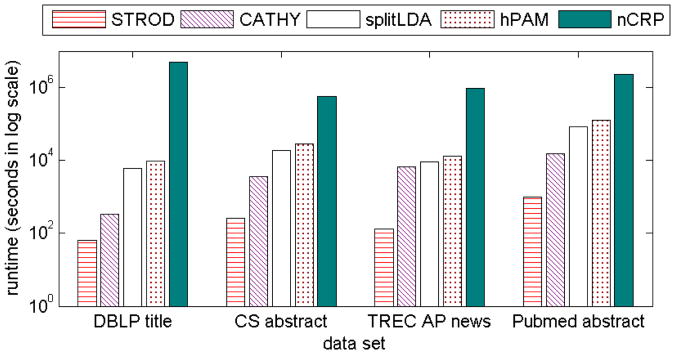
Figure 3 shows the overall runtime in these datasets. STROD is several orders of magnitude faster than the existing methods. On the largest dataset it reduces the runtime from one or more days to 18 minutes in total. CATHY is the second best method in short documents such as titles and abstracts because it compresses the documents into term co-occurrence networks. But it is still more than 100 times slower than STROD due to many rounds of EM iterations. splitLDA and hPAM rely on Gibbs sampling, and the former is faster because it recursively performs LDA, and considers fewer dependencies in sampling. nCRP is two orders of magnitude slower.
Figure 3. Total runtime on each dataset, H = 2, Ct = 5.
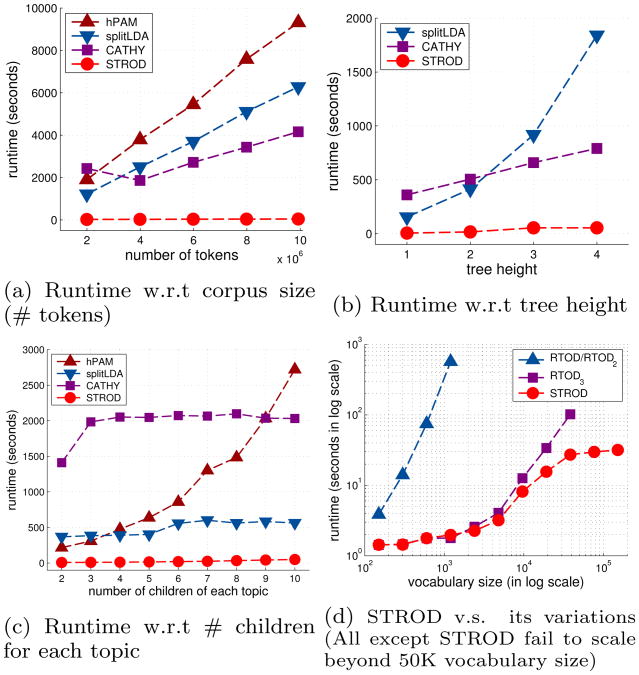
We then conduct analytical study of the runtime growth with respect to different factors. Figures 4a–4c show the runtime varying with the number of tokens, the tree height and the tree width. We can see that the runtime of STROD grows slowly, and it has the best performance in all occasions. The margin of our method over others grows quickly when the scale increases. In Figure 4b, we exclude hPAM because it is designed for H = 2. We exclude nCRP from all these experiments because it takes too long time to finish (>90 hours with 600K tokens).
Figure 4. Runtime with varying scale.
Figure 4d shows the performance in comparison with the variations of STROD. Both RTOD and RTOD2 fail to finish when the vocabulary size grows beyond 1K, because the third-order moment tensor M3(t) requires O(V3) space to create. RTOD3 also has limited scalability because the second order moment tensor M2(t) ∈V×V is dense. STROD scales up easily by avoiding explicit creation of these tensors.
5.2 Consistency
The second evaluation assesses the multi-run consistency of different algorithms. For each dataset, we sample 10,000 documents and run each algorithm 10 times and measure the variance among the 10 runs for the same method as follows. Each pair of algorithm runs generate the same number of topics, but their correspondence is generally unknown (STROD makes an exception with its ability to obtain a unique order of subtopics according to learned α). For example, the topic o → 1 in the first run may be close to o → 3 in the second run. We measure the KL divergence between all pairs of topical term distributions between the two runs, build a bipartite graph using the negative KL divergence as the edge weight, and then use a maximum matching algorithm to determine the best correspondence (top-down recursively). Then we average the KL divergence between matched pairs as the difference between the two algorithm runs. Finally, we average the difference between all 10 × 9 = 90 ordered pairs of algorithm runs as the final variance. We exclude nCRP in this section, since even the number of topics is not a constant after each run.
Table 2 summarizes the results: STROD has lowest variance in all the three datasets. The other three methods based on Gibbs sampling have variance larger than 1 in all datasets, which implies that the topics generated across multiple algorithm runs are considerably different.
Table 2. The variance of multiple algorithm runs in each dataset.
| Method | DBLP title | CS abstract | TREC AP news |
|---|---|---|---|
| hPAM | 5.578 | 5.715 | 5.890 |
| splitLDA | 3.393 | 1.600 | 1.578 |
| CATHY | 17.34 | 1.956 | 1.418 |
| STROD | 0.6114 | 0.0001384 | 0.004522 |
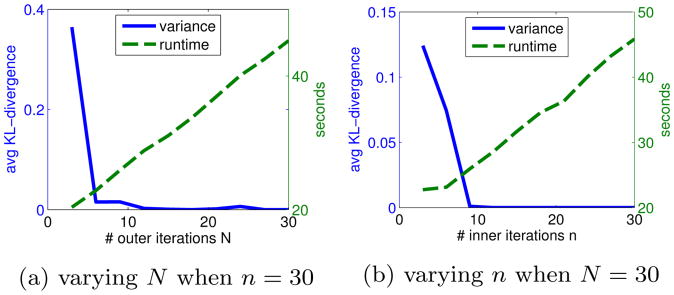
We also evaluate the variance of STROD when we vary the number of outer and inner iterations N and n. As shown in Figure 5, the variance of STROD quickly diminishes when the number of outer and inner iterations grow to 10. This validates the theoretical analysis of their fast convergence.
Figure 5. The variance and runtime of STROD when varying # outer and inner iterations N and n (CS abstract).
In conclusion, STROD achieves consistent performance with small runtime. It is stable and robust to be used as a hierarchy construction method for large text collections.
5.3 Interpretability
The final evaluation assesses the interpretability of the constructed topical hierarchy, via human judgment. We evaluate hierarchies constructed from DBLP titles and TREC AP news. For simplicity, we set the number of subtopics to be 5 for all topics. For hPAM, we post-process them to obtain the 5 strongest subtopics for each topic. For all the methods we use the same phrase mining and ranking procedure to enhance the interpretability. We do not include nCRP in this study because hPAM has been shown to have superior performance of it [20].
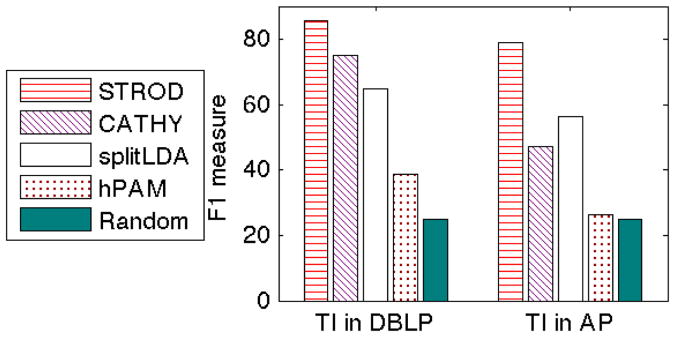
In order to evaluate the coherence of the hierarchy, we use an Topic Intrusion (TI) task which were proposed in [27]: Evaluators are shown a parent topic t and X candidate child topics. X – 1 of the child topics are actual children of t in the generated hierarchy, and the remaining child topic is not. Each topic is represented by its top-5 ranked phrases. Evaluators are asked to select the intruder child topic, or to indicate that they are unable to make a choice.
For this study we set X = 4. 160 Topic Intrusion questions are randomly generated. We then calculate the agreement of the human choices with the actual hierarchical structure constructed by the various methods. We consider a higher match between a given hierarchy and human judgment to imply a higher quality hierarchy. For each method, we report the F-1 measure of the answers matched consistently by three human judgers with CS background.
Figure 6 summarizes the results. STROD is the best performing method in both datasets. This suggests that the quality of the hierarchy is not compromised by the strong efficiency and consistency of STROD. As the tree goes deeper, splitLDA degrades in quality due to inclusion of irrelevant portion of each document. Compared to splitLDA, STROD does not assign a document entirely to a topic. In addition, STROD has a theoretically guaranteed inference method for expansion, which may also account for the superior quality.
Figure 6. Topic intrustion study.
A subset of the hierarchy constructed from CS abstract by ‘Expand’ is presented in Figure 7. For each non-root node, we show the top ranked phrases. Node o → 1 is about ‘data’, while its children involve database, data mining and bioinformatics. The lower the level is, the more specific the topic is, and the more multigrams emerge ahead of unigrams in general. This initial hierarchy helps users quickly see the main topics without going through all the documents. They can then use other operators to make small changes to the hierarchy to confidently and continuously refine the quality.
Figure 7. Sample of hierarchy generated by STROD (two phrases only differing in plural/single forms are shown only once).
6. Discussions
In this work, we tackle the efficiency and consistency challenge of interactive topical hierarchy construction from large-scale text data. We design a novel moment-based framework to build the hierarchy recursively. Our framework divides the construction task into simpler operations in which users can be interactively involved. To support these operations, we design a new model for topical hierarchy which can be learned recursively. For consistent inference, we extend a theoretically guaranteed tensor orthogonal decomposition technique to this model. Utilizing the special structure of the tensor in our task, we scale up the algorithm significantly. By evaluating our approach on a variety of datasets, we demonstrate a prominent computational advantage. Our algorithm generates consistent and quality topic hierarchy 100-1000 times faster than the state of the art, and the margin grows when the corpus size increases.
This invention opens up numerous possibilities for future work. On the application side, it is foundation for building new systems to support explorative generation of textual data catalogs. Existing choice is either fully manual or fully automatic. The former is high quality but labor-expensive, and the latter is the opposite. By adding interaction capability to automated methods, there is hope to reduce human effort and meanwhile allow users to have quality control. On the methodology side, the advantage of STROD can be further fulfilled by parallelization and adaptation to dynamic text collections.
Acknowledgments
Research was sponsored in part by the U.S. Army Research Lab. under Cooperative Agreement No. W911NF-09-2-0053 (NSCTA), National Science Foundation IIS-1017362, IIS-1320617, and IIS-1354329, HDTRA1-10-1-0120, and grant 1U54GM114838 awarded by NIGMS through funds provided by the trans-NIH Big Data to Knowledge (BD2K) initiative (www.bd2k.nih.gov), and MIAS, a DHS-IDS Center for Multimodal Information Access and Synthesis at UIUC.
Footnotes
Categories and Subject Descriptors: I.7 [Computing Methodologies]: Document and Text Processing; H.2.8 [Database Applications]: Data Mining
Contributor Information
Chi Wang, Email: chiw@microsoft.com.
Xueqing Liu, Email: xliu93@illinois.edu.
Yanglei Song, Email: ysong44@illinois.edu.
Jiawei Han, Email: hanj@illinois.edu.
References
- 1.Ahmed A, Ho Q, Teo CH, Eisenstein J, Xing EP, Smola AJ. Online inference for the infinite topic-cluster model: Storylines from streaming text. AISTATS. 2011 [Google Scholar]
- 2.Ahmed A, Hong L, Smola A. Nested chinese restaurant franchise process: Applications to user tracking and document modeling. ICML. 2013 [Google Scholar]
- 3.Anandkumar A, Ge R, Hsu D, Kakade SM, Telgarsky M. Tensor decompositions for learning latent variable models. Journal of Machine Learning Research. 2014;15:2773–2832. [Google Scholar]
- 4.Blei DM, Lafferty JD. Visualizing Topics with Multi-Word Expressions. arXiv:0907.1013. 2009 [Google Scholar]
- 5.Blei DM, Ng AY, Jordan MI. Latent dirichlet allocation. Journal of Machine Learning Research. 2003;3:993–1022. [Google Scholar]
- 6.Danilevsky M, Wang C, Desai N, Guo J, Han J. Automatic construction and ranking of topical keyphrases on collections of short documents. SDM. 2014 [Google Scholar]
- 7.El-Kishky A, Song Y, Wang C, Vossand CR, Han J. Scalable topical phrase mining from text corpora. VLDB. 2015 [Google Scholar]
- 8.Foulds J, Boyles L, DuBois C, Smyth P, Welling M. Stochastic collapsed variational bayesian inference for latent dirichlet allocation. KDD. 2013 [Google Scholar]
- 9.Fung BC, Wang K, Ester M. Hierarchical document clustering using frequent itemsets. SDM. 2003 [Google Scholar]
- 10.Griffiths T, Jordan M, Tenenbaum J, Blei DM. Hierarchical topic models and the nested chinese restaurant process. NIPS. 2004 [Google Scholar]
- 11.Griffiths TL, Steyvers M. Finding scientific topics. Proceedings of the National academy of Sciences of the United States of America. 2004;101(Suppl 1):5228–5235. doi: 10.1073/pnas.0307752101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hoffman M, Blei D, Wang C, Paisley J. Stochastic variational inference. Journal of Machine Learning Research. 2013;14:1303–1347. [Google Scholar]
- 13.Hofmann T. Unsupervised learning by probabilistic latent semantic analysis. Machine Learning. 2001 Jan;42(1-2):177–196. [Google Scholar]
- 14.Kim JH, Kim D, Kim S, Oh A. Modeling topic hierarchies with the recursive chinese restaurant process. CIKM. 2012 [Google Scholar]
- 15.Lawrie D, Croft WB. Discovering and comparing topic hierarchies. Proc RIAO. 2000 [Google Scholar]
- 16.Li A, Ahmed A, Ravi S, Smola AJ. Reducing the sampling complexity of topic models. KDD. 2014 [Google Scholar]
- 17.Li W, McCallum A. Pachinko allocation: Dag-structured mixture models of topic correlations. ICML. 2006 [Google Scholar]
- 18.Lindsey RV, Headden WP, III, Stipicevic MJ. A phrase-discovering topic model using hierarchical pitman-yor processes. EMNLP-CoNLL. 2012 [Google Scholar]
- 19.Liu X, Song Y, Liu S, Wang H. Automatic taxonomy construction from keywords. KDD. 2012 [Google Scholar]
- 20.Mimno D, Li W, McCallum A. Mixtures of hierarchical topics with pachinko allocation. ICML. 2007 [Google Scholar]
- 21.Newman D, Asuncion A, Smyth P, Welling M. Distributed algorithms for topic models. The Journal of Machine Learning Research. 2009;10:1801–1828. [Google Scholar]
- 22.Porteous I, Newman D, Ihler A, Asuncion A, Smyth P, Welling M. Fast collapsed gibbs sampling for latent dirichlet allocation. KDD. 2008 [Google Scholar]
- 23.Pujara J, Skomoroch P. Large-scale hierarchical topic models. NIPS Workshop on Big Learning. 2012 [Google Scholar]
- 24.Smola A, Narayanamurthy S. An architecture for parallel topic models. Proceedings of the VLDB Endowment. 2010;3(1-2):703–710. [Google Scholar]
- 25.Sontag D, Roy D. Complexity of inference in latent dirichlet allocation. NIPS. 2011:1008–1016. [Google Scholar]
- 26.Wallach HM. Topic modeling: beyond bag-of-words. ICML. 2006 [Google Scholar]
- 27.Wang C, Danilevsky M, Desai N, Zhang Y, Nguyen P, Taula T, Han J. A phrase mining framework for recursive construction of a topical hierarchy. KDD. 2013 [Google Scholar]
- 28.Wang C, Yu X, Li Y, Zhai C, Han J. Content coverage maximization on word networks for hierarchical topic summarization. CIKM. 2013 [Google Scholar]
- 29.Wang X, McCallum A, Wei X. Topical n-grams: Phrase and topic discovery, with an application to information retrieval. ICDM. 2007 [Google Scholar]
- 30.Yao L, Mimno D, McCallum A. Efficient methods for topic model inference on streaming document collections. KDD. 2009 [Google Scholar]
- 31.Zhai K, Boyd-Graber J, Asadi N, Alkhouja ML., Mr lda: A flexible large scale topic modeling package using variational inference in mapreduce. WWW. 2012 [Google Scholar]