Abstract
To validate a method for predicting the binding affinities of FabI inhibitors, three implicit solvent methods, MM-PBSA, MM-GBSA and QM/MM GBSA were carefully compared using sixteen benzimidazole inhibitors in complex with F. tularensis FabI. The data suggests that the prediction results are sensitive to radii sets, GB methods, QM Hamiltonians, sampling protocols, and simulation length, if only one simulation trajectory is used for each ligand. In this case, QM/MM-GBSA using 6 ns MD simulation trajectories together with GBneck2, PM3, and the mbondi2 radii set, generate the closest agreement with experimental values (r2= 0.88). However, if the three implicit solvent methods are averaged from six 1 ns MD simulations for each ligand (called “multiple independent sampling”), the prediction results are relatively insensitive to all the tested parameters. Moreover, MM/GBSA together with GBHCT and mbondi, using 600 frames extracted evenly from six 0.25 ns MD simulations, can also provide accurate prediction to experimental values (r2 = 0.84). Therefore, the multiple independent sampling method can be more efficient than a single, long simulation method. Since future scaffold expansions may significantly change the benzimidazole's physiochemical properties (charges, etc.) and possibly binding modes, which may affect the sensitivities of various parameters, the relatively insensitive “multiple independent sampling method” may avoid the need of an entirely new validation study. Moreover, due to large fluctuating entropy values, (QM/)MM-P(G)BSA were limited to inhibitors’ relative affinity prediction, but not the absolute affinity. The developed protocol will support an ongoing benzimidazole lead optimization program.
Keywords: radii sets, enoyl acyl reductase (FabI), implicit solvent models, molecular dynamics, quantum mechanics/molecular mechanics (QM-MM)
Introduction
Tularemia, a deadly zoonotic infection caused by the Gram-negative pathogen Francisella tularensis, is a viable bioweapon due to its ease of cultivation and aerosolization as well as its low infectious dose.1 Although treatments for tularemia are available, including aminoglycoside antibiotics, streptomycin, ciprofloxacin and tetracycline, a widespread outbreak of this disease may still be unmanageable due to their requirement for intravenous use (aminoglycosides, streptomycin) or contraindication for use in pregnant women and children (ciprofloxacin, tetracyclines).2 There is, therefore, a strong interest within the antibacterial research community in the identification and development of novel agents with improved physicochemical properties and activity against F. tularensis.
The bacterial fatty acid synthesis (FAS-II) metabolic pathway, which is responsible for the synthesis of fatty acid components of bacterial lipid membranes and energy stores, is an attractive antibacterial target. Distinct from its mammalian FAS-I counterpart, which consists of a single, large, multifunctional enzyme with low similarity, the bacterial FAS-II pathway is composed of separate enzyme steps with low similarity to FAS-I. The differences between FAS-I and FAS-II allow for the selective targeting of FAS-II enzymes, while minimizing disruption to the mammalian FAS-I pathway, a significant advantage in antibacterial drug design. The enoyl-[acyl-carrier-protein] reductase enzyme, FabI, catalyzes a key, rate-limiting reduction step in bacterial fatty acid synthesis and is considered to be one of the more attractive enzyme targets in the FAS-II pathway.
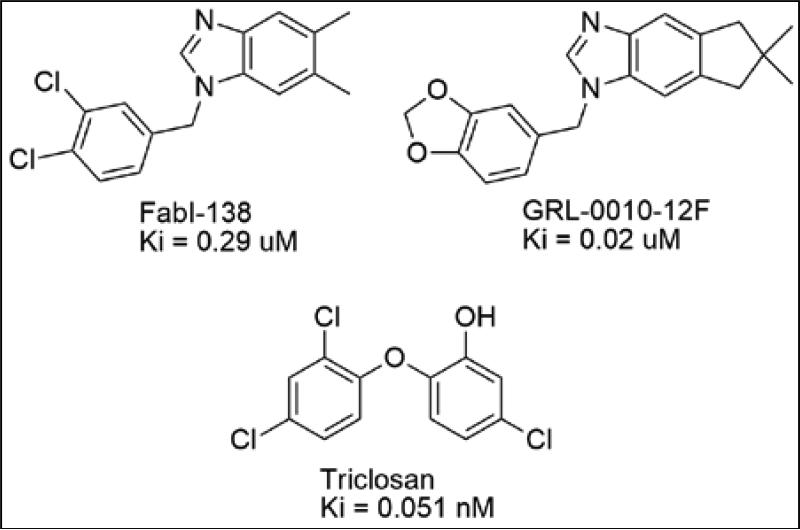
We have previously reported the identification of a series of benzimidazole compounds with FabI inhibitory activity as well as F. tularensis antibacterial activity using a novel shape/electrostatic virtual screening campaign.3 In addition to activity against F. tularensis, the benzimidazoles showed strong antibacterial activity against other Gram-positive and Gram-negative pathogens. Further, structural studies performed in-house revealed that the benzimidazole compounds bound to the FabI active site in a conformation that was unique from other known FabI inhibitors, including triclosan, a marketed antiseptic (Figure 1).4-6 This suggested the possibility that the benzimidazole compounds might have utility against F. tularensis strains bearing resistance to other FabI targeting antibacterials, including triclosan. Additional metabolic and toxicity studies showed that the benzimidazole scaffold possessed moderate metabolic stability and low cell toxicity.7 Taken together, the biological, microbiological, and pharmacokinetic data collected to date justify the further biochemical optimization of the benzimidazole compounds as a lead series for treatment of F. tularensis and possibly other bacterial infection.
Figure 1.
Representative Benzimidazole FabI Inhibitors and Triclosan. 4-6
The goal of the studies presented here was the development of a computational method that could predict the FabI binding affinity of benzimidazole compounds that were being proposed for synthesis and testing. The rationale was that a reliable computational affinity prediction protocol could allow for a more efficient and rapid lead optimization process by identifying compounds, prior to costly synthesis and testing, that were predicted to have high binding affinity to the FabI target. In previous work, we extensively studied various molecular docking and scoring algorithms for use in predicting relative FabI affinity, however these methods generally failed to accurately rank benzimidazole compounds by binding affinity in validation trials.3 This was likely due to insufficient conformational sampling of a flexible loop near the substrate/ligand binding site as well as inaccuracies in the scoring functions utilized. Herein, we report our studies of more advanced computational methods for predicting the binding affinity of the benzimidazole compounds to F. tularensis FabI, including MM-PBSA, MM-GBSA, and QM/MM-GBSA. Previous work has shown that the MM/P(G)BSA methods can accurately predict relative binding free energies of similar compounds using enhanced energy sampling from simulations combined with solvation energy estimations using implicit methods.8 We chose to explore these implicit solvent methods over more advanced explicit solvent methods, such as free energy perturbation and thermodynamic integration, as the higher computational expense of the latter methods would adversely impact the throughput of our planned lead optimization studies.9
Although MM-P(G)BSA methods have been used successfully in both virtual screening10,11 and lead optimization programs12-17, it has been shown that the results are sensitive to atomic charges, simulation length, entropy calculations, and sampling protocols which can lead to dramatic differences in affinity predictions using the same study system.18-21 Studies have also suggested that prediction results of MM-GBSA methods might be influenced by radii settings.22-29 Additionally, a recent study suggested that multiple independent simulations in MM-GBSA offered improved statistically converged results over one long MD simulation.30 Thus, it was also of interest to see if multiple independent samplings offer a better agreement between experimental and calculated binding free energy than a single, long MD simulation for the studied system. Lastly, the recently developed hybrid QM/MM-GBSA method31-34 has yet to be extensively compared with MM-GBSA methods with respect to the factors just mentioned.35
Within this context and our ultimate goal of developing the most suitable method to support our lead optimization program, we have performed a series of comparative trials using the F. tularensis FabI (FtFabI) structure and sixteen benzimidazole compounds with known affinity from experimental studies and several experimentally confirmed binding conformations. These studies were specifically designed to answer the following questions: (1) What is the best combination of radii settings, QM Hamiltonians, implicit solvent methods, and simulation length for the studied system? (2) If entropy calculations are included, will they improve the prediction results? (3) Can multiple independent samplings improve the prediction of binding free energy over the use of one long simulation for the methods studied? And ultimately, (4) Which optimized method offers the best predictive power in terms of the absolute and relative binding affinity for our study system?
Methods
Complex Preparation
The binding conformation of FtFabI-benzimidazole complexes were taken from co-crystal structures solved in-house (PDB codes: 3UIC, 4J3F, 4J4T).4,6 RESP atomic partial charges were assigned to benzimidazole ligands and the cofactor, NADH, with geometry optimization and the electrostatic potential calculations performed using HF/6-31G* and Gaussian 0936 in the R.E.D. server.37-39 The AMBER FF12SB force field and the general AMBER force field (GAFF)40 parameters were assigned to the protein and the ligand using antechamber in AMBER v12.41 A 10Å TIP3P water molecule octahedron box was set to solvate the complex system along with Na+ and Cl− counter-ions to neutralize the system.
Experimental Enzymatic Activity
The FabI enzyme reduces butenyl-CoA to butyryl-CoA utilizing the cofactor NADH. Enzyme activity was monitored by following the rate of decrease in fluorescence of NADH at 450 nm (excitation wavelength 340 nm). Detailed methods for the determination of the IC50 and Ki values of the benzimidazole compounds against FtFabI have been previously described.3,4,6 The compounds used in this study are shown in Supplementary Table 1, along withexperimental inhibition data. The experimental free energies of binding (ΔGbind) were calculated from Ki using Equation 1, where R is the ideal gas constant (1.9872×10−3 kcal K−1 mol−1) and T is the room temperature (300K).
| (1) |
Molecular Dynamics (MD) Simulations
The systems were first minimized using 5000 steps of steepest descent minimization using the Particle Mesh Ewald (PME) potential function. After minimization, the systems were heated from 0K to 300K over 50 picoseconds (ps) using the NVT ensemble with a 10 kcal/mol-Å weak restraint on the enzyme, cofactor and ligands. Following this, the systems were equilibrated over 50 ps at constant pressure (1 bar) and temperature (300K) using NPT equilibration. Next, a 6 nanosecond (ns) NPT production run was performed at 300 K and 1 bar. The following settings were activated in all of the equilibration and production run MD simulations: Langevin dynamics for temperature scaling, 2 ps as the pressure relaxation time, 8 Å electrostatic interactions cut off, the SHAKE bond length constraints of hydrogen atoms, and 1 fs time step. In the production runs, the MD simulation trajectories were saved every 2.5 ps for subsequent (QM/)MM-P(G)BSA analyses. The pmemd.MPI program in AMBER12 was used for all of the above minimizations and simulations.
MM-PBSA
The MM-PBSA calculations were performed using MMPBSA.py in AMBERTools13.42 When the PARSE, bondi, mbondi, and mbondi2 sets were applied, the MM-PBSA surface tension (α) and the non-polar free energy correction term (β) were set to 0.00542 kcal/mol-Å2 and 0.92, respectively, following the recommendation of the original PARSE radii study43 and the AMBER user manuals.41 An exterior dielectric constant of 80 and solute dielectric constant of 1 were used. 2,400 snapshots were taken evenly from the MD simulations trajectory from 0 to 6 ns in the MM-PBSA calculations.
MM-GBSA and QM/MM-GBSA
The (QM)/MM-GBSA calculations were performed using MMPBSA.py in AMBERTools13. We investigated several GB models in this study, including the pairwise model developed by Hawkins et al. (GBHCT),23 the model developed by Onufriev et al. (GBOBC),24 the optimized version of GBOBC (GBOBC2),25 the model developed by Mogan et al. to solve the so-called “bottle-neck” issue (GBNeck ),26 and the optimized version of GBNeck (GBNeck2).27 Additional details are provided in Supplementary Table 2. The bondi, mbondi, and mbondi2 radii sets were prepared using the antechamber program in AMBER12. In AMBERTools13, the default setting of MM-GBSA surface tension (α = 0.0072 kcal / mol Å2) and the non-polar free energy correction term (β = 0) were applied. In the QM/MM-GBSA, the benzimidazole ligand was treated as the QM region using the AM1, PM3 and PM6 semi-empirical Hamiltonian theories. The QM charge of the ligand was set to zero because none of the ligands in this study are expected to carry a formal charge at physiological pH. The remaining QM/MM-GBSA settings are identical to the above MM-GBSA section.
Entropy
The entropy calculations were performed using Normal Mode Analysis (NMA) in the MMPBSA.py program in AMBERTools13.44 The following were the settings for the entropy calculations: The distance-dependent dielectric constant was set to 1.0, and the energy gradient of minimization was 0.001 with 10,000 minimization cycles per snapshot. Due to limited computational resources, we used only 48 frames, which were evenly extracted from 0 to 6 ns of the MD trajectories for entropy calculations.
Multiple Independent MD Simulations
The multiple independent MD simulations were prepared using the same settings and starting structures described above, with the exception that the random starting velocities were applied by turning on the pseudo-random starting velocity generator (the “ig” flag in AMBER12). In order to compare the differences between these and single 6 ns MD simulations, the MD simulations were separated into six, 1 ns components. For the MM-PBSA and (QM/)MM-GBSA, 400 snapshots were taken evenly from each of the six, 1-ns MD simulation trajectories from 0 to 1 ns. Other settings for the MM-PBSA, MM-GBSA, and QM/MM-GBSA calculations for multiple MD simulations were as described above.
Results and Discussion
The Effect of MD Simulation Length on MM-PBSA
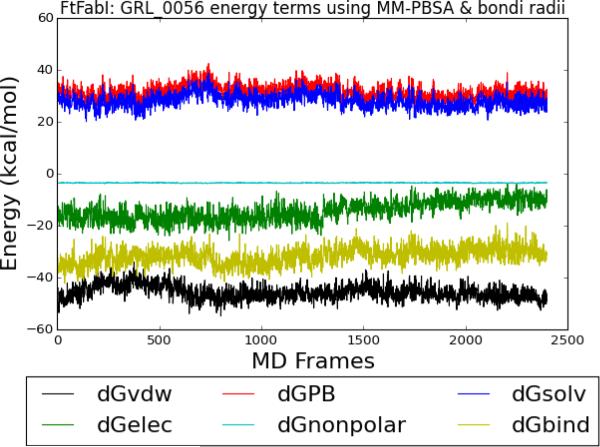
The coefficient of determination between experimental and predicted binding free energies using different MD trajectory lengths and radii settings in MM-PBSA calculations are summarized in Table 1. The MM-PBSA calculations based on the 0.25 to 2.00 ns MD trajectories were satisfactory (r2>0.70) in all bondi, mbondi, mbondi2, and PARSE radii sets. However, using data from MD trajectories equal to or longer than 2 ns for the MM-PBSA calculations seemed to lower the accuracy of prediction in all four radii settings. To further analyze the nature of the decrease in predictive power with longer MD simulation times, we first checked the MM-PBSA energy terms plot of FtFabI- GRL-0056 (Figure 2) and the rest of fifteen ligands (Supplementary Figure 1). The yellow line was the instantaneous enthalpy of binding (ΔGbind) and it can be readily seen that all the ΔGbind in the sixteen ligands using all the radii settings were readily converged. Therefore, it is likely that the decrease in predictive power along the MD simulation time frames is due to an amplification of force field errors along the MD simulation time frames, instead of non-converged energy in the system, as reported in the previous study.21
Table 1.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Different MD Trajectory Lengths and Radii Sets in MM/PBSA Calculations.a
| Radii Sets | R20.25ns | R20.5ns | R20.75ns | R21ns | R22ns | R23ns | R24ns | R25ns | R26ns |
|---|---|---|---|---|---|---|---|---|---|
| bondi | 0.78 | 0.82 | 0.83 | 0.82 | 0.74 | 0.61 | 0.49 | 0.4 | 0.36 |
| mbondi | 0.71 | 0.75 | 0.76 | 0.77 | 0.72 | 0.62 | 0.54 | 0.48 | 0.45 |
| mbondi2 | 0.79 | 0.82 | 0.83 | 0.82 | 0.74 | 0.61 | 0.49 | 0.43 | 0.37 |
| PARSE | 0.62 | 0.67 | 0.72 | 0.75 | 0.77 | 0.68 | 0.61 | 0.53 | 0.48 |
R2n: “R2” stands for coefficient of determination in the MM/PBSA calculation. Here 100, 400, 1200, 2400 MD simulation frames were evenly extracted from one 0.25, 1, 3, 6 ns MD simulation trajectories, respectively.
Figure 2.
FtFabI: GRL-0056 energy components using MM-PBSA and the bondi radii setting. Black, red, blue, green, cyan and yellow lines indicate the ΔGvdw, ΔGGB, ΔGsolvation, ΔGelectrostatic, ΔGnonpolar and ΔGbind terms respectively. The x axis is the frame number. Each frame is 2.5 ps. The total frame number is 2,400 frames, equal to 6 ns MD simulations.
The Effect of Radii Sets on MM-PBSA
The impact of four different radii sets (bondi, mbondi, mbondi2, and PARSE) are also summarized in Table 1. It can be clearly seen that bondi and mbondi2 gave almost identical predictive power since bondi and mbondi2 were optimized via similar theoretical frame works.27 Interestingly, the difference in predictive power between mbondi versus bondi and mbondi2 was also quite small. Considering the potential errors of the experimental binding free energy, these differences show little significance. Among the four radii sets, the PARSE radii offered the poorest correlation with experimental values using MD trajectories shorter than 2 ns (r2= 0.62 - 0.77). A possible explanation is that the GB radii sets (bondi, mbondi, and mbondi2) are more extensively parameterized in various atom types for each chemical element while the PARSE radii set has only one atom type for each chemical element, as discussed in previous studies. 21, 43 Finally, in Supplementary Table 3, one can clearly see that the three Born radii sets always generated smaller solvation energy terms (ΔGsolvation) and correspondingly more negative binding enthalpy values (ΔHbind) than the PARSE radii sets. A similar effect was noted in a previous study.21 A possible reason is that the three Born radii sets contain larger radii and larger corresponding dielectric boundaries than the PARSE radii set and therefore result in higher solvation energy terms when applying the three bondi radii sets. 21,23-26,43,45
The Effect of MD Simulation Length on MM-GBSA
The coefficient of determination of experimental and predicted binding free energies for different MD trajectory lengths and radii sets in MM-GBSA calculations are summarized in Table 2. The predictive power of the MM-GBSA method with longer simulations decreased in a manner similar to the MM-PBSA predictions. For all three radii sets, the MM-GBSA predictions based on MD trajectories less than or equal to 1 ns were in the satisfactory range (R2 > 0.7), while the predictive power dropped significantly when using MD trajectories larger than 1 ns. As above, the decrease in predictive power may be due to the amplification of force field errors. 21
Table 2.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Different MD Trajectory Lengths and Radii Sets in MM/GBSA Calculations.a
| Radii Sets | GB | R20.25nsa | R20.5ns | R20.75ns | R21ns | R22ns | R23ns | R24ns | R25ns | R26ns |
|---|---|---|---|---|---|---|---|---|---|---|
| bondi | GBHCT | 0.85 | 0.88 | 0.85 | 0.81 | 0.65 | 0.53 | 0.45 | 0.41 | 0.41 |
| mbondi | GBHCT | 0.81 | 0.83 | 0.8 | 0.75 | 0.59 | 0.51 | 0.45 | 0.43 | 0.44 |
| mbondi2 | GBHCT | 0.85 | 0.87 | 0.85 | 0.8 | 0.64 | 0.52 | 0.44 | 0.4 | 0.41 |
| bondi | GBOBC | 0.79 | 0.83 | 0.82 | 0.78 | 0.63 | 0.51 | 0.42 | 0.37 | 0.38 |
| mbondi | GBOBC | 0.68 | 0.71 | 0.7 | 0.67 | 0.52 | 0.43 | 0.37 | 0.35 | 0.36 |
| mbondi2 | GBOBC | 0.77 | 0.81 | 0.8 | 0.77 | 0.61 | 0.48 | 0.4 | 0.36 | 0.36 |
| bondi | GBOBC2 | 0.77 | 0.82 | 0.81 | 0.77 | 0.62 | 0.49 | 0.4 | 0.35 | 0.36 |
| mbondi | GBOBC2 | 0.59 | 0.64 | 0.62 | 0.59 | 0.42 | 0.31 | 0.25 | 0.23 | 0.24 |
| mbondi2 | GBOBC2 | 0.73 | 0.78 | 0.77 | 0.74 | 0.57 | 0.44 | 0.35 | 0.31 | 0.32 |
| bondi | GBNeck | 0.57 | 0.58 | 0.57 | 0.56 | 0.4 | 0.26 | 0.18 | 0.15 | 0.16 |
| mbondi2 | GBNeck | 0.52 | 0.53 | 0.53 | 0.52 | 0.36 | 0.23 | 0.16 | 0.13 | 0.15 |
| bondi | GBNeck2 | 0.63 | 0.68 | 0.6 | 0.6 | 0.52 | 0.5 | 0.49 | 0.48 | 0.5 |
| mbondi2 | GBNeck2 | 0.63 | 0.67 | 0.6 | 0.6 | 0.51 | 0.5 | 0.5 | 0.49 | 0.51 |
R2n: “R2” stands for coefficient of determination in the MM/GBSA calculation. Here 100, 400, 1200, 2400 MD simulation frames were evenly extracted from one 0.25, 1, 3, 6 ns MD simulation trajectories, respectively.
Interestingly, although the predictive power of GBNeck2 also decreased with longer MD simulations, the extent of the decrease was less than for the other four GB methods (R2 = 0.6 at 1 ns and R2 = 0.51 at 6 ns). This might suggest that GBNeck2 provided better agreement to the experimental values in terms of solvation energy and therefore offset the degree of predictive power diminishment. This will be discussed in more detail below in the QM/MM-GBSA section.
The Effect of Radii Sets on MM-GBSA
It is known that MM-GBSA is more sensitive to various radii sets than MM-PBSA, and earlier studies have suggested the optimal radii set (s) for each GB method (summarized in Supplementary Table 2).23-26,45 The mbondi radii set was a non-recommended radii setting for GBOBC. However, as shown in Table 2, in our studies the three different radii sets in GBOBC resulted in only minor differences. Thus, for this system, considering the potential errors in experimental free energy of binding, the differences between the predictive powers of the three radii sets for the GBOBC method can be safely ignored. In GBOBC, GBOBC2, GBNeck and GBNeck2, it is not surprising that the suggested radii sets, bondi and mbondi2, yielded nearly identical prediction results because mbondi2 is a modification of and very similar to bondi (Table 2).45 We did not include the mbondi set in the GBNeck and GBNeck2 calculations, since earlier studies did not recommend the mbondi setting in the GBNeck and GBNeck2 methods, and MMPBSA.py in the AMBERTools13 suite did not allow the mbondi radii set in the default GBNeck and GBNeck2 methods. Additionally, in GBOBC2, our data in Table 2 did suggest that the predicted binding free energy calculated by bondi and mbondi2 radii sets correlated better with the experimental binding free energy than the unfavorable mbondi settings.
The three radii sets and their corresponding effects on the solvation energy terms are summarized in Supplementary Figure 2 & Supplementary Table 4. When MM-GBSA calculations were performed under similar conditions (inhibitor, number of MD frames, GB method, and charges) using the different radii sets, the only energy terms showing significant changes are the polar energy term (ΔGGB), the total solvation energy term (ΔGsolvation), and the total free energy of binding, ΔGbind (the red, blue, yellow lines on top of each figure in Supplementary Figure 2 respectively and Equation 2). This is due to the fact that radii settings only affect ΔGGB and ΔGsolvation. From the ΔGGB energy curves in Supplementary Figure 2, bondi and mbondi2 result in nearly identical solvation energy values while mbondi consistently offered more positive ΔGGB values than bondi and mbondi2. These clear differences allow us to visualize the reason why bondi and mbondi2 suggested highly similar prediction results in all five GB methods.
| (2) |
Comparison of Generalized Born Methods
From Table 2, we can clearly see that GBHCT offered the best agreement with the experimental binding free energies (higher coefficient of determination) amongst the five GB methods using MD simulation trajectory data from 0.25 ns to 2 ns (R2 = 0.85 ~ 0.65). However, if we used data from MD simulation trajectories longer than 2 ns, GBHCT showed similar predictive performance compared to GBOBC, GBOBC2, and GBNeck2. Moreover, because GBOBC and GBOBC2 have a similar computational foundations, with only subtle differences in parameter settings, it is not surprising that GBOBC and GBOBC2 resulted in similar predictive power for the FtFabI-benzimidazole system. With respect to the difference between GBNeck and GBNeck2, GBNeck2 outperformed GBNeck as would be expected since GBNeck2 is an optimized version of GBNeck, and includes a higher number of parameters and a broader range of scaling factors.26
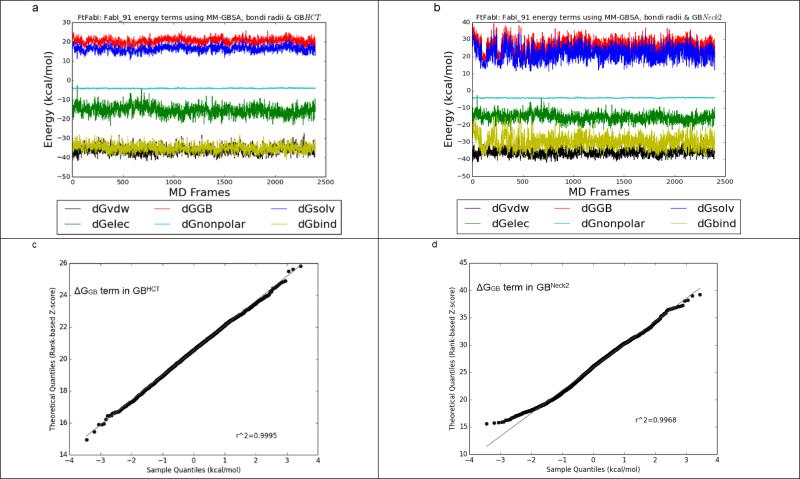
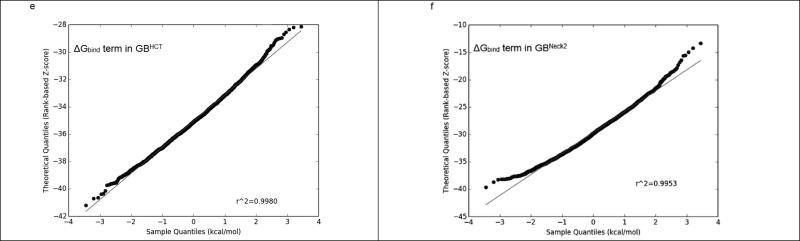
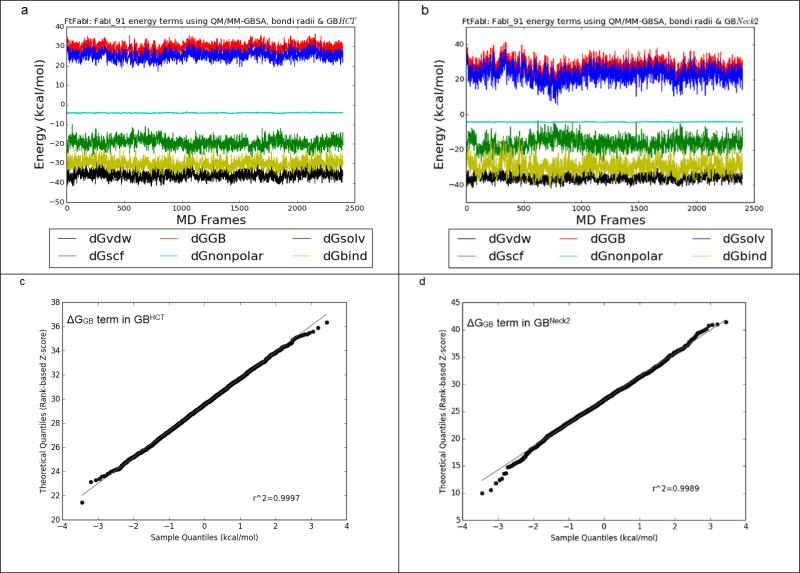
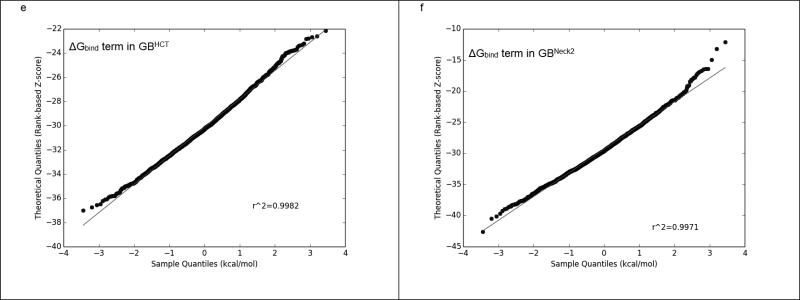
On the other hand, GBNeck2 behaved differently compared to all of the other four GB methods, as summarized in Figure 3 and Supplementary Figure 2. Even though the ΔGGB and ΔGbind terms calculated by GBHCT converged throughout the 6 ns trajectories (2,400 frames) and GBNeck2 converged after 500 ps (200 frames), the ΔGGB (the red line in Figure 3a & 3b) and ΔGbind (the yellow line in Figure 3a & 3b) terms in GBNeck2 had consistently greater fluctuation than with GBHCT and the other GB methods (Supplementary Figure 2). This was seen with all sixteen benzimidazole ligands (data not shown). Figures 3c and 3d show the Q-Q plots for ΔGGB using compound FabI 91, 6,000 ps (2,400 frames) using GBHCT and GBneck2 methods, respectively. Compared to the nearly straight line in Figure 3c (GBHCT ), the two slightly rising tails in Figure 3d (GBNeck2) suggest that the ΔGGB population calculated by GBNeck2 may be skewed, which might bias the average ΔGGB in GBNeck2. A similar effect can be observed in the Q-Q plot for ΔGbind calculated by GBHCT and GBneck2: the straighter line in Figure 3e (GBHCT ) suggests that ΔGbind calculated by GBHCT has a more normal distribution than that calculated using GBNeck2 (Figure 3e). Again, this may indicate that in calculations using GBNeck2, ΔGGB, ΔGsolvation, and ΔGbind might be slightly biased by the extreme values (outliers) and therefore provide less accurate prediction than the remaining four GB methods, at least using MD trajectories less than 3 ns.
Figure 3.
A. FtFabI: FabI 91 energy components using MM-GBSA, bondi radii and GBHCT. Black, red, blue, green, cyan and yellow lines indicate the ΔGvdw, ΔGGB, ΔGsolvation, ΔGelectrostatic, ΔGnonpolar and ΔGbind terms respectively. The x axis is the frame number. Each frame is 2.5 ps. The total frame number is 2,400 frames, equal to 6 ns MD simulations.
B. FtFabI: FabI 91 energy components using MM-GBSA, bondi radii and GBNeck2.
C. The quantile-quantile plot (Q-Q plot) of the ΔGGB term in GBHCT.
D. The Q-Q plot of the ΔGGB term in GBNeck2.
E. The Q-Q plot of the ΔGbind term in GBHCT.
F. The Q-Q plot of the ΔGbind term in GBNeck2.
Additionally, another reason why GBHCT, GBOBC, and GBOBC2 offered better agreement with experimental binding free energies than GBNeck1 and GBNeck2, at least for this FtFabI-benzimidazole system, is that the recently released GBNeck and GBNeck2 methods have thus far only been optimized using peptide-protein systems, not protein-small molecule systems.27 Future optimization of “neck region correction” GB methods covering non-peptide/non-protein systems will likely change this situation. As it stands, GBNeck1 and GBNeck2 are likely better suited than the GBHCT GBOBC, and GBOBC2 methods in predicting protein-protein binding free energies.
The Performance of QM/MM-GBSA
The Effect of Semi-Empirical QM Theory Levels on QM/MM-GBSA
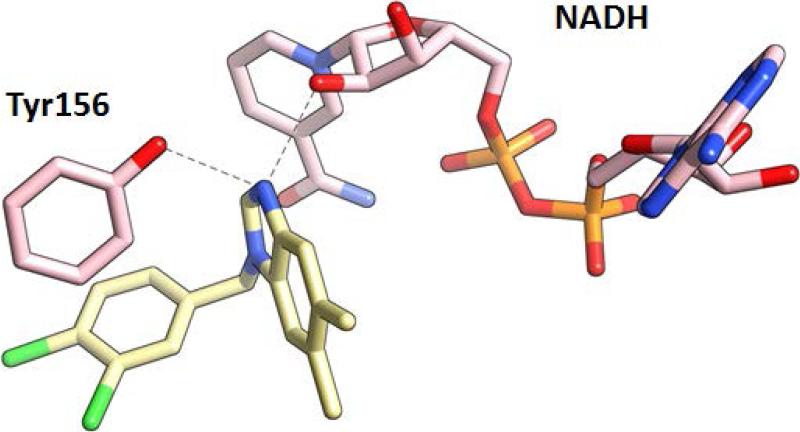
The effects of three commonly used semi-empirical QM theory levels, Parameterized Model number 3 (PM3),46,47 Austin Model 1 (AM1),48 and Parameterized Model number 6 (PM6)49 on QM/MM-GBSA are summarized in Tables 3 - 5. The PM3 Hamiltonian and QM-MM/GBSA together give the best agreement between experimental and predicted binding affinities, regardless of radii settings and GB methods (Table 3). The AM1 Hamiltonian and QM-MM/GBSA together resulted in a slightly worse accuracy than the PM3 Hamiltonian for all conditions (Table 4). Since the PM3 Hamiltonian is known to predict the intermolecular hydrogen bonds more accurately than the AM1 Hamiltonian,50 the PM3 Hamiltonian would be a better choice than the AM1 Hamiltonian for the benzimidazole inhibitors, which forms key intermolecular hydrogen bonds with FtFabI Tyr156 and the ribose on the nicotinamide ring of the cofactor NADH (Figure 4).4,6
Table 3.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Different MD Trajectory Lengths and Radii Sets in QM-MM/GBSA Calculations using the PM3 Hamiltonian.a
| Radii Sets | GB | R20.25nsa | R20.5ns | R20.75ns | R21ns | R22ns | R23ns | R24ns | R25ns | R26ns |
|---|---|---|---|---|---|---|---|---|---|---|
| bondi | GBHCT | 0.78 | 0.81 | 0.78 | 0.73 | 0.64 | 0.58 | 0.53 | 0.52 | 0.54 |
| mbondi | GBHCT | 0.76 | 0.79 | 0.75 | 0.69 | 0.59 | 0.56 | 0.54 | 0.55 | 0.57 |
| mbondi2 | GBHCT | 0.78 | 0.81 | 0.78 | 0.73 | 0.64 | 0.58 | 0.54 | 0.52 | 0.54 |
| bondi | GBOBC | 0.76 | 0.79 | 0.76 | 0.72 | 0.64 | 0.6 | 0.56 | 0.54 | 0.56 |
| mbondi | GBOBC | 0.72 | 0.75 | 0.71 | 0.67 | 0.57 | 0.55 | 0.53 | 0.54 | 0.56 |
| mbondi2 | GBOBC | 0.76 | 0.79 | 0.76 | 0.71 | 0.63 | 0.59 | 0.55 | 0.53 | 0.55 |
| bondi | GBOBC2 | 0.75 | 0.79 | 0.75 | 0.71 | 0.62 | 0.56 | 0.51 | 0.49 | 0.51 |
| mbondi | GBOBC2 | 0.72 | 0.75 | 0.71 | 0.64 | 0.51 | 0.47 | 0.44 | 0.44 | 0.46 |
| mbondi2 | GBOBC2 | 0.75 | 0.78 | 0.75 | 0.69 | 0.59 | 0.54 | 0.49 | 0.47 | 0.49 |
| bondi | GBNeck | 0.73 | 0.73 | 0.69 | 0.64 | 0.52 | 0.46 | 0.4 | 0.39 | 0.42 |
| mbondi2 | GBNeck | 0.72 | 0.72 | 0.68 | 0.63 | 0.51 | 0.44 | 0.38 | 0.37 | 0.4 |
| bondi | GBNeck2 | 0.62 | 0.66 | 0.62 | 0.65 | 0.69 | 0.76 | 0.79 | 0.82 | 0.86 |
| mbondi2 | GBNeck2 | 0.64 | 0.67 | 0.64 | 0.67 | 0.7 | 0.78 | 0.81 | 0.83 | 0.88 |
R2n: “R2” stands for coefficient of determination in the QM-MM/GBSA calculation. Here 100, 400, 1200, 2400 MD simulation frames were evenly extracted from one 0.25, 1, 3, 6 ns MD simulation trajectories, respectively.
Table 5.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Different MD Trajectory Lengths and Radii Sets in QM-MM/GBSA Calculations using the PM6 Hamiltonian.a
| Radii Sets | GB | R20.25nsa | R20.5ns | R20.75ns | R21ns | R22ns | R23ns | R24ns | R25ns | R26ns |
|---|---|---|---|---|---|---|---|---|---|---|
| bondi | GBHCT | 0.54 | 0.61 | 0.57 | 0.52 | 0.41 | 0.28 | 0.18 | 0.14 | 0.14 |
| mbondi | GBHCT | 0.49 | 0.55 | 0.51 | 0.46 | 0.36 | 0.30 | 0.26 | 0.25 | 0.27 |
| mbondi2 | GBHCT | 0.56 | 0.63 | 0.59 | 0.54 | 0.43 | 0.30 | 0.20 | 0.16 | 0.17 |
| bondi | GBOBC | 0.15 | 0.21 | 0.20 | 0.17 | 0.09 | 0.04 | 0.01 | 0.01 | 0.01 |
| mbondi | GBOBC | 0.13 | 0.18 | 0.16 | 0.13 | 0.07 | 0.05 | 0.04 | 0.03 | 0.04 |
| mbondi2 | GBOBC | 0.17 | 0.24 | 0.22 | 0.19 | 0.11 | 0.06 | 0.02 | 0.01 | 0.02 |
| bondi | GBOBC2 | 0.16 | 0.23 | 0.22 | 0.19 | 0.11 | 0.05 | 0.02 | 0.01 | 0.01 |
| mbondi | GBOBC2 | 0.12 | 0.17 | 0.15 | 0.11 | 0.05 | 0.02 | 0.01 | 0.01 | 0.02 |
| mbondi2 | GBOBC2 | 0.17 | 0.24 | 0.23 | 0.19 | 0.11 | 0.05 | 0.02 | 0.01 | 0.02 |
| bondi | GBNeck | 0.24 | 0.26 | 0.23 | 0.20 | 0.13 | 0.07 | 0.03 | 0.02 | 0.03 |
| mbondi2 | GBNeck | 0.26 | 0.29 | 0.26 | 0.23 | 0.15 | 0.09 | 0.05 | 0.04 | 0.05 |
| bondi | GBNeck2 | 0.52 | 0.57 | 0.55 | 0.56 | 0.56 | 0.57 | 0.57 | 0.60 | 0.64 |
| mbondi2 | GBNeck2 | 0.53 | 0.57 | 0.54 | 0.56 | 0.56 | 0.57 | 0.58 | 0.60 | 0.64 |
R2n: “R2” stands for coefficient of determination in the QM-MM/GBSA calculation. Here 100, 400, 1200, 2400 MD simulation frames were evenly extracted from one 0.25, 1, 3, 6 ns MD simulation trajectories, respectively.
Table 4.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Different MD Trajectory Lengths and Radii Sets in QM-MM/GBSA Calculations using the AM1 Hamiltonian.a
| Radii Sets | GB | R20.25nsa | R20.5ns | R20.75ns | R21ns | R22ns | R23ns | R24ns | R25ns | R26ns |
|---|---|---|---|---|---|---|---|---|---|---|
| bondi | GBHCT | 0.78 | 0.83 | 0.79 | 0.74 | 0.64 | 0.55 | 0.47 | 0.44 | 0.45 |
| mbondi | GBHCT | 0.74 | 0.78 | 0.73 | 0.69 | 0.58 | 0.53 | 0.49 | 0.48 | 0.50 |
| mbondi2 | GBHCT | 0.79 | 0.83 | 0.79 | 0.74 | 0.64 | 0.56 | 0.48 | 0.44 | 0.46 |
| bondi | GBOBC | 0.67 | 0.75 | 0.72 | 0.69 | 0.60 | 0.54 | 0.45 | 0.41 | 0.42 |
| mbondi | GBOBC | 0.60 | 0.67 | 0.63 | 0.60 | 0.51 | 0.48 | 0.43 | 0.42 | 0.44 |
| mbondi2 | GBOBC | 0.68 | 0.75 | 0.72 | 0.69 | 0.59 | 0.53 | 0.45 | 0.41 | 0.42 |
| bondi | GBOBC2 | 0.65 | 0.74 | 0.72 | 0.68 | 0.57 | 0.50 | 0.41 | 0.37 | 0.37 |
| mbondi | GBOBC2 | 0.61 | 0.68 | 0.64 | 0.58 | 0.46 | 0.40 | 0.34 | 0.33 | 0.35 |
| mbondi2 | GBOBC2 | 0.66 | 0.74 | 0.71 | 0.66 | 0.55 | 0.47 | 0.39 | 0.35 | 0.36 |
| bondi | GBNeck | 0.62 | 0.63 | 0.58 | 0.53 | 0.40 | 0.31 | 0.24 | 0.22 | 0.24 |
| mbondi2 | GBNeck | 0.62 | 0.63 | 0.58 | 0.53 | 0.40 | 0.31 | 0.24 | 0.22 | 0.24 |
| bondi | GBNeck2 | 0.55 | 0.61 | 0.60 | 0.62 | 0.64 | 0.69 | 0.70 | 0.74 | 0.79 |
| mbondi2 | GBNeck2 | 0.57 | 0.63 | 0.62 | 0.65 | 0.67 | 0.72 | 0.73 | 0.76 | 0.81 |
R2n: “R2” stands for coefficient of determination in the QM-MM/GBSA calculation. Here 100, 400, 1200, 2400 MD simulation frames were evenly extracted from one 0.25, 1, 3, 6 ns MD simulation trajectories, respectively.
Figure 4.
The FabI 138 inhibitor (pdb code: 3UIC) and other benzimidazole inhibitors (pdb codes: 4J1N, 4J3F, 4J4T) form key intermolecular hydrogen bonds with the FtFabI Tyr156 and the ribose on the nicotinamide ring of the cofactor NADH
The PM6 Hamiltonian is the recent advanced semi-empirical QM theory and it is believed to correct multiple defects in the AM1 and PM3 Hamiltonians.49,51 However, use of the PM6 Hamiltonian in QM-MM/GBSA resulted in the worst binding affinity prediction of the three semi-empirical QM theory levels here (Table 5). The PM6 Hamiltonian in QM-MM/GBSA using GBHCT, GBOBC, GBOBC2, and GBNeck radii sets resulted in no observed correlation between the predicted and experimental binding affinities (Table 5). The PM6 Hamiltonian in QM-MM/GBSA using GBNeck2 was the only case where a moderate accuracy was observed. The ΔGbind, ΔGGB, and the QM/MM-GBSA electrostatic term (Self Consistent Energy, ΔGscf) using the PM3 Hamiltonian are all converged (Supplementary Figure 3), similar to the AM1 and PM6 Hamiltonians (data not shown). A possible reason that the PM6 Hamiltonian performed poorly here is because in AMBER, the parameters of the PM6 Hamiltonian describing electrostatic interactions between QM and MM regions haven't been optimized and are borrowed from the PM3 Hamiltonian.41 However, since the PM6 Hamiltonian is more advanced and covers broader cases than the PM3 Hamiltonian, the PM3 parameters might not be exclusive enough for the PM6 Hamiltonian. The missing parameters of the PM6 Hamiltonian are estimated, as detailed in the AMBER manual.41 Therefore, the PM6 Hamiltonian requires more extensive tests, as pointed out in a previous study34 and the AMBER user manual.41 The future optimized PM6 parameters for electrostatic interactions between QM and MM regions are likely to significantly improve the PM6 Hamiltonian accuracy in the QM-MM/GBSA method within AMBER. Thus, since the PM3 Hamiltonian outperformed the AM1 and PM6 Hamiltonians in all conditions (MD simulation length, radii sets, etc.), only the PM3 Hamiltonian is considered in the following sections.
The Effect of MD Simulation Length on QM/MM-GBSA
The coefficient of determination between experimental and predicted binding free energies for different lengths of MD trajectories, various radii sets and semi-empirical QM methods in QM/MM-GBSA calculations, are summarized in Tables 3 - 5. It can be clearly seen that QM/MM-GBSA produced decreasing agreement with experimental binding free energies when longer MD trajectories were used with GBHCT, GBOBC1, GBOBC2, and GBNeck1 in all the tested semi-empirical methods. However, the extent of decreasing predictive power with simulation time was significantly less in QM/MM-GBSA than that observed in MM-GBSA when using GBHCT, GBOBC, GBOBC2, and GBNeck with PM3 and AM1 semi-empirical methods (Tables 2 - 4). This suggests that the extra QM and QM/MM terms in QM/MM-GBSA (Equation 3 & 4) may offset the amplification of “force field errors” and improve the predictive agreement with experimental binding free energies. With respect to GBNeck2 in QM/MM-GBSA using all the tested semi-empirical methods, surprisingly, the predictive power actually increased as the MD simulation lengths grew. The reason for this reversed trend compared to the other four GB methods can be traced back to the GBNeck2 results in MM-GBSA (Table 2). Although the predictive power of GBNeck2 was seen to decrease with longer MD simulations, the extent of decrease was smaller than the other four GB methods. Moreover, the differences in behavior of GBNeck2 between MM-GBSA and QM/MM-GBSA can be further visualized in Figures 3 & 5. The Q-Q plot for ΔGGB using GBneck2 suggests that ΔGGB in MM-GBSA (Figure 3d) has more outliers than ΔGGB in QM/MM-GBSA using the PM3 Hamiltonian (Figure 5d), which may bias the population mean and deteriorate the predictive results of the former. Similar results can be observed in the Q-Q plots of ΔGbind using GBneck2 (Figure 3f & 5f). It seems that the GBNeck2 and extra QM energy terms in QM/MM-GBSA together provide a better description to ΔGGB and ΔGbind compared with the MM-GBSA results, and therefore offset the force field errors which could diminish the predictive power along the MD trajectory length.
| (3) |
| (4) |
Figure 5.
A. FtFabI: FabI 91 energy components using QM/MM-GBSA, bondi radii and GBHCT. Black, red, blue, green, cyan and yellow lines indicate the ΔGvdw, ΔGGB, ΔGsolvation, ΔGSCF (Self Consistent Energy), ΔGnonpolar and ΔGbind terms respectively. The x axis is the frame number. Each frame is 2.5 ps. The total frame number is 2,400 frames, equal to 6 ns MD simulations.
B. FtFabI: FabI 91 energy components using QM/MM-GBSA, bondi radii and GBNeck2. One can see from the ΔGGB term (the red line) and the ΔGbind term (the yellow line) in GBNeck2 fluctuates wilder than the one in GBHCT (Figure 5a).
C. The quantile-quantile plot (Q-Q plot) of the ΔGGB term in GBHCT.
D. The Q-Q plot of the ΔGGB term in GBNeck2.
E. The Q-Q plot of the ΔGbind term in GBHCT.
F. The Q-Q plot of the ΔGbind term in GBNeck2.
The Effect of Radii Sets on QM/MM-GBSA
It has been previously noted by both AMBER and CHARMM developers that optimized radii specifically for QM Hamiltonians will advance the predictive power of QM/MM-GBSA methods.35,52 With an understanding of their potential limitations, we investigated the optimized MM-GBSA radii sets (bondi, mbondi, and mbondi2) with QM/MM-GBSA methods in these studies. Interestingly, all three radii sets were able to provide satisfactory agreements with experimental data (R2>0.70) using the five GB methods, various MD trajectory lengths, and the PM3 Hamiltonian, as discussed above and summarized in Table 3. Further, it can be clearly seen that the different radii settings yielded very similar results in both MM-GBSA (Table 2) and QM/MM-GBSA using the PM3 Hamiltonian (Table 3). The reason behind these similarities is that MM-GBSA and QM/MM-GBSA are analogous. Also, even though QM/MM-GBSA includes extra QM and QM/MM energy terms, some of these energy terms such as ΔGpolar<QM> and ΔGpolar<QM/MM> (Equation 3) require radii sets as part of their ΔGpolar mathematical functions. Therefore, QM/MM-GBSA showed a predictive sensitivity similar to MM-GBSA in several specific situations. First, the mbondi radii set yielded similar coefficient of determination to bondi and mbondi2 when using GBHCT. Second, the predictive power of bondi was always similar to mbondi2 in GBOBC, GBOBC2, GBNeck, and GB Neck2 since bondi and mbondi2 are alike in nature (discussed above). The only difference between MM-GBSA and QM/MM-GBSA in terms of radii sets can be seen in Table 3. In both GBOBC1 and GBOBC2 methods, the mbondi radii set showed similar predictive power to bondi and mbondi2 radii sets with QM/MM-GBSA, whereas mbondi results were always inferior to bondi and mbondi2 with MM-GBSA. The reason for these different behaviors of GBOBC and GBOBC2 in MM-GBSA and QM/MM-GBSA can be clearly visualized in Supplementary Figure 2 & Supplementary Table 4 (MM-GBSA) and Supplementary Figure 3 & Supplementary Table 5 (QM/MM-GBSA). While there is only one ΔGpolar term (MM ΔGpolar term) in MM-GBSA, QM/MM-GBSA includes extra QM and QM/MM ΔGpolar terms (Equation 3). Therefore, QM and QM/MM ΔGpolar terms together seemed to minimize the differences of the ΔGpolar term in the three tested radii sets, and the corresponding ΔGsolvation. On the other hand, while the MM-GBSA electrostatic term in AMBER is radii independent, the QM/MM-GBSA electrostatic term (Self Consistent Energy, ΔGscf in Figure 5a,b) is radii sensitive, as noted by Walker and Case.35 Therefore, the QM/MM-GBSA electrostatic terms varied slightly among the three tested radii sets (Figure 5 & Supplementary Table 5), while the MM-GBSA electrostatic terms were identical in the three tested radii sets. This also suggests that if one optimized radii sets for QM Hamiltonians, the QM/MM-GBSA should offer better descriptions, not only of ΔGsolvation, but also of ΔGelectrostatic.
Comparison of Generalized Born Methods on QM/MM-GBSA
With QM/MM-GBSA using the PM3 Hamiltonian (Table 3), it can be seen that the GBOBC method offered similar predictive power to GBOBC2. This is likely because both GB methods share similar underlying principles with respect to their scaling functions to treat the radii sets.24,25 Likewise, while GBHCT offered coefficient of determination similar to those of GBOBC and GBOBC2 in all the MD simulation time frames, GBHCT behaved differently to GBOBC and GBOBC2 in MM-GBSA. This was quite surprising at first glance since the method to treat radii sets in GBHCT is different from that of GBOBC and GBOBC2. One possible explanation for this behavior is that the extra QM and QM/MM ΔGpolar terms in QM/MM-GBSA are able to offset and minimize the differences between GBHCT, GBOBC and GBOBC2 in QM/MM-GBSA.35 On the other hand, in QM/MM-GBSA using the PM3 Hamiltonian (Table 3), the predictive power differences between the “neck correction” GB methods (GBNeck1 and GBNeck2) and “non-neck correction” methods (GBHCT, GBOBC1 and GBOBC2) were significant. It is likely that the underlying theories behind the “neck correction” GB methods and “non-neck correction” methods are dissimilar to the extent that the extra QM and QM/MM ΔGpolar terms in QM/MM-GBSA were unable to offset the differences between “neck correction” GB methods and “non-neck correction” methods. Finally, in both MM-GBSA and QM/MM-GBSA using the PM3 Hamiltonian, GBNeck2 still outperformed GBNeck, as GBNeck2 is the optimized version of the “neck correction” GB method.27
The Effect of Conformational Entropy
The effect of conformational entropy (48 frames) on MM-PBSA (2,400 frames) is summarized in Table 6 and on MM-GBSA and QM/MM-GBSA (2,400 frames) in Table 7. The numerical values for conformational entropy and the corresponding absolute binding free energy of MM-PBSA, MM-GBSA and QM/MM-GBSA are summarized in Supplementary Table 3, 4, & 5, respectively. It can be seen that after including entropy, the predictive power (coefficient of determination) of MM/PBS and MM-GBSA decreased significantly, regardless of radii sets or GB methods (Table 6 & 7). Interestingly, while the inclusion of entropy considerably reduced the predictive power of QM/MM-GBSA with GBNeck and GBNeck2, the negative effect of entropy inclusion on the predictive power of QM/MM-GBSA with GBHCT, GBOBC and GBOBC2 was less substantial (Table 7). It appears that the conformational entropy compromised the predictive power in the FtFabI-benzimidazole system due to large fluctuations.
Table 6.
Summary of the Impact of Entropy on Predicted Binding Free Energies of MD Trajectories of Different Lengths and Radii Sets in MM/PBSA Calculations.
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Radii Sets | R26nsa,b | R26nsc | R26nsd | R26nse |
| bondi | 0.36 | 0.06 | 0.21 | 0 |
| mbondi | 0.45 | 0.12 | 0.29 | 0 |
| mbondi2 | 0.37 | 0.06 | 0.22 | 0 |
| PARSE | 0.48 | 0.15 | 0.27 | 0.01 |
R2n: “R2” stands for coefficient of determination in the MM/PBSA calculation. Here 2,400 MD simulation frames were evenly extracted from 6 ns MD simulation trajectories.
2,400 frames calculated enthalpy & no calculated entropy
2,400 frames calculated enthalpy & 48 frames calculated entropy
48 frames calculated enthalpy & no calculated entropy
48 frames calculated enthalpy & 48 frames calculated entropy
Table 7.
Summary of Impact of Entropy on Predicted Binding Free Energies of MD Trajectories of Different Lengths and Radii Sets in MM/GBSA and QM-MM/GBSA Calculations
| MM/GBSA | QM-MM/GBSA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Radii Sets | GB | R26nsa,b | R26nsc | R26nsd | R26nse | Radii Sets | GB | R26nsa,b | R26nsc | R26nsd | R26nse |
| bondi | GBHCT | 0.41 | 0.24 | 0.37 | 0.14 | bondi | GBHCT | 0.54 | 0.52 | 0.54 | 0.48 |
| mbondi | GBHCT | 0.44 | 0.3 | 0.42 | 0.22 | mbondi | GBHCT | 0.57 | 0.59 | 0.59 | 0.58 |
| mbondi2 | GBHCT | 0.41 | 0.24 | 0.37 | 0.14 | mbondi2 | GBHCT | 0.54 | 0.54 | 0.54 | 0.50 |
| bondi | GBOBC | 0.38 | 0.12 | 0.31 | 0.04 | bondi | GBOBC | 0.56 | 0.51 | 0.56 | 0.41 |
| mbondi | GBOBC | 0.36 | 0.12 | 0.30 | 0.04 | mbondi | GBOBC | 0.56 | 0.54 | 0.57 | 0.49 |
| mbondi2 | GBOBC | 0.36 | 0.12 | 0.29 | 0.03 | mbondi2 | GBOBC | 0.55 | 0.52 | 0.55 | 0.43 |
| bondi | GBOBC2 | 0.36 | 0.13 | 0.27 | 0.04 | bondi | GBOBC2 | 0.51 | 0.45 | 0.49 | 0.36 |
| mbondi | GBOBC2 | 0.24 | 0.05 | 0.16 | 0.00 | mbondi | GBOBC2 | 0.46 | 0.42 | 0.43 | 0.35 |
| mbondi2 | GBOBC2 | 0.32 | 0.1 | 0.23 | 0.02 | mbondi2 | GBOBC2 | 0.49 | 0.45 | 0.46 | 0.35 |
| bondi | GBNeck | 0.16 | 0.00 | 0.07 | 0.02 | bondi | GBNeck | 0.42 | 0.28 | 0.35 | 0.14 |
| mbondi2 | GBNeck | 0.15 | 0.00 | 0.06 | 0.02 | mbondi2 | GBNeck | 0.4 | 0.28 | 0.34 | 0.15 |
| bondi | GBNeck2 | 0.5 | 0.07 | 0.42 | 0.06 | bondi | GBNeck2 | 0.86 | 0.47 | 0.75 | 0.42 |
| mbondi2 | GBNeck2 | 0.51 | 0.07 | 0.43 | 0.07 | mbondi2 | GBNeck2 | 0.88 | 0.52 | 0.76 | 0.46 |
R2n: “R2” stands for coefficient of determination in the MM/PBSA calculation. Here 2,400 MD simulation frames were evenly extracted from 6 ns MD simulation trajectories.
2,400 frames calculated enthalpy & no calculated entropy
2,400 frames calculated enthalpy & 48 frames calculated entropy
48 frames calculated enthalpy & no calculated entropy
48 frames calculated enthalpy & 48 frames calculated entropy
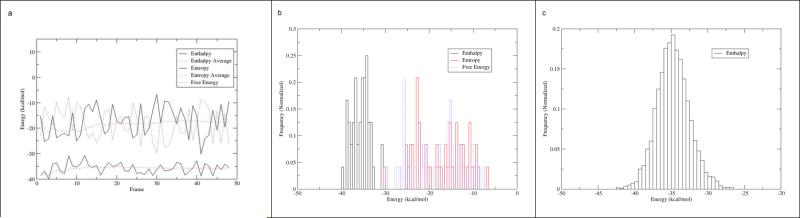
Further analysis of the effect of conformational entropy on absolute binding free energy is summarized in Figure 6. Figure 6a shows that, although the cumulative average of conformational entropy (upper dashed red line) converged in the 48 frames entropy calculation, the instantaneous conformational entropy (upper solid black line) fluctuated greatly (± 10 kcal/mol) compared to the cumulative average. Such huge fluctuations suggest that a higher number of frames in entropy calculation are needed to improve the quality of entropy predictions and therefore yield more accurate absolute binding free energy, as suggested in a previous study.21 Unfortunately, the high computational cost of entropy calculations prevented our further pursuit. For example, each FtFabI-benzimizadole entropy calculation in 48 frames took 120-140 hours on TACC Lonestar's 48 large memory nodes, which is equivalent to 23,000-26,000 XSEDE Service Units per FtFabI- benzimizadole set.
Figure 6.
A. The enthalpy, entropy and binding free energy components (48 frames) in the 6 ns MD simulation of FtFabI: FabI-135 using MM/GBSA, the bondi radii setting and GBHCT. The upper solid black and dash red line represents instanenous and cumulative average entropy respectively and the lower solid black and dash red line represents instanenous and cumulative average enthalpy. The blue line represents binding free energy.
B. The histogram view of the enthalpy, entropy and binding free energy (48 frames) in the 6 ns MD simulation of FtFabI: FabI-135 using MM/GBSA, the bondi radii setting and GBHCT.
C. The histogram view of the enthalpy (2,400 frames) in the 6 ns MD simulation of FtFabI: FabI-135 using MM/GBSA, the bondi radii setting and GBHCT.
Because accurate absolute binding free energy calculations rely on simultaneous error cancellation between the entropy and enthalpy terms, enthalpy calculated from 2,400 frames together with entropy calculated from 48 frames may not offer good quality absolute binding free energy predictions (Table 6, column 3 & Table 7, column 4 & 10). To investigate this, we calculated the absolute binding free energy using 48 frames MM-PBSA and (QM/)MM-GBSA enthalpy and 48 frames entropy. The corresponding calculated absolute binding free energy was then correlated with the experimental binding free energy, as summarized in Table 6, column 5 & Table 7, column 6 & 12. The results showed that the enthalpy from 48 frames (Table 6, column 4 & Table 7, column 5 & 11) did not correlate well with the experimental data. This is most likely because the sample size of 48 frames was insufficient. The 48-frame enthalpy from MM-GBSA, the bondi radii setting and GBHCT shown in the black histogram in Figure 6b, deviates significantly from the normal distribution seen for the 2,400-frame enthalpy histogram in Figure 6c. This suggests that the small sample size of 48 frames might offer a biased population mean. When the 48-frame enthalpy value was used with the 48-frame entropy value to calculate absolute binding free energy, the resulting value gave even worse agreement with the experimental binding free energy values (Table 6, column 5 & Table 7, column 6 & 12). This suggests that errors in entropy calculation using normal mode analysis here cannot be adequately cancelled using the enthalpy values from MM-PBSA and (QM/)MM-GBSA, even using the same MD frame samples for both calculations. Again, Figure 6a visualized the scenario here: Even though the instantaneous enthalpy from MM-GBSA (lower solid black line) was relatively stable, the “wild” instantaneous entropy (upper solid black line) still resulted in largely swinging and biased absolute free energy (blue dash line in Figure 6a) The histogram in Figure 6b visualized the distribution of 48 frames enthalpy from MM-GBSA (black), 48 frames entropy from normal mode analysis (red), and absolute free energy calculated from enthalpy minus entropy (blue). One can clearly see that entropy values in 48 frames distributed in a highly skewed shape with long double tails, which suggests the existence of extreme values. The extreme entropy values in some frames thus resulted in a skewed distribution with long double tails in absolute free binding energy (blue in Figure 6b). Thus, we will not include entropy calculation in future large scale benzimidazole prediction due to its high computational costs and relative inaccuracy.
Single MD Simulation Efficiency and Accuracy
MM-PBSA is about 60 times more computationally expensive (about 1 real world hour per 100 frames on TACC Lonestar using 48 CPU processors) than MM-GBSA and QM/MM-GBSA (about 1 real world minute per 100 frames on TACC Lonestar using 48 CPU processors). Therefore, MM-PBSA, together with bondi or mbondi2 settings using one 0.75-1 ns MD simulation trajectory (300-400 frames) can offer satisfactory predictive power (R2= 0.82-0.83) with 3-4 hours of computation. Alternatively, MM-GBSA using bondi/mbondi2 settings with a 0.5-0.75 ns MD simulation trajectory (200-300 frames) is able to achieve R2=0.85-0.88 with only 3-4 minutes of computation. Similarly, QM/MM-GBSA using GBHCT and bondi/mbondi2 settings with 0.5 ns MD simulation trajectory (200 frames) can achieve R2=0.81 with only 2 minutes of computation. This suggests that using one long MD simulation for large scale FtFabI-benzimidazole predictions, MM-GBSA and QM/MM-GBSA will be more economical choices than MM-PBSA.
Multiple MD Simulation Efficiency and Accuracy
The MM-PBSA and (QM/)MM-GBSA results based on multiple independent trajectories together with various radii settings are summarized in Table 8-10 accordingly. Table 8-10 show that the differences between the length of MD simulations and different radii settings were not significant in all MM-PBSA and (QM/)MM-GBSA runs. Using multiple independent samplings, the differences between various GB methods in (QM-)MM-GBSA were also trivial. However, compared to one long MD simulation trajectory (Tables 1-5), the predictive power using several short MD trajectories didn't decrease as it did when using longer MD simulation time frames (Tables 8-10), suggesting that multiple independent samplings can offset force field errors.
Table 8.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Different Multiple MD Trajectory Lengths and Radii Sets in MM/PBSA Calculations.
| Radii Sets | R20.25n | R20.5ns | R20.75 | R21ns |
|---|---|---|---|---|
| bondi | 0.77 | 0.73 | 0.73 | 0.75 |
| mbondi | 0.76 | 0.74 | 0.74 | 0.76 |
| mbondi2 | 0.77 | 0.73 | 0.73 | 0.76 |
| PARSE | 0.6 | 0.59 | 0.61 | 0.65 |
a R2n: “R2” stands for coefficient of determination in the MM/PBSA calculation. Here 600, 1200, 1800, 2400 MD simulation frames were evenly extracted from six 0.25, 0.5, 0.75, 1 ns MD simulation trajectories, respectively.
Table 10.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Multiple MD of Different Trajectory Lengths and Radii Sets in QM-MM/GBSA Calculations.a
| Radii | GB | R20.25nsa | R20.5ns | R20.75ns | R21ns |
|---|---|---|---|---|---|
| bondi | GBHCT | 0.76 | 0.75 | 0.75 | 0.75 |
| mbondi | GBHCT | 0.76 | 0.75 | 0.76 | 0.75 |
| mbondi2 | GBHCT | 0.76 | 0.75 | 0.75 | 0.75 |
| bondi | GBOBC | 0.73 | 0.72 | 0.72 | 0.72 |
| mbondi | GBOBC | 0.73 | 0.73 | 0.73 | 0.72 |
| mbondi2 | GBOBC | 0.73 | 0.72 | 0.72 | 0.72 |
| bondi | GBOBC2 | 0.73 | 0.72 | 0.72 | 0.72 |
| mbondi | GBOBC2 | 0.73 | 0.73 | 0.73 | 0.72 |
| mbondi2 | GBOBC2 | 0.73 | 0.72 | 0.72 | 0.71 |
| bondi | GBNeck | 0.68 | 0.67 | 0.67 | 0.67 |
| mbondi2 | GBNeck | 0.68 | 0.67 | 0.67 | 0.66 |
| bondi | GBNeck2 | 0.71 | 0.69 | 0.7 | 0.69 |
| mbondi2 | GBNeck2 | 0.71 | 0.7 | 0.71 | 0.7 |
R2n: “R2” stands for coefficient of determination in the QM-MM/GBSA calculation. Here 600, 1200, 1800, 2400 MD simulation frames were evenly extracted from six 0.25, 0.5, 0.75, 1 ns MD simulation trajectories, respectively.
Unlike using one long MD simulation, the predictive performance from multiple independent samplings was insensitive to various radii settings in all MM-PBSA and (QM/)MM-GBSA methods (Table 8-10). In MM-PBSA (Table 8), the three Born radii sets offered satisfactory predictive power (R2 > 0.7) while the PARSE radii setting was slightly worse (R2 in the 0.6 range). Using multiple independent samplings, the differences between (QM/)MM-GBSA were minimal. In (QM/)MM-GBSA together with multiple independent samplings (Table 9 & 10), the three “non-neck” correction GB methods (GBHCT, GBOBC, GBOBC2) behaved similarly but showed slight differences compared to the two neck correction GB methods (GBNeck and GBNeck2), which were similar to each other.
Table 9.
The coefficient of determination of Experimental and Predicted Binding Free Energies of Different Multiple MD Trajectory Lengths and Radii Sets in MM/GBSA Calculations.a
| Radii Sets | GB | R20.25nsa | R20.5ns | R20.75ns | R21ns |
|---|---|---|---|---|---|
| bondi | GBHCT | 0.84 | 0.83 | 0.82 | 0.82 |
| mbondi | GBHCT | 0.84 | 0.84 | 0.83 | 0.82 |
| mbondi2 | GBHCT | 0.84 | 0.83 | 0.82 | 0.82 |
| bondi | GBOBC | 0.81 | 0.8 | 0.8 | 0.8 |
| mbondi | GBOBC | 0.81 | 0.8 | 0.8 | 0.8 |
| mbondi2 | GBOBC | 0.81 | 0.8 | 0.8 | 0.8 |
| bondi | GBOBC2 | 0.81 | 0.79 | 0.79 | 0.79 |
| mbondi | GBOBC2 | 0.78 | 0.77 | 0.76 | 0.76 |
| mbondi2 | GBOBC2 | 0.8 | 0.78 | 0.79 | 0.78 |
| bondi | GBNeck | 0.73 | 0.7 | 0.71 | 0.71 |
| mbondi2 | GBNeck | 0.72 | 0.69 | 0.7 | 0.7 |
| bondi | GBNeck2 | 0.72 | 0.68 | 0.68 | 0.66 |
| mbondi2 | GBNeck2 | 0.72 | 0.69 | 0.68 | 0.66 |
R2n: “R2” stands for coefficient of determination in the MM/GBSA calculation. Here 600, 1200, 1800, 2400 MD simulation frames were evenly extracted from six 0.25, 0.5, 0.75, 1 ns MD simulation trajectories, respectively.
In terms of predictive power between the single, long MD simulation (Table 1-5) and multiple independent MD simulation (Table 8-10) methods, both provided similar predictive power using lower numbers of frames (600 and 1,200 frames). However, when larger numbers of frames were used, the predictive power decrease was negligible with the multiple independent simulation method but not with the single simulation. Taken together, these results suggest that methodology differences and errors may be minimized and averaged out using multiple independent samplings. With respect to computational efficiency, MM-PBSA is about 60-fold more computationally expensive than (QM/)MM-GBSA. Therefore, MM-GBSA together with GBHCT using six 0.25 ns multiple independent MD simulations (600 frames) can offer very good agreement, r2= 0.84 (Figure 7b), with experimental data after just 6 real world minutes of computation. Therefore, MM-GBSA and QM/MM-GBSA offer a better balance in terms of predictive power and computational efficiency than MM-PBSA with multiple independent samplings.
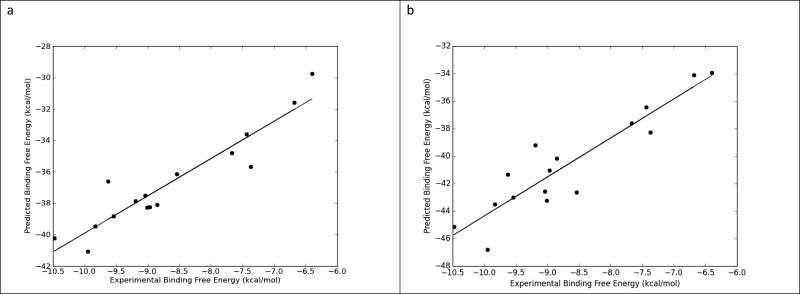
Figure 7.
A. The correlation plot between experimental and predicited binding free energy using QM-MM/GBSA, GBNeck2, mbondi2 & 2,400 frames evenly extracted from 6 ns long MD simulation trajectories (R2 = 0.88).
B. The correlation plot between experimental and predicited binding free energy using MM/GBSA, GBHCT, mbondi & 600 frames evenly extracted from six 0.25 ns long MD simulation trajectories (R2 = 0.84).
Conclusions
In this study, we have extensively compared three implicit solvent methods: MM-PBSA, MM-GBSA, and QM/MM-GBSA and the effects of radii sets, entropy, GB methods, QM Hamiltonians, sampling and simulation lengths using sixteen carefully chosen benzimidazole inhibitors of F. tularensis FabI. In the first part of the this study using one long MD simulation for each ligand (the traditional method), the various GB methods, QM Hamiltonians, and simulation lengths resulted in significantly different predictive power in MM-PBSA and (QM/)MM-GBSA results, while the effect of radii sets on prediction power is relatively milder. The QM/MM-GBSA method using GBNeck2, mbondi2, and the PM3 Hamiltonian setting with 2,400 frames extracted evenly from single 6 ns MD simulations offered the best agreement between predicted and experimental binding free energy (R2 = 0.88, Figure 7a).
The inclusion of conformational entropy compromised the agreement between predicted absolute binding free energy and experimental binding free energy due to large fluctuations in the calculated entropy values. Theoretically, using a larger number of frames in the entropy calculations might increase its accuracy, but the associated high computational costs might not be easily affordable. Therefore, the implicit solvent free energy methods in this study (MM-PBSA and (QM/)MM-GBSA) were limited to comparing relative binding free energies of similar ligands due to the absence of accurate entropies. However, for the purposes of developing a rapid tool for energy predictions for a lead optimization program focusing on highly similar compounds, conformational entropy may be safely ignored as the implicit solvent methods used in this study can still be powerful tools in compound prioritization.
In the second part of the study, the prediction is based on the average of six 1 ns MD simulations for each FtFabI-benzimidazole system. We called this type of sampling, “multiple independent sampling” or “Monte Carlo like MD sampling”. In general, implicit solvent methods based on multiple independent samplings are less sensitive on radii sets, MD simulation length, and GB methods. This feature might minimize the future need of an entirely new validation study, when (1) a new scaffold of the same therapeutic target is pursued and (2) the same scaffold with additional moieties, which result in distinct physiochemical properties (charges, etc.) and binding modes from the previous validation sets, bring in different sensitivities on various parameters.
Because the predictive power of the multiple sampling method showed little decrease with MD simulation time, it can offer the same or better predictive power compared with the use of a single, long simulation with lower number of MD frames. For example, MM/GBSA together with GBHCT and either bondi, mbondi or mbondi2, using 600 frames extracted evenly from six 0.25 ns MD simulations, can achieve a comparable agreement between predicted and experimental binding free energy (r2 = 0.84, Figure 7b) to QM/MM-GBSA using GBNeck2, mbondi2, and the PM3 Hamiltonian setting with 2,400 frames extracted evenly from 6 ns MD simulation (r2 = 0.88, Figure 7a). Therefore, the multiple independent sampling method can be more computationally efficient than a single, long simulation method.
Different implicit solvents methods bring varied accuracy. In this study, MM-GBSA and QM/MM-GBSA brings better accuracy and higher efficiency than MM-PBSA, in either the multiple independent sampling method, or the tradition single, long simulation method (Table 11a).
Table 11.
Summary of the Effect of Parameters on Predictive Power
| Traditional method | Multiple Independent Sampling | ||
|---|---|---|---|
| a. Accuracy of Implicit Solvent Methods | QM/MM-GBSA > MM-GBSA > MM-PBSA | QM/MM-GBSA ≈ MM-GBSA > MM-PBSA | |
| MM-GBSA & QM/MM-GBSA | |||
| Traditional method | Multiple Independent Sampling | ||
| b. Accuracy of GB Methods | GBNeck2 > GBHTC >= GBOBC = GBOBC2 > GBNeck | Differences are minimized | |
| MM-PBSA | |||
| Traditional method | Multiple Independent Sampling | ||
| c. Accuracy of Radii Settings | bondi = mbondi2 ≈ mbondi > PARSE | Differences are minimized | |
| MM-GBSA & QM/MM-GBSA | |||
| GB Method Names | AMBER igb flag | Traditional method | Multiple Independent Sampling |
| GBHCT | 1 | bondi = mbondi2 ≈ mbondia | Differences are minimized |
| GBOBC | 2 | bondia = mbondi2a ≈ mbondi | Differences are minimized |
| GBOBC2 | 5 | bondia = mbondi2a >≈b mbondi | Differences are minimized |
| GBNeck | 7 | mbondi2a,c ≈ bondi | Differences are minimized |
| GBNeck2 | 8 | mbondi2a,d ≈ bondi | Differences are minimized |
| QM/MM-GBSA | |||
| d. Accuracy of PM Hamiltonians | PM3 > AM1 > PM6 | ||
AMBER user manual recommended radii sets for the GB methods.
In MM-GBSA and GBOBC2: bondia = mbondi2a > mbondi. In QM/MM-GBSA and GBOBC2: bondia = mbondi2a ≈ mbondi
bondi might also work, but it might cause instability in the native peptide REMD type of simulation.
mbondi3 is recommended in the MD/REMD type of simulation.
The effect of GB methods on accuracy (Table 11b) is more evident in the traditional one long simulation method. Unlike four other GB methods, GBNeck2 can offer the best accuracy in the 6 ns time frame, without a decrease in accuracy along the MD simulation length in both MM-GBSA and QM/MM-GBSA. GBHTC could offer slightly better performance than GBOBC and GBOBC2. GBOBC and GBOBC2 offer the comparable results, since they share highly similar methodologies. Therefore, if the GB methods are applied on one MD trajectory for each ligand, the accuracy is GBNeck2 > GBHTC >= GBOBC = GBOBC2 > GBNeck. However, the differences between GB methods are largely minimized in the multiple independent sampling.
The effect of radii sets on small molecule binding free energy prediction is relatively mild in the traditional long MD method, comparing to other parameters (Table 11c). In MM-PBSA, the performance is bondi = mbondi2 ≈ mbondi > PARSE. In MM/GBSA together with GBHCT,GBOBC, GBNeck, and GBNeck2, the differences between radii sets are negligible. In MM/GBSA and GBOBC2, the non-recommended mbondi setting shows inferior performance than recommended bondi and mbondi2 settings. Moreover, the effect of radii sets on QM/MM-GBSA is highly similar to MM-GBSA, besides in GBOBC2, mbondi settings showed similar predictive power to bondi and mbondi2 with QM/MM-GBSA. On the other hand, the differences between radii sets are neutralized in the multiple sampling method.
QM Hamiltonians have a strong impact on QM/MM-GBSA results (Table 11d). In general, the performance is PM3 > AM1 > PM6. However, future optimized PM6 parameters may enhance the performance of the PM6 Hamiltonian in QM/MM-GBSA in AMBER.
To summarize, it is important, when optimizing computational protocols to predict binding free energy, to carefully investigate the optimal radii sets, entropy, sampling methods, GB methods, and QM Hamiltonians in (QM/)MM-P(G)BSA. Our results suggest that small deviations from optimized settings can have a significant impact on energy prediction results, not only for our FtFabI-benzimidazole systems, but potentially other similar systems amenable to such lead optimization methods. Lastly, because MM/GBSA together with GBHCT, mbondi, and 600 frames extracted evenly from six 0.25 ns MD simulations, provided accurate predictions efficiently, with less sensitivity on various parameters, this method will be applied to future large-scale lead optimizations of benzimidazole FabI inhibitors.
Supplementary Material
Acknowledgments
This work was supported in part by the National Institutes of Health Grant U01 AI077949. The computation resources were provided by the Texas Advanced Computing Center (TACC), Lonestar cluster at the University of Texas at Austin under the XSEDE Teragrid Grant TG-MCB090168. P.C.S was supported during part of this work by 13PRE-14800030, an American Heart Association pre-doctoral fellowship. K.E.H. was supported during a portion of this work by NIDCR 5T32-DE018381, UIC College of Dentistry, MOST Program. We thank the AMBER community, particularly Professors Adrian Roitberg, Carlos Simmerling, Ray Luo, Gerald Monard, Drs. Jason Swails, and Paul Gasper for AMBER technical support and helpful discussions.
Abbreviations
- AM1
Austin Model 1
- MD
Molecular Dynamics
- MM-PBSA
Molecular Mechanics - Poisson-Boltzmann Surface Area
- MM-GBSA
Molecular Mechanics - Generalized Born Surface Area
- QM/MM-GBSA
Quantum Mechanics / Molecular Mechanics - Generalized Born Surface Area
- FAS
Fatty Acid Synthesis
- FtFabI
Francisella tularensis FabI
- GAFF
general AMBER force field
- PME
Particle Mesh Ewald
- PM3
Parameterized Model number 3
- PM6
Parameterized Model number 6
- NMA
Normal Mode Analysis
- RMSD
root-mean-square deviation
- ΔGbind
binding free energy
- ΔHbind
binding enthalpy
- ΔGsolvation
solvation free energy
- ΔGGB
Generalized Born polar free energy
- ΔGPB
Poisson-Boltzmann polar free energy
Footnotes
Additional Supporting Information may be found in the online version of this article.
References and Notes
- 1.Christian MD. Crit Care Clin. 2013;29(3):717–756. doi: 10.1016/j.ccc.2013.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.World Health Organization; Geneva, Switzerland: 2007. [Google Scholar]
- 3.Hevener KE, Mehboob S, Su PC, Truong K, Boci T, Deng J, Ghassemi M, Cook JL, Johnson ME. Journal of medicinal chemistry. 2012;55(1):268–279. doi: 10.1021/jm201168g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mehboob S, Hevener KE, Truong K, Boci T, Santarsiero BD, Johnson ME. Journal of medicinal chemistry. 2012;55(12):5933–5941. doi: 10.1021/jm300489v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lu H, England K, am Ende C, Truglio JJ, Luckner S, Reddy BG, Marlenee NL, Knudson SE, Knudson DL, Bowen RA, Kisker C, Slayden RA, Tonge PJ. ACS Chem Biol: United States. 2009:221–231. doi: 10.1021/cb800306y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mehboob S, Song J, Hevener KE, Su P-C, Boci T, Brubaker L, Truong L, Mistry T, Deng J, Cook JL, Santarsiero BD, Ghosh AK, Johnson ME. Bioorganic & medicinal chemistry letters. 2015;25(6):1292–1296. doi: 10.1016/j.bmcl.2015.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhang YY, Liu Y, Mehboob S, Song JH, Boci T, Johnson ME, Ghosh AK, Jeong H. Xenobiotica. 2013 doi: 10.3109/00498254.2013.850553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Guimaraes CR, Cardozo M. J Chem Inf Model. 2008;48(5):958–970. doi: 10.1021/ci800004w. [DOI] [PubMed] [Google Scholar]
- 9.Homeyer N, Gohlke H. Journal of computational chemistry. 2013;34(11):965–973. doi: 10.1002/jcc.23218. [DOI] [PubMed] [Google Scholar]
- 10.Zhu T, Lee H, Lei H, Jones C, Patel K, Johnson ME, Hevener KE. J Chem Inf Model. 2013;53(3):560–572. doi: 10.1021/ci300502h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rastelli G, Del Rio A, Degliesposti G, Sgobba M. J Comput Chem. 2010;31(4):797–810. doi: 10.1002/jcc.21372. [DOI] [PubMed] [Google Scholar]
- 12.Pearlman DA. J Med Chem. 2005;48(24):7796–7807. doi: 10.1021/jm050306m. [DOI] [PubMed] [Google Scholar]
- 13.Steinbrecher T, Case DA, Labahn A. J Med Chem. 2006;49(6):1837–1844. doi: 10.1021/jm0505720. [DOI] [PubMed] [Google Scholar]
- 14.Wang J, Morin P, Wang W, Kollman PA. J Am Chem Soc. 2001;123(22):5221–5230. doi: 10.1021/ja003834q. [DOI] [PubMed] [Google Scholar]
- 15.Genheden S, Nilsson I, Ryde U. J Chem Inf Model. 2011;51(4):947–958. doi: 10.1021/ci100458f. [DOI] [PubMed] [Google Scholar]
- 16.Genheden S, Ryde U. J Chem Theory Comput. 2011;7(11):3768–3778. doi: 10.1021/ct200163c. [DOI] [PubMed] [Google Scholar]
- 17.Amaro RE, Cheng X, Ivanov I, Xu D, McCammon JA. Journal of the American Chemical Society. 2009;131(13):4702–4709. doi: 10.1021/ja8085643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Oehme DP, Brownlee RT, Wilson DJ. J Comput Chem. 2012;33(32):2566–2580. doi: 10.1002/jcc.23095. [DOI] [PubMed] [Google Scholar]
- 19.Hou T, Wang J, Li Y, Wang W. J Chem Inf Model. 2011;51(1):69–82. doi: 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Genheden S. J Comput-Aided Mol Des. 2011;25(11):1085–1093. doi: 10.1007/s10822-011-9486-1. [DOI] [PubMed] [Google Scholar]
- 21.Hou T, Wang J, Li Y, Wang W. Journal of chemical information and modeling. 2011;51(1):69–82. doi: 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nina M, Beglov D, Roux B. The Journal of Physical Chemistry B. 1997;101(26):5239–5248. [Google Scholar]
- 23.Hawkins GD, Cramer CJ, Truhlar DG. The Journal of Physical Chemistry. 1996;100(51):19824–19839. [Google Scholar]
- 24.Onufriev A, Bashford D, Case DA. J Phys Chem B. 2000;104(15):3712–3720. [Google Scholar]
- 25.Onufriev A, Bashford D, Case DA. Proteins. 2004;55(2):383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 26.Mongan J, Simmerling C, McCammon JA, Case DA, Onufriev A. J Chem Theory Comput. 2006;3(1):156–169. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nguyen H, Roe DR, Simmerling C. Journal of chemical theory and computation. 2013;9(4):2020–2034. doi: 10.1021/ct3010485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Roe DR, Okur A, Wickstrom L, Hornak V, Simmerling C. J Phys Chem B. 2007;111(7):1846–1857. doi: 10.1021/jp066831u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tan C, Tan Y-H, Luo R. J Phys Chem B. 2007;111(42):12263–12274. doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- 30.Genheden S, Ryde U. J Comput Chem. 2010;31(4):837–846. doi: 10.1002/jcc.21366. [DOI] [PubMed] [Google Scholar]
- 31.Seabra G. d. M., Walker RC, Elstner M, Case DA, Roitberg AE. J Phys Chem A. 2007;111(26):5655–5664. doi: 10.1021/jp070071l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Park K, Götz AW, Walker RC, Paesani F. J Chem Theory Comput. 2012;8(8):2868–2877. doi: 10.1021/ct300331f. [DOI] [PubMed] [Google Scholar]
- 33.Cho AE, Guallar V, Berne BJ, Friesner R. J Comput Chem. 2005;26(9):915–931. doi: 10.1002/jcc.20222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Götz AW, Clark MA, Walker RC. J Comput Chem. 2014;35(2):95–108. doi: 10.1002/jcc.23444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Walker RC, Crowley MF, Case DA. Journal of computational chemistry. 2008;29(7):1019–1031. doi: 10.1002/jcc.20857. [DOI] [PubMed] [Google Scholar]
- 36.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr., Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam NJ, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ö, Foresman JB, Ortiz JV, Cioslowski J, Fox DJG. Inc.; Wallingford CT: 2009. [Google Scholar]
- 37.Bayly CI, P. C., Cornell W, Kollman PA. J. Phys. Chem. 1993:10269–10280. [Google Scholar]
- 38.Dupradeau FY, Pigache A, Zaffran T, Savineau C, Lelong R, Grivel N, Lelong D, Rosanski W, Cieplak P. Phys Chem Chem Phys. 2010;12(28):7821–7839. doi: 10.1039/c0cp00111b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Vanquelef E, Simon S, Marquant G, Garcia E, Klimerak G, Delepine JC, Cieplak P, Dupradeau FY. Nucleic Acids Res. 2011;39(Web Server issue):W511–517. doi: 10.1093/nar/gkr288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA. Journal of computational chemistry. 2004;25(9):1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 41.Case DA, T. A. D., Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Hayik S, Roitberg A, Seabra G, Swails J, Goetz AW, Kolossváry I, Wong KF, Paesani F, Vanicek J, Wolf RM, Liu J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Cai Q, Ye X, Wang J, Hsieh M-J, Cui G, Roe DR, Mathews DH, Seetin MG, Salomon-Ferrer R, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. University of California; San Francisco: 2012. [Google Scholar]
- 42.Miller BR, McGee TD, Swails JM, Homeyer N, Gohlke H, Roitberg AE. J Chem Theory Comput. 2012;8(9):3314–3321. doi: 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- 43.Sitkoff D, Sharp KA, Honig B. The Journal of Physical Chemistry. 1994;98(7):1978–1988. [Google Scholar]
- 44.Pearlman DA, Case DA, Caldwell JW, Ross WS, Cheatham TE, Iii, DeBolt S, Ferguson D, Seibel G, Kollman P. Computer Physics Communications. 1995;91(1–3):1–41. [Google Scholar]
- 45.Nguyen H, Roe DR, Simmerling C. J Chem Theory Comput. 2013;9(4):2020–2034. doi: 10.1021/ct3010485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Stewart JJ. P. Journal of computational chemistry. 1989;10(2):209–220. [Google Scholar]
- 47.Stewart JJP. Journal of computational chemistry. 1989;10(2):221–264. [Google Scholar]
- 48.Dewar MJS, Zoebisch EG, Healy EF, Stewart JJP. Journal of the American Chemical Society. 1985;107(13):3902–3909. [Google Scholar]
- 49.Stewart JP. J Mol Model. 2007;13(12):1173–1213. doi: 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jurema MW, Shields GC. Journal of computational chemistry. 1993;14(1):89–104. [Google Scholar]
- 51.Stewart JP. J Mol Model. 2009;15(7):765–805. doi: 10.1007/s00894-008-0420-y. [DOI] [PubMed] [Google Scholar]
- 52.Pellegrini E, Field MJ. J Phys Chem A. 2002;106(7):1316–1326. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.