Measurement error and outcome distributions: Methodological issues in regression analyses of behavioral coding data

Abstract

Behavioral coding is increasingly used for studying mechanisms of change in psychosocial treatments for substance use disorders (SUDs). However, behavioral coding data typically include features that can be problematic in regression analyses, including measurement error in independent variables, non-normal distributions of count outcome variables, and conflation of predictor and outcome variables with third variables, such as session length. Methodological research in econometrics has shown that these issues can lead to biased parameter estimates, inaccurate standard errors, and increased type-I and type-II error rates, yet these statistical issues are not widely known within SUD treatment research, or more generally, within psychotherapy coding research. Using minimally-technical language intended for a broad audience of SUD treatment researchers, the present paper illustrates the nature in which these data issues are problematic. We draw on real-world data and simulation-based examples to illustrate how these data features can bias estimation of parameters and interpretation of models. A weighted negative binomial regression is introduced as an alternative to ordinary linear regression that appropriately addresses the data characteristics common to SUD treatment behavioral coding data. We conclude by demonstrating how to use and interpret these models with data from a study of motivational interviewing. SPSS and R syntax for weighted negative binomial regression models is included in supplementary materials.

As the literature on interventions for substance use disorders (SUD) has grown, research aims have shifted from a focus on testing treatment efficacy to identifying within-treatment processes and mechanisms that lead to reduced substance use (DiClemente, 2007; Doss, 2004; Kazdin & Nock, 2003; Longabaugh et al., 2005). Much of the research on mechanisms of change in SUD treatment has relied on behavioral coding to study within-session therapist and client behaviors, and the use of behavioral coding has led to some of our best data thus far on mechanisms of SUD treatment (e.g., see Magill et al., 2014).

Behavioral coding data have specific features that can violate the assumptions of regression models in psychology and addiction science. Specifically, common regression models assume that independent variables are measured without error, even though there can be a considerable degree of measurement error due to inter-rater disagreement when rating behaviors. As discussed in detail below, measurement error in independent variables can bias effect sizes and significance tests, leading to inaccurate results and conclusions. However, at present, measurement error is rarely accounted for in the statistical analyses of behavioral coding SUD research, despite the literature indicating that measurement error is notable and pervasive.

There appears to be limited awareness of the impact of measurement error in behavioral coding research and no consensus on methods for handling it statistically. In addition, behavioral coding data often violate other statistical assumptions, including the assumption that residuals are normally distributed and homoscedastic, since these data are often count- or proportion-based variables with substantial skew and heteroscedasticity. This issue has been discussed in the context of modeling alcohol consumption (e.g., Atkins, Baldwin, Zheng, Gallop, & Neighbors, 2013; Xie, Tao, McHugo, & Drake, 2013) but not within the context of behavioral coding data. Further, statistical analyses assume that the variables used for analysis (e.g., total counts of behaviors) are not confounded by other variables, but verbosity and session length can lead to confounding among count variables in coding data (Cohen, Cohen, West, & Aiken 2003).

The current manuscript reviews these characteristics of behavioral coding data and their implications for statistical analyses using theory, simulation, and real-world data analyses. Particular attention is focused on measurement error in independent variables, which can substantially impact statistical analyses but has received minimal attention in SUD research. In addition to critiquing current practice, the present article presents an improved approach to regression analysis that utilizes (a) weighted regression to account for measurement error in predictor variables, (b) count regression to account for non-normality in behavioral count data, and (c) offset terms and rates for covariates to account for differences in verbosity and session length.

Measurement Error has Implications for Regression Models

Motivational Interviewing (MI) is an efficacious treatment for SUDs (Hettema, Steele, & Miller, 2005; Lundahl & Burke, 2009) with a strong tradition of corresponding behavioral coding research. MI has proposed clinical models of how client and therapist verbal behaviors relate to one another and in turn lead to changes in client substance use (Miller & Rollnick, 2012; Miller & Rose, 2009). Behavioral coding research has tested these models empirically (Miller, Benefield, & Tonigan, 1993), for example, finding that therapist MI-consistent behaviors, such as open questions, complex reflections (i.e., adding meaning to what a client has said), and complex reflections of change (i.e., a complex reflection focused on reasons or commitments to reduce substance use) increase client change talk (i.e., statements indicating desires, reasons, or commitments to reduce substance use) and reduce sustain talk (i.e., statements indicating desires, reasons, or commitments to continue substance use; Moyers et al., 2007; Moyers & Martin, 2006; Moyers, Martin, Houck, Christopher, & Tonigan, 2009; Vader, Walters, Prabhu, Houck, & Field, 2010).

Much of the support for theories of causal chains in MI has been developed through behavioral coding performed by human raters. Human raters do not always agree, and most behavioral coding studies employ multiple raters to code a common subset of sessions to quantify the degree of disagreement among raters. Researchers often take two practical steps for working with multiply-rated sessions (i.e., sessions rated by two or more coders for the purpose of assessing reliability). First, inter-rater reliability is quantified for variables of interest, such as the frequencies of different codes, and only variables with good inter-rater reliability, determined using a pre-defined cutoff value (e.g., Cicchetti, 1994), are retained in model testing. Second, for sessions with two or more ratings, a single set of ratings from one coder is randomly selected to include in subsequent statistical analyses and other coders’ ratings are excluded in the main hypothesis testing (except hypotheses directly related to reliability analysis). Measurement error within the ratings is then given little or no further statistical consideration despite the implications of ignoring such error.

For a recent example, among the 16 studies in a meta-analysis of causal chain hypotheses in MI (Magill et al., 2014), most studies reported at least one behavioral coding variable with inter-rater reliability estimates that indicated only “fair” agreement (i.e., intraclass correlation coefficients [ICCs] between 0.40 and 0.60) or “poor” agreement (i.e., ICC < 0.40). Moreover, there is notable variability in how measurement error is treated within analyses. For example, approximately half of the same 16 studies excluded variables with poor agreement from statistical analyses, while other studies retained all coding variables in hypothesis testing even when agreement was poor. Most studies acknowledged that measurement error could affect the accuracy of statistical models when agreement was poor but did not further comment on the precise manner in which the results would be affected. Further, there was no discussion of the impact of measurement error on the results when reliability was better than “poor” but still not perfect (i.e., between 0.40 and 1.00), even though measurement error was often substantial for such variables. Although a detailed review of measurement error in MI or psychotherapy coding research is beyond the scope of the present study, these practices indicate that measurement error is prevalent across most studies, is often given little attention, and is often handled differently across settings.

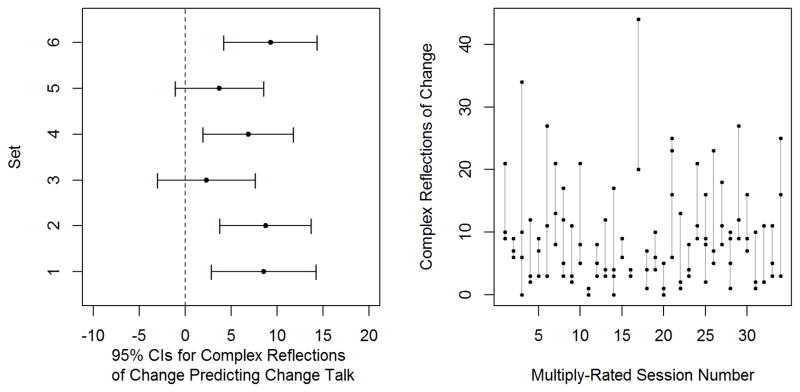
Standard regression models assume no measurement error in the independent variables (i.e,. predictor variables), and thus, behavioral coding data often violate this assumption. An example of this issue and its potential consequences are presented in the left panel of Figure 1, which shows six different 95% confidence intervals (CI) for regression coefficients of change talk predicted by complex reflections. Each coefficient and CI was created by randomly selecting a single set of ratings from sessions with multiple ratings (between two and four), using data from an MI coding study (Moyers et al., 2009; a full description of the study and data are provided later in the paper). The measurement error inherent in the data is seen in the lack of consistency over the various random samples; if there were little to no measurement error, the point estimates and CI should be virtually identical. Each combination of data produces a different point estimate for the effect of change talk predicted by complex reflections of change. Four of the combinations of the data indicate a significant relationship between change talk and complex reflections of change, whereas two combinations of rater scores fail to find a significant association. The measurement error in the independent variable is illustrated in the right panel of Figure 1, which shows the ranges of counts for complex reflections of change (y-axis) provided by different coders (separate dots connected by lines) for each multiply-rated session (x-axis).

Figure 1.

Left panel: point estimates and 95% confidence intervals for regression coefficient estimates of change talk predicted by complex reflections of change. Each point estimate estimates the association between complex reflections of change and change talk using different subsets of individual coders’ ratings from sessions that were coded by multiple raters. Right panel: ranges of complex reflections of change identified in multiply-rated sessions.

Although not commonly used in psychology or SUD research, appropriate methods for handling measurement error in regression have been developed and used in statistics and econometrics. These models are often referred to as error-in-variables (EIV) models (Fuller, 1987; Carroll et al., 1995). This literature has demonstrated that measurement error in independent variables causes bias in regression and typically underestimates regression coefficients, suggesting that the strength of association is weaker than it truly is and increasing type-II error rates. This is directly related to the issue of attenuation due to measurement error in standard correlation coefficients (Carmichael & Coen, 2008; Cragg 1994; Durbin, 1954). It is beyond the scope of the current article to give a full review of the EIV literature, and instead, we focus on one specific approach that is both appropriate for the types of behavioral coding data common to mechanisms-of-change research and straightforward to implement.

The approach we recommend is rooted in classical test theory (Lord & Novick, 1968). In psychometric measure development, each individual item is treated as an error-prone indicator of an underlying latent construct. Computing average values from two or more observations reduces the amount of random measurement error, producing a more accurate estimate of the true score for that session. As the number of observations of the same session increases, the averaged value generally moves closer to the true value, improving the accuracy of the estimate. Quite simply, taking an average over multiple ratings of the same (multiply coded) session is better than randomly selecting a single set of ratings. However, behavioral coding studies typically have a percentage of sessions that are multiply coded, and the remaining sessions are single coded. Thus, session scores that are averages of multiple raters will be more reliable than those that are from a single rater, because the former is averaging over measurement error whereas the latter is not. To incorporate the reliability from averaging, weighted regression can be used by giving the averaged ratings from multiply-coded sessions more weight in the analysis than ratings of single-coded sessions.¹ Moreover, using averaged ratings and weighted regression can easily extend to non-normally distributed outcomes, which are also common with behavioral coding data and are the next focus of our discussion.

Count Data as Outcomes are Different

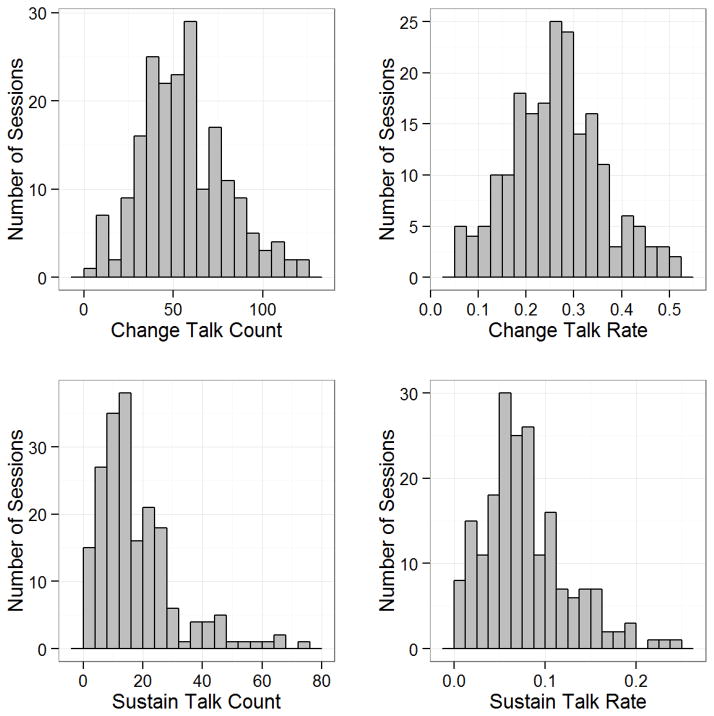
Commonly, behavioral coding variables reflect counts of different behaviors, such as sums of particular verbal utterances (e.g., simple reflections and open questions). Least squares linear regression models assume that residual errors of dependent variables are normally distributed and homoscedastic (i.e., constant across all fitted values). However, count data often violate this assumption because count data are bounded at zero and there is a direct relationship between the mean and variance with count variables, which typically produces heteroscedasticity and non-normal residuals (Atkins & Gallop, 2007; Atkins et al., 2013; Hilbe, 2011; Gardner, Mulvey, & Shaw, 1995). For example, histograms of two common dependent variables in MI coding studies, change talk and sustain talk, are shown in Figure 2. The sustain talk count variable has a lower mean than the change talk variable and therefore has greater skew. However, both variables are positively skewed. Converting these variables into rates (i.e., dividing them by the total number of client utterances) also results in positively skewed variables.

Figure 2.

Histograms of change talk (top row) and sustain talk (bottom row) using raw frequencies (left column) and rates (right column).

A common solution for reducing positive skew is to transform of the outcome, for example, using as the square-root or natural log transformation (O’Hara & Kotze, 2010). However, these approaches often lead to biased regression coefficients and inefficient standard errors (Maindonald & Braun, 2007; King, 1988). Alternatively, the generalized linear modeling (GLM) framework provides a robust method for performing regression on discrete count data (Atkins & Gallop, 2007; Atkins et al., 2013; Hardin & Hilbe, 2013; Hilbe, 2011; Xie et al., 2013).

In GLMs, independent variables (e.g., therapist code counts) are connected to the dependent variable (e.g., count of change or sustain talk) through a link function, which guarantees that predictions from the model are in the allowable range. For example, the negative binomial regression model uses a log link function, which guarantees that predictions are never negative. Furthermore, as the name implies, the negative binomial regression model does not assume normally distributed outcomes, but instead, assumes that the distribution of the outcome, conditional on the included predictors (i.e., similar to residuals in least-squares linear regression models), is a negative binomial random variable. Combining weighted regression for multiply coded sessions with count regression for count outcomes, we can formulate a much more appropriate regression model for behavioral coding data. However, particularly with codes that are counts of utterances within a session, there is one final consideration.

Variability in Session Length and Verbosity

Measurements of behavior counts over a specific time period (e.g., the length of a session) can be affected by variability in the length of the measurement period (e.g., different session lengths) and by the overall number of utterances within the time period (e.g., due to different speech rates). For example, a therapist using five complex reflections during a ten minute interview likely demonstrates higher quality MI than a therapist who uses five complex reflections during a 50 minute interview. For independent variables, a simple method for handling this issue is to convert the count covariates into a rate by dividing them by the total number of utterances per session that were made by the speaker.

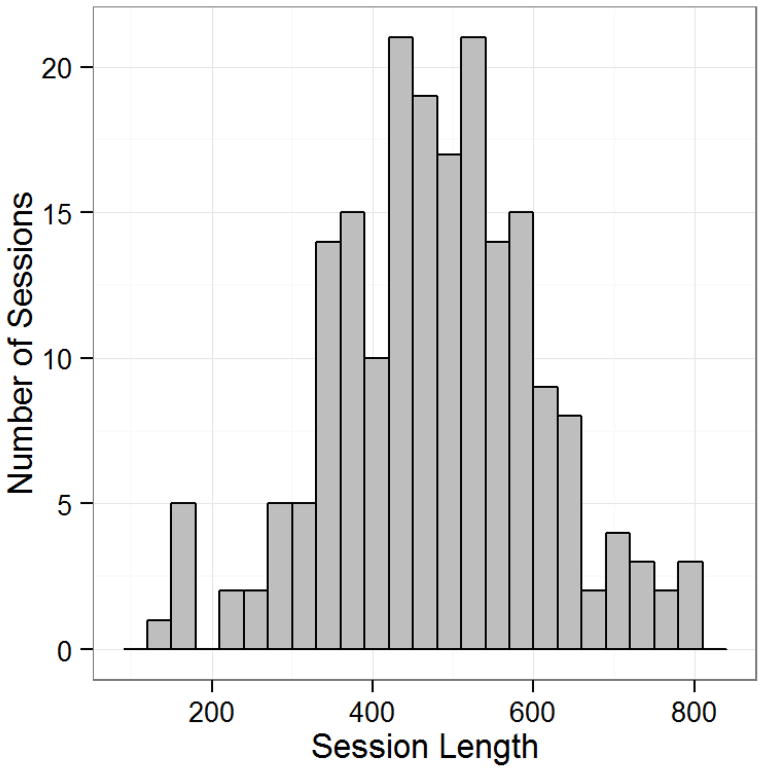
For count outcomes a similar conceptual approach is used, though the details are slightly different. GLMs for counts allow for an “offset” term, which in this case is simply a variable representing the length of exposure², such as the total number of client or therapist utterances in a session. The offset variable is typically defined as the natural log of the original exposure length variable. In psychotherapy coding studies, this variable will typically be (the natural log of) the total number of utterances made by the speaker.³ In the present data, session lengths (as measured by total number of utterances) varied notably across sessions (M = 479.8, SD = 130.1, range = 126 to 800; see Figure 3).

Figure 3.

Variability in number of codes per session.

Failure to account for variability in exposure length can bias regression results. For example, longer sessions would likely have a greater counts for all coding variables, and shorter sessions would likewise have fewer counts for all coding variables. This can cause different coding variables to appear more strongly associated with each other than they truly are because they are both mutual influenced by exposure length. Thus, to reduce the conflation of independent and dependent variables, we propose the following. First, use relative frequencies of behavior counts for independent variables, such as the proportion of behavior counts, which can be computed by dividing specific sums of each behavioral count by the total number of utterances made by the speaker. Second, use an offset term for dependent variables, such as the number of behavior codes in the full session for the client or therapist, which reduces the conflation between behavioral count frequencies and variability in length of the measurement period. Alternative measures of exposure could also be considered, such as the total amount of time that each speaker talks during a session; however, it is not common to measure per-speaker talk time in a session, and there is likely greater interest in controlling for the number of utterances in a particular session than in the amount of time it took to say them.

In summary, each of these three issues (measurement error, skewed count outcomes, and variable session length) can cause problems in the statistical analysis of behavioral coding data, including inaccurate standard errors, unreliable effect estimates, and inflated type-I and type-II errors. In general, this may increase the likelihood of obtaining misleading results and slow the progress of research on mechanisms of change in SUD treatments, potentially leading to misguided recommendations for therapists and treatment developers. These issues have often been neglected in existing behavioral coding studies, and the feasibility and results obtained using the recommended techniques have not been compared to methods that are typically used. Using both actual coding data as well as simulations, we explore these comparisons below.

Comparison of Statistical Models

Data

For the present study, we use behavioral coding data from 119 first-session tapes of Motivational Enhancement Therapy, a treatment protocol based on MI, from five Project MATCH sites (Project MATCH Research Group, 1997). These data were coded, analyzed, and reported in previous mechanisms of change research (Martin, Christopher, Houck & Moyers, 2011; Moyers et al., 2009). Client and therapist behaviors were rated by six trained coders using the SCOPE coding instrument (Martin, Moyers, Houck, Christopher, & Miller, 2005). The SCOPE provides total frequency counts of client and therapist behaviors, and in the present study we focus only on two client codes, change talk and sustain talk, and two therapist codes, complex reflections and complex reflections of change, and only focus on total frequencies of these counts (i.e., not sequential coding).

Comparing Regression Models: Normal vs. Poisson vs. Negative Binomial Regression

How do normal, Poisson, and negative binomial regressions compare to each other when modeling behavioral coding data? Two methods were used to compare regression models with different outcome distributions. First, deviance statistics (i.e., −2 times the log-likelihood) compared the fit of each model to the observed data. Second, a model-prediction version of deviance compared each model’s fit to new observations using a ten-fold cross validation procedure (James, Witten, Hastie, & Tibshirani, 2013). Specifically, the data were subdivided into 10 equal parts and a model was fit on 90% of the data. The resulting model was then fit to the remaining 10% of the data, and this process was repeated nine more times to predict outcomes for each of the ten subsets. As shown in Table 1, the negative binomial regression model had lower deviance (i.e., better fit to the data) and lower model-prediction deviance (i.e., better predictive performance) than the normal and Poisson regression models. This was especially the case for sustain talk, which had a heavier skew.

Table 1.

Average-Weighted Regression for Change Talk and Sustain Talk for Different Distributions.

	Distribution	-2LL (model fit)	-2PLL (predictive)
Change Talk	Normal	982	110
	Poisson	1348	150
	Negative Binomial	938*	105*
Sustain Talk	Normal	863	97
	Poisson	1183	135
	Negative Binomial	775*	88*

Note.

^*indicates best model fit and prediction

Example 2: Negative Binomial Regression with Varying Number of Raters

What effect does including multiple ratings of the same session have on parameter estimates? Using simulated data, we next show that there is a reduction of bias in parameter estimates when including multiple rater information in the presence of measurement error (i.e., non-perfect agreement among raters). Data were generated from a negative binomial distribution with measurement error in the dependent and independent variables. Independent variables were created to reflect different coder ratings with values that ranged from one to ten. A dependent variable was then simulated from a negative binomial distribution with a dispersion parameter of ten and a “true” regression coefficient of 0.5, which defined the relationship between the mean of the independent variables (i.e., the averaged coder ratings) and the dependent variable. Normally-distributed error variance was added to the independent variable ratings to represent measurement error, which was manipulated at three levels to produce inter-rater agreement ICCs approximately equal to 0.8, 0.6, and 0.4, corresponding to excellent, good-to-fair, and fair-to-poor agreement (Cicchetti, 1994) and representing values that are commonly obtained in MI coding studies. The latter of these values is often used as a cutoff point for inclusion in statistical analyses, although variables with ICCs below this have also been included in analyses in many MI coding studies.

Five hundred data sets were simulated under six study design scenarios. The first scenario included 100 sessions that were coded by only one rater (i.e., no multiply-rated sessions). The second scenario included 100 sessions that were coded by two raters. The third, fourth, and fifth scenarios included 100 sessions that were coded by three, four, and eight raters, respectively. The sixth scenario created a data set that was similar to the real SCOPE data described above, with 70% coded by one rater and 30% coded by 3 raters (i.e., 60 duplicate ratings). No specific rater bias was included (i.e., all measurement error had a mean of zero).

In the analysis, all scenarios with multiply-rated sessions used weighted regression using averages of the multiple ratings. In scenario six, heavier weights were given to sessions that were based on averages such that the values of the weights were equal to the number of ratings used for computing the average. The first scenario (with only one rater) most closely represents coding studies with multiple-raters in which a single set of ratings are randomly selected for the final analysis.

Table 2 shows the mean of the estimated regression coefficients across each condition. This example shows how the additional rater information can be included to reduce bias, shrink uncertainty, and increase precision in the parameter estimates. As additional ratings of the same sessions are included using averaging and weighting, the overall bias is reduced as represented by mean coefficient estimates that are closer to their true parameter value (i.e., 0.5). In scenarios with fewer overlapping ratings, the direction of the bias tended to systematically underestimate the true coefficient value. For example, when only one rater’s codes were used (scenario 1) and reliability ICCs were 0.8, indicating “excellent” reliability (Cicchetti, 1994), mean coefficients underestimated the true relationship of 0.50 as 0.40. But when two raters’ codes were used (scenario 2), the mean coefficient improved to 0.45, and when eight raters’ codes were used (scenario 5), mean coefficients improved to 0.48. These effects were stronger as reliability worsened to 0.6 and 0.4, when the use of a single rater underestimated the same coefficient as 0.29 and 0.19, respectively. Using weighted regression with two raters improved these estimates to 0.37 and 0.28, and using eight raters improved the estimates to 0.46 and 0.42. In all cases, the uncertainty (i.e., lack of precision in parameter estimates) also decreased as the number of raters increased, as represented by a decrease in standard deviations of coefficient estimates. Each of these phenomena are well-known and expected within EIV research (Carmichael & Coen, 2008; Cragg 1994; Durbin,1954). Finally, although the weighted regression approach with typical behavioral coding data (i.e., final row of Table 2) is superior to randomly selecting a single rater (i.e., first row), there is still bias and inefficiency even with this approach. The degree of bias and inefficiency are related to a variety of factors (e.g., degree of measurement error), but as expected, more ratings will lead to more accurate parameter estimation.

Table 2.

Bias and Uncertainty of Regression Coefficients for Different Numbers of Raters.

Scenario	No. of Raters per Session	Coefficient Estimates			No. of Duplicate Ratings
		ICC = 0.8 M (SD)	ICC = 0.6 M (SD)	ICC = 0.4 M (SD)
1	1	0.40 (0.026)	0.29 (0.034)	0.19 (0.039)	0
2	2	0.45 (0.022)	0.37 (0.029)	0.28 (0.034)	100
3	3	0.46 (0.019)	0.41 (0.024)	0.34 (0.029)	200
4	4	0.47 (0.016)	0.43 (0.022)	0.37 (0.028)	300
5	8	0.48 (0.013)	0.46 (0.016)	0.42 (0.021)	700
6	1–3	0.43 (0.023)	0.39 (0.033)	0.24 (0.036)	60

Note. All models were fit using weighted negative binomial regression.

Example 3: Regression with Variable Exposure Lengths

What kinds of problems can arise when predictor and outcome variables are both untransformed count variables? In this example, we demonstrate that the use of raw frequencies (i.e., total behavior counts) as both independent variables and dependent variables can lead to inflated regression parameter estimates and increased type-I error rates when exposure lengths are not constant. Data are again simulated to emulate the distributions in the SCOPE data described above for 119 sessions where the total number of codes per session varied randomly with a mean of 490 and standard deviation of 132. Then, rates of therapist reflections and client change talk were each randomly assigned to account for anywhere from 10% to 25% of the utterances observed within the session. Importantly, the rates for reflections and change talk were sampled independently and were therefore uncorrelated; thus, non-zero regression parameter estimates for change talk predicted by reflections would indicate a spurious relationship between these variables. Regression models were tested with and without an offset parameter for the dependent variable and by using either rates or raw frequencies of behavior codes for the independent variable, and the procedure was repeated 1,000 times.

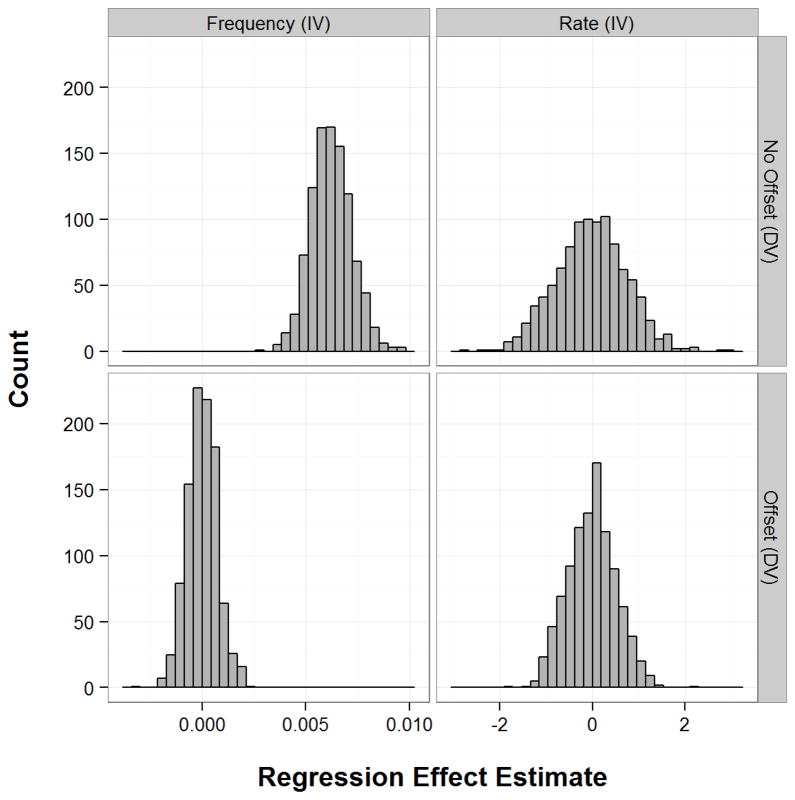
Histograms of parameter estimates for client change talk predicted by therapist reflections are presented in Figure 4. Models that omitted an offset parameter and used therapist behavior counts instead of rates (top-left panel of Figure 4) produced parameter estimates that were substantially positively biased, indicated by all regression coefficients being greater than zero despite the null relationship between rates of change talk and reflections that generated the data. In contrast, models that used an offset parameter (bottom-left panel of Figure 4), used rates instead of raw counts for the independent variable (top-right panel of Figure 4), or used both an offset parameter and rates of the independent variable (bottom-right panel of Figure 4) produced parameter estimates that were centered around the true value of zero.

Figure 4.

Simulated regression coefficient estimates for change talk predicted by therapist reflections. Data were generated using a true coefficient of zero (no relationship between change talk and therapist reflections).

In this case, the raw counts for the independent and dependent variables are both directly influenced by the total number of utterances within a session because longer sessions are likely to have a greater number of both codes and shorter sessions are likely to have a smaller number of both codes. The use of an offset parameter and converting independent variables from frequencies into rates eliminates the variables’ shared overlap with session length, producing results that more accurately capture the true null relationship between variables.

Model Comparisons using Real-World SCOPE Data

Finally, we demonstrate the use and interpretation of weighted negative binomial regression models by applying them to the real-world SCOPE data described above. First, a traditional linear regression model is estimated to predict client change talk from therapist complex reflections. The linear regression model does not account for error in independent variables, count outcome distributions, or variability in exposure. In addition, for multiply-coded sessions, a single coder’s ratings are randomly selected while the remaining ratings are discarded. The results, presented as Model 1a in Table 3, show that complex reflections are associated with change talk with an unstandardized regression coefficient of 0.65, p < .001, indicating that an increase of one therapist complex reflection corresponds with an expected increase of 0.65 client change talk statements. However, identically-structured models that select different single-coder ratings from the multiply-coded sessions are presented as Models 1b and 1c, each providing different regression coefficient estimates, 0.56 and 0.58, and different standard errors, t-test statistics, and p-values, p < .001 and p = .005.

Table 3.

Real-World Regression Model Results

Model		Estimate	SE	t or z	p
1a	Linear Regression (sample 1)
	Intercept	44.86	3.87	11.59	< .001
	Complex Reflections	0.65	0.18	3.58	< .001***
1b	Linear Regression (sample 2)
	Intercept	45.83	3.67	12.57	< .001
	Complex Reflections	0.56	0.16	3.45	< .001***
1c	Linear Regression (sample 3)
	Intercept	45.78	3.99	11.48	< .001
	Complex Reflections	0.58	0.20	2.89	.005**
2	Weighted Linear Regression
	Intercept	40.28	3.89	10.36	< .001
	Complex Reflections	0.80	0.18	4.48	< .001***
3	Weighted NB Regression
	Intercept	3.756	0.075	50.29	< .001
	Complex Reflections	0.015	0.004	4.04	< .001***
4	Weighted NB Regression, with offset
	Intercept	−1.3252	0.0521	−25.46	< .001
	Complex Reflections	−0.0005	0.0024	−0.19	.847
5	Weighted NB Regression, with offset and rate
	Intercept	−1.38	0.05	−25.46	< .001
	Complex Reflections (rate)	0.67	0.69	0.97	.333
6	Weighted NB regression with offset
	Intercept	−1.507	0.047	−32.69	< .001
	Complex Reflections of Change Talk	0.020	0.004	4.36	< .001***

Note. NB = negative binomial. t-values are presented for all linear regression models, z-values are presented for all negative binomial models.

^**p < .01,

^***p < .001 (not shown for intercept terms)

Next, weighted linear regression models are estimated in Model 2 that account for measurement error in independent variables by using averaging and weighting approach described above. The weighted linear regression model yields a regression coefficient of 0.80, p < .001, which is larger than each of the regression coefficients that were obtained using only single ratings. The standard error for the weighted linear regression model is similar to the standard errors provided by the non-weighted linear regression models, yielding larger z-test statistics, lower p-values, and therefore, greater statistical power.

In Model 3, a weighted negative binomial regression model is tested that accounts for the count distribution of the outcome variable. The model also indicates an association between complex reflections and change talk with a coefficient of 0.015, p < .001, which is markedly different than the coefficients found in Models 1a–1c and Model 2, in part because it is on a natural log scale instead of a linear scale. The negative binomial regression provides the expected estimate of the natural log of the count dependent variable, which for a model with one predictor variable can be written as

$$E(ln(y_i))={\beta }_0+{\beta }_1(x_i)$$

where E(ln(y_i)) is the expected value of the natural log of the dependent variable for observation i, β₀ and β₁ are regression coefficients for the intercept and independent variable found in the regression results, and x_i is the observed value for the independent variable for observation i. The raw coefficients in negative binomial regression models (e.g., β₁ above) are typically exponentiated (i.e., raised to the base e) and referred to as rate ratios (RR). In the present example, the RR is 1.015 and interpreted in the following way: For each one point increase in complex reflections, the mean of change talk increases by 1.5%. A one count increase in complex reflections, from 17.66 (the mean in the sample) to 18.66 would lead to expected (natural logs of) change talk of

$$E(ln(\mathit{Change}\mathit{Talk}))=3.756+0.015(17.66)=4.021$$

and

$$E(ln(\mathit{Change}\mathit{Talk}))=3.756+0.015(18.66)=\mathrm{4.036.}$$

When exponentiated, this indicates an expected increase by 0.85 (e^4.036 – e^4.021). This result is quite close to the regression coefficient from the weighted linear model, but note that the negative binomial regression is changing nonlinearly with the independent variable due to the dependent variable being predicted on a log scale (see Atkins et al., 2013 or Hilbe, 2011 for more detail).

In Model 4, an offset term is added to control for the variability in exposure lengths by entering the log of the total number of client utterances as an offset term, testing a final model that accounts for each of the three concerns raised in this paper. This yields a non-significant association between change talk and complex reflections with a regression coefficient estimate of −0.0005, p = 0.847, suggesting that the rates of change talk (rather than the raw frequencies) are not predicted by the number of complex reflections in a session. Likewise, Model 5 transforms the independent variable, therapist reflections, into rates by dividing the complex reflection frequencies by the total number of therapist utterances and still finds a non-significant association with a regression coefficient estimate of 0.67, p = 0.333. What appeared to be almost a one-for-one association between change talk and complex reflections in earlier models may actually have been confounded by a mutual dependence of both variables on session length.

In Model 6, a weighted negative binomial regression with an offset term is estimated which is nearly identical to Model 6, but the independent variable is replaced by therapist complex reflections of change talk rather than complex reflections more broadly defined. This alternative test is modeled after theories of MI, which have increasingly posited that therapists have a better chance at eliciting change talk if they specifically target change-related content in their reflections. A positive and significant association is found between change talk and complex reflections of change with a regression coefficient estimate of 0.020, p < .001. This suggests that although complex reflections, broadly defined, were unrelated to change talk (Model 4), a more specific form of complex reflections focused on change talk were associated with client change talk.

Conclusions

The present article presents weighted negative binomial regression with an offset term as a preferred method for testing relationships among behavioral coding variables. The examples presented here and in previous econometrics research show that this regression technique is improves the accuracy and precision of effect estimates. These issues are particularly salient for behavioral coding research, where measurement error is prominent, exists to varying degrees between codes and studies, and is often handled differently between studies. Although coding studies often employ methods to remedy poor inter-rater agreement (e.g., retraining or replacement of coders, revising coding manuals), low agreement may not always be avoidable, and even small amounts of measurement error can systematically bias results.

Researchers are at risk of reduced power and greater bias in regression coefficients, leading to greater risk of type-I and type-II errors, when there is measurement error in predictors, count-variable outcomes, and variability in exposure length. This was found in the real-world examples with the SCOPE data, in which the use of non-weighted linear regression reduced parameter coefficient estimates, produced greater deviance, and found a relationship between therapist complex reflections and client change talk that appeared to be confounded by speaker verbosity. The non-significant results in Model 4 of the example section were in fact useful findings which indicated that complex reflections, defined as a therapist statement that adds meaning to what a client has said, appear unlikely to elicit client change talk. If traditional regression techniques were used (i.e., models 1a–1c), it would be tempting to accept the positive association between complex reflections and change talk as evidence supporting theories of MI, which posit that therapist MI-consistent behaviors, which include complex reflections, may influence client change talk. However, the results found by using weighted negative binomial regression with an offset term revealed that change talk was more likely unrelated to complex reflections (models 4–5), but was related to complex reflections of change talk (model 6), leading to a different, and likely more accurate, recommendation that therapists use complex reflections of change rather than complex reflections in general to elicit change talk.

Although these regression models have features that may be unfamiliar to some (e.g., negative binomial distribution, log-link function, regression weights, and offset term), we believe that most researchers will be able to grasp these models both conceptually and practically. These models can be implemented with a few simple lines of code in many statistical software packages. R and SPSS syntax is provided in the supplementary materials to this paper, which may provide a starting point for using these models in practice. We encourage researchers who analyze behavioral coding data to gain familiarity with these models and use them with behavioral coding data.