Minimizing biases associated with tracking analysis of submicron particles in heterogeneous biological fluids

Abstract

Tracking the dynamic motion of individual nanoparticles or viruses offers quantitative insights into their real-time behavior and fate in different biological environments. Indeed, particle tracking is a powerful tool that has facilitated the development of drug carriers with enhanced penetration of mucus, brain tissues and other extracellular matrices. Nevertheless, heterogeneity is a hallmark of nanoparticle diffusion in such complex environments: identical particles can exhibit strongly hindered or unobstructed diffusion within microns of each other. The common practice in 2D particle tracking, namely analyzing all trackable particle traces with equal weighting, naturally biases toward rapidly diffusing sub-populations at shorter time scales. This in turn results in misrepresentation of particle behavior and a systematic underestimate of the time necessary for a population of nanoparticles to diffuse specific distances. We show here via both computational simulation and experimental data that this bias can be rigorously corrected by weighing the contribution by each particle trace on a ‘frame-by-frame’ basis. We believe this methodology presents an important step towards objective and accurate assessment of the heterogeneous transport behavior of submicron drug carriers and pathogens in biological environments.

1. Introduction

Analysis of the real-time motion of biological and synthetic particles, commonly referred to as single- or multiple-particle tracking (MPT) [1-3], is an increasingly popular approach to gaining insight into dynamic processes in living systems, such as the diffusion of proteins and lipids in cell membranes [4, 5], the kinetics and intracellular processes involved in viral infections [6, 7] as well as the mobility of pathogens in biofilms or mucus [8-10]. Because the motions of particles in an environment are governed by local viscous and elastic forces, particle traces from MPT can be further analyzed to infer the microstructural, rheological and barrier properties of different materials at the length scales relevant to nanoparticles and viral pathogens [11-14]. Particle tracking has been used extensively in the field of drug delivery, not only to characterize important barriers to drug delivery but also to quantify the extent to which engineered drug carriers can overcome these barriers. Indeed, MPT has enabled the development of nanoparticles capable of penetrating various mucus secretions [15-18], brain tissues [19] and other physiological gels [20-22], as well as investigations into the intracellular trafficking of nonviral gene carriers and polymeric nanoparticles [23-26].

Nevertheless, biological environments tend to be highly complex, often composed of a dense matrix of proteins, carbohydrates, cells and other biomacromolecules, and exhibiting a broad range of pore sizes. Particles introduced into such biological fluids will inevitably encounter varying degrees of steric obstruction and/or molecular interactions with the network. As particle sizes approach the characteristic mesh spacing of the network elements, the particles may exhibit increasingly heterogeneous motions, leading to orders of magnitude differences in mean squared displacements (MSD) and effective diffusivities (D_eff) within the same particle population. In addition, the same particles may also exhibit distinct affinity to network elements; for example, otherwise identical viruses with different numbers of surface-bound antibodies may possess different antibody-mucin avidity [9, 27], and variations in the surface properties within a population of synthetic nanoparticles may likewise result in heterogeneous interactions with the matrix constituents. Thus, accurate measurement of the true distribution of particle behavior is essential to correctly assess the transport kinetics of nano drug carriers and other nanoparticulates.

While an intrinsic advantage of particle tracking is that it offers a means of capturing heterogeneity across individual particle traces, particle tracking data can suffer from inherent biases. The conventional practice in particle tracking is to obtain video recordings of particles in a medium, track their movements to quantify 2D particle displacements over time, and finally compute ensemble averages and distributions across all traces. Numerous particle detection and tracking methods exist [28-30], but a common and critical technical challenge emerges when particle tracking is applied to sub-micron entities capable of rapid diffusion into and out of the plane of focus (or scanning volume for 3D imaging). Such rapid diffusion results in shorter traces recorded for the majority of faster particles, and longer traces recorded for slower particles. When particles exhibit heterogeneous behavior, the calculated ensemble MSD and D_eff at longer time scales inherently biases toward the slower subpopulation, since most fast-moving particle traces are too short to contribute MSD and D_eff values at these time scales. This fundamental limitation, discussed previously [31, 32], can only be lessened by longer tracking times or improved depth of tracking.

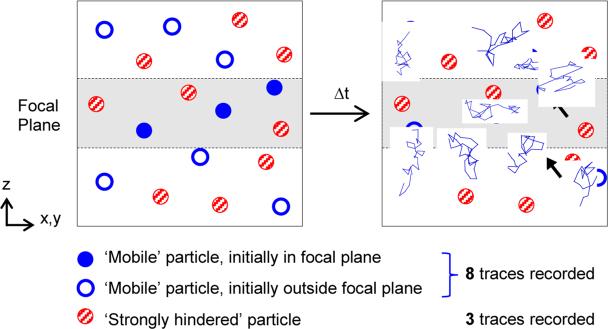
A less recognized and opposite bias occurs at shorter time scales, where relative contributions to the ensemble or distribution of MSD and D_eff skew towards faster particles. This bias naturally arises because (1) the same fast-moving particle may appear multiple times in the focal plane as distinct traces, and (2) distinct particles may enter and leave the focal plane throughout the movie, and the rate at which these processes occur increases with particle speed. This bias is conceptually illustrated in Fig. 1, which shows that particle tracking in a fluid containing an equal mixture of fast- and slow-moving particles would result in a much greater number of fast-moving vs. slow-moving particle traces using standard 2D particle tracking analysis. Overestimating the fast-moving fraction represents a potential major concern when assessing the performance of drug carriers, since for many applications efficacy is correlated to the fraction of the drug carriers that can penetrate a biological barrier. Here, we present a simple and rigorous algorithm to correct for this bias with 2D particle tracking data, without requiring 3D video microscopy.

Figure 1.

Schematic illustrating potential bias in particle tracking of heterogeneous systems. Particles that are trapped due to steric or adhesive interactions with the surrounding medium remain fixed in place, while those that avoid these interactions diffuse into and out of the focal plane. As a result, many more traces may be recorded in the focal plane for fast moving (‘Mobile’) particles vs. slow or trapped (‘Strongly hindered’) particles. Black arrows indicate moving particles for which two distinct traces were recorded due to the particles moving into and out of the focal plane multiple times.

2. Materials and Methods

2.1. Simulation of heterogeneous nanoparticle transport

We simulated 3D Brownian diffusion of a population of particles seeded at equal density in a defined volume with a bimodal distribution of effective diffusivity (D_eff), one centered at 0.001 μm²/s (corresponding to ‘strongly hindered’ particles) and another at 1 μm²/s (corresponding to ‘mobile’ particles) at a time scale of 0.0667 s (the time step of our simulation). These D_eff values are comparable to those we previously measured for muco-inert and muco-adhesive drug carrier nanoparticles in human mucus secretions [11, 16]. D_eff values were used to calculate a step size, and the locations of the particles from point to point were simulated following Marsaglia's method [33]. Briefly, the coordinates of a particle were determined by randomly selecting values x₁ and x₂ from independent uniform distributions on (−1, 1) such that $x_1^2+x_2^2<1$, and then calculating $\Delta x=d\cdot 2x_1\sqrt{1-x_1^2-x_2^2}$, $\Delta y=d\cdot 2x_2\sqrt{1-x_1^2-x_2^2}$, and $\Delta z=d\cdot (1-2(x_1^2+x_2^2))$, where d is the step size. Particle trajectories were ‘recorded’ if they were within a defined focal plane for a minimum of 5 frames, and trajectory segments for the same particle separated by more than 5 frames were treated as distinct traces.

2.2. Preparation of nanoparticles and viruses

Fluorescent, carboxyl-modified polystyrene beads (PS-COOH) sized 100 and 200 nm were purchased from Molecular Probes (Eugene, OR). PEGylated nanoparticles (PS-PEG) were prepared by conjugating 2 kDa amine-modified PEG (Rapp Polymere, Tuebingen, Germany) to PS-COOH particles via a carboxyl-amine reaction, as published previously [16, 34]. PS-COOH and PS-PEG solutions were adjusted to equal particle concentration based on fluorescence intensity and microscopy imaging. In acidic (pH ^~4) human cervicovaginal mucus (CVM) samples, PS-COOH nanoparticles are muco-adhesive and nearly always uniformly strongly hindered, while PS-PEG nanoparticles are muco-inert and nearly always uniformly fast-moving. Thus, a 50:50 mixture of the two in human CVM would mimic a heterogeneous particle population containing both strongly hindered and mobile particles in mucus. Fluorescent HSV-1 virions were prepared via expression of a VP22-GFP tegument protein construct, packaged at high copy numbers while maintaining native viral envelope integrity, as previously described [9]. Fluorescent, mCherry-Gag labeled HIV-1 virions pseudotyped with a YU-2 envelope were prepared similarly to previously described [8, 35].

2.3. Collection of human mucus

Human CVM was obtained from healthy female donors at random times in their menstrual cycles, following a protocol approved by the University of North Carolina Institutional Review Board (IRB), as previously described [16]. Briefly, undiluted CVM secretions, averaging 0.3 g per sample, were obtained from women using a self-sampling menstrual collection device; participants inserted the device into the vagina for at least 30 s, removed it, and placed it into a 50 mL centrifuge tube. Samples were centrifuged at 230 ×g for 2 min to collect the secretions. Samples used in this study had total anti-HSV-1 IgG <150 ng/mL, measured by whole virus ELISA as previously described [9]. Human airway mucus was obtained from healthy patients intubated for general anesthesia during elective surgery, following an IRB-approved protocol. After surgery, the endotracheal tube was removed from the patient, and mucus coating the tube was collected by centrifugation [36]. Airway mucus that was non-uniform in color or consistency or had visible blood contamination was discarded. Samples were stored at 4°C until microscopy, typically within 24 hours.

2.4. Multiple particle tracking in human mucus

Dilute particle solution (^~10⁸-10⁹ particles/mL, 1 μL or 5% v/v) was mixed gently into 20 μL of human mucus in custom-made chambers, and samples were incubated 1 hour at 37 °C before microscopy. The translational motions of the particles were recorded using an EMCCD camera (Evolve 512; Photometrics, Tucson, AZ) mounted on an inverted epifluorescence microscope (AxioObserver D1; Zeiss, Thornwood, NY), equipped with an Alpha Plan-Apo 100×/1.46 NA objective, environmental (temperature and CO₂) control chamber and an LED light source (Lumencor Light Engine DAPI/GFP/543/623/690). Videos (512 × 512, 16-bit image depth) were captured with MetaMorph imaging software (Molecular Devices, Sunnyvale, CA) at a temporal resolution of 66.7 ms and spatial resolution of 10 nm (nominal pixel resolution 0.156 μm/pixel) for 20 s. The tracking resolution was determined by tracking the displacements of particles immobilized with a strong adhesive, following a previously described method [37]. Trajectories were analyzed using MATLAB software, following methods originally developed in IDL by Crocker and Hoffman [1]. Sub-pixel tracking resolution was obtained by determining the precise location of particle centroids by light intensity-weighted averaging of neighboring pixels. As with simulation data, trajectories less than 5 frames in length were excluded, and trajectories belonging to the same particle were treated as distinct traces if separated by more than 5 frames.

2.5. Conventional vs. frame-by-frame MPT analysis

The coordinates of particle centroids for each individual trace were transformed into time-averaged mean squared displacements (MSD or <Δr²(τ)>), calculated as <Δr²(τ)>= [x(t + τ) − x(t)]² + [y(t + τ) − y(t)]² (where displacements x and y are functions of time t and time scale or time lag τ), and D_eff, calculated from MSD=4D_effτ, as previously demonstrated [8, 11, 16]. With conventional MPT analysis, ensemble averages and distributions of MSD or D_eff were calculated based on all traces without any weighting. For frame-by-frame MPT analysis, calculations were first performed at the individual frame level based only on particles present in that particular frame (i.e., capturing instantaneous ‘snapshots’ of particle behavior), before averaging across all frames in the movie. For example, the geometrically-averaged ensemble MSD was calculated by first averaging across the MSDs of particles present at each frame, and then averaging the resulting mean MSDs across all frames (Fig. S1). Trajectories of n ≥ 70 particles per frame and n ≥ 150 traces were analyzed for each experiment (see Table S1 for averages per dataset); note that the conventional minimum of 100 individual particle traces throughout the video typically corresponds n ≤ 40 particles per frame. Trapped particles were defined by D_eff < 10^−1.5 μm²/s at τ = 0.2667 s (time scale corresponding to a minimum trajectory length of 5 frames and a frame rate of 15 Hz). This cutoff was determined empirically based on multiple datasets of strongly hindered and mobile nanoparticles (e.g., PS-COOH and PS-PEG nanoparticles) in human mucus [11, 16]; for particles 200 nm and larger, a D_eff < 10^−1.5 μm²/s effectively means that the particles move much less than their diameters within 0.2667 s.

2.6. First passage time analysis

In order to demonstrate how the choice of conventional vs. frame-by-frame weighting can impact predictions of particle population behavior, we performed a first passage time analysis and calculated the expected time for 10% and 50% of a particle population to pass through a 50 μm thick layer of mucus. Given the diffusivity D of a particle, the probability that the particle has not passed through a layer of thickness L as of a given time t may be described by an explicit “survival function”. Using T to denote the time it takes for the particle to pass through the layer, the formula for this “survival function” is

$$P(T>t\mid D)=\frac{4}{\pi }\sum _{k=0}^{\infty }\frac{{(-1)}^k}{2k+1}exp\left(\frac{-{(2k+1)}^2{\pi }^{2}Dt}{4L^2}\right),$$

where exp is the exponential function and k is an integer from 0 to ∞. Suppose that a heterogeneous population of particles have individual diffusivities {D_i} with respective weights {w_i} where i ranges from 1 to the number of particles N. The expected fraction of particles that remain in the fluid layer as of time t is then equivalent to the following weighted survival function:

$$P(T>t)=\frac{{\sum }_{i=1}^{N}P(T>t\mid D_i)w_i}{{\sum }_{i=1}^N{w}_i}.$$

For the conventional weighting method, we set w_i for all i. For the frame-by-frame method, w_i is set to be the number of frames in which the i^th particle is present. For each weighting, we calculated the times t₁₀ and t₅₀ for which P(T > t₁₀) = 0.9 and P(T > t₅₀) = 0.5.

2.7. Statistical analysis

Data averages are presented as means with standard error of the mean (SEM), unless otherwise indicated. Statistical significance was determined by a one-tailed, Student's t-test (α = 0.05). For first passage time analysis, due to inherent variations in the first passage times for different data sets, statistical significance was determined for time estimates based on frame-by-frame analysis normalized to corresponding time estimates based on conventional analysis (a value of 1 indicates no difference).

3. Results

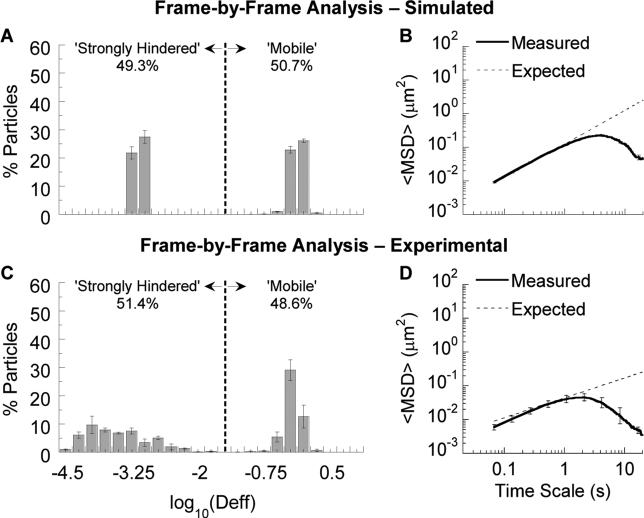
To measure the extent of the bias toward faster particles at shorter time scales and to evaluate methods to correct for it, we first obtained a ‘ground-truth’ dataset reflecting known particle heterogeneity in a complex environment by simulating 3D Brownian diffusion of a 50:50 mixture of randomly seeded ‘mobile’ and ‘strongly hindered’ particles (see Methods). Following conventional MPT analysis practice, we examined the D_eff distribution based on all traces. At a time scale of 0.2667 s (corresponding to a minimum of 5 frames per trace and a frame rate of 15 Hz), the D_eff distribution was markedly skewed towards the fast-moving particles (^~85% vs. the theoretical 50%; Fig. 2A). Only roughly 25% of traces were accounted for by particles present in the focal plane at the start of the simulation, while the remaining 75% were ‘excess’ traces due to these particles leaving and re-entering the focal plane multiple times, or to new particles entering the focal plane (Fig. S2; also see Table S1). Not surprisingly, the geometrically-averaged ensemble MSD (Fig. 2B) showed a similar bias toward the faster fraction at shorter time scales (^~10-fold higher than expected at a time scale of 0.2667 s).

Figure 2.

Application of conventional MPT analysis to simulated and experimental particle trajectory data. (A,C) D_eff distribution and (B,D) ensemble geometric average MSD based on simulated or experimentally measured particle traces, respectively. In (A,C), the vertical dashed line indicates the cutoff between strongly hindered and mobile particles (see Methods). In (B,D), expected MSD values are based on simulation parameters (B) or the geometric average of MSDs for PS-COOH and PS-PEG particles imaged separately (D). Error bars represent standard error across 3 independent data sets or mucus samples.

To validate this in silico prediction, we next performed MPT on an equal mixture of fluorescent 200 nm PEG-modified (PS-PEG; muco-inert and nearly uniformly fast-moving, see Fig. S3) and carboxyl-modified (PS-COOH; muco-adhesive and nearly uniformly strongly hindered) polystyrene beads introduced into human cervicovaginal mucus. Our results, in good agreement with the analysis of simulated data above, show that the D_eff distribution (Fig. 2C) was skewed substantially toward faster-moving particle fractions (again ^~85% vs. the theoretical 50%), and the geometrically-averaged ensemble MSD (Fig. 2D) was ^~5-fold greater at a time scale of 0.2667 s than the geometric average of the MSDs for PS-PEG and PS-COOH measured separately. Naturally, any subsequent analysis or derivation based on this dataset would overweigh contributions by the fast-moving subpopulations of PS-PEG particles, which would in turn result in artificial and significant overestimates of the true fraction of particles that can diffuse across a mucus layer of a given thickness over time.

To resolve this bias, we hypothesized that each instantaneous snapshot of an imaging volume approximately captures the distribution of particle behavior at that instant; in other words, the fraction of ‘mobile’ vs. ‘strongly hindered’ particles is approximately at steady state and thus time-independent over the time frame of analysis. Averaging across a series of snapshots over the duration of a recorded movie would in turn provide an accurate measure of the true heterogeneity of particle behavior within the imaging volume. In practice, this translates to first measuring the transport rates of individual particles across available frames/time scales, followed by calculating timescale-dependent MSD or D_eff at each frame based on the particles present in that particular frame, and finally averaging across all frames in the movie. This method results in a weighted averaging of particle contributions to MSD or D_eff calculations, which contrasts sharply with conventional particle tracking analysis that inherently assumes particles are present throughout the entire movie and averages across all particle traces regardless of the duration they are present in the focal volume.

We applied this ‘frame-by-frame’ approach to both the simulated and experimental data described above. Our proposed algorithm indeed recovered the 50-50 distribution of ‘strongly hindered’ vs. ‘mobile’ particles from simulation (Fig. 3A), with ^~50% mobile particles at each frame and an average of 49 ± 1% mobile particles across all frames and three independent datasets (Fig. S4A and B). In addition to closely matching the expected distribution of individual particle D_eff, the frame-by-frame ensemble average MSD also matched theoretical values well (Fig. 3B; <10% higher at a time scale of 0.2667 s compared to 10-fold higher previously). Applying the same approach to the experimental data, the average fraction of moving particles decreased from ^~84% when analyzed on a trace basis to ^~49% when analyzed on a frame-by-frame basis, in good agreement with the input 50:50 beads ratio. Likewise, the ensemble MSD was only ^~10% lower than the expected value, compared to 5-fold higher previously. For both simulated and experimental data, the small differences between theoretical values and measurements produced by the frame-by-frame method were statistically insignificant (p > 0.05). Finally, frame-by-frame analysis also accurately captured the true particle distribution across the full range of heterogeneity (Fig. S5; note for homogeneous populations that frame-by-frame analysis yields almost identical results as conventional analysis). This illustrates the broad utility of our approach, which can be applied to any particle population.

Figure 3.

Application of frame-by-frame analysis to simulated and experimental particle trajectory data. (A,C) D_eff distribution and (B,D) ensemble geometric average MSD. In (A,C), the vertical dashed line indicates the cutoff between strongly hindered and mobile particles (see Methods). Error bars represent standard error across 3 independent data sets or mucus samples.

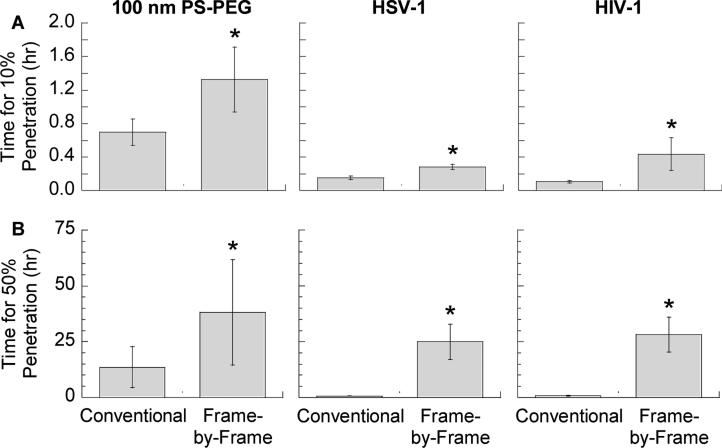
To illustrate the impact of tracking analysis approach on quantitative evaluation of the behavior of drug carrier nanoparticles in biological secretions, we compared first passage time estimates (i.e. the time needed for a particle to diffuse across a layer of defined thickness) for polymeric nanoparticles (d ^~ 100 nm) in human airway mucus, derived from conventional vs. frame-by-frame methods (Fig. 4). With the conventional method, the estimated time for 10% and 50% of the particles to diffuse across a 50 μm thick mucus layer, the approximate thickness of mucus lining the bronchial airways [38], was ^~0.8 and 16 hours, respectively. However, applying the frame-by-frame approach to remove systematic bias, the duration required was 1.6 and 46 hours, respectively, implying that a substantially lower fraction of the same nanoparticles would be able to penetrate airway mucus, and virtually all would be eliminated by mucociliary clearance. For drug delivery applications, this suggests a larger particle dose than previously estimated would be needed to achieve the desired therapeutic effect. Similar distinct conclusions are reached when we apply the analysis to HSV-1 and HIV-1 in human cervicovaginal mucus. Indeed, the time required for 50% of either HSV-1 or HIV-1 virions to penetrate a ^~50 μm thick mucus layer overlaying the vaginal epithelium [27] was 30-40 hours by frame-by-frame analysis (i.e., substantially longer than the estimated 12-24 hour mucus clearance rate), in sharp contrast to ^~1 hour by conventional estimate. The marked difference in the fraction of virions estimated to penetrate cervicovaginal mucus over time would substantially impact the amount of antiretroviral drugs or antibodies that must be dosed to block infection [9, 27]. These results underscore the importance of choosing the correct MPT analytical routine to quantify and interpret tracked particle traces.

Figure 4.

Effect of conventional vs. frame-by-frame analysis on estimates of the time required for (A) 10% or (B) 50% of particles to pass through a 50 μm thick mucus layer. Data is shown for 100 nm PS-PEG in human airway mucus, and HSV-1 and HIV-1 in human cervicovaginal mucus samples, in which the particles or virions exhibited heterogeneous transport behavior. Error bars represent standard error across 3 independent mucus samples. * indicates statistically significant difference compared to conventional analysis.

4. Discussion

Particle tracking is a powerful and popular tool for gaining insight into the transport dynamics or fate of drug carrier nanoparticles in biological environments, as well as the biochemical or biophysical interactions influencing particle motions. Unfortunately, the common practice of quantifying nanoparticle behavior based on simple summation and/or averaging of all tracked particle traces can result in misleading biases towards fast-moving subpopulations, and consequently far overestimate the extent to which drug carrier nanoparticles can overcome specific biological barriers. Here, we show that this bias can be easily rectified by the frame-by-frame analytical approach, which can be applied to any set of particle tracking data independent of particle speed or tracking algorithm. We believe this methodology presents an important step towards objective and accurate assessment of the heterogeneous transport behavior of submicron drug carrier particles, which may substantially impact conclusions about the efficiencies with which drug carrier nanoparticles penetrate biological barriers of interest, as well as conclusions about the microstructural and rheological properties of these barriers [11, 39].

The inherent bias in 2D particle tracking towards fast-moving populations at shorter time scales may be partially corrected by alternative approaches. For example, we and others [9, 16, 40] have previously performed tracking analysis only on nanoparticles that remain in the focal plane for a minimum of 50 frames, allowing us to obtain more accurate measurement of each individual particle trace at a timescale corresponding to 1 s or ^~15 frames (n = 35 data points within 50 frames). This effectively excludes from analysis a large number of fast-moving particles present for less than 50 frames in each specimen, which naturally reduces the bias towards fast-moving particles (Fig. S5). Nevertheless, this method is imperfect because (i) the appropriate minimum number of frames depends on the speed of the particles as well as thickness of the focal plane, and (ii) almost all fast-moving outlier fractions are omitted from analysis, making it impossible to accurately sample particle mobility. Only frame-by-frame analysis, with a low minimum number of frames required, is expected to consistently capture the true distribution (Fig. S6). Alternatively, Savin and Doyle previously proposed applying a normalized weight proportional to the duration of each trajectory to individual particle data before summing to obtain the mean MSD [32], and Mellnik et al. presented a method of analyzing trajectories grouped into statistically distinct clusters [41]. While these techniques are adept at deriving unbiased ensemble or cluster averages, they are not yet widely adopted, and may not readily provide an unbiased representation of heterogeneity in particle transport behavior, including the instantaneous distribution of particle transport rates. The method described here adds to the prior work by capturing the full distribution, including sub-populations of interest, as well as time-dependent phenomena. In conjunction with techniques such as sub-trajectory analysis [6], the frame-by-frame analysis approach may be applied to study, for example, the transport of drug carriers delivered with mucolytics that break down mucus over time, or the trapping of viruses in mucus by antibodies as they accumulate on the virus surface [27]. Lastly, a researcher should in theory obtain the same results as with our frame-by-frame averaging approach by tracking only particles that appear in the very first frame of each video. However, this method would require recording and analyzing many more videos to obtain the same level of confidence/accuracy.

Although the ‘frame-by-frame’ analytical approach can effectively minimize biases that result from inherent heterogeneity in particle motions, a number of limitations to particle tracking analysis remain that should be noted when applying MPT in the context of drug delivery. First, limited spatiotemporal resolution can result in static and dynamic errors, previously discussed by Savin and Doyle [42], particularly for small, inadequately labeled and/or fast moving particles. Second, because proportionally fewer fast-moving particles are tracked for long durations, the distribution skews toward slower particles at longer time scales; this bias cannot be corrected by the frame-by-frame averaging approach as it is a fundamental limitation of 2D particle tracking (Fig. 3B and D and Fig. S4C). While rapid 3D imaging would resolve this problem, the technological requirements continue to be prohibitive for most researchers. In particular, accurate 3D particle tracking necessitates a high frame rate to follow the motions of rapidly diffusing particles, as well as more complex tracking algorithms. As a result, 3D particle tracking remains far less popular than 2D particle tracking. Third, MPT analysis is predicated on the ability to accurately capture all particles while they are in the focal plane. Although a multitude of tracking algorithms exist, the high degree of noise in biological systems, often combined with low signal from inadequately labeled nanoparticles or viruses, can make identifying and tracking individual nanoparticulates challenging even for the most sophisticated of algorithms. Thus, in most instances, it is inadequate to blindly rely on the output of software trackers, and substantial human intervention continues to be necessary to ensure accurate tracking and proper elimination of imaging artifacts. Fourth, heterogeneity in a system may exist not only within each movie but also more globally throughout a sample; in such instances, a larger number of videos would be required to capture this level of heterogeneity.

In summary, multiple particle tracking is increasingly used to assess the transport behavior of drug and gene carriers in complex biological environments, such as the tumor microenvironment or the cell cytoplasm. We introduced here a simple yet rigorous analytical routine that avoids a common and significant pitfall with applying conventional multiple particle tracking analysis to submicron particles, which frequently results in substantial overestimation of particle diffusion kinetics. Our method of weighting particle traces on a ‘frame-by-frame’ basis is broadly applicable to analysis of all submicron particles independent of the particle speed, the nature of the specimen, or trace-linking algorithms, and represents an important improvement in the continued use of multiple particle tracking to enhance the delivery of therapeutics across major biological barriers.