Predicting Long-term Temperature Increase for Time-Dependent SAR Levels with a Single Short-term Temperature Response

Abstract

Purpose

Present a novel method for rapid prediction of temperature in vivo for a series of pulse sequences with differing levels and distributions of specific energy absorption rate (SAR).

Methods

After the temperature response to a brief period of heating is characterized, a rapid estimate of temperature during a series of periods at different heating levels is made using a linear heat equation and Impulse-Response (IR) concepts. Here the initial characterization and long-term prediction for a complete spine exam are made with the Pennes’ bioheat equation where, at first, core body temperature is allowed to increase and local perfusion is not. Then corrections through time allowing variation in local perfusion are introduced.

Results

The fast IR-based method predicted maximum temperature increase within 1% of that with a full finite difference simulation, but required less than 3.5% of the computation time. Even higher accelerations are possible depending on the time step size chosen, with loss in temporal resolution. Correction for temperature-dependent perfusion requires negligible additional time, and can be adjusted to be more or less conservative than the corresponding finite difference simulation.

Conclusion

With appropriate methods, it is possible to rapidly predict temperature increase throughout the body for actual MR examinations. (200/200 words)

Introduction

In MRI of the human body, a radiofrequency magnetic (B1) field is applied to excite nuclei to a state where they produce a detectable signal. In the conductive tissues of the human body, the B1 field induces electrical currents resulting in heating of tissues. This heating must be regulated by controlled application of the B1 field in order to avoid adverse effects, which can arise either if the temperature of the entire human body is escalated enough to cause discomfort or thermoregulatory distress, or if the temperature in a local region of the body is elevated for a sufficient degree and period of time to cause damage to tissues. The International Electrotechnical Commission has provided guidelines for the maximum temperature to be achieved by the whole body and any region within it (1). Although it is understood that temperature is more directly related to the hazards of RF heating than is the power absorbed per unit mass (Specific energy Absorption Rate; SAR), typically only SAR is used to ensure RF safety in MRI. This is partly due to the ability to relate transmitted RF power to SAR with a variety of methods, often involving numerical simulations of the human body for estimation of maximum local SAR, and partly to the perceived complexity and uncertainty which prediction of temperature from known transmitted power levels may add to the assurance of safety. For these reasons the IEC has also recommended limits on SAR for both the whole body and any 10-gram region within it (1), but it is ultimately temperature through time (or thermal dose) that is directly related to subject safety. Thus, methods to improve the accessibility and utility of temperature predictions and assessments for MRI should be pursued for meaningful safety assurance.

Data exists relating the likelihood of damage to specific tissues to the thermal dose within each tissue (2). There is some indication that such data may be used in future versions of safety guidelines (1). Importantly, different tissues have both different sensitivity to temperature through time (2) and different relations between SAR and temperature (3). Taken together, it is apparent that more meaningful estimates of safety could be made based on temperature through time than with SAR. To demonstrate that conservative real-time estimates of temperature through time throughout the human body are feasible during an MRI examination, which can contain many different sequences with different SAR levels, here we introduce a method for rapid, conservative temperature estimation based on application of a linear bioheat equation and with knowledge of the temperature response to a brief period of heating. For convenience, this will be referred to as the proposed Impulse Response (IR) based method, since it relies on impulse response-type concepts.

Theory

For any linear relationship between applied power and temperature change, if the temperature increase response to a brief period of heating can be characterized (with either calculation or experiment), then a convolution of that response with the timecourse of the heating will give an accurate prediction of the temperature through the entire timecourse. Linearity has been used to combine spatial precomputed temperature responses of multi-transmit array fields for safety evaluations for a fixed heating exposure (4, 5). In this work the superposition of thermal responses through time is used to compute temperature through the entire duration of an MRI exam with a time-varying spatial distribution of the fields.

As an example of what can be considered a linear relationship, consider the Pennes’ bioheat equation (6)

$$\rho c\frac{\partial T}{\partial t}=\nabla ·(k\nabla T)-W{\rho }_{bl}{c}_{bl}(T-T_{bl})+Q+\rho \mathit{SAR}$$ [1]

where c is heat capacity, ρ is tissue mass density, k is thermal conductivity, W is a parameter related to blood perfusion rate (7,8), Q is the heat generated by metabolism, SAR is Specific energy Absorption Rate and the subscript _bl indicates values for blood flowing in to the local region. This equation can be re-written as

$$\rho c\frac{\partial T}{\partial t}=\nabla ·(k\nabla T)-W{\rho }_{bl}{c}_{bl}T+W{\rho }_{bl}{c}_{bl}{T}_{bl}+Q+\rho \mathit{SAR}$$ [1a]

This equation remains linear in T for variable SAR and T_bl. By associating T_bl with core body temperature, which can increase during studies with high whole-body SAR, we can ensure increases in core body temperature are represented in calculations of local temperature. Eq.[1] remains linear if, for example, the continuity of the heat flow from the surface of the body is imposed using a linear boundary condition such as (9)

$$-k{(\nabla T·n_0)}_S=H(T_S-T_A)$$ [2]

where (∇T · n₀)_S indicates the temperature gradient normal to the skin surface at the surface of the skin, H is a heat loss coefficient that can be made to represent effects of convection and radiation, T_S is the local skin temperature, and T_A is the local air temperature. Heat loss due to perspiration can be included as published previously (9), however, only if they are assumed constant and not varying locally with local temperature.

The most important parameter that must remain time-invariant for Eq. 1 to remain linear is W. Because W is expected to increase with local temperature and serves to help remove heat from regions experiencing high temperature, the estimates of temperature that result from keeping W at a baseline level will be mostly conservative in calculating maximum local temperature for MRI applications (though perhaps not in tumors for applications with very strong temperature increase such as in hyperthermia (10)), meaning they should overestimate temperature in regions of high heating and thus help to ensure subject safety. Changes in W may be significant at high SAR, and can help to moderate local temperature increase (11). A challenge to including blood perfusion variations in simulations for safety assurance is in the significant differences in physiological responses between different human subjects (12). Even though keeping W constant is a conservative assumption, in some cases it can be less conservative than satisfying the SAR safety limits (13). Later in this work we will introduce a method to correct for temperature-dependent W, but for now W will be assumed constant through time at each location.

For any linear relationship it is possible to compute the absolute temperature T(r, t) at each location r and time t as given by the sum of an equilibrium temperature T₀(r) corresponding to a steady state temperature with no SAR applied, a temperature increase T_i(r, t) which depends on the spatial and temporal SAR distribution, and a temperature T_ibl(r, t), the increase in blood temperature of Eq. [1], or core body temperature. Absolute temperature can be determined at any time with the summation of T_i, T₀, and T_ibl.

$$T(r,t)=T_0(r)+T_i(r,t)+T_{\mathit{ibl}}(r,t)$$ [3]

From the linearity of Eq. [1], and from the definition in Eq. [3] it is possible to determine an independent relationship between SAR, blood temperature increase, and temperature increase which allows the implementation of a fast temperature computation method. If we define T_bl0 as the blood temperature at the initial equilibrium condition, T₀ as initial equilibrium local temperature, and ΔT_bl as the increase in blood temperature after the exam begins such that T_bl=T_bl0+ΔT_bl, then substituting [3] into [1] produces

$$\rho c\frac{\partial T_0}{\partial t}+\rho c\frac{\partial T_i}{\partial t}+\rho c\frac{\partial T_{\mathit{ibl}}}{\partial t}=\nabla ·(k\nabla T_0)+\nabla ·(k\nabla T_i)+\nabla ·(k\nabla T_{\mathit{ibl}})-W{\rho }_{bl}{c}_{bl}(T_0-T_{bl0})-W{\rho }_{bl}{c}_{bl}{T}_i-W{\rho }_{bl}{c}_{bl}{T}_{\mathit{ibl}}+Q+\rho \mathit{SAR}+W{\rho }_{bl}{c}_{bl}\mathrm{\Delta }{T}_{bl}$$ [4]

At thermal equilibrium with no SAR applied this becomes

$$\rho c\frac{\partial T_0}{\partial t}=\nabla ·(k\nabla T_0)-W{\rho }_{bl}{c}_{bl}(T_0-T_{bl0})+Q$$ [5]

assuming Q is time and temperature invariant.

Subtracting eq. [5] from eq. [4] we find

$$\rho c\frac{\partial T_i}{\partial t}+\rho c\frac{\partial T_{\mathit{ibl}}}{\partial t}=\nabla ·(k\nabla T_i)+\nabla ·(k\nabla T_{\mathit{ibl}})-W{\rho }_{bl}{c}_{bl}{T}_i-W{\rho }_{bl}{c}_{bl}{T}_{\mathit{ibl}}+\rho \mathit{SAR}+W{\rho }_{bl}{c}_{bl}\mathrm{\Delta }{T}_{bl}$$ [6]

Analogously, assuming that blood temperature increase ΔT_bl is independent of local SAR and local temperature, for linearity it is possible to separate eq. [6] into

$$\rho c\frac{\partial T_i}{\partial t}=\nabla ·(k\nabla T_i)-W{\rho }_{bl}{c}_{bl}{T}_i+\rho \mathit{SAR}$$ [7]

and

$$\rho c\frac{\partial T_{\mathit{ibl}}}{\partial t}=\nabla ·(k\nabla T_{\mathit{ibl}})-W{\rho }_{bl}{c}_{bl}{T}_{\mathit{ibl}}+W{\rho }_{bl}{c}_{bl}\mathrm{\Delta }{T}_{bl}$$ [8]

T₀(r) needs to be determined only once with any desired method and is not influenced by the application of external heat sources, but depends only on the properties of the body. On the contrary, T_i(r, t) is strongly affected by SAR(t) and T_ibl(r, t) by blood temperature increase. In this work we first focus on the fast computation of the term T_i which is the only one related to SAR, and then the same method is applied to the fast computation of the term T_ibl as a function of whole-body SAR through time.

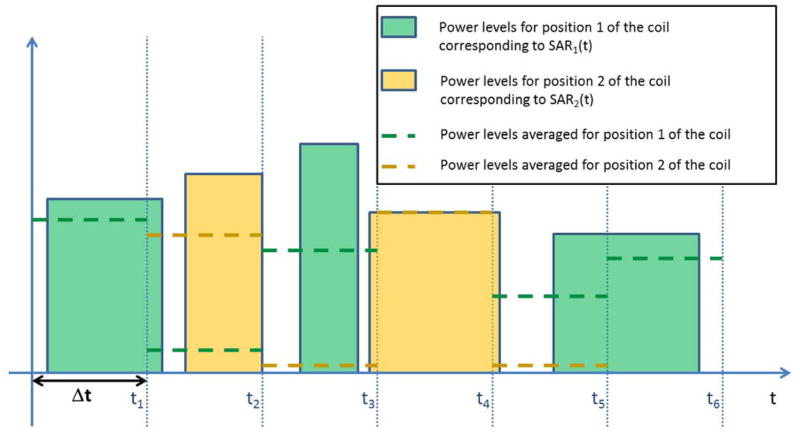
Assuming that the parameters in Eq. [7] except SAR and T_i are time invariant, the time dependent SAR(t) can be exactly described by a sequence of M SAR_m(t) spatial distributions each occurring at a different time (Fig. 1)

Figure 1.

Schematic of the power levels for two different real-time SAR distributions (solid bars), and the levels averaged over time segments having duration Δt (dashed lines).

$$\mathit{SAR}(t)={\mathit{SAR}}_1(t)+{\mathit{SAR}}_2(t)+\cdots =\sum _{m=1}^M{\mathit{SAR}}_m(t)$$ [9]

Here, each term SAR_m(t) could be associated with a different location of the subject in the magnet during a single exam or, in the case of parallel transmission, a different sequence with a pulse design resulting in a different SAR distribution. For the method of rapid prediction used here, time is then segmented into a finite number of steps, N, with pre-determined duration Δt and the variation of the intensity of each of these M unique SAR distributions through time is expressed in terms of a fundamental rectangular function SAR_m,0(t) having positive, constant amplitude c_m,0 for time 0 < t < Δt and no amplitude for t < 0 or t > Δt such that each SAR_m can be expressed

$${\mathit{SAR}}_m(t)=\frac{c_{m,1}}{c_{m,0}}{\mathit{SAR}}_{m,0}(t-\mathrm{\Delta }t)+\frac{c_{m,2}}{c_{m,0}}{\mathit{SAR}}_{m,0}(t-2\mathrm{\Delta }t)+\cdots =\sum _{n=1}^N\frac{c_{m,n}}{c_{m,0}}{\mathit{SAR}}_{m,0}(t-n\mathrm{\Delta }\mathrm{t})$$ [10]

where each single segment SAR_m,0(t − nΔt) has the same duration Δt and spatial distribution and is scaled in amplitude with the use of the constants c_m,n. The term c_m,n is calculated as the whole body SAR associated with the term SAR_m(t) in eq. [9] (SAR_m,wb) averaged over the n^th time interval

$$c_{m,n}=\frac{1}{\mathrm{\Delta }t}{\int }_{(n-1)\mathrm{\Delta }t}^{n\mathrm{\Delta }t}{\mathit{SAR}}_{m,wb}(t)dt$$ [11]

Substituting eq. [10] in eq. [9]

$$\mathit{SAR}(t)={\mathit{SAR}}_1(t)+{\mathit{SAR}}_2(t)+\cdots =\sum _{m=1}^M{\mathit{SAR}}_m(t)=\sum _{m=1}^M\sum _{n=1}^N\frac{c_{m,n}}{c_{m,0}}{\mathit{SAR}}_{m,0}(t-n\mathrm{\Delta }\mathrm{t})$$ [12]

and then, substituting eq. [12] into eq. [7], we find

$$\rho c\frac{\partial T_i}{\partial t}=\nabla ·(k\nabla T_i)-W{\rho }_{bl}{c}_{bl}{T}_i+\rho \sum _{m=1}^M\sum _{n=1}^N\frac{c_{m,n}}{c_{m,0}}{\mathit{SAR}}_{m,0}(t-n\mathrm{\Delta }\mathrm{t})$$ [13]

where the input heat source is seen as the series of N different heating periods or SAR segments, each of which can have contributions from any of M different SAR distributions, and where the contribution from each single segment with a given SAR distribution SAR_m,0(t − nΔt) satisfies eq. [7] as

$$\rho c\frac{\partial T_{im,n}}{\partial t}=\nabla ·(k\nabla T_{im,n})-W{\rho }_{bl}{c}_{bl}{T}_{im,n}+\rho \frac{c_{m,n}}{c_{m,0}}{\mathit{SAR}}_{m,0}(t-n\mathrm{\Delta }t)$$ [14]

generating the temperature increase T_im,n(r, t). Because of the linearity (14) of eq. [13], the solution T_i(r, t) is given by the sum of the M × N solutions of eq. [14]

$$T_i(r,t)=\sum _{m=1}^M\sum _{n=1}^N{T}_{im,n}(r,t)$$ [15]

In order to predict the temperature increase after a number of arbitrary SAR segments, for each spatial distribution SAR_m(t) it is necessary to first characterize (with any available method) the temperature increase response T_im,0(r, t), when a single segment SAR_m,0(t) is applied. For example, as in this work, the temperature response T_im,0 can be characterized with a numerical finite difference method, where its time steps would be a small fraction of Δt, the duration of segment SAR_m,0. Due to the linearity and the causality of eq. [13] and [14], each T_im,n(r, t) will differ from T_im,0 by a time shift nΔt and a scaling factor c_m,n/c_m,0:

$$T_{im,n}(r,t)=\frac{c_{m,n}}{c_{m,0}}{T}_{im,0}(r,t-n\mathrm{\Delta }t)$$ [16]

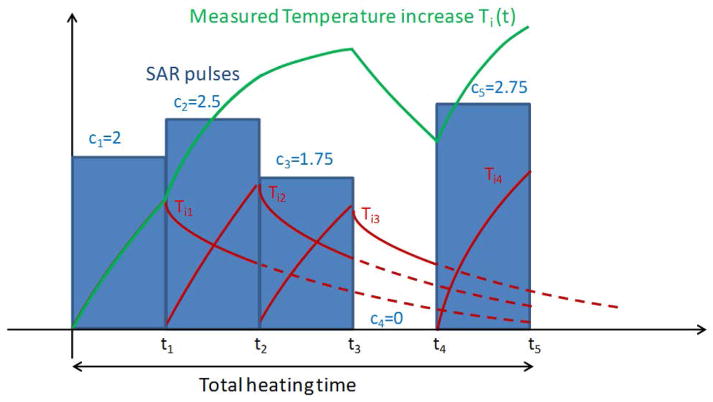
Once all the responses T_im,0(r, t) have been characterized, from eq. [15] and eq. [16] the temperature at any time during the series of SAR levels can be calculated by convolving the temperature response curves T_im,0(r, t) with the temporal sequence of N SAR scaling values, and summing this result for all M distributions, as shown in Fig. 2, according to the formula

Figure 2.

Schematic of the Impulse-Response calculation concept. A pre-determined baseline temperature increase response, T_i0, is shifted and scaled proportionally to the SAR levels averaged over each time segment (blue bars) to produce separate temperature increase responses (red curves) that can be summed to compute the overall resulting temperature (green curve).

$$T_i(r,t)=\sum _{m=1}^M\sum _{n=1}^N\frac{c_{m,n}}{c_{m,0}}{T}_{im,0}(r,t-n\mathrm{\Delta }t)$$ [17]

Consideration of Time-dependent Core Body Temperature, T_bl

For consideration of MRI where the system body coil is used for transmission, as in the majority of clinical imaging today, the potential effects of whole-body SAR on core body temperature should be considered. Here the blood temperature term T_bl in eq. [1] is computed with a method described previously (15) where core body temperature is related via a nonlinear model to a variety of factors including the heat absorbed by whole-body SAR (SAR_wb), heat generated by metabolism, and heat lost through respiration, perspiration, radiation, convection, and by conduction to the patient table. The mathematics for all this is described very thoroughly in the literature (15) and is not repeated here.

The computed blood temperature T_bl can be used either directly in Pennes’ bioheat equation as a time dependent parameter, or as an external excitation for fast temperature computation methods where the term W ρ_blc_blΔT_bl in eq. [8] is mathematically equivalent to a SAR distribution with the spatial distribution determined by the blood perfusion, and time-varying power levels determined by the value of blood temperature increase. In our work, we have used the first approach in the full finite difference method, and the second approach in the impulse response method presented here.

Periodic correction for temperature-dependent local blood perfusion

The human body has the ability to moderate temperature increases through several thermoregulatory mechanisms, one of which is the change of local blood perfusion. One model which correlates the parameter W in eq.[1] (which, again, is related to blood perfusion) and local temperature is (16)

$$W(r)=\{\begin{array}{cc}{W}_0(r)& T(r)\le 39°\mathrm{C}\\ W_0(r)(1+S_B(T(r)-39))& 39°\mathrm{C}<T(r)<44°\mathrm{C}\\ W_0(r)(1+5S_B)& T(r)\ge 44°\mathrm{C}\end{array}$$ [18]

where W₀ is the basal blood perfusion coefficient, and S_B is a coefficient set to 0.8 °C⁻¹.

The fast method presented here is based on the linearity of eq. [1], and the dependence of W on local temperature would make eq. [1] nonlinear. Here we propose a method to approximate the effects of changes in W in the fast IR-based method presented above.

If we express W as

$$W(r)=W_0(r)+\mathrm{\Delta }W(r,t)$$ [19]

then according to eq. [18],

$$\mathrm{\Delta }W(r,t)=\{\begin{array}{cc}0& T(r)\le 39°\mathrm{C}\\ W_0(r)S_B(T(r)-39)& 39°\mathrm{C}<T(r)<44°\mathrm{C}\\ W_0(r)5S_B& T(r)\ge 44°\mathrm{C}\end{array}$$ [20]

Substituting eq.[19] into eq.[1] yields

$$\rho c\frac{\partial T}{\partial t}=\nabla ·(k\nabla T)-W_0{\rho }_{bl}{c}_{bl}(T-T_{bl})-\mathrm{\Delta }W{\rho }_{bl}{c}_{bl}(T-T_{bl})+Q+\rho \mathit{SAR}$$ [21]

Let us now define

$$T_C=T_{NC}+\mathrm{\Delta }T$$ [22]

Where T_NC corresponds to the temperature obtained with the method with no correction for blood-temperature dependent perfusion corresponding to T as described in the previous sections, ΔT corresponds to a correction term due to the change in blood perfusion, and T_C is the corrected temperature.

Substituting eq. [22] in eq[1] yields

$$\rho c\frac{\partial (T_{NC}+\mathrm{\Delta }T)}{\partial t}=\nabla ·\left(k\nabla (T_{NC}+\mathrm{\Delta }T)\right)-W_0{\rho }_{bl}{c}_{bl}\left((T_{NC}+\mathrm{\Delta }T)-T_{bl}\right)-\mathrm{\Delta }W{\rho }_{bl}{c}_{bl}\left((T_{NC}+\mathrm{\Delta }T)-T_{bl}\right)+Q+\rho \mathit{SAR}$$ [23]

Eq.[23] can be separated exactly into two equations

$$\rho c\frac{\partial T_{NC}}{\partial t}=\nabla ·(k\nabla T_{NC})-W_0{\rho }_{bl}{c}_{bl}(T_{NC}-T_{bl})+Q+\rho \mathit{SAR}$$ [24]

(which has been solved as described in the previous sections), and

$$\rho c\frac{\partial \mathrm{\Delta }T}{\partial t}=\nabla ·\left(k\nabla (\mathrm{\Delta }T)\right)-W_0{\rho }_{bl}{c}_{bl}\mathrm{\Delta }T-\mathrm{\Delta }W{\rho }_{bl}{c}_{bl}\left((T_{NC}+\mathrm{\Delta }T)-T_{bl}\right)$$ [25]

Eq. [25] can be solved with use of a previously-demonstrated method of applying a low-pass spatial filter [17] that approximates the effects of thermal conduction (the first term on the right hand side of the equality) while computing the remaining terms analyitically, and provides a solution in a short time. All details for executing this method are given explicitly elsewhere [17]. The term ΔW in Eq. [25] is assumed to be constant through the time interval Δt: this is a reasonable assumption for time intervals Δt ≤ 60 s, considering that temperature change does not happen very rapidly, and given that temperature is the state variable in Eq.[25]. While SAR may change rapidly during an exam, within the bounds of common regulatory limits on SAR, temperature is naturally much more steady and slowly-varying.

Methods

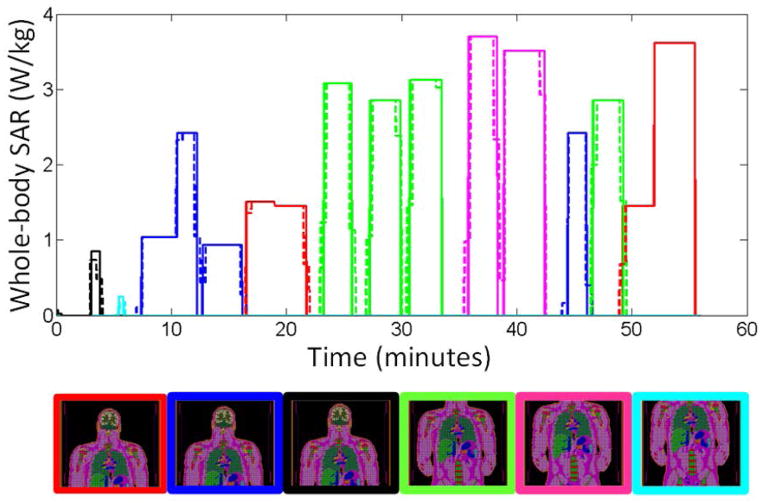
The approach described above was applied to the computation of temperature increase due to SAR absorption recorded from an actual whole-body spine exam, with high-SAR sequences and six different body positions, as shown in Figure 3. For each of the six positions of the body in the MR system, the electromagnetic fields and the corresponding SAR distribution were simulated for a body-sized birdcage coil, as shown in Fig. 5(a), operating at 128 MHz using commercial simulation software (XFDTD; Remcom, State College, PA). For all six SAR distributions the tissue temperature responses T_im,0(r, t) were obtained by applying a SAR segment of duration Δt =30 s and computed for the whole duration of the MRI exam. Temperature simulation was performed with in-house finite difference C++ code (3). In this method, thermal conduction to constant-temperature air is implemented directly at the outer surface of the body with Eq [1] as previously described and validated (3). The model for thermal simulations had a grid resolution of 5mm in each dimension and 891507 nodes in tissue. All calculations were executed on a computer workstation having 8 GB of RAM and eight 3 GHz CPU processors, though no parallel processing was used in this implementation. Temperature increases were computed by solving the Pennes’ Bioheat Equation with time-varying SAR and with time-varying core body (blood) temperature, and both with and without temperature-dependent perfusion following the methods described above. To calculate a thermal dose for comparison to what might actually cause damage in tissues, we also computed the Cumulative Equivalent Minutes at 43 °C (CEM43) as (2, 11) CEM43= ∫ R^{(43°C−T(t))}dt where R is 0.5 for T(t)>43 °C, 0.25 for 39 °C <T(t)<43 °C, and 0 for T(t)<39 °C.

Figure 3.

Whole-body SAR levels recorded throughout an actual spine exam (solid line) and the levels averaged over 30-second intervals for rapid calculation (dashed line). The position of the body in the coil at each time is indicated in the figure below the line plot with a border corresponding to the color of the line at that time. The length of these figures is set to indicate the portion of the body physically within the body coil at the given time.

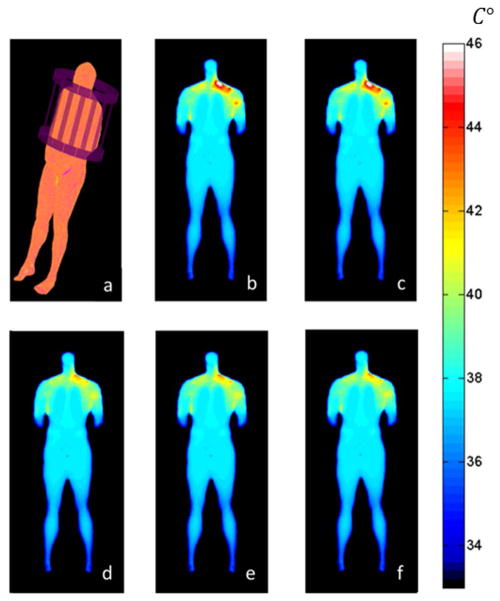
Figure 5.

Plots of (a) the geometry of the problem with a whole-body model in a birdcage coil at 128 MHz, and the temperature distribution on a coronal plane through the subject at the end of the exam (when temperature is highest) as calculated (b) with no allowance for temperature-dependent local perfusion using a full finite difference algorithm and (c) the fast IR-based method proposed here, and then with temperature-dependent blood perfusion using (d) a full finite difference algorithm and (e, f) the fast IR-based method with Δt = 30s (e), and Δt = 120s(f).

Accuracy of the method was assessed by comparing the calculated temperature distribution with that calculated using the full finite difference method with a timestep size of 1s (determined empirically to be near the largest to ensure stability and reliably produce accurate results), and where the SAR was not averaged over each Δt according to eq. [11]. Time evolution of the whole body SAR and local 10g SAR were averaged over 6 minute intervals (Fig. 4), and the maximum values were compared to the IEC safety limits. An examination of the effect of time step size on calculated temperature was performed by repeating the simulations with Δt =60,120,and 300 seconds.

Figure 4.

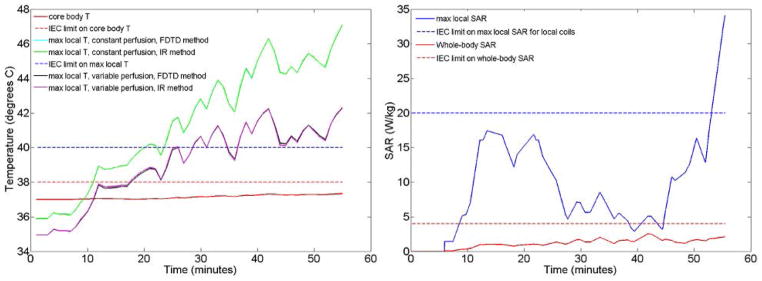
Key temperatures (left) and SAR levels (right) throughout the sequence simulated. Local temperature and local SAR are plotted for locations where absolute maximum local temperature and absolute maximum local 10g-averaged SAR occur. All SAR levels are averaged over a 6-minute sliding window in time for comparison to regulatory guidelines, which makes them fluctuate differently than the whole-body SAR in Fig. 3 which is interval-wise constant. Local temperatures curves have been plotted for both the finite difference and the impulse response computation methods, showing that they are almost indistinguishable from each other. Allowance for increase in local perfusion creates a less conservative and less restrictive prediction of local temperature. Maximum local temperature and maximum local SAR occur at different locations and have different behaviors through time. Also maximum temperature with constant and variable perfusion rates occur at different locations, as apparent from the different starting temperatures.

Results

Fig. 4 shows key SAR and temperature values throughout the exam simulated. Both the whole-body SAR and maximum 10g local SAR shown here are calculated as the 6-minute average for comparison to pertinent IEC limits. Whole-body SAR reaches a value of 2.53 W/kg, which does not exceed the limit of 4 W/kg in first level controlled operating mode. Core body temperature increases by about 0.35°C over the course of the exam and does not exceed the IEC limit of 38°C in this simulated high-SAR exam. The 10g local SAR, however, reaches a maximum value of 34 W/kg at the end of the exam (when relatively high-power pulse sequences are applied for longer than 6 consecutive minutes with the subject in a position with relatively high local SAR) which exceeds the IEC limit of 20 W/kg for local coils (there is currently no specified limit on local SAR for volume coils). Also local temperature, in the cases of both constant perfusion and temperature dependent perfusion, exceeds the recommended limit of 40°C. When no thermoregulatory effects are considered the maximum estimated temperature is 47.3 °C, while with temperature dependent perfusion the maximum value is equal to 42.3 °C, located in one shoulder. Here the maximum local temperature and maximum local SAR are plotted at locations where their absolute maximum values occur. These are two different locations since SAR and temperature do not always correlate well in space. Maximum local temperature and maximum local SAR also have very different behaviors through time. The CEM43 thermal dose at the location of maximum temperature increase was 2.25 minutes at the end of the exam, well below the 15 minute limit used previously (11).

Figure 5 shows the temperature distribution at the end of the examination as determined with a full Finite Difference calculation and with the proposed fast IR-based method both with and without allowance for temperature-dependent local perfusion. When no thermoregulatory effects are considered, the results obtained with the fast computation method predict a maximum temperature increase less than 1% from that of the full finite difference method. For this case, the method provides an accurate calculation of the temperature in a short time, capable of calculating the temperature rise throughout a one-hour exam in less than 2 minutes, while the computation time required for the full finite difference method on the same system is more than one hour. Thus using the fast IR-based method accelerates the calculation about 30-fold when Δt =30 s. When the time-varying local perfusion is included with the use of a low-pass spatial filter described in detail previously (17), the maximum temperature increase in the fast method is seen to differ by less than 8% from that in the full finite-difference method, with the fast method being more conservative. Our method with the addition of the spatial filter accelerates the calculation about 27-fold respect the full-finite difference method when Δt =30 s. Increasing Δt to 120s results in a very similar temperature distribution with approximately a 120-fold acceleration over the finite difference method.

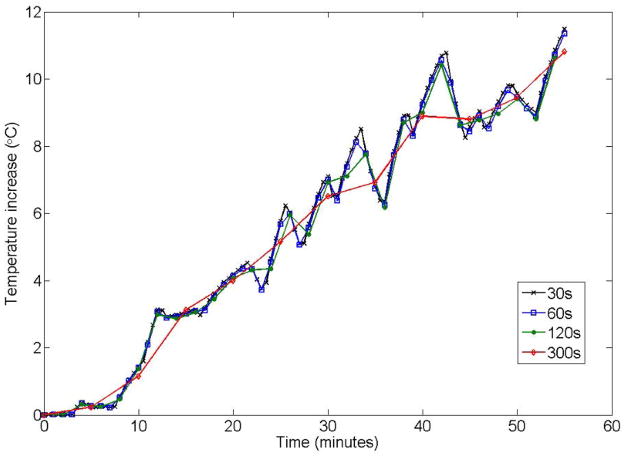
Figure 6 shows a comparison of temperature increase through time at the location of its maximum value when Δt =30,60,120, and 300 seconds. It is seen that the method is stable and that the temperature values are fairly accurate (matching the values at the smallest Δt and thus also for the full finite difference simulation) at the times they are calculated for all these choices of Δt, but that for larger values of Δt, detail in the temporal dimension is lost. In these simulations (for the SAR timecourse simulated here) values of Δt up to 120 seconds track changes in temperature through time due to fluctuations in SAR fairly well.

Figure 6.

Effect of Δt on calculated temperature. While choices of Δt up to 300s result in good accuracy at times when temperature is calculated explicitly, temporal resolution in the temperature timecourse is lost as Δt increases.

Discussion

Here we have described a method that utilizes a pre-determined tissue temperature response to a short period of heating in order to provide rapid, conservative calculation of the temperature throughout an entire exam. In our evaluations for a realistic MRI exam in an anatomical model, this fast IR-based method can utilize timesteps one to two orders of magnitude larger than a full finite difference method (yielding accelerations on the order of one to two orders of magnitude) depending on the temporal resolution desired. While in principle this approach could be used in real time for safety assessment purposes, for accurate use the pre-determined temperature response would need to be characterized either for the specific human subject in the magnet or for several human body models (4) to allow selection of a reasonable match to the geometry of each specific subject without being overly conservative. While it is possible to perform more advanced calculations accounting for more phenomena and heat transfer mechanisms (7, 18), inclusion of the mechanisms considered here should provide reasonable and conservative results in a very short time. In cases where pre-computed SAR distributions are currently used to determine local maximum SAR levels throughout the body during MRI, much of the necessary work for the proposed fast IR-based method is already available. The proposed method could potentially be used to perform real-time temperature prediction and adjustment of time-average sequence power levels to avoid exceeding unsafe temperatures or thermal doses. Here the characterization of the temperature response to a short period of heating with a given SAR distribution was performed with a full finite difference simulation. In principle, however, this characterization could be performed with a measurement of the tissue response to a brief period of heating (20). In this case, it may be possible to predict maximum temperature increase without the specific knowledge of the SAR spatial distribution, of the parameters distribution in the tissues, such as c, W, k, ρ, or the relationship among them but with the only assumption that they are time invariant and that the relationship is linear. Unfortunately, although MR methods used to measure temperature increase (21) have been used to measure that resulting from RF heating in phantoms and in vivo (22–24), there is currently no method that can do so accurately with high spatial resolution in all tissues with insensitivity to motion. The method could be further accelerated with parallel computing implementation, but it already provides results in a time short enough to allow real-time temperature prediction during an MRI exam. While larger values of Δt could provide even faster computation of the temperature increase, the duration of the time interval needs to be short enough that the length of the sequences of the exam is comparable with a multiple of Δt. With a Δt of 30s showing very good accelerations and accuracy, we did not see a need to explore larger increments here, but that could be the subject of future work. Towards future development and applications, our code can be shared with interested persons who contact the first author.

We have introduced versions of the proposed fast method that do and do not consider an increase in local perfusion. While not including variation in local perfusion may be considered conservative, it can also become too restrictive if MRI settings are limited according to its results. The methods we have introduced for considering changes in local perfusion are much less conservative than the approach that does not, but more conservative than a full finite difference simulation.

Our calculations indicate that the IEC-recommended limit on maximum local temperature for first-level control mode will be exceeded even though the limits for core temperature and increase in core temperature are not. The relationship between temperature and perfusion used here allows for a maximum perfusion rate that is 6 times the baseline value. In a recently-published work (11), maximum perfusion rates were allowed to reach much higher levels (maximum perfusion rate of 33 times the baseline in skin and 16 times the baseline in muscle and fat) with an exponential, rather than linear increase with temperature. Use of such relationships with our method should similarly reduce the restrictiveness of the predictions, and a single calculation allowing all perfusion rates to reach a maximum of 16 times the baseline levels in our model resulted in a maximum temperature of 41 °C. In that same work (11), a thermal dose limit based on CEM43 was shown to be less restrictive when temperature-dependent perfusion levels were allowed to increase with temperature. The limits chosen for CEM43 were 15 minutes in muscle, skin, fat, and bone, and 2 minutes elsewhere. In our work, at the location of maximum temperature increase was in muscle tissue and the CEM43 at that location was 2.25 minutes at the end of the exam, well below the 15 minute limit used previously (11).

It is important to note that maximum local temperature and maximum local SAR occur at different locations and have very different behavior through time. Given that it is temperature through time that is most relevant to safety, this difference through space and time illustrates the importance of moving beyond SAR alone in safety assurance for MRI.

The high rate of acceleration seen here would be expected to decrease as the number of voxels increases if mesh resolution (and thus timestep size in the full finite difference calculation) remain unchanged. Our method with the addition of the spatial filter accelerates the calculation about 27-fold respect the full-finite difference method, with the spatial filter requiring about 10% of the time. Indicating the total number of voxels with v, the computation time of our acceleration method based on the impulse response without the addition of the low-pass filter is proportional to v, as is the case for full finite difference methods. The computation time of the filter alone, which relies heavily on fast Fourier transforms, is proportional to v log v. T he filter itself is only applied to maximize accuracy of calculating the effects of perfusion rates differing from the baseline rate, and it is thus not applied if local temperatures do not exceed a certain threshold (39° in the model used here). For example, if a 1mm³ resolution had been used instead of the 5mm³ resolution of our model (a 125-fold increase in the number of voxels), the proposed method would be between 16 and 30 times faster than the full finite difference method neglecting the requirement for smaller timestep size in the full finite difference calculation, being higher in cases where the threshold temperature for increased perfusion is not reached for much of the exam, and it is about 16 in cases where high local temperatures exist from the beginning to the end of the exam. Considering the linear relationship between grid dimensions and time step size required for stability in the full finite difference approach, however, the method proposed here (which has no dependence of timestep size on spatial resolution) would be 80 to 150 times faster than the full finite difference method.

With choices of Δt larger than 30s, it is possible to get even greater acceleration rates. With Δt up to 300s the method is stable and gives accurate results, but with loss of temporal resolution (Fig. 6). Thus, the choice of Δt will be limited by the rate of fluctuations in SAR for a given exam. In the exam simulated here, Δt as large as 120 s was able to calculate fluctuations in temperature fairly well, and provide a 120-fold acceleration compared to the full finite difference method.

Here we have validated the method for a case with a human subject at several locations within a large volume coil. While we see no reason that the method would not also work for more local excitation coils or situations with regions of high local SAR (as may be experienced with conductive implants), validation of the method in these cases would require further study.

Conclusion

We have introduced a method for accelerating temperature calculations based on the analysis of the thermal impulse response of a subject to a short SAR segment. We have also included a method to approximate the effect of changes in blood perfusion due to local temperature increase. Hence, we have demonstrated that temperature throughout an entire human body can be calculated for an entire MRI examination very rapidly for real-time safety assurance. Results of the accelerated method match those of a full finite difference simulation very well. While temperature is more closely related to risk than is SAR, regular use of temperature in safety assurance for MRI would require a consensus regarding models of physical properties and physiological responses for conservative, but reasonable estimates.