Noncontact diffuse correlation tomography of human breast tumor

Abstract.

Our first step to adapt our recently developed noncontact diffuse correlation tomography (ncDCT) system for three-dimensional (3-D) imaging of blood flow distribution in human breast tumors is reported. A commercial 3-D camera was used to obtain breast surface geometry, which was then converted to a solid volume mesh. An ncDCT probe scanned over a region of interest on the mesh surface and the measured boundary data were combined with a finite element framework for 3-D image reconstruction of blood flow distribution. This technique was tested in computer simulations and in vivo human breasts with low-grade carcinoma. Results from computer simulations suggest that relatively high accuracy can be achieved when the entire tumor is within the sensitive region of diffuse light. Image reconstruction with a priori knowledge of the tumor volume and location can significantly improve the accuracy in recovery of tumor blood flow contrasts. In vivo imaging results from two breast carcinomas show higher average blood flow contrasts (5.9- and 10.9-fold) in the tumor regions compared to the surrounding tissues, which are comparable with previous findings using diffuse correlation spectroscopy. The ncDCT system has the potential to image blood flow distributions in soft and vulnerable tissues without distorting tissue hemodynamics.

1. Introduction

The current clinical standard for breast screening is x-ray mammography, with recent evidence confirming that mammograms offer substantial benefit for early cancer detection. However, mammography is hampered by a significant false-positive rate, which is especially high for women with dense breast tissue. The dense breast population is a particularly important subset of women because they experience higher incidence and mortality rates from the disease.^1,2 Other imaging diagnostic tools for breast cancers include x-ray computed tomography (CT), magnetic resonance imaging (MRI), positron emission tomography (PET), and ultrasonography.^3–5 Most of these imaging methods are prohibitively expensive and generally only provide tumor morphological information with low specificity. Moreover, some of these techniques (e.g., CT and PET) expose patients to ionizing radiation.^6,7

The autonomic growth and spread of malignant tumors are dependent on increased angiogenesis arising from the increased metabolic demand.⁸ Since functional alternations in tumors often appear earlier than detectable morphological changes, functional imaging of tumor hemodynamics and metabolism is a new strategy for early cancer diagnosis.⁹ Near-infrared (NIR) diffuse optical technologies provide a noninvasive and relatively inexpensive tool for functional imaging of tumor hemodynamics in deep microvasculature up to several centimeters.^10–13 The most commonly used NIR diffuse optical spectroscopy/tomography (DOS/DOT) can quantify total hemoglobin concentration (THC) and blood oxygen saturation (${\mathrm{StO}}_2$) in tumors.^14,15 DOS/DOT has been used over several decades to detect oxygenation alternations in breast tumors.^16–20 For example, THC was found up to 2-fold higher in malignant lesions than nearby healthy tissues.¹⁵ More recently, a novel NIR diffuse correlation spectroscopy (DCS) technique has also been developed for direct measurement of blood flow index (BFI) in deep tissues.²¹ A few pilot studies of breast tumors using DCS have found increased blood flow inside the tumor in contrast to surrounding normal tissues.¹⁰ Real-time monitoring of breast tumor blood flow response to neoadjuvant chemotherapy also demonstrated the potential of DCS for assessing cancer therapies.^22,23

Despite advances in DCS technologies, there have been limited imaging applications of diffuse correlation tomography (DCT) for tumor detection. An early probe–tissue contact-based DCT approach was applied to tissue phantoms²⁴ but was disadvantaged in vivo due in part to compression-induced hemodynamic alterations. A few noncontact-based DCT examinations have been conducted using the camera lenses positioned between a sample and optical fibers connected to source and detection elements.^25,26 These arrangements, however, were only tested on the brain of small animals with limited probing depth ($<5\mathrm{mm}$). Another limitation of these imaging studies was their reliance on analytical solutions that assumed a simple semi-infinite flat tissue geometry.

Our group has recently developed a novel noncontact DCT (ncDCT) system enabling three-dimensional (3-D) imaging of deep tissue blood flow distribution without contacting the tissue.^21,27,28 Our ncDCT system employs two sets of optical lenses to project source and detector fibers, respectively, onto the tissue surface. The separation of source and detector paths allows for the arrangement of large source–detector distances, thus enabling probing deep tissues up to centimeters. Furthermore, a finite-element-method (FEM) based facilitation of ncDCT image reconstruction for arbitrary tissue geometry is pioneered and integrated into an open software package (NIRFAST), designed originally for DOT.²⁹ Initial validation efforts for the innovative ncDCT system have been made using computer simulations and tumor-like phantoms on a simple slab-shaped tissue boundary (i.e., semi-infinite geometry).²¹

This paper reports our first step to adapt the ncDCT system for in vivo imaging of blood flow distribution in human breast tumors. We used a commercial 3-D camera (NextEngine, California) to obtain breast surface geometry and then converted it to a solid volume mesh for ncDCT image reconstruction. Computer simulations were carried out to characterize the performance of an ncDCT system for imaging an anomaly (tumor) with varied flow contrasts and depths inside the tissue volumes under different surface boundaries. The malignant tumors inside human breasts (determined by ultrasound imaging) were then scanned using the ncDCT probe, and high tumor-to-normal flow contrasts were observed in the reconstructed images. To the best of our knowledge, we demonstrate, in this report, the first 3-D blood flow contrast imaging of human breast tumors using the noninvasive ncDCT.

2. Materials and Methods

2.1. Noncontact Diffuse Correlation Tomography System

2.1.1. Instrumentation

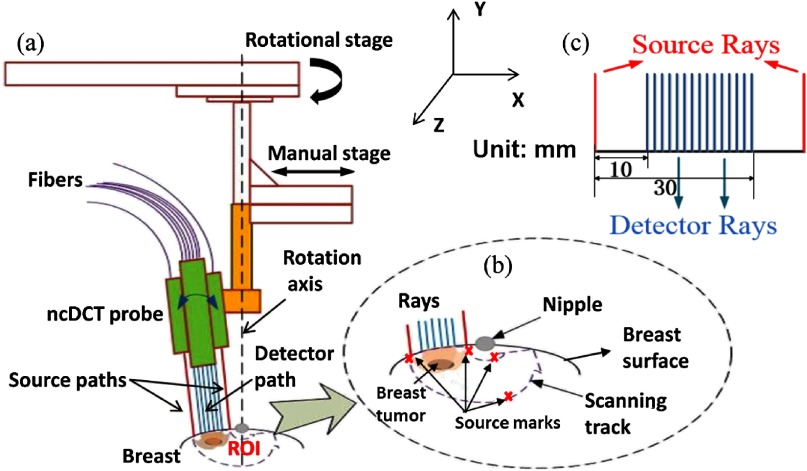
As reported previously,²¹ our ncDCT probe is a lens-focused apparatus, which has two identical source paths and one detector path configured in a linear array (Fig. 1). In each source path, output from a multimode source fiber (WF200/220/245, CeramOptec, Massachusetts) connected to a laser (825 nm) on the DCS instrument is projected onto the tissue through lenses [Figs. 1(a) and 1(b)]. Fifteen single-mode detector fibers (SM800-5.6-125, Fibercore, California) are equally spanned in the detector path connected to a detector array. The source–detector (S–D) separations vary from 10 to 30 mm, thus enabling up to $\sim 15\mathrm{mm}$ penetration depth [Fig. 1(c)].²¹ Two long coherence lasers at 825 nm (coherence length $>5\mathrm{m}$, CrystaLaser, Nevada) emit light to tissue through individual source paths, alternatively. The photons traveling through the tissue sample are collected by the detector array of 15 avalanche photodiodes (APD, Perkin Elmer, Canada) through the detector path. A multichannel autocorrelator (Correlator.com, New Jersey) takes the APD outputs and calculates 15 correlation functions simultaneously. A motorized stage was integrated into the optical system, which rotates the ncDCT probe around the nipple for scanning a region of interest (ROI) on the breast surface [Fig. 1(b)]. The outcomes from this scanning are the boundary data of intensity autocorrelation functions collected at hundreds of S–D pairs on the ROI (see the example in Fig. 4).

Fig. 1.

The schematic of the rotational probe in noncontact diffuse correlation tomography (ncDCT) system. (a) A motorized rotational stage was used to drive the ncDCT probe to scan over a region of interest (ROI) on the breast surface. The rotation axis was aligned through the nipple. (b) During ncDCT probe scanning, source and detector rays were adjusted to be perpendicular to the breast surface over the ROI. The two source pairs at first and last scanning steps were marked using a mark pen. (c) Fifteen detector fibers and two source fibers were projected on the breast surface with the S–D separations spanning from 10 to 30 mm.

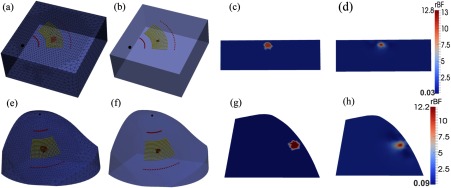
Fig. 4.

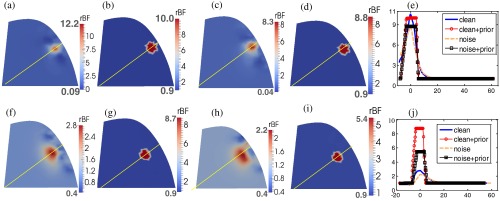
Recovery of anomaly blood flow contrasts inside the slab-shaped and breast-shaped volume meshes. A sphere anomaly with a diameter of 10 mm and 10-fold flow contrast was placed at 7 mm beneath the surface of background tissue volumes. (a) and (e) show the original assigned anomalies inside the volume meshes with sources and detectors aligned on the mesh surfaces; (b) and (f) show the reconstructed anomalies with full-width at half-maximum (FWHM) thresholds; (c) and (g) show the two-dimensional (2-D) cross-section views of original flow contrast distributions through the anomaly centers; (d) and (h) show the 2-D cross-section views of reconstructed flow contrast distributions.

2.1.2. Diffuse correlation spectroscopy/diffuse correlation tomography principle and noise model

In DCS theory, the correlation diffusion equation ²⁴ is used to model the propagation of electric field temporal autocorrelation function, $G_1(\mathit{r},\tau )=⟨E(\mathit{r},t)\cdot E^{*}(\mathit{r},t+\tau )⟩$, in biological tissues:

$$\nabla \left[\right(\frac{D(\mathit{r})}{v})\nabla G_1(\mathit{r},\tau )]-[{\mu }_{\mathrm{a}}(\mathit{r})+\frac{1}{3}{\mu }_{\mathrm{s}}^{\prime }(\mathit{r})k_0^2\alpha ⟨\mathrm{\Delta }{r}^2(\tau )⟩]G_1(\mathit{r},\tau )=-S(\mathit{r}),$$ (1)

where $\mathit{r}$ is the position vector, $v$ is the light speed in the medium, ${\mu }_{\mathrm{a}}(\mathit{r})$ is the medium absorption coefficient, ${\mu }_{\mathrm{s}}^{\prime }(\mathit{r})$ is the medium reduced scattering coefficient, $S(\mathit{r})$ is the source term, $k_0$ is the wavenumber of the incident light, and $D(\mathit{r})\equiv \upsilon /3[{\mu }_{\mathrm{s}}^{\prime }(\mathit{r})+{\mu }_{\mathrm{a}}(\mathit{r})]\approx v/3{\mu }_{\mathrm{s}}^{\prime }(\mathit{r})$ is the medium photon diffusion coefficient. The normalized electric field autocorrelation function $g_1(\mathit{r},\tau )=G_1(\mathit{r},\tau )/G_1(\mathit{r},0)$ is related to the light intensity autocorrelation function $g_2(\mathit{r},\tau )$ measured by DCS devices through the Siegert relation.¹¹ The decay of the correlation function depends on ${\mu }_{\mathrm{a}}(\mathit{r})$, ${\mu }_{\mathrm{s}}^{\prime }(\mathit{r})$, the mean square displacement $⟨\mathrm{\Delta }{r}^2(\tau )⟩$ of the moving scatterers inside the tissue, and a unitless factor $\alpha$ that represents the fraction of moving scatterers (primarily red blood cells) to total scatterers. A diffusion model $⟨\mathrm{\Delta }{r}^2(\tau )⟩=6D_B(\mathit{r})\tau$ is often employed with $D_B(\mathit{r})$ denoting the heterogeneous “effective” diffusion coefficient. The term $(1/3){\mu }_{\mathrm{s}}^{\prime }(\mathit{r})k_0^2\alpha ⟨\mathrm{\Delta }{r}^2(\tau )⟩$ in Eq. (1) is then reshaped as ${\mu }_{\mathrm{a}}^d(\mathit{r},\tau )=2{\mu }_{\mathrm{s}}^{\prime }(\mathit{r})k_0^2\alpha D_B(\mathit{r})\tau$, and is considered as “effective dynamic absorption”²¹ due to dynamic processes on the correlation with $\tau$. The combined $\alpha D_B(\mathit{r})$ term is referred to as BFI.^12,24,30

Because of the mathematical similarity of correlation diffusion equation [Eq. (1)]²⁴ and photon diffusion equation (for DOS/DOT),³¹ DCT is conceptualized as a formulation of DOT, which computes $G_1(\mathit{r},\tau )$ instead of photon fluence rate, by updating “static absorption” ${\mu }_{\mathrm{a}}(\mathit{r})$ to ${\mu }_{\mathrm{a}}^{\text{total}}(\mathit{r},\tau )={\mu }_{\mathrm{a}}(\mathit{r})+{\mu }_{\mathrm{a}}^d(\mathit{r},\tau )$, and reconstructing ${\mu }_{\mathrm{a}}^{\text{total}}(\mathit{r},\tau )$ instead of ${\mu }_{\mathrm{a}}(\mathit{r})$ only.²¹ The implementation of this concept into the FEM-based light transport and image reconstruction modules for modeling both complex geometries and heterogeneous media has been accomplished by adopting NIRFAST (for DOT)²⁹ as a shortcut.²¹

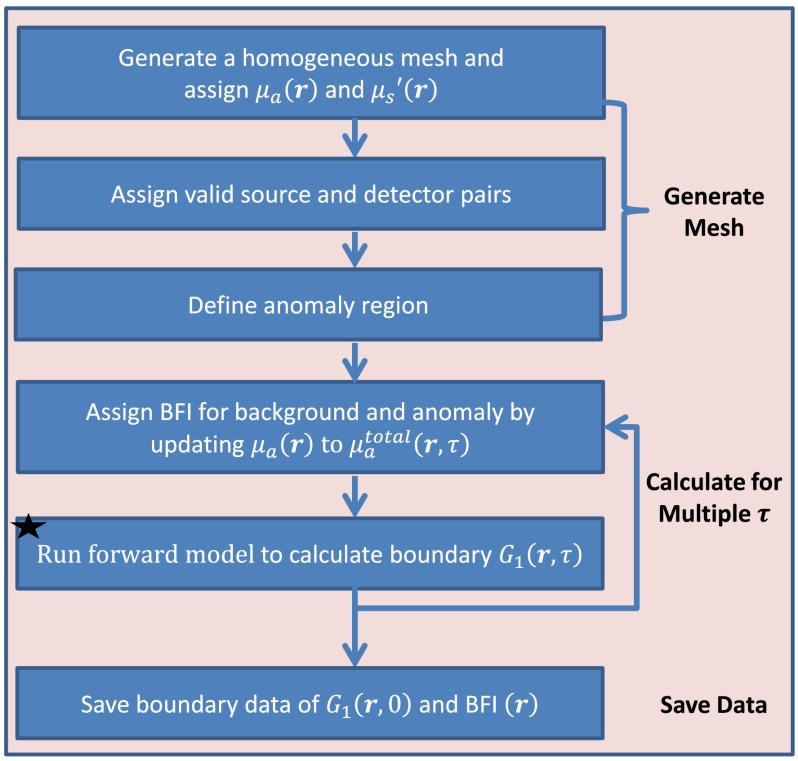
Figures 2 and 3 illustrate the main commands executed for solving the forward and inverse problems, respectively, in ncDCT using modified NIRFAST. A homogeneous background tissue volume mesh with assigned initial optical properties of ${\mu }_{\mathrm{a}}(\mathit{r})$ and ${\mu }_{\mathrm{s}}^{\prime }(\mathit{r})$ is first generated in the forward solution (see Fig. 2). All S–D pairs corresponding to the actual or simulated scanning of ncDCT probe are placed on the surface of the background mesh. However, only those with valid links between sources and detectors are configured as effective pairs for image reconstruction. An anomaly region (mimicking a tumor) inside the background volume mesh is then defined and assigned a BFI contrast relative to the surrounding background. Based on the designed distributions of BFIs, ${\mu }_{\mathrm{a}}^{\text{total}}(\mathit{r},\tau )$ is updated for each voxel inside the entire tissue volume within a certain range of $\tau$. The autocorrelation functions $G_1(\mathit{r},\tau )$ for multiple $\tau$ from all effective S–D pairs are then calculated by running the forward model. The boundary BFI data at all effective S–D pairs are then extracted by fitting $G_1(\mathit{r},\tau )$ to the analytical solution of Eq. (1) under semi-infinite homogeneous geometry. It is noted that even though the forward problem simulates the light propagation in breast tumor models, some commands (e.g., “Run forward model…”) are also executed for experimental data reconstruction.

Fig. 2.

Flowchart outlining the sequence and commands used in the modified NIRFAST to generate a forward model for ncDCT.

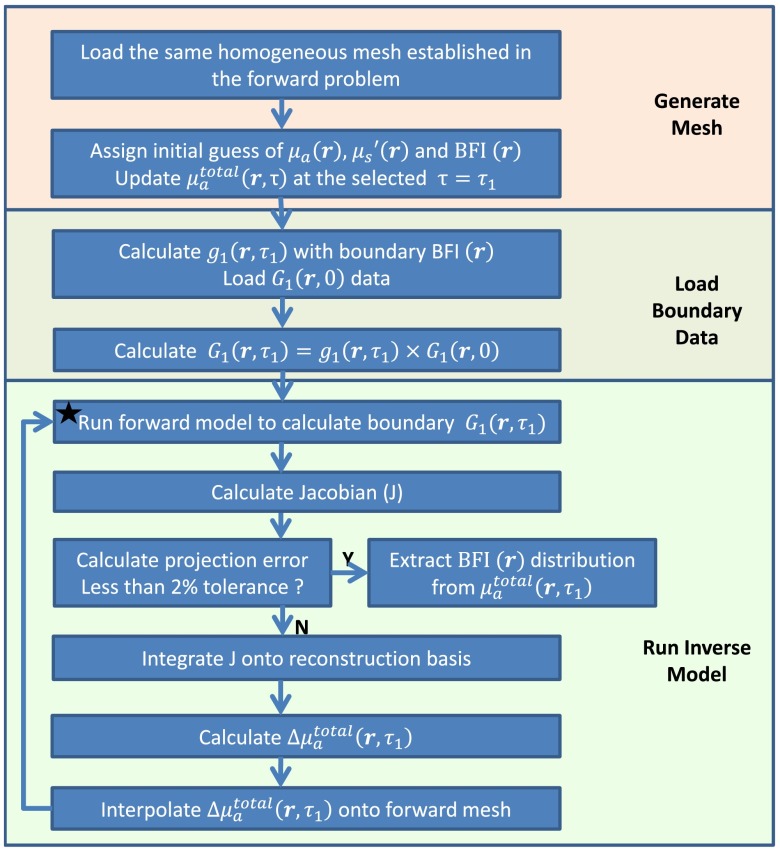
Fig. 3.

Flowchart outlining the sequence and commands used in the modified NIRFAST to solve diffuse correlation tomography inverse problem.

To evaluate noise influence on image reconstruction through simulations, randomized noise varying at different $\tau$ is generated based on a noise model originally derived for DCS.^32,33 The noise level depends on the detected photon count rate (i.e., light intensity) at each S–D pair, which is estimated using the light intensity detected from in vivo breast tissues (see Sec. 2.3). This noise is applied to the simulated $g_2(\mathit{r},\tau )$ curves. Multiple $g_2(\mathit{r},\tau )$ curves with noise are generated for each S–D pair and then averaged to improve the signal-to-noise ratio (SNR). This simulation mimics our in vivo measurements and data averaging process in human breasts (see Sec. 2.3). Finally, $g_2(\mathit{r},\tau )$ curves are converted to $G_1(\mathit{r},\tau )$ curves to generate boundary BFI data.

Solving the inverse problem for image reconstruction is conducted on a second mesh with a coarse finite element division (pixel basis)^29,34 (see Fig. 3). Initial values of background BFI and optical properties [${\mu }_{\mathrm{a}}(\mathit{r})$ and ${\mu }_{\mathrm{s}}^{\prime }(\mathit{r})$] along with the selected $\tau$ ($\tau ={\tau }_1$ was specifically noted in Sec. 2.2.1) are assigned to generate a homogeneous inverse mesh. The simulated or measured boundary BFI data are converted to $g_1(\mathit{r},\tau )$ at the selected $\tau$ using the semi-infinite analytical solution of Eq. (1),^27,33,35,36 and further converted to $G_1(\mathit{r},\tau )$ by multiplying with $G_1(\mathit{r},0)$. The boundary $G_1(\mathit{r},\tau )$ is then input into the inverse model to reconstruct the ${\mu }_{\mathrm{a}}^{\text{total}}(\mathit{r},\tau )$ distribution inside the entire tissue volume. The BFI distributions are finally extracted through the definition of ${\mu }_{\mathrm{a}}^d(\mathit{r},\tau )$.

2.2. Computer Simulation Protocols

We conducted several computer simulations to characterize the performance of the ncDCT system. The first simulation tested the abilities of ncDCT in recovery of an anomaly (tumor) beneath the surfaces of a slab and a female plastic mannequin breast (Sec. 2.2.1). The second simulation evaluated the reconstruction accuracies of the anomaly with varied depths and flow contrasts in the same plastic mannequin breast. The influence of noise on ncDCT image reconstruction was also assessed and compared with the results without noise (Sec. 2.2.2). The last simulation applied a priori structural knowledge of the anomaly in the inverse mesh to improve the accuracy of flow image reconstruction (Sec. 2.2.3).

2.2.1. Reconstructions of a tumor in slab-shaped and breast-shaped tissues

To evaluate the reconstruction of an anomaly inside a background tissue volume with a simple semi-infinite geometry, a slab volume [dimension (mm): $100(H)\times 100(W)\times 40(D)$] was first generated in SolidWorks® (Dassault Systemes, Massachusetts) and then segmented into finite elements using ANSYS® (ANSYS, Pennsylvania). A total of 15,996 nodes were created with node distances of 3 and 6 mm in the ROI and the surrounding region, respectively [Fig. 4(a)]. Different mesh resolutions were employed to reduce the total node number while maintaining appropriate spatial resolution in the ROI. The segmented mesh nodes and elements information were then input into MATLAB® (MathWorks, Massachusetts) to generate all mesh files needed for the simulations with modified NIRFAST. The slab volume mesh represented a healthy background tissue volume. A spherical anomaly with a diameter of 10 mm mimicking a tumor was then placed at the ROI center, and the anomaly centroid location was 7 mm beneath the surface of background tissue volume [Fig. 4(a)]. Optical properties for both tumor and background tissues were set homogeneous throughout the entire slab as ${\mu }_{\mathrm{s}}^{\prime }=6.00{\mathrm{cm}}^{-1}$ and ${\mu }_{\mathrm{a}}=0.06{\mathrm{cm}}^{-1}$. The blood flow indices for the background and anomaly were set as $1\times {10}^{-8}{\mathrm{cm}}^2/\mathrm{s}$ and $10\times {10}^{-8}{\mathrm{cm}}^2/\mathrm{s}$, respectively, resulting in a 10-fold flow contrast between the tumor and surrounding normal tissues [Fig. 4(c)]. The ncDCT probe with a linear S–D array scanning rotationally over the ROI was simulated for 21 steps with 3 deg/step to collect the boundary data [Fig. 4(a)], where coordinates were calculated with MATLAB. There were a total of 42 sources and 315 detectors distributed on the ROI. Thus, 630 ($315\times 2$) S–D pairs were effectively available and used for image reconstruction. The autocorrelation functions $G_1(\mathit{r},\tau )$ from the effective S–D pairs were calculated by the modified NIRFAST software with $\tau$ ranging from 0 to $3.2\times {10}^{-5}\mathrm{s}$ (50 consecutive $\tau$). Reconstruction was conducted on the same mesh with a pixel basis of $20\times 20\times 25$ and a ${\tau }_1=8.7\times {10}^{-6}\mathrm{s}$. The $\tau$ selection has been discussed in our previous publication.²¹ The presenting anomaly was extracted with the full-width at half-maximum (FWHM) criterion³⁷ on the reconstructed DCT image. The averaged BFI and the center location of the reconstructed anomaly were computed by averaging the BFIs and node coordinates within the anomaly.

In order to assess the ability of ncDCT for imaging a tumor inside breast, we conducted a computer simulation on a female plastic mannequin breast. The surface geometry of the mannequin breast with source marks of ncDCT [Fig. 1(b)] was scanned by a commercial 3-D camera (NextEngine, California), which was further converted to a solid breast tissue volume using SolidWorks. To align the sources and detectors of ncDCT on the breast model surface for image reconstruction, a scanning plane perpendicular to the breast surface and crossing the optical rays of 2 sources and 15 detectors was created in SolidWorks. The scanning plane was first aligned passing through the first pair of source marks and then rotated step-by-step around the rotation axis with an angle increment of 3 deg (Fig. 1), matching our experimental procedure [Fig. 4(a)]. At each step, the sources and detectors along the optical rays were projected onto the surface of the solid breast model.

Similar to the slab meshing, the solid breast volume was segmented into finite elements with node distances of 3 and 6 mm in the ROI and surrounding region. A solid volume mesh [largest dimension (mm): $100(H)\times 78(W)\times 70(D)$] with total nodes of 14,717 was generated for simulations. A spherical tumor with a diameter of 10 mm and a node distance of 3 mm was then placed at the ROI center, and the tumor centroid location was 7 mm beneath the breast surface [Fig. 4(e)]. For comparisons, we assigned the same optical properties and BFI contrast as those used in slab-tissue simulation. The boundary data were also collected in the same manner over the ROI on the breast surface. Identical breast-shaped mesh with a pixel basis of $20\times 20\times 30$ and ${\tau }_1=8.7\times {10}^{-6}$ s were used for image reconstruction.

2.2.2. Quantification of tumor location and flow contrast in the breast-shaped tissue

This simulation used the same tumor model in the breast-shaped mesh with the same configuration and optical properties, as assigned in Sec. 2.2.1 [see Fig. 4(e)]. The tumor was placed beneath the surface of the breast-shaped mesh with varied central depths from 7 to 15 mm at 1 mm increment/step. It is noted that breast tumors with their centroid locations within the sensitive region of diffuse light (i.e., the detected penetration depth of NIR light is $\sim 1/2$ of the S–D separation)^35,38,39 were our most interested study population, since more reliable reconstructions can be generated. At each depth, the tumor-to-normal flow contrast was increased from 0- to 20-fold at 5-fold increment/step. The reconstructed tumor depth was characterized as the shortest distance from the reconstructed anomaly center to the breast mesh surface. The measurement accuracy of the ncDCT system was assessed by quantifying the discrepancies between the reconstructed and assigned values in tumor central location and flow contrast.

To evaluate the noise influence on image reconstruction, we added noise on the subsets of boundary data collected from the tumor with 10-fold flow contrast throughout all varied depths. Forty $g_2(\mathit{r},\tau )$ curves with noises were generated and averaged at each effective S–D pair for DCT image reconstruction.

2.2.3. Reconstruction with a priori knowledge of tumor location and volume

To improve the reconstruction accuracy of anomaly blood flow contrast, the soft-constraint method^37,40–42 in NIRFAST package was tested in this simulation. A priori structural information of tumor (i.e., central location and tumor volume) was included in the inverse mesh by labeling the nodes in the inverse mesh according to the regions of tumor or surrounding tissues. A regularization matrix L was applied to the penalty term in the minimization function for the DCT inverse problem, which was equivalent to applying a Laplacian-type filter to minimize variation within each region. Simulations were done with the spherical anomaly (10-fold flow contrast and $\text{diameter}=10\mathrm{mm}$) placed at either 7 or 15 mm central depth beneath the breast surface and with or without noise.

2.3. In-Vivo Blood Flow Imaging of Human Breast Tumor

To explore the feasibility of an ncDCT imaging system in clinical applications, two female patients with low-grade carcinoma were recruited from University of Kentucky Comprehensive Breast Care Center, with signed informed consent approved by the University of Kentucky Institution Review Board. The patient lay in a supine position and the major tumor lesion inside the breast was determined by radiologists using ultrasound imaging prior to the optical measurement. The tumor mass margins along the radio direction were marked on the ultrasound images. The ncDCT probe was driven by a step motor to scan rotationally around the breast nipple over the region of breast tumor. The scanning procedures were similar to those described in Sec. 2.2.1. Briefly, 15 and 21 scanning steps were taken to cover the tumor bearing regions in the two breasts, respectively. Forty $g_2(\mathit{r},\tau )$ curves were collected from each S–D pair for each patient, and two source pairs at the beginning and ending steps of scanning were visually marked on the breast surface as the references for the alignment of sources and detectors on the surface mesh. The surface geometry of the breast with the source marks was then recorded by the 3-D camera for image reconstruction. Following the ncDCT measurement, a commercial frequency-domain tissue oximeter (Imagent, ISS, Illinois)⁴³ was used to measure ${\mu }_{\mathrm{s}}^{\prime }$ and ${\mu }_{\mathrm{a}}$ of the breast tissue at three different locations. The averaged ${\mu }_{\mathrm{s}}^{\prime }$ and ${\mu }_{\mathrm{a}}$ over the multiple sites were used as initial inputs for flow image reconstruction.

The solid breast mesh of the patient was created in the same way as that of the plastic mannequin breast (Sec. 2.2.1). Boundary BFIs on the breast mesh surface were then extracted by fitting the measured $g_2(\mathit{r},\tau )$ curves from effective S–D pairs. These boundary BFI data were then calibrated to the BFIs collected at the first scanning step, where the tissue underneath the probe was outside the tumor region and thus assumed to be homogeneous and healthy. The calibrated boundary data were finally used for DCT image reconstruction.

3. Results

3.1. Noncontact Diffuse Correlation Tomography Recovered an Anomaly Inside Both Slab-Shaped and Breast-Shaped Tissue Volumes with Similar Accuracies in Simulations

Figure 4 illustrates 3-D [Figs. 4(a), 4(b), 4(e), and 4(f)] and two-dimensional (2-D) cross-section [Figs. 4(c), 4(d), 4(g), and 4(h)] views of blood flow distributions in the slab-shaped (top panel) and breast-shaped (bottom panel) tissue volumes, respectively. Figures 4(a), 4(e), 4(c), and 4(g) show the originally assigned/simulated anomaly inside tissue volumes and Figs. 4(b), 4(f), 4(d), and 4(h) show the reconstructed results for comparisons. To clearly visualize the anomaly inside the tissue volume, 3-D background meshes were presented with 30% transparency of their original colors. The reconstructed anomalies were presented with FWHM thresholds in 3-D images [Figs. 4(b) and 4(f)] and without thresholds in 2-D cross-section views [Figs. 4(d) and 4(h)]. Table 1 summarizes the discrepancies between the assigned and reconstructed anomalies inside the slab-shaped and breast-shaped tissue volumes. These results indicate that the ncDCT system can recover the anomaly inside both slab-shaped and breast-shaped tissue volumes with similar accuracies.

Table 1.

Computer simulation results in recovering an anomaly^a inside slab-shaped and breast-shaped volume meshes.

	Anomaly central depth (mm)/% error	Anomaly diameter (mm)/% error	Peak flow contrast/% error	Average flow contrast/% error
Slab-shaped	6.4/8.6%	7.2/28%	12.8-fold/28%	9.3-fold/7%
Breast-shaped	6.6/5.7%	7.5/25%	12.2-fold/23%	8.1-fold/19%

^aA spherical anomaly with a diameter of 10 mm and 10-fold flow contrast was placed at 7 mm beneath the surface of background tissue volumes.

3.2. Higher Reconstruction Accuracy Achieved in Simulations when the Anomaly Was within the Sensitive Region of Diffuse Light

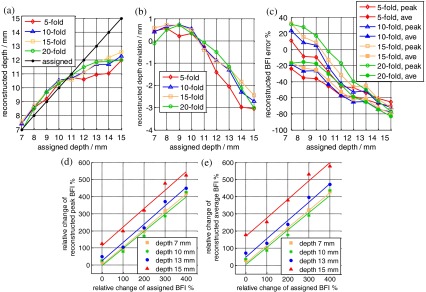
The reconstruction results with varied anomaly locations and flow contrasts are presented in Fig. 5. The discrepancies [Fig. 5(b)] between the reconstructed and assigned central locations of the anomaly were smaller than the mesh node distance (3 mm) at all depths. The reconstructed anomaly locations were more accurate in the sensitive region of diffuse light ($\text{errors}\le 0.5\mathrm{mm}$ at central $\text{depths}\le 10\mathrm{mm}$) compared to those in deeper depths.

Fig. 5.

Evaluation of reconstruction accuracy of ncDCT in the breast-shaped volume mesh. (a) and (b) show the center location and deviation of the reconstructed anomaly at different depths; (c) shows the percentage deviations of anomaly peak and average blood flow index (BFI) contrasts at different depths; (d) and (e) show the linear relationships between the assigned and reconstructed peak and average BFI contrasts at different depths.

Reconstruction errors in peak and average BFI contrast of the anomaly at varied center location and assigned flow contrasts are displayed in Fig. 5(c). The largest reconstruction errors in peak and average flow contrasts ranged from 31.4% to $-77.0\%$ and $-23.6\%$ to $-82.9\%$ respectively, through all varied depths and flow contrasts. Similarly, the reconstructed peak and average BFI contrasts were more accurate in the sensitive region of diffuse light (peak and average BFI underestimations $\le 27.8\%$ and 45.3%, respectively, at central $\text{depths}\le 10\mathrm{mm}$) compared to those in larger depths.

Figures 5(d) and 5(e) demonstrate the linear relationships between the assigned and reconstructed peak and average BFI contrasts. The relative anomaly flow contrast changes were well reconstructed from the chosen central depths of 7 mm (peak BFI: linear regression $\text{slope}=1.03$, $R^2=0.99$, and $p<0.001$; average BFI: linear regression $\text{slope}=1.02$, $R^2=0.99$, and $p<0.001$), 10 mm (peak BFI: linear regression $\text{slope}=1.01$, $R^2=0.97$, and $p<0.01$; average BFI: linear regression $\text{slope}=1.00$, $R^2=0.97$, and $p<0.01$), 13 mm (peak BFI: linear regression $\text{slope}=1.07$, $R^2=0.98$, and $p<0.01$; average BFI: linear regression $\text{slope}=1.07$, $R^2=0.98$, and $p<0.01$), and 15 mm (peak BFI: linear regression $\text{slope}=1.08$, $R^2=0.98$, and $p<0.01$; average BFI: linear regression $\text{slope}=1.08$, $R^2=0.98$, and $p<0.01$). The relationships between the assigned and reconstructed relative anomaly flow contrast changes from other tested depths were similar (results not shown here).

In total, these results indicate that relatively higher accuracies were achieved when the entire anomaly was within the sensitive depth of diffuse light. Also, even though the recovery of anomaly BFI contrasts was not as accurate as its location, the reconstructed anomaly BFI contrast changes were fairly accurate.

3.3. Noise Reduced Anomaly Recovery Accuracy in Simulations

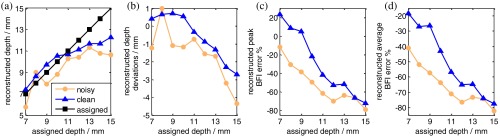
Figure 6 shows the ncDCT image reconstruction results with simulated noise added to the forward problem. For comparisons, images reconstructed from clean data (no noise) and noisy data are plotted together. When the anomaly volume was within the sensitive region of diffuse light (anomaly central $\text{depth}\le 10\mathrm{mm}$), the largest discrepancy between the reconstructed and assigned central locations of the anomaly was 1.2 mm [Fig. 6(b)], 0.8 mm greater than that (0.4 mm) without noise. Similarly, the largest reconstruction errors in peak and average flow contrasts were 33.2% and 31.0% larger than those reconstructed without noise [Figs. 6(c) and 6(d)]. Apparently, adding noise reduced reconstruction accuracies in recovery of the anomaly. However, the major conclusions drawn in Sec. 3.2 are still valid.

Fig. 6.

Noise influence on imaging accuracy of ncDCT. An anomaly was placed beneath the surface of the breast-shaped mesh with varied central depths from 7 to 15 mm. (a) and (b) show the center location and deviation of the anomaly at different depths, reconstructed with or without noise. (c) and (d) show percentage deviations of anomaly peak and average BFI contrasts at different depths, reconstructed with or without noise.

3.4. A Priori Knowledge of Anomaly Location and Volume Improved Flow Contrast Reconstruction in Simulations

Figure 7 demonstrates the improvements in the reconstruction of BFI contrasts using a priori knowledge of tumor location and volume in DCT image reconstruction. The top [Figs. 7(a)–7(e)] and bottom [Figs. 7(f)–7(j)] panels show the reconstructed results when the anomaly is at the central depth of 7 and 15 mm beneath the surface, respectively. In each panel, image results without/with a priori information and without/with noise are plotted, respectively. The transect plots [Figs. 7(e) and 7(j)] show the BFI distributions across the anomaly. The reconstruction accuracies in BFI contrasts were significantly improved when a priori knowledge of anomaly structural information was applied on data with and without noise. The peak/average BFI contrast errors were only 0.1%/4% (without noise) and 12.3%/12.3% (with noise), respectively, when using a priori structural information for the anomaly located in the sensitivity region of diffuse light [i.e., at the central location of 7 mm, Fig. 7(e)]. The BFI contrast improvement at the deeper central depth of 15 mm was also remarkable [Fig. 7(j)].

Fig. 7.

Comparison of anomaly reconstructions without and with a priori structural information. The top [(a)–(e)] and bottom [(f)–(j)] panels show the reconstructed flow contrast distributions of an anomaly (assigned a 10-fold flow contrast) located at 7 and 15 mm central depths, respectively. (a) and (f) show reconstructed results without the a priori structural knowledge of the anomaly; (b) and (g) show the reconstructed results with the a priori structural knowledge; (c) and (h) show the reconstructed results without the a priori structural knowledge and with noise. (d) and (i) show the reconstructed results with the a priori knowledge information and with noise. The flow contrast profiles crossing the yellow lines are shown in (e) and (j).

3.5. High Blood Flow Contrasts were Observed in Human Breast Tumors

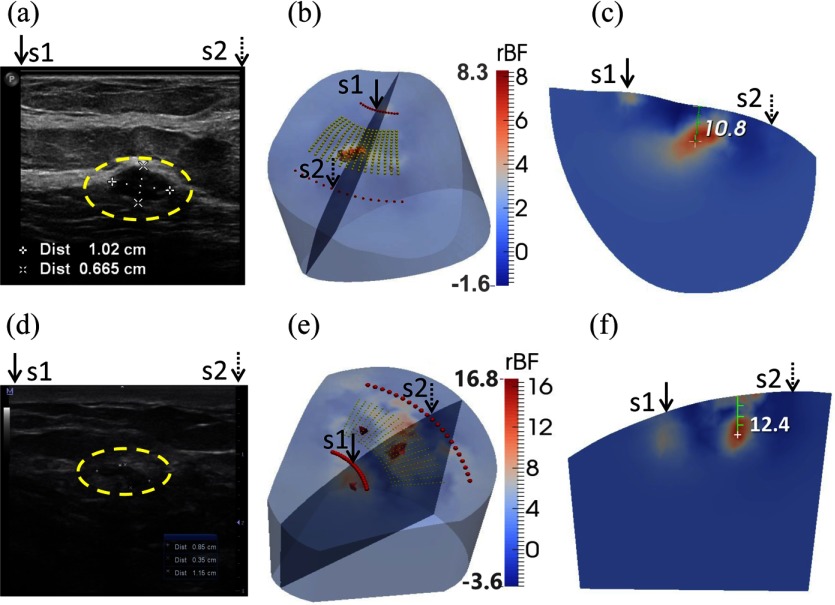
Two patients with low-grade carcinomas were imaged with our ncDCT system [Figs. 8(b), 8(c), 8(e), and 8(f)]. The first patient (P1) was a 59-year-old female who had ductal papilloma and low-grade adenocarcinoma in situ. According to the ultrasound imaging [Fig. 8(a)], the lesion with the dimension of $10.2\times 6.65{\mathrm{mm}}^2$ was located at 19.2 mm beneath the skin surface. For the comparison of ultrasound and ncDCT results, the cross-section view of tumor flow contrast image through the ultrasound imaging plane (along the line of ultrasound transducer) and across the overlapped two ncDCT sources (S1 and S2) is presented in the reconstructed 3-D image [Fig. 8(b)]. The dimension of the reconstructed tumor by ncDCT with the FWHM threshold was approximately $15.1\times 5.8{\mathrm{mm}}^2$ [Fig. 8(c)], which matched the ultrasound image [Fig. 8(a)]. However, the reconstructed tumor central location was 10.8 mm beneath the breast surface, which differed from the ultrasound image result (19.2 mm). The peak and average tumor blood flow contrasts were 8.3-fold and 5.9-fold, respectively. Note that measurement noise caused some artifacts with ${\mu }_{\mathrm{a}}^{\text{total}}(\mathit{r},\tau )$ lower than static ${\mu }_{\mathrm{a}}(\mathit{r})$ in the region bordering the reconstructed tumor, leading to some negative flow values.

Fig. 8.

Clinical examples of two low-grade carcinomas in situ. (a) Patient 1 (P1) ultrasound image taken from radio direction shows a $10.2\times 6.65{\mathrm{mm}}^2$ oval mass (inside the yellow dashed circle) with circumscribed margins parallel to the skin. The mass center is located at 19.2 mm beneath the skin surface. A core biopsy revealed a ductal papilloma with low-grade ductal adenocarcinoma in situ. (d) Patient 2 (P2) ultrasound image shows an $8.5\times 3.5{\mathrm{mm}}^2$ mass (inside the yellow dashed circle), located at 13.3 mm beneath the skin surface. A core biopsy revealed atypical ductal hyperplasia and low-grade carcinoma in situ. (b) and (e) show the reconstructed three-dimensional (3-D) tumor blood flow contrasts with FWHM thresholds for P1 and P2, respectively. The backgrounds are presented with 30% transparency of the original color clarity. For the comparison of ultrasound and ncDCT results, an ultrasound imaging plane along the transducer line and across the overlapped two specific sources (S1 and S2) is presented in the 3-D reconstructed image. (c) and (f) show the cross-section views of tumor flow contrast images through the ultrasound imaging planes, which can be directly compared to the 2-D ultrasound tumor images [(a) and (d)], respectively.

The second patient (P2) was a 49-year-old female, who had an atypical ductal hyperplasia and low-grade carcinoma in situ. Ultrasound images [Fig. 8(d)] show that the lesion centroid was located at 13.3 mm beneath the skin surface with the dimension of $8.5\times 3.5{\mathrm{mm}}^2$. Our ncDCT imaging results show a clear large tumor lesion with two small suspicious artificial anomalies [Fig. 8(e)]. The dimension of the reconstructed large tumor was approximately $12.3\times 5.1{\mathrm{mm}}^2$ [Fig. 8(f)] and its central depth was 12.4 mm beneath the breast surface, which fairly matched the ultrasound imaging result. The peak and average blood flow contrasts were 14.0-fold and 10.6-fold, respectively. Artifacts with negative flow values were also observed in the region bordering the reconstructed tumor.

The in vivo imaging results are consistent with our computer simulation results (see Secs. 3.1–3.3) in that the tumor central location can be accurately recovered when the tumor locates within the sensitive region of diffuse light.

4. Discussion and Conclusions

Since increased angiogenesis in breast tumor is commonly associated with blood flow increase, imaging of blood flow distribution in breast tissue is of great importance for tumor detection.⁸ The recently developed ncDCT in our laboratory provides a unique imaging tool for noncontact detection of tumor blood flow contrasts.²¹ We have previously demonstrated the ability of ncDCT for imaging blood flow contrast in tissue phantoms with a simple semi-infinite geometry.²¹ The remaining challenge of applying ncDCT for breast tumor imaging includes translating the FEM-based imaging algorithm to breast-shaped geometry and handling potential problems arising from the in vivo measurements. The goal of this study is to demonstrate the feasibility and evaluate the accuracy of ncDCT in detecting breast tumors.

Computer simulations were used to investigate the origins of flow reconstruction discrepancies. From the simulations, we observed similar reconstruction accuracies in blood flow contrasts and tumor central locations with slab-shaped and breast-shaped boundaries (see Fig. 4 and Table 1), indicating the ability of ncDCT for reconstructing tumor flow contrast in human breast with irregular geometry. Further simulations on breast-shaped geometry evaluated reconstruction accuracies when tumors had different flow contrasts and located at different depths. The results suggested that the reconstructed tumor location and flow contrasts were more accurate when the tumor volume was within the sensitive region of diffuse light (see Fig. 5). Based on photon diffuse theory, the penetration depth of diffuse light is $\sim 1/2$ of the S–D separation.^35,38,39 The largest S–D separation of ncDCT was 30 mm, allowing for a penetration depth up to $\sim 15\mathrm{mm}$. As such, it was not surprising that the reconstruction errors increased as the tumor center located at a depth deeper than 10 mm. The S–D separation (associated with light penetration depth) and SNR are two inter-related parameters that affect the utility of ncDCT. Future study should explore using source fibers with larger diameter to deliver greater light intensity for promoting the SNR and penetration depth.

In contrast to the recovery of tumor location, the reconstruction of tumor blood flow contrasts was more complicated. The reconstructed peak BFIs were overestimated when the tumor located closer to the breast surface and underestimated when the tumor located out of the sensitive region of diffuse light [see Fig. 5(c)]. By contrast, the reconstructed average BFIs were consistently underestimated. These observations are similar to those in DOT for reconstruction of tumor absorption contrasts.^44,45 It is known from the DOT practice that imaging sensitivity is higher at the shallow region beneath tissue surface.⁴⁶ Therefore, the reconstructed peak BFI from a single node close to the tissue surface tends to be overestimated. However, most of the reconstructed BFIs from the tumor node are prone to be underestimated due to the nature of inverse problem. Since the number of boundary data (S–D pairs) in ncDCT is much smaller than the unknowns to be solved (i.e., BFIs at all mesh nodes), the inverse problem is unstable,⁴⁷ leading to the underestimation.⁴⁴ In addition, according to the definition of ${\mu }_{\mathrm{a}}^{\text{total}}(\mathit{r},\tau )={\mu }_{\mathrm{a}}(\mathit{r})+{\mu }_{\mathrm{a}}^d(\mathit{r},\tau )$, BFI reconstruction errors come from both “static” and “dynamic” absorption coefficients. Therefore, dynamic flow contrast errors may be further enlarged by attributing all reconstruction errors of ${\mu }_{\mathrm{a}}^{\text{total}}(\mathit{r},\tau )$ to dynamic ${\mu }_{\mathrm{a}}^d(\mathit{r},\tau )$ while ignoring static errors of ${\mu }_{\mathrm{a}}(\mathit{r})$.

Similar to our previous findings,²¹ the relative changes of tumor flow contrasts can be accurately reconstructed in a large range of flow contrast variations [see Figs. 5(d) and 5(e)]. The observed linear relationships with a slope of close to “1” indicate the ability of ncDCT to capture tumor blood flow changes, which can be potentially used to longitudinally monitor tumor hemodynamic responses to interventions.

As expected, adding noise reduced the reconstruction accuracies (see Fig. 6). However, tumors can still be reconstructed clearly from the boundary data with noise (see Fig. 6), indicating the feasibility of ncDCT for in vivo breast tumor detection. More importantly, adding a priori knowledge of the tumor volume and location improved significantly reconstruction accuracy (see Fig. 7), which agrees with previous observations in DOT.^37,40,42

The results from the two patients with low-grade carcinoma showed higher blood flow contrasts in the tumor regions compared to the surrounding tissues (see Fig. 8). The reconstructed positions of the two tumors on the $x\text{-}y$ plane [see Figs. 8(c) and 8(f)] agreed well with ultrasound imaging results [see Figs. 8(a) and 8(d)]. The reconstructed tumor central depth from the second patient (P2) also matched the ultrasound image. For the first patient (P1), however, the reconstructed tumor central depth was at 10.8 mm beneath the breast surface, which did not match the ultrasound finding (19.2 mm). This was likely due to deep location of the tumor (P1), which was beyond the sensitive depth of diffuse light detected by our current system. To confirm this, we conducted computer simulations with the same location of tumor and similar level of measurement noise, and we found that the reconstructed tumor located at $\sim 8.5\mathrm{mm}$ beneath the breast surface (data are not shown). The simulation result agrees well with our in vivo measurement result.

Due to the difficulty of co-registering the 2-D ultrasound image and 3-D ncDCT image, it was not possible in this study to apply the a priori structural knowledge of tumors for improving the accuracy of image reconstruction in patients. Future study may utilize 3-D anatomical imaging modalities, such as MRI or CT, to obtain accurate priori structural information of the tumor.

The average tumor-to-normal flow contrasts of 5.9- and 10.6-fold observed from the two carcinomas are comparable to previously reported flow contrasts of 2- to 10-fold in breast tumors detected by DCS.^10,11 It should be noted that the tumor flow contrasts quantified previously by DCS may be underestimated due to the partial volume effect by the healthy tissues surrounding the tumor. In addition, the potential crosstalk between ${\mu }_{\mathrm{a}}$, ${\mu }_{\mathrm{s}}^{\prime }$, and BFI may also result in over- or underestimation of blood flow contrasts in both DCS and ncDCT.^33,35 According to the definition of ${\mu }_{\mathrm{a}}^{\text{total}}$, ${\mu }_{\mathrm{a}}$, ${\mu }_{\mathrm{s}}^{\prime }$ and $\alpha D_B$ variations cannot be completely separated unless they are independently measured. When assuming homogeneous ${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$ over the entire breast, the realistic heterogeneous ${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$ across the tumor can generate errors in tumor BFI contrasts. To overcome this limitation, a separate instrument enabling 3-D imaging of ${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$ distributions in the breast is needed (e.g., a frequency-domain or time-resolved DOT).^16,48–50

In conclusion, this paper reports the first flow image reconstruction results in human breast tumors using a novel ncDCT system. Results from computer simulations suggest that relatively high accuracy can be achieved when the entire tumor was within the sensitive region of diffuse light. Image reconstruction with a priori knowledge of the tumor volume and location can significantly improve the accuracy in recovery of tumor blood flow contrasts. In vivo imaging results from the two breast carcinomas show higher blood flow contrasts in the tumor regions compared to the surrounding tissues, which are comparable with previous findings. The noncontact design of the ncDCT system has the potential to be used for imaging blood flow distributions in soft and vulnerable tissues without distorting tissue hemodynamics.

Biographies

Lian He has recently graduated from the Department of Biomedical Engineering at the University of Kentucky. She has been working on the development of noncontact diffuse correlation spectroscopy/tomography (ncDCS/ncDCT) for noninvasive assessment of blood flow contracts in breast tumors. Her specialties include in vivo optical imaging system design, algorithm development, and clinical experiment design and data collection.

Yu Lin received his PhD degree in optical engineering in 2010. He was a postdoctoral scholar in the Department of Biomedical Engineering at the University of Kentucky and is now working in the College of Textile at NC State University. His research interests include digital color imaging in the textile industry, diffuse correlation spectroscopy/tomography in biological tissues, and multidiscipline applications with optical imaging technologies.

Chong Huang is a postdoctoral scholar in the Department of Biomedical Engineering at the University of Kentucky. His current research focuses on the development of noncontact diffuse correlation spectroscopy/tomography (ncDCS/ncDCT) and speckle contrast diffuse correlation spectroscopy (scDCT) for noninvasive assessment of blood flow and oxygenation in biological tissues. His specialties include optical/mechanical system design, signal processing, finite element analysis, physiological modeling, data collection, and image reconstruction.

Daniel Irwin is a graduate student in the Department of Biomedical Engineering at the University of Kentucky. His has been working on the development of noncontact diffuse correlation spectroscopy/tomography (ncDCS/ncDCT) and speckle contrast diffuse correlation spectroscopy (scDCT) for noninvasive assessment of blood flow contracts in animal and human tumors.

Margaret M. Szabunio is a professor of radiology and biomedical engineering, division chief of women’s radiology, and associate medical director of the Comprehensive Breast Care Center at the University of Kentucky. She has extensive experience in the detection of breast cancers and testing the efficacy of new therapeutic treatments.

Guoqiang Yu is an associate professor of the Department of Biomedical Engineering at the University of Kentucky. He has over 20 years of experience in the field of biomedical engineering and is currently leading a research group to develop various near-infrared diffuse spectroscopy and tomography systems for noninvasive imaging of deep tissue hemodynamics in animals and humans.