Etching of graphene in a Hydrogen-rich Atmosphere towards the Formation of Hydrocarbons in Circumstellar Clouds

Abstract

We describe a mechanism that explains the formation of hydrocarbons and hydrocarbyls from hydrogenated graphene/graphite; hard C–C bonds are weakened and broken by the synergistic effect of chemisorbed hydrogen and high temperature vibrations. Total energies, optimized structures, and transition states are obtained from Density Functional Theory simulations. These values have been used to determine the Boltzman probability for a thermal fluctuation to overcome the kinetic barriers, yielding the time scale for an event to occur. This mechanism can be used to rationalize the possible routes for the creation of small hydrocarbons and hydrocarbyls from etched graphene/graphite in stellar regions.

Introduction

Recent technological advances providing improved sensitivity in radio-astronomical receivers, and through the usage of large (sub)millimeter radio telescopes, have permitted to find numerous new chemical species in outer space. Several chemical processes lead to the formation of these molecules in gas-phase in space; e.g. ion-neutral, neutral-neutral, and radical-neutral reactions. In addition, reactions at the surface of the grains can also enhance the gas-phase abundance of these species when the temperature of dust grains increases above a critical value. Heating processes of dust grains can occur due to shocks, UV photon absorption from external sources, or by the proximity of a newly formed star. Nevertheless, the presence of complex molecules in photodissociation regions requires a continuous production mechanism that so far is not fully understood, although undestanding these chemical processes is crucial to study the chemical evolution of the interstellar gas in galaxies. Therefore, there is an increasing interest in detailed microscopic calculations leading to models that can explain the relative abundance of these molecules.

Carbonaceous particles are usually terminated on graphene/graphite-like layers or amorphous carbon, which may transform under heating to other stable forms of carbon. Clouds rich on silicates or carbonaceous dust grains are covered with ices (H₂O, NH₃, CH₄, CH₃OH, CO, …) providing support for the formation of different species. A paradigmatic example is the formation of the hydrogen molecule from atomic hydrogen; due to the presence of ices it is produced even at temperatures as low as 10 K, as demonstrated by laboratory experiments on circumstellar grain analogs and by Density Functional Theory (DFT) simulations.¹ On the other hand, in low-density clouds (diffuse) these particles are known to be clean of contaminants like ice, and a similar mechanism is lacking since the thermally activated process of molecular hydrogen formation would require temperatures T > 250 K to achieve a reasonable yield in times ranging between a few years to some thousands years.^2,3

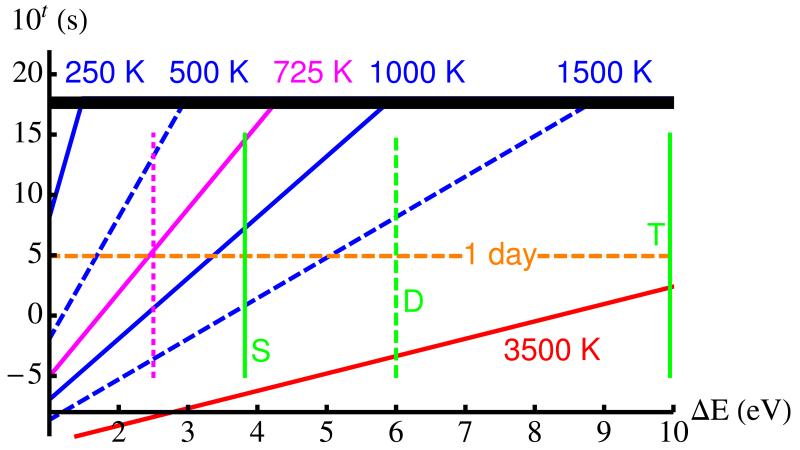
The opposite problem is the effect of atomic hydrogen on carbonaceous particles.⁵ It has recently attracted attention because of its potential to explain the formation of hydrocarbon molecules and all sort of radicals in space.⁶ These authors have described the high-temperature etching of SiC grains in a hydrogen-rich atmosphere in the laboratory. The main experimental observation is the formation of holes on a graphene surface. This is surprising since the typical energy stored in a C–C bond on graphene is ≥ 4 eV, and such a process would only happen on a time-scale of several years in pristine graphene at the temperature of the experiment (1000 K), cf. Fig. 1. Indeed, graphene is one of the known toughest materials in Nature, with a very large in-plane Young modulus of ≈ 1 TPa, which arises from the extraordinary efficiency of the sp² and π-like hybrid orbitals bonding C atoms on a honeycomb topology.⁷ Furthermore, bonding between C atoms is very versatile, resulting in a range of strengths from triple to single bonds, ≈ 10 eV to 4 eV per bond, respectively. Characteristic energies for the simple (S), double (D) and triple (T) carboncarbon bond are represented by vertical dashed lines in Fig. 1.⁸ Graphene is located on an intermediate region with a coordination order of about 1⅓ that corresponds to ≈ 4–5 eV per C–C bond. Such a kinetic barrier for the breaking of C–C bonds is too high for the process to take place at 1000 K on the observed experimental time scale, i.e. minutes. Owing to the exponential dependence with temperature of the Boltzmann factors such a process at 500 K would take an amount of time equivalent to the Age of the Universe and would not happen, while at the same time the solid-liquid phase-transition starting around 3500 K is correctly predicted to take place in about ms. We notice that a reduction of the barrier below 3 eV would be enough to allow such a process to happen on about a few minutes. Experiments run on heavily hydrogenated graphene make it clear that the presence of hydrogen does not eliminate these kinetic barriers,⁴ but we find that it acts to reduce their values so it can happen on a reasonable laboratory time scale, between miliseconds and minutes.⁶ Here we search for detailed mechanisms that can explain the catalytic-like activity of atomic hydrogen leading to the reported formation of holes in the graphene layer, as well as the nature of the fragments formed at the same time, i.e. hydrocarbons and radicals of various sizes.

Figure 1.

(color online). Blue lines give typical times (10^t in s) to overcome an energy barrier ( ΔE in eV) by picking up a thermal fluctuation at a temperature T (in K) between 250 and 3500 K. Characteristic energies for the simple (S), double (D) and triple (T) C–C bonds are represented by light-green lines. The top thick black horizontal line represent the total time since the big-bang (≈ 10¹⁰ years), and the middle horizontal orange dashed line represents 1 day. Around the blue 3500 K line the breaking of C–C bonds in the solid-liquid phase transition takes place in about ms. In agreement with experimental evidence,⁴ we expect a noticeable amount of defects to appear on the graphene layer after annealing at 725 K for about 1 day (solid and dashed magenta lines).

Methodology

In the ab-initio atomistic simulations, total energies, forces and stresses were minimized by using DFT as implemented in the plane-waves package Quantum Espresso.⁹ A perturbative van der Waals (vdW) correction was used to check for the effect of long-range interactions on the different configurations analyzed. For this purpose, we have used an empirical vdW R⁻⁶ correction to add dispersive forces to conventional density functionals within the DFT+D formalism.^10-12 This vdW contribution to the total energy is almost negligible around the transition states; it only becomes significative (~15%) when distances between the expelled fragments and graphene increases > 4Å, which only matters for a good description of energies at asymptotic distances. The Local Density Approximation (LDA) has been used for the exchange and correlation potential. It describes fairly well both the C–C and C–H bonds, and at the same time offers a most simple and clear conceptual frame. Similar conclusions have been reached by checking a few selected cases with a Generalized Gradient Approximations (GGA) to the exchange and correlation potential. Norm-conserving scalar-relativistic pseudopotentials have been used to model the ion-electron interaction.¹³

Models having from tens to hundreds of atoms have been considered to construct both finite-size clusters (labeled as C) and extended periodic-cell models (labeled as c). A k-space mesh of Δk ≤ 0.01 Å⁻¹, and an energy cutoff of 500 eV yielded total energies with an accuracy of ΔE ≈ ±0.05 eV (converged to a precision better than 10⁻⁶ eV). Optimized geometries were obtained with residual forces lower than 0.01 eV/Å, and stresses below 0.1 GPa. Besides enthalpies of formation, H, for a particular process the all important feature to ascertain its feasibility is the height of the barrier at the transition state (TS), ΔE. These TSs have been investigated within the climbing-image nudge elastic band (CI-NEB) approach^14-16 implemented in the Quantum Espresso package,⁹ where the initial, the final and all the intermediate image-states were free to fully relax. At this point, it is important to remark that the underlying chemistry of these systems is well represented by all the approximations adopted here, and we expect a good correlation with experimental data, as it is usually attained.^17-19

Results and discussion

A plausible mechanism that would allow the breaking of the strong in-plane C–C bonds should involve a transition state low enough to get from the initial to the final state in a meaningful time on the experiment time scale. Our simulations show that atomic hydrogen plays a dual role in this job. On the one hand, it chemisorbs on the graphene layer with an adsorption energy of ≈ 1 eV, and a small initial sticking barrier of ≈ 0.15 eV. This small barrier appears as a result of the induced deformation upon adsorption of H on the stiff planar graphene layer, where the sp² acquires a partial sp³ character.^20,21 On the other hand, hydrogen can adsorb on the edges of the newly created holes saturating the dangling bonds very effectively. That kind of C–H bond can store as much as 5 eV and it is characterized by vibrational frequencies that match the phonons of the graphene layer.⁷ Therefore, the C–H bond can effectively compete with the C–C bond making it possible to reduce transition barriers for various processes to reasonable amounts (see Fig. 2). Fig. 1 gives in a logarithmic scale the typical time in seconds of having a process with a transition barrier of ΔE (eV) at a temperature T (K). At the temperatures of interest (T > 500 K) we can safely neglect tunneling contributions and we assume that the probability for a thermal fluctuation to overcome the TS barrier is determined by the canonical Boltzmann factor,²²

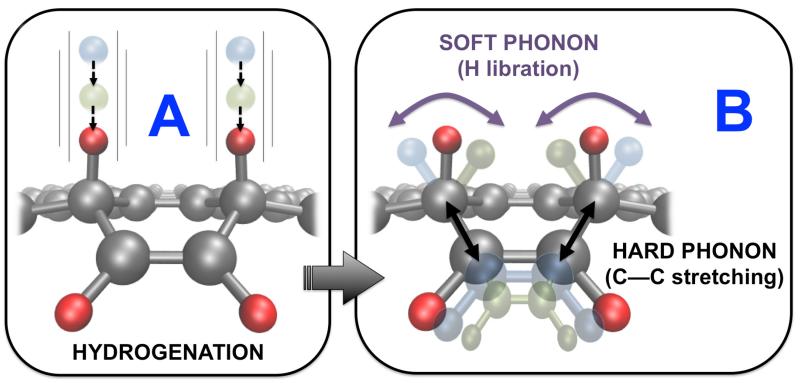
$$\Gamma ={\Gamma }_0{e}^{-\frac{\Delta E}{k_{B}T}}.$$ (1)

Since the exponential dominates the behaviour of this probability as a function of T we take the prefactor as a temperature-independent value. This prefactor Γ₀ is indeed determined by the combined action of a soft and a hard vibrational modes. We have calculated typical frequencies for these modes, the H libration (left panel in Fig. 2) comes around 300 cm⁻¹, while the C–C streching (right panel in Fig. 2) comes around 1000 cm⁻¹. These modes crucially determine the prefactor in such a way that if we imagine these frequencies tending to zero Γ₀ vanishes and the effect we are introducing would not be possible. On the other hand, the variation with the temperature of these values, or the difference between the soft and the hard modes, is totally negligeble compared with the exponential factor that changes by many orders of magnitude with small variations of T, whilst the prefactor mostly changes by one or two orders of magnitude at most. Therefore, the vibrational mechanism we have identified is at the same time crucial to understand the effect, but irrelevant to describe its variation with T. According to the aforementioned, the prefactor is here taken as a typical phonon Γ₀ = 1000 cm⁻¹. By propagation of errors, we find for typical temperatures of ≈ 1000 K, and typical energy barriers of ≈ 1 eV that uncertainties in the calculation of barriers of ≈ ±0.05 eV, and in the values of temperatures of ≈ ±10 K, result in Fig. 1 in fractional errors < 35%. These error bars, or even much higher values, are quite acceptable to draw conclusions since the rates change so quickly with the values of the barriers.

Figure 2.

(color online) Schematic mechanism to detach a C₂H₂ molecule from the edge of a hydrogenated graphene nano-ribbon. In step A hydrogen atoms are chemisorbed on nearby positions to progress towards a transition state under the combination of two phonons (step B). Once the H atoms have been inserted near the transition state the C–C bonds are weakened enough to be broken by thermal activation after annealing.

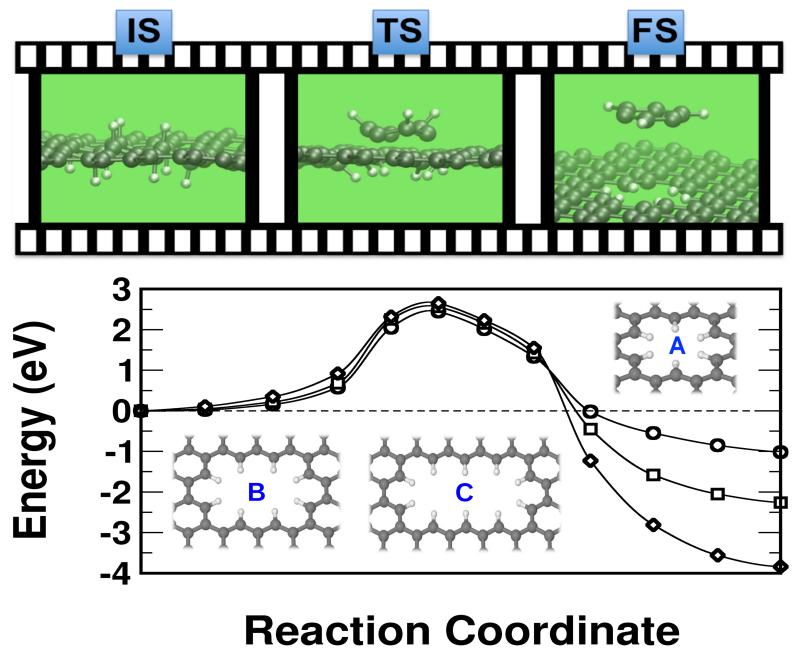
First, we discuss how a defective hole on a graphene layer can be created, as it has been observed in UHV-STM and AFM experimental images.⁶ We start by adsorbing a few H atoms on both sides of the graphene layer surrounding the region where the hole may appear and producing a sp³-like deformation on the layer. The role of chemisorbed atoms is to weaken first, and then to passivate the broken C–C bonds. Take as an example the extraction of a six C ring (see Fig. 3). It would be desirable from the point of view of the formation enthalpy to saturate this ring with H atoms to directly obtain benzene. However, this process involves too high barriers due to steric impediments from hydrogens in the extracted fragment and other hydrogens left in the layer. Instead, we find it is optimum to extract C₆H₃. The process starts by breaking the three C–C bonds that are left unsaturated in the fragment, and subsequently the three remaining ones. In the absence of chemisorbed hydrogen the formation of such a six-C ring hole has a barrier of +7.12 eV, which at 1000 K simply would not happen even in typical stellar times (see Fig. 1). Adsorption of atomic hydrogen drastically modifies this picture; values in Table 1 show how the transition state to extract C₆H₃ is reduced down to +2.43 eV, a process that now may take place in less than a second at 1000 K. The mechanism involves C–C stretching so a wagging mode of a nearby chemisorbed H can place the H closer to the middle of the C–C bond and can help to break it while forming at the same time a new C–H bond, cf. Fig. 2. The formation of a favourable configuration of chemisorbed hydrogen atoms depends on the available density of atoms impinging on the surface; the reference experiments have been performed under conditions where atomic H has been admitted in the UHV chamber up to a 10⁻⁶ mbars (≈ 10¹⁰ atoms/cm³), and temperature has been raised up to 1000 K.⁶ These conditions imply hydrogen saturation conditions, making likely to reach a favourable configuration, that then determines the shape of the hole. These experiments have been designed to mimick regions near red-giant stars between 3 to 15 stellar radii, where temperature ranges from 1500 K to 200 K, and hydrogen densities take values between 10¹¹ to 10⁶ atoms/cm³.²³ We remark that the enthalpy of formation for this particular C₆ hole is negative (−1.12 eV), therefore making the hole saturated with hydrogen and the fragment, C₆H₃, stable. A similar pattern follows for a large cluster labelled C in Table 1 with values of +2.81 and −0.82 eV for the barrier and the enthalpy of formation, respectively. The main difference between the periodic and finite-size simulations resides in the barriers to stick the hydrogen initially near the region to be etched. This is mainly due to the different elastic constants for a continuous layer and a small chunk of material that may be supported by some substrate or not. Finally, we analyze, for the case of the periodic system, the upstart of the scaling with the size of the hole formed, i.e. with the number of C atoms to be extracted, by considering 10 and 14 C atoms. These holes have been labeled in Fig. 3 with A, B and C, and in the continous lines marked with empty circles, squares and diamonds, respectively. Enthalpies of formation grow slowly with the size of the fragment tending to the saturation value to be found on very large systems. Interestingly enough, however, the transition state barriers tend to be nearly the same, indicating that the main difficulty to extract large fragments resides with the configurational statistical complexity more than with the chemistry. This can be fixed by introducing an abundant amount of hydrogen favoring the appearance of many different configurations; the holes observed would then correspond to the particular configuration realized on the graphene layer.

Figure 3.

(color online) Top: pictorial sketch of the initial (IS), transition (TS) and final (FS) states for the C₆H₃ dettachment. Bottom: Energy barriers to create holes of different sizes on an extended periodic graphene layer. (○) corresponds to the creation of a C₆ hole, (□) to a C₁₀ hole, and (◇) to a C₁₄ hole.

Table 1.

Perimetral length, P (Å), enthalpies of formation, H (eV), and transition states barriers, ΔE (eV), for different sizes of the hole (created by dettaching C₆H₃, C₁₀H₄ and C₁₄H₅). C and c indicate finite-size clusters and periodic-cell models, respectively.

	P(Å)	H (eV)		ΔE (eV)
Species		C	c	C	c
C6H3	9	−0.82	−1.12	2.81	2.43
C10H4	15	—	−2.35	—	2.56
C14H5	21	—	−3.96	—	2.65

According to the hole-creation mechanism proposed, the surrounding adsorbed H atoms helping to weaken C–C bonds and reducing the barrier to extract small fragments not involving any aromatic ring (such as a C atom, C₂, C₃, etc…), suffer steric impediments to be accommodated during the extraction of the fragment. As an example, if we apply the proposed mechanism to the extraction of a single C atom, or a CH functional group, from pristine extended graphene to create a hole, the barriers predicted by theory are in excess above 8 eV. This may be explained in terms that the hydrogen-saturated hole is left in a very stressed structural situation, with no reduction of the kinetic extraction barrier, in such a way that the event simply does not occur. This rationalization can be easily extended to the case of any aliphatic fragment leaving hydrogen-saturated holes in very structurally stressed situations. Besides, the fact that the C₆H₃ fragment is found to be the smallest optimal fragment to be extracted at a reasonable kinetic barrier can be justified following the same rationalization. If one analyzes within the proposed mechanism the case of the C₆H₆ (benzene) fragment, it is physically unfeasible because of another arising steric effect, and the impossibility of accommodating the H atoms (adsorbed on both graphene basal planes) during the extraction process. This occurs in the same way in attempting to analyze the extraction of the C₆H₅ and C₆H₄ fragments. Is in the extraction process of the C₆H₃ fragment where the mentioned steric impediment is not a problem anymore, since the C₆ skeleton is able to attach the 3 of the hydrogens weakening the C–C bonds from the side it is dettaching along. On the other hand, the extraction of the C₆H₂, and C₆H fragments yields values for the extraction kinetic barriers in excess above 5.5 eV; once again, these events simply would not occur.

In previous literature Elias et al.⁴ reports on a reversible process of charge and discharge of H on graphene, where the discharge is achieved by annealing up to a maximum of 723 K for 24 hrs. Higher temperatures resulted in damage of the graphene layer. As Fig. 1 (magenta line for 725 K) shows, in combination with our values in Table 1, our simulations predict the formation of holes in the graphene layer in a time-scale of approximately 24 hrs near T = 725 K, which is in good agreement with the observation of Raman spectra by Elias et al.,⁴ and the STM experiments beyond that critical temperature by Merino et al.⁶

Finally, we notice that in an elegant experiment Xie et al. have recently measured the etching of single graphene layer edges by hydrogen plasma at a rate of approximately 0.3 nm/min.²⁴ According to our model, to create a C₆ hole with a perimetral length of approximately 9 Å at the measured rate it would require a barrier of ≈ 2.85 eV, which is remarkably close to the values in Table I taking into account that our focus is on the general mechanism using arguments based in the order of magnitude of rates, not on the detailed values that we cannot expect to obtain with such accuracy.

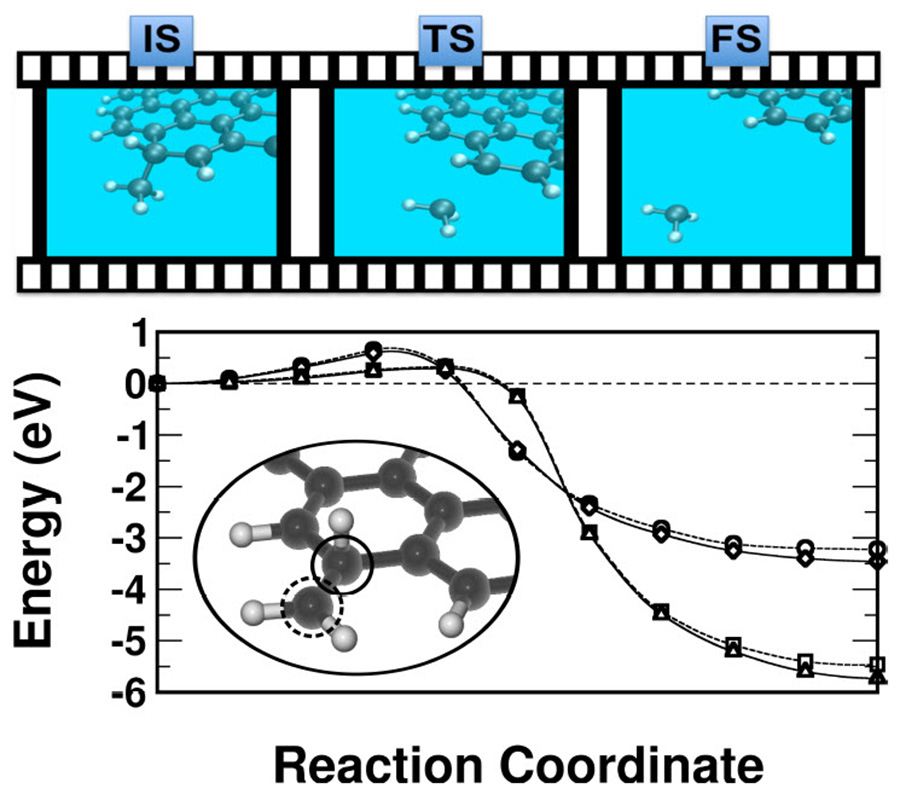
Second, we focus on the small molecules formed on the internal edges of the holes left on the surface, and in the external edges of the ejected fragments following the creation of a large defect on the layer. Table 2 shows a comparison between enthalpies and transition state barriers for a variety of small molecules. Formation of CH₂ and CH₃ involves the lowest barriers and the most stable systems, e.g. see discontinuous lines in Fig. 3. These two molecules can be formed on the external edges of graphene flakes, or on the internal edges of the hole (c). As an example of an straightforward mechanism on the edge of a hydrogen saturated nano-ribbon we draw an external C atom (surrounded by a dashed circle) attached to two H atoms and a third H chemisorbed on a top position in the nearby C (surrounded by a continuous circle). Barriers to form both CH₂ and CH₃ are similar since the important point here is the local geometry giving raise to the breaking of a C–C bond by insertion of a chemisorbed H. The more saturated with hydrogen the fragment, the lower are the barriers, and the formation enthalpies are more negative, since the C–C bond becomes weaker. This mechanism does not result in the formation of CH nor CH₄, although for opposite reasons. In the first case, the H chemisorbed on top position (continuous circle) finds it too favorable to bond to the second C (dashed circle) and cannot participate in the breaking of the C–C bond. In the second case, the second carbon atom cannot support the interaction with four H plus the first carbon atom. Nevertheless, CH₂ and CH₃ fragments dettached from hydrogenated graphene/graphite will capture environmental H atoms to spontaneously form CH₄.²⁵ Other fragments with higher C content, such as C₂H₂, C₂H₄, and C₂H₆, are not exothermic, but display reasonable formation barriers too. The inverse process, where the fragment joins the edge, is hindered by entropic orientational considerations and does not play an important role. The transition barriers for these molecules having two C atoms are higher than for those having just one C atom, but still reasonable if compared with typical times in the circumstellar medium. To complement the scenario, since these particles may be bombarded by charged particles in a realistic situation located near a star we have considered the breaking of C₂H₂ on a charged surface, leading to the anion C₂H₂⁻. The barrier for this case is of +2.20 eV, i.e. very similar to the one found on the inner side of the hole for the periodic system. The presence of the extra charge on the surface does not significantly alter the mechanism of breaking the relevant C-C bonds, and indicates that the abundance of anions and neutral species should be similar. Since the experiments have been performed on graphene formed on a SiC substrate we have additionally tested the influence of the layer immediately below the surface, the so-called buffer layer. For C₂H₂ we see a negligible change of the height of the barrier, from 2.35 eV to 2.33 eV. This finding manifests that the weak interaction between layers do not interfere with the strong chemical-like bonds broken and formed that explains the mechanism for etching of the layer, and assigns to the buffer layer a purely physical confining role.^20,26 Since in most cases graphene layers grown on metallic surfaces keeps also a weak interaction with the support, we expect the same principles to apply for those cases.

Table 2.

Enthalpies of formation, H (eV), and transition states barriers, ΔE (eV), to obtain different fragments from the inner part of the hole in the graphene layer. C and c indicate finite-size clusters and periodic-cell models, respectively.

	H (eV)		ΔE(eV)
Molecule	C	c	C	c
CH2	−3.22	−3.46	0.65	0.59
CH3	−5.46	−5.73	0.33	0.29
C2H2	+1.52	+1.33	2.35	2.18
C2H4	+0.81	+0.74	1.93	1.79
C2H6	−0.61	−0.82	1.48	1.67

Figure 4.

(color online) Top: pictorial sketch of the initial (IS), transition (TS) and final (FS) states for the CH₃ dettachment. Bottom: Energy barriers for the proposed mechanism of breaking a C–C bond in the edge of a H saturated graphene nano-ribbon. A chemisorbed H on top a C atom (continuous circle, referred in the text as the first C) moves towards a transition state located in between the second C (dashed circle) to create fragments like CH₂ (inset) or CH₃ (upper pannel). (○,□) CH₂ and CH₃ from a H saturated edge; and (◇,△) CH₂ and CH₃ from a H saturated hole.

Conclusions

Summarizing, in this letter we propose a mechanism underlying the formation of prototypical hydrocarbons, hydrocarbyls, and other polyaromatics from hydrogenated graphene. We have studied the formation of large holes on graphene upon atomic hydrogen adsorption and high-T annealing, as observed in experiments performed in the laboratory. These have been rationalized in terms of the adsorption of H atoms around the region where the hole is expected to appear. Chemisorbed atoms act to passivate broken bonds in synergy with phonons simultaneously weakening the hard C–C bonds. This is a temperature-activated process exhibiting typical barriers of around 3 eV, and occurs at 1000 K in a few minutes. Computed transition state energies are used to determine the Boltzman probability for a thermal fluctuation to overcome such a barrier, and the time scale for an event to occur, which is of paramount importance from the practical point of view. The proposed mechanism also sheds light into possible routes for the creation in the circumstellar medium of small hydrocarbons and hydrocarbyls, such as CH₂, CH₃, C₂H₂, C₂H₂⁻, C₂H₄ and C₂H₆.