Gradient-Induced Voltages on 12-Lead ECGs during High Duty-Cycle MRI Sequences and a Method for Their Removal considering Linear and Concomitant Gradient Terms

Abstract

Purpose

To restore 12-lead ECG signal fidelity inside MRI by removing magnetic-field gradient induced-voltages during high gradient-duty-cycle sequences.

Theory and Methods

A theoretical equation was derived, providing first- and second-order electrical fields induced at individual ECG electrode as a function of gradient fields. Experiments were performed at 3T on healthy volunteers, using a customized acquisition system which captured full amplitude and frequency response of ECGs, or a commercial recording system. The 19 equation coefficients were derived by linear regression of data from accelerated sequences, and used to compute induced-voltages in real-time during full-resolution sequences to remove ECG artifacts. Restored traces were evaluated relative to ones acquired without imaging.

Results

Measured induced-voltages were 0.7V peak-to-peak during balanced Steady-State Free Precession (bSSFP) with heart at the isocenter. Applying the equation during gradient echo sequencing, three-dimensional fast spin echo and multi-slice bSSFP imaging restored nonsaturated traces and second-order concomitant terms showed larger contributions in electrodes farther from the magnet isocenter. Equation coefficients are evaluated with high repeatability (ρ = 0.996) and are subject, sequence, and slice-orientation dependent.

Conclusion

Close agreement between theoretical and measured gradient-induced voltages allowed for real-time removal. Prospective estimation of sequence-periods where large induced-voltages occur may allow hardware removal of these signals.

Introduction

Physiological monitoring using a 12-lead ECG may be essential for MR imaging of patients with ischemic histories and acute-stroke, or during conduction of high-risk surgeries and interventions under MR guidance. However, ECG artifacts induced by the magnetic field gradients, whose amplitude may exceed the real ECG by one to two orders of magnitude, severely affect ECG trace quality and fidelity, and frequently lead to an inability to observe the true ECG (Fig. 1). Additional ECG artifacts are induced inside the MRI bore by the MagnetoHydrodynamic (MHD) effect, which are not addressed in this paper. Interested parties can view previous publications^{1, 2}.

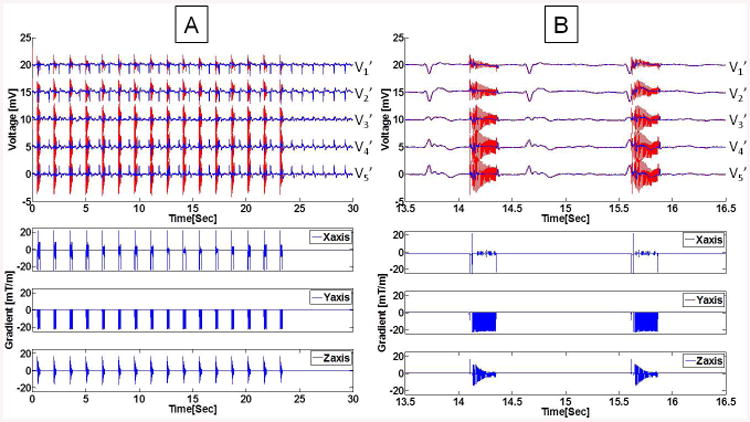
Figure 1.

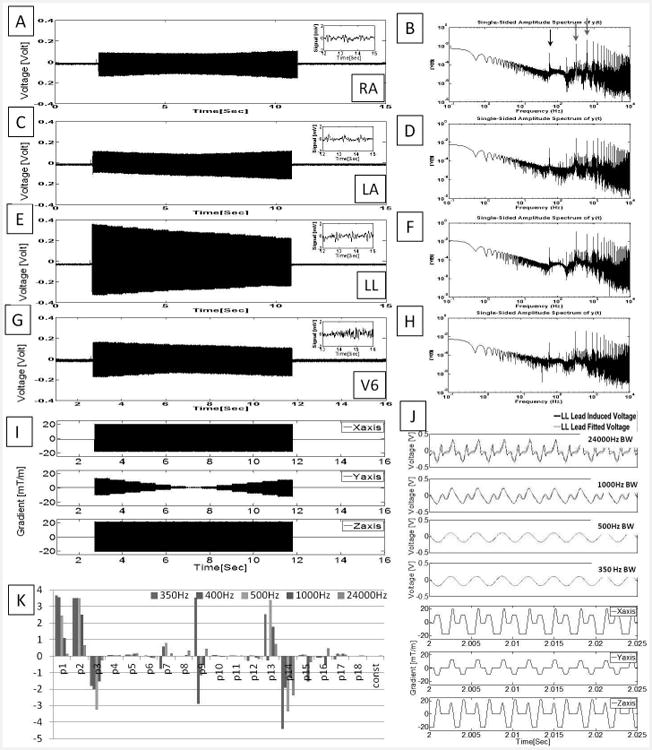
Unfiltered ECG traces recorded at a rate of 48 kHz during an axial bSSFP scan using acquisition Set-up I. (A, C, E, G)Voltages measured during imaging from three limb leads (LA, RA and LL) and the precordial lead with the largest induced voltage, V₆'. Insets showed 30Hz low-pass filtered ECG (in mV) extracted from the period without gradient activity. (B, D, F, H) Spectral analysis from 0.1-10KHz. Notable peaks (red arrows) are seen at the fundamental (320 Hz) and 2^nd harmonic (640 Hz) corresponding to the repetition time (TR) and at 60 Hz noise (black arrow). (I) Gradient waveforms simultaneously recorded while imaging. (J) Expanded induced noise in LL traces filtered below noted frequencies (black traces), overlaid on data fitted to the 19-parameter equation (green traces), and corresponding gradient waveforms (blue traces). (K) The 19-parameter plot for ECG traces with the bandwidths of (I), and their units are listed in Table 1. Note that even at 350 Hz bandwidth, some 2^nd order coefficients remain very large.

Removal of the induced voltages has been attempted using both hardware and software approaches. Commercial MRI compatible ECG systems employ 3-4 closely spaced ECG electrodes along with high-impedance (10 kΩ or more) transmission-lines to reduce the magnitude of the induced voltages. A dedicated hardware switching circuit was previously developed to reduce the gradient-induced artifacts in 12-lead MRI-conditional ECG by blocking/blanking ECG transmissions during all gradient ramps¹, which has been shown feasible at 1.5T in MR sequences with repetition times (TRs) > 4ms.

Most approaches apply strong (< 50 Hz) low-pass filters to the ECG traces to remove the high-frequency components in the induced voltages. This approach is limited, however, by the retention of low-frequency components of the gradient-induced voltages in the ECG traces, and it leads to distorted waveforms that are less useful for patient monitoring. Another approach used adaptive digital filters ^3-8 to reduce the ECG noise by detecting the gradient waveforms generated by the MR pulse sequences and modeling the noise responses as a linear time-invariant system to convolve with the temporal response of the gradients. It has been assumed that time derivatives of gradients are the major contributor in those studies, but a systematic derivation of the relationship between the gradients and the induced noise has not been demonstrated.

Each of the three gradient coils used in MRI generate magnetic fields in all three spatial directions during imaging, although imaging only makes direct use of the Z-component (B_z). Via Maxwell's equations, the time-varying gradients also generate electric fields in all directions. The distribution of induced electrical fields has been studied experimentally and theoretically due to its role in nerve stimulation. These studies have shown a linear relationship between the induced electric fields E and temporal derivatives of the magnetic field ∂B/∂t ^9-11. They also showed that, with the heart at the isocenter of the magnet, high voltages of approximately 0.6 V between the Right Arm (RA) and Left Leg (LL) can be generated in specific off-center body regions, such as thighs and shoulders, and that when the heart is not at the isocenter, the 12-lead ECG electrodes can record even higher voltages (2–5 V).

Other studies have examined the effect of time-varying gradients fields produced along the x and y directions (concomitant gradients), because they affect MRI images in specific sequences, such as phase-contrast velocity measurements, especially when imaging is performed far from the magnet isocenter ^12-14.

In this study we merge derivations from Maxwell's equations ¹¹ and concomitant field ¹⁴ to arrive at a theoretical equation that provides, to second order, the three components of the expected vectorial induced voltage at each ECG lead. All of the coefficients within this equation cannot be measured with conventional ECG electrodes, since these electrodes measure only the magnitude of the total vectorial field, not its individual components.

To obtain accurate estimates of the coefficients, we measured gradient-induced voltages during several MRI sequences using two experimental constructs. We also devised and tested a fast method to measure the coefficients, by executing abbreviated imaging sequences. Once all equation terms were established, we applied the equation in real-time to remove the gradient-induced voltages from ECG traces obtained during full-length high-duty-cycle MRI sequences and validated the quality of the induced-voltage removal.

Theory

We derived the gradient-induced voltages recorded by the 12-lead ECG electrodes based on the interaction of the electric fields induced by the three MRI gradient coils on the human body, using Maxwell's equations (see Appendix).

In the linear approximation, which results in a 7-parameter equation (Appendix equation A10), we assumed that only the z-component of the magnetic field induced by the gradients is relevant. This equation has dependencies on the gradients and on their temporal derivatives.

In the 2^nd order approximation, which becomes increasingly relevant when the ECG electrodes are placed further away from the MRI isocenter, we took into account the fact that the three gradient coils also create magnetic fields in the x and y directions. This fact was originally investigated in the context of the effect of these fields on MRI imaging further from magnet's center, and is referred to as concomitant field theory¹³. The equation (Appendix equation A15) we reached for the induced voltage S_k(t), where k represents individual ECG channel, defined as

$$S_k(t)=p_{1k}\frac{\partial G_x}{\partial t}+p_{2k}\frac{\partial G_y}{\partial t}+p_{3k}\frac{\partial G_z}{\partial t}+p_{4k}{G}_x+p_{5k}{G}_y+p_{6k}{G}_z+p_{7k}\frac{\partial G_x}{\partial t}{G}_x+p_{8k}{G}_x^2+p_{9k}\frac{\partial G_y}{\partial t}{G}_y+p_{10k}{G}_y^2+p_{11k}\frac{\partial G_z}{\partial t}{G}_z+p_{12k}{G}_z^2+p_{13k}\frac{\partial G_x}{\partial t}{G}_z+p_{14k}{G}_x\frac{\partial G_z}{\partial t}+p_{15k}{G}_x{G}_z+p_{16k}\frac{\partial G_y}{\partial t}{G}_z+p_{17k}{G}_y\frac{\partial G_z}{\partial t}+p_{18k}{G}_y{G}_z+C_k$$ (1)

The 2^nd order terms will be important, in the 12-lead ECG context, in two instances; (a)when the heart is at magnet isocenter (e.g. during cardiac imaging), the higher terms are expected to be large in the precordial leads V₅ and V₆, and in all the limb leads (RA, Left Arm (LA), LL), and (b) when other body organs are at isocenter (e.g. during imaging of the head, the knees, etc.), then the higher order terms can be important for all the 12-lead ECG leads, and much higher induced voltages may be observed, as also shown by numerical simulation.

Methods

Recording of 12-Lead ECG

We define gradient-duty-cycle as

$$\mathit{\text{GDC}}=\frac{(\mathit{\text{Total gradient activity time per cardiac cycle}})}{(\mathit{\text{Cardiac cycle time}})}$$ (2)

To enable observing the full amplitude and frequency spectrum of the ECG traces acquired during imaging under short TR and high- GDC (GDC>30%) conditions, the 12-lead MRI-conditional ECG system was modified from our previous setup, which was composed of transmission lines to reduce radiofrequency induction and switching circuits to remove induced voltages. ¹. These changes were required because 1) at higher gradient slew-rate and peak amplitude, the magnitude of the induced voltage, particularly in the limb and off-center precordial leads can be as high as 1 Volt, and 2) blocking signal transmission during high-GDC imaging results in the loss of most of the temporal information in real ECG traces.

In the data acquisition system shown in Fig. 2, each ECG channel, including the precordial leads V₁-V₆ and the limb leads RA, LL, LA, augmented Vector Right (aVR), augmented Vector Left (aVL), and augmented Vector Foot (aVF), entered the system via an unity-gain differential amplifier/delay-line (model AL181-25k-179A, TTE Incorporated, Los Angeles, CA), with the Right-Leg (RL) input acting as the reference voltage. This TTE unit utilized a 10-pole Chebyshev filter to provide an 80-μs signal delay and a 25 kHz low-pass frequency, replacing a previously used passive filter¹. It provided impedance matching between the human body and the front-end electronics, and preserved linear-phase, unity-gain, ECG traces without signal distortion and attenuation. A low-noise operational-amplifier adder (AD8674, Analog Devices, Norwood, MA) was placed before the single pole double throw (SPDT) switch, in order to correct for DC offsets introduced by the delay-line low-pass filter and the SPDT switch during periods when signal transmission was blocked¹. The front-end ECG analog output was acquired with a CompactRIO microprocessor (National Instruments, Austin, TX) for DC-offset monitoring. A feedback loop, with the feedback voltage controlled by a microprocessor, removed most of the DC offsets (down to 0.05mV) produced by the switch and the delay-line/ low-pass filter (data not shown).

Figure 2.

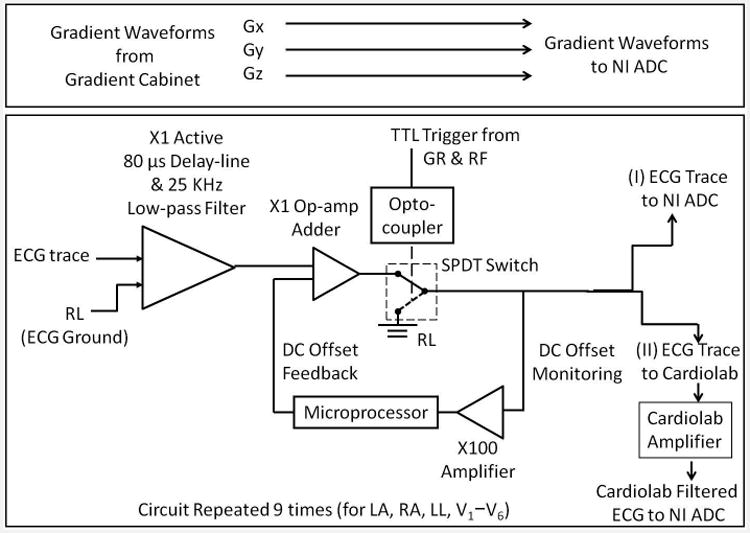
Block diagram of the MRI-conditional 12-lead ECG front end. The front end enabled patient-isolation via a differential pre-amp/delay-line at its input. It also allowed for blocking strong signals via a TTL-controlled single pole, double throw (SPDT) switch. The circuit had two outputs. Set-up I sampled ECG waveforms in their spectral form without any filtering, while Set-up II sampled using the CardioLab IT digital electrophysiology recording system.

We provided two methods for sampling the ECG traces (Fig. 2, rightmost):

Set-up I: In order to measure the full spectrum of the ECG signal, as well as the gradient induced voltages superimposed on the ECG signals, the circuit output was sent directly to a PCI-6251 Digital Acquisition (DAQ) board (National Instruments, Austin, TX) which digitized the ECG waveforms at a rate of 48 kHz. The maximum input voltage of the NI DAQ board was set at ±10 Volts, so none of the ECG traces were clipped. All ECG measurements were referenced to the RL lead.

Set-up II: In order to measure the ECG spectrum as it appears after filtering, the circuit output was sent to a CardioLab IT digital electrophysiology recording system (General Electric, Waukesha, WI) which applied Butterworth 1^st -order 0.05Hz high-pass and 3^rd -order 100Hzlow-pass filters to the input signal. The CardioLab amplifier gain was set to either 1000 or 100, which allowed precordial leads to be acquired without saturation. The CardioLab pre-processing and larger-input gain, relative to set-up I, resulted in a maximum input amplitude of ∼10 mV peak-to-peak (with the amplifier gain set at 1000) after the hardware filtering, so that most limb lead traces acquired during imaging were saturated, and their traces are therefore not shown in the context of set-up II. On the other hand, the noise figure of the precordial lead traces from CardioLab was superior to those obtained with set-up I, primarily due to the induction of 60 Hz noise present in the MRI operator room into the NI ADC. The ECG traces were output from CardioLab in analog form and re-digitized by the NI DAQ board. All measurements were referenced to the RL lead. The precordial lead traces $V_1^{\prime }$ to $V_6^{\prime }$ had each lead voltage (V₁ to V₆) subtracted by the Wilson Central Terminal (WCT) voltage, i.e. $V_k^{\prime }=V_k-\mathit{\text{WCT}}$, where WCT = (LL + RA + LA)/3 and k =1 to 6;

The x, y and z gradient waveforms were transmitted from the MRI gradient cabinet and digitized by the NI DAQ board simultaneously with the ECG traces, as illustrated in Fig. 2's top panel. The SPDT switching feature has been previously detailed ¹ and was not utilized in this study. Its possible role will be addressed in the Discussion section.

Data Processing

First, a clean ECG trace of a complete cardiac cycle, which will be referred to as a template, for a given ECG channel k was extracted from the portion of ECG traces acquired during pauses in acquisition (i.e., time periods without gradient activity). This template was then concatenated to align with an ECG trace acquired during gradient activity, which will be referred to as the corrupted ECG trace, for the same channel. By subtracting the clean ECG from the corrupted ECG trace for each channel, the gradient-induced ECG voltages S_k(t) were computed for all channels.

In the signal processing workflow (Fig. 3), a training step using a parallel imaging accelerated MRI pulse sequence, detailed in the Human studies section, was performed, during which ECG traces and gradient waveforms were recorded. To calculate the 19 coefficients of Eq. 1, a total of 4 steps (Fig. 3 left panel) consisted of performing numerical differentiation of the gradient waveforms, and calculating a template of clean ECGs for each channel by averaging over the QRS cycles without gradient-activity after these were adjusted to be of the same temporal duration, in cases of heart-rate variability.

Figure 3.

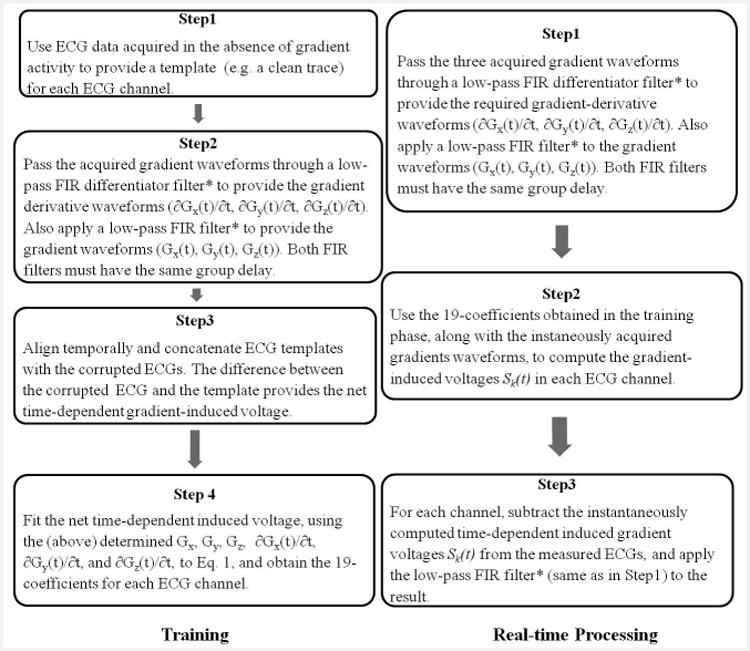
The workflow of training (left) and real-time processing (right) stages. The signal processing performed to remove the gradient-induced voltages consisted of two stages. A training stage followed by real-time induced-voltage removal during image acquisition with continuous display of restored ECG traces. *The FIR filter cut-off frequency was above 500Hz or above 200Hz for ECGs acquisition with Set-up I or II respectively, and has a group delay <5ms.

For data acquired with hardware Set-ups I or II, Finite Input Response (FIR) low-pass filtering with cut-off frequencies of above 500 or above 200 Hz, respectively, were applied to the gradient waveforms and their derivatives, removing higher-frequency components. For set-up II, this cut-off frequency aligned with filtering performed by the CardioLab system during ECG signal acquisition.

The template was then aligned with the corrupted ECG traces, with their difference providing the net gradient-induced voltage on each ECG channel, i.e. S_k(t) of Eq. 1. The over-determined system, with over 10⁵ data points per electrode for 19 unknowns, was solved by calculating the least-square solution (Matlab, Natick, MA), which delivered the 19 coefficients in Eq. 1 for each ECG channel. Total processing time was approximately 10 seconds on an HP XW8600 workstation.

After the training stage was completed, real-time processing was performed to remove the induced voltages (Fig.3 right panel), during the acquisition of a full-length MRI sequence, with the induced-voltage for each channel continuously calculated, based on Eq. 1, using the simultaneously acquired gradient waveforms as input. The computed induced voltage was then subtracted from the corresponding channel's corrupted ECGs, providing restored ECG signal in real-time (lag time of <5ms) during the imaging acquisition.

Performance Evaluation Parameters

The quality of the gradient-induced voltage removal was measured by computing the following metrics over complete cardiac cycles:

1. Fitting Assessment: Let s(n) and ŝ(n) represent the fitted and measured gradient-induced voltages, with n being the discrete time index. FIT estimates the goodness of the fit between s(n) and ŝ(n), and is defined as the following

   $$\mathit{\text{FIT}}=1-\sqrt{{\sum }_{n=1}^N{[s(n)-\widehat{s}(n)]}^2}/\sqrt{{\sum }_{n=1}^N{[\widehat{s}(n)-\overline{\widehat{s}(n)}]}^2}$$ (3)

2. Correlation Assessment: Let x(n) represent the clean ECG trace acquired with no gradient activity, and y(n) represent the restored ECGs during gradient-activity (i.e. the corrupted trace with the gradient-induced voltage removed), with n being the discrete time index. The cross-correlation coefficient CORR between x and y is

   $$\mathit{\text{CORR}}=\langle [x-{\mu }_x]\cdot [y-{\mu }_y]\rangle /{\partial }_x{\partial }_y$$ (4)

where 〈·〉 denotes the average over the observed time series, μ_x and σ_x are the mean and standard deviation of x, and μ_y and σ_y are the mean and the standard deviation of y.

We also studied the variation of the gradient induced voltage between different imaging orientations using the same imaging sequence, between imaging sequences, as well as between subjects with differing chest geometries. The repeatability of the parameter regression was analyzed by performing regression twice for each repeated acquisition, covering a range of slice orientations, and displaying the results in Bland-Altman plots.

Human Studies

For each subject, carbon fiber electrodes, as used in the previous study¹, were attached to the chest skin, and 12-lead ECG traces were acquired inside a Siemens Skyra 3T (peak gradient 45 mT/m, slew rate 200 mT/m/msec) scanner from 9 male healthy volunteers (age 38 ± 10 yr) under an approved institutional IRB with informed consent. All training stage ECG traces were collected during breath-holds, which were composed of interleaved periods in which the MR sequence was silent or running. In the real-time processing stage, ECG traces were also collected during breath-holds, excluding in a case when a volunteer was studied immediately after leg exercises inside the magnet bore, where the subject maintained shallow breathing. The amplitudes of the ECG traces reported throughout this paper are the initial values before the gain of the amplification system (i.e. the actual ECG voltages emanating from the human body).

Several non-ECG-gated MR sequences were performed, including 2D balanced Steady State Free Precession (bSSFP), 2D Gradient echo (GRE) and 3D Fast Spin Echo (FSE), and their acquisition parameters are listed in Table 2. MR imaging was performed covering the left-ventricle, with orientations along axial, coronal, sagittal and oblique directions. The full-resolution imaging sequences used an acceleration factor (GRAPPA) of 2, while the training sequences used higher parallel-imaging acceleration factors (GRAPPA = 6 - 8), thus skipping phase-encoding steps, but covering the full range of phase-encodings. Additionally, the training sequences were all single-slice sequences, while the full-resolution sequences utilized single- or multiple-(parallel)-slice acquisitions lasting 3-20 seconds.

Table 2.

Parameters of sequences performed during the ECG data acquisition. The sequence durations depended on the number of averages prescribed in the sequence.

	TR (ms)	TE (ms)	Flip Angle (°)	FOV (mm2)	ACQ Matrix	Slice Thickness (mm)	Receiver Bandwidth (Hz/pixel)	Total Duration (sec)
2D bSSFP	3.09	1.32	28	400 × 280	240 × 168	8	1490	3 - 5
2D GRE	20	1.97	25	300 × 300	128 × 128	5	1955	4 - 10
3D FSE	1500	151	120	280 × 192 × 54	256 × 176	1.5	500	20

Results

Set-up I: Full Bandwidth Acquisitions

Using Set-up I, we acquired the full amplitude and frequency spectrum of the 12-lead ECG traces, including the gradient-induced voltage component. The recorded voltages during a bSSFP acquisition reached up to700mV peak-to-peak (Fig. 1E). QRS complex features (i.e. a clean trace) could be observed after applying a 30-Hz low-pass filter (Fig. 1 A, C, E, G insets) to periods without gradient activity. As demonstrated in Fig. 1B, D, F, H, the gradient-induced voltages for bSSFP had frequency components within the ECG pass-band (up to 100 Hz) as well as at higher requencies. Multiple harmonics of the sequence repetition frequency (TR^-1 = 320 Hz) were observed. Regression of the LL lead traces to the 19-parameter equation exhibited a high-degree of agreement under several low-pass filter settings (Fig. 1J). Although the fitted parameters varied with filter settings (Fig. 1K), the 2^nd-order coefficients p9, p13 and p14 remained large values even at the lowest cut-off frequency setting.

Set-up II: Restricted Bandwidth Acquisitions

In our restricted bandwidth acquisitions using Set-up II, the commercial ECG recording system incorporated 100Hz low-pass filtering at signal input. Since the magnitude of the gradient- induced voltages was higher than 10 mV in the limb leads, resulting in saturated traces, we are only able to show results from the precordial leads.

An example of restored ECG traces during a GRE sequence is shown in Fig. 4. The lower three rows in Fig. 4A provided the recorded gradient waveforms during imaging. In an expanded view of the imaging period (Fig. 4B), it can be seen that the 19-parameter equation allowed sufficient removal of the spikes (in red), so that the restored ECG traces during imaging segments appeared almost identical to those observed outside the imaging interval, and the QRS complexes could be identified (black arrows in Fig. 4B). The performance evaluation is FIT = 0.71 ± 0.10 and CORR = 0.64 ± 0.12 across all precordial traces.

Figure 4.

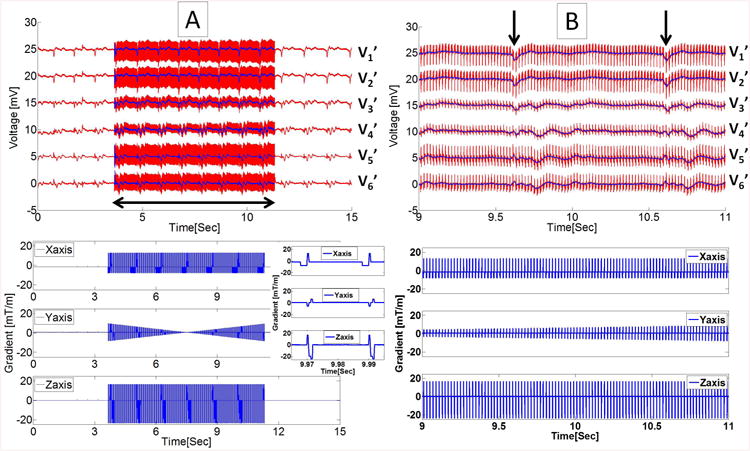
ECG signals, recorded with Set-up II during 20ms TR transverse GRE sequence. (A) Top panel displays recorded traces (red) and restored traces using 19-parameter fit (blue) for the precordial leads V₁'-V₆', and bottom panel shows the gradient waveforms recorded during the MRI acquisition (horizontal double-sided arrow). The inset shows zoomed view of gradient waveforms during two consecutive TRs. (B) The zoomed view of ECG traces shown in the top with R waves indicated by black vertical arrows, and corresponding gradient waveforms at bottom over a 2 sec period.

An example of ECG traces during 3D FSE acquisition is shown in Fig. 5A. In the expanded portion of the imaging interval (Fig. 5B), induced voltages of ∼5mV appeared at the beginning and end of each echo-train, during slab-select and slab-dephasing gradients along the X-axis. The 19-parameter function was able to largely remove these strong induced voltages, and the performance evaluation is FIT = 0.64 ± 0.10 and CORR = 0.86 ± 0.07 across all precordial traces. The induced-voltages also persisted at the end of each slice, for ∼0.1 seconds after the gradients are no longer pulsing. This residual voltage could be due to the “ringing” of CardioLab's receiver amplifier, which is not currently addressed in Eq. 1.

Figure 5.

Example of ECG traces during a coronal 3D FSE sequence, collected with Set-up II. (A) Imaging sequence consisting of 16 echo trains, followed by clean ECGs. The restored ECG signal, after subtraction of the 19-parameter system response function, resulted in the blue traces. (B) Expanded view of two FSE bursts show the strong induced voltage at the beginning and end of each echo train (red traces), which are not completely corrected by the 19-parameter equation. The echo train bursts fell in different cardiac cycle phases, due to the use of non-ECG-gated acquisition. V6' was acquired with low quality and omitted in this plot.

In cases of multi-slice bSSFP acquisition recorded in one subject, ECGs were recorded at a stable heart rate (Fig. 6A) and immediately after extensive exercise in the MRI (Fig. 6C) during which the heart rate varied between 90 to 70 beats per minute (BPM). The fitted parameters derived from the training data were sufficient for corrections of multiple parallel slice acquisitions under both conditions (Fig. 6A, C). The statistics of the 19-parameter fit (Fig. 6B, D) show that the fitting (FIT) is consistent across slices, and there are strong correlations (CORR>0.5) between the restored ECG traces and the true ECGs.

Figure 6.

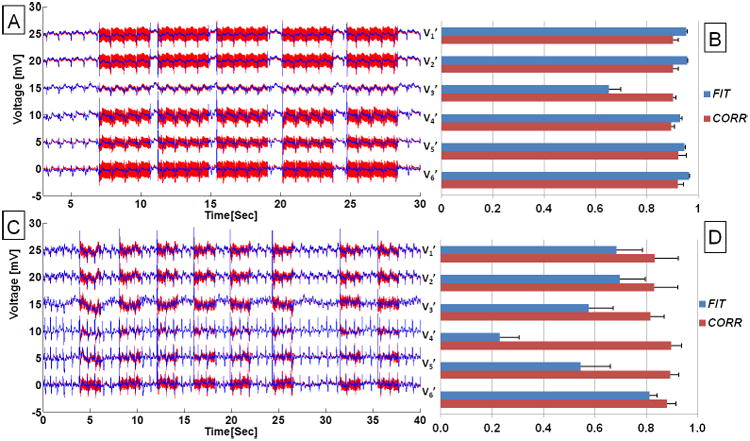
ECGs acquired in a volunteer during a multi-slice bSSFP full resolution acquisition. Precordial ECG traces acquired with set-up II during (A) a stable physiological condition, and (C) relaxation following leg exercises inside the scanner with heart rate dropping from 90 to 70 BPM. Red traces are acquired ECG traces and blue traces are after removal of gradient-induced voltages using the 19-parameter fit. (B, D) Bar plots showing statistics of fit for ECGs acquired and recovered during acquisition of the 5- and 8-parallel bSSFP slices, respectively. FIT and CORR were defined in Eq. 3 and 4, correspondingly.

Supplementary figures are provided to demonstrate, for ECG traces acquired during bSSFP, the importance of using the complete 19-parameter fit model. As shown in Supporting Figure S1B, there is an average of 12% improvement in the fitting error when adding second-order coefficients to the first-order coefficients, with >25% improvement observed in pericardial leads that are farther from isocenter (V₅ and V₆). When using first-order regression (Supporting Figure S2), there is a statistical significance (p <0.05) using all 7 parameters, versus only the gradient-time-derivatives or only the gradient-strength terms.

We also tested changes in regression parameters with varying TR, FOV, and the spatial resolution in bSSFP. The regression parameters remained unchanged when the spatial resolution stays the same, regardless of FOV changes. The importance of second-order coefficients increased concurrently with a strong reduction in TR of bSSFP, which could be due to an increasing importance of the 2^nd order coefficients when gradients along multiple axes are applied simultaneously.

Variation of Induced Voltages across Channels and Subjects

The variation of fitted parameters among 3 volunteers imaged with the same sagittal bSSFP sequence is displayed in vectorial format (Fig. 7A). For purposes of display ease, only the 1^st-order parameters p_1k – p_6k are plotted. It can be seen that the size of the parameters varies consistently between the precordial channels, with the gradient-strength terms p_4k – p_6k occuring largest in V₆′, which is the precordial electrode further closest to the induced hot-spots shown in Bencsik et al. ¹¹, while the gradient-time-derivative terms p_1k – p_3k vary in a different manner among subjects. The large variation in the size and vectorial orientation of the parameters among subjects, could result from inter-subject variations in the distribution of tissues, such as the size of the adipose fat layer and torso dimensions, which varied greatly among the subjects we imaged.

Figure 7.

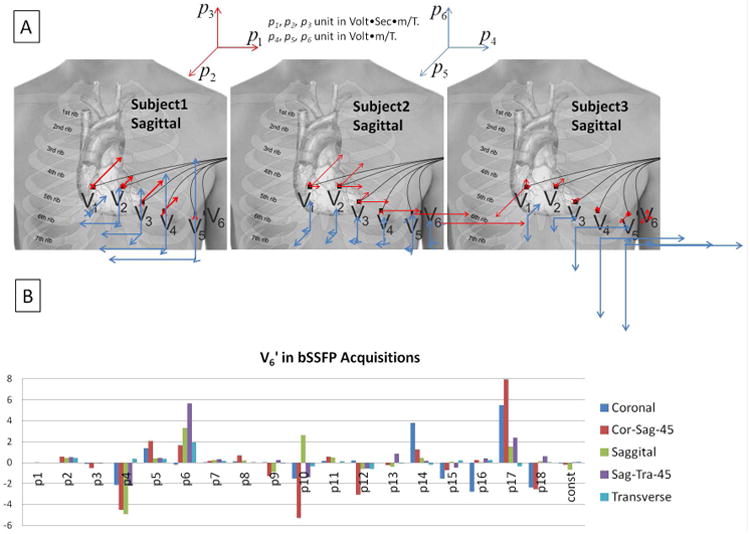
(A) The first 6 fitted parameters (1^st-order coefficients) for 3 subjects during sagittal bSSFP imaging with phase-encoding performed along the y direction (Anterior-Posterior). The 3D vector plots in the center illustrate graphically the size and direction of the coefficients for the precordial electrodes V₁'-V₆', with the origin of each vector placed at the approximate spatial position of the respective electrode. Red arrows denote p_1k – p_3k, which multiply the gradient derivatives along the 3 directions, and blue arrows denote p_4k – p_6k, which multiply the 3 gradients. A gradually increasing influence of the magnetic gradient fields on the ECG noise was observed from V₁' to V₆' in all subjects, although the magnitude of the gradient-induced voltage varied greatly among subjects. (B) Variation of the 19 fit coefficients during bSSFP acquisitions along different slice planes in a volunteer. Cor-Sag-45 and Sag-Tra-45 designate 45-degree oblique angles between the Coronal and Sagittal, and Sagittal and Transverse orientations, respectively.

The large variation of fitted parameters with different slice orientations is illustrated in Fig. 7B. As expected, the largest 2^nd order gradient-induced voltages are in the Cor-Sag-45 orientation, since during oblique acquisitions stronger gradients are applied, and multi-directional gradients are applied simultaneously.

Repeatability Experiments to Determine the Stability of Equation 1 Parameter Fitting

ECG traces were acquired during the same bSSFP sequence at two different times within the same imaging session. Data in each time was then regressed independently to examine the repeatability of the parameter evaluation algorithm, and is demonstrated in Bland-Altman plots for all 19 parameters (Fig. 8). The fitted parameters had a wide range because the repeated bSSFP sequences were acquired along various orientations. In addition, the Pearson's correlation coefficient for repeated evalulation of 19 parameters is ρ = 0.996 in average.

Figure 8.

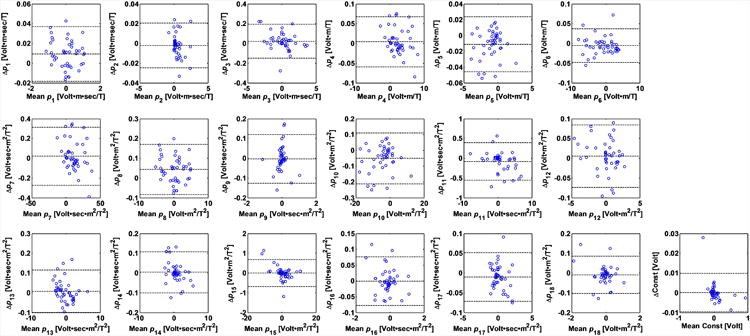
Repeatability measurement of the parameter fitting shown in Bland-Altman plots of all 19 parameters in their SI units listed in Table 1. The 3 dotted lines within each plot indicate upper 95% confidence interval, average, and lower 95% confidence interval of the parameter fitting. The vertical axis represents the difference of the parameters of the repeated scans, and horizontal axis represents the average of the parameters of the repeated scans. ECGs were collected twice during the acquisition of bSSFP sequences along each of 9 different spatial orientations. Since the fitted parameters varied as the orientation changes, a large variation in the fit parameter values can be observed (the abscissa of the graphs). Variations in the fitted parameters can be observed in the small size of the vertical dimension.

Discussion

This study has demonstrated that the magnitude of voltages induced by the MRI gradient coils is of the order of prior theoretical predictions ¹¹. We have shown, for the first time, the frequency spectrum of the induced voltages in the human body in the span of 0 to 24000Hz.

We have also demonstrated that the gradient-induced voltages can be characterized by a theoretically derived equation for the electric field. This equation closely fit the induced voltages observed in all the 12-lead ECG electrodes, during acquisition of all the MRI pulse sequences tested in this study. The fit quality was superior for GRE and bSSFP sequences, relative to 3D FSE. The computed induced voltages did not, however, capture the spikes at the beginning and end of each FSE burst, which may result from the non-linear response of the receiver to strong input signals. We also found that the analysis was sensitive to the temporal alignment between the template (acquired in the absence of gradient activity) to the corrupted traces acquired during imaging. The calculated 19 parameters varied between ECG channels, as predicted by Eq. 1, with the 2^nd -order coefficients playing a greater role for electrodes placed farther from the magnet isocenter.

A confounding result of our findings was the directional and sequence dependence of the regressed coefficients. Our explanation is the lack of vectorial components in Eq. 1's coefficients results from use of conventional ECG electrodes which measure the electric-field magnitude. The electric-field perpendicular to the surface is discontinuous at the boundary of the body and air. Each electrode, depending on its individual orientation (as determined by its placement on the body surface), measures some weighted sum of three electric-field components. As the imaging orientation changes, the field that arrives at the body surface is a different mix of these three components. Due to the sensitivity of ECG electrodes to each of these spatial electric fields, a different total induced voltage is measured. This issue was discussed previously in the context of ECG tomography¹⁵ It has been shown ¹⁰ possible to measure the individual field component using sophisticated electrode designs, which may resolve the individual factor contributing to each of the 19 coefficients (see Eq. A9 and A14), and further allow a single training scan for all orientations of a single sequence.

An additional limitation of Eq. 1 is the insufficient correction for the amplifier's non-linear response following the sudden arrival of strong input signals^16,17, which occurred frequently at the beginning of gradient bursts, leading to a DC offset, followed by an exponential relaxation (“ring-down”) period. The constant term (DC offset) in Eq. 1 deals with this effect to the lowest order, but a more general approach may include higher-order time-dependent components (e.g. Cons_1kt + Cons_2kt², where Cons_1k and Cons_2k are electrode-specific constants, and t is time.), or convolving Eq. 1 with an exponential-decay term.

In the future, it is possible to omit the training sequence, and resolve the fitting parameters iteratively during the first few gradient cycles (i.e. TRs) of the imaging sequence, such as those performed during dummy-cycles for establishing equilibrium magnetizations in the bSSFP and GRE sequences.

The current hardware circuit did not incorporate the electronic (SPDT) switch (Fig. 2I). In the future, the SPDT switch may be employed during the imaging sequence, to remove high-amplitude signals that cause amplifier saturation. Employing the switching feature, it might be possible to acquire limb lead traces with set-up II. The instances where large induced-voltages (spikes) occur within imaging sequences can be anticipated, once the coefficients of Eq. 1 are derived. Use of the switching feature also removes the need to perform low-noise acquisition over the full dynamic range of the gradient-induced voltage, which, as shown here, currently spans a 16-bit range (from 100 μV to 10 V). Because the amplitude of gradient-induced voltages is associated with the area of the conduction loops, in our 12-lead ECG setup, the gradient-induced voltages were larger due to the farther placements of electrodes, relative to 4-lead ECGs which are commonly acquired with shorter distances between leads. With the advent of higher-performance (higher slew rate and peak) gradient systems, the dynamic-range requirements are expected to increase.

Table 1.

The SI units of 19 parameters used in the system response function described in Eq. 1.

p1	Volt·m·sec/T
p2	Volt·m·sec/T
p3	Volt·m·sec/T
p4	Volt·m/T
p5	Volt·m/T
p6	Volt·m/T
p7	Volt·sec·m2/T2
p8	Volt·m2/T2
p9	Volt·sec·m2/T2
p10	Volt·m2/T2
p11	Volt·sec·m2/T2
p12	Volt·m2/T2
p13	Volt·sec·m2/T2
p14	Volt·sec·m2/T2
p15	Volt·m2/T2
p16	Volt·sec·m2/T2
p17	Volt·sec·m2/T2
p18	Volt·m2/T2
Const	Volt

Appendix: The ECG Gradient-Induced Voltage's explicit dependence on the MRI gradient fields

Dynamic magnetic fields B⃗ create electric fields E⃗, according to Maxwell's equation:

$$\nabla \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t},$$ (A1)

where ∇ × denotes the curl operator.

A. The First order approximation

The magnetic field in an MRI scanner can be expressed as:

$$\overrightarrow{B}={\overrightarrow{B}}_x+{\overrightarrow{B}}_y+{\overrightarrow{B}}_z={\overrightarrow{B}}_0+G_x\cdot {\overrightarrow{r}}_x+G_y\cdot {\overrightarrow{r}}_y+G_z\cdot {\overrightarrow{r}}_z,$$

where B⃗₀ is the static magnetic field of the MR magnet, and G_x, G_y, G_z are its spatial gradients.

Consequently, we can express the time varying magnetic field as:

$$\frac{\partial \overrightarrow{B}}{\partial t}=\frac{\partial (G_x\cdot {\overrightarrow{r}}_x)}{\partial t}+\frac{\partial (G_y\cdot {\overrightarrow{r}}_y)}{\partial t}+\frac{\partial (G_z\cdot {\overrightarrow{r}}_z)}{\partial t}$$ (A2)

which expands as

$$\frac{\partial \overrightarrow{B}}{\partial t}=(G_x\frac{\partial {\overrightarrow{r}}_x}{\partial t}+\frac{\partial G_x}{\partial t}\cdot {\overrightarrow{r}}_x)+(G_y\frac{\partial {\overrightarrow{r}}_y}{\partial t}+\frac{\partial G_y}{\partial t}\cdot {\overrightarrow{r}}_y)+(G_z\frac{\partial {\overrightarrow{r}}_z}{\partial t}+\frac{\partial G_z}{\partial t}\cdot {\overrightarrow{r}}_z)$$ (A3)

The magnetic field created by the gradient coils in the MRI scanner can be expressed as

$$\overrightarrow{B}(r,t)={\sum }_{i=1}^3{\overrightarrow{B}}_i$$ (A4)

where i represents the three gradient coils inside each MRI scanner.

Each gradient coil creates fields in all three spatial directions, so we write

$${\overrightarrow{B}}_i={\sum }_{j=1}^3{G}_{ij}\cdot {\overrightarrow{r}}_j,$$ (A5)

where j = x, y, z and $G_{ij}=\frac{\partial B_i}{\partial r_j}$

We commonly refer to the gradients used in MRI imaging, since only the z-component of the magnetic field is of interest for purposes of changing the phase of transverse spin magnetization, as G_x = G₁₃, G_y = G₂₃, G_z = G₃₃

We further assume that the electric field generated by the gradients can be expressed as a sum of decaying spherical waves, so that

$$\overrightarrow{E}={\sum }_m\frac{{\overrightarrow{E}}_m}{(r-r_m)}{e}^{-iL(r-r_m)},$$ (A6)

where E⃗_m is the initial amplitude, L is the wave-number, and r_m is the source location.

Therefore

$$\nabla \times \overrightarrow{E}\cong \overrightarrow{E}/r\text{when}|\frac{2\pi }{r-r_m}|<|L|$$ (A7)

which is true for ionic current flow (velocity outside heart is 20-30 cm/s ^18-22) at distances larger than ∼3 cm (at frequencies ≥ 10 Hz), from the sources.

Eq. A1 can therefore be expressed as

$${\sum }_{j=1}^3\frac{E_j}{r}=\frac{d}{dt}\left[{\sum }_{j=1}^3{\sum }_{i=1}^3{G}_{ij}\right]\cdot r_j+{\sum }_{j=1}^3{\sum }_{i=1}^3{G}_{ij}\cdot v_j,$$ (A8)

where E_j is the electric field along x, y or z direction and $v_j=\frac{d{r}_j}{dt}$ represents the velocity of electrically charged particles (e.g. ions) which change their position over time, so that they are affected by the spatially-varying electric fields and create fields of their own^{23, 24}.

By measuring the current flowing through each gradient coil in the system (a signal which is typically available in the gradient cabinet), we can determine:

G_x =G₁₃(t), and its time derivative $\frac{\partial G_{13}(t)}{\partial t}$

G_y =G₂₃(t), and its time derivative $\frac{\partial G_{23}(t)}{\partial t}$

G_z =G₃₃(t), and its time derivative $\frac{\partial G_{33}(t)}{\partial t}$

Here we make the following assumptions *

$$G_{11}(t)\cong K_{11}{G}_{13}=K_{11}{G}_x,G_{12}(t)\cong K_{12}{G}_{13}=K_{12}{G}_x,G_{21}(t)\cong K_{21}{G}_{23}=K_{21}{G}_y,$$

$$G_{22}(t)\cong K_{22}{G}_{23}=K_{22}{G}_y,G_{31}(t)\cong K_{31}{G}_{33}=K_{31}{G}_z,\mathit{\text{and}}{G}_{32}(t)\cong K_{32}{G}_{33}=K_{32}{G}_z$$

These K_ij are similar to the Maxwell terms used to reduce artifacts resulting from these magnetic fields in echo planar and phase-contrast imaging ^{12, 14}.

The constants K_ij are spatially dependent, and therefore are different for each surface electrode, so that we can further express Eq. A8 as

$$\begin{array}{l}{\sum }_{j=1}^3\frac{E_j}{r}=\frac{d}{dt}(G_{11}+G_{21}+G_{31})\cdot {\widehat{r}}_x+\frac{d}{dt}(G_{12}+G_{22}+G_{32})\cdot {\widehat{r}}_y+\frac{d}{dt}(G_{31}+G_{32}+G_{33})\cdot {\widehat{r}}_z+(G_{11}+G_{21}+G_{31}).{\widehat{v}}_x+(G_{12}+G_{22}+G_{32})\cdot {\widehat{v}}_y+(G_{13}+G_{23}+G_{33})\cdot {\widehat{v}}_z\\ =(K_{11}\frac{\partial G_x}{\partial t}+K_{21}\frac{\partial G_y}{\partial t}+K_{31}\frac{\partial G_z}{\partial t})\cdot {\widehat{r}}_x+(K_{12}\frac{\partial G_x}{\partial t}+K_{22}\frac{\partial G_y}{\partial t}+K_{32}\frac{\partial G_z}{\partial t})\cdot {\widehat{r}}_y+(\frac{\partial G_x}{\partial t}+\frac{\partial G_y}{\partial t}+\frac{\partial G_z}{\partial t})\cdot {\widehat{r}}_z+(K_{11}{G}_x+K_{21}{G}_y+K_{31}{G}_z)\cdot {\widehat{v}}_x+(K_{12}{G}_x+K_{22}{G}_y+K_{32}{G}_z)\cdot {\widehat{v}}_y+(G_x+G_y+G_z)\cdot {\widehat{v}}_z\end{array}$$ (A9)

This becomes, after regrouping of terms

$${\sum }_{j=1}^3\frac{E_j}{r}=\frac{\partial G_x}{\partial t}(K_{11}\cdot {\widehat{r}}_x+K_{12}\cdot {\widehat{r}}_y+{\widehat{r}}_z)+\frac{\partial G_y}{\partial t}(K_{21}\cdot {\widehat{r}}_x+K_{22}\cdot {\widehat{r}}_y+{\widehat{r}}_z)+\frac{\partial G_z}{\partial t}(K_{31}\cdot {\widehat{r}}_x+K_{32}\cdot {\widehat{r}}_y+{\widehat{r}}_z)+G_x(K_{11}\cdot {\widehat{v}}_x+K_{12}\cdot {\widehat{v}}_y+{\widehat{v}}_z)+G_y(K_{21}\cdot {\widehat{v}}_x+K_{22}\cdot {\widehat{v}}_y+{\widehat{v}}_z)+G_z(K_{31}\cdot {\widehat{v}}_x+K_{32}\cdot {\widehat{v}}_y+{\widehat{v}}_z)$$

or

$${\sum }_{j=1}^3\frac{E_j}{r}=\frac{\partial G_x}{\partial t}{p}_1+\frac{\partial G_y}{\partial t}{p}_2+\frac{\partial G_z}{\partial t}{p}_3+G_x{p}_4+G_y{p}_5+G_z{p}_6$$ (A10)

The system response function for the gradient-induced voltages measured at the 9 independent surface electrodes (k = 1, 2, … 9), in a 12-lead ECG experiment is

$$S_k(t)={\sum }_{j=1\cdot }^3{E}_{jk}\cdot r,$$ (A11)

where r is the distance from this electrode to the reference electrode (RL for most ECG systems) and ${\sum }_{j=1}^3.E_{jk}$ is the vectorial-summed field measured by the electrode. It can therefore be expressed as:

$$S_k(t)=p_{1k}\frac{\partial G_x}{\partial t}+p_{2k}\frac{\partial G_y}{\partial t}+p_{3k}\frac{\partial G_z}{\partial t}+p_{4k}{G}_x+p_{5k}{G}_y+p_{6k}{G}_z+C_k,$$ (A12)

where C_k is a constant parameter added to adjust for the DC offset frequently observed in the ECG amplifiers during the onset of strong input signals.

The values p_1k – p_6k and C_k are determined based on the measured ECG gradient-induced voltage S_k, the gradient waveforms G, and their time-domain derivatives $\frac{\partial G}{\partial t}$.

B. Second order approximation

Concomitant magnetic fields with a non-linear spatial dependence are present whenever a linear gradient is activated. Assuming x and y gradient coils are of the same design, but with a 90° coaxial rotation between them, and assuming they are placed symmetrically inside the bore, the concomitant magnetic field to the lowest order is expressed as ¹⁴

$$B_C(t)=\frac{1}{2B_0}\{G_x^2{Z}^2+G_y^2{Z}^2+G_z^2(\frac{x^2+y^2}{4})-G_x{G}_{z}xz-G_y{G}_{z}yz\}$$ (A13)

Note that the first three terms involve fields that are proportional to G², and the last two cross-terms are non-zero only when multiple gradient coils are activated at the same time.

We can then express the time derivatives of this field as

$$\frac{\partial B_C}{\partial t}=\frac{\partial G_x}{\partial t}{G}_x{Z}^2+2G_x^{2}Z{\widehat{v}}_z+2\frac{\partial G_y}{\partial t}{G}_y{Z}^2+2G_y^{2}Z{\widehat{v}}_z+(\frac{x^2+y^2}{4})\frac{\partial G_z}{\partial t}{G}_z+(\frac{2x{\widehat{v}}_x+2y{\widehat{v}}_y}{4})G_z^2-\frac{\partial G_x}{\partial t}{G}_{z}xz-G_x\frac{\partial G_z}{\partial t}xz-G_x{G}_z(z{\widehat{v}}_x+x{\widehat{v}}_z)-\frac{\partial G_y}{\partial t}{G}_{z}yz-G_y\frac{\partial G_z}{\partial t}yz-G_y{G}_z(z{\widehat{v}}_y+y{\widehat{v}}_z)$$ (A14)

Overall, grouping the first-order and second-order effects, the induced voltage S_k(t) can then be expressed as a 19-parameter function

$$S_k(t)=p_{1k}\frac{\partial G_x}{\partial t}+p_{2k}\frac{\partial G_y}{\partial t}+p_{3k}\frac{\partial G_z}{\partial t}+p_{4k}{G}_x+p_{5k}{G}_y+p_{6k}{G}_z+p_{7k}\frac{\partial G_x}{\partial t}{G}_x+p_{8k}{G}_x^2+p_{9k}\frac{\partial G_y}{\partial t}{G}_y+p_{10k}{G}_y^2+p_{11k}\frac{\partial G_z}{\partial t}{G}_z+p_{12k}{G}_z^2+p_{13k}\frac{\partial G_x}{\partial t}{G}_z+p_{14k}{G}_x\frac{\partial G_z}{\partial t}+p_{15k}{G}_x{G}_z+p_{16k}\frac{\partial G_y}{\partial t}{G}_z+p_{17k}{G}_y\frac{\partial G_z}{\partial t}+p_{18k}{G}_y{G}_z+C_k$$ (A15)

where the coefficients C_k, p_1k … p_18k are determined based on the ECG gradient-induced voltage S_k(t), the gradient waveforms G and their time-domain derivatives $\frac{\partial G}{\partial t}$.

The second order terms are expected to be largest in the ECG limb leads (LL, LA, RA), when the heart is placed at the magnet isocenter, since these leads are then farther away from the scanner's isocenter.

* Note that when ∇ × B⃗ = 0, which is not strictly valid for the 12-lead ECG case¹¹, since there are currents flowing in the body, simpler relationships exist between the G_ij. ¹⁴

$$G_{12}(t)=G_{21}(t)=0,G_{13}(t)=G_{31}(t)=G_x,G_{23}(t)=G_{32}(t)=G_y,G_{11}(t)=G_{22}(t)=-0.5G_z$$