Corneal Deformation Response and Ocular Geometry: A Non-invasive Diagnostic Strategy in Marfan Syndrome

Abstract

Purpose

To evaluate corneal air-puff deformation responses and ocular geometry as predictors of Marfan syndrome.

Design

Prospective observational clinical study

Methods

Sixteen investigator-derived, 4 standard Ocular Response Analyzer (ORA), and geometric variables from corneal tomography and optical biometry using Oculus Pentacam and IOL Master were assessed for discriminative value in Marfan syndrome, measuring right eyes of 24 control and 13 Marfan syndrome subjects. Area under the receiver operating characteristic (AUROC) curve was assessed in univariate and multivariate analyses

Results

Six investigator-derived ORA variables successfully discriminated Marfan syndrome. The best lone disease predictor was Concavity Min (Marfan syndrome 47.5 ± 20, control 69 ± 14, p = 0.003; AUROC = 0.80). Corneal hysteresis and corneal resistance factor were decreased (Marfan syndrome CH 9.45 ± 1.62, control CH 11.24 ± 1.21, p = 0.01; Marfan syndrome CRF 9.77 ± 1.65, control CRF 11.03 ± 1.72, p = 0.01) and corneas were flatter in Marfan syndrome (Marfan syndrome K_mean 41.25 ± 2.09 D, control K_mean 42.70 ± 1.81 D, p = 0.046). No significant differences were observed in central corneal thickness, axial eye length, or intraocular pressure. A multivariate regression model incorporating corneal curvature and hysteresis loop area (HLA) provided the best predictive value for Marfan syndrome (AUROC = 0.85).

Conclusions

This study describes novel biodynamic features of corneal deformation responses in Marfan syndrome, including increased deformation, decreased bending resistance, and decreased energy dissipation capacity. A predictive model incorporating HLA and corneal curvature shows greatest potential for non-invasive clinical diagnosis of Marfan syndrome.

Introduction

Marfan syndrome is an autosomal dominant connective tissue disorder caused by mutations in FBN1.¹ Clinical diagnosis currently conforms to the Ghent criteria, most recently revised in 2010.² These diagnostic criteria have evolved since the original description by Antoine-Bernard Marfan in 1896, reflecting challenges presented by a broad phenotypic spectrum and the age-dependent nature of individual abnormalities, as well as advances in our understanding of the genetic etiology of Marfan syndrome and differentiation from related conditions.^2–6 Early diagnosis is of crucial importance in Marfan syndrome due to the life-threatening sequelae of cardiac and vascular pathology. While the estimated prevalence of Marfan syndrome has been cited at 2–3 in 10,000, an exact prevalence is difficult to measure due to presumed under-diagnosis of this condition.^7,8

The role of the ocular examination in diagnosing Marfan syndrome has gained prominence with the revised Ghent criteria, as the presence of ectopia lentis with aortic dilation (Z-score ≥ 2) is currently sufficient for diagnosis.² However, the only other ocular feature officially considered in diagnosis is myopia greater than 3 diopters, which has questionable specificity for this condition.² The potential for ocular abnormalities to aid in diagnosis may be much greater than currently acknowledged, as fibrillin-1 microfibrils that are abnormally formed due to the disease-causing mutations FBN1, are widely distributed in the human eye.⁹ Histological study of fibrillin-1 microfibrils in the Marfan syndrome eye found differences in both quantity and quality of microfibrils, and it is possible that the impact of their malformation likely leads to global ocular changes.^10,11

Investigation of biomechanical and dynamic changes in tissues that contain abnormal fibrillin-1 is a reasonable next step in refining the approach to diagnosing Marfan syndrome. Abnormalities in corneal biomechanical properties, or more precisely, behavior as measured by the techniques utilized in the present study, have been detected in a variety of corneal disorders and postoperative conditions, including Fuchs' dystrophy,¹² post-LASIK eyes,^12,13 and in keratoconus,^12,14–16 a disease characterized by stromal degeneration and disruption of Bowman membrane, of which fibrillin-1 is a component.⁹ Differences between normal and Marfan syndrome corneas have been previously observed at the microscopic and clinical levels. Specifically, Iordanidou et al. evaluated Marfan syndrome corneas using confocal microscopy and found highly reflective interconnected lines between keratocytes in the extracellular matrix of over half of Marfan syndrome corneas, and brightly reflective particles in the endothelium in Marfan syndrome corneas exclusively.¹⁷ Additionally, clinical differences in corneal curvature have been observed repeatedly, as numerous studies have found the Marfan syndrome cornea to be flatter than non-Marfan syndrome corneas.^18–21 Based on these many observations of differences in the Marfan syndrome cornea, it is reasonable to suspect that corneal deformation responses in Marfan syndrome may also be altered.²⁰

Biomechanical behaviors of the cornea can be assessed in vivo using the Ocular Response Analyzer (ORA). To date, only one study has investigated the biomechanical behavior in the corneas of individuals with Marfan syndrome.²² Here we expand on the investigation of alterations in biomechanical behavior in corneas of individuals with Marfan syndrome, utilizing investigator-derived ORA variables described by Hallahan et al. and found to have high predictive value for detecting keratoconus.¹⁶ We assess the capacity of the corneal deformation responses to predict a diagnosis of Marfan syndrome both independently and in conjunction with geometric measurements of the Marfan cornea, including corneal curvature, central corneal thickness, and axial eye length. Through this investigation, we explore the possibility of a novel diagnostic algorithm that may be clinically useful in diagnosing future cases of Marfan syndrome.

Methods

Study design

This prospective, observational clinical study followed the tenants of the Declaration of Helsinki and complied with the Health Insurance Portability and Accountability Act. The project was prospectively approved by the Institutional Review Board of the Cleveland Clinic. Participants were evaluated between September 2012 and June 2013 and provided informed consent for the study.

Two groups of participants were included in this study. One group included individuals with a confirmed diagnosis of Marfan syndrome per the 1996 or 2010 Ghent criteria, based on clinical examinations from ophthalmology, cardiology, and medical genetics, and were all established patients from the Cole Eye Institute, Cleveland Clinic or University Hospitals Case Medical Center. Individuals who had undergone any kind of ocular surgery, or who only had a suspected diagnosis of Marfan syndrome were excluded from this study. The second group included healthy age-matched volunteers without history of Marfan syndrome or other connective tissue diseases or conditions that could affect the health and shape of the cornea such as keratoconus. In total, 13 right eyes of participants with a confirmed diagnosis of Marfan syndrome and 24 right eyes of age-matched controls were evaluated in this study.

Measurements

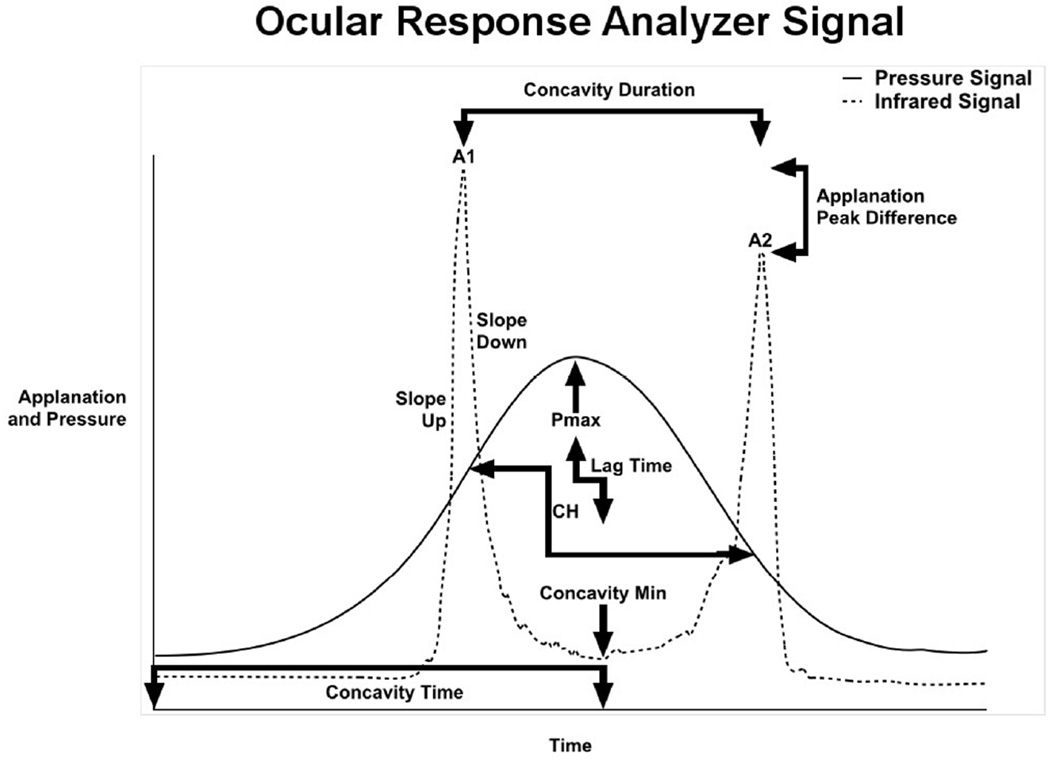
The ORA (Reichert Ophthalmic Instruments, Buffalo, NY) assesses corneal biomechanical behavior through measurement of corneal hysteresis (CH) and other features of the corneal deformation response. Hysteresis is a measurement of the energy absorptive capacity of viscoelastic tissues that undergo time-dependent strain upon deformation. The ORA measures corneal hysteresis through application of a variable air impulse to the central cornea with simultaneous monitoring of the magnitude of corneal deformation using an infrared electro-optical collimation detector system.¹² The pressure and deformation data can be exported for custom analysis. An illustrative example is provided in Figure 1, with the solid line depicting the pressure applied to the cornea, and the dotted line representing corneal deformation. The intensity of photons reflected off the cornea is greatest when the corneal surface is perpendicular to the detector, which occurs at relative applanation. The cornea passes through two points of applanation as it indents and regains shape. The ORA measures corneal hysteresis as the difference in external pressure at these two points of applanation, P1 and P2.¹²

Figure 1.

Graphical representation of selected Ocular Response Analyzer (ORA) signal output: The solid line depicts the pressure applied to the cornea, and dotted line depicts the reflection of infrared light off the cornea surface. Variabled are derived from aspects of the standard ORA waveform as shown here. Abbreviations: A1 is peak intensity at first applanation event; A2 is peak intensity at second applanation event; Pmax ia peak pressure applied, CH is corneal hysteresis.

The ORA also measures the corneal resistance factor (CRF), which is related to the same pressure values from which corneal hysteresis is derived. CRF is biased toward the pressure required to achieve applanation during inward deformation of the cornea due its definition by (P1 – ([kP2]). The constant k was set empirically by the manufacturer to 0.7 to increase association with central corneal thickness.¹² The ORA also provides two measurements of intraocular pressure, Goldmann-correlated and corneal compensated IOP, both of which are included as basic measurements in this study.

The 16 investigator-derived variables included in this study were previously described in detail.¹⁶ The variables were derived from specific aspects of the ORA waveform and are grouped accordingly. These groups include variables derived from applanation signal intensity (A1, A2, Applanation Peak Difference, Concavity Min, Concavity Mean), applied pressure (CRF, CH, P1, P2, P1P2Avg, Pmax), and response time (Concavity Duration, Concavity Time, Lag Time). Variables were also derived from combinations of these properties, including applanation signal intensity as a function of response time (Slope Down, Slope Up), pressure and applanation signal intensity (HLA), and pressure and time (Impulse). The relationship of many of these variables to the ORA waveform is depicted in Figure 1.

Measurements of ocular geometry were obtained in all patients at the same visit as ORA measurements and included axial eye length (IOL Master; Carl Zeiss Meditec, CA), as well as corneal curvature (mean simulated K values) and central corneal thickness using rotating Scheimpflug tomography (Pentacam; Oculus, Wetzlar, Germany).

Statistical analysis

The estimated sample size required to detect a 1 unit difference in CH at the 0.05 significance level was calculated using Minitab based on published standard deviations with 80% power. A group size of 10 was estimated to be sufficient. Mean and standard deviation values and 2-sample unpaired t-tests were calculated for all variables (Minitab v17, State College, PA).

To assess the predictive ability of the 23 measurements taken (including the standard and user-derived ORA variables, as well as geometric measurements), we first calculated the area under the receiver operating characteristic (AUROC) curve for each variable, and tested for significant differences in their predictive ability to correctly classify Marfan syndrome patients. These tests indicated no one variable was better than any of the others in this regard. We then generated multivariable models and tested the models for improvement in predictive ability relative to the simple univariate models. The 23 variables were first tested for independence from one another using the co-linearity diagnostic methods of condition indices and variance inflation factors.

The variables were tested in two groups, specifically, all variables together and the 16 investigator derived variables alone. The final assessment of the matrix indicated 10 of the variables from the list of 23 exhibited sufficient independence from one another (maximum condition index < 10, maximum VIF < 10). The results of a similar analysis for the 16 investigator derived variables indicated that 8 were sufficiently independent to be included in a multivariable study.

Two separate multivariable models were constructed using the two separate groups of independent variables. Multivariate backward logistic regression methods were used to generate reduced models for both sets of variables. A reduced model is one containing only statistically significant variables (p < .05). For both sets of variables, the final model reduced to two terms. These two terms were used to generate an AUROC curve and the resultant curve was tested against the various single variable model AUROC curves to check for improvement in sensitivity and specificity (SAS v9.3, SAS Institute, Cary, NC).

Results

Demographics and clinical findings in study participants are summarized in Table 1. The two diagnostic groups were successfully age matched. The two study groups were roughly similar ethnically, as both were predominantly Caucasian. Specifically, the Marfan syndrome group included 10 Caucasian (77%), 2 African American (15%), and 1 Hispanic (8%) participants. The control group included 17 Caucasian (71%), 4 Asian (17%), 2 Asian/Indian (8%), and 1 African American (4%) participants. The corneas of individuals with Marfan syndrome were significantly flatter than those of controls, with K_mean of 41.25 ± 2.09 diopters for Marfan syndrome corneas. There were no significant differences in the other basic measurements collected for the study participants, including corneal compensated intraocular pressure, Goldmann-correlated intraocular pressure, central corneal thickness, or axial length.

Table 1.

Comparison of age, intraocular pressure, and ocular geometry in Marfan syndrome and control groups

Variable	Control	Marfan syndrome	P-value
Number of eyes	24	13
Age	29.5 ± 11.7	33.5 ± 20.0	0.5
IOPcc (mmHg)	14.9 ± 3.3	15.5 ± 3.3	0.6
IOPg (mmHg)	15.2 ± 3.9	14.1 ± 3.1	0.4
Central Corneal Thickness (micron)	561.3 ± 23.9	552.5 ± 42.4	0.5
Corneal Curvature (Kmean, diopters)	42.70 ± 1.81	41.25 ± 2.09	0.046*
Axial Length (mm)	24.04 ± 1.31	24.61 ± 1.41	0.07

Abbreviations: IOPcc = corneal compensated intraocular pressure; IOPg = Goldmann-correlated intraocular pressure

Ocular response analyzer measurements are included in Table 2, including investigator-derived and 2 standard ORA biomechanical variables (CH, CRF). Six of the 16 investigator-derived variables and both standard variables were significantly different between the two groups. These included variables from three categories, those derived from applanation signal intensity (Group 1: Concavity Min, Concavity Mean), from pressure measurements (Group 2: Corneal Resistance Factor, Corneal Hysteresis, P1, P2, P1P2Avg), and from the combination of pressure and applanation signal intensity (Group 5: HLA).

Table 2.

Definition of air puff-derived corneal response variables and comparison in Marfan syndrome and control groups

Group	Variable	Operational Definition	Control	Marfan syndrome
			Mean ± SD	Mean ± SD	P-value
1: Applanation Signal Intensity	A1	Peak intensity of 1st applanation event	705 ± 89	629 ± 146	0.1
	A2	Peak intensity of 2nd applanation event	649 ± 80	567 ± 161	0.1
	Applanation Peak Difference	A2 – A1	−56 ± 105	−62 ± 106	0.9
	Concavity Min	Minimum applanation intensity between A1 and A2	69 ± 14	48 ± 20	0.003*
	Concavity Mean	Mean applanation intensity between A1 and A2	173 ± 25	145 ± 31	0.01*
2: Pressure Signal	CRF (mmHg)	Corneal Resistance Factor (P1 – 0.7P2)	11.0 ± 1.7	9.5 ± 1.6	0.01*
	CH (mmHg)	Corneal Hysteresis (P2 – P1)	11.2 ± 1.2	9.8 ± 1.7	0.01*
	P1 (mmHg)	Pressure at 1st applanation event	55.6 ± 7.2	47.9 ± 7.8	0.007*
	P2 (mmHg)	Pressure at 2nd applanation event	44.3 ± 6.1	38.1 ± 6.3	0.008*
	P1P2Avg (mmHg)	(P1+P2)/2	49.9 ± 6.6	43.0 ± 7.0	0.008*
	Pmax (mmHg)	Peak value of pressure signal	488.6 ± 40.1	470.6 ± 34.1	0.2
3: Temporal Response Variables	Concavity Duration (msec)	Time lapse between A1 and A2	10.88 ± 0.64	10.93 ± 0.53	0.8
	Concavity Time (msec)	Time from onset of applied pressure to Concavity Min	13.62 ± 3.65	13.34 ± 4.48	0.9
	Lag Time	Time between Pmax and Concavity Min	2.58 ± 2.75	2.35 ± 4.06	0.9
4: Applanation Intensity and Response Time	Slope Down (msec−1)	Negative slope of the 1st applanation peak, from peak to inflection point	−7 ± 205	−71 ± 189	0.4
	Slope Up (msec−1)	Positive slope of the 1st applanation peak, from inflection point to peak	84.5 ± 31.5	73.6 ± 34.4	0.4
5: Pressure and Applanation Intensity	HLA	Area enclosed by pressure vs. applanation function	38863 ± 13668	26412 ± 15699	0.03*
6: Pressure and Time	Impulse	Area under pressure vs. time curve	10063 ± 3228	10170 ± 2812	0.9

Abbreviations: CRF = Corneal Resistance Factor; CH = Corneal Hysteresis; HLA = Hysteresis Loop Area;

^*= statistically significant P-value

The AUROC values for all biomechanical and geometric variables that were found to have significantly better diagnostic capability than by chance are displayed in Table 3. The Youden index was utilized to identify cutoff values for each of these variables with corresponding sensitivity, specificity, positive and negative predictive values. When assessed individually, the best performing variable was Concavity Min (AUROC 0.80, cutoff 51.01, sensitivity 54%, specificity 96%), an indirect measurement of corneal bending resistance.

Table 3.

Comparison of the top performing corneal response variables and geometric measurements for distinguishing Marfan syndrome eyes from controls.

Group	Variable	AUROC	P value	Confidence Interval	Cutoff	Sensitivity (%)	Specificity (%)	PPV	NPV
1: Applanation Signal Intensity	Concavity Min	0.80	0.008	(0.65, 0.95)	51.01	54	96	88	79
	Concavity Mean	0.79	0.02	(0.63, 0.95)	163.33	85	67	58	89
2: Pressure	CRF (mmHg)	0.74	0.02	(0.57, 0.92)	10.30	85	63	53	88
	CH (mmHg)	0.77	0.01	(0.60, 0.94)	10.90	77	71	59	85
	P1 (mmHg)	0.76	0.01	(0.60, 0.93)	51.80	85	67	58	89
	P2 (mmHg)	0.75	0.01	(0.58, 0.92)	41.01	85	63	55	88
	P1P2Avg (mmHg)	0.76	0.01	(0.59, 0.92)	46.35	85	67	58	89
5: Pressure and Applanation Intensity	HLA	0.72	0.03	(0.54, 0.89)	26213.8 4	54	88	70	78
Geometric measurements	Corneal Curvature (Km, diopter)	0.72	0.04	(0.54, 0.90)	41.40 D	62	79	62	79

Abbreviations: CH = corneal hysteresis; CRF = corneal resistance factor; HLA = hysteresis loop area; AUROC = area under the receiver operating characteristic curve; PPV = positive predictive value; NPV = negative predictive value

Via backward elimination multivariable logistic regression, the combination of corneal curvature (K_mean) and HLA was found have greater predictive value for Marfan syndrome than any other individual variable or combination of variables, with an AUROC value of 0.85. Utilizing the regression equation in Table 4, measurement of HLA and corneal curvature may be used to generate the probability of a diagnosis of Marfan syndrome, with sensitivity 69%, specificity 92%, and positive and negative predictive values of 82% and 85% respectively.

Table 4.

Multivariate regression equation for prediction of Marfan syndrome disease phenotype based on measurement of Hysteresis Loop Area and corneal curvature

Equation	AUROC	Sensitivity	Specificity	PPV	NPV
Log(prob/(1−prob) = 39.35 −0.00012*HLA −0.859*KMean	0.84	69	92	82	85

Abbreviations: HLA = hysteresis loop area; AUROC = area under the receiver operating characteristic curve; PPV = positive predictive value; NPV = negative predictive value

Discussion

The clinical diagnosis of Marfan syndrome has been a challenge since its identification by Antoine Marfan over a century ago.³ Without a pathognomonic feature, diagnosis relies on an arbitrary combination of diagnostic criteria that have evolved as understanding of the disease and methods of detection have progressed.^2–6 Because of the continuing difficulties in making a clinical diagnosis, especially in mild or atypical cases, it is appropriate to consider novel strategies in evaluating the broad-reaching impact of fibrillin-1 mutations. To this effect, we utilized the Ocular Response Analyzer to characterize the corneal deformation responses of the Marfan syndrome cornea, and found that alterations in corneal biomechanical behavior can be a useful tool in the diagnosis of Marfan syndrome.

Use of the ORA to assess differences in corneal biomechanical behavior was recently shown by our group to be an effective means of predicting a diagnosis of keratoconus.¹⁶ Many groups have utilized this measurement approach to characterize ocular disease, either by assessing the standard ORA variables or through novel variables.^23,24 The investigator-derived variables considered in the present study assess specific aspects of the corneal response to air puff deformation, monitored through reflection of infrared light off the cornea surface.¹⁶ The variables relate to the applanation signal intensity, applied pressure, tissue response time, or these properties in combination. Through measurement of these variables in the Marfan syndrome cornea and controls, we observed several differences that shed insight into the probable effects of fibrillin-1 mutations on corneal biomechanical behavior. Specifically, lower Concavity Min and Concavity Mean observed in the study group indicates greater maximal deformation of the Marfan syndrome cornea. Lower P1, P2, and P1P2Avg demonstrate a lower amount of air pressure required for deformation. Additionally, decreased HLA, a comprehensive measurement of hysteresis described in detail previously, signifies decreased energy dissipation capacity of the Marfan syndrome cornea.¹⁶ In sum, these differences indicate that the cornea in Marfan syndrome has decreased resistance to bending, and may be less capable of dissipating energy from the external environment.

Many of these variables were found to have the capacity to predict a diagnosis of Marfan syndrome, with the best performing single variable being Concavity Min (Concavity Min 47.5 ± 20.0, AUROC 80). The high predictive value of Concavity Min along with its high specificity (96%) indicates that this measurement could have a role as a confirmatory test in the evaluation of a patient with a suspected diagnosis of Marfan syndrome. HLA could additionally be useful for helping to identify individuals with Marfan syndrome, as decreased HLA was found to have a high specificity (88%) for Marfan syndrome. A number of variables (Concavity Mean, CRF, P1, P2, and P1P2Avg) had moderately high sensitivity values (all 85%), which indicates these variables may be more helpful for Marfan syndrome screening.

Furthermore, considering the dynamic variables along with static corneal measurements, we found that the combination HLA with corneal curvature (K_mean) may also predict a diagnosis of Marfan syndrome in up to 85% of individuals. Of note, the combination of HLA and corneal curvature demonstrates greater predictive value than either variable independently, as each may predict the diagnosis of Marfan syndrome in 72% of patients when considered alone. The combination of Concavity Min and corneal curvature was also tested using multivariate analysis, however this combination did not perform better than single-predictor models. A regression equation incorporating HLA and corneal curvature is provided in this study and may be utilized in the clinical setting to estimate the probability of an individual having Marfan syndrome. Based on this equation we found that decreased values for corneal curvature and/or HLA increase the likelihood of the individual having a diagnosis of Marfan syndrome.

A 2008 article published by Rybczynski et al. examined the diagnostic power of the 1996 Ghent criteria, an analysis that was influential in the 2010 revisions.^2,25 These authors defined high diagnostic power as having a positive likelihood ratio (LR+) > 10, and found the best performing diagnostic criteria to include facial appearance (LR+ 13.47), ectopia lentis (LR+ 21.08), hypoplastic iris or ciliary muscle (LR+ 12.19), and dural ectasia (19.78).²⁵ Dilation of the ascending aorta, a cardinal feature of Marfan syndrome, had a slightly lower positive likelihood ratio of 6.35.²⁵ Additional ocular features examined included flat cornea (LR+ 5.22) and increased axial length of globe (LR+ 1.64). Myopia > 3D was not assessed.²⁵ In the present study, we can calculate that Concavity Min has a positive likelihood ratio of 12.9 (accounting for significant digits). This helps to contextualize the high diagnostic power of Concavity Min relative to the previously established criteria, suggesting it may be as strong, if not stronger, than many of the criteria currently used. It would be valuable to assess the positive likelihood ratios in a larger study in which all candidate variables are measured to allow direct comparison. In the present study we cannot directly compare corneal deformation responses such as Concavity Min to the systemic criteria of the study participants, as assessment of systemic features was not performed systematically on every individual prior to study entry, and there is insufficient data for a powered analysis. The importance of Concavity Min as a putative diagnostic is further supported by the fact that it outperformed corneal curvature in predicting a diagnosis of Marfan syndrome in the present study (AUROC for Concavity Min 0.80 and corneal curvature 0.72). Decreased corneal curvature has been observed as an ocular feature of Marfan syndrome in many previous studies^18–21 and was included as a minor diagnostic criterion in both the Berlin and 1996 Ghent criteria.^5,6 The greater diagnostic power of Concavity Min relative to corneal curvature in this study, as well the relatively high diagnostic performance of Concavity Min in comparison to the previous assessment of systemic criteria by Rybczynski et al, strongly supports consideration of corneal biomechanical behavior in future Marfan syndrome diagnostic schemes.

It is important to note that the mechanisms underlying corneal curvature differences in Marfan syndrome are not known. It is possible that the fibrillin-1 related changes in the Marfan syndrome eye might reflect generalized alterations in the whole eye, in contrast to the focal corneal weakening that is postulated to lead to corneal steepening in keratoconus.²⁶ Detection of similar changes in the variables measured by the ORA does not imply similar mechanisms of disease, but rather reflects a whole-eye response to the air puff, which can be influenced by extracorneal structures.²⁷

While the nature of the Marfan syndrome cornea as being significantly flatter is well supported, there is conflicting data in the literature regarding central corneal thickness. In this study we did not find a significant difference in corneal thickness between the Marfan syndrome and control groups. This finding in conjunction with a lack of measured difference in intraocular pressure between the two groups makes these factors unlikely to impact corneal biomechanical behavior as measured by the ORA. With regard to axial eye length, several previous studies have found the Marfan syndrome eye to be longer.^18,21,28 In the present study, there was a non-significant trend toward longer eyes in Marfan syndrome (p-value = 0.07), which is in agreement with prior studies. It is possible that we had insufficient study power to detect a significant difference in axial eye length (which further supports the strength of corneal biomechanical properties in distinguishing Marfan syndrome). It is also possible that only a small portion of individuals with Marfan syndrome have markedly longer eyes, and that the majority of individuals with Marfan syndrome have eyes of length within the normal range. This is supported by clinical observation, as well as in a previous study that found the distribution of axial eye length in Marfan syndrome to be positively skewed.²⁸

A previous study carried out by Kara et al. used the standard ORA variables to retrospectively assess the biomechanical behavior of the Marfan syndrome cornea.²² These authors found that corneal hysteresis, corneal resistance factor, and Goldmann-correlated intraocular pressure were significantly lower in Marfan syndrome eyes with ectopia lentis in comparison to Marfan syndrome eyes without ectopia lentis, however they did not find a difference between the Marfan syndrome eyes and controls. The disparity between results might be explained by differences in the participant demographics (the Kara et al. study was carried out in Istanbul, Turkey) or possibly due to a difference in the participant age, as the participants of their study were somewhat younger than in the current analysis, especially in view of the progressive worsening of the manifestations of Marfan syndrome with age.⁷ However, the most likely explanation is that the present study used custom variables shown to be more sensitive for discriminating disease-related biomechanical differences in other corneal conditions.¹⁶

The differences observed in corneal deformation responses between Marfan syndrome and control corneas is likely reflective of the global impact of aberrant fibrillin-1 microfibrils on the eye in general. Fibrillin-1 is expressed nearly ubiquitously in the eye, and is a known component of Bowman’s layer, the basement membrane of the corneal epithelium, which is the most anterior layer of the cornea.⁹ The architecture of the anterior-most 120 microns of the cornea has been shown to be responsible for corneal stability.²⁹ As differences in both quantity and quality of microfibrils in the Marfan syndrome eye have been observed histologically, it is reasonable to postulate that anomalous fibrillin-1 in Bowman’s layer could influence corneal biomechanical behavior as was observed here.^10,11,29

A stated goal of the 2010 Ghent criteria was to emphasize simplicity while maintaining accuracy in diagnosis of Marfan syndrome.² Incorporating measurement of corneal deformation responses and corneal curvature in the ophthalmologic evaluation of Marfan syndrome could be a next feasible step in the evolution of the Marfan syndrome clinical diagnostic criteria, improving detection while maintaining low invasiveness. Currently, evaluation of the ocular features of Marfan syndrome requires a slit lamp examination with a fully dilated pupil, assessing for sometimes subtle displacement of the lens and qualitative abnormalities of the zonule fibers. The exam should be performed by an ophthalmologist who is trained to detect minor lens displacements. Also, the pupil in Marfan syndrome has been observed to dilate slowly or insufficiently⁶ which can present a practical difficulty in the clinical assessment of the position of the lens. Measurement of corneal deformation responses and corneal curvature are obtained using non-contact devices, can be performed by a trained technician, and do not require pupillary dilation. This presents a significant diagnostic advantage in assessing corneal deformation responses and corneal curvature.

We acknowledge the current study has a small sample size. However, a priori sample size calculations and the final statistical analysis suggest that the sample sizes obtained were sufficient to detect a meaningful difference, and the results support the case for continued investigation of corneal biomechanical behavior as an aid in the diagnosis of Marfan syndrome. With regard to variance, our previous studies using the ORA in a variety of patient populations demonstrated low levels of variance. In patients with keratoconus, the portion of variance explained by IOP ranged 5–16% for the top 5 disease-predicting variables (8% for Concavity min).¹⁶ In individuals who underwent myopic LASIK and PRK, the variance in biomechanical changes by the most strongly correlating variables was less than 11%.³⁰ Regarding potential fluctuation among examiners, nearly all of the ORA measurements in this study were performed by the same person. However, based on clinical experience, we have not observed noticeable fluctuation in ORA measurements by different examiners. A previous study carried out by Sullivan-Mee et al., showed reproducibility of the standard ORA measurements between different exmaminers.³¹ In the present study, four measurements were taken of the right eye, and the measurement with the highest waveform score (or best score value, the instrument’s internal measurement of reliability) was included in statistical analysis. Finally, the analysis of significance performed here intrinsically accounts for variance, as a significant result implies a mean difference that surpasses the variance of the measurement.

This study paves the way for continued investigation into the potential for corneal biomechanical behavior to aid in the diagnosis of Marfan syndrome. Since completion of this study, the Corvis ST was released by Oculus, which directly images deformation of a corneal optical section using a high-speed Scheimpflug camera. Application of similar analyses for assessing subtle alterations in corneal deformation responses to emerging technologies such as the Corvis-ST may enhance our understanding the biomechanical impact of aberrant fibrillin-1 on the cornea and lead to continued refinement of our evolving strategies for diagnosing Marfan syndrome.

While ectopia lentis is a cardinal feature of Marfan syndrome, an estimated 40% of individuals with Marfan syndrome do not have subluxated lenses.¹⁸ A future goal of our team is to determine the ability of these ORA investigator-derived variables to correctly predict a diagnosis of Marfan syndrome in individuals who do not have ectopia lentis, and thus pose a greater diagnostic challenge. We also intend to investigate the relationship between altered corneal biomechanical behavior and the systemic features of Marfan syndrome. By seeking out unique, low risk means to diagnose Marfan syndrome in those individuals with a more subtle phenotype, and recognizing patterns in ocular and systemic features, we hope to improve the ability to effectively diagnose this condition.

Biography

Lauren Beene is a first year resident in Pediatrics at Rainbow Babies & Children’s Hospital, University Hospitals Case Medical Center in Cleveland, Ohio. She is very grateful for the opportunities she had to learn and grow while carrying out this research project as a medical student under the mentorship of Dr. Elias Traboulsi and Dr. William J. Dupps.