Abstract
Purpose:
Deformable image registration (DIR) plays an important role in dose accumulation, such as incorporating breathing motion into the accumulation of the delivered dose based on daily 4DCBCT images. However, it is not yet well understood how the uncertainties associated with DIR methods affect the dose calculations and resulting clinical metrics. The purpose of this study is to evaluate the impact of DIR uncertainty on the clinical metrics derived from its use in dose accumulation.
Methods:
A biomechanical model based DIR method and a biomechanical-intensity-based hybrid method, which reduced the average registration error by 1.6 mm, were applied to ten lung cancer patients. A clinically relevant dose parameter [minimum dose to 0.5 cm3 (Dmin)] was calculated for three dose scenarios using both algorithms. Dose scenarios included static (no breathing motion), predicted (breathing motion at the time of planning), and total accumulated (interfraction breathing motion). The relationship between the dose parameter and a combination of DIR uncertainty metrics, tumor volume, and dose heterogeneity of the plan was investigated.
Results:
Depending on the dose heterogeneity, tumor volume, and DIR uncertainty, in over 50% of the patients, differences greater than 1.0 Gy were observed in the Dmin of the tumor in the static dose calculation on exhale phase of the 4DCT. Such differences were due to the errors in propagating the tumor contours from the reference planning 4DCT phase onto a subsequent 4DCT phase using each DIR algorithm and calculating the dose on that phase. The differences in predicted dose were more subtle when breathing motion was modeled explicitly at the time of planning with only one patient exhibiting a greater than 1.0 Gy difference in Dmin. Dmin differences of up to 2.5 Gy were found in the total accumulated delivered dose due to difference in quantifying the interfraction variations. Such dose uncertainties could potentially be clinically significant.
Conclusions:
Reductions in average uncertainty in DIR algorithms by 1.6 mm may have a clinically significant impact on the decision-making metrics used in dose planning and dose accumulation assessment.
Keywords: deformable registration, dose accumulation, stereotactic body radiotherapy, biomechanical modeling, hybrid registration
1. INTRODUCTION
Stereotactic body radiation therapy (SBRT) is an effective treatment option in various anatomical sites. However, due to the high dose per fraction in SBRT, even small geometric uncertainties in defining and targeting the anatomy on the planning and treatment delivery images could potentially reduce the therapeutic ratio and increase the risk of normal tissue toxicity.1 Geometric uncertainties, patient setup, breathing motions, tumor response, and radiation-induced edema may lead to changes which compromise the delivery of the planned dose.2,3 Therefore, it is important to understand and quantify the uncertainties in the delivered dose in SBRT patients by accurate accumulation of dose over the course of treatment.1,4
Cone-beam computed tomography (CBCT), as one of the available medical imaging technologies, has been extensively used in image-guided radiotherapy (IGRT).5 CBCT has shown daily changes in the anatomy that rigid alignment cannot correct. Deformable image registration (DIR) determines the voxel to voxel correspondence between different images, enabling the propagation of planning contours and the accumulation of the delivered dose. Dose accumulation, summing the dose delivered to the same voxel of tissue tracked over the course of treatment through DIR, can help us understand how these uncorrected errors affect the deviation of the delivered dose compared to the planned dose distribution.
Although several studies have reported on retrospective dose accumulation in the lung,6–8 it has not translated into prospective clinical trials and widespread use. This is due in part to limitations in the implementation of the process into clinical workflow, but also due to the lack of a clear understanding of how the uncertainties associated with DIR algorithms impact the applications of the DIR especially in SBRT.9 Previous studies showed that intensity-based DIR algorithms can be erroneous in homogeneous regions of images.10 However, through the use of inverse consistency (IC), intensity-based DIRs can improve dose accumulation results.11,12 These studies highlight the need to relate clinical decision parameters (e.g., minimum dose to the target and maximum dose to the normal tissue) to the uncertainty in DIR algorithms on dose accumulation results.
The purpose of this work is to quantify the impact of DIR uncertainty on the clinical parameters calculated from DIR-based dose accumulation. To illustrate the concept, morfeus, a biomechanical model based DIR, and a newly developed Hybrid version, which combines a limited scope intensity-based DIR in series with morfeus leading to a reduction in the uncertainty of 1.6 mm on average,13 will be used to perform dose accumulation in lung SBRT patients. The results of this work show its potential to be used for further quantification of the relationship between geometric and dosimetric uncertainties in DIR-based dose accumulation.
2. METHODS AND MATERIALS
Ten nonsmall cell lung cancer (NSCLC) patients previously treated with SBRT over 3 or 4 fractions were used for this retrospective analysis. Each patient was previously planned for SBRT with the gross tumor volume (GTV) and dose calculations performed on the end exhale phase of 4DCT using an internal target volume (ITV) constructed from the breathing motion observed on the 4DCT and a planning target volume (PTV) margin of 5 mm. All the patients were treated with 6 MV energy using 3D conformal delivery technique and IGRT by 4DCBCT. 4DCBCT scans with ten breathing phases were acquired for each fraction just prior to the delivery of the treatment. For all patients with (*) sign in their number of beams in Table I, a subset of beams were non-coplanar. The prescribed dose ranged from 48 to 60 Gy, as shown in Table I. V20 was defined as the percent of the lungs’ volumes excluding the GTV that received greater than 20 Gy. Two patients (9 and 10) had each two GTVs treated with two separate plans. Dose heterogeneity index (DHI) proposed by Ding et al.14 was used to determine the level of inhomogeneity of the plan within the PTV. The 4DCT and 4DCBCT had the same voxel size of 0.9 × 0.9 × 2.5 mm3. In some cases for 4DCBCT, the resolution was slightly higher with 0.8 × 0.8 × 2.0 mm3. The inhale and exhale dose grids which were imported from the treatment planning system (TPS) (pinnacle v9.2, Philips Medical Systems, Madison, WI) had a voxel size of 2.5 × 2.5 × 2.5 mm3, which was larger than those of the 4DCT and 4DCBCT images.
TABLE I.
Planning information.
| Patient No. | No. of beams | Prescription | Location | V20 | DHI |
|---|---|---|---|---|---|
| 1 | 9* | 60 Gy/3 | RL | 3.5 | 14.2 |
| 2 | 7* | 54 Gy/3 | LLL | 7 | 17.4 |
| 3 | 9* | 60 Gy/3 | LL | 7.8 | 27.5 |
| 4 | 9* | 48 Gy/4 | RL | 2.6 | 13.0 |
| 5 | 9* | 48 Gy/4 | RL | 2.4 | 10.6 |
| 6 | 9* | 48 Gy/4 | RL | 1.3 | 19.9 |
| 7 | 9* | 60 Gy/3 | RLL | 7.9 | 21.4 |
| 8 | 9* | 54 Gy/3 | LL | 5 | 18.5 |
| 9,1 | 10* | 48 Gy/4 | RUL | 2.0 | 19.6 |
| 9,2 | 9* | 48 Gy/4 | RLL | 2.0 | 16.7 |
| 10,1 | 9* | 48 Gy/4 | LLL | 11.2 | 23.3 |
| 10,2 | 9* | 48 Gy/4 | RUL | 11.2 | 11.8 |
| Average | N/A | N/A | N/A | 5.3 | 17.8 |
Note: RL, right lung; LL, left lung; LLL, left lower lobe; RLL, right lower lobe; and RUL, right upper lobe.
2.A. Modeling and deformable image registration
For each patient, 3D tetrahedral models of the lungs, body, and the GTV(s) were created from contours on the end-inspiration 4DCT in the TPS, as previously described.13 Additional normal tissues, including esophagus, trachea, central bronchus, and heart were also modeled by assigning appropriate material properties to subsets of body tetrahedrons (using their imported contours from TPS to classify the tetrahedrons to the tissue).
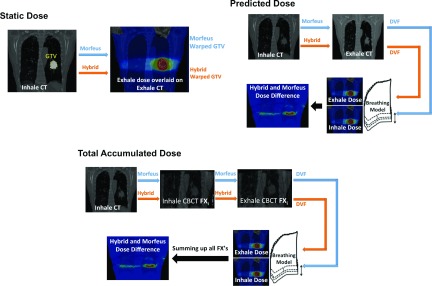
To model the breathing motion defined by the 4DCT, the inhale 4DCT image was deformed to the exhale 4DCT (predicted dose, Fig. 1). To model the interfraction motion of patient over the course of treatment and the intrafraction breathing motion at the time of treatment, the inhale 4DCT image was deformed to the inhale 4DCBCT at the treatment fraction and then to the exhale 4DCBCT image (accumulated dose, Fig. 1). Both morfeus, a biomechanical model based DIR and a recently developed Hybrid technique, which combines morfeus with an intensity-based registration algorithm, were used to model the breathing motion as well as interfraction motions. In morfeus, a guided surface projection algorithm (hypermorph, Altair Engineering, Troy, MI) was used to determine the boundary conditions by comparing the surface of primary and secondary lung finite element method (FEM) models. Linear elastic material properties were assigned to each organ creating a heterogeneous multiorgan model.15 The deformations were then determined by solving for displacements of internal nodes using commercial physics solver software (abaqus, ABAQUS, Inc, Pawtucket, RI).
FIG. 1.
Schematic overview of the dose scenario calculations using DIR. In the static dose, the DIR-warped contour from inhale to exhale is used to calculate Dmin based on the exhale dose grid. In the predicted dose, both inhale and exhale grids (imported from TPS) together with the DIR deformation vector field (DVF) are used in a breathing model to cumulate the dose in six weighted steps to include variant contribution of each of the dose grids in the breathing dose. The accumulated dose is the sum of each fraction’s (denoted by FXi in the figure) breathing doses. For each fraction, the inhale CT is first registered to inhale CBCT to account for setup and interfraction motions. Next, the inhale CBCT is registered to exhale CBCT to provide the DVF for the breathing model. The total accumulated dose is the sum of all fractions. The number of fractions is 3 or 4 depending on the patient’s plan. In all three dose experiments, two sets of results are obtained by separate application of morfeus and the Hybrid DIR method.
The second DIR algorithm, the Hybrid method, was performed by refining the deformations obtained by morfeus through a B-spline based intensity-based registration (Drop, Munich, Germany).16 In the hybrid process, it was ensured that the refinement step produces small magnitude differences with a guaranteed positive Jacobian resulting in an overall biomechanically plausible estimation of the ground truth deformations. The Hybrid method reduces the local residual uncertainties in morfeus results as demonstrated in Ref. 13 and confirmed in Sec. 3.A.
2.B. Model validation
Target registration error (TRE) was used to evaluate the uncertainty of the deformable registration. TRE was calculated based on the Euclidean distance of corresponding anatomical points selected on the inhale and exhale planning CT images. A minimum of 29 (average of 33) points per lung per patient were selected by an expert. Effort was made to select the points with the highest possible spatial dispersion throughout the lung regions. The intraobserver variability was calculated by having the same expert (MV) reselect the points on the exhale CT when shown the points on the inhale CT. The GTV contour manually drawn on the inhale CT was mapped onto the exhale CT using both morfeus and Hybrid. The Dice similarity coefficient (DSC) was computed between the mapped GTV and the manually drawn GTV on the exhale CT. In addition to DSC, the difference in the center of gravity (COG) of the tumor on the inhale and exhale CT was measured and compared to the COG shift calculated from morfeus and Hybrid.
Quantification of the DIR uncertainty (using both morfeus and Hybrid) was also performed using the DSC and the surface distance (based on Hausdorff distance) values obtained for each registration step in each fraction. The GTVs were contoured on each pair (inhale and exhale) of the 4DCBCT images from each fraction. The GTV contours mapped from the inhale CT onto each 4DCBCT using the DIR and the manually drawn GTV contours on the each 4DCBCT image were used to calculate the DSC and the surface distance values for each patient’s tumor over the entire treatment course.
2.C. Static, predicted, and accumulated dose
Figure 1 illustrates the three different dose terminologies in this paper, static, predicted, and accumulated dose, using a schematic of how they are calculated. The experiments were designed to build on each previous step, as outlined in Fig. 1.
Static dose refers to the clinical plan on the exhale phase of the 4DCT, which accounts for the breathing motion through the use of an asymmetric PTV margin, but does not account for the normal tissue motion in and out of the PTV during breathing motion. In the static dose case, the uncertainty in DIR impacts the mapping of the GTV contour from the inhale CT to the exhale CT and the quantification of the dose delivered to the warped GTV when the GTV is in the exhale breathing position only (i.e., there is no dose accumulation in this initial step). As shown in Fig. 1, static dose, different dose values can be obtained with different warped GTVs from inhale to exhale position using each DIR algorithm. Thus, the entire reported dose in the static dose case is influenced by the DIR uncertainty. Here, comparisons can also be made to the actual GTV position as visualized and contoured on the exhale 4DCT image and the dose calculated to the known GTV location (static dose, Fig. 1). This level of gold standard is not possible for the following two experiments.
The predicted dose (Fig. 1) calculates an estimate of the delivered dose based on the breathing motion observed on the 4DCT obtained at the time of treatment planning. The accumulation is performed based on DIR results and a previously published periodic asymmetric probability density function method to model the breathing motion between inhale and exhale states.17 For each tetrahedral element, dose is determined based on the relative time weights reflecting the asymmetry of the breathing cycle.18 This dose represents an estimate of the dose that would be delivered assuming perfect daily image guidance and consistent breathing motion from 4DCT at each fraction. The dose for each tetrahedral element is the summed in six breathing increments from the inhale to the exhale state. In the predicted dose case, the uncertainty in the DIR impacts the mapping of the GTV contour onto the inhale image as well as the accumulated dose, which is determined from tracking the tissue between CT images based on the DIR. Since the dose is calculated over a breathing cycle rather than just one extreme phase (as it is computed in the static dose), the impact of DIR-based uncertainties on the clinical metrics is expected to be less in the predicted dose case than in the static dose case. Because, the largest dose changes occur at the extreme exhale phase where DIR uncertainties are largest. However, in the predicted dose, whereby the dose is summed in six weighted increments including the exhale step, the exhale dose has limited contribution in the overall dose.
The accumulated dose (Fig. 1) calculates the dose delivered based on the 4DCBCT obtained at the start of each treatment fraction. This accounts for unresolved anatomical differences between the reference position at treatment planning and the corresponding reference position at each fraction of treatment delivery (3 or 4 treatment fractions), as well as variations in the breathing motion determined from the 4DCBCT. For each treatment fraction, DIR-based dose accumulation (using both morfeus and the Hybrid DIR algorithm) was performed using the exhale 4DCBCT and the inhale 4DCBCT to account for residual setup uncertainties, changes in the patient position, and the breathing motion observed just prior to the delivery of the treatment fraction. The dose accumulation is the summation of the breathing dose over all fractions. The breathing dose in each fraction is calculated in a process similar to the predicted dose but based on deformation vectors mapping inhale CBCT to exhale CBCT. In the accumulated dose case, the uncertainty in the DIR impacts the mapping of the GTV contour onto the exhale and inhale CBCT images as well as the accumulated dose between exhale and inhale and across all fractions.
2.D. Dose accumulation parameters
A standard method of reporting the dose to the tumor is the use of the minimum dose to a small (less than 0.5 cm3) volume of the tumor.19 Therefore, the sensitivity of this parameter, minimum dose to 0.5 cm3 of the tumor (denoted as Dmin), was used to quantify the impact of the uncertainty in DIR-based dose accumulation. Dmin was calculated for the static dose, predicted dose, and accumulated dose using morfeus and Hybrid to determine the sensitivity of the Dmin parameter on the DIR uncertainty.
Wilcoxon signed rank test was used to determine whether the difference in Dmin results obtained using each of the DIR algorithms was statistically significant. Wilcoxon signed rank test is especially useful for Dmin in this study since the normal distribution assumption regarding the Dmin data could not be made. A similar test was performed for the TRE validation, COG mapping, and DSC values to determine the statistical significance. Linear regression model was used to test the statistical relationship between planning and geometric error parameters and various Dmin. Adjusted R2 value was obtained for the overall regression, and p-values were reported to indicate whether each parameter was statistically significant in predicting Dmin.
3. RESULTS
3.A. Validation of DIR (inhale 4DCT-exhale 4DCT)
Table II summarizes the uncertainty of the two DIR methods using the overall TRE as well as DSC for the tumor contour propagation. The average TRE for the Hybrid method is 1.2 ± 1.0 mm compared to 2.8 ± 1.6 mm using morfeus (p = 0.002). The intraobserver variability was within the voxel size of the images.13 The DSC was on average increased by 0.13 using Hybrid compared to morfeus (p = 0.002); however, the range of improvement was up to 0.33. The Euclidean distance between the inhale and exhale tumor (GTV) COG is also shown in Table II. On average, the COG motion of the GTV between inhale and exhale was 4.9 mm. The average residual error in predicting the COG of the GTV on the exhale image, when using DIR to map the contour, was 2.9 mm using morfeus and reduced to 0.9 mm using the Hybrid registrations (p < 0.0005).
TABLE II.
TRE, GTV COG error, and Dice using morfeus and Hybrid DIR methods for inhale to exhale CT registrations. N is the number of landmarks for TRE calculations in both lungs.
| TRE (mm) | GTV COG error (mm) | Dice index for tumor | ||||||
|---|---|---|---|---|---|---|---|---|
| Patient No. | morfeus | Hybrid | N | No. registration | morfeus | Hybrid | morfeus | Hybrid |
| 1 | 1.8 ± 1.1 | 0.8 ± 0.4 | 63 | 3.9 | 1.7 | 1.0 | 0.82 | 0.82 |
| 2 | 2.7 ± 1.3 | 1.0 ± 0.6 | 63 | 7.9 | 4.3 | 0.7 | 0.72 | 0.88 |
| 3 | 3.2 ± 2.6 | 1.5 ± 1.7 | 68 | 5.4 | 2.5 | 0.8 | 0.87 | 0.95 |
| 4 | 3.9 ± 3.5 | 1.5 ± 1.6 | 63 | 2.9 | 3.3 | 0.6 | 0.69 | 0.87 |
| 5 | 2.6 ± 1.7 | 1.1 ± 1.2 | 107 | 5.1 | 0.6 | 0.2 | 0.92 | 0.95 |
| 6 | 2.6 ± 1.6 | 0.8 ± 0.4 | 59 | 0.6 | 5.9 | 0.8 | 0.45 | 0.78 |
| 7 | 3.2 ± 1.8 | 1.7 ± 1.1 | 61 | 7.3 | 2.7 | 1.7 | 0.82 | 0.85 |
| 8 | 2.9 ± 1.4 | 1.2 ± 1.2 | 59 | 8.9 | 3.1 | 0.7 | 0.82 | 0.91 |
| 9,1 | 2.4 ± 1.3 | 1.0 ± 0.5 | 58 | 3.5 | 2.4 | 0.3 | 0.81 | 0.92 |
| 9,2 | N/A | N/A | N/A | 2.5 | 2.6 | 2.3 | 0.57 | 0.74 |
| 10,1 | 2.5 ± 1.0 | 1.3 ± 1.2 | 59 | 0.9 | 4.5 | 0.4 | 0.36 | 0.78 |
| 10,2 | N/A | N/A | N/A | 9.9 | 1.4 | 1.2 | 0.86 | 0.85 |
| Average | 2.8 ± 1.6 | 1.2 ± 1.0 | 66 | 4.9 | 2.9 | 0.9 | 0.73 | 0.86 |
3.B. Static dose—Impact of DIR-based contour mapping on single state dose assessment
In the first experiment, the DIR algorithms were used to map the GTV contour from the inhale CT to the exhale CT where the planning dose grid is available from the TPS, as well as the actual GTV contour. To understand how uncertainties in DIR algorithms lead to differences in Dmin, the geometric deviation from the original exhale GTV contour (the planning GTV) measured by the DSC, a surface distance (based on Hausdorff distance), DIR-mapped exhale tumor volume differences, and DHI of the plan was reported in Table III. The Dmin difference between the two DIR algorithm was significantly different (p = 0.05). The largest Dmin differences were present in patients 3 and 6 with over 3 Gy differences. Both patients had high DHI indicating high dose heterogeneity within the PTV which increases the chance of sensitivity of Dmin to geometric errors measured by DSC and volume differences. Patient 3 had a substantial (8.4 cm3) change in the GTV volume manually contoured on the inhale and exhale 4DCT. Linear regression analysis showed that DHI, volume, DSC, and surface distance differences could predict Dmin differences with adjusted R2 = 0.81 and p-values of 0.424, 0.003, 0.007, and 0.806 for each parameter, respectively. The analysis indicates that the selected parameters were able to describe 81% of the variations in Dmin differences. Although, in this experiment, DHI and surface distance differences did not statistically significantly contribute in predicting Dmin differences possibly due to small number of patients. Nevertheless, summarizing the relationship between these parameters and Dmin in practical ranges shows promise in identifying the potentially significant Dmin differences. As shown in Table III, over 50% (n = 10) of the patients with more than 1 Gy difference exhibited at least three of the following three characteristics: DHI > 15, volume differences > 5%, DSC differences > 0.08, and surface distance differences > 1.5 mm.
TABLE III.
Difference between morfeus and Hybrid in the static and predicted dose scenarios.
| Patient No. | DHI | Difference in predicted GTV volume (cm3) (% out of total GTV volume) | Surface distance difference (mm) (morfeus–Hybrid) | Dice difference (morfeus–Hybrid) | Static Dmin difference (Gy) (morfeus–static plan) | Static Dmin difference (Gy) (Hybrid–static plan) | Static Dmin difference (Gy) (morfeus–Hybrid) | Predicted Dmin difference (Gy) (morfeus–Hybrid) |
|---|---|---|---|---|---|---|---|---|
| 1 | 14.2 | 0.4 (5%) | 0.0 | 0.01 | 1.1 | 1.0 | 0.1 | 0.2 |
| 2 | 17.4 | 0.1 (2%) | 0.9 | −0.16 | 0.8 | 0.0 | 0.8 | 0.4 |
| 3 | 27.5 | 8.4 (19%) | 3.0 | −0.08 | 3.3 | 0.1 | 3.2 | 1.1 |
| 4 | 13.0 | 0.0 (1%) | 2.5 | −0.18 | 0.9 | 0.3 | 0.6 | 0.5 |
| 5 | 10.6 | 0.2 (6%) | 0.7 | −0.03 | 0.3 | 0.3 | 0.0 | 0.1 |
| 6 | 19.9 | 0.4 (8%) | 2.8 | −0.33 | 1.8 | 1.2 | 3.0 | 0.4 |
| 7 | 21.4 | 0.2 (1%) | 2.1 | −0.03 | 1.9 | 1.8 | 0.1 | 0.8 |
| 8 | 18.5 | 0.8 (3%) | 1.5 | −0.09 | 3.3 | 2.1 | 1.2 | 0.6 |
| 9,1 | 19.6 | 0.2 (4%) | 0.0 | −0.10 | 1.0 | 0.1 | 0.9 | 0.8 |
| 9,2 | 16.7 | 0.1 (5%) | −1.5 | −0.17 | 2.5 | 0.7 | 1.8 | 0.7 |
| 10,1 | 23.3 | 0.0 (1%) | 0.9 | −0.42 | 0.3 | 1.2 | 1.5 | 0.5 |
| 10,2 | 11.8 | 0.4 (6%) | −0.3 | 0.01 | 2.0 | 1.3 | 0.7 | 0.3 |
| Average | 17.8 | 0.9 (N/A) | 1.1 | −0.13 | 1.6 | 0.8 | 1.2 | 0.5 |
3.C. Predicted dose—Impact of DIR-based dose accumulation over a breathing cycle
The differences between the predicted doses (the DIR-based accumulated dose using the breathing motion modeled from 4DCT) using the DIR algorithms are presented in the far right column of Table III. The Dmin differences between the DIR algorithms were approaching significant (p = 0.08) with larger than 1 Gy in patient 3 only. Linear regression model revealed that DHI, volume, DSC, and surface distance differences were 55% (R2 = 0.55) predictor of variations in Dmin difference with p-values of 0.009, 0.885, 0.229, and 0.805, respectively. Despite the subtlety of the predicted dose differences, the results of Table III show that when all of the three criteria related to the plan and DIR uncertainty (DHI > 15, volume differences > 5%, DSC differences > 0.08, and surface distance differences > 1.5 mm) are met, it is still expected to encounter over 1 Gy in the predicted Dmin difference. Previously, Rosu et al.22 investigated the magnitude of changes over a breathing cycle. They found that the largest differences in the dose due to breathing motion from inhale to exhale did not exceed 2% in the point dose and were limited to <0.5% using various clinical metrics. In the current study, the breathing motion was linearly modeled using two extreme phases of inhale and exhale with the help of DIR. The dose was accumulated in six weighted increments, which led to less pronounced effect of the extreme phases, and thus, Dmin differences were subtle compared to the static dose where only the variations on exhale dose were examined.
3.D. Accumulated dose—Impact of DIR-based dose accumulation over treatment fractions
In the last experiment, the total accumulated dose (the DIR-based accumulated dose that accounts for residual uncertainties at treatment delivery and the breathing motion modeled from 4DCBCT just prior to treatment delivery) was calculated using both DIR methods. The differences in Dmin in the GTV as well as DSC, surface distance, and DIR-mapped GTV volume difference statistics were obtained for each tumor in each patient. Adjusted R2 value of 0.53 with p-values of 0.175, 0.988, 0.122, and 0.028 was obtained using a linear regression model for DHI, volume, DSC, and surface distance differences in predicting Dmin differences. Table IV shows that patients 2, 3, and 7 had greater than 2 Gy differences in Dmin. For patients 3 and 7, DSC, surface distance differences, DHI, and tumor volumes were over 0.08, 1.5 mm, 20, and 27 cm3, respectively. Dmin differences between the two DIR algorithms were not statistically significant (p = 0.27). Dosimetric uncertainties due to geometric differences in DIR algorithms can be more amplified when the tumor volume is large and DHI is high (more heterogeneity in the plan). For patient 2, although the tumor volume and DHI were lower compared to previous patients, the dosimetric difference was substantial due to high DSC difference. For the remaining patients, one (or more) of the four parameters (DSC, surface distance, volume, and DHI) was too small to produce any substantial difference in Dmin in the tumor. The result of Table IV indicates that for tumor volumes > 25 cm3, when the DHI > 20 reductions of DIR uncertainty (i.e., DSC differences > 0.08 and surface distance difference > 1.5 mm) may result in Dmin difference of more than 1 Gy in the accumulated dose assessment.
TABLE IV.
The differences between final accumulated doses using morfeus and Hybrid methods. In DSC and surface distance difference, values in brackets show the worst and the best performance cases of the Hybrid compared to morfeus, respectively.
| Patient No. | DHI | % of DIR-mapped GTV volume difference (morfeus–Hybrid) | Surface distance difference (mm) (morfeus–Hybrid) | Dice difference (morfeus–Hybrid) | Dmin difference (Gy) (morfeus–Hybrid) |
|---|---|---|---|---|---|
| 1 | 14.2 | 28.4 ± 10.0 (11.1,37.6) | −0.4 ± 0.3 (−0.5,0.7) | 0.05 ± −0.01 (0.12,−0.05) | 0.0 |
| 2 | 17.4 | 23.8 ± 4.0 (16.8,27.1) | 2.1 ± 0.9 (1.0,5.2) | −0.08 ± 0.04 (0.01,−0.17) | 2.1 |
| 3 | 27.5 | 20.1 ± 4.1 (15.2,25.1) | 3.9 ± −0.1 (2.9,6.5) | −0.09 ± 0.01 (−0.06,−0.11) | 2.5 |
| 4 | 13.0 | 26.5 ± 14.6 (5.0,41.7) | 1.2 ± 0.5 (0.9,4.5) | −0.13 ± 0.06 (0.07,−0.36) | 0.3 |
| 5 | 10.6 | 6.4 ± 4.2 (1.0,14.6) | 1.3 ± 0.6 (0.5,3.2) | −0.14 ± 0.09 (−0.01,−0.29) | 0.2 |
| 6 | 19.9 | 14.1 ± 8.1 (0.0,26.0) | 2.4 ± 0.3 (2.6,5.0) | −0.18 ± 0.03 (−0.06,−0.27) | 0.1 |
| 7 | 21.4 | 9.5 ± 4.2 (4.7,14.3) | 1.9 ± 0.2 (2.3,4.0) | −0.08 ± 0.00 (−0.02,−0.14) | 2.2 |
| 8 | 18.5 | 4.6 ± 4.5 (0.5,13.2) | 0.5 ± 0.9 (−0.7,2.6) | −0.05 ± 0.06 (0.01,−0.11) | 0.5 |
| 9,1 | 19.6 | 11.8 ± 9.7 (0.8,30.8) | 0.8 ± 0.1 (0.7,1.7) | −0.13 ± 0.06 (0.01,−0.33) | 0.5 |
| 9,2 | 16.7 | 2.1 ± 1.2 (0.3,3.8) | 0.1 ± 0.1 (−0.4,4.7) | −0.01 ± 0.00 (0.10,−0.19) | 0.4 |
| 10,1 | 23.3 | 25.4 ± 6.4 (15.2,33.1) | 0.4 ± 0.4 (0.1,1.7) | −0.20 ± 0.08 (0.01,−0.40) | 0.2 |
| 10,2 | 11.8 | 15.2 ± 9.3 (2.4,31.7) | 1.2 ± 0.2 (0.9,4.4) | −0.02 ± 0.03 (0.02,−0.10) | 0.3 |
| Average | 17.8 | 28.4 ± 10.0 (11.1,37.6) | 1.3 ± 0.4 (0.8,3.7) | −0.1 ± −0.04 (0.01, −0.24) | 0.8 |
4. DISCUSSION
This study investigated the impact of uncertainties in DIRs on a clinical decision-making dosimetric parameter in lung SBRT. Such information is important as in the field of radiation oncology, the utilization of DIR increases. Four-dimensional planning has been shown to provide better prediction of dose distribution than the conventional 3D planning.9 However, it is important to understand how the DIR uncertainty impacts the dose accumulation so that the uncertainty associated with the DIR-based dose accumulation metrics can be understood.
The relationship between the uncertainties in the dose parameter (Dmin) and the combinational effect of other factors including DSC, DHI, and GTV volume aid in the generation of guidelines for which the uncertainties of DIR may lead to clinically relevant dosimetric uncertainties. This is consistent with what Hardcastle et al.12 concluded: the larger the spatial error in high gradient regions, the larger the dosimetric uncertainty. In addition, this study is also consistent with the study by Yu et al.,20 which showed that increased DIR uncertainty can lead to more substantial dose discrepancies. In the current study, the quantitative measurement of DIR uncertainty (DSC and surface distance) when combined with other patient-specific properties such as tumor volume and planning heterogeneity (as an indicative of dose gradient) was shown to be an important indication of dosimetric uncertainty.
Deformable image registration plays a significant role in dose accumulation applications. In this study, the impact of the accuracy of DIR was investigated on the static, predicted, and total accumulated dose. Depending on the heterogeneity of the radiation plan in the tumor, a tumor volume change of 19% (between inhale and exhale), a 0.08 difference in DSC, and a minimum of 1.5 mm difference in surface distance (when mapping a GTV contour onto an alternative static plan) could affect Dmin by over 3 Gy (patient 3). The biomechanical based DIR (morfeus) did not apply any boundary conditions to the GTV directly, so the change in the GTV volume (due to variable representation of the tumor on inhale and exhale 4DCT) was not modeled, leading to a remarkable DSC and surface distance discrepancy for this patient. Large discrepancy in tumor volume results in a greater possibility of covering different doses within a highly heterogeneous plan (manifested by DHI). When the DIR results were used through the breathing motion model to calculate the predicted dose, the dosimetric differences were reduced to 1 Gy (Table III), due to the decrease in the weight of the dose from one particular breathing position. Summation of the dose over the course of treatment using different DIR algorithms involved more complex geometric variations. These variations measured by DSC, surface distance, and percent of volume difference statistics combined with other relevant factors (dose heterogeneity of the plan and the tumor volume) resulted in up to 2.5 Gy differences in the minimum dose delivered to 0.5 cm3 volume (Dmin) of the tumor. Such dosimetric discrepancies may have clinical significance.
Clinical implications of DIR-based dose accumulation outcomes should be interpreted in the context of the geometric uncertainties associated with the DIR algorithm. These results suggest that the uncertainty in Dmin when using DIR-based dose accumulation may be greater than 1 Gy if the DIR-based accumulation has the uncertainties of 1.6 mm and if three or more of the following criteria are met: (1) DHI of the plan is larger than 15, (2) and (3) DIR-based contour mapping leads to a DSC and surface distance differences in the tumor exceeding 0.08 and 1.5 mm, respectively, or (4) tumor volume difference is larger than 5%. The linear regression analysis showed the importance of each or a combination of these parameters in a specific dose scenario. By increasing the number of patients, it would be expected to observe better correlation between the uncertainty of Dmin and possibly all four criteria listed above. In the current preliminary study, it was found that in presence of these criteria, the likelihood of a greater than 1 Gy uncertainty in Dmin is 50% when assessing the static dose on a single breathing phase, 10% for the predicted dose, and 30% for the accumulated dose for a SBRT treatment.
Despite the lack of a ground truth accuracy measure for DIR application in clinical images, geometric and dosimetric investigations as performed in the current study can help us to move toward more reliable estimates of the true accuracy. Landmark- and surface-based techniques to assess accuracy, as were used in this study, are the only component of the process to fully understand the accuracy, reliability, and behavior that are necessary prior to the clinical use of any DIR algorithm. The development and implications of additional voxelwise methods of validating DIR algorithms, such as Jacobians, unbalanced energy (UE), and IC are under investigation for clinical usage.21 Furthermore, correlating the dosimetric impact of DIR uncertainties will inform clinicians of the clinical importance of the use of DIR (i.e., Dmin or similar planning parameters) compared to geometric measures, such as TRE.
ACKNOWLEDGMENTS
This work is supported by the U.S. National Institutes of Health Grant No. 5RO1CA124714 and a grant from the Ontario Institute for Cancer Research. The authors wish to thank Dr. Andrea Bezjak, the Addie MacNaughton Chair in Thoracic Radiation Oncology, for her assistance in obtaining the data.
REFERENCES
- 1.Jaffray D. A., Lindsay P. E., Brock K. K., Deasy J. O., and Tomé W., “Accurate accumulation of dose for improved understanding of radiation effects in normal tissue,” Int. J. Radiat. Oncol., Biol., Phys. 76(3), S135–S139 (2010). 10.1016/j.ijrobp.2009.06.093 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rosu M., Chetty I. J., Balter J. M., Kessler M. L., McShan D. L., and Ten Haken R. K., “Dose reconstruction in deforming lung anatomy: Dose grid size effects and clinical implications,” Med. Phys. 32(8), 2487–2495 (2005). 10.1118/1.1949749 [DOI] [PubMed] [Google Scholar]
- 3.Siker M. L., Tomé W. A., and Mehta M. P., “Tumor volume changes on serial imaging with megavoltage CT for non–small-cell lung cancer during intensity-modulated radiotherapy: How reliable, consistent, and meaningful is the effect?,” Int. J. Radiat. Oncol., Biol., Phys. 66(1), 135–141 (2006). 10.1016/j.ijrobp.2006.03.064 [DOI] [PubMed] [Google Scholar]
- 4.Kupelian P.A. et al. , “Serial megavoltage CT imaging during external beam radiotherapy for non–small-cell lung cancer: Observations on tumor regression during treatment,” Int. J. Radiat. Oncol., Biol., Phys. 63(4), 1024–1028 (2005). 10.1016/j.ijrobp.2005.04.046 [DOI] [PubMed] [Google Scholar]
- 5.Sonke J.-J., Zijp L., Remeijer P., and van Herk M., “Respiratory correlated cone beam CT,” Med. Phys. 32(4), 1176–1186 (2005). 10.1118/1.1869074 [DOI] [PubMed] [Google Scholar]
- 6.Flampouri S., Jiang S. B., Sharp G. C., Wolfgang J., Patel A. A., and Choi N. C., “Estimation of the delivered patient dose in lung IMRT treatment based on deformable registration of 4D-CT data and Monte Carlo simulations,” Phys. Med. Biol. 51(11), 2763–2779 (2006). 10.1088/0031-9155/51/11/006 [DOI] [PubMed] [Google Scholar]
- 7.Hugo G. D., Campbell J., Zhang T., and Yan D., “Cumulative lung dose for several motion management strategies as a function of pretreatment patient parameters,” Int. J. Radiat. Oncol., Biol., Phys. 74(2), 593–601 (2009). 10.1016/j.ijrobp.2008.12.069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lu W. et al. , “Deformable registration of the planning image (kVCT) and the daily images (MVCT) for adaptive radiation therapy,” Phys. Med. Biol. 51(17), 4357–4374 (2006). 10.1088/0031-9155/51/17/015 [DOI] [PubMed] [Google Scholar]
- 9.Chan M. K., Kwong D. L., Ng S. C., Tong A. S., and Tam E. K., “Experimental evaluations of the accuracy of 3D and 4D planning in robotic tracking stereotactic body radiotherapy for lung cancers,” Med. Phys. 40(4), 041712 (11pp.) (2013). 10.1118/1.4794505 [DOI] [PubMed] [Google Scholar]
- 10.Kirby N., Chuang C., Ueda U., and Pouliot J., “The need for application-based adaptation of deformable image registration,” Med. Phys. 40(1), 011702 (10pp.) (2013). 10.1118/1.4769114 [DOI] [PubMed] [Google Scholar]
- 11.Bender E. T., Hardcastle N., and Tome W. A., “On the dosimetric effect and reduction of inverse consistency and transitivity errors in deformable image registration for dose accumulation,” Med. Phys. 39(1), 272–280 (2012). 10.1118/1.3666948 [DOI] [PubMed] [Google Scholar]
- 12.Hardcastle N., Bender E. T., and Tomé W. A., “The effect on dose accumulation accuracy of inverse-consistency and transitivity error reduced deformation maps,” Australas. Phys. Eng. Sci. Med. 37, 321–326 (2014). 10.1007/s13246-014-0262-0 [DOI] [PubMed] [Google Scholar]
- 13.Samavati N., Velec M., and Brock K., “A hybrid biomechanical intensity based deformable image registration of lung 4DCT,” Proc. SPIE 9034, 90343J (2014). 10.1117/12.2043560 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ding C., Chang C.-H., Haslam J., Timmerman R., and Solberg T., “A dosimetric comparison of stereotactic body radiation therapy techniques for lung cancer: Robotic versus conventional Linac-based systems,” J. Appl. Clin. Med. Phys. 11(3), 212–224 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Al-Mayah A., Moseley J., and Brock K., “Contact surface and material nonlinearity modeling of human lungs,” Phys. Med. Biol. 53(1), 305–317 (2008). 10.1088/0031-9155/53/1/022 [DOI] [PubMed] [Google Scholar]
- 16.Glocker B., Komodakis N., Tziritas G., Navab N., and Paragios N., “Dense image registration through MRFs and efficient linear programming,” Med. Image Anal. 12(6), 731–741 (2008). 10.1016/j.media.2008.03.006 [DOI] [PubMed] [Google Scholar]
- 17.Balter J. M., Lam K. L., McGinn C. J., Lawrence T. S., and Ten Haken R. K., “Improvement of CT-based treatment-planning models of abdominal targets using static exhale imaging,” Int. J. Radiat. Oncol., Biol., Phys. 41(4), 939–943 (1998). 10.1016/S0360-3016(98)00130-8 [DOI] [PubMed] [Google Scholar]
- 18.Brock K., McShan D., Ten Haken R., Hollister S., Dawson L., and Balter J., “Inclusion of organ deformation in dose calculations,” Med. Phys. 30(3), 290–295 (2003). 10.1118/1.1539039 [DOI] [PubMed] [Google Scholar]
- 19.Bradley J.D. et al. , “A randomized phase III comparison of standard-dose (60 Gy) versus high-dose (74 Gy) conformal chemoradiotherapy with or without cetuximab for stage III non-small cell lung cancer: Results on radiation dose in RTOG 0617,” in ASCO Annual Meeting Proceedings (2013). [Google Scholar]
- 20.Yu H., Zhang S.-X., Wang R.-H., Zhang G.-Q., and Tan J.-M., “The feasibility of mapping dose distribution of 4DCT images with deformable image registration in lung,” Bio-Med. Mater. Eng. 24(1), 145–153 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Li S. et al. , “Voxel-based statistical analysis of uncertainties associated with deformable image registration,” Phys. Med. Biol. 58(18), 6481–6494 (2013). 10.1088/0031-9155/58/18/6481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rosu M., Balter J. M., Chetty I. J., Kessler M. L., McShan D. L., Balter P., and Ten Haken R. K., “How extensive of a 4D dataset is needed to estimate cumulative dose distribution plan evaluation metrics in conformal lung therapy?,” Med. Phys. 34(1), 233–245 (2007). 10.1118/1.2400624 [DOI] [PubMed] [Google Scholar]