Abstract
Accurate modeling of the molecular environment is critical in condensed phase simulations of chemical reactions. Conventional quantum mechanical/molecular mechanical (QM/MM) simulations traditionally model non-electrostatic non-bonded interactions through an empirical Lennard-Jones (LJ) potential which, in violation of intuitive chemical principles, is bereft of any explicit coupling to an atom’s local electronic structure. This oversight results in a model whereby short-ranged exchange-repulsion and long-ranged dispersion interactions are invariant to changes in the local atomic charge, leading to accuracy limitations for chemical reactions where significant atomic charge transfer can occur along the reaction coordinate. The present work presents a variational, charge-dependent exchange-repulsion and dispersion model, referred to as the charge-dependent exchange and dispersion (QXD) model, for hybrid QM/MM simulations. Analytic expressions for the energy and gradients are provided, as well as a description of the integration of the model into existing QM/MM frameworks, allowing QXD to replace traditional LJ interactions in simulations of reactive condensed phase systems. After initial validation against QM data, the method is demonstrated by capturing the solvation free energies of a series of small, chlorine-containing compounds that have varying charge on the chlorine atom. The model is further tested on the SN2 attack of a chloride anion on methylchloride. Results suggest that the QXD model, unlike the traditional LJ model, is able to simultaneously obtain accurate solvation free energies for a range of compounds while at the same time closely reproducing the experimental reaction free energy barrier. The QXD interaction model allows explicit coupling of atomic charge with many-body exchange and dispersion interactions that are related to atomic size and provides a more accurate and robust representation of non-electrostatic non-bonded QM/MM interactions.
I. INTRODUCTION
Combined quantum mechanical/molecular mechanical (QM/MM) simulations are powerful tools in the study of chemical reactions taking place while embedded within large biological scaffolds and/or in condensed phase environments. These hybrid methods are typically orders of magnitudes more efficient than fully quantum mechanical approaches, although recent advances in the development of reactive quantum mechanical force fields have greatly narrowed this gap.1–4 QM/MM methods have been successfully applied in the study of enzymes,5–7 catalytic RNAs,8–10 ligand binding,11–13 acid dissociation constants,14–16 and small molecule reactions occurring in solution.17–20
Combined QM/MM approaches leverage the strengths associated with of both QM methods and MM simulations by allowing a typically small, localized reactive region requiring explicit treatment of electronic degrees of freedom to be modeled within a large, complex condensed phase environment. The overall reliability of QM/MM simulations depends critically on both the accuracy of the chosen QM and MM models as well as the treatment of the QM/MM interaction. Considerations such as the size of the reactive region and the specific chemistry occurring within it must be considered when choosing the QM method. The accuracy of MM force field model depends simultaneously on its functional form and the empirical parameters used to describe the underlying potential. The MM model is typically chosen as to best represent key features of the environment surrounding the QM region. The most advanced force field treatments include accurate descriptions of electrostatic interactions and have explicit consideration of many-body polarization. While such potentials are very promising, these force fields are typically less computationally efficient than their traditional non-polarizable counterparts and, in many cases, have parameters which either have a somewhat limited chemical scope or have not been as fully matured through critical assessment to the level of those employed by the more simple force fields. Because of these reasons, the vast majority of QM/MM simulations currently utilize conventional, point-charge force fields in the study of condensed phase reactions.
The QM and MM regions interact with each other through a QM/MM boundary. Most generally, both bonded and non-bonded interactions are treated over this division. Bonded interactions are required when the QM/MM boundary falls between two or more covalently bound atoms. A variety of specialized methods; including link atoms,21,22 pseudoatoms,23,24 and generalized orbital methods;25,26 have been developed to model this interaction. Non-bonded interactions can be further subdivided into electrostatic and non-electrostatic terms.
The QM/MM non-bonded electrostatic interactions can be treated using different embedding techniques that can be broadly separated into three categories: mechanical, electrostatic, or polarized embedding.27 Electrostatic embedding enters the electrostatic potential due to fixed, static MM point charges directly into the QM Hamiltonian as an external potential to polarize the QM density that results from a self-consistent field (SCF) procedure. This scheme generally provides greater accuracy than mechanical embedding,28 where static point charges are assigned to QM atoms and electrostatics are treated classically as Coulomb interactions between point charges. If the MM force field is itself an explicitly polarizable model then a polarized embedding29,30 scheme can be adopted, where MM polarizable charges/multipoles are allowed to respond to the QM charge density in some way.
The QM/MM non-electrostatic non-bonded interactions include short-ranged exchange repulsion and mid/long-ranged dispersion interactions. Conventional QM/MM methods handle this term using the Lennard-Jones (LJ) model,31–33 which is also the most commonly employed non-electrostatic non-bonded model used by MM force fields. However, unlike the electrostatic QM/MM interactions in electrostatic and polarized embedding methods, the LJ model for non-electrostatic non-bonded QM/MM interactions is not explicitly coupled to the quantum mechanical wave function, meaning these interactions cannot adjust to changes in the chemical environment. In order to account for this issue, atoms in different chemical environments are assigned different LJ interactions, and much like many MM force fields adopt the concept of an atom type—a prescription in which parameters for an atom are inherited based on specific local electronic and chemical bonding environment. Within this framework, each atom type is given a unique set of fixed LJ parameters.34 Given that traditional MM force fields do not allow for the formation or destruction of chemical bonds this strategy provides a practical mechanism for modeling these interactions, provided that the scope of LJ parameters in the force field is wide enough to model a diverse range of intermolecular interactions. However, in the case of QM/MM simulations, the bonding environment can and in fact often does change. As such, adhering to the notion of assigning fixed atom types to reactive QM atoms is impractical and unsound. In careful QM/MM studies, LJ parameters for QM atoms are developed to produce an overall reasonable, balanced reaction profile that strives to eliminate artifacts due to having atoms whose assigned atom types might misrepresent changes in the chemical identity of those atoms over the course of the modeled chemical reaction. However, in doing so the accuracy of the solvation properties of individual states along the reaction pathway is sacrificed. Frequently, it is not possible to select a single LJ parameterization which can simultaneously reproduce quantitative reaction barrier data while obtaining accurate solvation free energies for the reactant and product states.
One partial solution to this issue is to use so-called adaptive QM/MM methods,35–37 where the QM and MM representations of molecules turn on/off as they enter/leave a larger “reactive zone.” In principle QM models account for changes in exchange repulsion and dispersion interactions as a function of the electronic structure. By using these methods and by pushing the QM/MM boundary further away from the reaction zone, the problems associated with static LJ potentials could be greatly reduced. While this approach is conceptually appealing and has been demonstrated to be successful if carefully applied, it is also more computationally demanding than traditional methods and will only have clear benefits if the QM model used is superior to the MM force field at representing solvation properties. For instance, the application of approximate semiempirical, Hartree-Fock, or small basis set density-functional QM models have been shown to often be inferior to a carefully parameterized MM water model for describing the physical properties of liquid water. Alternatively, one could replace the conventional, static LJ QM/MM interaction with one which is explicitly coupled to the QM electronic structure. Recent studies have pioneered this type of approach by directly linking the extent of charge delocalization to the electronic structure of the system, effectively allowing the charge of more negative species to appear more diffuse.38,39
This work introduces a new model that explicitly couples atomic charge with many-body exchange and dispersion interactions. The QXD (Charge-dependent eXchange and Dispersion) model allows the seamless modulation of non-electrostatic, non-bonded interactions in a chemically intuitive and meaningful way with changes in local atomic charge. As atoms become more negatively charged, they become larger and softer with regard to their interactions with surrounding MM atoms. In this way, the model is able to better represent the QM/MM interaction non-locally along the reaction coordinate.
In the present work, we examine a well-studied benchmark reaction of the chloride ion attack on methylchloride using a specific reaction parameterization semiempirical QM model40 in a solution of non-polarizable MM water while treating electrostatic QM/MM interactions via electrostatic embedding. This combination of QM and MM models is widely used in combined QM/MM studies of biological reactions, a target application area for which the hope is that the methods introduced here will have future impact. The remainder of the manuscript will be broken into four parts: (1) Sec. II in which the QXD model is developed, (2) Sec. III which outlines details as to how the QXD model was parameterized and integrated into a QM/MM framework, and (3) Sec. IV which presents, compares, and discusses simulation results for solvation free energy calculations and reaction free energy profiles involving chloride ion attack to methylchloride, and (4) a section which summarizes the main conclusions of the work and places its importance into a broader context.
II. BACKGROUND THEORY
The QXD model replaces the traditional LJ treatment of non-classical interactions in the QM/MM Hamiltonian for QM atoms. It allows QM atoms to effectively “change size” in accordance to fluctuations in local charge, as determined by the single-particle density matrix. QXD does this task through a series of equations which closely follow previous work of Giese and York.41 However, unlike the initial work where the energy was added as a post-SCF correction term, present here is a variational formulation that is integrated with the SCF procedure which provides simple expressions for the gradients needed to obtain forces when used in molecular dynamics calculations.
A. QM/MM simulations
During QM/MM simulations the total potential energy, E, can be written as
| (1) |
where R is an array of atomic positions, q is a set of MM charges, and P is the atomic orbital (AO) representation of the QM total density matrix. This term is defined as
| (2) |
where Pσ is the spin-resolved density matrix,
| (3) |
and nσ and Cσ are the spin-resolved orbital occupation numbers and molecular orbital (MO) coefficients, respectively, and where μ and ν index atomic orbital basis functions.
EQM(R, P) is the QM region’s ab initio self-energy, EMM(R, q) is the MM energy, and EQM/MM(R, P, q) is the interaction energy of the QM region with the MM region. For a given set of atomic positions and MM charges, the total energy is minimized with respect to changes in the QM region’s MO coefficients under the constraint that the MOs remain orthonormal. When the energy is extremized under these constraints, the following stationary condition (the Roothaan-Hall equation) is satisfied:
| (4) |
where Sμν = ∫χμ(r) χν(r) d3r is the AO overlap matrix, and is the spin-resolved Fock (or Kohn-Sham) matrix,
| (5) |
where is QM method’s Fock matrix in the absence of the MM atoms, and is an effective external electronic chemical potential that causes the QM density to respond to the MM environment. The self-consistent field procedure is as follows: 1. Given a set of trial MOs, compute the density matrix. 2. From the density matrix, compute the energy and Fock matrix. 3. If the change in the energy is small, and Eq. (4) is satisfied, then exit. 4. Construct a new set of trial MOs and go to step 1. Typically, a new guess is made by solving Eq. (4) for Cσ.
B. LJ QM/MM interaction potential
In conventional QM/MM implementations, EQM/MM is expressed in terms of non-bonded electrostatic interactions and LJ potentials,
| (6) |
where is the electrostatic interaction, is the bonded interaction, and is the non-bonded interaction term. As discussed in the introduction, can be entirely avoided if the QM/MM boundary does not cross any covalent bonds. The present work will be examining systems which are entirely subsumed by the QM region and no chemical bonds intersect the boundary, so this term will be ignored to avoid unnecessary complication. Furthermore, if the LJ interaction is assumed to represent the non-classical QM/MM interactions, the total QM/MM interaction can be expressed as
| (7) |
where
| (8) |
and ELJ,ac is the LJ potential31,42,43
| (9) |
The LJ expression can be separated into two distinct, but coupled parts. The first representing exchange-repulsion and the latter models the attractive, dispersion interactions.
C. QXD QM/MM interaction potential
The QXD model replaces the QM/MM LJ interactions with a charge-dependent functional form. The systems considered in this work do not explicitly cross the QM/MM boundary, so any specialized treatment of this type of interaction will be ignored. The total QXD energy can be written as
| (10) |
where
| (11) |
where Qa ≡ Qa(P) is the Mulliken charge of QM atom a
| (12) |
| (13) |
and Za is the nuclear charge of atom a.
The charge-dependent QXD van der Waals energy consists of exchange-repulsion and dispersion components,
| (14) |
EX,ac treats the exchange-repulsion as being proportional to the overlap of atomic densities, which Eq. (18) models as the overlap of Slater functions S(r; ζ) = (ζ3/8π) e−ζr. The approximate relationship between exchange-repulsion and atomic overlap was recognized 40 years ago44 and then further developed into an anisotropic repulsion model by Wheatley.45 Recently, similar formalisms have gained popularity in the GEM force field.46 The model used in the present manuscript is based on previous work by Giese,41 which replaces the rigorous treatment of the electron density with an empirical model that can be tuned for high-accuracy while providing a means for incorporating charge-dependence. Specifically, the charge dependence is introduced via the Slater exponents,
| (15) |
ED,ac is a damped R−6 dispersion model, whose C6 dispersion coefficient is proportional to the atomic dipole polarizability, α, and an “effective number of electrons,” Neff. Charge dependence is introduced by making α and Neff a function of atomic charge,
| (16) |
| (17) |
The QXD model depends on the empirical parameters: sa, ζ0,a, ζq,a, Neff,0,a, α0,a, αq,a. The values of Neff,0,a, which on atomic number, were developed by Pellenq and Nicholson47 and are used directly without modification, that is, Neff,0,a is not treated as a parameter to be optimized. The expressions for EX,ac and ED,ac are summarized as follows:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
In the limit ζc → ζa, Eq. (18) reduces to
| (26) |
The Fock matrix correction for the QXD QM/MM model [Eq. (11)] is
| (27) |
where
| (28) |
and ∂EQXD/∂Qa|R,q is obtained from elementary chain-rule derivatives of Eqs. (14)–(25). Modern charge-fitting procedures could be used to more accurately represent local atomic charge, such as ESP fitting48–52 or CMX53–57 charges. However, early tests indicated that regardless of which charge model was used the end results were not significantly different, but rather lead to slightly different optimized parameters, as the changes in charge were highly correlated and internally consistent within the semiempirical framework. Similar results have been demonstrated previously for Mulliken and CM2 charge changes calculated with linear-scaling semiempirical methods.58 These findings, combined with the simplicity of the Mulliken charge mapping into the density matrix and ease of incorporation into the Fock matrix for variational self-consistency, led to use of these charges as a basis for the semiempirical QXD model. It is expected that the parameters developed here are not likely transferable to other quantum methods, and the use of Mulliken charges might not be appropriate for other quantum methods which might use large, delocalized basis sets.
Upon reaching SCF convergence, the atomic gradients of atom a are
| (29) |
where
| (30) |
III. COMPUTATIONAL METHODS
This section describes computational details involving the implementation, parameterization, and validation of the QXD model for interaction energies, molecular dynamics simulations, and free energy calculations. First, we outline how the QXD model can interact with traditional force fields. Second, a protocol for comparing LJ and QXD QM/MM interactions to high-level quantum data using gas-phase scans is provided. Third, MD simulation protocols to calculate solvation free energies used in the parameterization of QXD are shown. Finally, the MD protocol for free energy profile simulations used to validate the QXD QM/MM interaction model is described.
A. The QXD interface with modern force fields
The first step in implementing the QXD correction is to interface it with existing QM/MM frameworks. The QXD model would be inconvenient to use if special parameters would have to be redeveloped for all MM atom types. Fortunately, we have found that the LJ parameters used in current MM force fields can be suitably “mapped” into QXD parameters through a series of approximate expressions. These expressions are purely empirical, and details, including their motivation, are described in the supplementary material, Section S1.97
Therefore, the QXD parameters of the MM atoms are obtained directly from their LJ parameters using the prescription described below, whereas the QXD parameters of the QM atoms are parameterized for the specific QM Hamiltonian used. The description of the QM atom QXD parameters is discussed in Sec. IV C.
The prescription for mapping the MM atom LJ parameters to QXD parameters begins by removing their charge-dependence within the QXD model ζq,c = 0 and αq,c = 0. The approximate relations between the remaining adjustable parameters in the QXD model to the and Rmin,c ≡ (1/2) Rmin,cc LJ parameters are
| (31) |
| (32) |
| (33) |
Parameters A-F neither depend on atom-type nor atomic number and can be used universally (the numerical values are listed in atomic units): A = 9.4423, B = 0.4111, C = 2.8208, D = 3.7893, E = − 0.0192, and F = − 0.7249. The Gc parameter depends on atomic number, as to keep the mapping expressions consistent with the Pellenq and Nicholson values of Neff,0,c used within the dispersion potential.47 Values for Gc have been parameterized for elements H, C, N, O, and Cl by fitting the QXD van der Waals interaction energies to reproduce the LJ energy for a large number of atom-type pairs. The numerical values of these parameters are (listed in atomic units): GH = 32.7324, GC = 19.0422, GN = 18.2066, GO = 17.5986, and GCl = 15.1066. A detailed comparison of the mapped QXD interactions with respect to the LJ potential is presented in Sec. IV A.
B. Specific reaction parameterization Hamiltonian
Solvation free energies of chlorine containing compounds and a prototype reaction of a chloride anion attacking methylchloride will be examined to validate the QXD QM/MM interaction model. This reaction has been extensively studied59–63 and is generally well understood, lending credence as a system for benchmarking new computational models. For all QM/MM calculations reported here, we employ the recently developed Specific Reaction Parameterization (SRP) AM1 Hamiltonian for Cl− attack on CH3Cl that has been demonstrated to accurately model this reaction in both the gas phase and in solution.40 All non-QXD atoms in QM/MM simulations and calculations performed will use the LJ parameters provided in Table I.
TABLE I.
Lennard-Jones Parameters. Parameters used to determine the non-electrostatic, non-bonded interactions in conventional QM/MM and other molecular dynamics simulations. The LJCl− chlorine parameters are taken from the work of Joung and Cheatham64 and are specifically tailored to be used with a TIP4P-Ew solvent, while the LJCH3Cl were independently parameterized to capture the solvation free energy of methylchloride. Other parameters are from the ff99 AMBER force field.65 Rmin,c and εc, values are in Å and kcal/mol, respectively.
| Element | Rmin,c | εc | |
|---|---|---|---|
| Solvent | O | 1.775 931 | 0.162 75 |
| H | 0.000 0 | 0.000 0 | |
| Solute | C | 1.908 0 | 0.086 0 |
| H | 1.487 0 | 0.015 7 | |
| LJCl−: Cl | 2.760 0 | 0.011 661 5 | |
| LJCH3Cl: Cl | 1.448 9 | 0.457 866 2 |
C. QXD validation against high-level quantum calculations
Gas-phase adiabatic scans of a water probe of various molecules of interest were carried out via constrained optimization to demonstrate the viability and flexibility of the QXD interaction model, while also achieving a base line departure point for solution phase parameters. In these scans the quantum-level water is constrained to the TIP4P-Ew66 geometry. The electronic degrees of freedom and the geometry of the molecule of interest were allowed to relax. The water probe is oriented with the hydrogen atoms facing the particle of interest the and the axis of the scan bifurcating the hydrogen-oxygen-hydrogen angle. High-level calculations were performed with the Gaussian09 software suite67 in conjunction with the GaussView tool.68 using the M06-2X functional69 at the mixed 6-31+g(d,p)//6-311++g(3df,2p) level using an ultrafine integration grid for both the geometry and energy evaluations, with tight SCF and optimization criteria. Gas phase QXD scans were performed in the AMBER12 software package70 with the water probe represented by an MM TIP4P-Ew model and an infinite non-bonded cutoff was employed. QXD parameters were optimized via steepest descent optimization in conjunction with a direction set minimization routine, utilizing a Boltzmann weighted chi-squared protocol with additional weighting for reproducing the zero and minimum of the interaction energy.
D. QXD parameterization and thermodynamic integration
Solution phase Thermodynamic Integration (TI) simulations were performed with the AMBER12 software package70 in TIP4P-Ew66 to parameterize the QXD model for condensed phase simulations. All simulations use periodic boundary conditions (PBCs) with a particle mesh Ewald treatment for long-range electrostatics, the QM/MM long-range interaction switch fix, tight density convergence, and a SCF convergence criteria set to 1.0 × 10−10. A tighter density and SCF convergence criteria was desirable due to the importance of accurately modeling the electronic density as it now more directly impacted QXD interactions with the surrounding MM environment.
Parameters are refined through the use of dual-topology, single coordinate TI71–74 simulations to accurately calculate solvation free energies using the thermodynamic cycle shown in Figure 1. TI mixes Hamiltonians of two different potential states (V0 and V1) to calculate the free energy between those states by moving the system along an artificial, alchemical pathway,
| (34) |
where
| (35) |
Simulation protocol was tested for accuracy, examining box size and long-range electrostatic effects. The protocol was adjusted accordingly to eliminate any systematic errors. Following the thermodynamic cycle in Fig. 1, contributions from each leg can be analyzed separately for their contributions to the total solvation energy. Of particular note; the gas phase legs of the cycle involving adjusting non-bonded terms can be ignored as, by design, the contribution to the overall solvation free energy is zero. The gas phase MM to QM leg, designated as ΔG6, is required to correct for differences in arbitrary zeros of the QM and MM representations. Parameterization of QXD is hastened through intelligent division of the cycle and by minimizing the free energy differences experienced in each individual step. To this end, trial LJ parameters were created for each species to approximate their solvation free energy accurately, allowing for the ΔG4 step to be repeatedly run to test small adjustments of QXD parameters without needing additional simulations of other areas in the thermodynamic cycle. Each leg of the thermodynamic cycle is divided into eleven evenly spaced windows from λ = 0.0 to λ = 1.0 with a linear coupling scheme (k = 1) with the exclusion of the calculation of ΔG1. In this transformation a softcore potential scheme75 is used to avoid the “end-point catastrophe” when disappearing a LJ sphere in solution. The endpoint windows in these legs are moved to λ = 0.05 and λ = 0.95. Data were processed using a smoothing Akima spline (and in softcore cases, also extrapolated to the endpoint values of 0.0 and 1.0) to the free energy ∂V/∂λ plots and then those splines were integrated with respect to λ to calculate the free energy contribution from each change. NPT equilibration of the system was run for 250 ps to allow for solvent and box size relaxation. Afterwards, each λ window was NPT equilibrated for an additional 250 ps. Finally, NVE production was ran for 250 ps, analyzed and used in parameterization of the QXD model.
FIG. 1.
Thermodynamic cycle for QXD parameterization. Shown is the cycle used for calculating the solvation free energies for the parameterization of the charge-dependent QM/MM interaction model, QXD. Cycle legs shown in black are simulated using alchemical perturbation (where needed) and the leg in red is the target free energy. For cycles not using QXD, those legs are ignored.
Only the si, ζi(0), ζq,i, αi(0), and αq,i were treated as free parameters, the Neff,i parameters being taken from literature values.47 Data used to parameterize the QXD model were separated into training and testing sets. The training set consisted of solvation free energies for the chloride anion, methylchloride, and carbon tetrachloride molecules, as this set represented diverse charge states of chlorine. The testing set consisted of solvation free energies for the other molecules listed in Table II, as well as the free energy profile for chloride ion attack to methylchloride. Due to the length of the simulations required to obtain solvation free energies in accord with the thermodynamic cycle shown in Figure 1, a step-wise procedure was adopted whereby initial values for the QXD parameters for Cl were taken from fitting to gas-phase QM interaction energy curves at the M06-2X 6-31+G(d,p)//6-311++G(3df,3p) level. In order to reduce the degrees of freedom and conditioning of the fitting problem, this initial curve fitting was performed using LJ parameters which were then mapped into charge-static QXD parameters in accord with Equations (31)–(33), and then a single charge-dependent QXD parameter set was created to capture the three charge-static curves. These parameters were then used for optimization by exploring parameter space in discrete increments ( 5% or less of the initial values) in order refine individual training set molecule solvation free energies. Once QXD interaction curves were determined for each molecule, a single QXD parameterization was created by direction set refinement to these curves and TI simulation to obtain solvation free energy results. During optimization of the QXD parameters for Cl, it was found that small adjustment of the charge-dependent QXD parameters for C and H, which were needed to balance the charge dependence of Cl, was required to get very good fits.
TABLE II.
Comparison between traditional and QXD models. Calculated QM/MM solvation free energies for a series different chlorine-containing compounds, using two parameterizations of the traditional Lennard-Jones model, one made to produce the chloride solvation free energy and the other to capture the CH3Cl solvation free energy, and then a single parameterization of the QXD density-dependent interaction model. Free energies provided are in kcal/mol.
| ΔG, solvation free energy | ||||
|---|---|---|---|---|
| Compound | Experimental79–84 | LJCl− | LJCH3Cl | QXD |
| Cl− Anion | −89.1 | −89.21 | −125.67 | −89.64 |
| CH3Cl | −1.02 to 0.31 | 5.64 | 0.34 | 0.53 |
| CH2Cl2 | −1.90 to −0.65 | 8.11 | 0.14 | −1.37 |
| CHCl3 | −1.78 to −0.38 | 11.43 | 0.62 | 0.33 |
| CCl4 | −0.64 to 1.10 | 14.66 | 2.37 | 1.20 |
| CCl3CHCl2 | −2.32 to −0.24 | 17.63 | 1.51 | 0.28 |
| CCl3CCl3 | −1.57 to −0.93 | 33.84 | 4.53 | 2.94 |
E. Free energy profiles with QXD
The manuscript will then examine the attack of a chloride ion on methylchloride as an example reaction where there is a large amount of charge transfer along the reaction coordinate (RxC).76 General simulation protocol is identical to the QM legs of the thermodynamic cycle which were outline in the previous section. Initial NPT simulations for solvent and box size equilibration were ran for 250 ps followed by another 150 ps of NPT equilibration at each different RxC window. Finally, 150 ps of NVE production was ran and used for analysis. The RxC is defined as a linear combination of orthogonal degrees of freedom, R1-R2, where R1 and R2 are defined as the distance between the attacking/leaving chloride and the carbon atoms. Umbrella windows were evenly spaced every 0.2 Å between RxC values of −3.5 Å and 3.5 Å with force constants ranging from 60 kcal/(mol/Å) and 24 kcal/(mol/Å) depending on location in the RxC. Additional windows between −0.8 Å and 0.8 Å with force constants ranging between 200 kcal/(mol/Å) and 184 kcal/(mol/Å) were used to ensure adequate sampling about the transition state of the reaction. Simulation results were analyzed using vFEP77,78 to obtain the solution phase free energy profile.
IV. RESULTS AND DISCUSSION
In this section the main results the manuscript are discussed. First, the performance of the interface between QXD and traditional QM/MM models will be reviewed and discussed. Next, comparisons will be drawn between the QXD model and the LJ model in their ability to reproduce high-level gas phase interaction curves. Third, the parameterization of QXD for reproducing experimental solvation free energies of various chlorine containing species will be assessed. Fourth, free energy profile results of the previous parameterization for the attack of chloride on methylchloride will be examined. Finally, an overall perspective of the QXD model and its future directions are discussed.
A. Integration of the QXD model into conventional QM/MM frameworks using LJ mapping relations
Integration of QXD into conventional QM/MM frameworks is key to facilitate wide-spread use of the model. Toward this end, an empirical model (Eqs. (31)–(33), see Sec. III) was developed that, as seen in Figure 2, is capable of transforming traditional LJ parameters into charge-static terms which operate within a QXD framework. Differences between the mapped QXD and the LJ interaction curves were tested with thermodynamic integration simulations and found to be negligible with respect to statistical uncertainties typically on the order of 0.1 kcal/mol or less. With this empirical mapping, quantum mechanical atoms that have fully charge-dependent QXD parameters can interact with MM atoms that have static (fixed-charge) QXD parameters derived from their LJ parameters.
FIG. 2.
Lennard-Jones interactions compared with corresponding mapped parameter QXD interactions. Shown are various atom-atom (X–O; X = O, P, S, C) interactions for both traditional Lennard-Jones and QXD models, with QXD charge-independent parameters generated from the interfacing equations which allow for on-the-fly conversion of LJ interactions into a form which can be used with the new QXD charge-dependent interaction model.
B. Robustness of the QXD model for gas-phase interactions
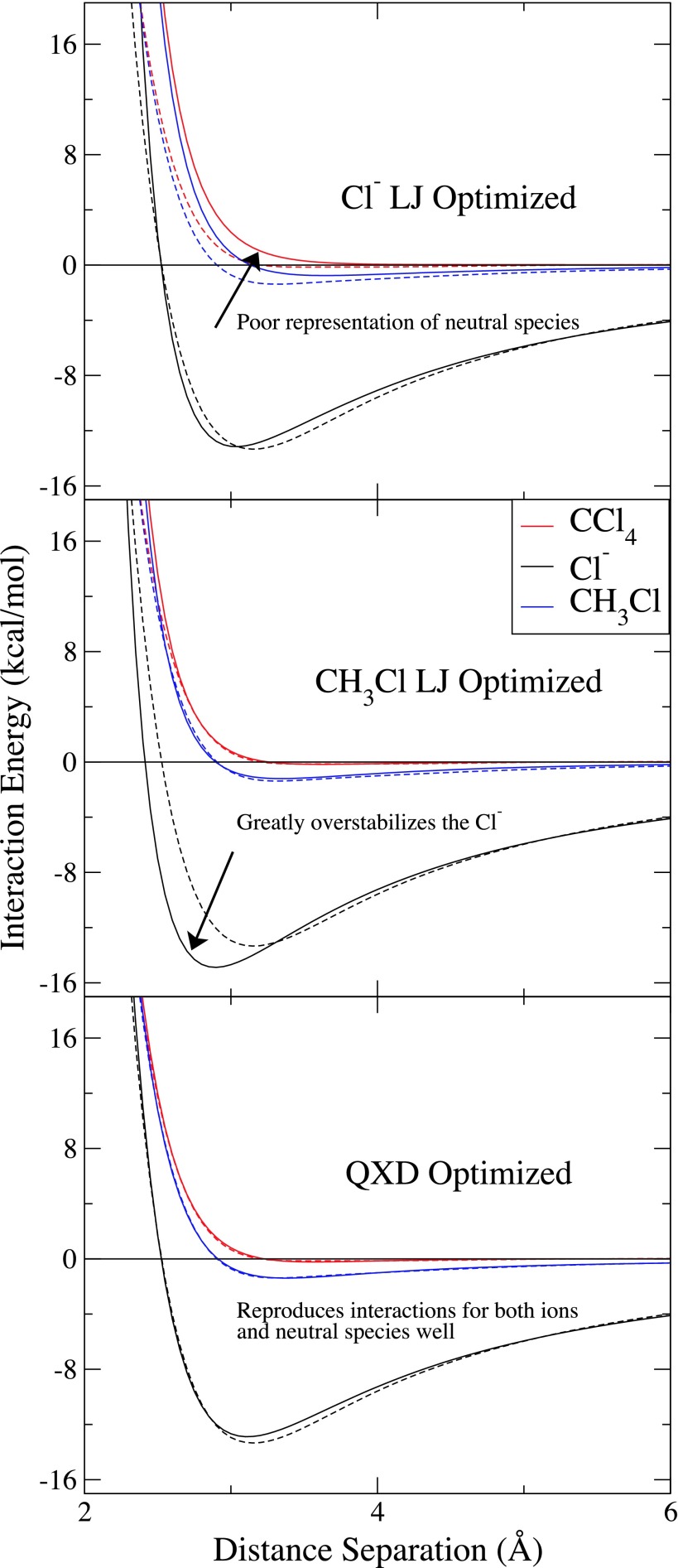
High-level adiabatic QM scans were created to demonstrate the flexibility of the QXD model in reproducing interactions of systems through various charge-states. Initially, two different sets of LJ parameters were optimized to reproduce the high-level scans of the chloride anion and of the methylchloride molecule, respectively. Then, one set of QXD parameters, with full charge-dependent interactions, was optimized to best reproduce all three of the reference potentials shown. Potentials from these optimizations and the resulting scans are shown in Figure 3.
FIG. 3.
Comparative X–H2O gas phase LJ and QXD interactions. Gas phase QM/MM adiabatic energy curves (solid lines) of chlorine containing compounds (X = Cl−, CH3Cl, and CCl4) interacting with a water probe are compared to a high-level quantum benchmark (dashed lines). Water geometry was fixed to emulate a TIP4P-Ew water. Shown are the results from interactions with LJ parameters optimized to reproduce the Cl− reference energy (top), LJ parameters optimized to reproduce the CCl4 reference energy (middle), and QXD with full charge dependent interactions (bottom).
The charge-dependent QXD model stands as a marked improvement when compared to the conventional LJ model in its ability to capture the high-level gas-phase data. The two different LJ 12-6 potentials each reasonably model the interaction for which they were parameterized to reproduce; however, each fails to simultaneously capture the other interactions within a single parameterization. When trying to recapitulate the Cl− interaction, the LJ potential drastically under-stabilizes the neutral chlorinated species. Likewise, when the LJ potential is parameterized to model the methylchloride interaction the neutral particles (CH3Cl and CCl4) interaction curves reasonably well; however, the parameterization significantly over-stabilizes the chloride anion. Without the ability to respond to changes in local electronic environment, the LJ potential lacks the flexibility to represent atoms over a wide range of charge states. The QXD model, on the other hand, is able to accurately capture all of the high-level quantum data with the small exception that there is a slight deviation in the Cl−/water interaction curve.
The discrepancy between QXD and the high-level reference data at the minimum of the interaction curve is likely due to the limited electronic degrees of freedom in the semiempirical and MM models. Despite the high-level water having its geometry fixed to that of the TIP4P-Ew water model, differences between the reference and the QXD scans arise because the electronic density about the atoms of the high-level reference are still allowed to fully polarize. The QM/MM simulations do not allow the electronic density about the chloride anion (and, clearly, around the MM water) to relax as freely as the high-level reference and thus the quantum scans gain additional stabilization beyond what the QXD model can compensate for. Nonetheless, the QXD model demonstrates greater flexibility and robustness in capturing interactions at varied local charge state than the traditional LJ model and represents a significant improvement over the LJ potential in recapitulating high-level quantum data.
C. QXD and LJ QM/MM solvation free energies
QM/MM solvation free energies were calculated through the use of TI and were used in the parameterization of chlorine QXD atoms for solution phase simulations. Parameters for carbon and hydrogen atoms were provided from the mapping equations with additional charge dependence assigned to these atoms to prevent artificial charge transfer between atoms. Chlorine parameters were adjusted to best reproduce the experimental solvation free energy data; the resulting parameters can be found in Table III.
TABLE III.
QXD parameters for chlorine containing compounds. Shown are the QXD parameters used in the present work to accurately predict the solvation free energy for the series of chlorine containing compounds, and the free energy profile for chloride attack to methyl chloride. The optimization procedure is described in detail in Sec. III.
| Type | si | ζi(0) | ζq,i | αi(0) | αq,i | Neff,i |
|---|---|---|---|---|---|---|
| Cl/Cl− | 11.300 | 1.970 | −0.225 | 26.31 | 0.300 45 | 5.551 |
| C | 21.308 | 2.487 | −0.215 | 8.553 | 0.000 00 | 2.657 |
| H | 5.2423 | 3.078 | −0.205 | 1.746 | 0.000 00 | 0.824 |
The QXD model for non-bonded QM/MM interactions shows promise in accurately capturing experimentally known solvation free energies over a series of chlorine-containing compounds and represents a marked improvement over the results obtained when employing a traditional LJ model. While individual sets of parameters in either model could be generated to reproduce the solvation free energy for a single given species, the QXD model is able to accurately replicate experimental solvation free energies of several different species in a variety of local electronic states, while the LJ potential is incapable of this task. For comparison, data from QXD and two sets of LJ parameters can be found in Table II. The LJ parameter sets used where chosen to represent two different chlorine “atom types”: one set that accurately reproduces the solvation free energy of a chloride anion, LJCl−, and another set that captures the methylchloride solvation free energy, LJCH3Cl.
The LJCl− set of parameters accurately reproduces the chloride anion solvation free energy, at −89.21 kcal/mol; however, for all other species it consistently undersolvates the charge neutral species. This is especially notable on molecules containing several chlorine atoms, such as hexachloroethane which is undersolvated by nearly 35 kcal/mol. This behavior is expected for this parameterization as a strong repulsive potential is required to overcome the extremely favorable charge/partial-charge interactions that the chloride ion would experience in solution. As the traditional LJ model cannot respond to changes in the local electronic density, the “size” of the chlorine atoms represented in the non-ionic species are the same as those for the chloride anion. From a physical standpoint, given that the local atomic charge around a chlorine atom in a neutral species is considerably less than that of a chloride anion with full −1 charge, the interactions should reflect the smaller, harder character and have a steeper repulsive wall and closer contact distance. Thus, the LJCl− parameter set causes the chlorine atoms in the molecular compounds to interact as if they were too large and soft, reducing the ability of water to effectively solvate.
The LJCH3Cl set of parameters captures the solvation free energy of methylchloride, reproducing the upper experimental range at 0.34 kcal/mol. Also, because the methylchloride is electronically more similar to several other molecules in the test set than the chloride anion, the LJCH3Cl parameterization generally out performs the LJCl− set as a whole. However, it still fails dramatically is several cases. Most predominately, the chloride anion is oversolvated by approximately 35 kcal/mol. Furthermore, while the methylchloride has the appropriate amount of solvation, the hexachloroethane molecule remains undersolvated by approximately 5.5 kcal/mol. Similar arguments could be made as in the previous paragraph as to why these results are not unexpected. The static nature of the LJ potential means that if the atom being modeled is in a different local electronic environment, then new parameters must be generated to accurately model the non-bonded interactions.
The QXD model, however, is able to capture the solvation free energies for nearly all species with errors of approximately 1.0 kcal/mol or less. The QXD model provides a much more accurate representation of the non-bonded interactions, reproducing solvation free energies for both the chloride anion, at −89.64 kcal/mol, and the methylchloride molecule, at 0.53 kcal/mol. Error can be seen in the hexachloroethane molecule, undersolvating the species by about 4 kcal/mol; however, this number is still in better agreement with experiment than either of the individual LJ models. QXD overcomes the limitations of the LJ model by allowing the non-bonded interaction to adjust to changes in the local electronic density and to behave in a more physically realistic manner. As seen in Table II, more accurate solvation results can be achieved when using the QXD model within a single parameterization than with the tradition LJ potential. The accuracy gained through QXD model does have some computational overhead associated with the evaluation of the modified exchange repulsion and dispersion interactions that must be recomputed at each step of the SCF procedure, and in our current implementation, this introduces a factor of around two in the simulation time relative to the conventional LJ QM/MM model. The ability of the QXD model to adjust to different electronic environments may ultimately allow the need for atom types to be eliminated in QM/MM calculations, which will have particular impact in studies of chemical reactions where local charge changes along the reaction coordinate.
D. QXD and LJ free energy profiles
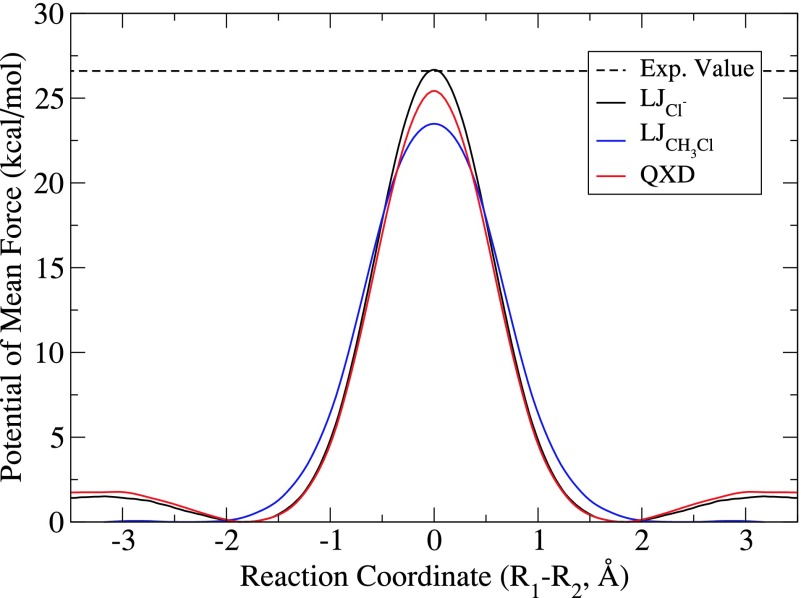
Free energy profile simulations were performed in order to test the effects of the QXD model on the attack barrier of a chloride anion reacting with methylchloride. In previous studies,40 the traditional LJ model was shown to accurately capture this reaction barrier while using the LJCl− parameters set. The QXD parameter set used for these simulations is the set used to recapitulate experimental solvation free energies outlined in Subsection IV C. Results of these simulations, and comparisons to the standard LJ model with both the LJCl− and LJCH3Cl parameter sets, can be seen in Figure 4.
FIG. 4.
Comparative LJ and QXD free energy profiles for the attack of chloride on methylchloride. Free energy profiles were run to examine the effects of the different parameter sets for the traditional LJ potential and the QXD charge-dependent potential had on the attack barrier of the symmetric reaction of Cl− with methylchloride. The simulated free energy barriers for the LJCl−, LJCH3Cl, and QXD (26.5, 23.5, and 25.4 kcal/mol) parameterizations are compared to the experimental value (26.5 kcal/mol estimated from the rate constant).
The QXD model predicts the attack barrier for the reaction of a chloride anion on methylchloride to be 25.4 kcal/mol, roughly 1 kcal/mol less than the experimentally estimated value of 26.5 kcal/mol. The LJCl− and LJCH3Cl parameter sets bracket the QXD reaction barrier: the LJCl− set, which as discussed above produces the worst solvation free energies for neutral chlorine-containing compounds, matches very closely the experimental Cl− attack barrier, whereas the LJCH3Cl set underestimates the barrier by about 3 kcal/mol. The reason for the somewhat fortuitous agreement of the LJCl− parameter set with the experimentally estimated barrier is discussed in more detail below.
E. Discussion of errors
While the results of the current study are encouraging, it is nonetheless important to point out limitations that remains within the scope of the current work. The QXD model provides an improved representation of QM/MM non-electrostatic non-bonded interactions by allowing the character of atoms, in terms of their contribution to exchange repulsion and dispersion interactions, to adjust based on the underlying charge distribution. Nonetheless, the applied QM/MM protocol has additional shortcomings not directly associated with the QM/MM interaction that arise from (1) the lack of explicit many-body response of the MM solvent, and (2) the inflexibility inherent in the minimal valence basis set used in the semiempirical quantum model. Both of these limitations factor directly into the parameterization of the models presented here and thus warrant discussion in order to properly interpret results.
Without the appropriate many-body response of the MM solvent, differently charged QM species will experience electrostatic interactions with the same set of unpolarized MM charges on the water molecules. Further, the minimal valence basis set used in the semiempirical quantum model systematically underestimates the electronic polarization response, and this error becomes worse as anionic charge increases.41 In the extreme cases, such as that of a Cl− anion in isolation, the orbitals are fully occupied, leaving no virtual orbitals available for polarization. Each of these effects requires compensating adjustment of the non-electrostatic non-bonded parameters (i.e., LJ or QXD) to overcome their shortcomings in an effort to reproduce experimental solvation free energies.
There is a large body of the literature85–90 that specifically examines the importance of polarization and quantum many-body effects for modeling a solvated chloride anion. While the degree to which polarization plays a roll in correctly predicting the solvation free energy and long-range solvent structure of the chloride anion is still debated, it is clear that some amount of polarization (in both the solute and the solvent) is required if both of these observables are to be accurately be represented. The mismatch of the polarization effect on Cl− and CH3Cl at different stages along the reaction coordinate is more difficult to correct within the scope of the current work. For instance, in Sec. IV D, the QXD model predicts the attack barrier for the reaction of a chloride anion on methylchloride to be 25.4 kcal/mol, roughly a kcal/mol under the experimentally observed value of 26.5 kcal/mol. The LJCl− parameter set, on the other hand, agrees with experiment to within the statistical error of the calculation which, in retrospect, may not be all that surprising because the LJ terms are consistent with the solvation free energy of a non-polarizable MM Cl− anion, and due to the minimal valence basis set, the QM Cl− anion also lacks polarization. The lower barrier of the LJCH3Cl parameter set, which models the Cl atoms as being smaller, reflects the preferential stabilization of the transition state where both Cl atoms carry a significant charge (approximately 0.89 e in the simulation, see supplementary material97).
As mentioned in the introduction, despite its limitations, the present QXD model is introduced within a QM/MM framework that uses a specific reaction parameter semiempirical QM model in combination with a traditional non-polarizable MM force field. This type of QM/MM model is frequently used to study of biological reactions that often require treatment of a fairly large quantum region, on the order of 50-200 atoms, necessitating a fast QM model. The extensive MM region surrounding the active site is most often modeled by an established static charge force field. It is the hope that the QXD model will ultimately lead to improved QM/MM models for this important application area. In moving toward that goal, it should be recognized that the errors inherent in this choice of QM/MM model become coupled with the parameterization of the QXD model for the QM/MM interaction. However, we argue that introducing a model whereby the exchange repulsion and dispersion interactions of QM atoms are allowed to adjust based on the underlying charge distribution is, at least, and incremental improvement to the alternative of the ubiquitous assumption that these interactions do not depend on electronic structure. Further, the present approach is a systematic first step in the sense that we first consider a QM/MM model using a non-polarizable MM force field such that only atoms in the QM region change their charge distribution and require charge-dependent QXD parameters. It is likely that the use of polarizable force fields, where the charge distribution is also changing in the MM region, may also require the non-electrostatic non-bonded interactions to adjust accordingly.
Future work has promise to overcome both of the limitations described herein. Recently, methods have been recently introduced41,91 that use “chemical potential equalization”92 to overcome the problem of poor modeling of electronic response properties with approximate QM models without increasing the size of the minimal valence basis set (and thus remaining highly efficient). Further, the ongoing development of polarizable force fields93–95 and quantum mechanical force fields (QMFFs)3,4,96 poses a possible solution to seamlessly allow mutual polarization and other many-body quantum effects to be modeled for very large systems with practical efficiency.
V. CONCLUSION
Herein we develop a charge-dependent QXD model for exchange and dispersion interactions in QM/MM simulations that is demonstrated to accurately capture the reaction barrier of the attack of a chloride anion on methylchloride (within approximately 1 kcal/mol) while simultaneously predicting experimental solvation free energies for a series of chlorine-containing compounds. This represents a feat which conventional LJ models fail to accomplish. Additionally, QXD has demonstrated superior flexibility over LJ models by being able to accurately recapitulate high-level gas-phase intermolecular interactions.
As it currently stands, the QXD QM/MM interaction model offers an attractive alternative to traditional LJ interactions for chemical reactions or other processes where changes in local atomic charge occur. An advantage of the QXD model is that it surmounts the problem of pre-assigning non-bonded parameters based on “atom types” corresponding to a particular chemical environment. The QXD model may therefore be useful in simulations of pKa values and pKa shifts, allowing for the correct response in the non-classical terms of key residues in large biopolymers at different catalytic steps in a reaction pathway. Furthermore, the QXD methodology could be applied to next-generation quantum mechanical force fields, which still do not explicitly couple the non-bonded, non-electrostatic interactions directly to the underlying electronic structure.
Acknowledgments
The authors are grateful for financial support provided by the National Institutes of Health (No. GM107485 to D.Y.). Computational resources were provided by the Minnesota Supercomputing Institute for Advanced Computational Research (MSI) and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant No. OCI-1053575, with Project No. TG-MCB110101 (D.Y.).
REFERENCES
- 1.van Duin A. C., Dasgupta S., Lorant F., and Goddard W. A. III, J. Phys. Chem. A 105, 9396 (2001). 10.1021/jp004368u [DOI] [Google Scholar]
- 2.Xie W. and Gao J., J. Chem. Theory Comput. 3, 1890 (2007). 10.1021/ct700167b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Giese T. J., Huang M., Chen H., and York D. M., Acc. Chem. Res. 47, 2812 (2014). 10.1021/ar500103g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Giese T. J., Panteva M. T., Chen H., and York D. M., J. Chem. Theory Comput. 11, 451 (2015). 10.1021/ct500799g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Senn H. M. and Thiel W., Curr. Opin. Chem. Biol. 11, 182 (2007). 10.1016/j.cbpa.2007.01.684 [DOI] [PubMed] [Google Scholar]
- 6.Topol I. A., Cachau R. E., Nemukhin A. V., Grigorenko B. L., and Burt S. K., Biochim. Biophys. Acta 1700, 125 (2004). 10.1016/j.bbapap.2004.04.007 [DOI] [PubMed] [Google Scholar]
- 7.Devi-Kesavan L. S., Garcia-Viloca M., and Gao J., Theor. Chem. Acc. 109, 133 (2003). 10.1007/s00214-002-0419-x [DOI] [Google Scholar]
- 8.Lee T.-S., Silva Lopez C., Giambaşu G. M., Martick M., Scott W. G., and York D. M., J. Am. Chem. Soc. 130, 3053 (2008). 10.1021/ja076529e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wong K.-Y., Lee T.-S., and York D. M., J. Chem. Theory Comput. 7, 1 (2011). 10.1021/ct100467t [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Banáš P., Jurečka P., Walter N. G., Šponer J., and Otyepka M., Methods 49, 202 (2009). 10.1016/j.ymeth.2009.04.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cho A. E., Guallar V., Berne B., and Friesner R., J. Comput. Chem. 26, 915 (2005). 10.1002/jcc.20222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jorgensen W. L. and Tirado-Rives J., J. Comput. Chem. 26, 1689 (2005). 10.1002/jcc.20297 [DOI] [PubMed] [Google Scholar]
- 13.Antony J., Grimme S., Liakos D. G., and Neese F., J. Phys. Chem. A 115, 11210 (2011). 10.1021/jp203963f [DOI] [PubMed] [Google Scholar]
- 14.Kamerlin S. C. L., Haranczyk M., and Warshel A., J. Phys. Chem. B 113, 1253 (2009). 10.1021/jp8071712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gao J., Li N., and Freindorf M., J. Am. Chem. Soc. 118, 4912 (1996). 10.1021/ja960021m [DOI] [Google Scholar]
- 16.Jensen J. H., Li H., Robertson A. D., and Molina P. A., J. Phys. Chem. A 109, 6634 (2005). 10.1021/jp051922x [DOI] [PubMed] [Google Scholar]
- 17.Gregersen B. A., Lopez X., and York D. M., J. Am. Chem. Soc. 126, 7504 (2004). 10.1021/ja031815l [DOI] [PubMed] [Google Scholar]
- 18.Lopez X., York D. M., Dejaegere A., and Karplus M., Int. J. Quantum Chem. 86, 10 (2002). 10.1002/qua.1601 [DOI] [Google Scholar]
- 19.van der Kamp M. W. and Mulholland A. J., Nat. Prod. Rep. 25, 1001–1014 (2008). 10.1039/B600517A [DOI] [PubMed] [Google Scholar]
- 20.Radak B. K., Harris M. E., and York D. M., J. Phys. Chem. B 117, 94 (2013). 10.1021/jp3084277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Antes I. and Thiel W., J. Phys. Chem. A 103, 9290 (1999). 10.1021/jp991771w [DOI] [Google Scholar]
- 22.Reuter N., Dejaegere A., Maigret B., and Karplus M., J. Phys. Chem. A 104, 1720 (2000). 10.1021/jp9924124 [DOI] [Google Scholar]
- 23.Zhang Y., Lee T.-S., and Yang W., J. Chem. Phys. 110, 46 (1999). 10.1063/1.478083 [DOI] [Google Scholar]
- 24.Zhang Z., Xu L., Wang G., Shao C., and Jiang L., Comput. Theor. Chem. 1043, 38 (2014). 10.1016/j.comptc.2014.05.013 [DOI] [Google Scholar]
- 25.Pu J., Jiali Gao P., Donald P., and Truhlar G., ChemPhysChem 6, 1853 (2005). 10.1002/cphc.200400602 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pu J., Gao J., and Truhlar D. G., J. Phys. Chem. A 108, 632 (2004). 10.1021/jp036755k [DOI] [Google Scholar]
- 27.Senn H. M. and Thiel W., Top. Curr. Chem. 268, 173 (2007). 10.1007/128_2006_084 [DOI] [Google Scholar]
- 28.Lin H. and Truhlar D. G., Theor. Chem. Acc. 117, 185 (2007). 10.1007/s00214-006-0143-z [DOI] [Google Scholar]
- 29.Gao J., J. Comput. Chem. 18, 1061 (1997). [DOI] [Google Scholar]
- 30.Zhang Y., Lin H., and Truhlar D. G., J. Chem. Theory Comput. 3, 1378 (2007). 10.1021/ct7000107 [DOI] [PubMed] [Google Scholar]
- 31.Lennard-Jones J. E., Proc. Phys. Soc. 43, 461 (1931). 10.1088/0959-5309/43/5/301 [DOI] [Google Scholar]
- 32.Freindorf M. and Gao J., J. Comput. Chem. 17, 386 (1996). [DOI] [Google Scholar]
- 33.Freindorf M., Shao Y., Furlani T. R., and Kong J., J. Comput. Chem. 26, 1270 (2005). 10.1002/jcc.20264 [DOI] [PubMed] [Google Scholar]
- 34.Senn H. M. and Thiel W., Angew. Chem., Int. Ed. 48, 1198 (2009). 10.1002/anie.200802019 [DOI] [PubMed] [Google Scholar]
- 35.Bulo R. E., Ensing B., Sikkema J., and Visscher L., J. Chem. Theory Comput. 5, 2212 (2009). 10.1021/ct900148e [DOI] [PubMed] [Google Scholar]
- 36.Nielsen S. O., Bulo R. E., Moore P. B., and Ensing B., Phys. Chem. Chem. Phys. 12, 12401 (2010). 10.1039/c004111d [DOI] [PubMed] [Google Scholar]
- 37.Park K., Götz A. W., Walker R. C., and Paesani F., J. Chem. Theory Comput. 8, 2868 (2012). 10.1021/ct300331f [DOI] [PubMed] [Google Scholar]
- 38.Hou G., Zhu X., Elstner M., and Cui Q., J. Chem. Theory Comput. 8, 4293 (2012). 10.1021/ct300649f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Riccardi D., Schaefer P., Yang Y., Yu H., Ghosh N., Prat-Resina X., K o¨nig P., Li G., Xu D., Guo H. et al. , J. Phys. Chem. B 110, 6458 (2006). 10.1021/jp056361o [DOI] [PubMed] [Google Scholar]
- 40.Kuechler E. R. and York D. M., J. Chem. Phys. 140, 054109 (2014). 10.1063/1.4863344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Giese T. J. and York D. M., J. Chem. Phys. 127, 194101 (2007). 10.1063/1.2778428 [DOI] [PubMed] [Google Scholar]
- 42.Weeks J. D., Chandler D., and Andersen H. C., J. Chem. Phys. 54, 5237 (1971). 10.1063/1.1674820 [DOI] [Google Scholar]
- 43.Verlet L., Phys. Rev. 159, 98 (1967). 10.1103/PhysRev.159.98 [DOI] [Google Scholar]
- 44.Kita S., Noda K., and Inouye H., J. Chem. Phys. 64, 3446 (1976). 10.1063/1.432637 [DOI] [Google Scholar]
- 45.Wheatley R. J. and Price S. L., Mol. Phys. 69, 507 (1990). 10.1080/00268979000100371 [DOI] [Google Scholar]
- 46.Piquemal J., Cisneros G., Reinhardt P., Gresh N., and Darden T. A., J. Chem. Phys. 124, 104101 (2006). 10.1063/1.2173256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pellenq R. and Nicholson D., Mol. Phys. 95, 549 (1998). 10.1080/00268979809483189 [DOI] [Google Scholar]
- 48.Breneman C. M. and Wiberg K. B., J. Comput. Chem. 11, 361 (1990). 10.1002/jcc.540110311 [DOI] [Google Scholar]
- 49.Besler B. H., K. M. Merz, Jr., and Kollman Peter A., J. Comput. Chem. 11, 431 (1990). 10.1002/jcc.540110404 [DOI] [Google Scholar]
- 50.Chirlian L. E. and Francl M. M., J. Comput. Chem. 8, 894 (1987). 10.1002/jcc.540080616 [DOI] [Google Scholar]
- 51.Singh U. C. and Kollman P. A., J. Comput. Chem. 5, 129 (1984). 10.1002/jcc.540050204 [DOI] [Google Scholar]
- 52.Dupradeau F., Pigache A., Zaffran T., Savineau C., Lelong R., Grivel N., Lelong D., Rosanski W., and Cieplak P., Phys. Chem. Chem. Phys. 12, 7821 (2010). 10.1039/c0cp00111b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Thompson J. D., Cramer C. J., and Truhlar D. G., J. Comput. Chem. 24, 1291 (2003). 10.1002/jcc.10244 [DOI] [PubMed] [Google Scholar]
- 54.Brom J. M., Schmitz B. J., Thompson J. D., Cramer C. J., and Truhlar D. G., J. Phys. Chem. A 107, 6483 (2003). 10.1021/jp0301002 [DOI] [Google Scholar]
- 55.Li J., Xing J., Cramer C. J., and Truhlar D. G., J. Chem. Phys. 111, 885 (1999). 10.1063/1.479199 [DOI] [Google Scholar]
- 56.Li J., Williams B., Cramer C. J., and Truhlar D. G., J. Chem. Phys. 110, 724 (1999). 10.1063/1.478180 [DOI] [Google Scholar]
- 57.Li J., Zhu T., Cramer C. J., and Truhlar D. G., J. Phys. Chem. A 102, 1820 (1998). 10.1021/jp972682r [DOI] [Google Scholar]
- 58.Khandogin J. and York D. M., Proteins 56, 724 (2004). 10.1002/prot.20171 [DOI] [PubMed] [Google Scholar]
- 59.DeTar D. F., J. Org. Chem. 45, 5174 (1980). 10.1021/jo01313a030 [DOI] [Google Scholar]
- 60.Zhao X. G., Tucker S. C., and Truhlar D. G., J. Am. Chem. Soc. 113, 826 (1991). 10.1021/ja00003a015 [DOI] [Google Scholar]
- 61.Hu W.-P. and Truhlar D. G., J. Am. Chem. Soc. 117, 10726 (1995). 10.1021/ja00148a015 [DOI] [Google Scholar]
- 62.Gertner B. J., Whitnell R. M., Wilson K. R., and Hynes J. T., J. Am. Chem. Soc. 113, 74 (1991). 10.1021/ja00001a014 [DOI] [PubMed] [Google Scholar]
- 63.van Bochove M. A. and Bickelhaupt F. M., Eur. J. Org. Chem. 4, 649 (2008). 10.1002/ejoc.200700953 [DOI] [Google Scholar]
- 64.Joung I. S. and Cheatham T. E. III, J. Phys. Chem. B 112, 9020 (2008). 10.1021/jp8001614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wang J., Cieplak P., and Kollman P. A., J. Comput. Chem. 21, 1049 (2000). [DOI] [Google Scholar]
- 66.Horn H. W., Swope W. C., Pitera J. W., Madura J. D., Dick T. J., Hura G. L., and Head-Gordon T., J. Chem. Phys. 120, 9665 (2004). 10.1063/1.1683075 [DOI] [PubMed] [Google Scholar]
- 67.Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A. et al. , gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009. [Google Scholar]
- 68.Dennington R. II, Keith T., Millam J., Eppinnett K., Hovell W. L., and Gilliland R., Gaussview, Version 3.09, Semichem, Inc., Shawnee Mission, KS, 2003.
- 69.Zhao Y. and Truhlar D. G., Theor. Chem. Acc. 120, 215 (2008). 10.1007/s00214-007-0310-x [DOI] [Google Scholar]
- 70.Case D. A., Darden T. A., Cheatham T. E. III, Simmerling C. L., Wang J., Duke R. E., Luo R., Walker R. C., Zhang W., Merz K. M. et al. , AMBER 12 (University of California, San Francisco, CA, 2012). [Google Scholar]
- 71.Straatsma T. P. and McCammon J. A., Annu. Rev. Phys. Chem. 43, 407 (1992). 10.1146/annurev.pc.43.100192.002203 [DOI] [Google Scholar]
- 72.Pearlman D. A., J. Chem. Phys. 98, 8946 (1993). 10.1063/1.464453 [DOI] [Google Scholar]
- 73.Kirkwood J. G., J. Chem. Phys. 3, 300 (1935). 10.1063/1.1749657 [DOI] [Google Scholar]
- 74.Mitchell M. J. and McCammon J. A., J. Comput. Chem. 12, 271 (1991). 10.1002/jcc.540120218 [DOI] [Google Scholar]
- 75.Steinbrecher T., Mobley D. L., and Case D. A., J. Chem. Phys. 127, 214108 (2007). 10.1063/1.2799191 [DOI] [PubMed] [Google Scholar]
- 76.Bergsma J. P., Gertner B. J., Wilson K. R., and Hynes J. T., J. Chem. Phys. 86, 1356 (1987). 10.1063/1.452224 [DOI] [Google Scholar]
- 77.Lee T.-S., Radak B. K., Pabis A., and York D. M., J. Chem. Theory Comput. 9, 153 (2013). 10.1021/ct300703z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lee T.-S., Radak B. K., Huang M., Wong K.-Y., and York D. M., J. Chem. Theory Comput. 10, 24 (2014). 10.1021/ct400691f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Schmid R., Miah A. M., and Sapunov V. N., Phys. Chem. Chem. Phys. 2, 97 (2000). 10.1039/A907160A [DOI] [Google Scholar]
- 80.Chamberlin A. C., Cramer C. J., and Truhlar D. G., J. Phys. Chem. B 112, 3024 (2008). 10.1021/jp076682v [DOI] [PubMed] [Google Scholar]
- 81.Mackay D. and Shiu W. W., J. Phys. Chem. Ref. Data 10, 1175 (1981). 10.1063/1.555654 [DOI] [Google Scholar]
- 82.Sander R., Atmos. Chem. Phys. Discuss. 14, 29615 (2014). 10.5194/acpd-14-29615-2014 [DOI] [Google Scholar]
- 83.Hiatt M. H., J. Chem. Eng. Data 58, 902 (2013). 10.1021/je3010535 [DOI] [Google Scholar]
- 84.Kang H., Choi H., and Park H., J. Chem. Inf. Model. 47, 509 (2007). 10.1021/ci600453b [DOI] [PubMed] [Google Scholar]
- 85.Stuart S. J. and Berne B. J., J. Phys. Chem. 100, 11934 (1996). 10.1021/jp961076d [DOI] [Google Scholar]
- 86.Jorgensen W. L. and Severance D. L., J. Chem. Phys. 99, 4233 (1993). 10.1063/1.466077 [DOI] [Google Scholar]
- 87.Perera L. and Berkowitz M. L., J. Chem. Phys. 95, 1954 (1991). 10.1063/1.460992 [DOI] [Google Scholar]
- 88.Jungwirth P. and Tobias D. J., J. Phys. Chem. A 106, 379 (2002). 10.1021/jp012059d [DOI] [Google Scholar]
- 89.Tobias D., Jungwirth P., and Parrinello M., J. Chem. Phys. 114, 7036 (2001). 10.1063/1.1360200 [DOI] [Google Scholar]
- 90.Serr A. and Netz R. R., Int. J. Quantum Chem. 106, 2960 (2006). 10.1002/qua.21121 [DOI] [Google Scholar]
- 91.Kaminski S., Giese T. J., Gaus M., York D. M., and Elstner M., J. Phys. Chem. A 116, 9131 (2012). 10.1021/jp306239c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.York D. M. and Yang W., J. Chem. Phys. 104, 159 (1996). 10.1063/1.470886 [DOI] [Google Scholar]
- 93.Lopes P. E. M., Roux B., and A. D. MacKerell, Jr., Theor. Chem. Acc. 124, 11 (2009). 10.1007/s00214-009-0617-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Ponder J. W., Wu C., Ren P., Pande V. S., Chodera J. D., Schnieders M. J., Haque I., Mobley D. L., Lambrecht D. S., R. A. DiStasio, Jr. et al. , J. Phys. Chem. B 114, 2549 (2010). 10.1021/jp910674d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Chaudret R., Gresh N., Narth C., Lagardère L., Darden T. A., Cisneros G. A., and Piquemal J.-P., J. Phys. Chem. A 118, 7598 (2014). 10.1021/jp5051657 [DOI] [PubMed] [Google Scholar]
- 96.Giese T. J., Chen H., Huang M., and York D. M., J. Chem. Theory Comput. 10, 1086 (2014). 10.1021/ct401035t [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.See supplementary material at http://dx.doi.org/10.1063/1.4937166 E-JCPSA6-143-009547 for all materials stated to be in the supplementary materials.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4937166 E-JCPSA6-143-009547 for all materials stated to be in the supplementary materials.