Abstract
Purpose:
Magnetic resonance imaging (MRI) is capable of providing valuable real-time feedback during medical procedures, partly due to the excellent soft-tissue contrast available. Several technical hurdles still exist to seamless integration of medical devices with MRI due to incompatibility of most conventional devices with this imaging modality. In this study, the effect of local perturbations in the magnetic field caused by the magnetization of medical devices was examined using finite element analysis modeling. As an example, the influence of the geometric and material characteristics of a transurethral high-intensity ultrasound applicator on temperature measurements using proton resonance frequency (PRF)-shift thermometry was investigated.
Methods:
The effect of local perturbations in the magnetic field, caused by the magnetization of medical device components, was examined using finite element analysis modeling. The thermometry artifact generated by a transurethral ultrasound applicator was simulated, and these results were validated against analytic models and scans of an applicator in a phantom. Several parameters were then varied to identify which most strongly impacted the level of simulated thermometry artifact, which varies as the applicator moves over the course of an ablative high-intensity ultrasound treatment.
Results:
Key design parameters identified as having a strong influence on the magnitude of thermometry artifact included the susceptibility of materials and their volume. The location of components was also important, particularly when positioned to maximize symmetry of the device. Finally, the location of component edges and the inclination of the device relative to the magnetic field were also found to be important factors.
Conclusions:
Previous design strategies to minimize thermometry artifact were validated, and novel design strategies were identified that substantially reduce PRF-shift thermometry artifacts for a variety of device orientations. These new strategies are being incorporated into the next generation of applicators. The general strategy described in this study can be applied to the design of other interventional devices intended for use with MRI.
Keywords: MRI, thermometry, artifact, ultrasound, symmetry
1. INTRODUCTION
All materials have some level of magnetic susceptibility and can, therefore, acquire a magnetization when exposed to an external magnetic field. Even though many of the materials used in medical devices, such as titanium or silver, are not traditionally considered magnetic, they do generate weak distortions in a uniform magnetic field. When these devices are moved in or around a patient during a magnetic resonance imaging (MRI) scan, the low-level magnetic field distortions can still cause substantial deterioration of the image.1 In spite of these technical challenges, there has been sustained interest in integrating interventional procedures with MRI due to the excellent spatial resolution and soft-tissue contrast achieved with this imaging modality.
MRI-guided high-intensity focused ultrasound (MR-HIFU) therapy is an example of an emerging interventional procedure where targeting, monitoring, and evaluation of therapy are performed completely within a MRI scanner. This enables noninvasive ablation of soft tissue to be performed with a high degree of precision. High-intensity ultrasound energy is transmitted to a target volume in the body from an external or intracavitary device, which generates irreversible tissue destruction through thermal coagulation. One application, primarily involving intracavitary devices, is the treatment of localized prostate cancer. Early HIFU treatments for localized prostate cancer utilized ultrasound guidance.2,3 Recent advances in MRI technology, however, have become available which enable more accurate in vivo targeting and online control.4–6 MR-HIFU devices are also under development to evaluate their utility in humans for the treatment of uterine fibroids,7 as well as cervical,8 brain,9,10 liver,11 and bone disorders. Research is ongoing to expand the indications for this technology.
MRI is used to ensure accurate targeting of ultrasound energy and to provide real-time monitoring of heating with high spatial accuracy. This enables accurate control over the thermal dosimetry pattern during treatment. The proton resonance frequency (PRF)-shift technique12 is most commonly used to measure temperature during MR-HIFU and is usually achieved by a phase subtraction of images acquired during heating from a baseline or reference scan acquired prior to heating. The PRF-shift technique is particularly susceptible to magnetic field distortions, since it is a phase-based technique with a sensitivity of −0.01 ppm/°C.12 Even small changes to the magnetic field can appear as an apparent change in temperature of several degrees. The main technique used to account for distortions is to record a reference scan prior to any heating. While ultrasound heats the target area, measurements are taken and the relative phase between the measurements and the reference scan is used to compute the heating. In practice, a reference scan is recorded only once at the beginning of the procedure. In the transurethral prostate application, the ultrasound beam is rotated about its axis at an angular rate of several degrees per minute. During this time, changes in phase are assumed to be due to heating, though the constantly changing orientation of the applicator necessarily introduces a time varying magnetic field which manifests as local phase changes as well.
Several approaches have been proposed to account for spatiotemporal variations in the magnetic field including multibaseline,13,14 referenceless,15,16 and hybrid17 thermometry techniques, as well as techniques based on modeling the nature of the magnetic field distortion from external transducers.18 These methods have an important role in obtaining accurate thermometry under time varying magnetic field conditions and are complementary to effective device design that seeks to minimize the amount of artifact generated in the first place. Efforts have been made to design devices with materials whose magnetic susceptibility is closely matched to that of water,19,20 although this is not possible for all components. For example, there is no piezoceramic material, which is used to generate ultrasound energy for HIFU, whose magnetic susceptibility is close to that of water. This can result in undesirable magnetic susceptibility-induced temperature artifacts that must be reduced using strategies other than material selection.
The goal of this study was to evaluate the influence of geometric and material characteristics on the temperature artifacts associated with PRF-shift thermometry for a transurethral applicator designed for the treatment of localized prostate cancer.4 These results may also prove useful in developing HIFU devices for other anatomical sites. In this specific application, the temperatures measured in the prostate gland during treatment with PRF-shift thermometry are used as real-time feedback to control the pattern of heating precisely, making distortions on thermometry measurements critical to the role thermometry plays during treatment delivery. PRF-shift thermometry is typically accurate to within 1–2 °C; hence, it is desirable to keep artifacts to this level or below. An error of more than a few degrees will cause significant distortions to the treatment volume.
2. METHODS
2.A. Transurethral ultrasound applicator
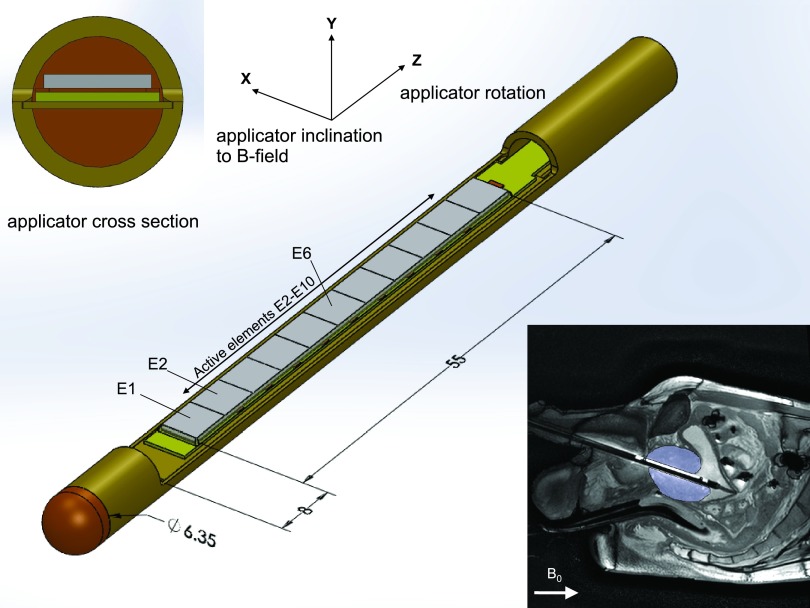
The transurethral ultrasound applicator, shown in Fig. 1, is comprised of a lead zirconate titanate (PZT) transducer, which is 4 mm wide, 55 mm long, and approximately 0.5 mm thick, embedded in a brass tube. The rectangular PZT transducer (DeL Piezo Specialties, LLC, FL) is segmented into 11 elements (each 5 mm long) enabling independent power and frequency control along the span of the prostate gland. The section of the tube above the PZT is cut away and replaced with a thin PET (Vention Medical, New Hampshire) window to enable sound transmission radially outward into the prostate. Degassed water is circulated through the applicator during treatment to couple sound transmission out of the device and to provide cooling for the transducers. Cross-sectional views of the device, as well as a sagittal MR image of it inserted into a patient, are shown as insets in Fig. 1.
FIG. 1.
Applicator design. Brass tube with polymide end cap. In the center, a section of tube is removed to provide exposure of a rectangular transducer element to the surrounding tissue. This window is covered by a thin vinyl membrane (not pictured). A circuit board and floor plate, on which the transducer rests, are approximately centered in the applicator along the y-axis. All rotations are of right-handed sense, as are the coordinate axes. Insets at top–left and bottom–right show a cross section of the device and a sagittal MR image of the device being used in a patient, respectively. The prostate gland is indicated in the MR image.
The materials used in the construction of the applicator are nonmagnetic by conventional standards but are slightly paramagnetic or diamagnetic, within the same order of magnitude as water23 (χv ≈ − 9.05 × 10−6).1 The material with the poorest equivalence to the magnetic susceptibility of water is the PZT transducer. A value for the volume susceptibility of the PZT material used in this device could not be found and was measured in-house using an Evans balance (Johnson Matthey, MK1, PA) to be χv = 48.62 × 10−6. The tube is made from brass alloy 260 (also measured in house, χv ≈ − 10.37 × 10−6). The plastic tip is made from polyimide (χv ≈ − 9.02 × 10−6, Keyser 1989). Electrical signals are transmitted down copper lines on a printed circuit board (PCB) and connect to brass connectors (Lemo, Switzerland). There is also a small air space between the transducer and PCB to prevent sound from being radiated from the backside of the transducer. Air has a susceptibility similar to vacuum (χv = 0), causing a slight mismatch to the surrounding water. The volume of this region, however, is so small that it caused no appreciable effect magnetically.
The high level of MRI-compatibility of the device results in no appreciable distortion of magnitude MR images used during treatment planning, as shown in the anatomical inset of Fig. 1. This is essential in order to achieve precise spatial positioning of the device within the prostate during treatment. The small magnetic field distortions produced by the rotating device have a measurable impact, however, on PRF-shift MR thermometry measurements, especially in the immediate vicinity of the device. Device rotation about the z-axis during treatment violates the assumption of static field disturbances in conventional phase-subtraction PRF-shift thermometry, resulting in thermometry artifacts. In order to treat the full prostate volume, which surrounds the urethra, the beam must be swept through a complete 360° rotation. During this time, heating is occurring due to ultrasound energy delivery, and the pattern of magnetic distortion is changing as the orientation of the applicator changes in the magnetic field.
Inclination of the applicator about the x-axis may vary depending on treatment setup. This can have substantial impact on the pattern and magnitude of the resulting artifact. In prostate treatment applications, the device is inserted into the urethra of a subject lying supine in the magnet. In this case, the natural orientation of the device is approximately 20°– 22° inclined to the main magnetic field, as shown in Fig. 1. For simplicity, rotations of the applicator about the z-axis will be referred to simply as rotations, and rotations about the x-axis will be referred to as the inclination of the applicator. The term orientation will be used to describe the overall rotations after the device is inclined, about the x-axis, and then rotated, about the z-axis. The Cartesian coordinate system used and the sense of rotation are both right-handed, as shown in Fig. 1.
2.B. Calculation of device-induced magnetic field distortions
The magnetic distortions due to even simple shapes, such as a cube, are sufficiently complex that analytical solutions become prohibitive due to the number of terms required and their complexity. This is generally true for most electromagnetic problems without a symmetry aligned to a convenient coordinate system such as a point charge in spherical coordinates, or an infinite plane of current in Cartesian coordinates. Thus, calculations of the magnetic field distortions caused by the transurethral applicator were performed using numerical methods. COMSOL® Multiphysics 4.3a (COMSOL, Inc., Sweden) was used to calculate magnetostatic effects with no hysteresis and examine magnetic field strength, H, that results from the magnetization of a material, M, as a function of its volume magnetic susceptibility,
| (1) |
which approximates the situation for medical devices in MRI to high accuracy. For clarity, vector valued quantities are bolded, while scalar variables are in normal type.
The simulations of the applicator and its components were performed against a background of water, to simulate the presence of human tissue, in a static 3 T magnetic field. Calculations were performed in 3D to account for all components of the vector-valued magnetization and resulting magnetic fields. The 3D geometry of the ultrasound applicator was created within COMSOL, and simulations were performed using the magnetic fields, no currents (mfnc) package in the AC/DC module. Only stationary studies were performed because there are no time-dependent phenomena of interest in this application. Calculations utilized iterative solutions, with the successive over-relaxation (SOR) method having the most reliable convergence to solution. Of note, the relative tolerance in the accuracy of the calculation was made smaller, i.e., more accurate, from the default 10−6 to 10−10 due to the materials being simulated having comparatively small susceptibilities. The magnitudes of the magnetic distortions were on the same order as the variation in susceptibilities, i.e., 10−6. Hence, the default tolerance gave errors of the same magnitude as the changes in the magnetic field being computed. A tolerance of 10−8 was sufficient to see the pattern of artifact clearly with errors on the order of a few percent, and a value of 10−10 made any residual computational errors negligible. Some small errors, on the order of a few percent, are reintroduced when values are interpolated between mesh points to generate a pixelated image. This results in a very slight mottling of the field, visible in Figs. 2 and 3 on close inspection. This amounts to an error of much less than a single degree in the final computed temperature artifact. The accuracy of the calculations was first confirmed by comparing with published analytical solutions for spheres and cylindrical geometries,1 prior to simulation of the applicator. These calculations demonstrated agreement to within the relative tolerance specified.
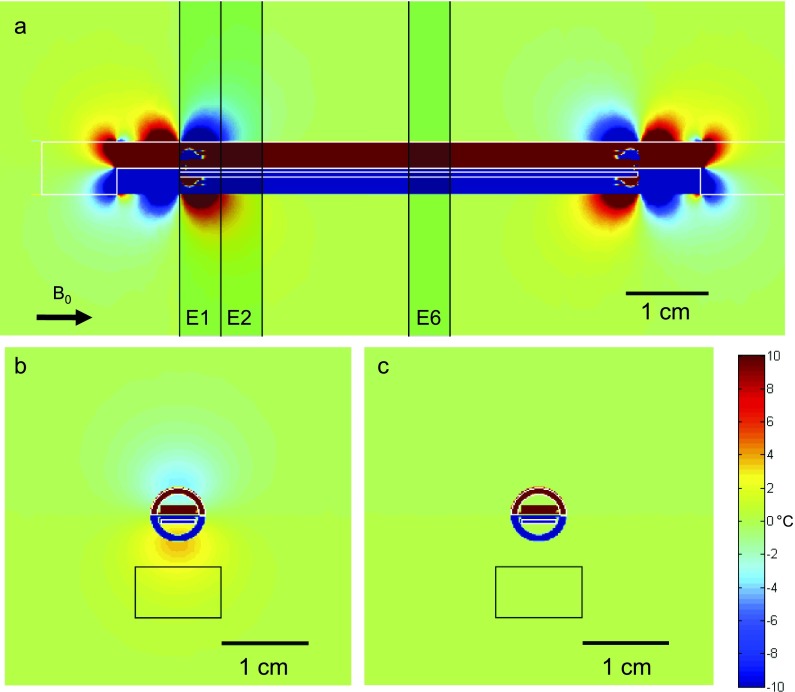
FIG. 2.
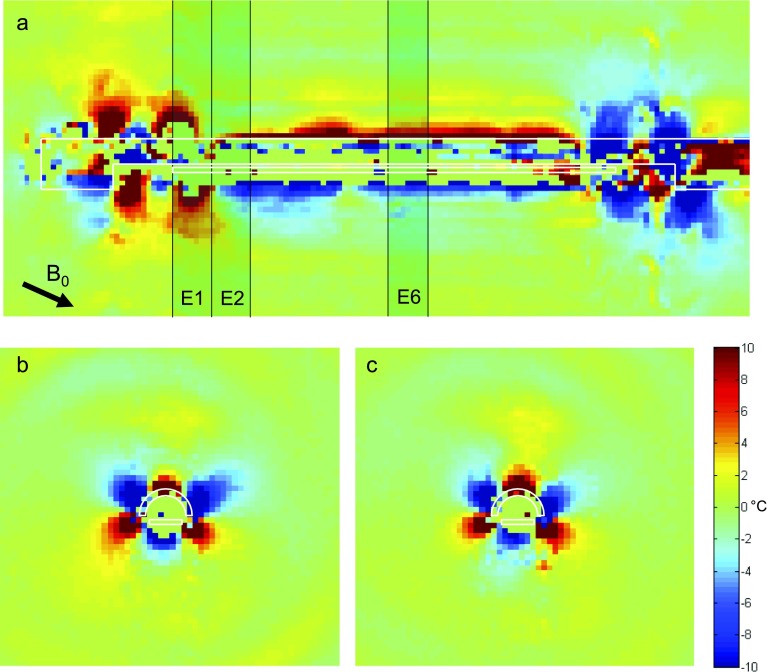
Simulation. A simulated scan of the temperature artifact due to changing magnetic fields around the applicator (whose transducer was offset from the center by approximately 0.2 mm) after a 180° rotation of the applicator about its long axis. The applicator inclination to the B0-field is 0° relative to the applicator (shown by arrow at bottom left of sagittal plot). The three axial slices examined most are shown as shaded rectangles in the top sagittal view (a). The slices are each 5 mm thick, aligned with the transducer elements. In (b) and (c), the temperature artifact after a 180° rotation is shown for the 1st active element (E2) and the center element (E6). The artifact is characterized by the range of temperature artifacts in the target box in front of the transducer where sonication will be occurring. The black bars in each plot indicate a scale at 1 cm. Note the more pronounced artifact at the 1st active element vs the center element.
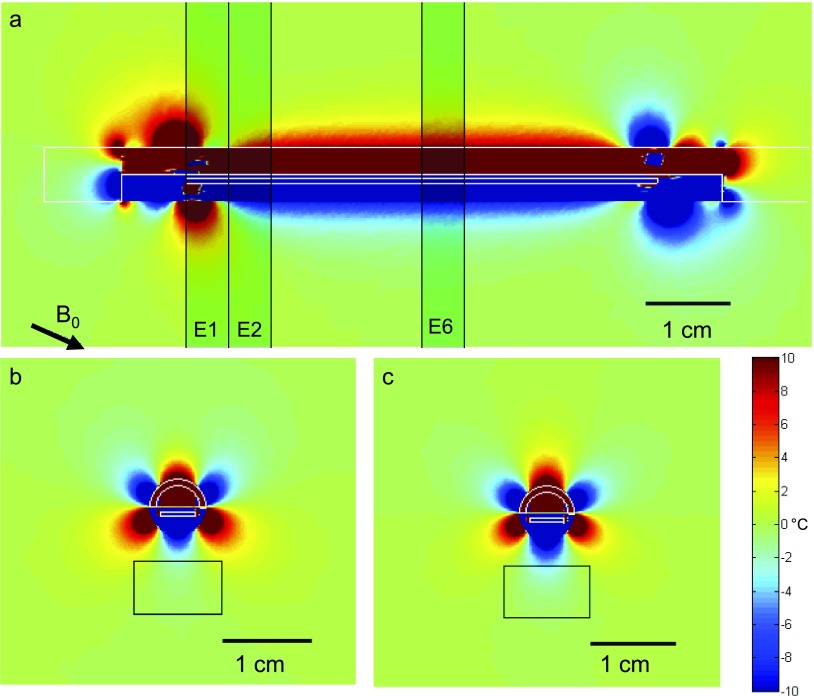
FIG. 3.
Simulation. The same format as Fig. 2 is used, although here the inclination of the applicator is −22.5°.
For each simulation, the orientation of the device relative to the background magnetic field B0 was specified and the resulting magnetic field, Btot, was determined as a 3D block of vector-valued data. COMSOL accomplishes this calculation, in this case, by solving the equation for magnetic flux conservation,
| (2) |
where Btot can be expanded in terms of the background field B0 and the field due to the magnetization of components, described in terms of the magnetic scalar potential Vm,
| (3) |
Typically, magnetic fields require a vector potential, but in this case, there are no free currents, only steady-state magnetizations; thus, the magnetic potential can be described in terms of a scalar field. Each voxel contains a vector describing the total magnetic field at that point, which can be interpreted as a linear combination of the background field plus some distortion, dB, introduced by the magnetization of the applicator: Btot = B0 + dB. During imaging, only the component of Btot aligned with the bore of the magnet, , is responsible for changes in the resonant frequencies measured. As a practical note, however, this distinction makes little actual difference in this case. That is, , since the angle between Btot and is very small. Similarly, the component of dB aligned with B0 adds to the magnitude linearly, while the components of dB orthogonal to B0 only change the length to second order. Typical magnetic susceptibilities of MRI compatible materials are of the order 10−5. This means dB will be of order 10−5, while the difference between and is of order 10−10. Consequently, this dot product can be, and has been, ignored in these numerical calculations.
The 3D vector field computed prior to any applicator rotation served as the reference scan. The applicator was then rotated to a new orientation and another block of data calculated. This second 3D vector field was the measurement scan. Within this 3D block of data, which represented the entire volume surrounding the device, analysis was limited to a region of interest (ROI) where active sonication would be taking place.
The ROI was confined to a target box (10 × 6 × 5 mm) centered above the transducer element being examined. This target box demarcated an area typically being treated within the prostate in which the accuracy of the temperature measurements was most critical. Regions closer to the device contained sharp thermal gradients, from the high temperatures generated in tissue by the ultrasound to the lower temperature of the water flowing through the device. The limited spatial resolution of imaging (1–2 mm) precluded accurate characterization of this gradient. The end of the box furthest away from the transducer element represented distances where the artifacts from the device were negligible. The width of the box was chosen to encompass the critical regions leading and lagging the ultrasound beam during treatment as the device rotated.
The corresponding ROI in the reference scan was then isolated and the magnitudes of the magnetic field in the ROIs were averaged over the 5 mm slice thickness in the z-direction to simulate the finite slice thickness in a real MR image. The now 2D scalar images for the region of interest in the measurement and reference scans were then subtracted to yield the change in magnetic field magnitude: ΔB = |B0 + dBmeas| − |B0 + dBref|, which was used to calculate the expected level of PRF thermometry artifact, dT, as described below.
In practice, the temperature change in a voxel is computed using the phase shift between the reference scan, ϕ0, and the measurement scan, ϕ1. The difference between these phases can then be used to calculate the change in temperature using
| (4) |
where dT is the measured change in temperature in °C, α is a constant equal to −0.01 ppm/°C, γ is a constant equal to 2.7 × 108 rad T−1 s−1, TE is the echo time for the imaging acquisition (typically 15 ms), and B0 is the magnitude of the static field of the MRI. In contrast to phase measurements in an actual MRI, the change in the magnetic field magnitude, dB, can be read out directly from the simulation output. The equation ϕ = γTE|B| relates changes in magnetic field magnitude to changes in phase. Thus, Eq. (4) can be recast in terms of dB directly, rather than in terms of the physical observable ϕ,
| (5) |
Computations of de novo applicator orientations are computationally intensive. To speed computations for arbitrary orientations, the field distortions for arbitrary applicator orientations, dB, were computed through vector superposition of computed basis fields. The basis fields are those generated when the background field is aligned with each of the three principle coordinate directions. That is, for a background field aligned with the unit vector , the field distortions dB are given as a linear combination of the field distortions when the background field is aligned with the x, y, and z axes. This is equivalently stated by the following linear equation:
| (6) |
where dBij is the ith component of dB when the background field is oriented in the j-direction. These superpositions are less computationally intensive and can be further hastened by limiting postprocessing to the ROI, which is not possible in de novo simulations.
To summarize, the following steps are followed to calculate the temperature artifacts around the interventional device: (1) a wireframe model of the applicator is made in (or imported from a CAD model into) COMSOL, and the various material properties (primarily magnetic susceptibilities) are assigned. (2) The vector-valued magnetic field around the applicator is then computed for static fields aligned in the x, y, and z directions. (3) Superpositions of these solutions are then used to compute the field for two device orientations (since rotating the device is equivalent to rotating the field in the opposite direction). The first is the reference scan where the device is inclined relative to the static field by some amount, which accounts for the angular inclination relative to the magnet bore as shown in Fig. 1. Another field is then computed at that same inclination with a rotation of the applicator by some amount about its long axis. (4) The difference between the two field calculations is taken and the magnitude multiplied by the appropriate constants to calculate the temperature difference around the device caused by the rotation.24
Using the above methods, the pattern of artifacts around the current applicator design was simulated and validated against phantom studies. Then, various design parameters were systematically varied, and the resulting temperature artifacts in selected target boxes were quantified in terms of the median, range, and interquartile cutoffs for the artifacts contained therein. The latter studies examined whether design principles used in the current applicator design, such as the use of materials with susceptibilities closely matched to that of water, was appropriate. They also examined more novel modifications in an attempt to find design improvements that had not been previously considered.
2.C. Experimental verification
Experimental thermometry measurements in a phantom were used to verify the simulations results. A transurethral ultrasound applicator with the same construction as the one simulated was inserted into a cylindrical phantom containing a tissue-mimicking gel material (Zerdine®, CIRS, Inc., VA). The cylindrical phantom was placed into a clinical head coil on a 3 T MR scanner (Achieva 3T, Philips Healthcare, The Netherlands). A MRI-compatible rotational motor4 was connected to the applicator to rotate it to desired angles about its axis, and the entire assembly was imaged with the applicator along the main magnetic field (0°) and at a −22° inclination (±1°).25
At each orientation, a sagittal MR image was acquired along the applicator in the 0° and 180° rotational positions. The images were acquired using a segmented EPI sequence with the following parameters: FOV = 160 mm, slice thickness = 5 mm, matrix size = 228 × 221 (voxel size ≈0.67 mm), TE = 15 ms, TR = 391 ms, and EPI factor = 13. More details on the sequence and its performance in vivo for prostate imaging can be found in Ref. 21. In addition, a series of axial images, transverse to the applicator, was acquired with the same acquisition settings, but centered on each element in the transducer (i.e., 11 slices). From these images, the spatial temperature artifact was calculated and compared with the simulation predictions.
2.D. Influence of geometric characteristics
The main parameters of interest in applicator design relate to the size, shape, and location of the transducer. The transducer is essentially the only component of substantial volume in the applicator that has a magnetic susceptibility substantially different from that of water. It is also located directly within the region where images are acquired during treatment. Consequently, it is the main source of artifact due to magnetic effects, and modification of its design is the most likely to result in substantial artifact reduction. A preliminary design feature included dummy elements (i.e., nonactive elements flanking the active elements of the transducer), in an attempt to push edge effects of transducer magnetization out of the area being actively sonicated. The temperature artifact due to magnetic effects was systematically examined above each transducer element. The extent to which artifacts diminished with distance from the edge of the transducer, and as a function of applicator orientation, was then examined.
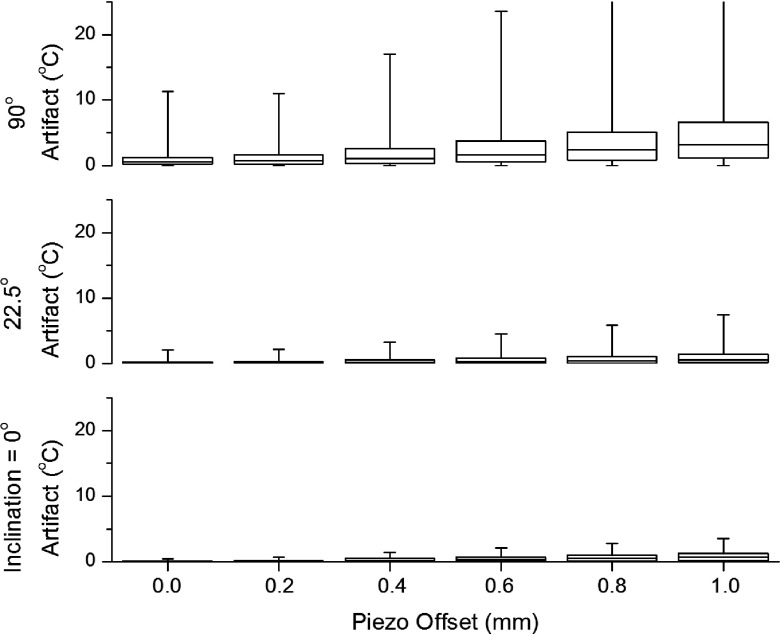
The location of the transducer within the applicator was also varied. The original applicator design cut a window out of the brass tube through half the thickness of the tube, resulting in the brass floor plate being flushed with the central axis of the applicator. This geometry resulted in the transducer, once mounted on the PCB and placed on the floor plate, being 0.76 mm above centerline. Simulations were conducted with the transducer y-displaced in 0.1 mm increments from the center of the applicator, while holding the x and z positions fixed. A range of displacements, above and below center, was simulated. To give an accurate sense of the artifact generated, artifacts in the target box were collated over multiple applicator rotations, in 30° increments. The median, range, and interquartile ranges of the compiled list were then examined. These statistics were analyzed as a function of transducer offset within the applicator for three inclinations (0°, 22.5°, 90°).26
2.E. Influence of material properties
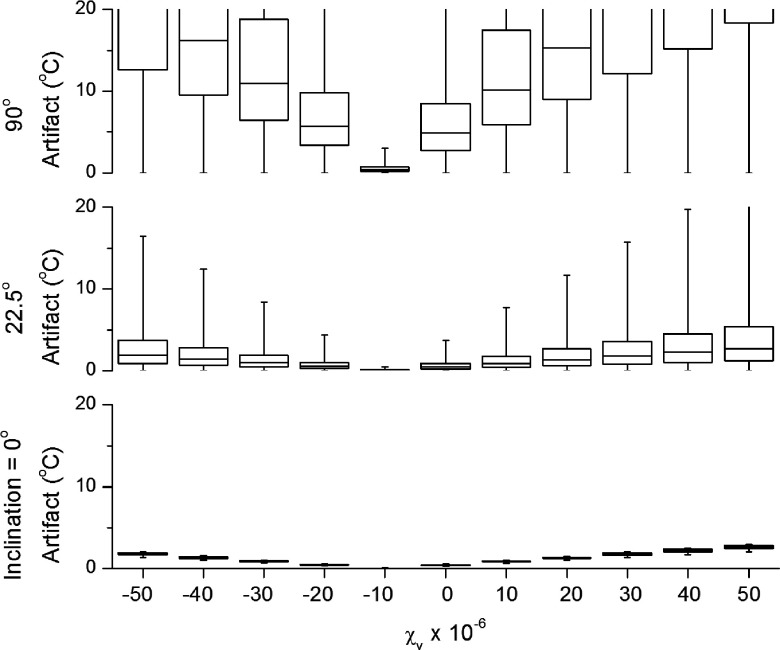
Finally, the magnetic susceptibilities of the applicator components were examined. Again, the resulting artifacts in the target box were compiled over a full rotation of the applicator, in 30° increments. In practice, the materials suitable for applicator construction give only a few discrete values for available magnetic susceptibility. In a simulation, however, it is possible to vary these parameters freely to identify how the temperature artifact depends on component susceptibility. The brass for the main body of the applicator is intentionally matched closely to the susceptibility for water. Simulations were performed for various susceptibility values for the brass. The consequences of small variations in the susceptibility of the transducer were also examined.
2.F. Variation of artifact with applicator rotation
The artifact around the applicator was expected to vary with both the rotation angle of the device and its inclination relative to the magnetic field. Polar plots of the artifact as a function of applicator rotation were generated to understand better what applicator orientations were most problematic. These plots were also used to determine whether compiling data in 30° increments were sufficient to capture artifact variation during a full rotation of the applicator.
3. RESULTS
3.A. Validation of simulations with phantom studies
Figure 2 shows simulated sagittal and axial views of the spatial temperature artifact occurring after 180° rotation of the applicator, for a device oriented parallel to the main magnetic field. A 180° rotation is used because this is easily visualized in the sagittal view, and it is where the maximum artifact often occurred for the current applicator design. The sagittal and axial views are both numerically integrated over a 5 mm slice thickness to simulate the signal that would be seen in a MRI scan. Figure 2(a) is a sagittal view showing the concentration of this artifact predominantly at the ends of the PZT transducer, where it extends radially outside the applicator. From the axial images 2(b) and 2(c), it is clear that the artifact decreases substantially from the first element to the 2nd and is progressively lower all the way to the 6th (center) element where it is almost entirely within the applicator. This increased artifact at the first element justifies the incorporation of dummy elements in the current design. The axial views also show the target box, within which the spatial temperature artifact is quantified. Here, the box is shown in front of the transducer after rotating the device 180°.
Figure 3 shows the spatial temperature artifact after 180° rotation for the same device inclined −22.5° to the main magnetic field (similar to the clinical situation for prostate treatment). The sagittal view in Fig. 3(a) depicts how the spatial temperature artifact now extends beyond the device boundary for most of the transducer length. In addition, the increased spatial artifact at the edges of the transducer is still present (although less symmetric compared to the case when the device is aligned with the magnetic field) and slightly larger in magnitude. The axial views at transducer elements E2 [Fig. 3(b)] and E6 [Fig. 3(c)] show that the artifact is more consistent across all elements and has much more structure than the previous case at 0°. Although not shown, the spatial artifact increases even more at 90° orientation relative to the main magnetic field. In both of these cases, the justification for the dummy elements is weaker because the artifact is fairly constant for most of the transducer length.
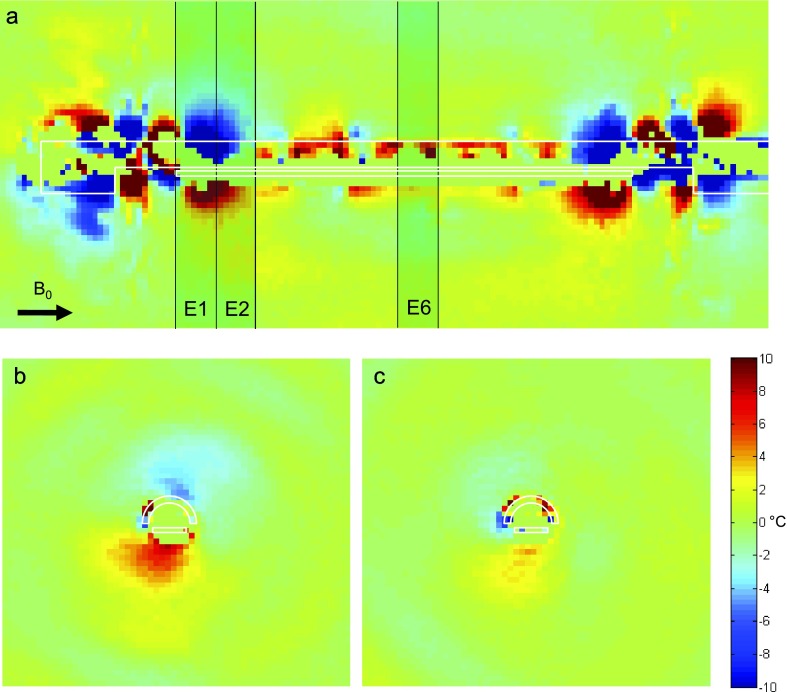
Figures 4 and 5 show the spatial temperature artifact measured experimentally at inclinations of 0° and −22.5°, respectively. Each figure shows a sagittal image, and the corresponding axial slices through the transducer elements E2 and E6, after a 180° rotation of the applicator. The general pattern and degree of artifact show good agreement between Figs. 2 and 4 and between Figs. 3 and 5. The major lobes of artifact are concentrated at the tips of the transducer in both simulation and experiment and both demonstrate the expected lobe rotation after inclination of the applicator. The fairly constant artifact along the length of the transducer is visible in both scans, with the level of artifact increasing at the higher inclination. Finally, in the axial slices, the overall dipole-like artifact at the 0° inclination agrees well between simulation and experiment, as does the six-lobed artifact seen in the axial images of the −22.5° inclination scan.
FIG. 4.
Phantom scan. Experimental data for a 180° applicator rotation in a phantom at 0° inclination. The pattern of thermal artifact is similar to the pattern shown from the simulation in Fig. 2. In the axial slice centered on first active element (E2), there is more significant artifact than at center element (E6), as expected. The pattern of artifact seen in the axial slices has a bipolar character in the vertical direction, similar to that seen in Fig. 2. The transducer in this applicator was offset from the center by approximately 0.2 mm.
FIG. 5.
Phantom scan. Experimental data for a 180° applicator rotation in a phantom at an inclination of −22°. The pattern of thermal artifact is similar to the pattern shown from the simulation in Fig. 3. In the axial slices, first active element (E2) and center element (E6) show more artifact compared to the lower inclination in Fig. 4. The pattern of artifact seen in the axial slices has the same six-lobed character seen in the simulation in Fig. 3.
3.B. Primary design considerations
The following analyses show the lower and upper ranges, 2nd and 3rd quartile outer boundaries, and the median of the absolute value of compiled temperature artifacts in the target boxes. The sign of the artifact is generally less important than its magnitude, and examining the absolute magnitude prevents having a median of zero in most cases and allows the impact of parameters to be visualized more clearly. These values are indicated by the whiskers, box, and line, respectively. These studies identify novel design modifications, particularly aligning the transducer with the axis of rotation, which substantially reduce artifact. They also validate the use of dummy elements and water-matched susceptibility materials.
The effect of changing the vertical position, i.e., the y-position, of the entire transducer is shown in Fig. 6. The results are shown for the slice around first active element (E2) only because this is the element over which artifacts are generally largest. Placing the transducer in the center of the applicator produces a clear minimum in the artifact generated, within about ±0.1 mm. The data for dummy element (E1) as a function of vertical position of the entire transducer are not shown since no treatment or imaging slice is placed here. The reason for this reduction in artifact is that the pattern of distortion around the transducer is, very grossly, cylindrically symmetric. The alignment of this distortion with the axis of rotation of the device does not reduce the magnitude of the distortion, but it does make the distortion between the reference scan and subsequent measurement scans more similar. That is, centering the transducer does not reduce the level of magnetic artifact created by the applicator, but it does make this artifact less variable as the applicator is rotated. Thus, the magnetic distortions that do exist, and are unavoidable to some extent, are more similar to the reference scan and thus better accounted for in the phase subtraction between the thermometry measurement and reference scans. Prior designs concentrated on minimizing magnetic distortion, but the actual goal is the reduction of thermometry distortions. This small leap of logic yields a valuable guiding principle: even substantial magnetic distortion will not cause thermometry artifact if it remains constant between the reference and thermometry measurement scans.
FIG. 6.
Artifact by transducer offset. The temperature artifact quartiles for first active element (E2) of the applicator over the course of a full 360° rotation are plotted as a function of transducer offset at three different applicator inclinations: 0°, 22.5°, and 90°. There is a substantial benefit to keeping the transducer near the center, as this reduces the temperature artifact for all applicator inclinations. In this plot, the effect is not strongly dependent on precise positioning of the transducer, as seen in a moderate flattening of the artifact when the transducer is within 0.2 mm of center. These data provide a rough upper bound to the level of artifact, which is comparable or reduced for more central elements in the transducer array. The artifact behaves in a symmetrical fashion for negative transducer offsets (not shown).
Thus, in general, aligning the symmetry of a magnetic distortion with symmetry of the motion used will reduce artifact. In this case, aligning the approximately cylindrically symmetric magnetic distortion with the axis of rotation substantially reduces thermometry artifact. In other applications, where linear motion might be used, the goal would be to make distortions constant along the length of the device in the direction of motion.
Indeed, a 180° flip of the applicator gives virtually no artifact if the transducer is centered. This is in stark contrast to the current design where this is the rotation at which artifact is most severe, as shown in Figs. 2–5. Consequently, the previous assumption that the maximum artifact occurs at an applicator rotation of 180° is no longer valid. Simulations showed maximal artifact occurred anywhere between 45° and 315° of applicator rotation, depending on the position of the transducer and the inclination of the magnetic field.
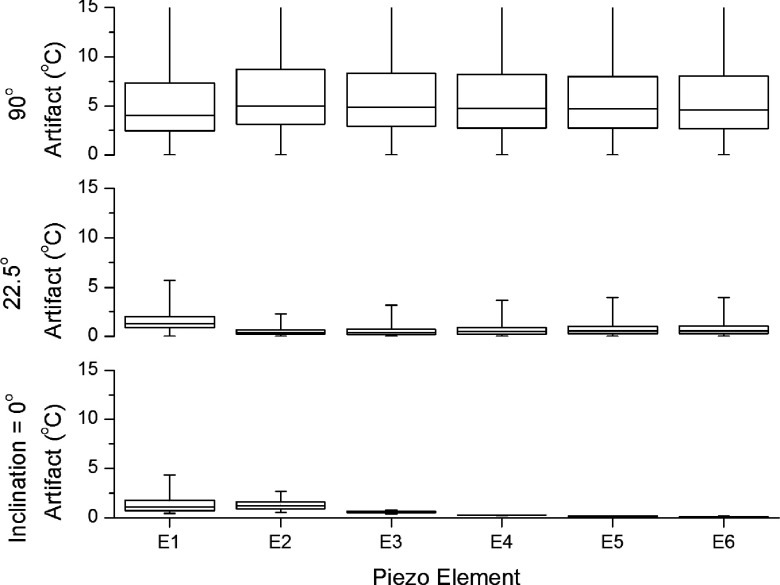
After centering of the transducer, the use of dummy elements was among the most valuable design features. Validation of this technique for the current, offset, and design is shown in Fig. 7. Here, the spatial temperature artifact within each target box as a function of transducer element is shown. The sharp increase in the level of artifact near the edges of the transducer is readily apparent. This demonstrates that the reduction provided by the dummy elements can be as substantial as providing several degrees of artifact reduction and is valuable over the full rotation of the applicator. Dummy elements are valuable in a centered design as well, though the effect is not as dramatic because the thermometry artifact, even near the ends of the transducer, is small. The elements, running from the edge of the transducer closest to the applicator tip to the center of the transducer, are labeled E1–E6 along the horizontal axis. Voxels located in the part of the target box farthest away from the transducer generally had near-zero artifact regardless of the simulation parameters. Thus, artifact can generally be assumed to vanish at distances beyond about 1.2 cm from the applicator, and the extent of the lower whisker is almost always near zero.
FIG. 7.
Artifact by element—centered transducer design. Simulated values of the temperature artifact within the target box plotted as quartiles for the first 6 transducer elements, in a centered transducer design. E1 is the element closest to the tip and E6 being the central element. Artifacts in the target box are compiled for all orientations from 0° through 360°, in 30° increments. Since the magnitude of the artifact is generally symmetrical between the first and last elements of the transducer, only the first 6 of 11 elements are plotted. Also, the artifact is symmetric between positive versus negative rotations due to the bilateral symmetry of the applicator. The box indicates the 2nd–3rd quartile range with the thin line in the middle indicating the median of the compiled artifact values. The whiskers show the total range of artifact within the target box over the course of a full rotation. At low applicator inclinations, edge effects near the tips of the transducer are important. As the inclination increases, artifact becomes greater in magnitude and more uniform along the transducer.
For an applicator inclination of 0°, there is almost no artifact over sixth transducer element (E6), the center element. The artifact is concentrated at E1 due to edge effects and decreases quickly over the first two elements. This validates the intuitive need for having E1 as an inactive “dummy” element. At an applicator inclination of 0°, the transducer is magnetized along its length, similar to a bar magnet, resulting in the field being concentrated at the tips. The transducer is 11 elements long, but the artifact occurs in a symmetric fashion about the center. Thus, E11 looks very similar to E1, except for a mirroring of the artifact pattern. Thus, only half the transducer is shown to improve the clarity of the plots. At 90°, the transducer is magnetized perpendicular to its broadest face. This can be interpreted as magnetic field lines being induced perpendicular to the sonicating surface of the transducer, which causes a much stronger artifact that is almost constant along the transducer length and falls off more gradually. The artifact still falls off to near 0 °C within the target box as indicated by the lower whiskers in the plot for 90°, but reaches values greater than 15 °C closer to the device. It is unlikely that an orientation of much more than 30° to the field of the MRI would ever be realized for the transurethral application here; however, results for orientations at 90° serve to demonstrate the general behavior of artifact over the entire range of applicator orientations. This information may be useful in developing applicators for other anatomical sites that may require larger angles, such as intracranial applications.
Perhaps the most intuitive design point is the use of materials with susceptibilities matched to that of water. Figure 8 shows the effect of changing the magnetic susceptibility of the brass used to make the body of the applicator. These results are for a centered transducer design, though the results are generally similar for the current design. Results shown are only for the target box above E2. The results confirm what intuition might suggest that matching the susceptibility of the device housing to that of water results in the lowest spatial temperature artifact. This artifact increases linearly as the susceptibility of the brass deviates from the susceptibility of water. This deviation is symmetric in magnitude for susceptibilities above and below that of water. The primary source of magnetic distortions for a 0° orientation occurs at the edges of the window cut into the brass. As a result, only the elements near the edge of the window are affected: E1, E2, E10, and E11; artifact falls off rapidly as distance from the edge increases. For devices inclined relative to the main field, the magnetization of the tube is increasingly perpendicular to the long axis of the applicator. This causes a substantial asymmetry because the region of the window has only magnetized water, while the opposite side of the applicator has magnetized brass. Only in the case of the brass being matched to water does the magnetization in the region of the window, and the corresponding region opposite it has the same magnetization. In this case, symmetrizing the magnetization and minimizing the overall magnitude are both accomplished by the same change. That is, matching the tube susceptibility to that of water both eliminates distortions in the magnetic field and can be regarded as magnetically equivalent to a perfectly symmetric tube with no window cut in it.
FIG. 8.
Artifact by susceptibility—centered transducer design. Artifact as a function of tube material susceptibility for an applicator with a centered transducer. Boxes and whiskers follow the same scheme as previous figures. The minimum artifact occurs, as one might expect, when the brass most closely matches water (about −9 × 10−6). Interestingly, this is not true for the current applicator design with a slightly offset transducer. The current design shows a minimum at a susceptibility of +10 × 10−6, when the tube is partially matched to the PZT.
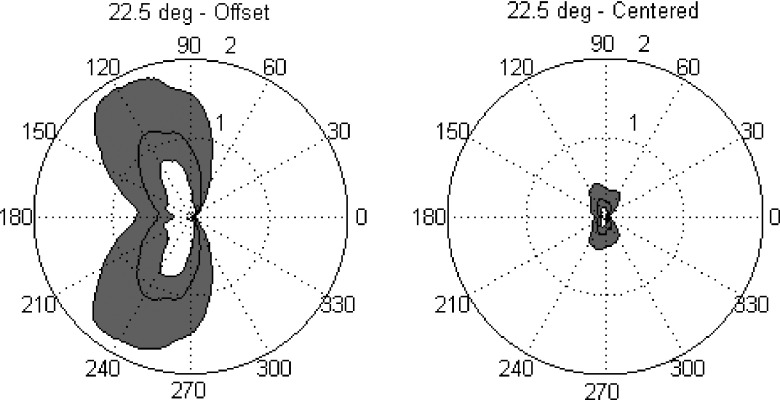
The overall character of the artifact as the applicator rotates can be seen in Fig. 9. Here, polar plots illustrate the substantial reduction in artifact at all angles of rotation when the transducer is centered. These results are plotted for a typical inclination of 22.5°, above the first active element of transducer (E2). For clarity, only the second to third interquartile range of artifact, and median, was plotted as a function of applicator rotation. The left plot is for the current applicator design with the transducer offset 0.74 mm from the applicator centerline. Thermal artifact is identically zero at 0° because this is where the reference scan is taken. In this case, at an applicator inclination of 22.5°, the maximum artifact is not at 180°, even for the offset design. This is because the edge effects from the magnetization along the y- and z-directions partially cancel for transducer element selected (E2). Interestingly, this cancellation effect can actually be maximized in the offset design by mismatching the brass tube susceptibility from water, in the opposite direction. This is neither valuable in the centered design, however, nor is it as effective as a centered design with a water-matched tube. The maximum value of artifacts in the centered transducer design was 0.4, 2.0, and 11.3 °C for inclinations of 0°, 22.5°, and 90°, respectively. These represent a dramatic improvement over the artifacts caused by the current offset transducer prototype.
FIG. 9.
Polar plots of artifact—comparison of offset and centered transducer designs. In each plot, the temperature artifact within the target rectangle above 1st active element (E2) is plotted as a function of applicator rotation. Radial values are in degrees centigrade, with the 1 and 2 °C levels indicated by a dotted, and solid outer, circle, respectively. The azimuthal coordinate indicates the rotation of the applicator in degrees of arc. Each plot contains three polar curves, delineating the external boundaries of the second and third quartiles of artifact within the target rectangle, as well as the median artifact value in the target rectangle. The area encompassed by these middle two quartiles is shaded for readability, with the median artifact visible as a line inside the gray area. The left and right plots contrast the artifact behavior for a transducer offset by 0.74 mm (left) versus a centered transducer (right). A dramatic improvement in artifact at all rotations is apparent for the centered transducer design compared to the original offset design. This reduction in artifact, by approximately a factor of 5, is similar across different transducer elements and applicator inclinations. In general, artifact increases in both designs for elements near the ends of the transducer array and as the inclination of the applicator increases. The pronounced relative minimum in artifact at 180° in the off-center design was unexpected and is due to a complicated partial cancellation of the fields due to the y- and z-magnetizations of the transducer. Both plots are computed for an applicator inclination of 22.5°.
3.C. Other considerations
In addition to the above major findings, a variety of other parameters were explored. These included examinations of transducer thickness and edge shape, and the size of window in the brass housing and the shape of its edge. As noted above, it is the roughly cylindrical symmetry of the transducer that makes centering it so successful at reducing thermometry artifact. From the design principle of maximizing symmetry, creating a square cross section transducer was considered but this was not successful in reducing thermometry artifact.
The dependence of thermometry artifact on transducer thickness, or equivalently, acoustic resonant frequency, was relatively minor, with temperature artifacts remaining less than 1 °C even for transducers of 1.0 mm thickness at 0° inclination, and less than 5 °C at 22.5° inclination. There is little detriment in selecting a transducer thickness for whatever resonant frequency is desired. This dependence on thickness was more pronounced for inclinations of 90° where the maximum artifact grew, in a roughly linear fashion, from less than 5 °C for a 0.1 mm thick transducer up to 20 °C for 1.0 mm thick transducers. The level of artifact, especially the lower three quartiles, remains low for most transducer thicknesses and inclinations, but artifact does become steadily higher with increasing thickness. This increasing artifact with thickness is a strong enough effect that a square cross section transducer produces more thermometry artifact than the current, rectangular cross section, design. That is, a square cross section does increase the symmetry of magnetic distortions, but this is more than offset by the increased magnetic moment of a thicker transducer. This result underscores the importance of validating intuition with numerical simulations. It is difficult to know how the interplay between reducing the magnetic distortions and symmetrizing them will balance out in a final design.
Other manipulations were explored in an effort to find other configurations to minimize artifact. The window in the brass was made shorter than the transducer to check whether such an overhang of brass over the edges of the transducer would shield the edge effects at all, but very little effect was found. Cutting the edges of the window at a slope to make the sudden change from a hemicylinder to a full cylinder, a more gradual change gave only a very minor reduction in artifact. This effect was small even for brass not matched to water and is likely of little value for water-matched brass designs. Finally, the effect of changing the susceptibility of the transducer material was tested and did not change the character of the artifact in any qualitative way. Ideally, matching the transducer susceptibility to water would provide the best artifact reduction. Piezocomposite materials might achieve this criterion, which is an important advantage; however, the power handling characteristics of these materials are inferior to PZT, an important consideration for these minimally invasive device designs.
The versatility of numerical solutions enables parameters to be varied in potentially complex ways. In an attempt to minimize the artifacts caused by the edge of the transducer, various modifications to the edges of the transducer were attempted including gradual tapers of varying profiles: cusped, elliptic, linear, even variable-density perforations, to provide a gradual change in magnetization in an effort to reduce edge effects. Tapers reduced the artifact by only 10%–20% at best but needed to be much longer than the current dummy element length. Perforations of increasing density near the ends of the transducer, in an effort to create gradual change in bulk susceptibility, appear inferior to tapers and are difficult to machine in brittle PZT.
4. DISCUSSION
Suppression of spatial temperature artifact is achieved primarily in two ways. First, the magnitude of the magnetic distortions can be minimized by matching the susceptibility of the brass in the applicator housing to that of the background water. Second, the pattern of magnetic distortion can be made more cylindrically symmetric, by centering the transducer, such that distortions that are present are canceled better by the reference scan. The magnetization of the applicator was minimized overall by selecting materials of appropriate susceptibility. Then, by making the components with the largest degree of magnetization as symmetric as possible, and aligning this symmetry with the motion used, the pattern of magnetic distortions was kept as constant as possible between the reference scan and the subsequent thermometry scans.
Alternative approaches were considered including acquiring multiple reference scans at a variety of rotational positions of the device and using these to better match the images acquired during heating as the device rotated. In theory, this can eliminate the artifact that occurs due to rotation, and promising results were observed experimentally in tissue-mimicking phantoms. The method degraded in vivo since the rotation of the device was often not purely axial. Nonetheless, there may still be a role for this approach in combination with the device design efforts explored in this study, especially for device orientations close to 90°.
In practice, centering of the transducer yields the greatest reduction of artifact of all the parameters tested. This is partly because the majority of the applicator was susceptibility matched to water from the first stages of design, a strategy that has been validated in these studies. Other modifications were more difficult to design and did not provide sufficient improvement to warrant their implementation. The more effective strategies discussed here are currently being implemented in a next generation applicator device, though these devices are not yet available for empiric validation. It is our hope that these results will be able to inform the future design of devices outside our immediate application as well.
From the standpoint of maximizing symmetry, the transducer should be centered and of a cylindrical geometry. This is a design feature in some devices,22 although there are tradeoffs against the beam width and a resulting decrease in the gain of the transducer. A lower aspect ratio to the transducer’s cross section would enhance its symmetry. Here as well, design considerations must be balanced, as the width of the transducer affects radiated beam width and power, while the thickness of the transducer will affect the acoustic resonant frequencies of the crystal and the total magnetic moment.
Given a water-matched housing and centered transducer, there are a number of other manipulations of applicator design that can be made but most have comparatively minor effects on the artifact generated. Among these are the dummy elements that have been used in the current design. The dummy elements still help to move the edge effects away from the area being sonicated, but the improvement provided in a centered transducer design is smaller than in the original offset design.
A very important result obtained from the simulations was that ultrasound frequency (which translates into transducer thickness) did not have a major influence on the spatial temperature artifact for the range typically used for intracavitary applications.
Device orientation was, in fact, the most important parameter influencing the spatial temperature artifact around the device. Effects that are unimportant at some applicator inclinations become much more important at others. For applications such as prostate where the device orientation is restricted to a small range of angles, this variation can be considered constant. However, for applications such as interstitial treatments in the brain, where devices may be inserted into the skull at arbitrary angles, this effect must be considered.
5. CONCLUSIONS
The distortions of MRI-based temperature measurements due to the magnetization of an interventional device have been examined using finite element analysis methods. Several design strategies that were assumed to be effective in initial designs of the transurethral HIFU applicator were validated as being effective. These include matching the magnetic susceptibilities of the materials used to the surrounding medium, as closely as is practical, and the use of dummy elements at the ends of the transducer to move the fringing fields away from the region of interest. Beyond this, the new technique of matching device symmetry to the motion used was identified, which yielded significant improvements when used in conjunction with the prior strategies. In this case, the applicator was made more rotationally symmetric by centering the transducer to the axis of rotation. This also had the added benefit of moving the transducer farther away from the applicator window and, thus, the target box where temperature measurements are made. Finally, the reduction of the volume of components whose susceptibilities cannot be matched well to water was also found to be effective. In the case of this applicator, this meant minimization of air volume behind the transducer and making the transducer as thin as possible without compromising function. These principles can be generalized, in roughly descending order of importance, into the following three statements: 1. Minimize the magnetization of the device, either by matching susceptibilities of materials or by reducing the volume of the most mismatched components. 2. Minimize the change in any remaining magnetization between the reference scan and the measurement scans, which is accomplished by matching the symmetry of the device to the symmetry of the motion used. 3. Moving component edges away from the region of interest minimizes artifact due to fringing fields in the region of interest.
In addition to these qualitative statements, it is still important to perform quantitative analysis of any new geometries or materials. Such quantitative results enable design optimization when two of the above strategies are in conflict. For example, in this case, it was found that reducing the total volume of the transducer by making it thinner resulted in more artifact reduction than attempting to make the transducer more symmetric by giving it a square cross section. Several of the improvements found in this study are being incorporated into the next generation applicator design and should enable more accurate temperature measurements during treatment. Currently, the maximum artifact generated during a typical treatment is approximately 4 °C in the region of the target box, while most voxels have an artifact of less than 2 °C. This is adequate but not ideal for prostate therapy monitoring. The modifications identified here will reduce the artifact at any given voxel to half of this figure or less at most rotations, as evidenced in Fig. 9. There still remain unanswered questions about how to reduce artifact at high angles of inclination most effectively. More sophisticated design changes may also allow successful strategies for shielding to be created. Finally, future developments in software algorithms may enable more sophisticated artifact reduction.
ACKNOWLEDGMENTS
The authors would like to thank fellow group member Aaron Boyes for constructing the transurethral devices and providing information about their design. This study was supported by NIH Grant No. 1R21CA159550.
REFERENCES
- 1.Schenck J. F., “The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds,” Med. Phys. 23(6), 815–850 (1996). 10.1118/1.597854 [DOI] [PubMed] [Google Scholar]
- 2.Crouzet S., Murat F., Pasticier G., Cassier P., Chapelon J., and Gelet A., “High intensity focused ultrasound (HIFU) for prostate cancer: Current clinical status, outcomes and future perspectives,” Int. J. Hyperthermia 26(8), 796–803 (2010). 10.3109/02656736.2010.498803 [DOI] [PubMed] [Google Scholar]
- 3.Uchida T., Nakano M., Hongo S., Shoji S., Nagata Y., Satoh T., Baba S., Usui Y., and Terachi T., “High-intensity focused ultrasound therapy for prostate cancer,” Int. J. Urol. 19(2), 187–201 (2012). 10.1111/j.1442-2042.2011.02936.x [DOI] [PubMed] [Google Scholar]
- 4.Chopra R., Baker N., Choy V., Boyes A., Tang K., Bradwell D., and Bronskill M. J., “MRI-compatible transurethral ultrasound system for the treatment of localized prostate cancer using rotational control,” Med. Phys. 35(4), 1346–1357 (2008). 10.1118/1.2841937 [DOI] [PubMed] [Google Scholar]
- 5.Diederich C. J., Nau W. H., Kinsey A., Ross T., Wootton J., Juang T., Butts-Pauly K., Rieke V., Chen J., Bouley D. M., and Sommer G., “Catheter-based ultrasound devices and MR thermal monitoring for conformal prostate thermal therapy,” in Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC (IEEE, 2008), pp. 3664–3668. 10.1109/IEMBS.2008.4650002 [DOI] [PubMed] [Google Scholar]
- 6.Partanen A., Yerram N. K., Trivedi H., Dreher M. R., Oila J., Hoang A. N., Volkin D., Nix J., Turkbey B., Bernardo M., Haines D. C., Benjamin C. J., Linehan W. M., Choyke P., Wood B. J., Ehnholm G. J., Venkatesan A. M., and Pinto P. A., “Magnetic resonance imaging (MRI)-guided transurethral ultrasound therapy of the prostate: A preclinical study with radiological and pathological correlation using customised MRI-based moulds,” BJU Int. 112(4), 508–516 (2013). 10.1111/bju.12126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fruehauf J. H., Back W., Eiermann A., Lang M. C., Pessel M., Marlinghaus E., Melchert F., Volz-Köster S., and Volz J., “High-intensity focused ultrasound for the targeted destruction of uterine tissues: Experiences from a pilot study using a mobile HIFU unit,” Arch. Gynecol. Obstet. 277(2), 143–150 (2008). 10.1007/s00404-007-0435-0 [DOI] [PubMed] [Google Scholar]
- 8.Wootton J. H., Hsu I. C., and Diederich C. J., “Endocervical ultrasound applicator for integrated hyperthermia and HDR brachytherapy in the treatment of locally advanced cervical carcinoma,” Med. Phys. 38(2), 598–611 (2011). 10.1118/1.3512803 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Canney M. S., Chavrier F., Tsysar S., Chapelon J. Y., Lafon C., and Carpentier A., “A multi-element interstitial ultrasound applicator for the thermal therapy of brain tumors,” J. Acoust. Soc. Am. 134(1), 1647–1655 (2013). 10.1121/1.4812883 [DOI] [PubMed] [Google Scholar]
- 10.Kangasniemi M., Diederich C. J., Price R. E., Stafford R. J., Schomer D. F., Olsson L. E., Tyreus P. D., Nau W. H., and Hazle J. D., “Multiplanar MR temperature-sensitive imaging of cerebral thermal treatment using interstitial ultrasound applicators in a canine model,” J. Magn. Reson. Imaging 16(5), 522–531 (2002). 10.1002/jmri.10191 [DOI] [PubMed] [Google Scholar]
- 11.Mast T. D., Barthe P. G., Makin I. R., Slayton M. H., Karunakaran C. P., Burgess M. T., Alqadah A., and Rudich S. M., “Treatment of rabbit liver cancer in vivo using miniaturized image-ablate ultrasound arrays,” Ultrasound Med. Biol. 37(10), 1609–1621 (2011). 10.1016/j.ultrasmedbio.2011.05.850 [DOI] [PubMed] [Google Scholar]
- 12.Ishihara Y., Calderon A., Watanabe H., Okamoto K., Suzuki Y., Kuroda K., and Suzuki Y., “A precise and fast temperature mapping using water proton chemical shift,” Magn. Reson. Med. 34(6), 814–823 (1995). 10.1002/mrm.1910340606 [DOI] [PubMed] [Google Scholar]
- 13.Vigen K. K., Daniel B. L., Pauly J. M., and Butts K., “Triggered, navigated, multi-baseline method for proton resonance frequency temperature mapping with respiratory motion,” Magn. Reson. Med. 50, 1003–1010 (2003). 10.1002/mrm.10608 [DOI] [PubMed] [Google Scholar]
- 14.de Senneville B. D., Mougenot C., and Moonen C. T. W., “Real-time adaptive methods for treatment of mobile organs by MRI-controlled high-intensity focused ultrasound,” Magn. Reson. Med. 57, 319–330 (2007). 10.1002/mrm.21124 [DOI] [PubMed] [Google Scholar]
- 15.Salomir R., Viallon M., Kickhefel A., Roland J., Morel D. R., Petrusca L., Auboiroux V., Goget T., Terraz S., Becker C. D., and Gross P., “Reference-free PRFS MR-thermometry using near-harmonic 2-D reconstruction of the background phase,” IEEE Trans. Med. Imaging 31(2), 287–301 (2012). 10.1109/TMI.2011.2168421 [DOI] [PubMed] [Google Scholar]
- 16.Rieke V., Vigen K. K., Sommer G., Daniel B. L., Pauly J. M., and Butts K., “Referenceless PRF-shift thermometry,” Magn. Reson. Med. 51(6), 1223–1231 (2004). 10.1002/mrm.20090 [DOI] [PubMed] [Google Scholar]
- 17.Grissom W. A., Rieke V., Holbrook A. B., Medan Y., Lustig M., Santos J., Mcconnell M. V., and Pauly K. B., “Hybrid referenceless and multibaseline subtraction MR thermometry for monitoring thermal therapies in moving organs,” Med. Phys. 37(9), 5014–5026 (2010). 10.1118/1.3475943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Salomir R., de Senneville B. D., and Moonen C. T. W., “A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility,” Concepts Magn. Reson., Part B 19B(1), 26–34 (2003). 10.1002/cmr.b.10083 [DOI] [Google Scholar]
- 19.Astary G. W., Peprah M. K., Fisher C. R., Stewart R. L., Carney P. R., Sarntinoranont M., Meisel M. W., Manuel M. V., and Mareci T. H., “MR measurement of alloy magnetic susceptibility: Towards developing tissue-susceptibility matched metals,” J. Magn. Reson. 233, 49–55 (2013). 10.1016/j.jmr.2013.05.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chapelon J. Y., Cathignol D., Cain C., Ebbini E., Kluiwstra J. U., Sapozhnikov O. A., Fleury G., Berriet R., Chupin L., and Guey J. L., “New piezoelectric transducers for therapeutic ultrasound,” Ultrasound Med. Biol. 26(1), 153–159 (2000). 10.1016/S0301-5629(99)00120-9 [DOI] [PubMed] [Google Scholar]
- 21.Ramsay E., Mougenot C., Köhler M., Bronskill M., Klotz L., Haider M. A., and Chopra R., “MR thermometry in the human prostate gland at 3.0T for transurethral ultrasound therapy,” J. Magn. Reson. Imaging 38(6), 1564–1571 (2013). 10.1002/jmri.24063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Prakash P., Salgaonkar V. A., and Diederich C. J., “Modelling of endoluminal and interstitial ultrasound hyperthermia and thermal ablation: Applications for device design, feedback control and treatment planning,” Int. J. Hyperthermia 29(4), 296–307 (2013). 10.3109/02656736.2013.800998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Susceptibility can be represented in a variety of ways depending on whether the susceptibility is given in terms of mass, volume, or molar volume. In the case of volume susceptibility quoted here, the value is unitless and is given using the conventions of SI measurement.
- 24.Strictly speaking only the component of the field perpendicular to the radio frequency coils contributes to the Larmor frequency, in this case the z-component. The difference between the total field magnitude and the projected magnitude along the z-axis was negligible in this case, and this projection operation was often omitted in numerical computations.
- 25.The phantom setup inclines the applicator downward, at a negative angle, to mimic the orientation during patient care.
- 26.Temperature artifacts are the same, except with reversed sign, for equal inclinations in the opposite direction.