Accuracy of respiratory motion measurement of 4D-MRI: A comparison between cine and sequential acquisition

Abstract

Purpose:

The authors have recently developed a cine-mode T2*/T1-weighted 4D-MRI technique and a sequential-mode T2-weighted 4D-MRI technique for imaging respiratory motion. This study aims at investigating which 4D-MRI image acquisition mode, cine or sequential, provides more accurate measurement of organ motion during respiration.

Methods:

A 4D digital extended cardiac-torso (XCAT) human phantom with a hypothesized tumor was used to simulate the image acquisition and the 4D-MRI reconstruction. The respiratory motion was controlled by the given breathing signal profiles. The tumor was manipulated to move continuously with the surrounding tissue. The motion trajectories were measured from both sequential- and cine-mode 4D-MRI images. The measured trajectories were compared with the average trajectory calculated from the input profiles, which was used as references. The error in 4D-MRI tumor motion trajectory (E) was determined. In addition, the corresponding respiratory motion amplitudes of all the selected 2D images for 4D reconstruction were recorded. Each of the amplitude was compared with the amplitude of its associated bin on the average breathing curve. The mean differences from the average breathing curve across all slice positions (D) were calculated. A total of 500 simulated respiratory profiles with a wide range of irregularity (Ir) were used to investigate the relationship between D and Ir. Furthermore, statistical analysis of E and D using XCAT controlled by 20 cancer patients’ breathing profiles was conducted. Wilcoxon Signed Rank test was conducted to compare two modes.

Results:

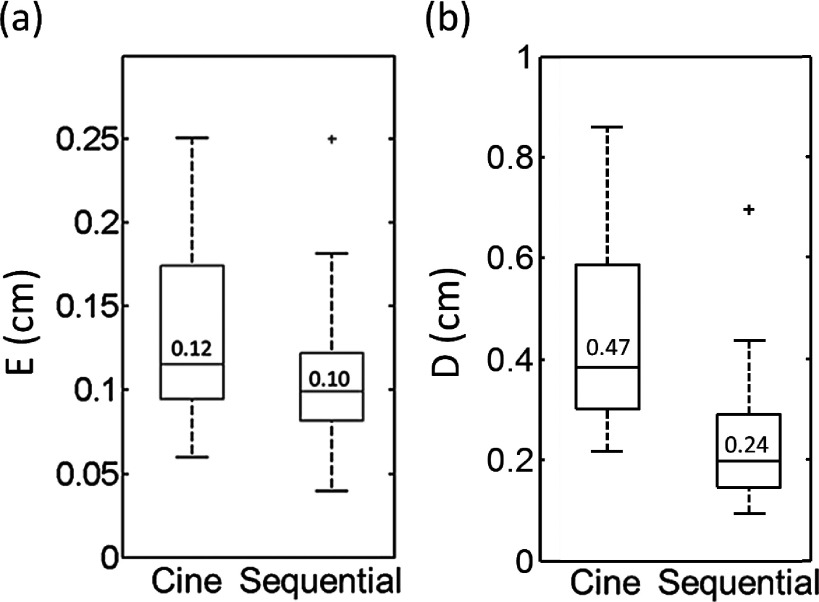
D increased faster for cine-mode (D = 1.17 × Ir + 0.23) than sequential-mode (D = 0.47 × Ir + 0.23) as irregularity increased. For the XCAT study using 20 cancer patients’ breathing profiles, the median E values were significantly different: 0.12 and 0.10 cm for cine- and sequential-modes, respectively, with a p-value of 0.02. The median D values were significantly different: 0.47 and 0.24 cm for cine- and sequential-modes, respectively, with a p-value < 0.001.

Conclusions:

Respiratory motion measurement may be more accurate and less susceptible to breathing irregularity in sequential-mode 4D-MRI than that in cine-mode 4D-MRI.

1. INTRODUCTION

Respiratory motion affects the thorax and abdomen radiation therapy in several different aspects, inducing potential errors in target volume determination and treatment delivery.^1–3 4D computed tomography (4D-CT) technique has been widely used as the clinical standard for imaging respiratory motion, especially for tumors in the thorax.^4–6 In particular, 4D-CT can be used to determine patient-specific internal target volume (ITV) and the optimal motion management strategy for the patient.⁷ Furthermore, respiratory-gated techniques were also developed to assisted motion management, used in imaging techniques (such as respiratory-gated PET/SPECT)^8–10 and therapy techniques. Recently, 4D magnetic resonance imaging (4D-MRI) has been developed for imaging respiratory motion for abdominal cancers,^11–14 owning to its high soft-tissue contrast and no-known ionizing radiation hazard.^15–17 A number of 4D-MRI techniques have been reported in the literature to date,^11,18–23 which can be generally categorized into two types: (1) prospective 4D-MRI, in which respiratory trigger system is used to preselect respiratory amplitudes to achieve 4D-MRI image acquisition by employing fast 2D (Refs. 18, 19, and 24) or 3D MR sequences^11,20,21 to acquire images at different respiratory amplitude levels and (2) retrospective 4D-MRI, in which 2D slice images are acquired continuously using fast 2D MR sequences,^{22,23,25–28} with a respiratory signal recorded simultaneously during the image acquisition process. The acquired 2D MR images are then retrospectively sorted according to the respiratory phases or amplitudes.

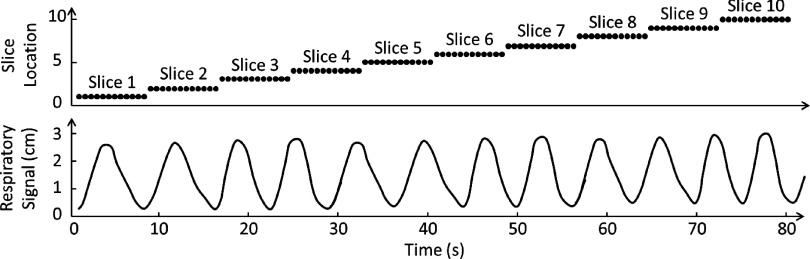
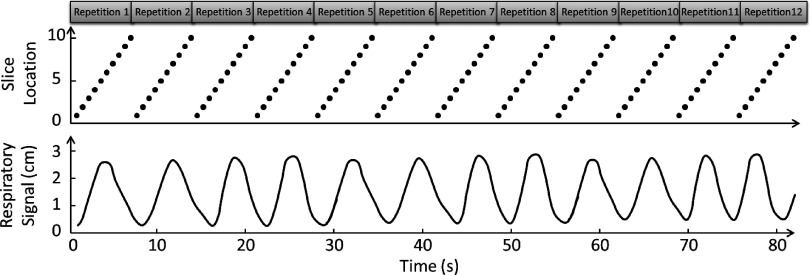
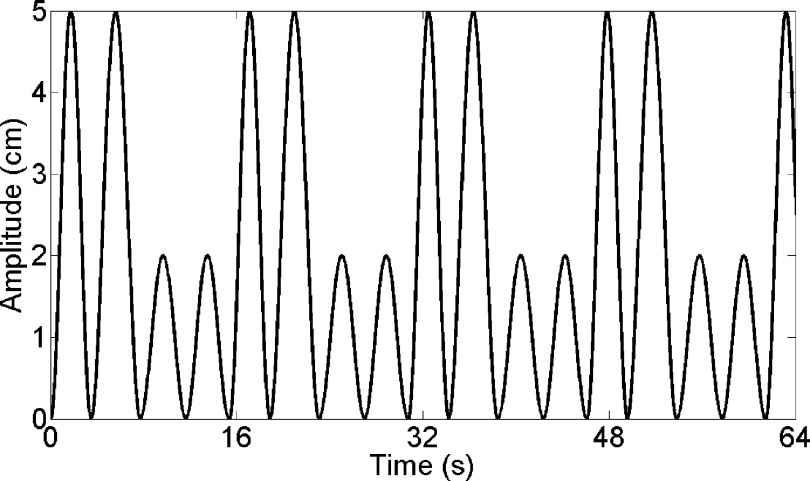
Most of current retrospective 4D-MRI techniques acquire images in the cine-mode,^27,28 as illustrated in Fig. 1. In the cine-mode 4D-MRI, 2D MR images are continuously acquired at the same slice position for a period of time, and then the process is repeated at multiple slice positions to cover the entire volume of interest (VOI). Several groups used this image acquisition mode. For example, Remmert et al. implemented a T1-weighted 4D-MRI technique with retrospective sorting and slice stacking of 2D MRI cine images.²² Cai et al. developed a T2*/T1-weighted 4D-MRI technique using body area (BA) as the respiratory surrogate.^27,28 This technique acquires images in the cine-mode utilizing a true fast imaging with steady state precession (TrueFISP) MR sequence with fast frame rate (3–10 fps). On the other hand, some other retrospective 4D-MRI techniques acquire images in the sequential-mode,^25,26 as illustrated in Fig. 2. In the sequential-mode 4D-MRI, 2D MR images are acquired sequentially (could be ascending, descending, or interleaved) to cover the VOI and the sequential image acquisition process is repeated a number of times to ensure adequate sampling of all respiratory phases at each slice position. For example, Liu et al. employed a T2-weighted half-Fourier acquisition single-shot turbo spin-echo (HASTE/SSFSE) MR sequence for 4D-MRI image acquisition.²⁵ This sequence was selected for 4D-MRI due to its high frame rate (∼2 fps) and the high tumor contrast with T2-weighting. Tryggestad et et al. developed a T2*/T1-weighted 4D-MRI technique with fast imaging employing steady-state acquisition (TrueFISP/FIESTA) MR sequence. Both groups used sequential image acquisition mode for 4D-MRI image acquisition.

FIG. 1.

Illustration of cine image acquisition mode for 4D-MRI. This acquisition mode acquires 2D images continuously at the same slice position for a period of time, and then the process is repeated at multiple slice positions to cover the entire VOI. Each black dot represents one 2D-MR image acquisition. The respiratory signal is simultaneously recorded for 4D-MRI retrospectively sorting purpose.

FIG. 2.

Illustration of sequential image acquisition mode for 4D-MRI. This image acquisition mode repeatedly acquires 2D MR images sequentially for the volume of interest. Each black dot represents one 2D-MR image acquisition. The respiratory signal is simultaneously recorded for 4D-MRI retrospectively sorting purpose.

There are many similarities between the cine-mode and the sequential-mode 4D-MRI techniques. For example, both of them require high imaging frame rate and recording of synchronized breathing signals. Nevertheless, there are fundamental differences between the two. In particular, they are distinctly different in the criteria of achieving data sufficient condition (DSC) in 4D image acquisition,^25–28 i.e., images of all sorting bins have been acquired for all slice positions. In the cine-mode 4D-MRI, DSC can be simply achieved by setting the imaging time per slice position (cine duration) to be longer than the patient’s breathing period. In the sequential-mode, achieving DSC becomes less straight forward because the assignment of respiratory phase to images is a very random process as a result of breathing variation. Since the sequential acquisition does not continuously acquire images at the same slice position, it is difficult to predict when the image acquisition of all respiratory phases will be finished at each slice location. We have shown in our previous study that DSC is affected by multiple factors, including imaging frame rate, sorting method, number of repetitions, number of slices, number of sorting bins, initial respiratory phase at the start of image acquisition and patient’s breathing period and breathing variation.²⁵

While both the cine and the sequential image acquisitions can be effectively used for 4D-MRI, as demonstrated by previous studies, there could be systematic differences in 4D-MRI quality between the two methods due to their fundamentally different image acquisition schemes. In particular, it is expected that respiratory motion measurement accuracy and the effects of breathing variation will be different using the two image acquisition scheme. The purpose of this study is therefore to quantitatively evaluate the performance of 4D-MRI techniques using cine- and sequential-modes, particularly their accuracy of motion measurement with different breathing variation. Large number of subject samples with different breathing patterns may be preferable for a convincing comparison; however, it is not efficient or practical to acquire a large number of patients’ data. In our study, we simulated cine-mode and sequential-mode 4D-MRI techniques using a 4D digital human phantom embedded with a hypothesized tumor and evaluated the accuracy of tumor motion trajectories measured from the simulated 4D-MRI, using the input signal as references. The mean amplitude error across all slice positions was also measured. In addition, we investigated how breathing irregularity affects the 4D-MRI tumor motion accuracy for both image acquisition modes.

2. METHODS AND MATERIALS

2.A. Digital phantom simulation study

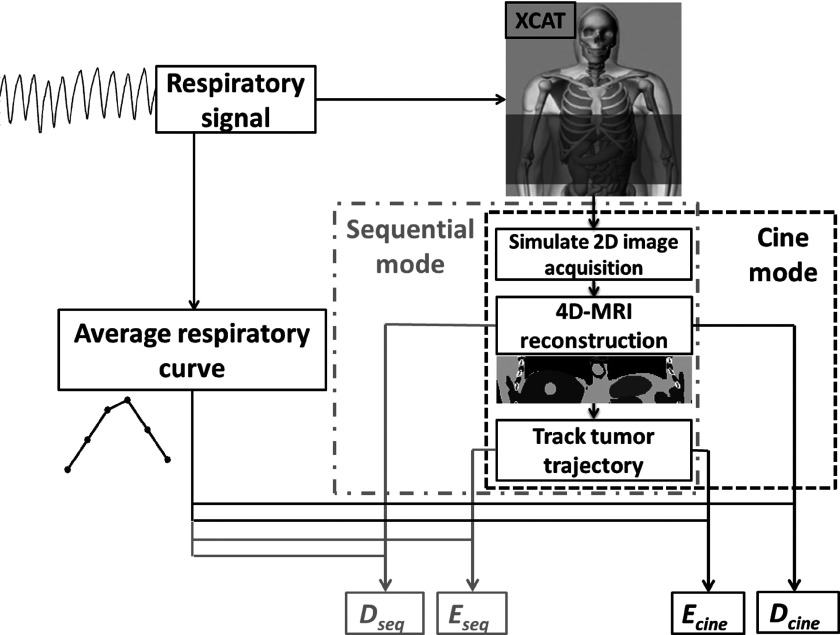
To evaluate and compare the performance of the cine-mode and the sequential-mode 4D-MRI techniques, we conducted virtual experiments on a 4D digital extended cardiac-torso (XCAT) digital human phantom^29–31 by simulating step-by-step the image acquisition and reconstruction of the two 4D-MRI techniques.^{25,27,32–36} An in-house developed matlab program was built to facilitate the simulation and evaluation. Figure 3 illustrated the overall study design and workflow of the digital phantom simulation study. A subset of the XCAT phantom was generated from the mid-thorax to mid-abdomen regions and used in this study. The XCAT phantom was generated in the activity mode for MRI-like image appearance where the signal intensities of the organs and tissues were assigned using values derived from HASTE/SSFSE MRI images. The acquisition mode of that sequence is in sequential-mode.²⁵ Although cine-mode 4D-MRI is achieved by using TrueFISP/FIESTA sequences,^27,28 the same image intensity assignment is used in the cine-mode 4D-MRI XCAT simulation for image quality comparison purpose. The HASTE/SSFSE MRI image intensities were selected for both simulations also because it provided T2-weighted signals, which have a high tumor-to-tissue contrast. Tumor size and respiratory motion pattern were also set to be the same between two modes. In other words, all the basic imaging parameters were set to be the same to compare the image acquisition mode. Only 4D-specfic factors were varied to understand how the performances of the 4D-MRI techniques are influenced by respiratory motion variation from the 4D perspective. In particular, the respiratory motion of the XCAT phantom was controlled by a customizable input signal. Maximum diaphragm motion in superior–inferior (SI) direction was set to be 30 mm; and maximum chest surface motion in anterior–posterior (AP) direction was set to be 10 mm. No motion was input in medial-lateral (ML) direction. A hypothesized spherical tumor of 40 mm in diameter was inserted at the center of the liver.

FIG. 3.

Flow chart of quantification of 4D-MRI respiratory motion measurement accuracy for both sequential and cine image acquisition mode.

To simulate cine-mode or sequential-mode 4D-MRI, a series of volumetric datasets of the 4D XCAT phantom was first generated in the same imaging frame rate of the actual 2D MR sequence (e.g., 2 fps). This resulted in a large number of volumetric XCAT image datasets, each corresponding to a different breathing status. These datasets would be the digital moving phantom that we would simulate image acquisition process on. Second, one single slice 2D XCAT image was extracted from each volumetric XCAT image dataset, mimicking the image acquisition as the real MR sequence does. The extraction of the 2D images can be carried out in either cine- or sequential-mode, following the corresponding scheme as shown in Figs. 1 and 2. Third, the extracted 2D images were used to reconstruct 4D-MRI using sorting methods that we have previously developed for both modes.^25,27

Simulated imaging parameters in the XCAT phantom study were the following: in-plane resolution: 256 × 256; voxel size: 2.5 mm; slice thickness: 3 mm; total number of slices: 30; frame rate: 2 Hz; total number of 4D-MRI phase bins: 6. For the cine-mode, the scanning time for each slice was 8 s, and the total scanning time was 240 s. For the sequential-mode, the total scanning time was set to be long enough (300 s) to ensure sufficient sampling of all respiratory phases for 4D-MRI reconstruction.²⁵

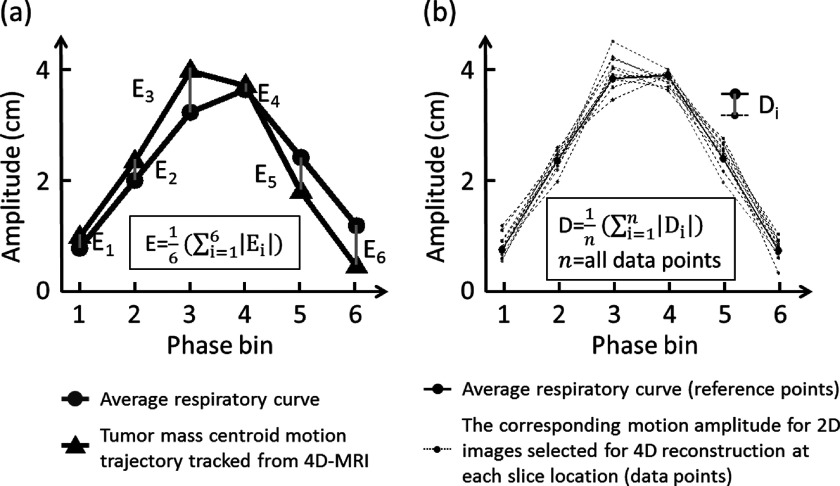
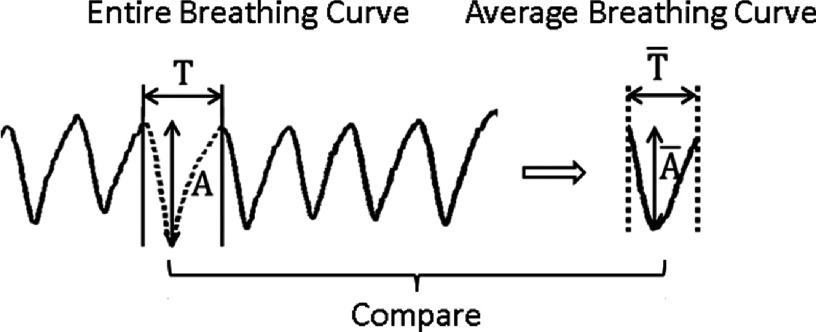
To quantitatively assess the accuracy of respiratory motion measurement of 4D-MRI, two evaluating metrics were calculated and compared between the cine-mode 4D-MRI and the sequential-mode 4D-MRI. The first metric is the error in tumor motion trajectory (E). The motion trajectory of the hypothesized tumor was first measured from the simulated 4D-MRI images using an in-house developed motion tracking algorithm that was based on maximum cross-correlation,^28,37 and then compared to an average respiratory curve derived from the input signal to determine E. As shown in Fig. 4(a), E was calculated as the phase-averaged absolute difference in tumor motion amplitude between the two curves. E was determined for both the cine-mode 4D-MRI and the sequential-mode 4D-MRI, and labeled as E_cine and E_seq, respectively. It should be noted that E evaluates the performance of 4D-MRI only in terms of tumor motion; it does not evaluate the performance of 4D-MRI at nontumor regions.

FIG. 4.

Illustration of the determination of E and D.

To assess the overall performance of 4D-MRI of the entire volume, we introduced a second evaluating metric, the mean difference from the average breathing signal across all slice positions (D). The determination of D includes 3 steps: (1) derive the average breathing cycle from the input breathing signal and (2) generate individual breathing cycle for each slice position. During 4D-MRI reconstruction, each selected MR image corresponded to a data point in the input breathing signal, and each data point has an unique set of phase and amplitude. The individual breathing cycle is generated by sorting the selected data points of that slice position based on respiratory phase. Each phase image at a particular slice position has corresponding respiratory amplitude that can be read from the respiratory signal recorded simultaneously with external surrogate. Based on these recorded amplitude information, individual breathing cycle for each slice position can be generated; (3) compare all individual breathing cycles to the average breathing cycle to determine D, as shown in Fig. 4(b). D was calculated for both the sequential-mode 4D-MRI and cine-mode 4D-MRI and was labeled as D_seq and D_cine, respectively.

In order to demonstrate the image quality difference between the two 4D-MRI techniques, we designed a particular respiratory motion to control XCAT, and reconstructed the 4D-MRI using the two techniques with different image acquisition modes as an example. The respiratory motion for this example case is shown in Fig. 5.

FIG. 5.

A particular respiratory motion we designed to demonstrate the image quality difference between the two 4D-MRI techniques.

2.B. Effects of breathing variation

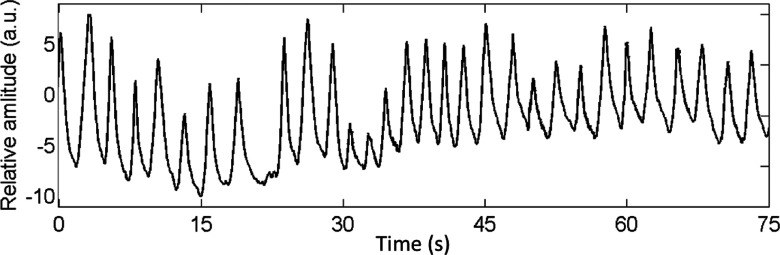
Breathing variation is a key factor that affects the image quality of 4D-MRI. Due to the difference in image acquisition scheme, the two 4D-MRI techniques (cine-mode and sequential-mode) are expected to have different yet unknown sensitivities to breathing variation. It is therefore of interest to study the effect of breathing variation on the image quality of 4D-MRI and compare it between the cine-mode and sequential-mode 4D-MRI techniques. To do this, we performed simulation studies using the XCAT digital phantom that was controlled by 20 different real cancer patients’ real-time position management (RPM) breathing profiles. One example of the RPM signal is illustrated in Fig. 6. It shows the beginning 75 s of the RPM signal of the first patient. Evaluating metrics E_seq and E_cine were derived from simulation 4D-MRI; D_seq and D_cine were derived for each RPM breathing profile and were compared between the cine-mode and the sequential-mode using the Wilcoxon Signed Rank test.

FIG. 6.

One example of the patients’ RPM signal.

Furthermore, to systematically evaluate the relationship between breathing variation and 4D-MRI image quality, we constructed 500 irregular respiratory profiles with a wide range of breathing irregularities, which was defined as

$${\displaystyle \text{Ir}=\sqrt{{({\sigma }_{\mathrm{amplitude}}/\overline{A})}^2+{({\sigma }_{\mathrm{period}}/\overline{T})}^2}}$$ (1)

where Ir is the respiratory irregularity and σ_amplitude and σ_period are the variance of amplitude and period of each individual breathing cycle. $\overline{A}$ and $\overline{T}$ are the average amplitude and the average period of each breathing profile.

For a respiratory profile, each individual cycle on the profile will be assigned an amplitude value (A_i) and a period time value (T_i). There is a variation range for the A_i and T_i. The range depends on the Ir of the respiratory profile. The value of A_i and T_i were randomly generated with a Gaussian distribution. The values of A_i subject to a Gaussian distribution of $N(\mu =\overline{A},\sigma ={\sigma }_{\mathrm{amplitude}})$ and the values of T_i subject to a Gaussian distribution of $N(\mu =\overline{T},\sigma ={\sigma }_{\mathrm{period}})$. The relationship between the Ir of the breathing profile and Gaussian distribution parameters is showed in formula (1). We then determined D_seq and D_cine for each breathing profile using the method as mentioned above and studied the relationships between D and Ir.

3. RESULTS

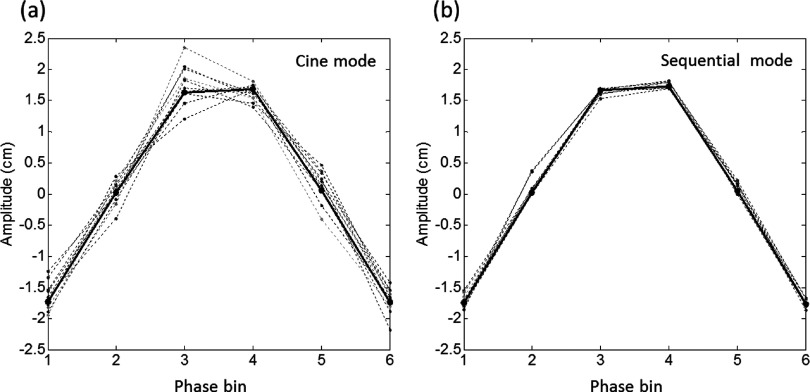
Fig. 7 shows an example of a six-phase 4D-MRI data sorting results for the cine and sequential image acquisition modes. The solid curves represent the average breathing curve. The dashed curves represent the sorted breathing cycles of different slice locations. It can be seen that sequential-mode resulted in more consistent breathing cycles among different slice positions than the cine-mode, indicating potentially better 4D-MRI image quality and more accurate respiratory motion measurement with sequential-mode acquisition.

FIG. 7.

Example of 4D-MRI data sorting results for the cine-mode (a) and the sequential-mode (b) image acquisition. The black solid curves represent the average breathing curve. The dashed curves represent the sorted breathing cycles of different slice locations.

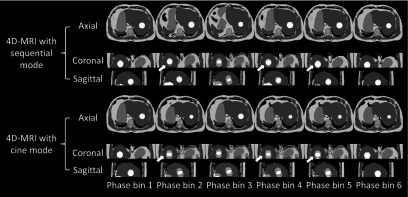
The example of 4D-MRI images reconstructed using the technique with cine image acquisition mode and the technique with sequential image acquisition mode are displayed in Fig. 8. The respiratory motion for this example case is shown in Fig. 5. The comparison shows the image quality difference between using the two techniques.

FIG. 8.

An example of 4D-MRI images reconstructed using the technique with cine image acquisition mode and the technique with sequential image acquisition mode. White arrows pointed out some image quality differences showed between 4D-MRI reconstructed using the two techniques.

Fig. 9 shows the comparisons between the cine-mode and the sequential-mode for evaluating metrics E (a) and D (b) from the XCAT phantom study. It can be seen that tumor motion measurement was significantly more accurate in the sequential-mode than in the cine-mode: the mean E_cine was 0.12 cm and the mean E_seq was 0.10 cm (p-value = 0.02). Furthermore, the mean D_cine was 0.47 cm and mean D_seq was 0.24 cm (p-value < 0.001), indicating the overall image quality of 4D-MRI is better in sequential-mode than in the cine-mode.

FIG. 9.

Comparison between the cine-mode and the sequential-mode for E (a) and D (b) from the XCAT phantom study.

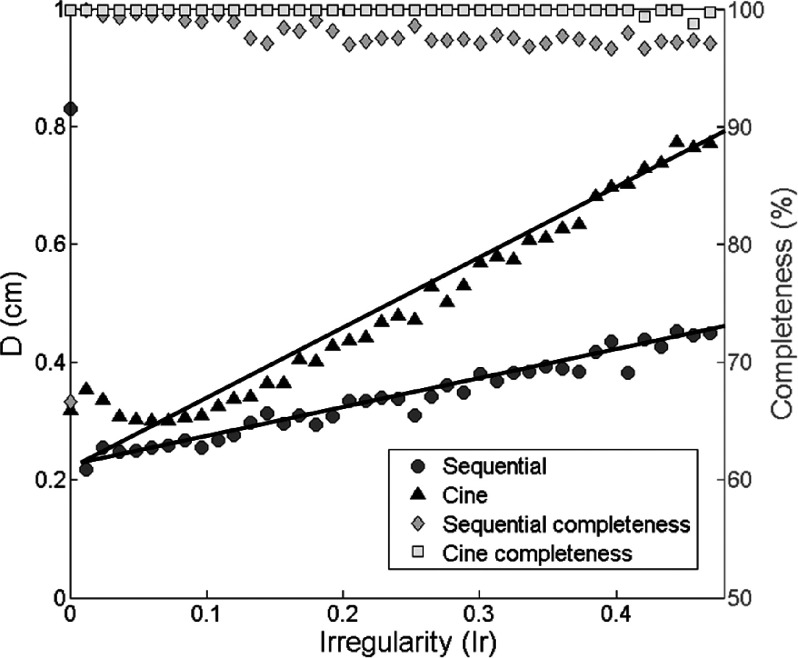
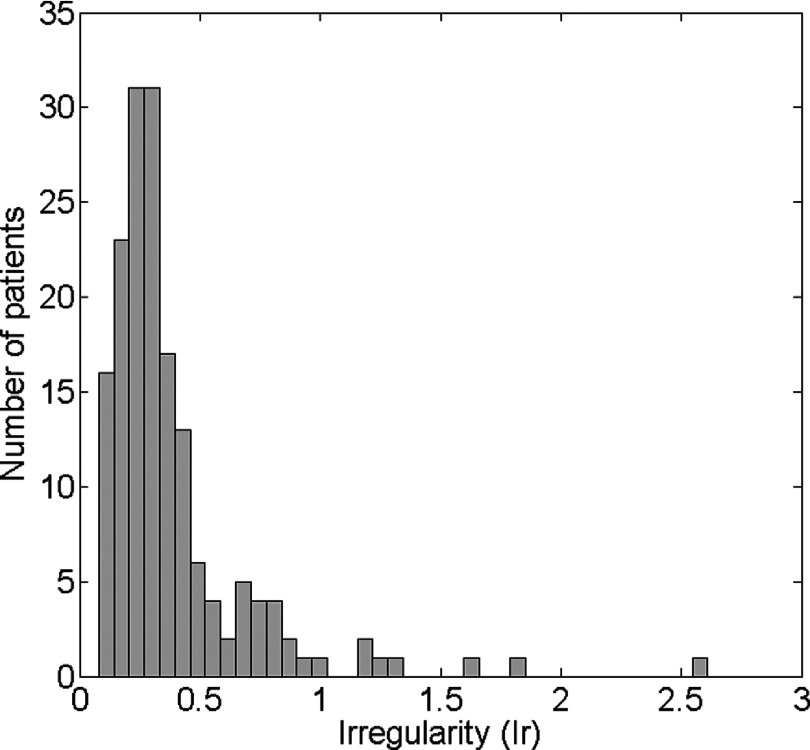
Fig. 10 shows the relationships between Ir and D derived using the 500 irregular breathing profiles for the cine-mode (triangles) and sequential-mode (circles). The image data acquisition completeness for different Ir with cine-mode (squares) and sequential-mode (diamonds) are also illustrated in the figure as references. It was observed that D_cine is consistently larger than D_seq, and D_cine increases faster as Ir increases than D_seq. Linear regression resulted in D_seq = 0.47 × Ir + 0.23 and D_cine = 1.17 × Ir + 0.23. Based on our measurement of 167 cancer patients’ breathing profiles, the median breathing Ir value is 0.39. The Ir values distribution is shown below in Fig. 11. The median value and the distribution imply that the sequential-mode would generally provide better image quality of 4D-MRI than the cine-mode. It is worth notice that when Ir is very small, D_seq could be higher than D_cine and D_seq decreases as Ir increases. This was in fact caused by data insufficiency in the sequential-mode, as indicated by its data completeness curve. When Ir is small, i.e., breathing is more regular, it takes longer time to acquire all necessary data to meet the DSC for the sequential-mode 4D-MRI, i.e., the image data acquisition completeness is low. Conversely, DSC for the cine-mode 4D-MRI can be easily met by setting the cine-duration longer than one breathing period.

FIG. 10.

Relationship between D and Ir. Linear regression resulted in D_seq = 0.47 × Ir + 0.23 and D_cine = 1.17 × Ir + 0.23.

FIG. 11.

Ir values distribution measured from 167 cancer patients’ RPM breathing profiles.

4. DISCUSSION

In this study, we compared the respiratory motion measurement accuracy between the cine-mode 4D-MRI and the sequential-mode 4D-MRI techniques and investigated how breathing irregularity influenced the 4D-MRI image qualities through a simulation study using the XCAT digital phantom. Our results showed that the sequential-mode consistently provided more accurate respiratory motion information than the cine-mode, independent of patients’ breathing irregularity.

Differences between sequential and cine image acquisitions also include the total image acquisition time. In our comparison study, the image acquisition time settings are based on the published 4D-MRI image sorting and reconstruction methods,^25,27 and to meet the DSC of 4D-MRI image acquisition. For example, assuming a frame rate of 2 Hz for image acquisition and 30 slices to be imaged, the total image acquisition time for sequential mode would be approximately 20 repetitions × 30 slices × 1/2 Hz = 300 s, where the number of repetitions (20) is estimated based on our previous work²⁵ to ensure data sufficient condition was met. On the other hand, under the same condition, the total image acquisition time for cine-mode would be approximately 8 s/slice × 30 slices = 240 s, where 8 s/slice is the cine duration per slice that was set to be slightly greater than the typical period of breathing cycle (3–7 s) to ensure all respiratory phases can be acquired for each slice.

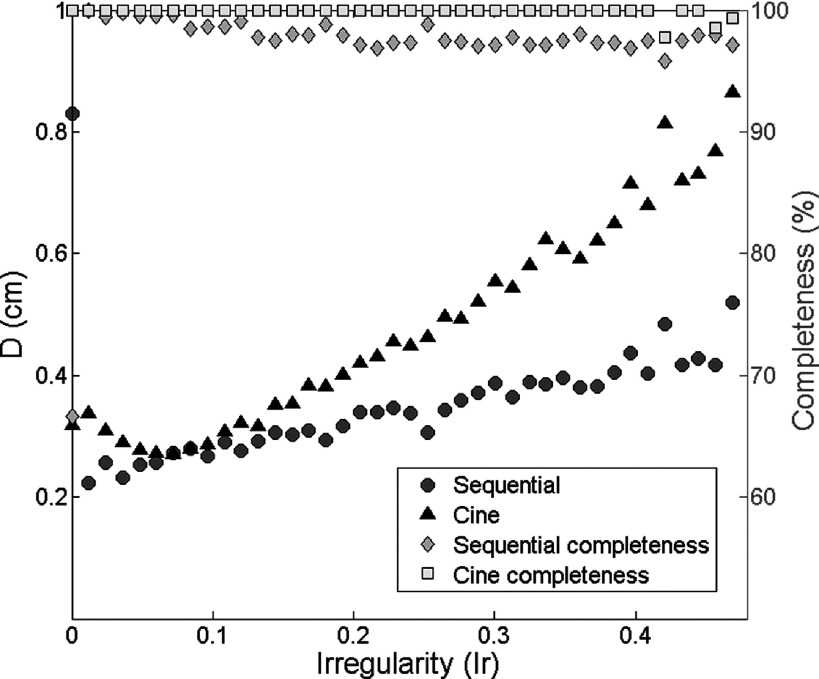
However, it is worth to investigate the 4D-MRI techniques’ performances when the image acquisition time is the same using the two image acquisition modes. One additional simulation study using the 500 pure simulated breathing profiles with different Ir was conducted. The image acquisition time for each slice location with cine image acquisition mode was extended to 10 s, and the time settings for sequential image acquisition mode were kept. The results are shown in Fig. 12. Compared to Fig. 10, the comparison results between cine-mode and sequential-mode are almost the same. D_cine is still consistently larger than D_seq, and D_cine increases faster as Ir increases than D_seq.

FIG. 12.

Relationship between D and Ir for cine-mode and sequential-mode image acquisition in the additional simulation study. The image acquisition time for each slice location with cine image acquisition mode was extended to 10 s, and the time settings for sequential image acquisition mode were kept.

It can be noticed that TR, TE, sequence, tumor size, and image SNR will affect the comparisons. It will be ideal to include all factors for a complete study. However, these factors are basic imaging parameters and are not 4D-specfic factors. What is more interesting from the 4D perspective is that to understand how the performances of the 4D-MRI techniques are influenced by respiratory motion variation, which is the focus of the current study. It will be of great interest to study the effects of these factors on 4D-MRI image quality in our future clinical trials.

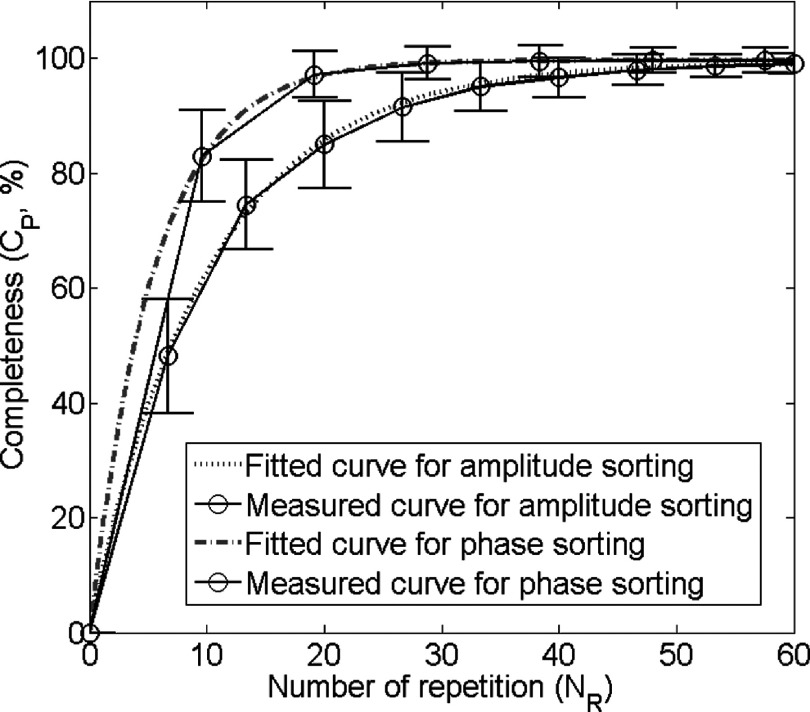
In our study, only phase-sorting method was applied and investigated. Although amplitude-sorting is also an important sorting method, it was not included because it cannot be applied to the two 4D-MRI techniques investigated in this study. For the 4D-MRI technique with cine acquisition,²⁷ a novel image-based respiratory surrogate, the body area, was employed in the original study. It does not provide consistent amplitude information between slices as its value reflects patient’s anatomical size, not breathing amplitude. Therefore, amplitude-sorting cannot be applied. For the 4D-MRI technique with sequential acquisition,²⁵ we employed a result-driven phase-sorting technique in the original study. This sorting method was used, as an oppose to the amplitude-sorting, due to its superiority in imaging time. Figure 13 shown below compares the data completion curves for the sequential 4D-MRI technique using phase-sorting and amplitude-sorting. It can be seen that in order to achieve at least 95% of data completion (which was approved to be sufficient for 4D-MRI reconstruction), 19 repetitions are needed in the phase-sorting method and 36 repetitions are needed in the amplitude-sorting method. Since phase-sorting significantly reduce imaging time, it is selected for the sequential 4D-MRI technique. For the above described reasons, although studying amplitude-sorting is a relevant topic, it has minimal practical meaning as the two 4D-MRI techniques do not use amplitude-sorting in reality.

FIG. 13.

Completeness curves measured and fitted using phase-sorting method and amplitude-sorting method. This is the simulation result using 29 patients’ RPM breathing traces. Gray straight lines show that in order to achieve data sufficient condition for 4D-MRI reconstruction, about 19 repetitions are needed using phase-sorting method, while about 36 repetition are needed using amplitude-sorting method.

It is worth mention that with sequential image acquisition, it is possible to further improve 4D-MRI motion measurement by removing data points of high irregularity from the dataset for 4D-MRI reconstruction. This can be realized by setting an irregularity filter above which the corresponding data points will be discarded for reconstruction. For a given breathing profile, we can calculate the average breathing curve and compare its period and amplitude with that of each individual cycle. To generate 4D-MRI with less breathing irregularity, only MR images that satisfy the following condition will be used:

$${\displaystyle \left\{\begin{array}{c}\hfill \left|\frac{A}{\overline{A}}-1\right|<\text{threshold}\hfill \\ \hfill \left|\frac{T}{\overline{T}}-1\right|<\text{threshold}\hfill \end{array}\right.,}$$ (2)

where A and T represent the amplitude and the period of an individual cycle, and $\overline{A}$ and $\overline{T}$ are the average amplitude and the average period of the whole breathing curve. The threshold can be preset to control the ratio of period and amplitude for each individual cycle with average breathing curve, as shown in Fig. 14. If the threshold is too small, most of the data will be filtered out, leading to insufficient data for 4D-MRI reconstruction. If the threshold is too large, filtering effect becomes less obvious. As an example, we tested a breathing irregularity threshold of 80% in the 4D-MRI reconstruction of the 20 patients’ XCAT simulation study. As a result, E_seq was found to decrease by 10% as compared to that without irregularity filter. These preliminary results implied that the motion measurement accuracy of 4D-MRI might be further improved in the sequential-mode 4D-MRI by selectively removing data points of high irregularity.

FIG. 14.

Illustration of breathing irregularity filter for sequential image acquisition.

It should be noted that the irregularity filter method as described above can only be applied to the sequential-mode, but not to the cine-mode. As shown in Fig. 1, the cine-mode acquires all phase images continuously at one slice location before moving to the next slice location. Filtering out an irregular breathing cycle in the cine-mode means removing all MR images at the corresponding slice location, leading to incomplete 4D-MRI reconstruction. Capability of applying irregular filter is a unique feature and an advantage of the sequential-mode 4D-MRI as compared to the cine-mode 4D-MRI.

There are some limitations of this study. First, the 4D image quality was evaluated only in the SI direction. There are many other metrics that can be used to comprehensively evaluate respiratory motion accuracy demonstrated on 4D-MRI, for instance, tumor motion in other directions and tumor volume variation during respiratory motion. Second, we only evaluated the respiratory motion accuracy of 4D-MRI. We did not assess other aspects of 4D-MRI image quality, such as tumor contrast and target volume. The usefulness of 4D-MRI relies on its good performances in all of these aspects, and therefore we should clarify that this study only demonstrated that sequential-mode is superior to the cine-mode only in terms of motion accuracy and not the overall image quality which is yet to be determined. A more comprehensive comparison in 4D-MRI image quality between sequential-mode and cine-mode will require a carefully designed patient study.

5. CONCLUSION

Compared to the conventional cine-mode 4D-MRI, the sequential-mode 4D-MRI may provide more accurate motion measurement and is less susceptible to breathing irregularity.