Optimizing swept-tone protocols for recording distortion-product otoacoustic emissions in adults and newborns

Abstract

Distortion-product otoacoustic emissions (DPOAEs), which are routinely used in the audiology clinic and research laboratory, are conventionally recorded with discrete tones presented sequentially across frequency. However, a more efficient technique sweeps tones smoothly across frequency and applies a least-squares-fitting (LSF) procedure to compute estimates of otoacoustic emission phase and amplitude. In this study, the optimal parameters (i.e., sweep rate and duration of the LSF analysis window) required to record and analyze swept-tone DPOAEs were tested and defined in 15 adults and 10 newborns. Results indicate that optimal recording of swept-tone DPOAEs requires use of an appropriate analysis bandwidth, defined as the range of frequencies included in each least squares fit model. To achieve this, the rate at which the tones are swept and the length of the LSF analysis window must be carefully considered and changed in concert. Additionally, the optimal analysis bandwidth must be adjusted to accommodate frequency-dependent latency shifts in the reflection-component of the DPOAE. Parametric guidelines established here are equally applicable to adults and newborns. However, elevated noise during newborn swept-tone DPOAE recordings warrants protocol adaptations to improve signal-to-noise ratio and response quality.

I. INTRODUCTION

Distortion product otoacoustic emissions (DPOAEs) are evoked when two or more pure tones are presented simultaneously to the ear; intermodulation distortion generated around the overlap of waves evoked by the primary tones travels back into the ear canal where it is measured by the microphone, amplified, and averaged. DPOAEs are used routinely for the assessment of cochlear function and hearing in auditory experiments with humans and laboratory animals, most notably, transgenic mice. They are also integrated into the standard audiologic test battery in the hearing clinic as they provide a noninvasive metric of nonlinearity—a hallmark of the healthy cochlea—and a remote probe of outer hair cell integrity. In humans, DPOAEs are roughly associated with audiometric threshold (Gorga et al., 1993); the greater the hearing loss, the more reduced the DPOAE, and once hearing thresholds exceed a moderate degree of sensorineural hearing loss, they become unmeasurable at most stimulus levels. DPOAEs have become ubiquitous in the laboratory and hearing clinic as well as a staple of neonatal hearing screening programs.

A. Dual source DPOAE

We now understand that lower sideband DPOAEs (those generated at frequencies lower than the primary tones that evoke them) include at least two components, nonlinear distortion and linear reflection. Distortion is generated at the overlap of the waves evoked by the primary tones and travels both back to the ear canal and also apicalward to its characteristic frequency place (e.g., 2f₁–f₂); here, energy is thought to be backscattered off of naturally existing mechanical irregularities and reflected back toward the stapes (Shera and Guinan, 1999). In the ear canal, the vector sum of these two components—distortion and reflection—produces the total DPOAE commonly utilized in the audiology clinic and laboratory (Shera and Guinan, 1999; Talmadge et al., 1999; Knight and Kemp, 1999, 2000, 2001; Kalluri and Shera, 2001).

Because the two DPOAE components have different delays, the total DPOAE shows quasi-periodic frequency fine structure, reflecting the alternating constructive and destructive interference between these components. The distortion component is typically the dominant contributor to the DPOAE under most common protocols (i.e., moderate-high levels and f₂/f₁ ≈ 1.22). However, if stimulus parameters are strategically chosen to maximize the strength of cochlear reflections, fine structure becomes pronounced because interference is increased. DPOAE fine structure can be problematic when frequencies are chosen arbitrarily for hearing assessment or study because the tester does not know whether the measured emissions fall at minima or maxima in the spectrum. Ideally, one would record DPOAEs with the needed resolution to select test and analysis frequencies carefully so as to define each ear's characteristic fine structure pattern, including its periodicity, which may provide clues about cochlear health (Reuter and Hammershøi, 2006; Abdala and Dhar, 2012; Poling et al., 2014).

Achieving sufficient resolution to define DPOAE fine structure requires excessive time if using conventional data collection schemes. Measuring DPOAEs at closely spaced frequencies is impractical and prohibitive if done with sequential primary-tone pairs presented at discrete frequencies. The alternative to this standard mode of OAE stimulus presentation is to employ tones the frequencies of which are swept continuously rather than being presented one at a time.

B. Swept-tone OAEs

Paradigms using swept-tones to evoke OAEs have been studied and developed over the last decade (Choi et al., 2008; Long et al., 2008; Bennet and Özdamar, 2010; Kalluri and Shera, 2013). Tones are swept upward or downward in frequency continuously at a specified rate, and post hoc analysis of the signal recorded at the microphone is conducted to produce estimates of emission amplitude and phase. The analysis used to compute these estimates from swept-tone OAE recordings varies. Choi and colleagues (2008) applied a digital heterodyne method, which was based on discrete Fourier transform and involves spectral shifting of the stimulus-frequency otoacoustic emission (SFOAE) and low-pass filtering. A traditional application of Fourier analysis has also been applied to swept-tone OAEs and, perhaps more commonly, a modeling technique using least-squares-fitting (LSF) (Long et al., 2008; Kalluri and Shera, 2013). Kalluri and Shera (2013) compared these three analysis techniques for producing estimates of SFOAE amplitude and phase and determined that although digital heterodyning and Fourier analysis were computationally more efficient, the LSF was less vulnerable to noise and artifacts in the measured waveform. Unlike the other two methods, the LSF uses prior knowledge to generate a model for the OAE and how it varies across time (Kalluri and Shera, 2013).

The LSF technique is typically applied to the average of many sweeps measured in the ear canal (Long et al., 2008; Kalluri and Shera, 2013); however, in this study, we modified the analysis procedure to apply LSF to each sweep and then take the complex average of all sweep-based estimates to get the DPOAE estimate. To apply LSF modeling, the time waveform recorded at the microphone is segmented into chunks or analysis windows, and models for the primary tones (f₁, f₂) and the DPOAE (e.g., 2f₁–f₂) are created. Signals within specified analysis windows are then determined by LSF fitting, which minimizes the sum of the squared residuals between the model and the data. The LSF analysis can be thought of as a moving bandpass filter with varying center frequencies that correspond to the frequency of the OAE (Long et al., 2008).

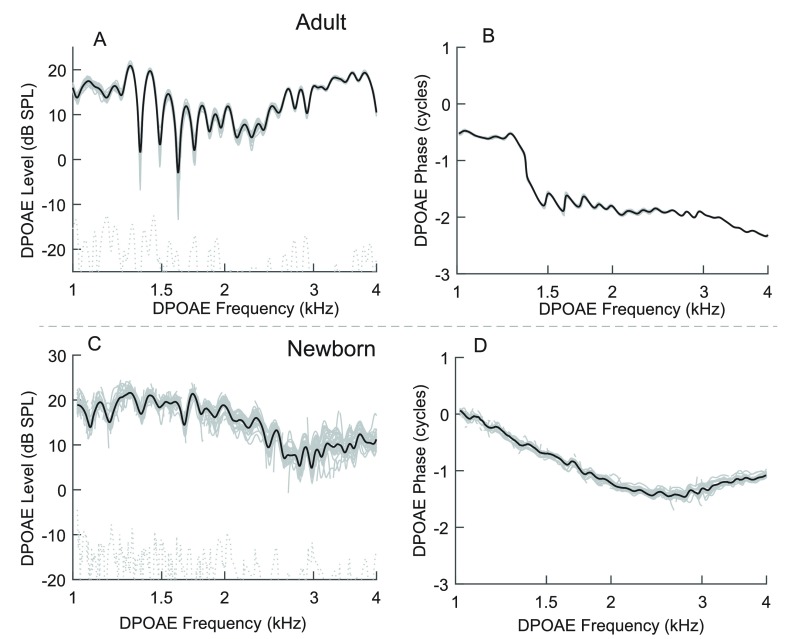
OAEs evoked with swept tones and analyzed with an LSF technique produce estimates of amplitude and phase that are similar to those generated with discrete tones (Long et al., 2008; Kalluri and Shera, 2013; Abdala et al., 2015). The data collection, however, is much more efficient and rapid, and resolution is unparalleled because one can analyze the sweep at any desired frequency to produce OAE estimates. The black line in Figs. 1(A) and 1(C) show examples of average DPOAE spectra from one adult and one newborn ear (including ∼640 points across frequency) derived from swept-tone presentation and LSF analysis. The definition of the DPOAE fine structure is outstanding, and phase ambiguities are easily resolved with this degree of frequency resolution.

FIG. 1.

(A) and (B) DPOAE recorded with swept tones and analyzed in one adult ear (sweep rate: 0.5 octave/s, analysis-window duration: 125 ms). The thin gray lines represent DPOAE level and phase estimates from each of 24 individual sweeps. The thicker black line is the complex average derived from the individual sweep-based estimates. The noise floor is shown as dotted light gray. (C) and (D) DPOAE from one newborn ear recorded and analyzed in the same way as described for the adult ear, however, with more sweeps (n = 32). The thin gray lines in all panels depict the variance of repeated DPOAE estimates within an ear and provide a measure of intra-subject response stability.

Parametric study of optimal sweep rates and analysis-window durations for recording DPOAEs over a broad frequency range has not been conducted in adults and newborns. The precision of the LSF technique for estimating amplitude and phase of the total DPOAE (both components together) depends on selecting appropriate combinations of sweep rate and analysis-window durations for least squares fitting. For example, if the analysis window is too long for the sweep rate employed, the reflection component of the DPOAE is missed in the LSF modeling and the estimated total DPOAE will consist mostly of nonlinear distortion (Long et al., 2008; Long et al., 2009; Abdala et al., 2015). Conversely, if the LSF analysis window is too short, the uncertainties in the model and the reliability of the fit suffer (Kalluri and Shera, 2013). Hence proper analysis parameters are crucial to successful recording of swept-tone DPOAEs.

Once the optimal parameters for OAE swept-tone presentation and LSF analysis are defined and the effect of manipulating these parameters on the resulting OAE estimates well understood, there appears to be no obvious benefit in using discrete tones for measuring OAEs to assess hearing at only a handful of frequencies. The conventional discrete-tone methods slow down OAE recording, making it less likely to obtain sufficient SNR for reliable measurement, in particular when challenging populations are being tested such as newborns. Swept-tone OAE protocols are particularly useful for the neonatal population (Abdala and Dhar, 2010, 2012; Abdala et al., 2013; Abdala et al., 2014), which sometimes offers limited moments of quiet recording time and produces elevated and erratic noise.

This study tests the key parameters that must be selected when measuring DPOAEs via swept tones and analyzing them with LSF-based techniques. We establish an optimal set of values that allows for the capture and accurate estimate of the total DPOAE, including both distortion and reflection energy. The conceptual underpinnings of the DPOAE swept-tone method have been described in the initial development of the method (Long et al., 2008), but evaluation across a broad parametric space has not been undertaken and the impact of parametric manipulation across frequency and age has not been explored. In this study, we (1) use multiple outcome measures and statistical tests to study the effect of combined changes in rate and LSF analysis-window duration, (2) determine how parameters must be adjusted with frequency to accommodate latency shifts in the reflection component of the DPOAE, and (3) include neonates to determine whether the optimal parameters for this group are similar to those specified for adults.

II. METHODS

A. Subjects

Subjects were 15 normal-hearing young adults (mean age = 21.2 yr; range = 18–29 yr) and 10 healthy term neonates (mean gestation = 39 weeks) tested between 24 and 72 h after birth. The adult group included 2 males and 13 females; 11 right and 4 left ears, all with audiometric thresholds <15 dB hearing level (HL) and no history of ear disease. Newborn subjects passed a routine hearing screening with a click-evoked auditory brain stem response at 35 dB HL. They included four males and six females, four right and six left ears. Mean 1- and 5-min APGAR scores, which are indicators of neonatal health at birth, were 8.8 and 9 (on a scale of 1–10). Average newborn birth weight was 3148 g (6.94 lbs).

B. Instrumentation and DPOAE protocol

Signals were generated and DPOAEs recorded using an Apple MacBook Pro laptop controlling a MOTU 828 mk II audio device (44.1 kHz, 24 bit). The output of the MOTU was appropriately amplified and fed to Etymotic Research ER-2 insert phones coupled to the subjects' ears through the sound tubes of an Etymotic Research ER10B+ probe microphone assembly. The output of the microphone was pre-amplified and passed through an analog high-pass filter with 300-Hz cutoff frequency before being digitized by the MOTU and stored on disk.

Newborns were tested within a sound-attenuated isolette (Eckles ABC-100) providing between 25 and 40 dB attenuation in the Infant Auditory Research Lab within the Neonatology Ward of LAC+USC hospital. Newborn testing was always conducted by a pair of researchers: one attending to the newborn throughout the entire test, watching for movement and probe slippage, while the other implemented the data collection protocol. DPOAEs were recorded with primary tone levels L₁,L₂ of 65,65 dB sound pressure level (SPL) at a fixed primary frequency ratio, f₂/f₁, of 1.22. The primary frequencies were swept upward logarithmically at rates, r, of 1, 0.5, 0.125 octave/s for DPOAEs from 1 to 4 kHz and 0.5, 0.125, and 0.0625 octave/s for DPOAEs from 4 to 8 kHz.¹ Sweep rates were changed after every pair of sweeps and were presented in a pseudo-random order with a 1-s pause between presentations.

Calibrated stimuli were delivered to each subject's ear after estimating the depth of probe insertion from the half-wave resonance in the ear canal. Associations between half-wave resonance and insertion depth were established earlier in a coupler. Based on individual estimates of probe-insertion depth, we selected the best filter to approximately equalize level across frequency at the tympanic membrane (Lee et al., 2012). This calibration technique allowed us to reduce the effect of ear-canal standing waves, which can lead to erroneous estimates of stimulus level for high-frequency stimuli. In newborns, standing-wave errors are less problematic below 6–8 kHz because the ear canal is shorter than the adult canal (Abdala and Keefe, 2012). To expedite testing with newborns, the measurement of the half-wave resonance peak was conducted in 20 newborn ears a priori and found to be 9600 Hz; hence, the corresponding filter was applied to all infant subjects.

Adult ears were presented with 24 frequency sweeps at all but the slowest sweep rates (0.125 and 0.62 octave/s) where 16 sweeps were presented; infant ears were presented 32 sweeps at all but the slowest sweep rates where 24 sweeps were presented. In some analyses of the impact of doubling the number of sweeps contributing to each average, fewer sweeps were included in DPOAE estimates. Each adult subject was tested in all sweep-rate and frequency conditions whereas only two of the newborn subjects contributed to both low- and high-frequency segments. The other eight newborns contributed either low- or high-frequency data, producing a total of six newborn ears in each condition.

For a subset of nine adult subjects, DPOAEs were also recorded in the more traditional manner using pure tones presented at discrete frequencies and analyzed with a conventional FFT. The discrete-tone and swept-tone measures were always taken during the same test session, using the same probe fitting and counter-balanced presentation. For discrete-tone recording, we presented primary tones in three frequency segments: 1–1.5, 2–3, and 4–6 kHz with 0.005 octave step resolution (∼110 points per segment). Discrete-tone DPOAEs were recorded for 4 s per data point and a 0.5 s pause between points with the same primary levels and f₂/f₁ ratio as the swept-tone OAEs.

DPOAE phase at 2f₁–f₂ was corrected for phase variation of the primaries by subtracting 2ϕ₁–ϕ₂, where ϕ_1,2 are the measured phases of the stimulus tones at f_1,2. Phase was then unwrapped by sequentially adding appropriate multiples of ±360° to all points.

C. Analysis

1. Least squares fitting

DPOAE level and phase estimates were obtained using a LSF algorithm. Recall that in the LSF technique, models for the primary tones and DPOAE of interest are fit to the microphone signal by minimizing the sum of the squared residuals between the model and the data (Long et al., 2008; Kalluri and Shera 2013). The noise floor is estimated by taking the difference between adjacent sweep pairs and applying the LSF to this difference trace.

The LSF is conducted on small chunks of overlapping Hann-windowed data with specified duration. The analysis-window duration specifies the length of the segment modeled to derive estimates of the DPOAE. In this study, we applied analysis windows with durations Δt = 31, 62, 125, 250, and 500 ms with a constant step size of Δt/20. These various windows were paired with sweep rates, r = 1, 0.5, 0.125, and 0.0625 octave/s and the optimal parameters for DPOAE measurement determined using the outcome variables specified in Sec. II C 4. OAEs < 4 kHz were recorded with r = 1, 0.5 and 0.125 octave/s rates and OAEs > 4 kHz recorded with r = 0.5, 0.125 and 0.0625 octave/s rates. The analysis-window duration multiplied by the sweep rate gives an indication of the bandwidth of frequencies represented in each LSF analysis window, termed here analysis bandwidth or BW. For example, a 0.5 octave/s rate paired with Δt = 125 ms results in an analysis bandwidth of approximately 0.06 octave (0.125 s × 0.5 octave/s = 0.0625 octave).² For any given rate, r, the analysis-window duration, Δt, must be chosen to specify the target analysis bandwidth that will capture the total DPOAE.

2. Artifact rejection

We did not implement a real-time automated artifact rejection. For both adult and newborn data collection, the tester watched the time waveform recorded at the ear canal microphone on the monitor and if a spike was noted, the recording was paused by the tester and the entire sweep was aborted. A new sweep was initiated once subject state was appropriate. This scheme was inefficient because entire sweeps (of up to 24 s) could be discarded due to one transient spike.

A post hoc artifact rejection was implemented based on the noise floor. We eliminated any DPOAE level estimate whenever (1) the noise estimate exceeded 5 dB SPL and (2) the OAE estimate deviated from average DPOAE level by more than 3 dB. If more than half of the points in any given DPOAE sweep were eliminated by this process, the entire sweep was deleted from the data set. Only 5% of newborn sweeps were eliminated under this criterion; no adult sweeps were eliminated. An additional SNR criterion was applied to the data requiring the DPOAE level be at least 3 dB above the noise floor. (Note that actual SNRs were usually much better than this relatively liberal criteria as reported in Sec. III; this criterion was implemented so as to retain points reflecting minima in fine structure which are nearer the noise floor.) Once the combined artifact-rejection and SNR criteria were implemented, 70% of data points from the newborn group and 90% from the adult group remained for analysis.

3. Intra-subject standard error of the mean (SEM)

To obtain a robust average DPOAE, it is necessary to present multiple sweeps. We exploited this requirement to calculate intra-subject repeatability. Rather than apply the LSF to the average recorded signal (averaged from 16 to 32 sweeps), we applied LSF to each sweep individually to generate multiple estimates of the complex DPOAE pressure. The levels and phases of these individual pressures are shown by the thin gray lines in Fig. 1; the black lines show the level and phase of the final DPOAE pressure, obtained as the complex average of the individual estimates. At each frequency, we then calculated the standard error of the mean DPOAE (SEM) for each individual ear.³ The intra-subject SEM provides a metric of test-retest reliability and an overall indicator of the quality of the average. The lower the value of the intra-subject SEM, the lower the variation among individual sweep estimates contributing to the DPOAE; hence, the more stable the estimate.

4. Outcome measures

We examined the impact of changing recording and analysis parameters (such as the sweep rate, analysis-window duration, OAE frequency, and the number of sweeps contributing to an average) on DPOAEs recorded from adults and newborns. To determine optimal parameters, four outcome measures were calculated: (1) the match between gold-standard discrete-tone DPOAEs and swept-tone DPOAEs, (2) inter-subject variability or scatter of DPOAE level data as measured in standard deviations, (3) DPOAE noise floor and signal-to-noise measures, and (4) intra-subject variability as measured by the standard error of the mean and 95% confidence intervals (as described in the preceding text). By employing these measures, we were able to determine the swept-tone parameters that produced the most valid DPOAEs (re: conventional DPOAE measures), the tightest data set among subjects, the most reliable data within a subject, and the data with the best SNR. Additionally, we have provided a basic comparison of the test time required to produce comparable estimates of the DPOAE using conventional discrete-tone DPOAE measurements versus swept-tone measurements.

III. RESULTS

A. Data quality

DPOAE data showed excellent noise immunity. Adult group mean SNR calculated as the difference between average DPOAE levels and noise floor binned into third-octave intervals ranged from 18 to 30 dB across frequency with no single SNR measure for any one adult subject showing <12 dB. In newborns, group mean SNR ranged from 16 to 28 dB across frequency with no single value for any one neonate showing <11 dB. These DPOAE levels are generally within the range reported for adults and newborns using similar methodology (Abdala and Dhar, 2010, 2012). Average adult DPOAE levels ranged from 1 to 12 dB SPL across frequency while newborn DPOAE levels ranged from 3 to 15 dB SPL, resulting in ∼3 dB higher mean DPOAE amplitude in newborns compared to adults.

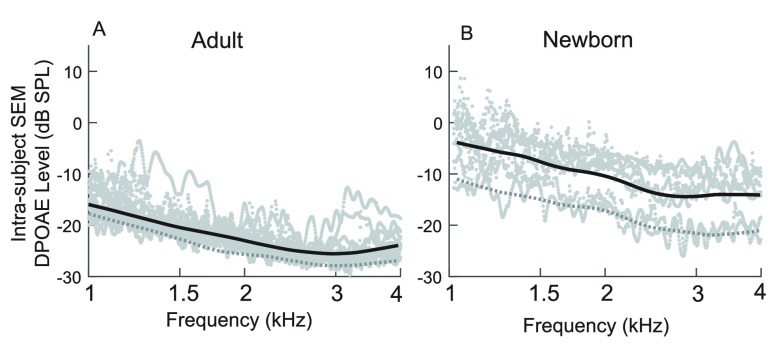
We calculated intra-subject stability of DPOAE level averages by assessing the repeatability of individual sweeps within the average. As described in Sec. II (and shown in Fig. 1), we applied the LSF to each sweep rather than the average, allowing us to calculate a within-ear standard error of the mean (SEM) by analyzing variance among the sample of sweeps. Figure 2(A) provides the individual intra-subject SEM calculated in pressure and converted to dB SPL for each adult (gray dots) and a loess line showing the central tendency for the group. Figure 2(B) displays these same data for newborns.

FIG. 2.

The standard error of mean (SEM) for adult and newborn estimates of DPOAE level. This intra-subject SEM was calculated for all subjects from repeated sweep-based estimates [see Figs. 1(A) and 1(C)], first in pressure and then converted to dB SPL. This procedure allows for a measure of within-ear stability and provides a metric of response quality for each subject. The group SEM was determined by fitting a loess trend line to the individual functions; it approximates group-noise floor measurements, which are shown as dotted lines. In adults, the group noise floor is within a few dB of the calculated intra-subject SEM. In newborns, within-ear variability is greater than in adults and the SEM is notably higher than the group noise floor suggesting other sources of variance.

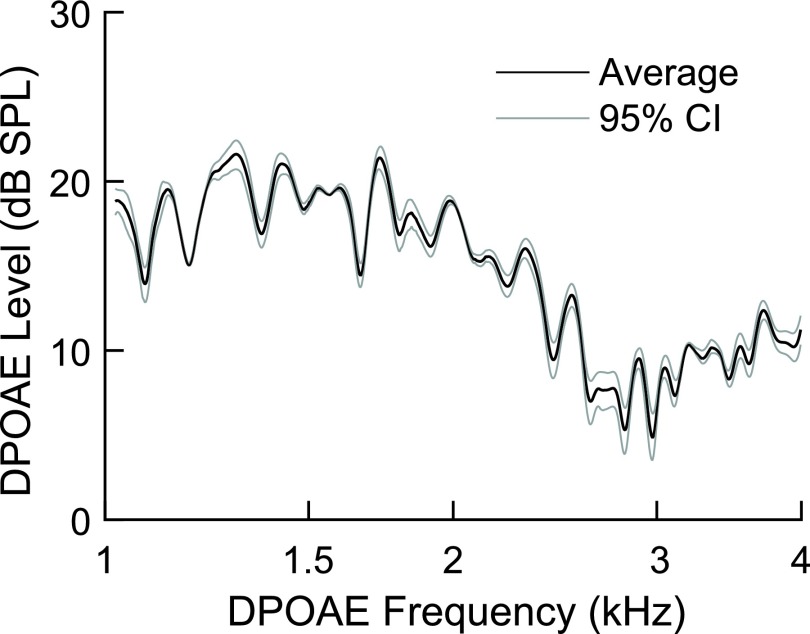
Intra-subject SEM were converted to 95% confidence intervals in Fig. 3 for one newborn ear. DPOAE level is shown as a thick black line with 95% CIs (thin lines) plotted around the mean. One clear observation from Figs. 2 and 3 is that the responses are more stable in adult ears where the SEM ranges from −12 to −25 dB SPL across frequency and approximates the average group noise floor, which is shown by a dotted line. In newborns, the intra-subject SEM ranged from −4 to −15 dB. Also, more outliers were noted among individual ears, suggesting that DPOAEs for any given newborn were less repeatable than in an adult ear. For adult subjects, the match between the group SEM and measured noise floor indicates that the errors in DPOAE calculations were explained by measurement noise and not a systematic undetected source. This suggests repeatable data and good intra-subject stability in our adult subjects. In newborns, the match was not as close, suggesting that in addition to the measured noise floor, other variability exists which influences the DPOAE estimates. Newborn data are known to be less stable in general and show elevated noise (Abdala and Dhar, 2012).

FIG. 3.

Intra-subject SEM measures provide a metric of response quality or test-retest reliability within an ear and can be converted into 95% confidence intervals (CI) around the complex average. As an example, sweep-based CIs are shown here for DPOAEs recorded in one newborn ear.

B. The effect of LSF analysis-window duration on DPOAE estimates

Figure 4 displays DPOAE phase and level fine structure in one adult (AB) and one newborn (CD) ear to illustrate the trends in data with a fixed sweep rate, r = 0.5 octave/s, and five different values of the analysis-window duration, Δt. We can see that the longest LSF analysis windows, 250 and 500 ms, reduced DPOAE fine structure and smoothed the response excessively. This pattern was observed for all adult and neonatal subjects tested. Long LSF windows broaden the bandwidth of frequencies included in the fit and consequently produce spectral smoothing. With a fixed sweep rate, the duration of the analysis window, Δt, determines the band of frequencies analyzed for any given fit. The bandwidth of frequencies represented for each Δt is shown by the horizontal bars (plotted re: the frequency axis) in Fig. 4(A). The smoothing produced by long windows reduces DPOAE fine structure because it effectively eliminates the reflection component from the estimated DPOAE.

FIG. 4.

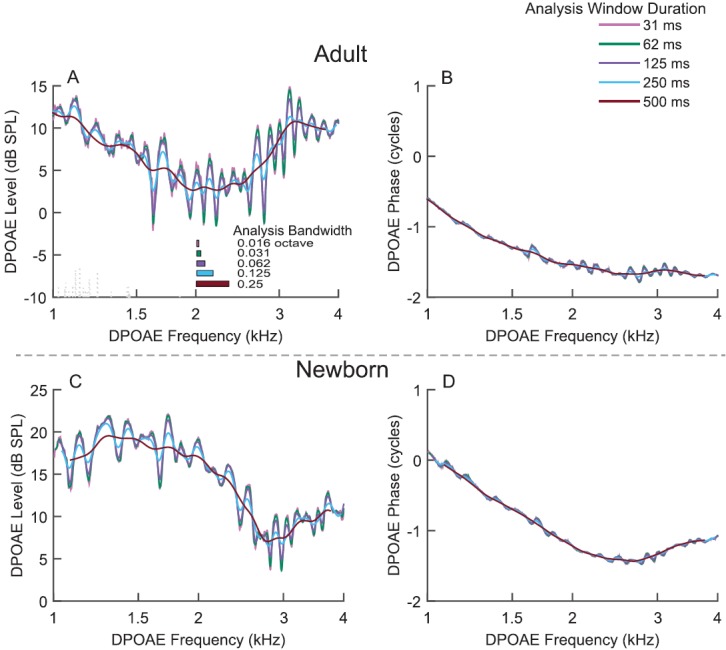
(Color online) DPOAE level and phase recorded with a fixed sweep rate of 0.5 octave/s and analyzed with five analysis-window durations in one adult and one newborn subject. The longer windows smooth the DPOAE excessively and do not preserve fine structure. The shortest window produces additional oscillations riding atop the larger fine structure. Both 62 and 125 ms preserve DPOAE fine structure well and appear to be optimal analysis windows for this sweep rate. The analysis bandwidth associated with each window condition is shown by the length of the horizontal bars plotted near the frequency axis; the longer the window, the broader the bandwidth (and the smoother the DPOAE).

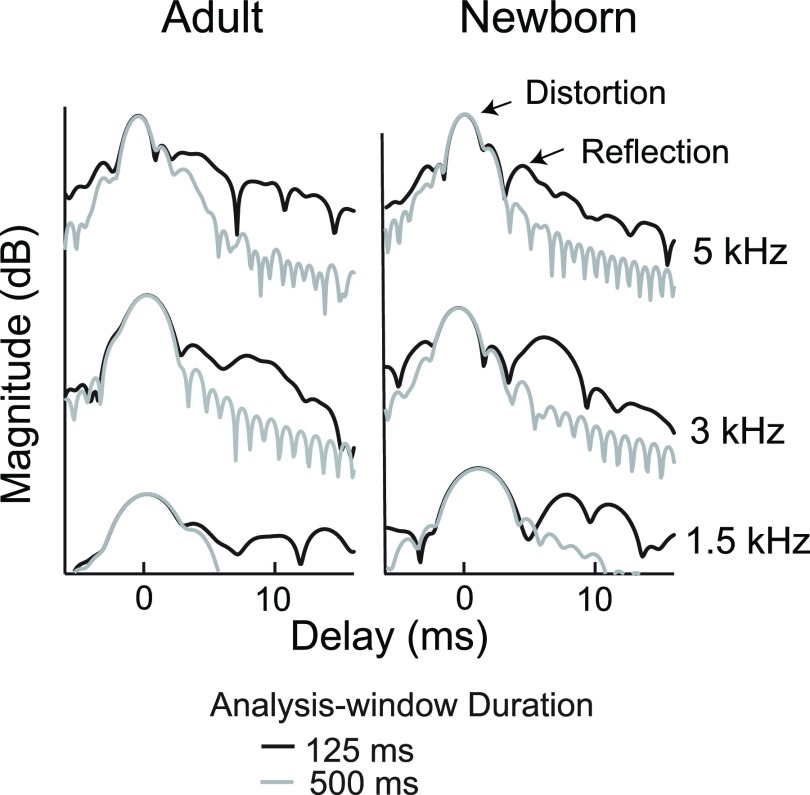
Figure 5 further explicates this effect in the time domain. Segments from an inverse FFT analysis centered at 1.5, 3, and 5 kHz are shown for one adult and one newborn ear. The black lines represent DPOAEs recorded with fixed r = 0.5 octave/s and Δt = 125 ms. A relatively large short-latency lobe, the distortion component of the DPOAE, is evident as is a smaller reflection component around 5–10 ms. The gray lines are DPOAEs recorded with the same sweep rate but analyzed with a long analysis window of 500 ms. This condition leaves the distortion component unchanged while eliminating reflection energy. The result is that DPOAE estimates are increasingly dominated by distortion.

FIG. 5.

Time-domain analyses of DPOAE in one adult and one newborn ear for three frequency segments. The longer analysis windows smooth the total DPOAE by eliminating contributions from the reflection component as shown in these exemplars. The large dominant lobe around 0 ms is the distortion component of the total DPOAE and is equally present for analyses with both a short (125 ms) and long (500 ms) window. The smaller lobe noted at ∼5–10 ms is the reflection component of the DPOAE, and its energy is reduced when analyzed with a 500 ms window. The longer window produces spectral smoothing and reduces reflection energy in the DPOAE.

The shortest analysis window applied, 31 ms, not only preserved fine structure but also produced fast oscillations riding atop the larger structure. These oscillations are not informative to the DPOAE estimates we are interested in. They could be noise or could reflect longer-latency multiple internal reflections as many had periods that were close to half of the larger fine structure period. If analysis windows are too short, uncertainties are introduced into the fitting procedure and can make estimates noisy, which may be the case for the 31 ms analysis-window data shown in Fig. 4 (Kalluri and Shera 2013).

The 62 and 125 ms analysis windows preserve DPOAE fine structure best and provide a robust estimate of the total DPOAE. Both analysis windows used in conjunction with r = 0.5 octave/s capture the distortion and reflection components of the DPOAE as noted by the robust fine structure and do not produce excessive smoothing; nor do they include noisy or non-informative oscillations riding atop the larger fine structure. Which of these two acceptable window durations—62 and 125 ms—is best for capturing the total DPOAE and estimating its amplitude? Four outcome measures were applied to address this question. Although both adult and newborn data are shown in each analysis, there were insufficient newborn observations within each of the two frequency conditions to conduct statistical age comparisons. Newborn data are included to display trends in relation to adult data, which were statistically tested to determine optimal parameters.

1. Match with discrete-tone DPOAEs

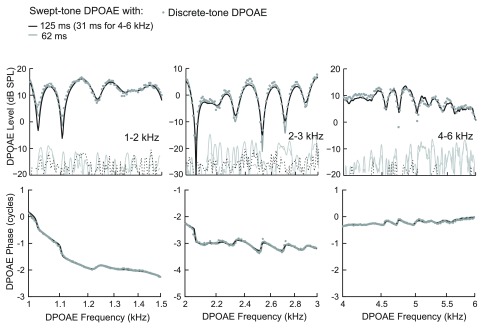
We compared swept-tone (ST) DPOAE level estimates obtained with a fixed rate (r = 0.5 octave/s) and the two analysis-window durations thought to best preserve DPOAE fine structure (62 ms, 125 ms) to DPOAE estimates calculated with standard discrete-tone (DT) presentation and FFT-based analysis in the same ears. This comparison was conducted for adults only because infants did not allow sufficient test time to complete both protocols. ST-DT differences were calculated for both analysis-window durations; the smaller the difference, the more closely the ST result estimated the DT result. Figure 6 shows the ST-DT match for level and phase in one adult ear over three half-octave frequency bands. There was no significant difference in the match for the two windows deemed optimal (note that for the highest frequency segment, the comparison was between 31 and 62 ms analysis windows; the need for high-frequency adjustments are described in the following text). Therefore with fixed r = 0.5 octave/s, no difference was apparent in the accuracy with which either of these two analyses windows approximated the gold standard discrete-tone DPOAE from 1 to 8 kHz.

FIG. 6.

DPOAE level (top panels) and phase (bottom panels) in three half-octave bands for one adult subject. DPOAEs were collected and analyzed using traditional discrete-tone presentation with FFT analysis (small gray dots) and swept-tones with LSF-based analysis and the two optimal window durations: 62 and 125 ms (or 31 and 62 ms for the higher-frequency segment). The swept-tone analysis approximated discrete-tone DPOAE fine structure within a few dB, and the difference in accuracy of the match among analysis-window conditions was statistically insignificant.

The group average DT-ST differences in three frequency segments (1–1.5, 2–3, and 4–6 kHz) were 0.03, 0.08, and 0.31 dB, respectively. In the lower two frequency bands, no subject had greater than 1.1 dB difference between swept and discrete tone DPOAEs. In the higher frequency band, only one of nine adult subjects had a 3 dB difference between swept- and discrete-tone DPOAE level estimates. These values are well within natural test-retest repeatability of DPOAE level as calculated from intra-subject SEM data (Fig. 2). Average 95% CIs for intra-subject variability were 1.5 and 2.5 dB for the low- (1–4 kHz) and high-frequency (4–8 kHz) ranges, respectively, in the adult group. Newborns showed slightly higher intra-subject variability, averaging CIs of ∼3 dB in both low- and high-frequency ranges. These CIs, which define the natural variance within any given subject, equal or exceed the differences calculated between ST and DT estimates of DPOAE level, suggesting a satisfactory match for both 62 and 125 ms analysis-window durations.

2. Inter-subject variability

DPOAE inter-subject variability, as measured with standard deviations (SD) of DPOAE level estimates, is also equivalent for Δt = 62 and 125 ms as confirmed by a one-way analysis of variance (ANOVA) conducted on the adult data (p = 0.87). Newborns showed this same trend. For adults and newborns, both 62 and 125 ms analysis windows produced SDs that ranged from 3 to 6 dB across frequency, confirming the absence of a significant analysis-window duration effect on DPOAE data scatter among subjects.

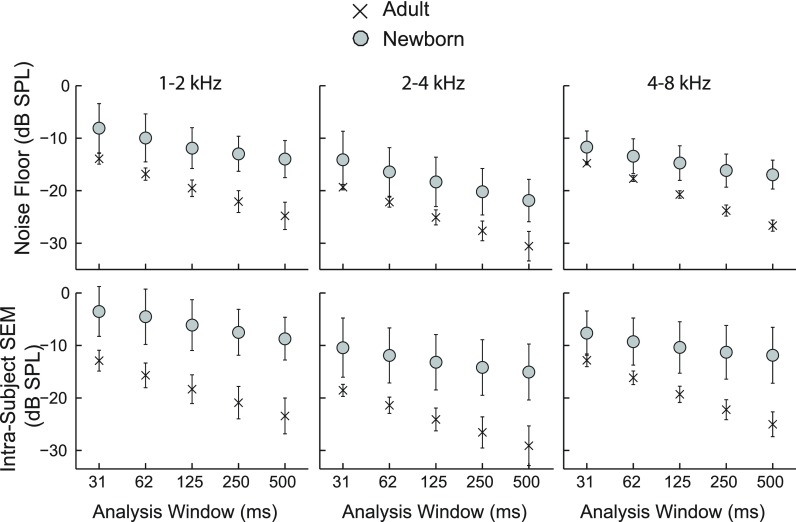
3. Noise floor and SNR

The DPOAE noise floor and SNR were calculated in octave-wide intervals for all Δt values (31, 62, 125, 250, 500 ms) to assess the effect of analysis-window duration on estimates of the noise. The upper panels in Fig. 7 show mean noise floor data for both adults and newborns for the three frequency segments as a function of window duration. As evident, noise floor estimates are reduced as Δt is lengthened. Repeated measures ANOVAs conducted on adult data confirmed a main effect of Δt on both noise and SNR (not shown): 1–2 kHz noise: f = 85, p < 0.0001 and SNR: f = 7.3, p < 0.0001; 2–4 kHz noise: f = 100, p < 0.0001 and SNR: f = 6.5, p = 0.0002; 4–8 kHz noise: f = 531, p < 0.0001 and SNR: f = 6.8, p = 0.0001. This finding suggests that of the two windows best preserving DPOAE fine structure—62 and 125 ms—the longer window is preferable because it produces a reduced noise estimate and enhanced SNR. The doubling of analysis-window duration produced an average “noise reduction” effect of ∼3 dB in adults but only 1–2 dB in newborns. The smaller effect in newborns is a result of our offline artifact-rejection algorithm, which is less effective at eliminating spurious measurements when longer analysis windows are used. (Longer windows tend to smooth out and reduce the effects of artifacts, making them less noticeable and therefore less likely to trigger outright rejection of the buffer.) Because newborns are more prone to artifacts, the reduced rejection rate affected the newborn more than the adult data.

FIG. 7.

The top panel shows the effect of analysis-window duration on DPOAE noise floor. The bottom panel shows the effect of analysis-window duration on intra-subject SEM measures for the adult and neonatal age groups. The longer the analysis window, the lower the noise floor, the better the SNR (data not shown here), and the more stable and repeatable the response within an ear. Error bars represent ±1 standard deviation.

4. Intra-subject repeatability

Intra-subject SEM for DPOAE level were calculated in octave-wide bands for five analysis-window conditions in adult and newborn subjects. The bottom row of panels in Fig. 7 shows that the longer the window, the smaller the intra-subject SEM. Repeated measures ANOVAs conducted on adult data confirm that intra-subject SEM were significantly decreased as analysis-window duration increased (1–2 kHz: f = 34, p < 0.0001; 2–4 kHz: f = 41, p < 0.0001; 4–8 kHz: f = 118, p < 0.0001), indicating that for any given ear, DPOAE data were more stable and the sweeps contributing to the average more repeatable as Δt became longer. However, as we established from data in Fig. 4, the longest analysis windows also eliminate reflection components of the DPOAE. Therefore among those windows that adequately capture the total DPOAE, the longest of them should be used to maximize response stability. Thus for a 0.5 octave/s sweep, Δt = 125 ms is preferable to Δt = 62 ms. This guideline suggests that for the 1–4 kHz frequency range, DPOAEs are optimized if the analysis bandwidth, BW, is kept constant at ∼0.06 octave (0.125 s × 0.5 octave/s). Modifications of this bandwidth guideline will be considered for frequencies >4 kHz. Note that when r is changed, Δt must also be varied to maintain a constant BW; these two parameters should be changed in concert to capture and measure the total DPOAE effectively.

C. Varying sweep rates

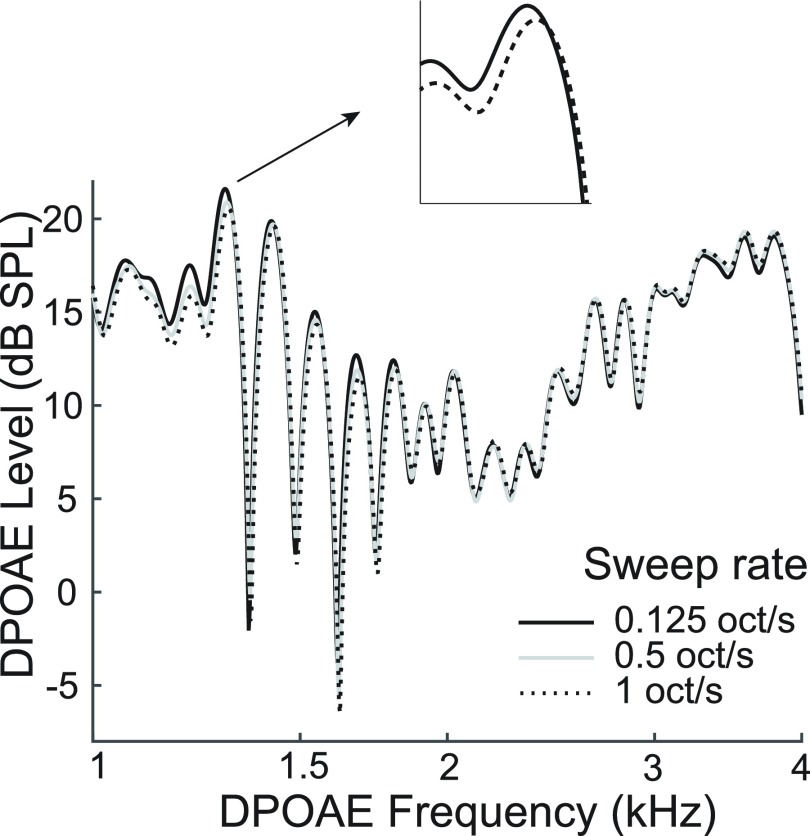
Using BW = 0.06 octave should result in comparable DPOAE estimates regardless of the sweep rate. To test this, we compared DPOAE level and phase measured using three different sweep rates, r. The value of Δt was chosen to maintain the target analysis bandwidth, BW = rΔt (i.e., Δt = 62 ms for r = 1 octave/s, Δt = 125 ms for r = 0.5 octave/s, and Δt = 500 ms for r = 0.125 octave/s). Figure 8 shows representative data from one adult ear illustrating the strong similarity among the DPOAEs measured at the three sweep rates. A repeated-measures ANOVA of the effect of r on adult DPOAE levels (binned into third-octave intervals) found no effect at any frequency. So long as a constant analysis bandwidth is maintained, overall DPOAE estimates are nearly identical, even when rates as fast as 1 octave/s are employed.

FIG. 8.

DPOAE level in one adult ear to illustrate the effect of sweep rate on DPOAE fine structure. (The analysis bandwidth was fixed at 0.06 octaves for each rate and optimal analysis-window durations were applied.) Fine structure peaks often shift as sweep rate is increased from 0.125 to 1 octave/s. The inset magnifies this change for one of these peaks. The average peak shift was 3–7 Hz for adults and 6–12 Hz for newborns, suggesting an effect of sweeping rate on OAE phase.

However, some fine-structure peaks in Fig. 8 shift rightward to slightly higher frequencies as r increases. The inset of Fig. 8 shows a zoomed segment illustrating this shift. Increasing r from 0.125 to 0.5 octave/s yields an average peak shift of ∼3 Hz in adults and ∼6 Hz in newborns, and increasing r from 0.125 to 1 octave/s yields an average shift of ∼7 Hz in adults and ∼12 Hz in newborns. Notwithstanding the constant analysis bandwidth, these results suggest that faster sweep rates induce shifts in the relative phase of the two DPOAE components, whose interference produces the observed fine-structure pattern. Small frequency shifts of this sort have been reported previously, and attributed to shifts in the phase of the reflection component (Henin et al., 2011; AlMakadma et al., 2015).

Sweep rates also affect noise floor estimates when the number of sweeps contributing to the average is kept constant. For faster rates, shorter analysis windows must be used to keep the analysis bandwidth in each window constant. As shown from Fig. 7, the elevation in noise floor and reduction in SNR due to shortening of the analysis window can be as high as 9 dB. Increased noise will require more time to achieve a criterion SNR even though the sweep rate is faster. Therefore, using a 1 octave/s rate, although intuitively the most rapid testing condition, adversely affects noise-floor estimates; the expected benefits of halving the recording time may be negated by the additional averaging required to achieve adequate SNR.

D. High-frequency adjustments

Our finding that an LSF analysis window/sweep rate combination producing an analysis bandwidth of 0.06 octave can be used to optimize DPOAE swept-tone measurements is based on data below 4 kHz. Figure 9 shows DPOAE data recorded with a fixed 0.5 octave/s sweep rate and multiple analysis-window durations for higher-frequency DPOAEs from 4 to 8 kHz. The optimal sweep rate/analysis window combinations (and corresponding analysis bandwidth, BW) for high-frequency DPOAE recordings differ from those required for low-frequency recordings for reasons illustrated by the inset in Fig. 9. The inset displays reflection-source OAE delay measures from two previous studies: the SFOAE delays are shown by a dashed trend line, and delays for the separated reflection component of the DPOAE are shown by a solid trend line, both measured in groups of normal-hearing adults. Past work has shown that these two reflection-source OAEs are basically equivalent (Kalluri and Shera, 2007). Although we are interested in defining optimal strategies to record the total DPOAE, to achieve this goal, we must consider the frequency-dependent phase behavior of the reflection component. The inset of Fig. 9 indicates that delays (measured in periods) from reflection-source OAEs become longer with increasing frequency.

FIG. 9.

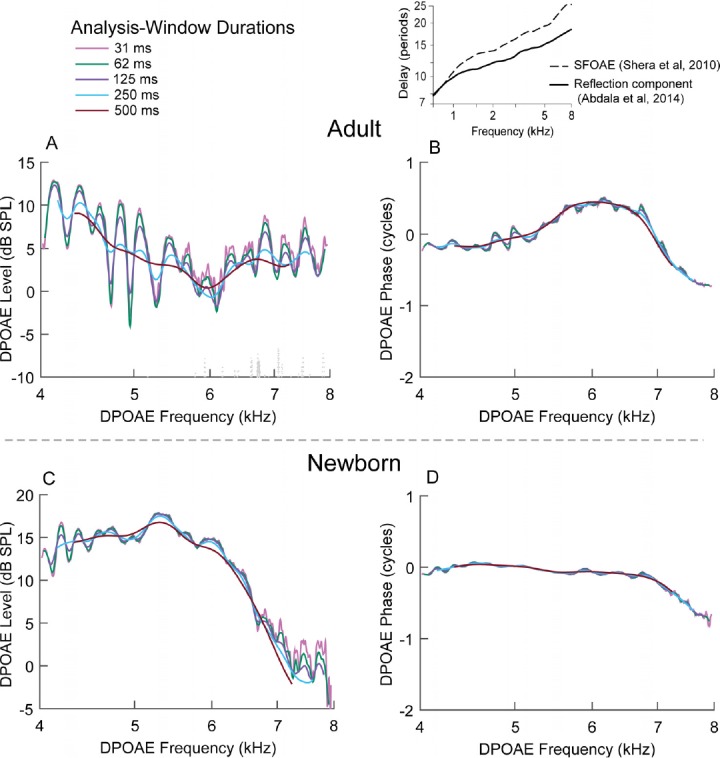
(Color online) The inset displays data from two previous studies showing reflection-component delays (Abdala et al., 2014) and stimulus-frequency OAE delays (Shera et al., 2010) expressed in periods. Both confirm longer delays with increasing frequency. To accommodate the shifting latency of the reflection-component, analysis-window duration (and bandwidth) must change with increasing frequency. (A)—(D) show DPOAE level and phase recorded and analyzed with a fixed sweep rate of 0.5 octave/s and five analysis-window durations in one adult (A) and (B) and one newborn (C) and (D) for frequencies from 4 to 8 kHz. The trends are similar to those shown in Fig. 4 except that shorter analysis windows and narrower bandwidths are required for DPOAEs at higher frequencies. Analysis windows of 31 ms and 62 ms best preserve DPOAE fine structure. Following the convention of using the longest analysis-window duration that captures the total DPOAE, among these options, the optimal analysis window for the 4–8 kHz data is 62 ms (which corresponds to a 0.03 octave bandwidth).

As a result of the frequency-dependent latency of reflection OAEs, optimal parameters for capturing and estimating the total DPOAE must shift as frequency increases. Using the same reasoning applied to DPOAEs in Fig. 4, DPOAEs recorded from 4 to 8 kHz have an optimal analysis window of 62 ms (with fixed r = 0.5 octave/s). This value of Δt best preserves DPOAE fine structure in this frequency range while reducing noise most effectively and providing the most stable DPOAE measures. The analysis bandwidth associated with this Δt and r = 0.5 octave/s is 0.03 octave. Clearly to compensate for the changing latency of the reflection component with frequency, the optimal relationship between r and Δt (and the resulting BW) must be adjusted. More ideal ways to implement this adjustment are considered in Sec. IV.

E. Estimating the distortion component

Although this study investigated the optimal parameters and strategies for recording the total DPOAE in adults and newborns, it is possible to estimate the distortion component without increasing test-time and with minimal post hoc analysis. This can be done by reanalyzing the sweep with a long analysis window (see line in Fig. 4). The longer-latency reflection component can be eliminated with a 500 ms window and fixed 0.5 octave/s sweep rate because under these conditions, the LSF analysis window will be wide enough to smooth out fine structure and eliminate the reflection component. In the past, we have estimated the distortion component of the total DPOAE by using inverse FFT processing (Abdala and Dhar, 2010, 2012). During inverse fast Fourier transformation (IFFT), the DPOAE complex pressure measured in the frequency domain is multiplied by a moving window of constant relative bandwidth. Time-domain filters are applied to each window to extract the target DPOAE component based on its latency then the filtered windows of data are transformed back to the frequency domain and the level and phase of each component reconstructed. Our IFFT methods and standard parameters have been detailed in previous publications (e.g., Abdala and Dhar, 2010, 2012). Here, we applied this IFFT protocol to data from the 15 adult subjects to compare level estimates of the distortion component derived from the IFFT to the LSF-based technique of using fast rates with long windows.

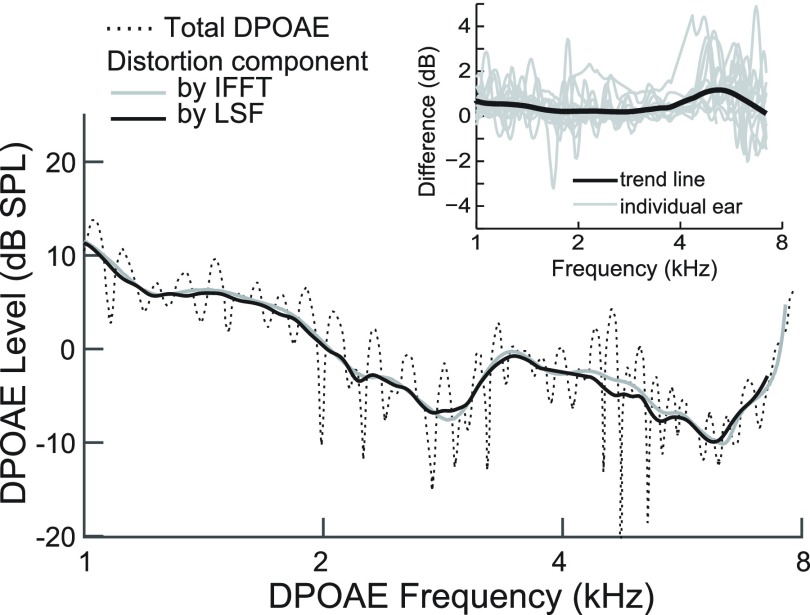
Figure 10 displays the total DPOAE measured in one adult ear (dashed line) with the distortion-component estimates of this same ear extracted via each of these two techniques: IFFT (black) and LSF windowing (gray). The inset shows a trend line of the difference between estimates in distortion-component level as calculated by the two methods (black line) and the individual differences (gray lines). The mean difference in distortion-component level between methods varied from 0.2 to 1.5 dB and was 0.4 dB overall. Both methods produce comparable estimates of the distortion component of the DPOAE.

FIG. 10.

Although this study focuses on the optimal parameters for the collection of the total DPOAE (including both distortion and reflection components), a rapid way to isolate the distortion component from the reflection component of the response is to use a long window, 500 ms, with a too-fast sweeping rate, 0.5 octave/s. This effectively isolates the shorter-latency distortion energy from the later reflection energy. The main panel displays DPOAE fine structure from one adult ear (dotted line) and the distortion component of the DPOAE extracted using an inverse FFT (gray line) versus the above-described LSF-based method (black line). The two distortion-component measures are nearly indistinguishable. This is further elucidated for group data by the inset, which displays individual differences in dB for all adult subjects as thin gray lines and a loess trend line superimposed in black. The average overall difference between IFFT and LSF-based estimates of the distortion component was 0.4 dB.

F. Results summary

Our results confirm that across a three-octave frequency range, the swept-tone DPOAE paradigm generates DPOAE estimates in adults and newborns similar to those generated in more traditional ways using discrete-tone primaries. The findings also confirm that one must consider and change sweep rate and analysis-window duration in concert to maintain a constant analysis bandwidth of frequencies within each least squares fit. We found that below 4 kHz an analysis bandwidth of approximately 0.06 octave was ideal (e.g., 0.5 octave/s with 125 ms analysis window; or 0.125 octave/s with a 500 ms analysis window) and above 4 kHz, an 0.03 octave analysis bandwidth was optimal (e.g., 0.5 octave/s with 62 ms analysis window). Sweep rates as fast as 1 or 0.5 octave/s appropriately estimate DPOAE fine structure. However, the fastest rate produces higher noise floors (poorer SNR) and may be too fast unless additional averaging is employed, especially for newborns, who have intrinsically elevated noise floors. Newborns show the same optimal parameters for DPOAE swept-tone recording and analysis as do adults. Nevertheless test adaptations may be warranted in this age group to decrease the elevated noise.

IV. DISCUSSION

Otoacoustic emissions are being recorded more frequently with tones swept continuously across frequency rather than presented at discrete frequencies. The advantages are readily apparent as data are collected rapidly, allowing for more sweeps per average, which leads to notably improved SNR. Additionally, estimates are obtained at small frequency intervals providing enhanced resolution to resolve ambiguities in phase unwrapping with precision and preserve fine structure while allowing for more accurate separation of DPOAE components.

The efficiency of swept-tone OAE protocols is generally greater than that of traditional discrete-tone methods. In this study, we presented both swept- and discrete-tones to nine adult ears, allowing us to make a direct comparison of the test time required for each approach. For the optimal parameters identified here (0.5 octave/s; 125 ms analysis window from 1 to 4 kHz; 62 ms analysis window from 4 to 8 kHz), using the full complement of sweeps available for each age and a 1 s pause between sweeps, we find that a high-resolution DPOAE, such as the one shown in Fig. 1, requires ∼4.3 min of test time for newborns assuming a 20% rejection rate and ∼2.7 min of test time for normal-hearing young adults assuming a 5% rejection rate. The discrete-tone measurement across a comparable frequency range (see Fig. 6) requires ∼40 min, even with no artifact-rejection factored in. (Note that for the ear shown in Fig. 6, the 4-s recording time used at each discrete frequency gives an SNR comparable to that of the swept-tone method at low frequencies and 3–6 dB better at high frequencies.) If we wish to approximate a clinical DP-gram by recording the discrete-tone DPOAE with a resolution of only ∼6 points per octave, it is possible to obtain a result in ∼8–10 min (assuming 5%–10% artifact rejection and 1–2 min of pausing throughout recording). However, even the measurement of this low-resolution discrete-tone DP-gram is two to three times slower than the swept-tone protocol and sacrifices frequency resolution that permits the definition of DPOAE fine structure, the elimination of phase-wrapping ambiguities, and the separation of DPOAE components.

A. Basic guidelines

The swept-tone OAE paradigm does not simply alter the stimulus presentation modality but also applies a non-FFT-based analysis scheme such as LSF modeling. This technique takes short segments (or LSF analysis-windows) of the ear canal signal and applies models of the primaries and the emission to extract estimates of DPOAE level and phase. The bandwidth of frequencies included within each model or fit is determined by the sweep rate combined with the duration of the analysis window. Therefore, measuring DPOAEs using the swept-tone paradigm and LSF requires the specification of a number of measurement and analysis parameters. For logarithmic sweeps, these parameters include

$$\begin{array}{c}r=\text{sweep}\hspace{0.17em}\text{rate}\hspace{0.17em}(\text{oct}/\mathrm{s}),\\ N_{\text{avg}}=\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{sweeps}\hspace{0.17em}\text{averaged},\\ BW=\text{LSF}\hspace{0.17em}\text{analysis}\hspace{0.17em}\text{bandwidth}\hspace{0.17em}(\text{oct}).\end{array}$$

Using these values, related quantities, such as the total recording time per octave (N_avg/r) or the duration of the analysis window (BW/r), can be computed.

Our results indicate that optimal measurement of the DPOAE requires that the analysis bandwidth (BW) be small relative to the expected DPOAE fine-structure period [see Fig. 4(A) to compare BW with DPOAE fine structure spacing]. Because the fine-structure period measured in octaves varies with frequency, the bandwidth, BW, should be varied correspondingly—either continuously or in some stepwise fashion in order that it span a roughly constant fraction of the DPOAE fine-structure spacing at all frequencies. The analysis window needed to produce a specified analysis bandwidth has a duration (Δt) given by

$$\Delta t=BW/r.$$ (1)

If the bandwidth, BW, varies with frequency, then so must the corresponding analysis-window duration, Δt (assuming the sweep rate, r, is independent of frequency).

Although analysis bandwidths that are small relative to the fine-structure period are needed for measuring the total DPOAE, reducing the bandwidth too much has adverse effects on the noise floor (Fig. 7). In the absence of artifacts (i.e., “non-Gaussian” events of the sort that appear especially prevalent in infants), one expects the noise floor at any given frequency to scale inversely as the square root of the total measurement time contributing to the DPOAE estimate. Thus

$$\text{NF}\sim {\text{NF}}_1/\sqrt{N_{\text{avg}}\Delta t}={\text{NF}}_1\hspace{0.17em}\sqrt{r\hspace{0.17em}/\hspace{0.17em}(N_{\text{avg}}\hspace{0.17em}BW)\hspace{0.17em}},$$ (2)

where NF₁ is the noise floor expected when analyzing a single sweep (N_avg = 1) using an analysis window of 1 s (Δt = 1 s). Equation (2) predicts that when the number of sweeps (N_avg) is held fixed, doubling the analysis window duration decreases the expected noise floor by $\sqrt{2}$ (or 3 dB), in good agreement with the trends seen in the adult data of Fig. 7.

Equations (1) and (2) allow one to appreciate how changes in the parameters such as sweep rate affect the measurement. For example, to increase the sweep rate, r, while leaving the analysis bandwidth, BW, unchanged requires decreasing the analysis-window duration, Δt. However, preserving the measurement noise floor while decreasing Δt requires a compensating increase in the number of sweeps presented and averaged, N_avg.

B. Measuring DPOAEs with swept tones

Prior to this report, the stimulus parameters that optimize measurements of DPOAE level and phase across a broad frequency range and maximize signal to noise had not been systematically examined. Additionally, there had been no studies defining these parameters in infants although this is the group for whom the swept-tone OAE technique might be most beneficial in a clinical setting. Also notable is the lack of published data exploring higher frequency swept-tone DPOAE measurement; this is particularly important given that the reflection component of the DPOAE shows frequency-dependent delays (Schairer et al., 2006; Kalluri and Shera, 2007; Abdala et al., 2014). In this study, we systematically examined the effects of analysis-window duration for a fixed sweep rate, varied sweep rates for fixed analysis bandwidths, and the effects of frequency and age on DPOAE levels, phase and SNR using swept-tone presentation and LSF analysis techniques.

The results of this study suggest that for DPOAEs< 4 kHz, rates as rapid as 0.5 octave/s analyzed with LSF windows of 125 ms duration produce DPOAE level and phase estimates comparable to the discrete-tone DPOAE. Additionally, this combination produces noise floors that are favorable. Although a slightly shorter window (62 ms) provides for an equally good match to DPOAE discrete-tone values, it produces an approximately 3 dB increase in the estimated noise floor rendering a 125 ms window duration preferable. It is possible to go faster and sweep at 1 octave/s; however, there is some shift in the DPOAE fine structure at this rate. More importantly, the faster rate requires a shorter analysis window (i.e., 31 or 62 ms), which produces noise floors that are 3–6 dB higher than those noted for the suggested combination of a slightly slower rate, i.e., 0.5 octave/s with a 125 ms analysis window. Therefore the trade-off in time-savings with the faster rate is likely to be complicated by the requirement for more averaging to overcome the elevated noise floor and achieve adequate SNR.

Although our focus is on measuring the total DPOAE rather than its components, we found that using an analysis bandwidth of ∼0.25 octave isolated the distortion component and produced estimates of component phase and amplitude matching other signal processing techniques such as the inverse FFT. Thus if one wishes to isolate distortion as a marker of cochlear nonlinearity, one can eliminate reflection energy in this manner. In accordance with the relation BW = rΔt, the required 0.25 octave analysis bandwidth can be achieved by combining a long analysis window (Δt = 500 ms) with a fast sweep rate (r = 0.5 octave/s).

Isolating the reflection component of the DPOAE is more involved and will be addressed in a planned companion paper probing various methods for separating source contributions to the DPOAE. Nevertheless a preliminary metric of reflection contributions can be obtained simply by subtracting the distortion component from the total DPOAE. This gross calculation contains all longer-latency multiple internal reflections in addition to the primary reflection from the 2f₁–f₂ site. Multiple internal reflections are not typically apparent in the DPOAE fine structure recorded using discrete tones and do not appear to be informative.

C. High-frequency adjustments

There is a caveat to our aim of keeping analysis bandwidth constant across frequency during LSF-based analysis of swept-tone DPOAEs. At higher frequencies, we want a narrower analysis bandwidth to adapt to frequency-dependent shifts in reflection-component latency. To capture the reflection components of the DPOAE in the estimate, we must shorten the analysis window to accommodate this shifting delay. With a fixed sweep rate, a shorter analysis window produces a narrower analysis bandwidth (i.e., 0.5 octave/s× 62 ms = 0.031 octave).

Another way to think about the shifting bandwidth as a function of frequency is by considering DPOAE fine structure. Our aim is to keep the same number of fine structure periods represented in each analysis window across frequency; this will ensure that the same number of cycles of reflection-component phase is included in each analysis window. Because fine structure periodicity changes with frequency, the analysis-window duration must change across frequency. If sweep rate is fixed and analysis window changed, this change produces an effective change in the analysis bandwidth included in each LSF fit.

We recognized and adjusted to this need for a varying analysis bandwidth across frequency by considering two gross frequency categories, i.e., 1–4 kHz versus 4–8 kHz. And by adjusting our target bandwidth from ∼0.06 to ∼0.03 octave, we were able to achieve our basic goal of preserving fine structure and capturing both DPOAE components. However, the better option is to have an analysis bandwidth that changes continuously with frequency so that analysis windows are adapted smoothly to approximate changes in the reflection-component latency rather than impose an arbitrary division between two low- and high-frequency segments. Applying only two analysis windows across a three-octave frequency range cannot appropriately mimic the frequency dependence of changing reflection-component delays shown in the Fig. 9, inset.

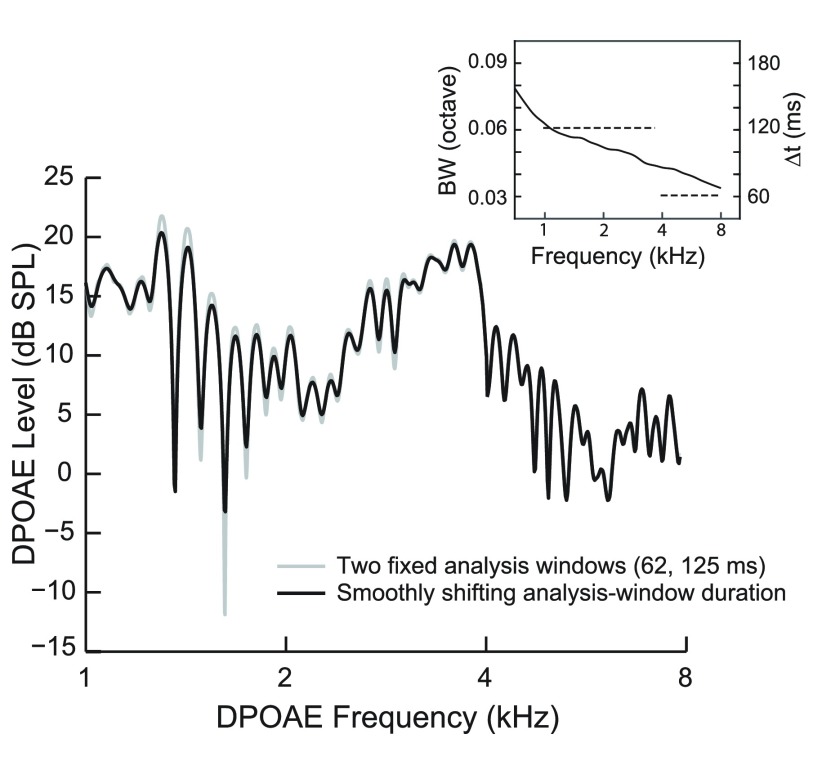
In the inset of Fig. 11, we derived a preliminary analysis-window function based on the reflection-component delay data from normal-hearing adult ears in a previous study (Abdala et al., 2014). This provided a template for the shift in analysis bandwidth required to capture the reflection elements of the total DPOAE as well as the nonlinear distortion component. The inset shows analysis bandwidth, BW, changing across DPOAE frequency (r = 0.5octave/s), approximating the frequency-dependent shift in reflection-component latency. The associated analysis-window duration is displayed on the right y axis. To achieve this, the duration of analysis window, $\Delta t,$ was varied with frequency according to the following formula:

$$\hspace{0.17em}\Delta t=\alpha /(N_{\mathrm{R}}(f_{\text{oae}}(t))\cdot d\text{ln}(f_{\text{oae}}(t))/dt)\hspace{0.17em},$$ (3)

where $f_{\text{oae}}(t)$ describes how the OAE frequency changes with time, $N_{\mathrm{R}}$ is the reflection-component delay measured in periods, and $\alpha$ is a constant chosen to yield a bandwidth of 0.0625 octave at 1 kHz. For logarithmically swept tones at rate r, the function $d\text{ln}(f_{\text{oae}}(t))/dt\hspace{0.17em}$ becomes r $\hspace{0.17em}\text{ln}2$. The main panel in Fig. 11 shows the application of this smoothly shifting analysis-window function to DPOAEs collected from one adult ear (black line) compared to DPOAEs analyzed with the two optimal windows established earlier: Δt = 125 ms for 1–4 kHz; and 62 ms for 4–8 kHz (gray line). Although differences are not strongly evident in this one exemplar, smoothly shifting analysis windows across frequency are expected to show enhanced precision in capturing reflection-component energy compared to a gross two-window solution. A more comprehensive exploration of this issue is warranted to detect systematic benefits of an analysis bandwidth that shifts smoothly with frequency.

FIG. 11.

The inset in this figure illustrates the desired function between frequency and both analysis-window duration (Δt) and associated analysis bandwidth (BW) to optimize DPOAE measurements and include both components. The dashed horizontal lines represent the two fixed analysis-window durations determined to be optimal for DPOAEs above/below 4 kHz, i.e., 62 and 125 ms. This function was derived from DPOAE reflection-component delays reported in Abdala et al. (2014). The main panel of this figure displays DPOAE level analyzed with smoothly shifting analysis windows which follow the inset function (black) compared to DPOAE level analyzed using only two fixed analysis-windows (gray).

In this study, we did not test the effect of stimulus level on DPOAEs evoked with swept-tones and analyzed with LSF. However, past work has shown that DPOAE reflection-component delays are level-dependent (Mauermann and Kollmeier, 2004; Abdala et al., 2011). Using normal-hearing adult DPOAE data from Abdala et al. (2011), we estimate that the reflection-component phase rotates an additional 0.7–2.8 cycles from 1 to 4 kHz when DPOAEs are measured at L₁, L₂ levels of 45, 35 versus 65, 55 dB SPL; at 8 kHz, the additional phase rotation at the lower levels increases to ∼5.5 cycles. Although these changes are notably less than the total phase rotation across frequency (see Fig. 11, inset), they may warrant adjustments when recording OAE input/output functions at high frequencies. Other accommodations for lowered stimulus levels might include a slower sweep rate and correspondingly long analysis-window durations to enhance SNR since the OAE will be reduced in amplitude.

D. Optimizing newborn measurements

Measures of DPOAE level, phase, and SNR were similarly affected by parametric changes in analysis-window duration, sweep rate, and DPOAE frequency in adults and newborns. This suggests that the same optimized protocol can be applied to both age groups. However, the elevated noise floor and poorer response stability in the neonatal group (see Figs. 2 and 3) differentiate infant swept-tone OAEs from those of adults and suggest that test adaptations may be warranted. This is especially important because one could argue that clinically applied OAEs are most useful in the screening and detection of hearing loss in this age group.

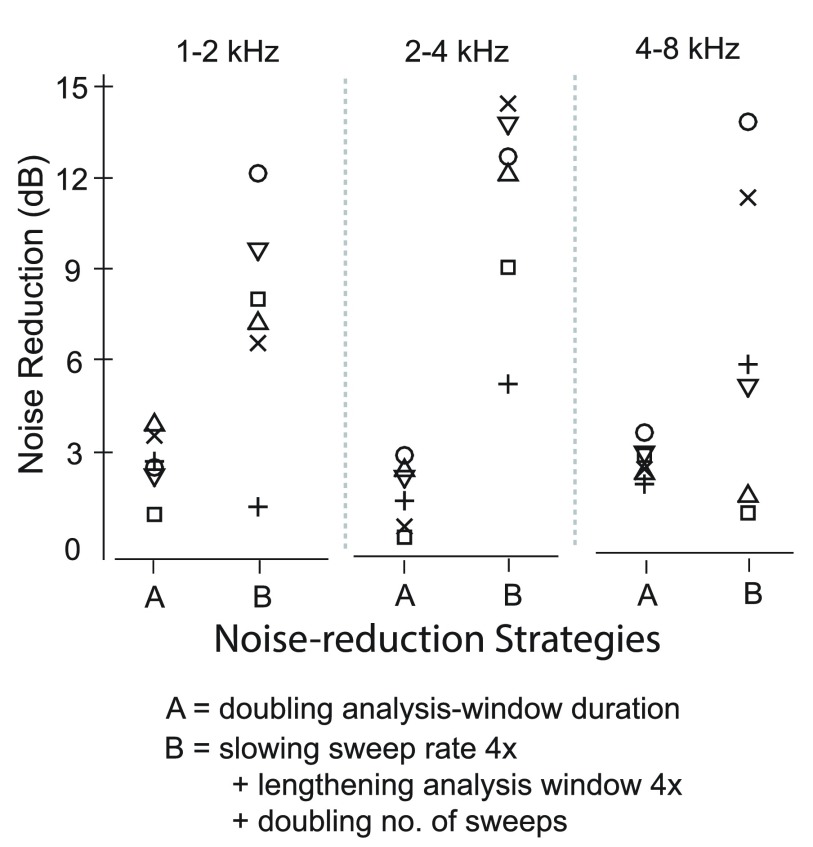
We have established that doubling the duration of analysis windows decreases noise floor estimates by ∼1–2 dB in newborns. This “noise reduction” effect can be combined with other strategies to enhance DPOAE swept-tone recordings in this challenging subject group. Figure 12 plots DPOAE results from six newborn ears in three octave-wide bands using two noise-reduction strategies. (Note: no artifact-rejection or SNR criteria were applied to infant data for this analysis). Strategy A doubles the analysis-window durations (from 62 to 125 ms for low-frequencies and 31 to 62 ms for the high-frequency band) and produces a ∼2 dB improvement in noise (termed “noise reduction”). Strategy B is a combined approach, presenting a sweep rate that is four times slower, an analysis window that is four times longer, and twice as many sweeps. Together, combined modifications produced average reductions in the noise floor ranging from 6.5 to 11 dB although the effect is idiosyncratic among newborns. These combined modifications plus the implementation of efficient real-time artifact rejection procedures will improve swept-tone OAE recordings in newborns by reducing noise and providing a more reliable DPOAE measure. The downside of this approach is that each of these modifications prolongs data collection, which can be problematic in newborns who provide limited periods of quiet for testing. Whether the benefit of these combined modifications outweighs the investment in time will need to be evaluated on a case-by-case basis. However, the only way to make an informed choice is to understand how each of these manipulations impacts the DPOAE and noise floor.

FIG. 12.

The effect of two strategies on noise estimates in 10 neonates (each ear denoted by a separate symbol). “Noise reduction” is the improvement in noise floor re: baseline (analysis window of either 31 or 62 ms depending on frequency, and sweep rate of 0.5 octave/s) The larger the dB value, the more effective the noise reduction. Strategy A shows that the doubling of analysis windows produces approximately 2 dB reductions in noise floor (as expected from data shown in Fig. 7) for all newborns across frequency. Strategy B shows data from the same newborns after applying combined modifications: (1) slowing down the sweep rate to 0.125 octave/s; (2) lengthening the analysis window to 500 ms; and (3) doubling the number of sweeps contributing to each average. These combined strategies produce additional noise floor reductions, some as great as 14 dB.

We did not employ a real-time artifact-rejection strategy for DPOAE data collection in this study because it was not available at the time of testing. Such an algorithm has since been developed for swept-tone OAEs (Kalluri and Shera, 2013) and is currently being refined for application in newborns. The online artifact rejection employs an adaptable threshold based on each subject's baseline noisiness and eliminates short data segments where noise has exceeded a given dB SPL criteria. It has the advantage of allowing real-time adaptation of the data-collection process; that is, a rejected segment can be replaced by another more reliable segment via presentation of additional sweeps until some stopping criteria is reached.

In summary, although newborns do not require different parameters than adults to capture the swept-tone DPOAE, they are likely to benefit from adaptations that reduce noise, such as slowing the sweep rate, lengthening the analysis window, including more sweeps in an average, and employing an online artifact-rejection process.

E. Measuring intra-subject reliability of DPOAEs

Here we exploited the need for repeated sweep presentation to generate a measure of sweep-to-sweep repeatability for DPOAE estimates within each ear. We refer to this measure as the intra-subject standard error of the mean (SEM) or confidence interval (CI). It is not difficult to imagine how this sort of variability metric could be incorporated into a clinical assessment protocol, in particular if monitoring the ongoing effect of some ototoxic treatment, on cochlear health, for example, or the effects of industrial noise. The natural sweep-to-sweep variance of one ear could help determine with more precision when the effects produced by a noxious agent begin to damage the ear. Additionally, the intra-subject SEM can be used to reliably differentiate an ear with hearing loss or other auditory pathology from normal ears by considering natural within-subject variability. An ear with excessive response variability from run to run might be deemed of poor quality and differences between it and that of a normative template might not be considered reliable enough for a diagnosis. Sweep-based estimates of repeatability also have research utility if acceptable criteria are developed to establish a given subject's data as highly repeatable or conversely, of insufficient quality.

V. CONCLUSIONS

The presentation of tones swept across frequency for OAE testing and LSF modeling to estimate OAE level and phase provides an efficient alternative to conventional OAE recording. DPOAE swept-tone techniques produce responses similar to DPOAEs recorded with discrete tones but in a much-reduced time frame. Additionally, they provide unparalleled frequency resolution. One of our goals was to provide parametric study of and guidelines for the application of swept-tone OAE paradigms. We have defined the stimulus and analysis parameters that impact both the DPOAE and measurement noise to provide a deeper understanding of the various influences and factors that shape the swept-tone DPOAE. We found that the optimal protocols appear equally applicable to newborns and adults although some adaptations are warranted in newborns. This study did not probe the optimal methods for the separation of the dual DPOAE sources: reflection and nonlinear distortion. Because most applications of the DPOAE in humans and laboratory animals record the total DPOAE, we focused on optimizing this measure. A companion paper will address component separation of the DPOAE using swept-tones. We conclude that if the parameters are chosen carefully, recording the DPOAE with continuously sweeping tones and least squares fit modeling across a broad range of OAE frequency, provides a robust alternative to conventional recording strategies in both adults and newborns.