Distributions of experimental protein structures on coarse-grained free energy landscapes

Abstract

Predicting conformational changes of proteins is needed in order to fully comprehend functional mechanisms. With the large number of available structures in sets of related proteins, it is now possible to directly visualize the clusters of conformations and their conformational transitions through the use of principal component analysis. The most striking observation about the distributions of the structures along the principal components is their highly non-uniform distributions. In this work, we use principal component analysis of experimental structures of 50 diverse proteins to extract the most important directions of their motions, sample structures along these directions, and estimate their free energy landscapes by combining knowledge-based potentials and entropy computed from elastic network models. When these resulting motions are visualized upon their coarse-grained free energy landscapes, the basis for conformational pathways becomes readily apparent. Using three well-studied proteins, T4 lysozyme, serum albumin, and sarco-endoplasmic reticular Ca²⁺ adenosine triphosphatase (SERCA), as examples, we show that such free energy landscapes of conformational changes provide meaningful insights into the functional dynamics and suggest transition pathways between different conformational states. As a further example, we also show that Monte Carlo simulations on the coarse-grained landscape of HIV-1 protease can directly yield pathways for force-driven conformational changes.

I. INTRODUCTION

Proteins are often regarded as the work force of cells, and understanding their actions requires an understanding of their dynamics. Experimental protein structures, whether determined by X-ray crystallography, NMR spectroscopy, or by high resolution cryo-electron microscopy,^1,2 shed light about the structure and function of diverse proteins. However, the structures individually only provide a static snapshot of the protein. But collectively, multiple structure determinations of the same or closely related proteins can inform us directly about its dynamics. Even mutants, it is now being realized, have structures and motions falling primarily along the same limited dynamics pathways.^3,4 Wolynes, Onuchic, and Dill^5–14 have all pointed out the importance of understanding the energy landscapes. Understanding the dynamic distributions of the different structures and their energetics upon the landscape is a crucial step in understanding structure-function relationship in proteins. Recently, Nussinov and Wolynes¹⁵ have pointed out how useful it is to interpret biomolecular function within the framework of energy landscapes and can help to explain diverse phenomena ranging from the effects of ligand binding¹⁶ to the effects of mutations^17–19 on protein stability.

Predicting dynamics information, given the 3D structure of a protein, has been a topic of a huge body of research. Molecular dynamics (MD)^20,21 and Monte Carlo (MC) methods^22,23 are the most commonly employed techniques for extracting such dynamics information. Despite their proven success, these methods remain computationally intensive and limited in the time-scales that can be thoroughly investigated. On the other hand, coarse-grained (CG) methods such as those used in the elastic network models (ENMs) offer a convenient and quick alternative to all-atom models. Coarse-grained ENMs successfully model the dynamics of most proteins, even though the interactions between amino acid residues are represented by extremely simple Hooke’s-law springs. The most popular ENMs are the Gaussian network model (GNM)²⁴ and the anisotropic network model (ANM).²⁵ In addition to being able to accurately predict residue position fluctuations, the low-frequency modes predicted by ENMs often capture the functionally relevant conformational changes evident in multiple crystal structures, for a wide variety of proteins^26,27 including even the largest molecular structures such as viral capsids²⁸ and ribosome.^29–32

The number of available structures in the protein databank (PDB)³³ has been growing exponentially. While there is remarkable diversity in the variety of type of structures in the PDB, many of them are indeed structures of the same protein or its close homologs and many more belong to the same protein fold. These multiple structures of the same or closely similar proteins in many cases provide an excellent sampling of the possible conformational states, analogous to what one would obtain from simulations such as MD or Monte Carlo. Previous works have shown the close correspondences between motions inherent in sets of structures in the PDB and motions extracted from analysis of MD trajectories³⁴ or predicted motions from theoretical models.^35–37 Surprisingly, little effort is being made to systematically explore the conformational space by using the different structures of the same protein already available in the PDB.

Given a set of structures (either experimental or those generated from MD simulations), perhaps the most common method of extracting useful dynamics information is principal component analysis (PCA),^38,39 and when applied to protein samples generated from MD termed essential dynamics.⁴⁰ PCA is a statistical method based on covariance analysis, which can transform high dimensional data from the original space of correlated variables into a highly reduced space of independent variables (i.e., principal components or PCs). By performing PCA to reduce the dimensionality, most of a system’s variance will usually be captured by a small subset of the PCs. This is one of the primary advantages of performing PCA; that it greatly reduces the dimensionality of the dynamics space (originally of the order of number of residues) to a few dominant motions of the protein. PCA has been applied extensively to analyze trajectory data from MD simulations to find a protein’s essential motions.^41,42

Earlier, Howe⁴³ used PCA to classify structures in NMR ensembles automatically, according to the correlated structural variations, and the results have shown that two different representations of the protein structure, the C^α coordinate matrix and the C^α-C^α distance matrix, gave equivalent results and permitted the identification of structural differences between conformations. Teodoro et al.⁴⁴ applied PCA to a dataset composed of many conformations of HIV-1 protease and found that PCA transformed the original high-dimensional representation of protein motions into a low-dimensional one that provides the dominant protein motions. PCA has also been employed to characterize diverse biomolecular phenomena such as protein folding pathways from MD simulations,^45–47 the mechanism of prion action,⁴⁸ and others.

Recent studies have also shown that the most important motions (PCs) extracted from sets of experimental structures correspond well to the modes predicted by using coarse-grained models such as elastic network models.^35–37 Software to perform PCA on sets of protein structures is currently supported by software packages such as Maven⁴⁹ from our lab, ProDy⁵⁰ from the Bahar group, as well as Bio3d⁵¹ from grant.

PCs involved in the largest scale motions are often associated with the functional mechanism of a protein⁵² and thus also provide a convenient reduced coordinate system upon which to construct energy landscapes as a basis for describing conformational changes, and even to treat protein folding.⁴⁵ Even though the energy landscape of a protein can be rugged and high dimensional,⁵ using the PCs as coordinates for the landscapes can usually reveal the dominant low energy regions and pathways for conformational changes.⁴⁷ There have also been recent attempts to use PCA for internal coordinates⁵³ rather than Cartesian coordinates to construct free-energy landscapes.^54–56 Free energies along the PCs are traditionally calculated from the negative logarithm of the probability distribution function of structures along each PC (Ref. 46) as ΔG = − kTlogP_ij, where k is the Boltzmann constant, T the temperature, and P_ij the joint probability density function of structures along a pair of PCs, PC_i and PC_j. But this assumes that the simulation samples the entire conformational space accessible to the protein, which is not necessarily true. A more accurate picture of the energy landscape can be obtained if the conformational space (at least along the most significant directions of motion) is explicitly sampled and the relative energies of structures in different regions of the landscape can be computed. Here, we propose a new method of combining the PCs from sets of experimental structures with our previously successful free energy estimates⁵⁷ to construct the free energy landscapes of a group of 50 well studied proteins.

The free energy Δ G of a system is defined as Δ V − TΔ S, where Δ V and Δ S are measures of the energy and entropy of the system, respectively. Given the difficulties in computing interaction energies for proteins by using first principles, the empirical statistical or knowledge-based potentials have emerged as a convenient method to estimate potential energies of proteins. They have been tested out extensively at the CASP (Critical Assessment of Structure Prediction) competitions⁵⁸ and have proven themselves to be superior to other types of potentials. Knowledge-based potentials are calculated based on the preference of amino acid contacts between different residues in a database of known structures under the assumption that the global free energy minimum is the native structure of the protein. Pairwise (two-body) statistical contact potentials were pioneered by Tanaka and Scheraga⁵⁹ and subsequently developed and extended by Miyazawa and Jernigan^60,61 and Sippl.⁶² Since then, with increased availability of structures in the PDB, many different two-body potentials have been developed and have found applicability for a variety of protein problems ranging from protein tertiary structure prediction^63,64 and protein-protein interaction prediction^65–67 to protein design.^68,69

The dense packing of residues in globular proteins means that two-body potentials are likely not sufficient to capture the 3-dimensional cooperative nature of multiple interactions,^70–72 and it has been suggested that higher-body potentials are necessary for tasks like protein structure prediction. To address this, three-body⁷³ and four-body potentials⁷⁴ have been developed. Our own four body potentials^75,76 capture the cooperative nature of interactions among amino acid residues in addition to incorporating differences between buried and exposed residues and the interactions between backbone and side chains. In addition, we have also developed an optimized potential function⁷⁷ combining the long-range four body potentials with short-range potentials.⁷⁸ This optimized potential when combined with entropy measures obtained from coarse-grained computational methods such as the ENMs^57,79 can provide estimates of free energy that have already proven to be extremely powerful in identifying native protein-protein complexes from sets of docked poses.⁵⁷ We therefore combine information about preferred directions of motions from PCs with free energy information to present coarse-grained free energy landscapes for proteins. These show the pathways for the limited conformational changes described by the set of dominant motions.

The paper is organized as follows: First, we discuss how to collect a dataset of proteins for this type of analysis and how to construct free energy landscape for these proteins by combining principal components and free energy estimates. Then, we analyze and discuss in detail the energy landscapes of three well known proteins and discuss how the energy landscapes can be interpreted in the context of the motions extracted from each dataset. As a further step, we also show how Monte Carlo simulations on these coarse-grained free energy landscapes can provide transition pathways for force-driven conformational changes in proteins.

II. THEORY AND METHODS

A. Datasets

The PDB³³ provides a clustering of all the chains by using CD-HIT (Cluster Database at High Identity with Tolerance)^80,81 at different levels of specified sequence similarity. In order to identify all the structures which are highly similar to one another in the PDB, we have utilized clusters obtained at 95% sequence similarity cutoff, from the PDB (as of November 2014). In other words, all protein chains in each cluster are at least 95% identical in sequence to each other. After obtaining these clusters, only monomeric proteins were retained for the analysis. However, with more careful alignment of oligomers, this methodology can handle multimeric proteins as well. Each of the members of these sets is aligned using the multiple structural alignment (MSA) tool MUSTANG⁸² and the alignment is manually edited to remove any obvious mismatches or indels. Proteins within each set often have stretches of residues lacking position coordinate information (resulting in gaps in the alignment), and these structures have been removed from the sets. Guided by the MSA, the PDB files of the structures are processed using our own Perl scripts to retain only residues present in all the structures within each set (i.e., not including positions having gaps in the MSA). Care is taken so as not to include any structures having gaps in the middle of the protein. This processed dataset of the position coordinates for each residue in the set of proteins constitutes the data used to perform PCA. Following this selection process, we obtain 50 proteins from which at least 45 structures are retained. The complete list of PDB IDs for all the 50 sets of proteins used in this study are provided in Table S1 in the supplementary material⁸³ and the distribution of root-mean-square deviations (RMSDs) within the dataset of structures is provided in Fig. S1 in the supplementary material.⁸³

B. PCA

The dataset for PCA, Ξ_n×p, is the matrix of position coordinates (x, y, and z) of the C^α atoms in an aligned set of proteins for n structures each having the total number of variables, p = 3N, where N is the number of residues in each structure. Then the p × p dimensional variance-covariance matrix C has elements,

$${\displaystyle c_{ij}={\sum }_{k=1}^n({\xi }_{ki}-{\overline{\xi }}_i)({\xi }_{kj}-{\overline{\xi }}_j)/(n-1),\forall \hspace{0.17em}1\le i,j\le 3N.}$$ (1)

Each diagonal term is the variance of each position coordinate and the cross diagonal terms are the covariances. Here, ξ_ki refers to the value of the ith variable (x, y, or z) for the kth structure in the dataset Ξ_n×p and ${\overline{\xi }}_i$ refers to the mean of the ith variable. The covariance matrix C can be decomposed as C = EΔE^T, where the columns of E are the eigenvectors e_k∀1 ≤ k ≤ 3N, which are the linearly independent, orthogonal vectors along directions of the variations in the data and the eigenvalues are the elements of the diagonal matrix Δ. The eigenvalues are sorted in order, and each eigenvalue is directly proportional to the amount of the variance it captures. The projections of the points on each eigenvector are called the PCs and are obtained as columns of the matrix P_n×3N = Ξ_n×3N × E_3N×3N. The PC scores are calculated as projections of the mean centered data onto the PCs, obtained as columns of the matrix ${\mathit{P}}_{n\times 3N}=(\mathit{\xi }-({\overrightarrow{1}}_{p\times 1}\times {\overline{\mathit{\xi }}}^{{}^T})){\mathit{E}}_{3N\times 3N}$, where ${\overline{\mathit{\xi }}}^{{}^T}$ is the transpose of the mean vector of position coordinates. The ith row of the matrix P correspondingly gives the PC scores of structure i in the dataset.

C. Knowledge based potential functions

The potential energies for the structures are estimated as an optimized linear combination of three different in-house statistical potential functions: four-body sequential potential,⁷⁵ four-body non-sequential potential,⁷⁶ and short-range potentials;⁷⁸ as in our previous work.⁵⁷ Four-body refers to close groups of four amino acids that can interact,

$${\displaystyle V_{\mathit{opt}}=V_{4\text{-}\mathit{body}\mathit{seq}}+0.28*V_{4\text{-}\mathit{body}\mathit{non}\text{-}\mathit{seq}}+0.22*V_{\mathit{short}\mathit{range}}.}$$ (2)

The weights for the four-body sequential and four-body non-sequential potential terms were obtained previously⁷⁷ by minimizing the RMSD of best decoys from homology modeling targets of CASP8⁸⁴ to their corresponding native structures using particle swarm optimization (PSO).⁸⁵ Please refer to our previous work⁷⁷ for more details about how the weights for each potential terms were optimized.

D. Structural entropy evaluation

In order to obtain a reliable measure of the entropy of a system, we use coarse-grained models of protein dynamics referred to as ENMs.^24,25,86,87 In ENMs, the molecules are represented using bead-spring models in a simplified manner (for the coarse-grained cases usually the beads are the C^α atoms of proteins, i.e., one bead per residue, which is what has been used here) and are assumed to interact with only the physically close beads (within a specified distance cutoff, taken here as 7 Å). Here, we specifically use the GNM²⁴ in which the equilibrium fluctuations of the beads are assumed to be isotropic and normally distributed. The spring stiffness (γ) between all the beads is assumed to be the same (γ = 1). The potential energy of the system is then simply proportional to the sum of squares of displacements of all the beads from their equilibrium positions. Mean square fluctuations of the C^α atoms computed from the GNM (obtained as diagonal elements of the pseudoinverse of the connectivity or Kirchoff matrix) have been shown to agree well with the experimental temperature factors for many different crystal structures, and also to agree with the variabilities observed in sets of structures.^35,36 The entropies for the structures are directly computed as the sum of mean square fluctuations of all the C^α atoms⁵⁷ as computed with the GNM,

$${\displaystyle \mathrm{\Delta }S\propto {\mathrm{\Gamma }}^{-1}={\sum }_{i=2}^N\frac{1}{{\lambda }_i}\left(M_i{M}_i^T\right),}$$ (3)

where N is the number of residues in the structure, M_i is the ith mode vector from the GNM, λ_i the corresponding square frequency, Γ the system’s Kirchoff or connectivity matrix, and Γ⁻¹ its pseudo-inverse.

E. Construction of energy landscapes

The first few eigenvectors from PCA capture the most important directions of motions from the set of structures, and these provide convenient coordinates for constructing free energy landscapes. By using the PC vectors, representative structures can be sampled along the first few eigenvectors under the assumption of linearity provided the conformational changes are not overly large. The distribution of structures along the PC axes (the mean-centered projections of the structures onto the eigenvectors) indicates the similarities and dissimilarities between the various structures in the dataset. Usually there are clusters within the dataset, by viewing their distribution.

In order to obtain a free energy landscape, we choose to focus on the most important motions, along the PC1-PC2 coordinates, considered as grid points. Consider a dataset of (x, y, z) coordinates, Ξ_n×3N of n structures with N residues each. Performing PCA on this dataset as described above yields 3N eigenvectors e_k ∀ 1 ≤ k ≤ 3N. For this study, we consider only the first two eigenvectors (e₁ and e₂) which capture the largest fraction of the variance in the data of any pair of such coordinates. Representative structures were sampled uniformly at equally spaced points along the PC1 and PC2 directions to yield a rectangular grid where the extrema of the grid are dictated by the extrema in the PC scores of all of the crystal structures. For this, the coordinates of each representative structure on the grid are obtained relative to the coordinates of a central structure (closest to the origin) on the grid, R₀. The 3D coordinates R_1×3N of a structure R on the PC1-PC2 grid at position (R_i, R_j) are obtained using the coordinates of the central structure on the grid R⁰ as

$${\displaystyle {\mathit{R}}_{1\times 3N}={\mathit{R}}_{1\times 3N}^0+\left(R_i-R_i^0\right)\times {\mathit{e}}_1+\left(R_j-R_j^0\right)\times {\mathit{e}}_2,}$$ (4)

where $(R_i^0,R_j^0)$ are the PC1-PC2 scores of the central structure on the PC grid and e₁ and e₂ are the eigenvectors corresponding to PC1 and PC2.

The free energy of a representative structure is measured as

$${\displaystyle \mathrm{\Delta }G=\mathrm{\Delta }V-a\mathrm{\Delta }S,}$$ (5)

where the energy contribution ΔV is obtained from V_opt (as in Eq. (2)) and the entropy contribution ΔS is obtained from the GNM fluctuations (Eq. (3)). The value of a cannot be determined universally for all proteins because the entropy term depends on various factors such as the size of the protein. The value of a is taken to be a variable and is optimized for each protein as the value that places the largest number of structures in lowest energy regions of the landscape, as discussed in Section III.

Once the free energies for each of the representative structures is computed, the values are visualized as a contour along the PC1-PC2 coordinate space and the contour plot is colored spectrally according to the order VIBGYOR (with violet corresponding to regions of lowest energy and red corresponding to regions of highest energy). The experimental structures are plotted in this space on top of the contours. Usually, the experimental structures fall into lower free energy regions of such a contour plot, subject to some uncertainties arising from additional conformational variabilities from additional PCs beyond the first two that are being ignored.

F. Generation of a transition path between two structures on the free energy landscape

In order to show an example of how to obtain the transition pathway between two different forms of a protein, we have chosen to perform force applications using Monte Carlo simulations on HIV-1 protease. This approach builds on the Hessian matrix computed from coarse-grained ANM and generates a displacement vector in response to an external force perturbation vector based on linear response theory^88,89 to relate the response behavior to the equilibrium fluctuations in the unperturbed state. This displacement vector can be represented as

$${\displaystyle {\mathrm{\Gamma }}_i^{-1}\cdot F_i=\mathrm{\Delta }{R}_i,}$$ (6)

where the matrix Γ⁻¹ is equivalent to the inverse Hessian and F_i is the external force vector applied on residue i with component directions (F_x, F_y, F_z), and ΔR_i is the displacement vector in Cartesian coordinates for residue i.

We have developed a pipeline (unpublished) to perform randomly directed force perturbations at sites where exothermic events occur. To understand the conformational changes in HIV-1 protease, where the binding process itself is exothermic,^90,91 we have added forces on the residues close to the flaps, where the major conformational changes take place. Any extremely large forces that could rupture bonds would clearly fall outside the range of linear responses, so we apply small iterative forces. In this way, we will avoid large disruptions, but permit new contacts between two nodes to form during a transition. We use a Metropolis Monte Carlo approach,⁹² which follows a series of steps (deformations) that are mostly downhill on the energy landscape, but with occasional uphill steps. Instead of accepting all steps during a simulation, we accept some and reject others using the Metropolis decision criterion. We have integrated this MC scheme with our elastic network based force perturbation method.

The Metropolis decision criterion uses only the four-body potential energy of the newly generated state m in comparison with the four-body energy of the previous state,

$${\displaystyle p=\left\{\begin{array}{ll}1,\hfill & V_m\le V_{m-1}\hfill \\ exp\left(-\frac{V_m-V_{m-1}}{kT}\right),\hfill & V_m>V_{m-1}\hfill \end{array}\right.,}$$ (7)

where p is the probability for accepting the newly generated structure in the MC simulation. V_m the four-body energy of the newly deformed structure, V_m−1 the four-body energy of the previous structure, k the Boltzmann constant, and T the temperature. In other words, any newly generated conformation lower in energy than the previous conformation will always be accepted, while the probability of accepting a newly generated conformation is lower if the newly generated conformation has a four-body energy higher than at the previous step.

III. RESULTS

A. Distribution of crystal structures in low energy regions of the landscape

One of the principal aims of this study is to learn whether the crystal structures are located in low free energy regions of the landscape. If the experimentally determined structures do reside in the low free energy regions on the landscape, this supports the conformational selection point of view for the protein under study. In other words, we can assume that the protein is in a state of dynamic inter-conversion between the conformations corresponding to the low free energy regions and different triggering events such as binding of a ligand, introduction of a mutation, or a chemical reaction may shift the equilibrium in favor of some slightly different conformations.

In order to test this hypothesis, we choose 50 proteins of interest (selected on the basis of having at least 45 experimental structures each). Next, we construct the free energy landscape for the proteins by computing the free energies of the structures obtained by deforming the structures along the first two pairs of PCs on an equally spaced rectangular grid. Let us assume that the entire grid produces a scale of free energies from G_min (lowest free energy) to G_max (highest free energy). The free energy of each crystal structure is assumed to be that of the closest grid point. We then consider a set of percentiles G_i ∀ i ∈ {0, 5, 10, …, 100} of the crystal structures on the free energy scale of the whole grid. If the free energy of the crystal structures was predominantly in low energy regions of the entire landscape, we would expect the higher percentile values to be closer to the lowest free energy on the grid, G_min. For this, we compute the normalized energy difference δ_i from G_min for each percentile value G_i relative to G_max (the highest free energy in the grid),

$${\displaystyle {\delta }_i=\frac{G_i-G_{\mathit{min}}}{G_{\mathit{max}}-G_{\mathit{min}}},i\in \{0,5,10,\dots ,100\}.}$$ (8)

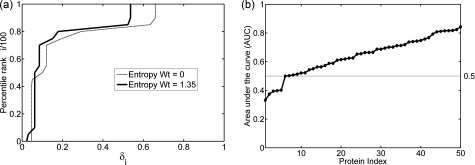
We then plot the scaled percentile rank i/100 against the normalized energy difference of each percentile value, δ_i ∀ i ∈ {0, 5, 10, …, 100} (Eq. (8)). This plot can be considered analogous to the receiver operating characteristic (ROC) curve used in machine learning: for higher percentile rank i corresponding to lower δ_i, the curve is shown in Fig. 1(a). As in the ROC, we can use the area under the curve (AUC) as a measure of the tendency for experimental structures to lie in low energy regions. Higher AUC values mean that the energies of the experimental structures with respect to the entire landscape grid are lower. For each of the 50 sets of proteins, AUC values were calculated for different values of the entropy weight “a” from Eq. (5) to find an optimal value for a. Fig. 1(a) shows the plot of percentile rank i vs δ_i curve for sarco-endoplasmic reticular Ca²⁺ ATPase (SERCA). The optimum value of a obtained is 1.35 with an AUC (red curve) of 0.84 vs. 0.81 (blue curve) when the entropy term was not included.

FIG. 1.

Measures of the distribution of the experimental structures in the low free energy regions of the landscapes. (a) Plot of percentile rank i/100 against the normalized free energy difference δ_i from the lowest free energy in grid for sarco-endoplasmic reticular Ca²⁺ ATPase (SERCA). Without including the entropy term, the area under the curve (AUC) is 0.81 (thin line), while for the entropy weight a = 1.35, the AUC increases to 0.84 (thick line). (b) Plot of AUC (sorted) for optimal weight of the entropy term for all 50 proteins investigated in this study. The AUC for 43 out of 50 cases is above 0.5 suggesting that the crystal structures are located in lower energy regions of the free-energy landscape.

Table S2 in the supplementary material⁸³ shows the maximum AUC values and the corresponding optimal values of a for all 50 proteins under study. If the crystal structures were not found to be preferentially located in low energy regions of the landscape, then the curve would be close to the diagonal from the origin which would result in an AUC of 0.5. In our dataset, we find that 43/50 proteins (86%) show an AUC above 0.5 (Fig. 1(b)). Interestingly, for a number of proteins, including the entropy term does not improve the AUC, whereas for some, it does improve the behavior significantly. We hypothesize that for at least those cases that improve the AUC when the entropy term is included; there is a significant entropic contribution to the conformational change. In Sections III B–III E, we discuss in detail the energy landscapes derived from the sets of experimental structures for three well studied proteins: lysozyme, serum albumin, and SERCA.

B. Case study I: T4 lysozyme

Lysozyme is an enzyme found in various plants and animals and is primarily used as a first line of defense against bacteria. In humans, it is found in many bodily secretions including saliva, tears, mucus, and milk as well as the secondary (granulocyte specific) granules of neutrophils and serves as a part of the innate immune system. It causes bacterial lysis by hydrolyzing the 1,4-β-glycosidic linkages between the N-acetyl muramic acid (NAM) and N-acetyl d-glucosamine (NAG) residues in peptidoglycan cell walls of bacteria.⁹³ Several types of lysozymes have been identified in diverse organisms, but the most important classes of lysozymes are the chicken-type (C-type), virus type (V-type), and goose type (G-type).

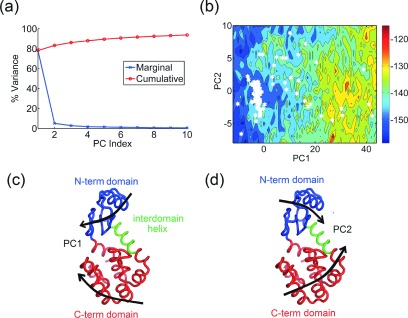
Discovered by Fleming in 1922,^94,95 lysozyme was not only one of the first proteins whose 3D structure was solved using X-ray crystallography^96,97 but also a first protein for which a detailed catalytic mechanism was proposed. Since then, more than 1500 structures of different members of the lysozyme superfamily have been determined using X-crystallography and NMR spectroscopy. After filtering structures with missing residues and outliers, we obtain 218 structures for human lysozyme (C-type), 183 structures for T4 lysozyme (V-type), and 586 structures for hen egg-white lysozyme (C-type). Here, we discuss results for the set of T4 lysozyme structures. The crystal structure⁹⁸ of the T4L protein (162 residues) shows that it is comprised of two domains, the N-terminal domain (residues 15-65), and the C-terminal domain (residues 80-162) connected by an inter-domain helix (residues 66-80) with a deep cleft between them where the peptidoglycan backbone of the bacterial cell wall binds. PCA on the set of 183 T4 lysozyme structures results in the first three PCs capturing an unusually high fraction of the variance in the first three PCs, with 78%, 5%, and 2% of the total variance, respectively (Fig. 2(a)). Both PC1 (Fig. 2(c)) and PC2 (Fig. 2(d)) correspond to combinations of hinge bending motion of the two domains with respect to each other and a twisting of the domains (refer to supplementary movies S1 and S2 for animations of the PCs⁸³). The difference between the two PCs is that the motions are at an angle of approximately 90° relative to one another. The hinge-bending motion between the two domains in T4L has previously been well documented as an intrinsic property of T4L based on experimental structures of various mutants.^99–101 This motion was also reported from MD simulations^102–104 and shown to be highly similar to the principal motions extracted from a set of crystal structures.¹⁰³ In addition, this motion was also characterized extensively in both hen-egg white¹⁰⁵ and human lysozymes¹⁰⁶ using normal mode analysis. The hinge-bending motion of the domains has been considered to be the functional motion for the entry of substrate and the release of products.

FIG. 2.

Bacteriophage T4 lysozyme. (a) Percentage of variance captured by the first 10 PCs from a set of 183 T4 lysozyme structures. (b) and (c) Visualization of PC1 and PC2 on the protein structure (thick black arrows) as a combination of hinge-bending and twisting motions of the N-term domain (blue) with respect to the C-term domain (red). (d) Energy landscape of human lysozyme along the PC1-PC2 coordinates (entropy weight a = 0). Crystal structures are denoted by white hexagons. The large cluster at lower values of PC1 corresponds to closed structures whereas the open structures are more broadly scattered along PC1 and PC2.

Upon projecting the structures onto the PCs (mean centered projections, also referred to as PC scores), it can be seen that most of the structures fall into a low energy cluster located at low values of PC1. The free energy landscape (as discussed in Section II) along PC1-PC2 is shown in Fig. 2(b). These are the structures where the two domains are “closed” with respect to one another and correspond to a conformation with bound ligand where the protein can be considered “closed.” On the other hand, the “open” forms of T4L are scattered along PC2 for a range of higher values in PC1. This is quite different from what we have observed for many other proteins where there are tighter clusters of open and closed forms. This broader unusual distribution possibly suggests that the two hinge motions may be coupled to each other and that at higher values of PC1, the structures can be sampled uniformly along each of the two PCs. The AUC was 0.69 suggesting that the crystal structures fall into low energy regions of the energy landscape.

C. Case study II: Human serum albumin (HSA)

Serum albumin (HSA) is the most abundant blood protein in mammals and is essential for maintaining the proper osmotic balance between body fluids inside blood vessels and tissues.¹⁰⁷ It is also the primary carrier of many hydrophobic molecules¹⁰⁸ in the blood such as steroids, fatty acids, thyroid hormones, and hemin and also transports certain metal ions like Cu²⁺ and Ca²⁺. Structurally, HSA is a globular protein (585 amino acids) comprised of several helices organized into three domains:¹⁰⁹ domain I (residues1-195), domain II (residues196-383), and domain III (384-585), which are homologous in both sequence and structure but arranged in an asymmetric fashion. Each of these domains can be divided into subdomains A and B where the subdomains IA, IB, and IIA can be thought of as forming a head for the molecule with IIB, IIIA, and IIIB forming a tail¹⁰⁹ giving the protein overall a heart shape.¹⁰⁸

The versatility of serum albumin to bind diverse water insoluble ligands ranging from fatty acids to metal ions is attributed to the diverse binding sites present on its domains. There are at least six major sites where ligand association occurs. Of the various ligand binding sites, the one on subdomain IIIA is the most active and preferentially accommodates several ligands.¹¹⁰ The primary binding sites for fatty acids and bilirubin are IIA and IIIA with their pockets located in similar regions containing hydrophobic side chains and gated by two helices A-h5 and A-h6. It is believed that the binding ability of these pockets is due to the strategic positioning of W214, K199, and Y411 which limit accessibility to solvent.^107,108 In addition, since IIA and IIIA share a common interface, the binding of ligands to one of the domains can affect the conformation and binding ability of the other.

We perform extensive analysis on a set of 99 structures of HSA for the stretch of residues 5-558 with no gaps. PCA on this set results in PC1, PC2, and PC3 capturing 85%, 7%, and 2% of the total variance, respectively (Fig. 3(a)). In PC1, domain I rotates as a single unit relative to domain III providing access to the ligand binding pocket within subdomain IIIA (Fig. 3(c)). PC2 involves a motion of subdomain IIIB relative to subdomain IB, providing access to the ligand binding site on IB. In addition, PC2 also involves a breathing motion of the helices A-h5 and A-h6 of subdomain IIIA, which is most likely responsible for the gating of this versatile pocket (Fig. 3(d)). It is worth noting that both PC1 and PC2 are motions involved in restricting access to the crucial IIIA binding pocket (see animations of the PCs in supplementary movies S3 and S4⁸³).

FIG. 3.

Human serum albumin (HSA). (a) Percentage of variance captured by the first 10 PCs from the set of 99 HSA structures. (b) Visualization of PC1 on the protein structure—domain I (red + magenta) rotates and moves away from domain III (blue + cyan) providing access to the ligand binding site on subdomain IIIA (cyan). (c) Visualization of PC2—subdomain IIIB (blue) moves away from subdomain IB (red) providing access to its ligand binding site. In addition, the two helices governing access to the binding site on subdomain IIIA (cyan) open and close in a breathing motion. (d) Energy landscape of HSA along PC1-PC2 (entropy weight a = 0). Crystal structures are denoted by white hexagons. The two largest clusters are clearly located in lowest energy regions (see free energy scale on the right hand side, from blue favorable to red unfavorable).

PC1 and PC2 separate the set of 99 structures into three primary clusters (Fig. 3(b)), with one cluster at high values of PC1 corresponding to structures with the domain I rotated and open to provide access to the domain IIIA binding pocket; a second cluster at low values of PC1 and high values of PC2 (structures with domain III closed and blocking access to the IB binding site) and a third cluster at low values of PC1 and low values of PC2 (representing structures with domain III open). We construct the free energy landscape for this set of proteins and obtain an AUC of 0.77 suggesting that a majority of the crystal structures fall into the minima of the free energy landscape. In addition, the landscape also clearly shows possible low energy transition paths between the different clusters.

D. Case study III: SERCA

SERCA is a Ca²⁺ ATPase found on membranes of the sarcoplasmic reticulum (SR) in muscle cells. The primary function of SERCA is the reuptake of Ca²⁺ ions (an active transport process) from the cytosol of muscle cells into the lumen of the SR (for internal storage of Ca²⁺) during muscle relaxation using energy derived from ATP hydrolysis. In other words, it is essential for maintaining a proper concentration of Ca²⁺ in the cytosol of muscle cells. There are several isoforms of SERCA encoded by three different genes which were reviewed in detail by Misquitta et al.¹¹¹

Early on, site-directed mutagenesis^112–115 and cryo-electron microscopy¹¹⁶ have elucidated extensive information about the structure and function of the various domains of the protein. The 994 residue protein is an integral membrane protein consisting of a large head on the cytoplasmic side, a small flexible stalk, and a transmembrane (TM) domain comprised of 10 TM helices and associated loops in the lumen of the SR. A crystal structure¹¹⁷ of the SERCA1a isoform (most abundant form) from rabbit fast-twitch skeletal muscle revealed that the cytoplasmic head consists of three domains: domain A (actuator) involved in the gating mechanism regulating the binding and release of Ca²⁺, domain N (nucleotide-binding) that binds ATP and ADP, and domain P (phosphorylation) containing residue D351, which is phosphorylated as part of the transport cycle reaction. A transport mechanism has been described¹¹⁸ in the form of a cycle to consist of two main conformations E1 and E2, where the E1 (open) conformation has high affinity for Ca²⁺ and binds it from the cytoplasm whereas the E2 (closed) conformation has low affinity for Ca²⁺ and releases it into the SR lumen. The transition from E1 to E2 proceeds through the phosphorylated states E1P and E2P and involves large conformational rearrangements and rotation of the N and A domains.

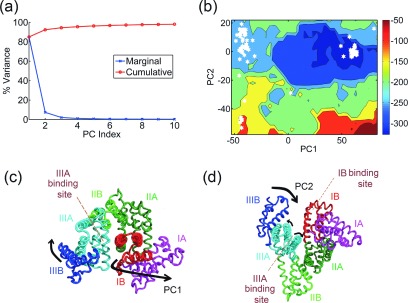
Several structures of SERCA are available from the PDB that sample multiple conformational states of the transport cycle which makes its analysis by PCA worthwhile. We compiled a dataset of 63 structures of rabbit SERCA1a and performed PCA on this set, which results in the PCs 1-3 capturing ∼57%, 27%, and 11% of the total variance, respectively (Fig. 4(a)). PC1 when visualized appears as a twisting motion of the actuator and nucleotide-binding domains whereas PC2 corresponds to a hinge-bending motion of the actuator and nucleotide-binding domains toward each other (Figs. 4(c) and 4(d)). Since the A-domain is linked to three helices of the TM domain through highly flexible linkers, it has been suggested previously that the rotation of the A domain could play a key role in the rearrangement of helices that open the gate to release Ca²⁺ into the lumen¹¹⁹ (see supplementary movies S5 and S6 for animations of the PCs⁸³).

FIG. 4.

Sarco-endoplasmic reticular Ca²⁺ ATPase (SERCA). (a) Percentage of variance captured by the first 10 PCs from the set of 63 SERCA structures. (b) Visualization of PC1—twisting motion of the N (green) and A (red) domains against each other whereas the TM domain (gray) remains relatively rigid. (c) Visualization of PC2 as an opening-closing motion of the N and A-domains towards each other. (d) Free energy landscape of the molecule along PC1-PC2 (entropy weight a = 1.35). Crystal structures are denoted by white hexagons.

When the structures are projected onto PC1 and PC2, they distinctly separate into two major clusters: one cluster at low values of PC1 and PC2 corresponding to E2 (closed) structures and another at high values of PC1 and PC2 corresponding to E1 (open) structures. Two minor clusters are also observed at high values of PC1 and low values of PC2, and these correspond to structures where the A and N domains have rotated, but a hinge-bending motion between the two domains has not occurred. The free energy landscape obtained from our analysis is shown in Fig. 4(b). The optimum weight for the entropy term obtained is 1.35 corresponding to an AUC of 0.84, again suggesting that most of the crystal structures fall into low energy regions of the energy landscape. One interesting feature of this landscape that differs from those of other proteins investigated is that the low energy basins corresponding to clusters are not connected to others by low free energy paths. This can be understood by interpreting the landscape in the context of the SERCA transport cycle which requires external energy in the form of ATP. This further shows that these coarse-grained free energy landscapes are powerful enough to identify high energy barriers that cannot be crossed without significant additional energy (e.g., ATP or guanosine triphosphate (GTP) driven mechanisms in proteins).

E. Predicting the transition pathway between the open and closed forms of HIV-1 protease

When there are two or more distinct conformations for a protein, it becomes important to understand how the protein passes between these conformations. For example, many proteins have a “closed” conformation after they bind their ligands and an “open” conformation when they have released the ligands. Using the intensely studied protein HIV-1 protease as an example, we show that transition paths between the open and closed conformations can be predicted by using the free energy landscapes.

HIV-1 protease is a retroviral aspartyl protease responsible for cleaving newly synthesized polyproteins to produce mature proteins in the infectious HIV virion. The protein is composed of two symmetrical identical subunits (each 99 residues long).¹²⁰ Each monomer consists of three domains: a flap domain (residues 33-62), a core domain (10-32 and 63-85), and a terminal domain (1-4 and 96-99). The active site is composed of the D25-T26-G27 amino acid triad from both the monomeric units and the protein functions only in the dimeric form.

Given its importance as a primary target for HIV therapy, more than 300 structures of this protein have been solved using X-ray crystallography in complex with diverse ligands. In addition, this protein has been a subject of extensive study by computational simulations, especially molecular dynamics.^121–125 Previous work³⁵ from our lab has shown that the principal motions extracted from sets of X-ray and NMR structures or snapshots from MD simulations of the protein agree well with the motions predicted by ANM. Crystal structures of mutants as well as MD simulations have identified distinct closed and open conformations of the protein. The flaps are assumed to open up, allowing for the binding of substrate and the release of products. Here, we discuss the transition between the open and closed forms within the context of free-energy landscapes generated using a set of 304 experimental structures of the protein.

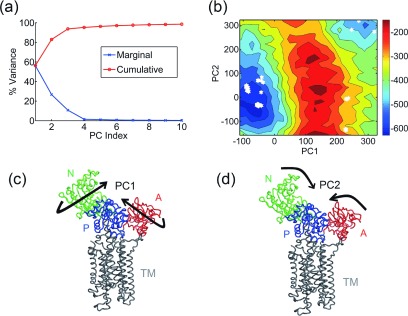
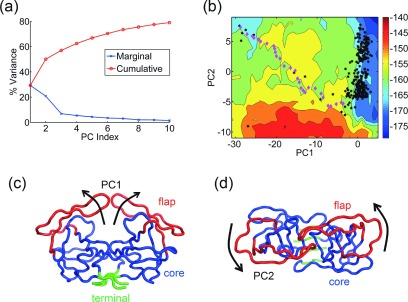
The PCs obtained from a set of 304 structures are shown in Fig. 5. The first three PCs capture 30%, 21%, and 7% of the total variance, respectively (Fig. 5(a)). PC1 is an opening and closing motion of the flaps resulting in significant changes for the ligand binding space (Fig. 5(c)). PC2 (Fig. 5(d)) is a twisting motion of the flaps (see animations in supplementary movies S7 and S8⁸³). When the intermediate structures along the transition pathway (discussed in Section II F) are projected onto the free energy landscape (Fig. 5(b)) from the set of structures, it can be seen that they fall on a relatively low free energy path between the two conformations. There are a few energy barriers which the protein crosses to reach the final state, but most interestingly the transition path passes through the regions of the landscape where experimental structures are located. Recall that in this Monte Carlo simulation, only energies and not entropies have been considered in making the decisions for the steps taken, so the path when plotted on the free energy surface does not follow the lowest free energy path. This suggests that the free energy landscapes obtained by the use of this method can guide the probable transition pathways between structures.

FIG. 5.

Predicted conformational transition pathway for HIV-1 protease. (a) Percentage of variance captured by the first 10 PCs from the set of 304 HIV-1 protease structures. (b) Visualization of PC1—opening and closing of the flap domains (red) against the core domain (blue). The terminal domain is shown in green. (c) Visualization of PC2—twisting motion of the flaps (red). (d) Free energy landscape of the molecule along PC1-PC2 (entropy weight a = 1.3). Crystal structures are denoted by black hexagons, while intermediate structures along the predicted transition pathway are shown as magenta diamonds. The predicted transition pathway follows a relatively low-energy path on the landscape along a diagonal path and passes close to several experimental intermediate forms.

IV. CONCLUSIONS

In this work, we have exploited the availability of multiple structures for groups of closely related proteins in the PDB to understand conformational changes in the context of their free energy landscapes constructed by combining knowledge based potential functions with entropy terms from elastic network models. By using principal components as a suitable coordinate system for landscape construction, we have been able to map out the free energetics of conformational changes along the most important directions of motion for several proteins. It has been found that most of the crystal structures tend to lie in regions of relatively low free energies. However, we also find cases where there were lower free energy regions on the landscape where a structure has not yet been observed. In principle, for cases such as these, it may be possible to pursue these analyses to suggest mutants that would occupy these lower free energies regions.

Further investigations are required to establish with certainty whether the conformational changes from higher order less important principal components affect in any significant way the free energy landscapes. The cases where the first few principal components are dominant should be the most reliable cases, but approximations to account for the effects of some higher order, less important motions can be developed in future studies.

Our analysis also sheds light on the two contrasting views about conformational changes in proteins: the conformational selection hypothesis or induced fit. According to the conformational selection hypothesis, proteins exist in equilibrium among their different conformations and a trigger (such as a binding event) causes a shift in the equilibrium towards one of the states. This can be contrasted with the induced-fit hypothesis where the protein is assumed to exist in one conformation only and where a triggering event such as binding induces a change in conformation of the protein. We find from our analysis of a set of 50 proteins that most of the crystal structures do occur in regions of relatively low free energy on coarse-grained landscapes. With the exception of a few cases (e.g., T4 lysozyme), the structures are clustered along the PC coordinate and each of these clusters can be considered to represent a conformation of the protein. Further, the clusters seem to occupy a low free energy basin within the conformational space and are often connected to each other through narrow low free energy paths (which suggest possible transition paths between the conformations), as can be seen from the landscapes of T4 lysozyme, serum albumin, or HIV-1 protease. However, in a few cases (e.g., SERCA), the clusters are separated from each other by high energy barriers. These can be considered to represent cases that require extra energy (from ATP or GTP interactions) which is not considered in our calculations. In summary, our analysis suggests that such coarse-grained free energy landscapes of proteins can be used to shed light on the extent to which conformational selection or induced fit is operative in a system. From the present point of view, interpretation of the difference between conformational selection and induced fit can be made directly from the free energy landscapes. Whenever the conformations are accessible without requiring passage over high energy barriers, this would be conformational selection, but when there are high free energy barriers, this would require induced fit arising from favorable interactions with the ligand.