Laminar microvascular transit time distribution in the mouse somatosensory cortex revealed by Dynamic Contrast Optical Coherence Tomography

Abstract

The transit time distribution of blood through the cerebral microvasculature both constrains oxygen delivery and governs the kinetics of neuroimaging signals such as blood-oxygen-level-dependent functional Magnetic Resonance Imaging (BOLD fMRI). However, in spite of its importance, capillary transit time distribution has been challenging to quantify comprehensively and efficiently at the microscopic level. Here, we introduce a method, called Dynamic Contrast Optical Coherence Tomography (DyC-OCT), based on dynamic cross-sectional OCT imaging of an intravascular tracer as it passes through the field-of-view. Quantitative transit time metrics are derived from temporal analysis of the dynamic scattering signal, closely related to tracer concentration. Since DyC-OCT does not require calibration of the optical focus, quantitative accuracy is achieved even deep in highly scattering brain tissue where the focal spot degrades. After direct validation of DyC-OCT against dilution curves measured using a fluorescent plasma label in surface pial vessels, we used DyC-OCT to investigate the transit time distribution in microvasculature across the entire depth of the mouse somatosensory cortex. Laminar trends were identified, with earlier transit times and less heterogeneity in the middle cortical layers. The early transit times in the middle cortical layers may explain, at least in part, the early BOLD fMRI onset times observed in these layers. The layer-dependencies in heterogeneity may help explain how a single vascular supply manages to deliver oxygen to individual cortical layers with diverse metabolic needs.

1. Introduction

Blood flow [1, 2], delivered by major cerebral arteries to the microvasculature, supplies oxygen to support the metabolic requirements of normal brain function. While the importance of cerebral blood flow is well-known, microvascular flow distribution at the site of oxygen delivery is also critical to the biophysics of oxygen extraction and consequently, the interpretation of functional neuroimaging signals based on blood oxygenation. In particular, the transit time of blood through the pre-capillary arterioles and capillary bed, where most oxygen is delivered to tissue [3], determines the maximal fraction of oxygen molecules that can be extracted from the vasculature through diffusion [4]. Additionally, the time lag between an increase in blood flow and the resulting microvascular oxygenation increase is determined, in part, by the transit time. Thus, transit times contribute to the kinetics of functional neuroimaging signals based on blood oxygenation [5]. Particularly, in order to correctly interpret observable laminar kinetics in blood-oxygen-level-dependent functional Magnetic Resonance Imaging (BOLD fMRI) [6–10], laminar differences in transit times, if present, must be accounted for. Thus, transit time is a fundamental microcirculatory parameter of importance to both oxygen delivery and the kinetics of functional neuroimaging signals.

As capillaries are heterogeneous in topology and flow supply may be non-uniform, blood may travel between an artery and vein by numerous paths through the capillary bed. Rather than a single transit time, these paths are characterized by a distribution of transit times [11]. Recently, it was demonstrated theoretically that this capillary transit time heterogeneity, the standard deviation of this distribution, potentially leads to non-uniform oxygen extraction in micro-domains [12]. Moreover, it was shown that the transit time distribution, rather than mean transit time (MTT) alone, most directly determines the maximum oxygen extraction that a capillary bed can support [12]. Recent theoretical work has implicated pathological transit time heterogeneity in a number of diseases including stroke [13], ischemia [14], Alzheimer’s disease [15], traumatic brain injury [16], and diabetic nephropathy [17], leading to renewed interest in this subject. In spite of these theoretical studies highlighting the importance of transit time distribution, efficient and robust experimental methods that quantify this distribution at the capillary level have been lacking.

Neuroimaging techniques such as Positron Emission Tomography (PET) can indirectly determine MTT from the central volume theorem [18], as the ratio of cerebral blood volume (CBV) to cerebral blood flow (CBF) [19]. In Magnetic Resonance Imaging (MRI), the passage of a CBV tracer through the vasculature after bolus injection [20] can be used to comprehensively assess hemodynamics. In particular, if residue functions, describing the fraction of tracer present in the vasculature over time, can be determined by fitting procedures, then CBF, CBV, and MTT can all be determined after an intravenous bolus injection [21]. Importantly, information about the transit time distribution is inherently contained in fit residue functions [22]. However, arteriovenous transit time distributions based on residues from MRI bolus tracking inherently average all capillary paths and provide no spatial information within a voxel. Thus, laminar or localized transit time distributions are not accessible with macroscopic bolus tracking and imaging techniques.

Optical techniques such as laser Doppler flowmetry [23], diffuse correlation spectroscopy [24], and laser speckle flowmetry [25] use statistical metrics to determine the motion of scattering from red blood cells (RBCs). However, the shape of the power spectrum or autocorrelation function measured by these techniques provides little information about the underlying velocity distribution [26], and the spatial distribution of flow across micro-vessels is lost due to multiple scattering events. Moreover, the variable and unknown scattering properties of biological tissue (and consequently the number of dynamic vs. static scattering events) make absolute quantification challenging using these methods.

Optical microscopy of flow in microvessels can determine the transit time distribution, particularly if used in conjunction with a connectivity graph [27]. Two-photon microscopy (2PM) line scans across vessels can quantify velocity and flux, but require individual sampling of vessels which can be time consuming [28]. Although alternative methods, not based on oriented line scans, can be applied [29], scanning speeds, penetration depths, and fields-of-view remain limited. Fluorescent tracer kinetic-based techniques have been applied with 2PM using bolus injections, albeit with penetration depths limited to a few hundred microns [30], only a fraction of the rodent cortical thickness. Doppler Optical Coherence Tomography (OCT) can assess flow in arteriolar supply zones [31], but operates most accurately in large vessels with a well-defined cross-sectional flow profile, rather than capillaries. Recently, decorrelation-based [32–36] OCT metrics of capillary speed or count-based [37] OCT metrics of capillary speed, flux, and density have been developed. These methods are high throughput, but require calibration of the focal spot size to relate either decorrelation rate or pulse width to RBC speed. As light propagates deeper into scattering tissue, the focal spot degrades in a manner that depends on tissue-specific scattering properties, and can be difficult to calibrate. Thus, decorrelation or count-based metrics are less reliable deep in the cortex where the focal spot degrades in a spatially (and possibly time-) varying manner. Hence quantification of capillary flow parameters in deep cortical layers remains challenging.

Here, we introduce Dynamic Contrast Optical Coherence Tomography (DyC-OCT), a new technique based on cross-sectional imaging of intravascular tracer kinetics, for measurement of capillary transit time distributions at the microscopic scale. After validation, we apply this new technique to comprehensively characterize the transit time distribution across the mouse neocortex. We focus on addressing the following questions: Could the distribution of transit times across cortical depths plausibly account for laminar differences in BOLD fMRI? Do layer-specific differences in transit time heterogeneity correlate with differing metabolic requirements of individual cortical layers?

Our results clearly show earlier transit times and less transit time heterogeneity in the middle cortical layers. The early transit times in the middle cortical layers provide one possible explanation for laminar variations in fMRI BOLD onset time that does not invoke laminar variations in activation kinetics. The low transit time heterogeneity in layer 4 may explain, in part, how the vascular supply optimizes oxygen extraction efficacy to match the higher metabolic needs of this layer. More broadly, the new DyC-OCT technique affords a novel perspective of microvascular networks, with the unique capability of simultaneously measuring transit time distributions across cortical laminae.

2. Methods and Materials

Optical Coherence Tomography (OCT) [38] focuses a beam of light into tissue and measures the backscattered or backreflected light from different depths in the tissue. Beam scanning generates depth-resolved images, similar to B-mode ultrasound. In the brain, imaging depths up to and exceeding 1 mm are possible with OCT at 1300 nm. A number of OCT angiography methods have been developed for the visualization of blood vessels within scattering tissue [39–43]. Recently, a highly sensitive OCT angiography method was proposed to separate both dynamic and static signals in cortical tissue [44].

One of the strengths of OCT in clinical applications has been the fact that imaging can be performed without contrast agents. Here, we instead use the OCT angiography technique to observe time-resolved changes in the dynamic signal during the passage of an exogenous tracer through the imaged field-of-view. For this study, an FDA-approved intravenous nutritional supplement called Intralipid, recently shown to enhance contrast in steady-state Doppler OCT images following intravascular injection [45], was used. Indicator-dilution theory was then applied to the dynamic scattering signal to extract quantitative information about the mouse neocortical hemodynamics following bolus injection.

2.1 Optical Coherence Tomography (OCT) System Setup

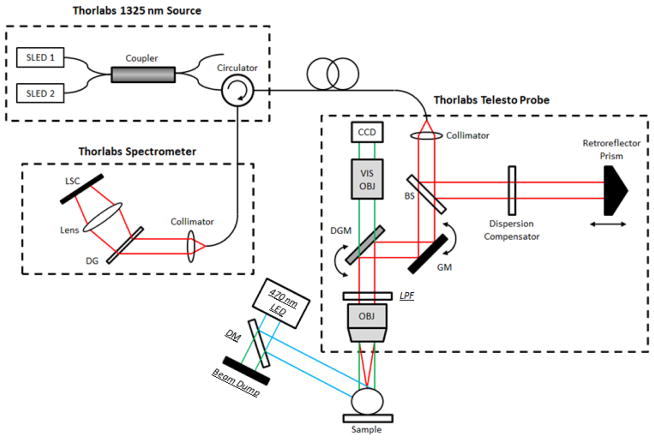
A 1325 nm spectral / Fourier domain OCT microscope [46] was used to image the mouse neocortex, as shown in Figure 1. The light source consisted of two superluminescent diodes combined to yield a bandwidth of over 100 nm. The theoretical axial (depth) resolution, after computational spectral shaping of the raw spectrum, was 7 μm in air (5.3 μm in tissue). The spectrometer, with a 1024 pixel InGaAs line scan camera, was operated at 91 kHz. Imaging was performed with a 5x objective, yielding a transverse resolution of 15 microns, and a 10x objective, yielding a transverse resolution of 7.5 microns. The system sensitivity, the minimum sample reflectivity that can be detected, was 91 dB.

Figure 1.

Imaging setup. By modifying a Thorlabs Telesto 1325 nm OCT system, spatially co-registered dynamic fluorescence and OCT imaging was performed simultaneously. The schematic for this system is shown with the following abbreviations: SLED – Superluminescent Diode, LSC – Line Scan Camera, DG – Diffraction Grating, DM – Dichroic Mirror, GM – Galvanometer Mirror, DGM – Dichroic Galvanometer Mirror, LPF – Long-Pass Filter, OBJ – Objective Lens, VIS – Visible, BS – Beam Splitter, CCD – Charge-Coupled Device Camera. Italicized and underlined labels denote components added to enable fluorescence imaging. Due to the spatial constraints imposed by the commercial probe, the long-pass filter, used to reject stray excitation light, was placed in the OCT beam path. This caused an estimated 15% excess loss in OCT signal intensity. Components for fluorescence imaging were removed when the fluorescence channel was not used. Cyan lines denote excitation light, green lines represent light with a wavelength in the emission spectrum, and red lines represent the OCT beam with a center wavelength of 1325 nm.

2.2 Modified Setup for Simultaneous OCT and Fluorescence Imaging

In order to acquire spatially and temporally co-registered fluorescence and OCT data, the imaging setup was temporarily modified, as noted in Figure 1. To collect fluorescence light, a wide-field camera built into the OCT probe for alignment of the sample was used. A narrow-bandwidth 470-nm LED light source was used for excitation and was additionally short-pass filtered with a 490-nm dichroic mirror. To reject backscattered excitation light, an absorptive 515-nm long-pass filter was placed in front of the camera. Due to the spatial restrictions of the enclosed commercial OCT probe, this filter had to be placed in the path of the OCT beam which is believed to cause ~15% round-trip drop in OCT signal intensity.

2.3 Animal Preparation

The animal procedures were approved by the Institutional Animal Care and Use Committee at UC Davis. Male C57/BL6 mice (n = 10; 20–35 grams) were used in this study. The mice were initially anesthetized with 1.5% v/v isoflurane with a gas mixture of 80% air and 20% oxygen. After successful induction of anesthesia, the mice were mounted on a stereotactic frame with continued delivery of 1–1.5% v/v isoflurane, modulated as necessary to maintain healthy and steady breathing throughout the surgical and imaging procedures. Once in the frame, the scalp was retracted, the fascia was removed, and the skull was cleaned and dried using a gauze pad. Using a progressively finer series of dental burrs, a ~3 × 3 mm² region of the skull lateral to the midpoint between lambda and bregma was thinned to within ~30 μm in thickness. This made the skull more transparent, and enabled imaging of the somatosensory cortex through the thinned region without requiring an invasive craniotomy. A 5 mm diameter coverglass was glued to the thinned region. A large ball joint attached to the stereotactic frame was used to position the mouse such that the coverglass was perpendicular to the beam path. Throughout the surgical and imaging procedures, the animal’s core temperature was maintained at 37 degrees Celsius using a heating blanket (Harvard Apparatus USA). Anesthetic levels were titrated carefully by an investigator experienced in monitoring the breathing rate and pattern to maintain end-tidal pCO2 levels around 4%, as measured by a capnometer (Columbus Instruments).

2.4 Bolus Injection Protocol

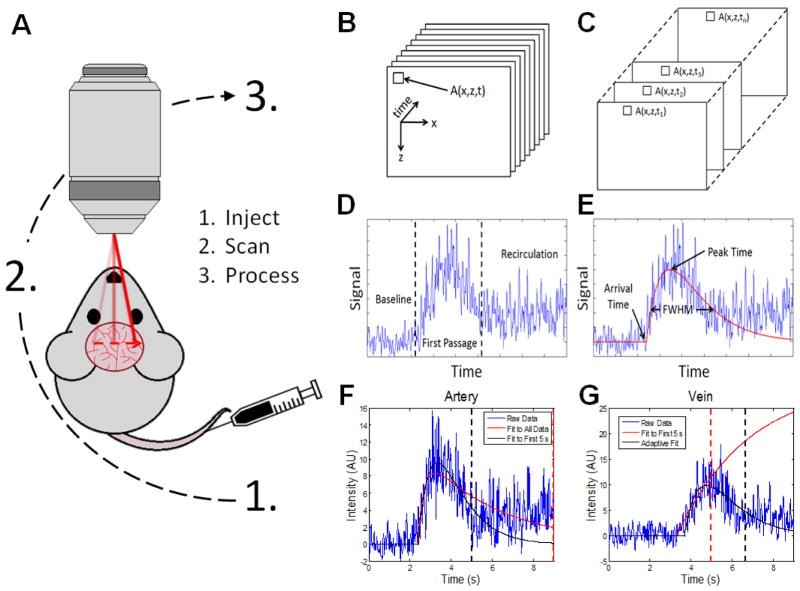
A tracer bolus was injected into the tail vein using either a 27 or 31 gauge syringe as shown in Figure 2A. The bolus was restricted to ~100 μL (3 mL/kg weight, representing approximately 3.8% of the mouse blood volume) to minimize changes in cortical hemodynamics due to the bolus itself. Furthermore, the bolus was injected quickly (~0.5 seconds) to approximate an idealized delta input function and maximize the DyC-OCT signal. In practice, input delta functions could not be achieved due to transit time dispersion from the injection site to the cortex. For the DyC-OCT measurements, Intralipid 20% was used as the contrast agent. For the simultaneous DyC-OCT and fluorescence measurements, a 4:1 mixture of Intralipid 20% and saline-dissolved fluorescein isothiocyanate–dextran (FITC-dextran) was used. The final FITC-dextran concentration was 5% weight by volume.

Figure 2.

DyC-OCT image acquisition and processing. DyC-OCT imaging produces 3-D stacks of data which are then processed along the temporal axis by fitting a model to the indicator-dilution response represented by the OCT signal at every (x,z) location. A) DyC-OCT follows a simple imaging protocol in which an OCT tracer is injected via the tail vein, repeated B-scans are acquired at the region-of-interest directly following injection, and the acquired data is processed. B) DyC-OCT generates a 3-D stack of temporally-resolved B-scans at the region-of-interest as the tracer passes through. C) Selection of the temporal profile associated with a single location. D) A typical DyC-OCT signal showing a baseline level before the bolus arrives, a sharp increase followed by slow decrease in signal with the first passage of the tracer bolus, eventually settling at a level higher than baseline due to recirculation of the tracer. E) Second-Order Plus Dead Time (SOPDT) model fitting and extraction of features such as arrival time, FWHM, and peak time. F) Recirculation degrades the accuracy of the model’s fit. The red dotted line associated with the poor fit, shown in red, marks the cutoff point which includes recirculation. The black dotted line associated with the better fit, shown in black, marks a cutoff at 5 s that avoids recirculation. G) However, when the same 5 s cutoff from F) (red dotted line) is used in a different vessel, the fit, shown in red, is poor. A better fit, shown in black, is achieved using an adaptively determined cutoff (black dotted line). For this reason, the cutoff for fitting was adaptively determined for each vessel.

2.5 DyC-OCT Imaging Protocol

To capture the change in scattering signal as the bolus passes through the vasculature, repeated B-scans, or cross-sectional images, of the same area were acquired to generate a 2-D time-resolved cross-section of the cortex. 1000 B-scans, consisting of 1024 axial scans each, were acquired every 13 ms (77 Hz) along a 1–2.5 mm lateral span of the cortex to observe the dynamic signal change due to tracer passage over a time window of 13 seconds starting at the time of tracer injection. An appropriate imaging plane was selected based on several criteria. The first step for imaging selection was to ensure placement occurred over the somatosensory cortex, using the skull sutures as a guide. Next, a region for imaging was chosen that contained at least one large artery and one large vein to ensure that the distribution of microvascular hemodynamic information covered all vascular compartments. After this, the final location within the somatosensory cortex was determined by the penetration depth of the scan to ensure vessels were measured from as many cortical layers as possible. Visibility of deeper layers was affected by a number of factors including surface vessel position and thinned-skull window quality, which means that the optimal imaging position changed slightly from animal to animal.

2.6 Fluorescence Imaging Protocol

To validate the DyC-OCT methods, spatially and temporally co-registered DyC-OCT and fluorescence measurements were acquired in surface vessels of the mouse cortex. A custom LabView program was used to simultaneously acquire wide-field fluorescence images and B-scans over the same region-of-interest at a rate of 30 Hz.

2.7 Data Processing

Several methods were developed to analyze the DyC-OCT data both parametrically and non-parametrically on a pixel by pixel basis.

2.7.1 OCT Angiography

OCT angiograms were produced by removing the static scattering component of the OCT signal [44]. This was accomplished by performing a complex subtraction, or high-pass filtering, along the slow axis of repeated B-scans. This subtraction removes the static scattering components, which do not change over time, while highlighting the areas where the scattering signal does change, as in vasculature with blood flow. This angiogram was further improved by applying a phase correction before the complex subtraction to account for sub-pixel axial movement.

2.7.2 DyC-OCT Signal

The DyC-OCT data was acquired as a series of repeated B-scans (Figure 2B). First the static-scattering components of the signal were removed using angiography methods described above to improve detection of the tracer signal. This generates a second series of repeated angiogram frames, one fewer in number than the original series. The time-resolved dynamic signal at a given pixel can be obtained by extracting the values of that pixel from each angiogram frame over time (Figure 2C). The passage of the tracer at a given pixel causes a change in the dynamic signal shown in Figure 2D that has several distinct features. First, the baseline (pre-injection) value is attributed to the RBC scattering signal before the tracer arrives. Second, a sharp increase in signal as the tracer passes through for the first time is followed by a slower decrease. Third, settling of the signal at a level higher than baseline, due to recirculation of the temporally dispersed tracer, is observed. This occurs when the injected tracer passes through the body, returns to the heart, and is pumped back through the imaging plane. This typically happens before complete decay of the tracer signal. For all steps below, the angiogram data was averaged 3x laterally 3x axially and 3x temporally to reduce speckle noise.

2.7.3 Signal Increase Mask

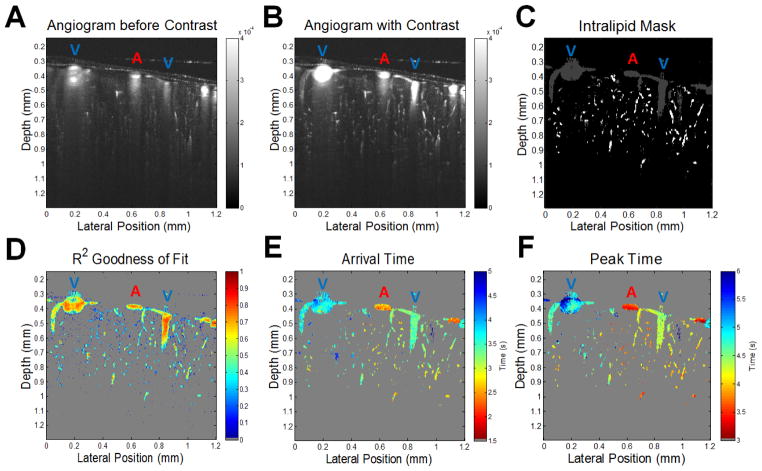
The first step in visualizing this data is to determine the increase in the angiogram signal caused by the tracer bolus shown in Figure 3A–B. A baseline signal is determined by averaging the first 1 to 2 seconds of data before the bolus arrives. Then the global maximum of the signal during the measured time course is determined after additional temporal averaging to reduce noise. The maximum signal divided by the baseline yields the relative increase in signal. The next step is to threshold out the background noise to create a mask of the vasculature where the tracer has traveled as shown in Figure 3C. To do this, the mean and standard deviation of the noise in the signal increase map are measured by using a region of air above the skull. The threshold for the mask was set 4 standard deviations above this noise floor corresponding to ~35% increase in signal to isolate regions of interest in the data and to reduce processing time.

Figure 3.

DyC-OCT cross-sectional mapping of the mouse cortex. Pixel-by-pixel analysis of the DyC-OCT signal following bolus injection of a contrast agent, reveals functional information about microvascular networks in the mouse cortex. Surface arteries and veins, marked with a blue “V” or red “A” respectively, were identified prior to DyC-OCT imaging through inspection of an enface angiogram. A–B) Intralipid (contrast) injection significantly increases the angiogram signal in the vasculature in the imaged cross-sectional plane. C) The gray and white masks show where the increase in angiogram signal exceeded the noise threshold. The white mask represents the vessels that were further analyzed after size and goodness of fit thresholding. Large vessels and noise (gray mask) were rejected. D) Goodness of the model’s fit shows that the best fits correspond to regions with a large signal increase. E–F) The arrival times and peak times of the tracer, extracted from them SOPDT model, separate arteries and veins, and illustrate capillary heterogeneity.

2.7.4 Parametric Model

To quantify parameters such as bolus duration and arrival time, a second-order plus dead time (SOPDT) model is used after subtracting off the baseline signal. This phenomenological model shown in Figure 2E uses arrival time (θ), signal frequency (ω), amplitude (A), and dampening (ξ) variables to generate a curve similar to the angiogram signal over time for each point. In the Laplace (s) domain this model is given by:

$$\mathrm{G}(\mathrm{s})=\frac{e^{-\theta s}}{s^2+2\xi \mathrm{\omega }\mathrm{s}+{\mathrm{\omega }}^2}$$ (1)

In practice, however, the model is converted to the time (t) domain for faster fitting.

$$\mathrm{g}(\mathrm{t})=\text{Au}(\mathrm{t}-\theta )\left[\frac{e^{\omega (t-\theta )\left(\sqrt{{\xi }^2-1}-\xi \right)}-e^{\omega (\theta -t)\left(\sqrt{{\xi }^2-1}+\xi \right)}}{\left(2\omega \sqrt{{\xi }^2-1}\right)}\right]$$ (2)

In the above equation, u is the Heaviside (unit step) function. A study comparing indicator-dilution models shows that the SOPDT model fits indicator-dilution curves better than the traditional gamma-variate model [47].

2.7.5 Fit Optimization and Quality Control

The variables in the SOPDT model were optimized using a non-linear least-squares method after subtraction of the baseline signal and normalizing the signal to fall approximately between 0 and 1. Because tracer recirculation invalidates the bolus model (Eq. (2)) after the recirculation time (Figure 2F), only the time window before recirculation occurs should be used for fitting. If a single cutoff time for the fitting window is used across the entire data set (Figure 2G), the fit will be poor in vessels with recirculation times before or after the cutoff. To achieve the best fit, the model was applied twice under different conditions. First, a generic cutoff time, typically between 6.5–13 seconds, was used for every point in the map. For some points, this cutoff time was too early and for others it was too late, so the model fit was not optimal overall; however, a relatively accurate arrival time was still extracted. Next, the model was fit again using a pixel-wise time window determined by the “adaptive” recirculation cutoff time, obtained by adding a constant, typically ~3 seconds, to the arrival time determined by the first fit. This second fit was more accurate across the observed wide range of arrival times (Figure 2G).

The first fit was made using initial parameter values that are physiologically likely based on experimental observations. The arrival time (θ) was given an initial value of 2 seconds based on the average time it takes the bolus to arrive at the destination from the time of injection and was additionally constrained to be greater than zero. The damping parameter (ξ) was given an initial value that was critically damped and was constrained to be critically damped or over damped to avoid non-physiological oscillations in the fit. The frequency term (ω) was initially set to 0.2 Hz and was also constrained to be greater than zero to prevent the SOPDT fit from inverting. Finally the amplitude (A) was given an initial value of 1 as the signal had already been normalized. The amplitude term was included to allow for better fits when the noise was high and, similarly to the frequency term, was constrained to be greater than zero to prevent the fit from inverting. The second fit, which used the adaptive time window described above, then used the optimized fit parameters from the first fit as its starting parameters. Once the adaptive window fit had been made, several quality control measures were taken. First, any fits that had R² goodness of fit values less than 0.3 were removed. Additionally, fits with damping parameters that were too high were rejected as this can cause the fit to plateau in a non-physiological shape. Finally, fits which approximated delta functions, in which the arrival, peak, and return times were too close together to be physiologically possible, were removed. These steps ensured that the Intralipid signal was accurately measured and that poor or erroneous fits were rejected.

2.7.6 Microvessel Selection

After a final map of the transit characteristics had been generated as shown in Figure 3E–F, individual vessels were automatically segmented and studied. Because the focus of this study is to examine microvascular transit kinetics, the macrovascular networks were thresholded out as shown in Figure 3C. As many vessels were imaged at an angle, their areas presented in the imaging plane may be larger than their true cross-sectional areas. To prevent these microvessels from being inappropriately rejected and to estimate the radii as accurately as possible, steps were taken to estimate the true cross-sectional areas. Ellipses were fit to each vessel, and the ratio of the minor axis length to the major axis length of each ellipse was multiplied with the measured area to correct for the angle and to obtain a more accurate estimate of the cross-sectional area and radius. Vessels were rejected if their corrected cross-sectional areas were greater than 800 μm² which corresponds to an estimated radius of ~16 μm. A histogram of the estimated radii of the sampled vessels across all animals (Supplemental Figure 1C) clearly shows that macrovessels have been excluded.

2.7.7 Layer-Dependent Analysis

Features of the DyC-OCT data were analyzed as a function of depth in the cortex. Here, we examined the DyC-OCT signal in the microvasculature to study trends associated with different layers. Cortical layer boundaries were approximated from the Allen Mouse Brain Atlas (2011) [48, 49]. By combining white light images of the OCT scan location on the mouse skull with information from cross-sectional images, the slice location could be accurately determined in brain atlas coordinates. The atlas, providing both cortical region and layer information, was used to determine cortical layer boundaries for the imaged region of interest, and to remove any vessels not located in the somatosensory cortex. Layer thicknesses, used for partitioning data, were averaged over the range of stereotaxic coordinates where OCT imaging was performed. Averaged thicknesses were used due to the finite extent of OCT images, and the difficulty of imaging deep into the cortex at precisely the same stereotaxic coordinates in each animal, due to variability in surface vasculature, as described in Section 2.5.

2.7.8 Transit Time Distribution Quantification

Indicator-dilution theory shows that if a tracer is injected into a vascular network, and the tracer concentration is measured at an upstream location and a downstream location, then the transit time distribution (TTD), or transport function, of the network connecting the two points can be calculated. The venous signal (proportional to the venous concentration) is equal to the TTD convolved with the arterial signal (proportional to the arterial concentration) as shown here where c_v and c_a are the venous and arterial concentrations respectively, * denotes a convolution, and h(t) is the TTD [50]:

$${\mathrm{c}}_v(\mathrm{t})=({\mathrm{c}}_a\ast \mathrm{h})(\mathrm{t})$$ (3)

Furthermore, the central volume theorem allows us to calculate the CBF with knowledge of the mean transit time (MTT) and cerebral blood volume (CBV), or the CBV given the CBF and MTT [50]:

$$\text{CBV}=\text{CBF}\times \text{MTT}$$ (4)

The relationship between the DyC-OCT signal in venous vasculature related to the signal in connected arterial vasculature is given by a convolution with the TTD described in equation 3. To extract a quantitative measure of the TTD from two measured signals, a discrete deconvolution can be performed either on the raw data or on a fit to the data. The noise and recirculation effects in the raw signal may cause poor deconvolution and extraction of the TTD, so the modeled signals may also be used. Because a convolution in the time domain is the same as a multiplication in the transform domain, the deconvolution can also be directly calculated from the SOPDT model as a division of the venous signal by the arterial signal in the frequency domain followed by an inverse Laplace transform.

$$\mathrm{h}(\mathrm{t})\approx {\mathcal{L}}^{-1}\left\{\frac{{\omega }_v^2}{{\omega }_a^2}{e}^{-({\theta }_v-{\theta }_a)s}\frac{s^2+2{\xi }_a{\omega }_{a}s+{\omega }_a^2}{s^2+2{\xi }_v{\omega }_{v}s+{\omega }_v^2}\right\}$$ (5)

Here h(t) is the TTD, ℒ⁻¹ denotes the inverse Laplace transform, and the a and v subscripts denote arterial and venous/capillary fitted parameters respectively. As h(t) is typically taken to be a probability density function, it has been normalized to ensure an area of one. The MTT can then be determined as the centroid of the TTD.

3. Results

The results are organized as follows: first, validation of the DyC-OCT technique is described. Second, the analysis of bolus arrival time, the most robust DyC-OCT measure, as a function of cortical depth and layer, is described. Third, bolus peak time is shown to correlate well with the MTT of the TTD function. Last, since bolus peak time can be robustly measured and is a proxy for mean transit time, analysis of bolus peak time is also presented across cortical depths and layers.

3.1 Validation

As shown in Figure 3A–B, the Intralipid bolus transiently increases the angiogram signal in vasculature. The relative increase was used to form a binary mask to restrict subsequent fitting analysis (Figure 3C). Based on fitting, parameters describing tracer kinetics in individual vessels over the cortical depth could then be visualized as images (Figure 3D–F). These images showed expected clear differences between arteries (A) and veins (V) based on arrival times or peak times alone. Moreover, as shown in Supplemental Figure 2, the arrival times in a dural vessel increased from upstream to downstream, with a profile consistent with laminar, non-mixing flow streams. Importantly, cerebral blood flow (CBF), as measured by Doppler OCT in surface vessels, did not change during either the injection or the bolus passage (Supplemental Figure 3).

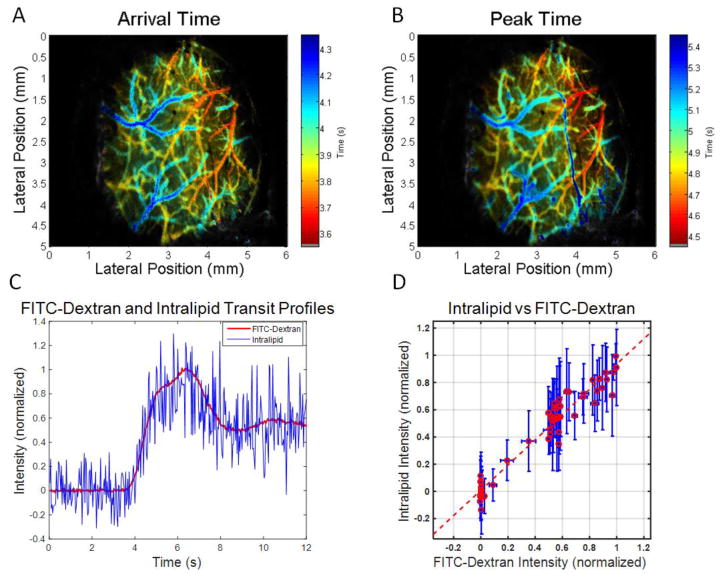
Intralipid was believed to behave as a blood plasma tracer due to its relatively small mean particle diameter of 226 nm [51], over an order of magnitude smaller than the diameter of RBCs. In order to validate Intralipid as a plasma tracer, its kinetics were compared to those of FITC-dextran during injection and imaging of a mixture containing both. By performing spatially and temporally co-registered DyC-OCT and fluorescence imaging, transit profiles of both tracers could be acquired with a single injection. In spite of the larger variance of the Intralipid signal, attributed to speckle noise, transit profiles at the same location in a vein were highly correlated as shown in Figure 4C. These profiles show a strong, linear relationship in Figure 4D with an R² value of 0.94 and p ≪ 0.0005. The DyC-OCT error bars get larger as the signal level increases, due to the multiplicative nature of speckle noise. Due to the incoherent nature of fluorescence emission, fluorescence imaging is not affected by speckle noise and has lower signal variance. These results indicate that although speckle increases the noise in the concentration curves, Intralipid kinetics are highly correlated to those of a standard fluorescent plasma tracer [52] at the cortical surface, supporting the application of DyC-OCT to measure transit times.

Figure 4.

DyC-OCT validation. Simultaneous and co-registered dynamic fluorescence and DyC-OCT show that Intralipid dilution curves are similar to those of FITC-Dextran (a blood plasma tracer), after a simultaneous bolus injection containing both. Wide-field dynamic fluorescence images and OCT B-scans were acquired at a rate of 30 Hz over the same field of view. A–B) By applying the processing methods described in Figure 3 to dynamic fluorescence data, en face arrival time and peak time maps were generated for the superficial vasculature. C) Normalized DyC-OCT (blue) and fluorescence (red) intensity signals corresponding to the passage of their respective tracers through the same vein location. D) The strong linear relationship (dotted red line) between the two signals is shown to have an R² value of 0.94 and p ≪ 0.0005. Data were binned in segments of 0.2 seconds with vertical error bars showing the standard deviation of the OCT signal and horizontal error bars showing the standard deviation of the fluorescence signal within each temporal bin.

Further validation of DyC-OCT was performed by comparing the arrival times from two consecutive injections in the same field of view in the same mouse brain. Measurements were shown to be highly repeatable in larger vessels with estimated radii between 9 and 16 μm; however, error between the two measurements increases as the vessel size decreases (Supplemental Figure 4). While this discrepancy may be partially due to the effects of averaging fewer pixels in the smaller vessels, physiological factors are also believed to contribute. These factors may include fluctuations in microvascular flow patterns [28] and changes in breathing or level of anesthesia, although changes in blood viscosity due to the injections [53] cannot be ruled out as sources of error.

3.2 Arrival Time Analysis

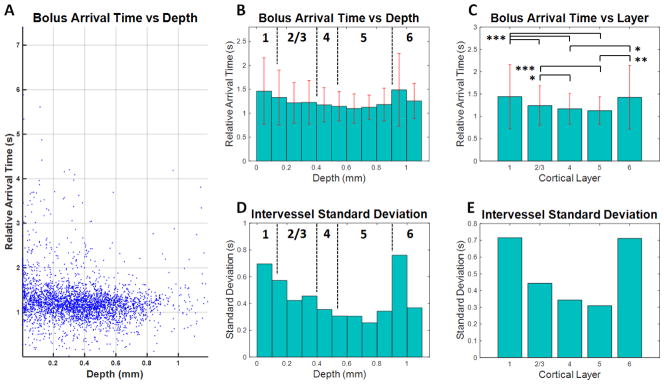
In order to describe the laminar arrival time distribution across cortical depths, data from DyC-OCT experiments in 10 animals were grouped either according to cortical depth (Figure 5B) or according to cortical layer (Figure 5C). These data sets were temporally aligned by using the earliest mean arrival time from the supplying macrovasculature. After alignment, the earliest arrival time was subtracted from all vessels, such that the earliest vessel had an arrival time of 0. An alternate alignment based on the mean arrival time across all microvessels in each animal was also tested and yielded similar results (Supplemental Figure 5 & Supplemental Figure 6). In summary, the minimum arrival time was identified in layer 5, around 600–700 microns in depth, and the middle cortical layers (layers 4–5) displayed the shortest arrival times on average.

Figure 5.

Arrival time as a function of depth in the mouse somatosensory cortex. By segmenting the arrival time maps from 10 different mice, transit time trends associated with the microvasculature were revealed. Large vessels were excluded based on size (exclusion criteria: radius > 16 μm). A) Relative arrival times in microvessels from all 10 mice are presented as a function of depth. Each point is the mean arrival time within a single microvessel. B) The mean arrival time decreases with depth down to the middle cortical layers (layers 4–5), followed by an increase in layers 5–6. Estimated boundaries of different cortical layers are shown as dotted black lines and standard deviations are shown as red error bars. C) When layer-averaged arrival times were compared across mice, the middle cortical layers displayed shorter arrival times. Statistical testing used the Kruskal-Wallis test followed by Tukey’s Honestly Significant Difference test to account for multiple comparisons (* p < 0.05, ** p < 0.005, and *** p < 0.0005). D–E) The intervessel standard deviation also decreased with depth down to the middle cortical layers, reaching a minimum in layer 5.

The trend of decreasing arrival time with increasing depth was statistically significant in each subject up to 650 microns after accounting for heteroscedasticity using a weighted least squares linear regression (p < 0.05). Standard deviations were large superficially, mainly due to the presence of a distribution of vessels with long arrival times (Figure 5A). The trend of decreasing arrival times with depth persisted even after the group with long arrival times was removed (Supplemental Figure 7B–C). More rigorous analysis was also performed by selecting only microvessels with self-consistent parameter fits, as indicated by low intravessel standard deviations (Supplemental Figure 8). This analysis showed that the findings of lowest mean peak times and standard deviations in the middle cortical persisted even after the removal of less reliable vessels from the data set. Therefore, these statistical “outliers”, causing deviation from a Gaussian distribution, were not due to measurement error (Supplemental Figure 8) and came from a number of different animals (Supplemental Figure 9A–B), and hence, should be considered as physiologically relevant.

By analyzing the distribution of arrival times at different cortical depths, the laminar dependence of transit time heterogeneity, as measured by the standard deviation of microvascular arrival times, was also examined. Depth and layer-dependent trends in heterogeneity (Figure 5D–E) were similar to mean arrival time trends, albeit more pronounced. The minimum heterogeneity covered from the layer 4–5 boundary to deeper in layer 5, around 500–800 microns in depth. The middle cortical layers additionally displayed the least heterogeneity on average. Removal of the long arrival time group as described above reduced the standard deviation in the superficial layers, but the trend of decreasing heterogeneity down to layer 5 persisted (Supplemental Figure 7E). Furthermore, the observed layer-dependence of heterogeneity is not a result of the alignment of the data as it was observed in each individual animal (Supplemental Figure 9B).

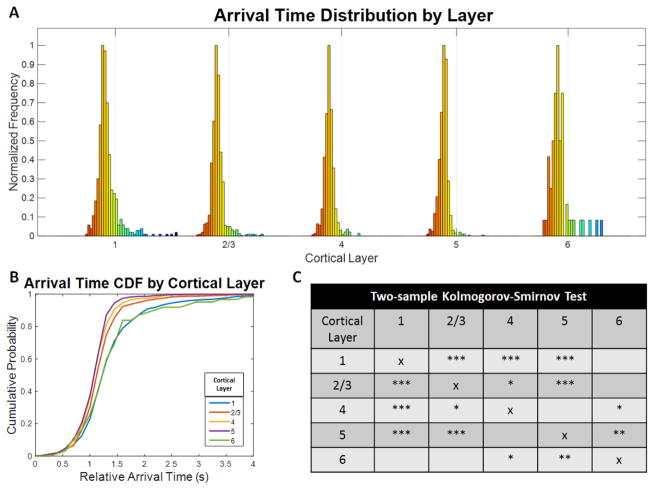
Histogram analysis of the arrival time distributions within each layer further revealed significant layer-dependent changes (Figure 6). The distribution widths become smaller when moving deeper to the middle cortical layers. Two-sample Kolmogorov-Smirnov tests were applied to each pair of layers and corrected with the Bonferroni correction for multiple comparisons. Statically significant differences in the layer-dependent distributions were observed for 7 out the 10 layer pairs, which further supports laminar differences in the cortical microvasculature.

Figure 6.

Arrival time distributions in each layer of the mouse somatosensory cortex. A) The arrival time distributions in microvasculature vary across cortical layers. The color indicates relative arrival time where red is earlier (more arterial) and blue is later (more venous). The gray line marks a 2 second arrival time in each distribution. The middle cortical layers show narrower distributions with fewer long arrival time vessels. B) The cumulative probability functions for the arrival time distributions of each layer shown in A) emphasize layer dependencies with layers 4 and 5 showing the earliest and least heterogeneous arrival times. C) Two-sample Kolmogorov-Smirnov tests were applied to each pair of layers and corrected for multiple comparisons using the Bonferroni correction and show that 7 out of 10 layer pairs are statistically significant. The number of asterisks denotes the level of statistical significance (* p < 0.05, ** p < 0.005, and *** p < 0.0005).

3.3 Peak Time Analysis

While bolus arrival time and peak time were the most precisely estimated temporal measures derived from DyC-OCT, the mean transit time (MTT) (or centroid) of the transit time distribution (TTD) is more directly related to oxygen delivery [12]. The MTT can be estimated from the deconvolution of two signals as described in Equation 5; however its correct interpretation requires connectivity information. To estimate the MTT without a connectivity map, an approximate arterial input function was derived from the average profile of the superficial supplying artery with the shortest arrival time. This assumed that the profile of the arterial input function was similar to other supplying arteries due to the high speed and lower probability of dispersion throughout the arterial macrovascular network. With this estimated arterial input function, TTDs and MTTs were determined for each point using Equation 5. Any points with arrival times earlier than the input function were rejected from analysis as they could not physiologically be connected to the chosen artery. Peak time, on the other hand, shares some characteristics of the estimated MTT, but does not require connectivity assumptions to accurately quantify. Supplemental Figure 10 shows the relationship between bolus arrival time, peak time, and estimated MTT. While MTT and peak time increase with arrival time (Supplemental Figure 10A–B), a stronger linear relationship (black line) is observed between MTT and peak time (Supplemental Figure 10C). In summary, the linear relationship suggests that bolus peak time can be viewed as a proxy for MTT.

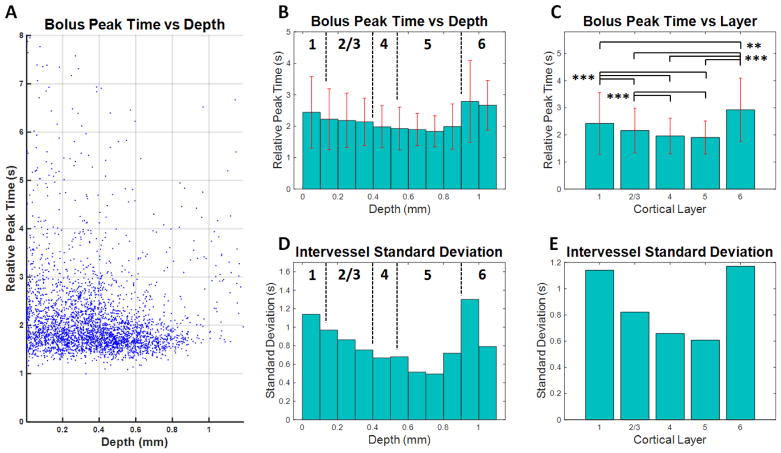
In order to describe the laminar peak time distribution across cortical depths (Figure 7A), data from DyC-OCT experiments in 10 animals were grouped either according to cortical depth (Figure 7B) or according to cortical layer (Figure 7C), similar to arrival time. In summary, the minimum mean peak time was identified in layer 5, around 700–800 microns in depth (Figure 7B–C). As with arrival time, the standard deviations were smallest in layer 5 (Figure 7E), around 600–800 microns (Figure 7D), indicating less heterogeneity. When averaged by layer, the shortest peak times and least heterogeneity were again found in the middle cortical layers. More rigorous analysis was also performed by selecting only microvessels with self-consistent parameter fits, as indicated by low intravessel standard deviations (Supplemental Figure 11). This analysis showed that the findings of lowest mean peak times and standard deviations in the middle cortical persisted even after the removal of less reliable vessels from the data set.

Figure 7.

Peak time as a function of depth in the mouse somatosensory cortex. By segmenting the peak time maps from 10 different mice, transit time trends associated with the microvasculature were revealed. Large vessels were excluded based on size (exclusion criteria: radius > 16 μm). A) Relative peak times in microvessels from all 10 mice are presented as a function of depth. Each point is the mean peak time within a single microvessel. B) The mean peak time decreases with depth down to layer 5, around 700–800 microns followed by an increase in layers 5–6. Estimated boundaries of different cortical layers are shown as dotted black lines and standard deviations are shown as red error bars. C) When layer-averaged peak times were compared across mice, the middle cortical layers (layers 4–5) displayed shorter peak times. Statistical testing used the Kruskal-Wallis test followed by Tukey’s Honestly Significant Difference test to account for multiple comparisons (** p < 0.005 and *** p < 0.0005). D–E) The intervessel standard deviation also decreased with depth, reaching a minimum in layer 5 around 600–800 microns.

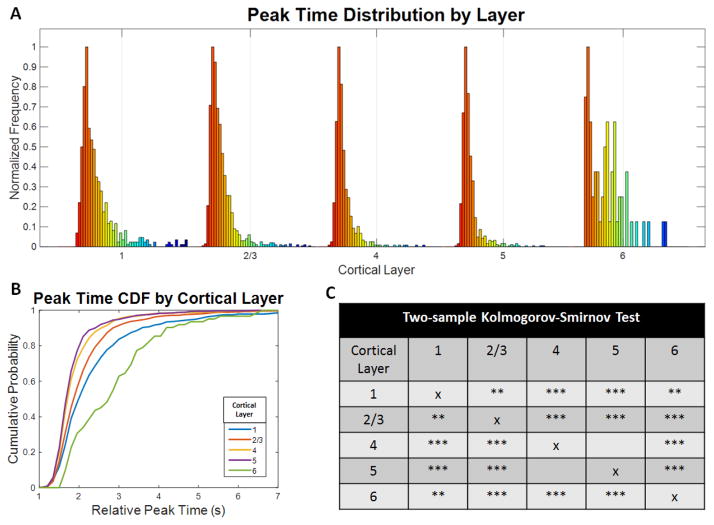
Histogram analysis of the peak time distributions within each layer was performed (Figure 8). The distribution widths differed between cortical layers, with layers 4 and 5 being the narrowest. Two-sample Kolmogorov-Smirnov tests were applied to each pair of layers and corrected with the Bonferroni correction for multiple comparisons. Statically significant differences in the layer-dependent distributions were observed for 9 out the 10 layer pairs, which further supports laminar differences in the cortical microvasculature.

Figure 8.

Peak time distributions in each layer of the mouse somatosensory cortex. The peak time distributions in microvasculature vary across cortical layers. The color indicates relative peak time where red is earlier (more arterial) and blue is later (more venous). The gray line marks a 4 second peak time in each distribution. Layer 4 shows a substantial decrease in width compared to the other layers. B) The cumulative probability functions for the peak time distributions of each layer shown in A) emphasize layer dependencies with layers 4 and 5 showing the earliest and least heterogeneous peak times. C) Two-sample Kolmogorov-Smirnov tests were applied to each pair of layers and corrected for multiple comparisons using the Bonferroni correction and show that 9 out of 10 layer pairs are statistically significant. The number of asterisks denotes the level of statistical significance (* p < 0.05, ** p < 0.005, and *** p < 0.0005).

3.4 Summary

In summary, our data, analyzed a number of different ways, consistently showed statistically significant laminar trends in both transit time and heterogeneity. Overall, both arrival time (Figure 5B–C) and peak time (Figure 7B–C) were shortest in the middle cortical layers, with shortest times generally observed around layer 5. Similar trends were observed for the standard deviation of arrival time (Figure 5D–E) and peak time (Figure 7D–E). Notably, while layer 5 tended to exhibit earlier transit times and lower heterogeneity, statistical comparisons between layers 4 and 5, based either on average values (Figure 5C, Figure 7C) or distributions (Figure 6C, Figure 8C), were not significant after correction for multiple comparisons.

4. Discussion

Though the cortex is supplied and drained at the pial surface via a single microvascular network [27], neuronal activity and metabolism [54, 55] vary across the cortical column. The laminar adaptations of the microvasculature to the specific needs of the individual cortical layers are of importance not only for understanding cerebral energetics, but also for the interpretation of BOLD fMRI. In particular, previous studies have shown that the highly metabolically active layer 4 possesses the highest capillary density [56], arteriole branching density [27], and blood flow [57], and is also the site of the earliest BOLD signals [6–10]. However, transit time is a critical parameter that links hemodynamics to oxygen extraction [4]; yet has been understudied. Here, we demonstrated, validated, and applied DyC-OCT specifically for the purpose of studying the transit time distribution in microvascular networks. The layer-resolved measurements in the mouse neocortex enabled by our methods have led to a number of novel findings.

4.1 Laminar Distribution of Transit Times

This study showed that the middle cortical layers of the somatosensory cortex have the earliest microvascular transit times (Figure 5C, Figure 7C) as well as the lowest microvascular transit time heterogeneity (Figure 5E, Figure 7E). In agreement with results from the somatosensory cortex, pooled data from the posterior parietal and visual cortices (n = 8) also showed decreases in arrival time, peak time, and their standard deviations from the superficial to middle cortical layers (data not shown). The recently published angioarchitecture of the mouse neocortex [27] offers clues to explain these observations (Supplemental Figure 12). In particular, the superficial cortical layers contain relatively more venule branches and fewer arterioles [27], leading to a more venous-weighted microvascular network. By contrast, layer 4 and the middle cortical layers contain more arteriolar branches and fewer venular branches [27]. Layer 4 has the largest capillary density [56] and a higher flow as well [57]. Taken together, these data suggest that the microvasculature in layer 4, with relatively more arteriolar microvessels and fewer venular microvessels, should have a shorter and more homogenous transit time distribution, as demonstrated here. The deeper cortical layers show an increase in both transit time (Figure 5C, Figure 7C) and heterogeneity (Figure 5E, Figure 7E), possibly due to lower flow speeds and longer paths traversed by the arterioles that reach the deep cortex. Reported findings in cortical layer 6 should be interpreted cautiously due to the smaller number of vessels (Supplemental Figure 1) and animals (Supplemental Figure 9) for that layer. We assume that delays in arteriolar transit near the cortical surface, where speeds are high (~10 mm/s) [58], do not appreciably affect the more superficial transit time distributions. The transit time characteristics of white matter will be assessed in future studies.

4.2 Relationship to Laminar BOLD

Laminar BOLD offers the exciting prospect of deciphering afferent and efferent activity based on temporal or amplitude differences in the BOLD signal in different layers [10]. Since the BOLD signal primarily depends on deoxyhemoglobin, it can be affected by the complex interplay of CBF, CBV, and the cerebral metabolic rate of oxygen consumption. In fact, laminar variations in arteriolar dilation timing, with the earliest responses coinciding with the input cortical layers, have been proposed as potential explanations for laminar BOLD [59]. However, it is also well-known that transit time is an important contributor to the delay of the BOLD response after an increase in blood flow [5]. Our results highlight an alternative explanation for laminar BOLD fMRI timing profiles based only on the baseline transit properties of the microvasculature. In particular, our results show that the microvascular transit times are earliest in the middle cortical layers, a fact that alone predicts earlier BOLD onset times in the middle cortical layers (Figure 5B–C, Figure 7B–C). Our results do not contradict prior work, including, a recent elegant study that showed a restructuring of the BOLD kinetics consistent with denervation induced plasticity [10]. Rather, our results highlight that alternative explanations based on transit time distribution constraints should be considered as potential contributors to the BOLD response kinetics. Moreover, the notable variations in transit time distribution with depth (Figure 5A, Figure 7A) suggest that accurate models of fMRI BOLD must be founded on measurements across the entire cortical column, not just the cortical surface.

4.3 Implications for Oxygen Delivery

The classical picture of oxygen delivery assumes a single capillary with a maximal oxygen extraction inversely proportional to blood transit time [60]. However, heterogeneity of transit times among capillaries, where present, can impede efficacy of oxygen extraction [12] relative to this classical model. Here we suggest that laminar differences in microvascular transit time distributions (Figure 5A, Figure 7A) imply differences in efficacy of oxygen extraction between cortical layers. Moreover, we argue that these differences enable the cortex to accommodate the diverse metabolic needs of cortical layers through a single vascular supply.

Layer 4, the most metabolically active cortical layer [61–63], resides in the middle of cortex, though its blood supply must derive from the pial surface network. Moreover, supplying arterioles diving from the pial surface are known to lose oxygen through diffusion [64], thus reducing the available oxygen supply to deeper cortical layers. The cortex is known to cope with this design problem by directing more blood flow to layer 4 than the other layers [57]. This might be achieved passively through the angioarchitecture [27], or actively through laminar regulation of arteriolar tone [59]. Aside from blood flow, our results suggest that the cortex may also address this design problem, at least in part, through tailoring transit time heterogeneity to different cortical laminae. The laminar transit time distribution suggests that the cortical microvasculature is adapted to optimize oxygen extraction efficacy (low heterogeneity) in the middle cortical layers, perhaps even at the expense of less efficacious oxygen extraction (high heterogeneity) in other cortical layers (Figure 5D–E, Figure 7D–E). This finding is consistent with the hypothesis that transit time heterogeneity is optimized to deliver oxygen precisely where it is most needed.

Whether transit time heterogeneity is fully specified by the angioarchitecture, or can be actively controlled (dependent on or independent from blood flow) remains to be determined. The laminar transit time distribution should be investigated during functional activation [65] as well as during microvascular dysfunction. A more detailed picture of how metabolic needs are met under these conditions will require additional, simultaneous measures of flow and oxygenation.

4.4 Methodological Assessment and Future Directions

A major advantage of the DyC-OCT technique is that, even though the focal spot size degrades beyond ~0.5 mm in highly scattering brain tissue [66], quantitative transit time data are obtained at > 1 mm cortical depth. This is because the transit times are derived from a time course (Figure 2) that does not depend on the precise image resolution. As long as microvessels can be isolated in DyC-OCT, transit times are expected to be accurate.

Several limitations of the DyC-OCT methodology, as implemented here, provide directions for future work. First, a notable feature of Intralipid as a DyC-OCT contrast agent is that it seems to act as a plasma tracer, as evidenced by similar transit kinetics to FITC-dextran (Figure 4). The layer-dependent blood plasma kinetics demonstrated here are likely to be correlated with red blood cell flow kinetics. Nevertheless, future DyC-OCT tracers can be developed that more closely mimic red blood cell transit kinetics. Second, the best estimates of TTD are achieved when the arterial input approximates an “impulse” or delta function. For our injections, the tracer underwent temporal dispersion from the site of intravenous injection to the cortical arterioles that feed the capillary beds measured in this study. Future work will investigate shorter bolus injections at alternative sites of administration in closer proximity to the cerebral vasculature where transit times are to be measured. Shorter boluses will also enable measuring further into the tails of the TTD, though the short recirculation time in the mouse would remain a limitation. Next, while DyC-OCT enables simultaneous interrogation of large numbers of capillaries, it will need modifications (i.e. closely spaced boluses) to quantify more rapid changes on the second scale, such as those during functional activation [59].

DyC-OCT data remain somewhat ambiguous in the absence of detailed vascular anatomy. A long transit time in a particular microvessel branch could have one of two plausible interpretations; either the branch is on the venular end of the branching tree, or the branch is poorly perfused. Ascertaining which of these possibilities is true requires determining branch order and comparing the particular microvessel branch in question to other branches of similar order. Thus, although this study investigated ensemble microvascular transit time characteristics without regard to branching sequence, future studies will investigate transit times in the context of compartment (arteriolar, capillary, venular) and branching order determined from a vascular graph [27]. We believe that this approach would provide more direct insight into how transit time characteristics relate to the angioarchitecture. Another related direction is to use data derived from DyC-OCT with advanced graphing and modeling methods to more accurately simulate blood flow through complex microvascular networks.

The use of isoflurane anesthesia has the potential to affect the reported DyC-OCT measurements. Isoflurane is a known vasodilator and has been reported to significantly increase CBF in a dose-dependent fashion [67], as compared to an awake state [68]. Higher CBF due to the anesthesia could cause shorter arrival and peak times, as compared to awake mice. If trends in transit time are impacted by active regulation of vascular tone, anesthesia could represent a confound [69]; anesthesia would be less problematic if transit time trends are governed primarily by the angioarchitecture. Future DyC-OCT studies could evaluate the laminar differences in tracer kinetics, if any, under the effects of isoflurane versus other anesthetic agents.

Last, it should be stated that standard deviations of individual arteriovenous transport functions could, in principle, have been determined and used as a measure of heterogeneity here, as was done in previous studies [11, 70]. Due to the unique capillary-level resolution enabled by DyC-OCT, we opted to analyze variability in transit time parameters amongst capillaries instead. Spatial variability in microvasculature is closely related to more conventional measures of heterogeneity [70].

5. Conclusions

DyC-OCT, a method based on imaging the kinetics of an intravascular contrast agent, was developed to study the transit time distribution in microvascular networks in cross-section at the single-capillary level. Dilution curves identical to those obtained with a fluorescent plasma label at the cortical surface were shown, thus validating the technique. Then, transit times were measured simultaneously across the entire depth of the cerebral cortex in mice. The results demonstrate a clear laminar distribution, with the shortest microvascular transit times and heterogeneity observed in the middle cortical layers. These trends are consistent with the known cortical angioarchitecture of the mouse, and may help to explain the onset time kinetics of the BOLD fMRI response. Moreover, they shed light on how a single vascular network tailors its transit time distribution to meet diverse metabolic needs of individual cortical layers. DyC-OCT affords a new perspective of cortical microvascular networks, and may prove to be a useful tool to investigate heterogeneity in microvascular flow patterns that impact oxygen extraction from the capillary bed.

Highlights.

• We introduced Dynamic Contrast Optical Coherence Tomography (DyC-OCT).

• DyC-OCT was validated using fluorescence imaging in the mouse somatosensory cortex.

• Shortest microvascular transit times were located in the middle cortical layers.

• Minimum transit time heterogeneity was found in the middle cortical layers.

• Results help interpret the laminar kinetics of BOLD fMRI and cerebral energetics.

Glossary

DyC-OCT

Dynamic Contrast Optical Coherence Tomography