Wavelet-based clustering of resting state MRI data in the rat

Abstract

While functional connectivity has typically been calculated over the entire length of the scan (5-10 min), interest has been growing in dynamic analysis methods that can detect changes in connectivity on the order of cognitive processes (seconds). Previous work with sliding window correlation has shown that changes in functional connectivity can be observed on these time scales in the awake human and in anesthetized animals. This exciting advance creates a need for improved approaches to characterize dynamic functional networks in the brain. Previous studies were performed using sliding window analysis on regions of interest defined based on anatomy or obtained from traditional steady-state analysis methods. The parcellation of the brain may therefore be suboptimal, and the characteristics of the time-varying connectivity between regions are dependent upon the length of the sliding window chosen. This manuscript describes an algorithm based on wavelet decomposition that allows data-driven clustering of voxels into functional regions based on temporal and spectral properties. Previous work has shown that different networks have characteristic frequency fingerprints, and the use of wavelets ensures that both the frequency and the timing of the BOLD fluctuations are considered during the clustering process. The method was applied to resting state data acquired from anesthetized rats, and the resulting clusters agreed well with known anatomical areas. Clusters were highly reproducible across subjects. Wavelet cross-correlation values between clusters from a single scan were significantly higher than the values from randomly-matched clusters that shared no temporal information, indicating that wavelet-based analysis is sensitive to the relationship between areas.

1. Introduction

Resting state MRI has become a powerful and popular tool for the study of network activity in the brain. It is widely used to study human cognition and is sensitive to alterations caused by disorders of the brain (Hedden et al., 2009; James, 2009; Kennedy and Courchesne, 2008; Liao et al.; Rombouts et al., 2005; Sorg et al., 2007; van Meer et al.; Wang et al., 2007). Traditionally, functional connectivity has been assumed to remain stationary over the course of a scan (5-10 minutes), but it is well known that cognitive processes occur on much shorter time scales (seconds). Recent studies have shown that the BOLD signal exhibits dynamic properties on a similar time scale (Chang and Glover, 2010; Handwerker et al.; Hutchison et al., 2012; Keilholz et al., 2012; Magnuson, 2010; Majeed et al., 2011; Majeed et al., 2009). Majeed first demonstrated that the BOLD signals exhibit intrinsic spatiotemporal organization in rats (Majeed et al., 2009) and in humans (Majeed et al., 2011), showing that there are aspects of activity which are not captured by traditional analysis techniques that examine only ‘steady-state’ relationships. Chang and Glover (2010) focused on the relationship between the posterior cingulate cortex (PCC) and other brain areas, demonstrating that the correlation between these areas varied over time and that the temporal variability was greater than would be expected by chance. A recent report by Hutchison et al. demonstrates that similar dynamics occur in anesthetized monkeys (Hutchison et al., 2012). Most of the existing demonstrations of dynamic connectivity (other than the studies by Majeed et al., which used an autoregressive pattern-finding algorithm to create templates of common BOLD spatiotemporal patterns) have used seed regions selected by the user and either wavelet coherence (Chang and Glover, 2010) or sliding window correlation (Chang and Glover, 2010; Handwerker et al.; Hutchison et al., 2012; Keilholz et al., 2012) to demonstrate changing connectivity over time. Ideally, however, voxels would be clustered into groups that share similar characteristics to minimize the loss of information that can be caused by averaging. This is particularly true for dynamic analysis, where it is important to minimize variations in the timing information from all members of a cluster. Wavelets are ideally suited to dynamic analysis of resting state data, as they provide a representation of the signal in the time-frequency plane. Previous work has shown that different networks have characteristic spectral ‘fingerprints’ (Cordes et al., 2001; Mantini et al., 2007). Wavelet analysis also has the potential to provide superior sensitivity to variations over time than sliding window approaches, as the range of scales obtained during the transform in some sense correspond to using a range of windows, which may reduce loss of sensitivity to short-lived states caused by averaging.

In this paper, we describe a clustering method based on wavelet decomposition that groups areas with similar frequency profiles and temporal properties using a hierarchical algorithm. When applied to resting state MRI data from the rat, clusters localized well with known anatomical areas and tended to form bilateral cortical or subcortical groups. A preliminary examination of the wavelet cross correlation calculated between homologous clusters in opposite hemispheres showed that correlation was greater than when calculated for randomly matched areas. This suggests that the wavelet-based analysis allows the detection of periods of coordinated activity and has the potential to identify meaningful temporal dynamics.

2. Materials and Methods

All experiments were performed following guidelines set by the Institutional Animal Care and Use Committee (IACUC) of Emory University. Four male Sprague–Dawley rats (200–300 g) were chosen from data acquired for another study (Keilholz et al., 2013) (Magnuson et al., 2014). The preparation is described briefly below. These rats represent the best specimens collected for the study and were selected based on image quality, lack of motion, and physiological stability. A preliminary analysis for each rat indicated that cross-correlation based on a seed manually chosen in primary somatosensory cortex (SI) resulted in a typical pattern of localized bilateral correlation (Pawela et al., 2008; Williams, 2010; Zhao et al., 2008). Three scans from each rat were analyzed.

2.1. Animal preparation

Each rat was anesthetized with 2% isoflurane mixed with 1:1 oxygen and room air, and maintained at 1.5% isoflurane during setup. Heart rate and blood oxygen saturation percentage were recorded with a pulse oximeter placed on the rear left paw. Body temperature was monitored with a rectal thermometer and maintained at approximately 37° C using an adjustable warm water pad. Respiratory rate was also monitored by using a pressure-sensitive balloon placed under the rat's chest. The rat was then placed in the MRI cradle and the head was secured with a bite bar and ear bars.

After setup was completed, the rat was given a subcutaneous bolus injection of 0.025 mg/kg dexmedetomidine (Domitor, Pfizer, Karlsruhe, Germany). Five minutes after the bolus, isoflurane was discontinued, and fifteen minutes later, a subcutaneous infusion of 0.05 mg/kg/hr dexmedetomidine was initiated to maintain anesthesia for the duration of the experiment (Weber et al., 2006). Approximately eighty minutes after the initial dexmedetomidine bolus, the infusion dosage was increased to 0.15 mg/kg/hr (3x initial infusion rate) for maintaining anesthetic depth, in accordance with the protocol established in (Pawela et al., 2009).

2.2. Image acquisition and processing

All images were acquired on a 20 cm bore 9.4 T Bruker BioSpec magnet interfaced to an AVANCE console (Bruker, Billerica, MA). An actively decoupled imaging protocol was used, with a 7 cm volume coil for RF transmission and a 2 cm surface coil for signal reception. A FLASH image was acquired in three planes and a single slice was positioned over the primary somatosensory cortex (SI) based on known anatomical markers. Manual shimming was conducted on this slice to obtain maximum SNR and spatial homogeneity. Each resting state scan was acquired using a single-shot gradient echo EPI sequence with the following parameters: Repetitions = 1000, TR = 500ms, TE = 15ms, total scan time = 8 minutes 20 seconds, slice thickness = 2mm, FOV = 2.56cm × 2.56cm, matrix size = 64 × 64. Approximately ten resting state scans were acquired from each animal. The aim of the original study was to examine time-dependent effects of anesthesia. To avoid those effects for the current study, only three scans that occurred after the animal reached ‘steady state’ were used.

2.3. Seed-based functional connectivity analysis

All fMRI data processing and analysis was performed using code written in MATLAB (MathWorks, Natick, MA). The time course from each voxel was linearly detrended (detrend function), followed by FIR band pass filtering between 0.01 Hz – 0.3 Hz. For each rat, regions of interest (2 × 2 pixels) were manually selected based on the unfiltered image in primary somatosensory cortex (SI), secondary somatosensory cortex (SII), and caudate putamen (CP) by comparison with an atlas (Paxinos, 1998). Pearson correlation was calculated between the average time course from each ROI and all other voxels in the brain.

2.4. Wavelet-based clustering

All analysis was performed using code written in Matlab utilizing Wavelet Toolbox primary functions. For each scan, the brain was segmented manually to minimize contributions from muscle or scalp. The raw, unfiltered time course from each voxel in the brain was normalized to zero mean and unit variance, and the discrete wavelet transform (DWT) was used to decompose the signal into a multiresolution approximation (MRA) with j=5 levels of resolution, using a Daubechies wavelet (db7) with p=7 vanishing moments, and resulting support size of N=2p-1=13 points. At each level of the decomposition, the approximation coefficients (ca) and detail coefficient (cd) are computed using the following relations

$$\{\begin{array}{c}c{a}_J\left[k\right]=f\left(t\right),{\varphi }_J\left[k\right]\hfill \\ c{d}_j\left[k\right]=f\left(t\right),{\psi }_j\left[k\right]\hfill \end{array}\phantom{\}}j=1,2,\dots \mathrm{J},k\in \mathbb{Z}$$ (1)

where f (t) represents the voxel time signal as function of time only, ϕ and Ψ are the scaling and the wavelet functions, and J is the maximum level of the MRA decomposition (Mallat, 1989). Moreover, in Eq. (1), k is the discrete index that spans the samples of the coefficients, and it depends of the length of f (t) and on the wavelet selected for analysis.

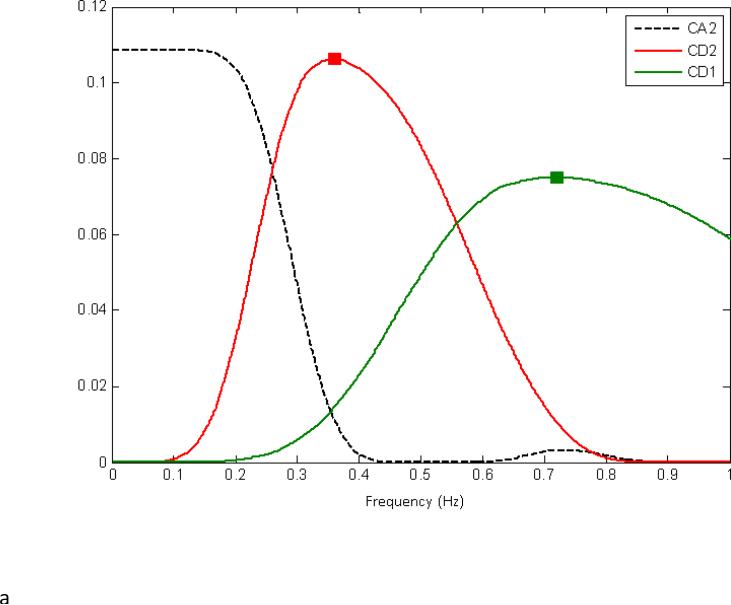
Clustering was then performed using the computed wavelet coefficients at each level of the MRA as features for an agglomerative clustering algorithm. For comparison purposes, the raw voxel signal was also used as feature for the clustering algorithm. The algorithm uses Ward's linkage as linkage function, which minimizes the total within-cluster variance. A more detailed description of this algorithm can be found in (Medda et al., 2012). Clustering was performed for each scan from each rat. Based on comparison to the rat brain atlas (Paxinos, 1998) and with a priori knowledge of the frequencies likely to be involved in functional connectivity (typically below 0.3 Hz in the rat anesthetized with dexmedetomidine (Magnuson, 2010; Majeed et al., 2009; Williams, 2007)), the approximation coefficients at level j=2 (ca2) and the detail coefficients at level j=3 (cd3) were chosen for further investigation. These features are characterized by a frequency spectrum that defines the frequency sensitivity of the wavelet in the 0 to FS/2 range. The wavelet decomposition for j=2 is composed of the approximations for level j=2, and the details for levels j=1,2. The power spectrum associated with this decomposition can be seen in Figure 1A., where the lowpass filter (ca2) has a transition at about 0.26Hz, and a flat band response until 0.13Hz. If we consider j=3, then the wavelet transform is comprised of the approximation for j=3, and the details for j=1,2,3. The power spectrum associated with this decomposition can be seen in Figure 1B, where the highpass filter at level 3 (cd3) is characterized by a peak response of 0.18 Hz and a transition bandwidth that goes from 0.13 Hz to 0.28 Hz. Here, the transition bandwidth is defined as the bandwidth of the wavelet function between two transition points, and a transition point is defined as that frequency for which the frequency response of a wavelet at level j is equal to the frequency response of the wavelet at level j+1. The same is valid for the transition between wavelet and scaling function. After wavelet decomposition, the number of clusters was varied from 6 to 10 to examine the effect of the parameter on the parcellation of the resulting clusters.

Figure 1.

The power spectrum associated with the wavelet decomposition for j=2 (A) and j = 3 (B). For j = 2, the wavelet decomposition is composed of the approximations for level j=2, and the details for levels j=1,2. The lowpass filter (Ca2) has a transition at about 0.26Hz, and a flat band response until 0.13Hz. For j = 3, the wavelet transform is comprised of the approximation for j=3, and the details for j=1,2,3. The power spectrum associated with this decomposition can be seen in Figure 1B, where the highpass filter at level 3 (Cd3) is characterized by a peak response of 0.18 Hz and a transition bandwidth that goes from 0.13 Hz to 0.28 Hz. The frequency ranges associated with Ca2 and Cd3 overlap with the frequencies of the BOLD fluctuations most commonly used to map functional connectivity in rats, and these coefficients were chosen for further examination.

2.5. Power spectra

To examine the sensitivity of wavelet-based clustering to region-specific spectral characteristics, the power spectrum was calculated for the average unfiltered BOLD time course from each cluster using Welch's method (Hamming window, 200 image segments, 50% overlap) (Hayes, 1996). The resulting plots show the approximate power as a function of frequency averaged over the entire time course of the scan. In contrast to the combination of spectral and temporal information obtained with the MRA decomposition, the power spectra contain only frequency information.

2.6. Wavelet-based correlation analysis

To compare wavelet-based clustering to traditional cross-correlation approaches, all parcellations were manually separated in the midline so that each resided in only one hemisphere. To facilitate comparisons to previous findings using seed-based analysis, clusters that approximately corresponded to the anatomical locations ofSI, SII, motor cortex (MI), and CP were selected from all rats and pooled for further analysis. In some scans, no cluster was localized to one or more of the anatomical regions and data from that region was not used in the analysis.

Wavelet correlation between clustered time series was computed for each pair of interhemispherically symmetric clusters using the wavelet transform of the average signal for each cluster. The wavelet correlation between two time series is defined on the coefficients of the maximal overlap DWT (MODWT)¹, a non-decimated version of the orthonormal DWT. Unlike the DWT, the MODWT is not an orthogonal transform, but it is invariant to translations and can be computed on any size signal (Percival and Walden, 2000). If the MODWT coefficient of signals from two voxels X and Y at level j is indicated with $W_j^{\left(X\right)}\left[n\right]$ and $W_j^{\left(Y\right)}\left[n\right]$, the wavelet correlation between X and Y at scale j can be defined as a correlation coefficient between two random variables

$${\rho }_j^{\left(XY\right)}=\frac{cov\left\{W_j^{\left(X\right)}\left[n\right],W_j^{\left(Y\right)}\left[n\right]\right\}}{\sqrt{var\left\{W_j^{\left(X\right)}\left[n\right]\right\}\mathsf{C}var\left\{W_j^{\left(Y\right)}\left[n\right]\right\}}}$$ (2)

Therefore $-1\le {\rho }_j^{\left(XY\right)}\le 1$. In (2), the quantity $cov\{W_j^{\left(X\right)}\left[n\right],W_j^{\left(Y\right)}\left[n\right]\}$ indicates the wavelet cross-covariance between the MODWT of X and Y. When applied to the analysis of the wavelet parcellation obtained from the technique described in paragraph (2.4), the wavelet correlation as defined in (2), is a scaled version of the wavelet cross-covariance, and expresses the relative variation of the two signals on a level-by-level basis between clusters. Because the cross-spectra density is defined as the Fourier transform of the cross-covariance, when considering the wavelet cross-correlation computed for each level of a MRA decomposition, a level-by-level decomposition of the cross-spectra density between the two signals is obtained. For an estimate of how the activity of two regions covaries as a function of time, the wavelet cross-correlation is computed for each pair of bilateral clusters from the same brain. This is compared with the wavelet cross-correlation of clusters that were randomly matched across subject and across scan and should therefore share no temporal information.

3. Results

Wavelet-based hierarchical clustering was performed on the raw signal and the detail and approximation coefficients for five levels of decomposition. An example is shown in Figure 2. For all levels, clusters were typically bilaterally symmetrical and localized to cortical or subcortical anatomical areas. Each approximation and detail coefficient can be associated with a corresponding region in the frequency spectrum usually described by the transition points between two wavelets at level j and j+1 or between a wavelet and a scaling function at level j. These regions are referred to as ‘pseudo-frequencies’. Moreover, the wavelet functions are also characterized by the center frequency, which is the predominant frequency in the wavelet frequency spectrum of interest. The corresponding pseudo-frequencies for ca1-5 and cd 1-5 are given in Table 1. Clusters based on some features, including approximation coefficients for levels four and five (ca4, ca5) and detail coefficients for levels 1 and 2 (cd1, cd2), appear scattered rather than spatially localized and are likely a result of low signal to noise ratio (SNR) in the voxel time series. However, even for these features, some cluster localization is preserved in the cortex. It is clear that different scales contain different information, as the parcellation of both cortical and subcortical structures varies based upon the scale used. For further examinations of reproducibility, we chose to focus on ca2 and cd3, which exhibit good cortical and subcortical parcellation and have pseudo-frequencies that overlap with frequencies commonly used for functional connectivity mapping in the rat (Magnuson, 2010; Majeed et al., 2009; Williams, 2010). These frequencies exhibit significant coherence with slow electrical activity (Pan et al., 2013).

Figure 2.

Wavelet-based clustering for different signal features from one scan from one rat. The image at top is based on clustering of the raw signal (S); the middle row is based on approximation coefficients 1-5; and the bottom row is based on detail coefficients 1-5. For all levels, clusters were typically bilaterally symmetrical and localized to cortical or subcortical anatomical areas. Clusters based on some features, including approximation coefficients for levels four and five (Ca4, Ca5) and detail coefficients for levels 1 and 2 (Cd1, Cd2), appear scattered rather than spatially localized. However, even for these features, some cluster localization is preserved in the cortex. It is clear that different scales contain different information, as the parcellation of both cortical and subcortical structures varies based upon the scale used.

Table 1.

Wavelet pseudo-frequencies for cal-5 and cdl-5 and relative center frequencies

	Approximations	Details	Details Center Frequency
j=1	0 ÷ 0.52 Hz	0.52 ÷ 1 Hz	0.70 Hz
j=2	0 ÷ 0.26 Hz	0.26 ÷ 0.559 Hz	0.36 Hz
j=3	0 ÷ 0.13 Hz	0.13 ÷ 0.279 Hz	0.18 Hz
j=4	0 ÷ 0.065 Hz	0.065 ÷ 0.139 Hz	0.09 Hz
j=5	0 ÷ 0.0325 Hz	0.0325 ÷ 0.0698 Hz	0.045 Hz

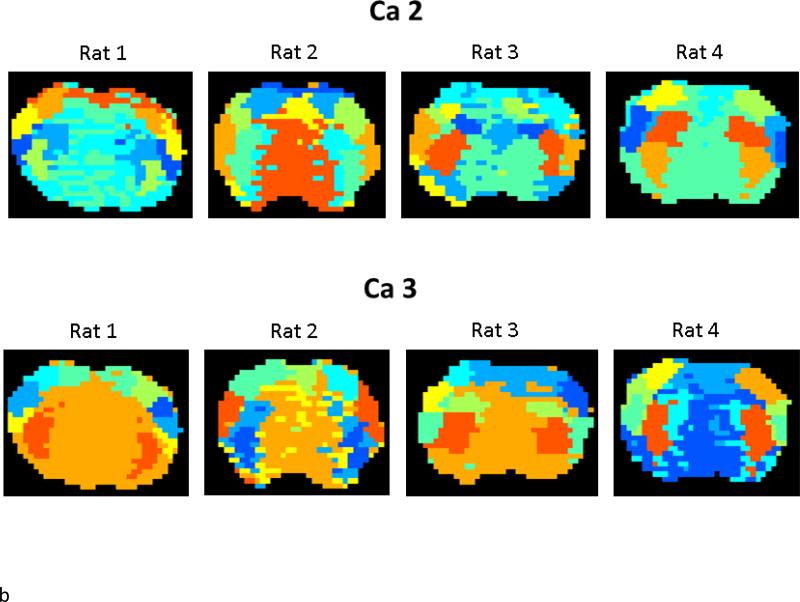
To demonstrate the reproducibility of the clusters obtained based on ca2 and cd3, Figure 3 shows all three scans from a single rat along with example scans from all four rats. While variability is certainly present, all scans exhibit mostly bilateral clusters localized to cortical and subcortical regions. Typically, the cortex is segmented into three to four clusters, including one in medial areas, one in lateral cortex, and one to two in between. These clusters roughly correspond to MI, SI, and SII. The subcortical clusters typically comprise one or two groups in the CP. The remaining clusters tend to be less spatially specific and are probably not anatomically relevant.

Figure 3.

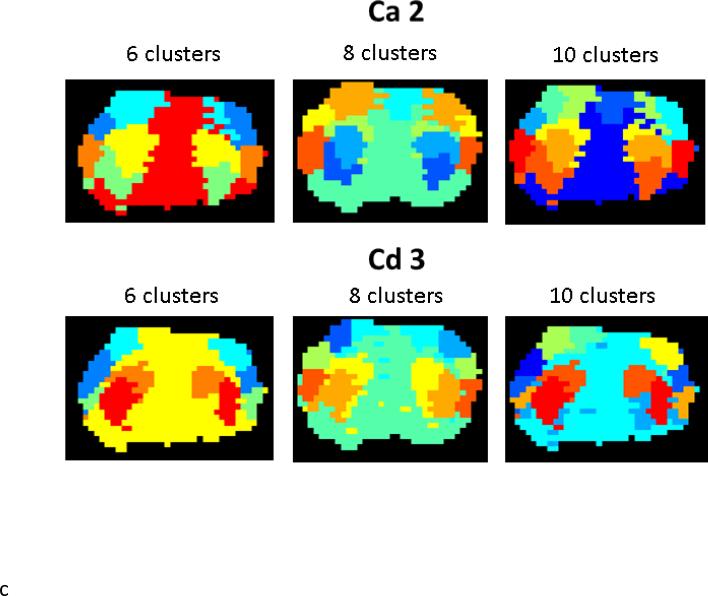
A) Wavelet-based clustering for all three scans from a single rat for Ca2 (top) and Cd3 (bottom). B) Wavelet-based clustering for an example scan from each rat. While variability is present, all scans exhibit mostly bilateral clusters localized to cortical and subcortical regions. The cortex is typically parcellated into three to four clusters, including one in medial areas, one in lateral cortex, and one to two in between. These clusters roughly correspond to MI, SI, and SII. The subcortical clusters typically comprise one or two groups in the CP. The remaining clusters tend to be less spatially specific. C) Impact of the initial cluster estimate for K=6,8,10 on one data set. For both Ca2 and Cd3-based clusters, the primary effect of increasing the cluster size is to parcellate the cortex into more numerous smaller groups.

While this clustering technique is data-driven, it does require an initial estimate of the number of expected clusters K. Figure 3C demonstrates the impact of the initial cluster estimate for K=6,8,10 on the same data set. For both ca2 and cd3-based clusters, the primary effect of increasing the cluster size is to parcellate the cortex into more numerous smaller groups. We chose to use a cluster size of K=8 for the remaining work, as it provides the closest approximation into the division of the cortex into MI, SI, and SII that we would expect based on anatomy. Fewer clusters tend to provide less parcellation of medial cortical areas and larger cluster sizes often subdivide subcortical clusters into small clusters that lack anatomical rationale.

The clusters produced with K=8 also match well in size with the pattern of functional connectivity observed using traditional seed-based correlation. Figure 4 shows wavelet-based clustering for ca2 and cd3 along with functional connectivity maps created using seeds in SI, SII, and CP. While the size of the ‘connected’ areas depend on the chosen threshold, it is clear that fairly large areas of strong correlation are present, comparable in size to the clusters obtained from the wavelet decomposition. Wavelet-based clustering, however, has the advantage of being data-driven and not biased by the choice of seed location.

Figure 4.

Clusters based on Ca2 and Cd3 for one rat (rat 4), along with seed-based correlation for the same scan. Seeds were chosen in SI, SII, and CP to demonstrate the extent of correlation. The networks obtained with traditional seed-based correlation match the size and location of the wavelet-based clusters well.

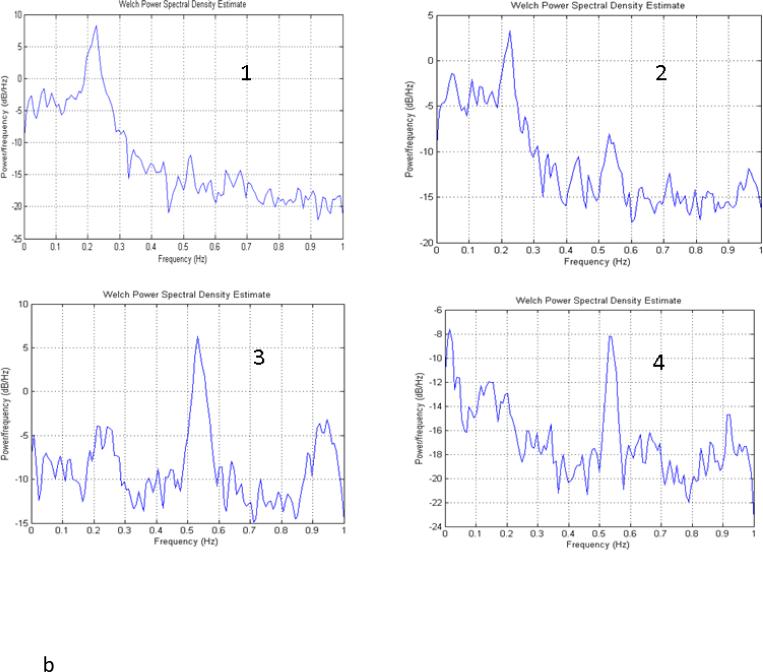
One of the advantages of wavelet-based clustering is that it considers both spectral and temporal information. Figure 5 shows the distinctive spectral fingerprints of the raw time courses of the clusters obtained from ca2, from one of the collected data sets. Lateral cortical areas (clusters 1 and 2 for this scan) exhibit a strong peak near 0.2 Hz, in agreement with previous findings (Majeed et al., 2009; Williams, 2010). Clusters 3 and 4 contain a large peak between 0.5 and 0.6 Hz that is likely to be related to respiratory and/or cardiac noise. Clusters 5 and 6 cover SI and exhibit high power in a broad range of low frequencies (<0.25 Hz). Cluster 5 appears to contain a greater contribution from physiological noise in the 0.5-0.6 Hz range than cluster 6, which may be the reason that SI is divided into two unilateral groups rather than contained in one bilateral group in this example. Clusters 7 and 8, which contain the CP, exhibit power in the low frequencies with a gradual falloff, rather than the plateau and steep falloff seen in SI.

Figure 5.

Power spectra for each cluster obtained based on Ca2 for one scan from one rat. Lateral cortical areas (clusters 1 and 2) exhibit a strong peak near 0.2 Hz. Clusters 3 and 4 contain a large peak between 0.5 and 0.6 Hz that is likely to be related to respiratory and/or cardiac noise. Clusters 5 and 6 cover SI and exhibit high power in a broad range of low frequencies (<0.25 Hz). Cluster 5 has a greater contribution from a peak a little above 0.5 Hz than cluster 6, which may be the reason that SI is divided into two unilateral clusters rather than contained in one bilateral cluster in this example. Clusters 7 and 8, which contain the CP, exhibit power in the low frequencies with a gradual falloff, rather than the plateau and steep falloff seen in SI.

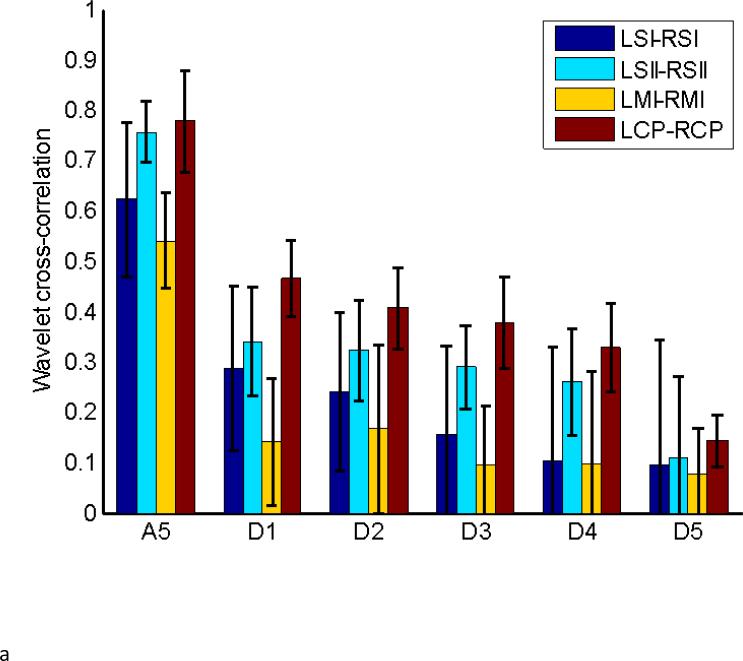
To further examine the sensitivity of wavelet analysis to coordinated changes in wavelet power over time, clusters that approximately correspond to left and right SI, MI, SII, and CP were selected for each data set, based on clustering of the whole brain obtained for ca2 and cd3. In analogy to seed-based correlation, the wavelet cross-correlation as defined in (2) was computed for the full wavelet decomposition for each pair of homologous regions in left and right hemispheres from the same subjects. As a control, the same was done using areas that were randomly matched across different scans and different subjects, destroying any common temporal information between the signals. A summary that includes the standard deviation of the computed wavelet cross-correlation for the homologous group is given in Table 2, while a summary of the results obtained from comparisons across randomly matched subjects are given in Table 3. Figure 6A shows the results for the homologous set of Table 2, while Figure 6B shows the results for the randomly matched subjects of Table 3.

Table 2.

Wavelet cross-correlation for homologous contralateral areas for each wavelet coefficient.

	ca5	cd1	cd2	cd3	cd4	cd5	CC
LSI-RSI	0.62±0.15	0.29±0.16	0.24±0.16	0.16±0.17	0.10±0.22	0.10±0.25	0.49±0.12
LSII-RSII	0.76±0.06	0.34±0.11	0.32±0.10	0.29±0.08	0.26±0.11	0.11±0.16	0.56±0.18
LMI-RMI	0.54±0.10	0.14±0.13	0.17±0.17	0.09±0.12	0.10±0.18	0.08±0.09	0.36±0.17
LCP-RCP	0.78±0.10	0.47±0.08	0.41±0.08	0.38±0.09	0.20±0.15	0.14±0.05	0.25±0.13

For comparison, the cross correlation from seed-based analysis on the same data reported in (14) is shown at the far right. All pairs of areas show the greatest correlation in the ca5 coefficients, followed by cd1 and cd2. In the labels, L represents left hemisphere; R represents right hemisphere.

Table 3.

Wavelet cross-correlation for regions across randomly across different scans for different subjects.

	ca5	cd1	cd2	cd3	cd4	cd5
LSI-RSI	−0.03±0.05	−0.02±0.15	0.00±0.11	−0.00±0.11	−0.03±0.13	−0.03±0.04
LSII-RSII	−0.00±0.08	−0.11±0.15	−0.10±0.15	−0.10±0.13	−0.09±0.10	−0.04±0.03
LMI-RMI	0.01±0.05	−0.05±0.11	−0.04±0.16	−0.02±0.05	−0.00±0.04	−0.01±0.04
LCP-RCP	0.09±0.07	0.05±0.14	0.07±0.10	0.02±0.11	−0.02±0.13	−0.01±0.03

In the labels, L represents left hemisphere; R represents right hemisphere.

Figure 6.

Wavelet cross-correlation for homologous regions in left (L) and right (R) hemispheres for real data (A) and randomly-matched data (B). Correlation in the Ca5 band is higher than for Cd1-5 for all pairs of areas in the real data. Correlation for all coefficients in the randomly-matched data is close to zero, as expected.

The values in Figure 6A obtained for the homologous set are considerably higher than the ones shown in Figure 6B for randomly matched areas. In particular, correlations for the ca5 coefficients are higher than the others from the same set, and show a contained spread in standard deviation. In general, the wavelet coefficients associated with lower frequency bands exhibit stronger correlation. Cross-correlation values between a 2×2 voxel seed in each region and a 2×2 voxel ROI in the opposite hemisphere were calculated for another study on the same data set, but using standard lowpass filtering and analysis (Keilholz et al., 2013). These values are shown in Table 2 for comparison. CP exhibits the highest correlation for all wavelet coefficients but the lowest seed-based correlation, a discrepancy that may result from the much smaller ROIs used for the seed-based measurement.

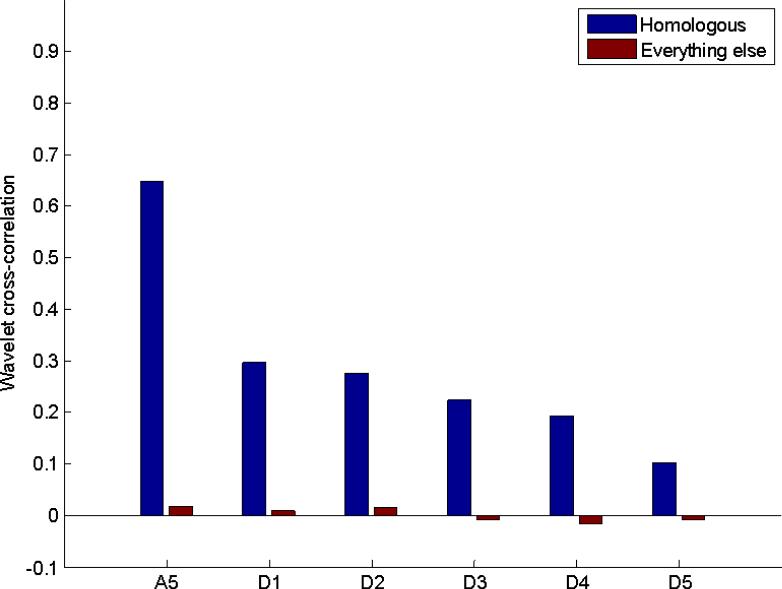
In contrast to the data from homologous cortical areas, analysis of the values in Table 3 show that almost all correlations are very close to zero, indicating that no time-frequency correlation exists between randomly matched signals. Previous analysis of this data set showed that both real and randomly-matched time courses exhibited similar variation over time when sliding window correlation was calculated. However, the histograms of correlation coefficients for the randomly-matched data approximated a normal distribution, while those of the homologous areas were shifted and skewed towards positive values (Keilholz et al., 2012). The current results are in agreement with the previous findings, showing that only data that share temporal information exhibit positive wavelet correlation. To further compare homologous and randomly-matched data, the wavelet correlations computed for homologous regions across the same subject as an average of the values in Table 2 and Table 2 across SI, SII, MI, and CP versus randomly selected regions is shown in Figure 7.

Figure 7.

Average correlation for all pairs of homologous areas in the real and randomly-matched data for Ca5 and Cd1-5. Correlation based on Ca5 is highest, with correlation based on Cd5 lowest. Correlation for all coefficients in the randomly-matched data is near zero.

4. Discussion

Wavelet-based clustering has potential advantages for functional connectivity analysis due to its sensitivity to both the frequency content and the temporal evolution of the BOLD signal over time. The spatially-localized clusters obtained based on wavelet decomposition were typically bilateral and corresponded well to known anatomical divisions. The spatial extent of the clusters depended on the number of clusters chosen, but with the parameters used for this study, was comparable to the size of areas exhibiting significant correlation to a seed region. Clear distinctions were observed between cortical and subcortical regions. While this study is a very preliminary exploration of the use of wavelet-based analysis for resting state MRI, the results are promising and support a fuller investigation of the use of the technique.

Comparison to previous study

The same data was previously examined using sliding window correlation between regions of interest chosen based on an atlas (Keilholz et al., 2012). Both methods found that the variation over time was more different from randomly-matched time courses in homologous areas. More extensive comparisons are difficult, however, since in this study the average signal from a fairly large area was used, in comparison to the 2×2 seeds examined in the previous work. Also, while clusters were roughly assigned to anatomical regions, spatial variation was present across rats, and in one animal a cluster may encompass 75% SI and 25 % MI, while in the next, it could cover 75% SI and 25% SII.

Comparison to other methods

Seed-based correlation requires selection of a region of interest and identifies networks of voxels that have high average correlation across the entire scan. In contrast to seed-based correlation techniques, wavelet analysis is data-driven and not biased by the selection of the seed. In many ways, it is similar to independent component analysis (ICA), which also can extract networks in a data-driven manner. Low-dimensionality ICA identifies networks where the relationship between areas is assumed stable over the entire course of the scan. Higher dimensionality ICA, however, tends to result in localized nodes, and average time courses from each node can be used to examine the temporal variations in relationships between areas. Wavelet-based analysis is attractive in that it explicitly considers both the spectral and temporal properties of the signal, but direct comparisons of the two methods will be necessary to determine if either has an advantage for dynamic network analysis.

Extension to human subjects

This work was performed in the anesthetized rat to take advantage of the high SNR and temporal resolution available for single-slice imaging on the 9.4 T MRI and to allow for future multi-modal studies where simultaneous electrical recording can provide a ‘gold standard’ for MRI-based network dynamics. However, as in rats, it has been shown that particular areas of the human brain also exhibit distinctive spectral properties and relationships that vary over time (Chang and Glover, 2010; Mantini et al., 2007), which suggests that wavelet analysis should be equally applicable to human data. Ideally, the images should be acquired with a rapid sampling rate and a large number of samples should be obtained to take full advantage of the method's capabilities. Current advances in rapid functional imaging are making it possible to acquire whole brain images in humans in a fraction of a second (Moeller et al.; Posse et al.), which will facilitate future applications of wavelet analysis.

Group based vs individual analysis

For this first demonstration, clustering was performed individually for each scan. However, a simple extension would allow group analysis similar to that used with ICA. Images can be registered to a common space and concatenated, then clustered based on the wavelet transform of the concatenated signal. This approach has the advantage of combining all data in a single framework and facilitating comparisons. However, it assumes that the temporal dynamics of the interactions between areas are the same for different rats, which may or may not prove true. Our initial investigation identified particular states that were only found in subsets of the population, possibly due to the use of single slice data (Keilholz et al., 2013).

Preprocessing

Global signal regression is a somewhat controversial part of the pre-processing pipeline for resting state MRI data, and was not performed in this study (Murphy et al., 2009). Similarly, no filtering or physiological noise correction was performed, though these steps are commonly used prior to analysis. Minimal processing of the rsMRI data was used because one of the strengths of the wavelet analysis approach is that it considers the relative contribution of different frequencies and provides insight into the contributions from different processes. For example, in Figure 5, it can be seen that left and right SI fall into separate clusters, which corresponds to a greater presence of high frequency activity (probably respiratory noise) on one side. It may be possible to improve the anatomical relevance of clustering by minimizing physiological noise using RETROICOR (Glover et al., 2000). However, as shown here, the use of wavelet analysis can also provide insight into the relative levels of physiological noise. As dynamic analysis and segmentation also consider frequency information, the subsequent processing could be limited to only the lower frequencies to avoid respiratory contributions.

Wavelet details and approximations

In this study, clustering was performed separately on the approximation coefficients and the detail coefficients obtained from each level of the discrete wavelet transform. Two features, ca2 and cd3, were chosen for further study based on the anatomical relevance of the clusters obtained and the frequency ranges of greatest sensitivity. However, other coefficients also contain anatomically-specific information that is discarded when a single coefficient is used for clustering. We are currently developing an approach based on the wavelet packet transform, a natural expansion of the multiresolution approximation framework of the wavelet transform. Wavelet Packets provide a uniform segmentation of the spectrum in $[0,\frac{Fs}{2}]$ allowing for a better representation more clear relation between spatial clusters and frequency features.

Dynamic analysis of rsMRI data

Dynamic analysis of spontaneous BOLD fluctuations is still a new area, and several studies using sliding window analysis have shown that strong variations in correlation over time can be observed in multiple areas and species (Chang and Glover, 2010; Handwerker et al.; Hutchison et al., 2012; Keilholz et al., 2012). However, similar dynamics are sometimes observed in randomly-matched or modeled signals (Handwerker et al.; Keilholz et al., 2012). One of the challenges in sliding window analysis of network dynamics is that the length of the window must be specified and the ideal window size is unknown. To examine network dynamics, in the future we plan to temporally segment the average time course from each wavelet-based cluster into periods of stable wavelet power, thus empirically determining the ideal window size at each point in the scan.

While it is anticipated that wavelet-based analysis will be useful in the study of network dynamics, it should be noted that in its current implementation, it will not be able to detect propagating patterns of activity that manifest as phase differences across the cortex as seen in (Magnuson, 2010; Majeed et al., 2011; Majeed et al., 2009). The clustering algorithm used in this preliminary approach could also be improved by considering the spatial location and/or contiguity of the voxels. The number of clusters was determined empirically for this feasibility study, but we plan to employ measures of wavelet entropy in future efforts to determine the optimal number.

As the field grows, it will be necessary to find methods that can identify changes that are most likely to be related to the function of the brain. Some studies have linked network dynamics to behavior as a first step (Thompson et al., 2012), and others are pursuing multimodal approaches that can link dynamics to more direct measures of neural activity. In either case, it will be necessary to maximize the separation and detection of signals that demonstrate relevant variations over time, and wavelet analysis is a promising candidate. As shown here, the method can cluster voxels based on their spectral and temporal properties, providing a ‘connectivity’ map without the use of a seed pixel. We anticipate that clustering voxels with similar spectral and temporal properties will improve sensitivity to dynamic network interactions. As the volume of data from each study increases, data-driven analysis will play an increasingly important role in summarizing the results and identifying key features.