Abstract
Diffusion MRI (dMRI) can provide invaluable information about the structure of different tissue types in the brain. Standard dMRI acquisitions facilitate a proper analysis (e.g. tracing) of medium-to-large white matter bundles. However, smaller fiber bundles connecting very small cortical or sub-cortical regions cannot be traced accurately in images with large voxel sizes. Yet, the ability to trace such fiber bundles is critical for several applications such as deep brain stimulation and neurosurgery. In this work, we propose a novel acquisition and reconstruction scheme for obtaining high spatial resolution dMRI images using multiple low resolution (LR) images, which is effective in reducing acquisition time while improving the signal-to-noise ratio (SNR). The proposed method called compressed-sensing super resolution reconstruction (CS-SRR), uses multiple overlapping thick-slice dMRI volumes that are under-sampled in q-space to reconstruct diffusion signal with complex orientations. The proposed method combines the twin concepts of compressed sensing and super-resolution to model the diffusion signal (at a given b-value) in a basis of spherical ridgelets with total-variation (TV) regularization to account for signal correlation in neighboring voxels. A computationally efficient algorithm based on the alternating direction method of multipliers (ADMM) is introduced for solving the CS-SRR problem. The performance of the proposed method is quantitatively evaluated on several in-vivo human data sets including a true SRR scenario. Our experimental results demonstrate that the proposed method can be used for reconstructing sub-millimeter super resolution dMRI data with very good data fidelity in clinically feasible acquisition time.
Keywords: Super resolution reconstruction, diffusion MRI, spherical ridgelets, compressed sensing
1. Introduction
Diffusion-weighted Magnetic Resonance Imaging (dMRI) is a key technique for studying the neural architecture and connectivity of the brain. It utilizes multiple 3-dimensional diffusion-weighted images to probe the water diffusivity along various directions. Its importance has been proven in clinical settings for investigating several brain disorders such as Alzheimer's disease, schizophrenia, mild traumatic brain injury etc. [1, 2]. However, low signal-to-noise ratio (SNR) and acquisition time limits the typically spatial resolution of dMRI to the order of 2 × 2 × 2 mm3. Consequently, dMRI has been mainly used to study medium-to-large white matter structures. Further, partial volume effects (PVE) which occur at the interface of different tissue types (gray-white, gray-CSF (cerebrospinal fluid) and white-CSF) can have significant effect on the measured diffusion properties and can lead to erroneous inferences [3, 4]. While some of the effects of CSF contamination can be removed using free-water modeling [5], yet large voxel sizes can lead to erroneous results in tractography. Consequently, increasing the spatial resolution of dMRI is imperative for investigation of small white-matter fascicles originating in small cortical and sub-cortical gray matter structures (such as, substantia nigra or sub-thalamic nucleus).
Reducing the voxel size of dMRI is challenging because the SNR is directly proportional to the voxel size if the readout time is fixed, see [6, page 163]. Although SNR could be enhanced by averaging multiple acquisitions, the increase in SNR is proportional to the square root of the number of averages. For example, reducing the voxel size from 2 × 2 × 2 mm3 to 1 × 1 × 1 mm3 requires 64 averages to obtain equivalent SNR, which makes it impractical to use such an “averaging” scheme in current clinical setting. Recently, several methods have been proposed to obtain high-resolution (HR) dMRI data. These methods can be classified into two categories based on their acquisition strategies. The first group of methods obtain high spatial resolution using a single low-resolution image via intelligent interpolation. These type of methods have been widely used for natural images [7] and more recently for MRI [8, 9] and dMRI [10, 11]. Though, these methods preserve and enhance certain anatomical details, their performance still largely depends on the original image resolution, as pointed out in the work of [11].
The second group of methods use the concept of super-resolution to obtain high resolution data from multiple LR image volumes acquired according to specific sampling schemes. A HR image is estimated by intelligently fusing the LR images. This type of method was initially studied in [12] for reconstruction of HR images using multiple LR stereo images. It has since been applied to obtain HR anatomical MRI images [13, 14, 15] by employing sub-pixel-shifted scans along the slice-select dimension. In the field of diffusion MRI, it was first proposed in [16] to obtain high resolution diffusion tensor images. The authors in [17] used acquisition from three orthogonal directions to perform super-resolution, while the authors in [18] use a generalized version with arbitrary slice acquisition direction to obtain HR images. However, in most these methods, super-resolution was applied independently to each individual diffusion weighted volume and the correlation between diffusion signals in q-space was not taken into account during the reconstruction process. As a result, each of the LR images were either acquired or interpolated on the same set of diffusion gradients prior to obtaining the complete dMRI volume. Further, all of the LR volumes have to be corrected for EPI (echo-planar imaging) distortions, which are different for different slice-select directions. This requires accurate non-rigid registrations and blip-up blip-down acquisitions as in [19] for correcting the distortions, making the acquisition time significantly long. To address this problem, more recently, [20] introduced a method that used the diffusion tensor imaging (DTI) technique to model the diffusion signal in q-space. It was extended in [21, 22] to allow the LR images to be acquired along different sets of gradients in q-space. Though this approach does reduce acquisition time and is robust to motion, a very simplistic diffusion tensor model is not appropriate for modeling more complex diffusion phenomena (crossing fibers). The proposed work is a generalization of this technique with no parametric model assumed about the diffusion signal and thus recovers the true underlying signal in its most general form (for a given b-value). A preliminary version of this paper has been accepted for publication in the conference on Information Processing in Medical Imaging (IPMI) 2015.
Our contributions
In this paper, we propose to combine the concepts of compressed sensing and super-resolution to reconstruct very high resolution diffusion data. In particular, we focus on a specific q-space sampling scheme known as high angular resolution diffusion imaging (HARDI) which uses several diffusion measurements at a single b-value shell [23, 24]. The proposed CS-SRR method reconstructs a HR image using multiple LR data sets which are also under-sampled in q-space. As illustrated in Figure 1, given three thick-slice data sets that are sub-pixel-shifted along the slice-select dimension and have N1, N2 and N3 gradient directions, respectively, we reconstruct a thin-slice high resolution dMRI data set that has N1 + N2 + N3 gradients. Being a non-parametric method, the proposed approach is capable of resolving crossing of multiple fiber-bundles in the reconstructed high resolution image.
Figure 1.
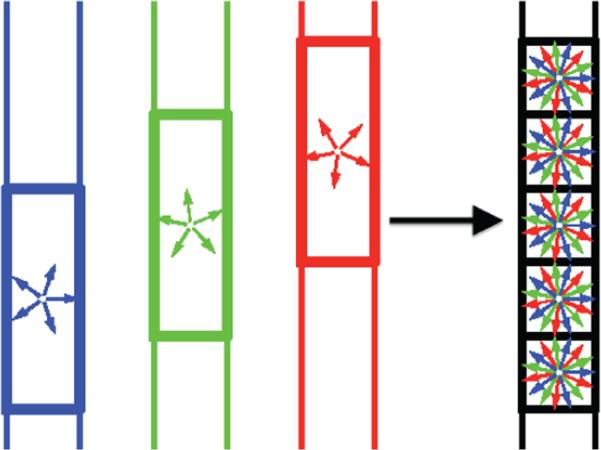
An illustration of the proposed CS-SRR scheme: a high-resolution image is reconstructed using three overlapping thick-slice volumes with down-sampled diffusion directions.
The proposed method uses spatial and q-space regularization techniques for reconstructing HR diffusion data. Additionally, we incorporate a-priori knowledge about the tissue type (gray, white or CSF) from a high-resolution T1-weighted image to adaptively reconstruct the HR diffusion data. Compressed sensing reconstruction from under-sampled data in q-space is achieved by means of a sparsifying basis of spherical ridgelets [25], whereas sparsity and smoothness in the spatial domain is incorporated by means of total-variation(TV) regularization. We design a convex cost functional and introduce an efficient optimization algorithm based on ADMM for solving the CS-SRR problem. We quantitatively evaluate the performance of our method by comparing short and long range fiber connectivity as well as the estimated diffusion measures such as fractional anisotropy (FA) and mean diffusivity or trace. The performance is evaluated for a synthetic scenario using the human-connectome-project (HCP) data set and in a true SRR scenario, whereby quantitative comparison is made between high resolution data obtained using the proposed CS-SRR method and that obtained directly from the MR scanner (from repeated scans). We should note that, to the best of our knowledge, this is a first instance of combining compressed sensing and super-resolution to reconstruct the HR diffusion signal without any modeling assumptions of the diffusion process. The proposed acquisition and reconstruction scheme allows to reduce the scan time significantly (up-to 3 times) compared to the standard super-resolution reconstruction, which would require at-least 3 times more measurements than the proposed method. We thus expect the proposed method to be of great utility for future neuroimaging studies.
2. Background
In this section, we provide a brief background on diffusion-weighted MRI, spherical ridgelets and the compressed sensing technique, which will be used subsequently in the proposed CS-SRR algorithm.
2.1. Diffusion-weighted Imaging
Diffusion MRI is a favorite research tool for investigating the neural architecture and the connectivity of the brain. The ensemble average diffusion propagator (EAP) is usually estimated from the diffusion measurements to describe the average displacement of water molecules within a voxel during the sampling period, which provides important structural information about the underlying tissue. In the narrow pulse setting (for single pulse field gradient experiment), the diffusion signal S(q) is related to the EAP P(r) via the Fourier transform given by [26]
with being the normalized diffusion signal and S(q), S(0) being the diffusion signal along the gradient direction q and at the origin, respectively. The vector q in q-space is an experimentally controlled parameter with where γ is the gyromagnetic ratio and δ is the duration of the diffusion sensitizing gradient whose magnitude and orientation are determined by the vector G.
Various of methods have being devised to estimate the EAP from E(q) measured at different points in q-space [27, 28, 29, 30, 31, 32]. A classical method is Diffusion Tensor Imaging (DTI) [33] which models E(q) using a Gaussian function with a single fiber orientation. Consequently, it cannot model complex fiber architectures such as crossings and kissing fibers. To resolve this issue, High Angular Resolution Diffusion Imaging (HARDI) technique was introduced, which involves acquiring diffusion signal on a single q-shell along several gradient directions [34]. This technique requires a lot less time and measurements than those that estimate the entire EAP. Various estimation methods [23, 24, 35, 36, 37] have been proposed for analyzing the HARDI data to resolve complex angular structures. These methods are subsequently used in tractography algorithms [38, 39] to study brain connectivity.
In this paper, we focus on the HARDI scheme and introduce a method that uses a set of LR dMRI acquired on the same q-shell to recover high spatial resolution dMRI data. For this purpose, we use the spherical ridgelet functions introduced in [37] to model the diffusion signal in q-space at each voxel. Spherical ridgelets form a basis for representing functions on a unit sphere. In particular, it has been demonstrated that diffusion signals over a single b-shell can be sparsely represented in this basis [37]. This allows the use of the theory of compressed sensing (CS) for accurate reconstruction of HARDI data from sparse samples. In the following, we provide the principal concepts behind spherical ridgelets and compressed sensing.
2.2. Spherical ridgelets
Spherical ridgelets are constructed following the fundamental principles of wavelet theory. For and ρ ∈ (0, 1), let κ(x) = exp{–ρx(x + 1)} be a Gaussian function. Further, we let
for j = 0, 1, 2 . . .. The spherical ridgelets with their energy spread around the great circle supported by a unit vector is given by
| (1) |
where Pn denotes the Legendre polynomial of order n, κ−1(n) = 0, ∀n and
To construct a finite over-complete dictionary, we follow the method in [25, 40] and restrict the values for the resolution index j to a finite set {−1, 0, 1}. For each resolution index j, the set of all possible orientations are discretized to a set of Mj = (2j+1m0 + 1)2 directions on the unit sphere with m0 being the smallest spherical order resulting in k0(m0) ≤ ε for some predefined 0 ≤ ε < < 1 (e.g. ε = 10−6). To this end, for each j, a total of Mj orientations are chosen so that the set of over-complete spherical ridgelets are given by
The spherical ridgelet basis functions have been shown to provide a sparse representation of the dMRI signal. In particular, it was shown in [25] that a suitable implementation of spherical ridgelets can be used for reliable reconstruction of HARDI signals from as few as 16 diffusion encoded scans. Moreover, in the Sparse Reconstruction Challenge for Diffusion MRI (SPARC) held during the workshop on Computational Diffusion MRI (CDMRI) 2014, the spherical ridgelets based method was one of the best methods in reconstructing HARDI signals acquired from a physical phantom, see http://projects.iq.harvard.edu/sparcdmri/results for more details. However, the work in [25] did not incorporate an isotropic basis function to sparsely represent nearly isotropic signal as in the cortical gray matter or CSF areas. Consequently, we expanded the basis of spherical ridgelets with an isotropic function. Thus, the set of functions that is used to represent the diffusion signal is
where ψiso denotes a constant function on the unit sphere. For convenience, we denote the functions in Ψ as ψ1, ψ2, . . . , ψM with ψ1 = ψiso.
2.3. Compressed sensing
Let Eb(u) be the normalized diffusion signal at a b-shell along the direction u. Using the set of functions Ψ, we assume that the diffusion signal can be represented as
| (2) |
where only a few of the cm's are non-zero. Given the diffusion signal measured at a set of N diffusion-encoding orientations , one can recover the diffusion signal on the whole sphere by estimating the representation coefficients cm in (2). For this purpose, we let denote the vector of the diffusion signal whose nth entry is equal to Eq(un) and let the values of ϕm for m = 1, . . . , M at the N acquisition locations be stored in a N × M matrix A defined as
Each column of A is scaled such that it has unit norm. Thus the measurement s can be represented as
where c denotes the vector of representation coefficients and μ denotes the measurement noise. Since the number of measurements, N, is usually much smaller than M, it is an underdetermined problem to estimate c. On the other hand, the vector c has very few non-zero entries. Thus, the representation coefficient of the signal can be estimated by solving
| (3) |
where ∥c∥0 denotes the number of non-zero entries of c and ε denotes the level of measurement noise. However, being a combinatorial problem, (3) is computationally intractable for most practical problems.
The theory of compressed sensing provides a mathematical foundation for accurate and efficient recovery of signals that can be sparsely represented in a basis [41, 42]. In recent years, it has been widely used in many areas of signal processing [43] and in MRI [44]. In (3), if the optimal c is sufficiently sparse and if the columns of A have low coherence, then the solution of (3) can be robustly recovered by solving the following convex optimization problem [41]:
| (4) |
where ∥c∥1 denotes the norm of c. From the Lagrangian multiplier method, the solution of (4) equals to that of
| (5) |
for some λ ≥ 0. This setup has been successfully used in [37, 25, 40] to reconstruct dMRI signals from sparse measurements. Several minimization algorithms [45, 46, 47, 48] exist for solving (5).
For this particular application of estimating diffusion signals in the SRR scenario, we modify the method in the following two aspects to improve the performance: First, we restrict the representation coefficients to be nonnegative. Second, we use a weighted -minimization algorithm so as to allow for imposing different weighting coefficients for the isotropic basis function for different brain tissues. For example, the diffusion signal in CSF areas is isotropic, hence, we impose much smaller penalty for selecting the isotropic basis element in such isotropic areas. Incorporating this fact, we introduce the following modified -minimization problem:
| (6) |
where all the entries of c are constrained to be nonnegative, ◦ denotes the element-wise multiplication and the weighting vector has the form
with w ≥ 0 weighs the penalty for choosing an isotropic basis function. The value of w is larger in white and gray matters areas than in CSF areas. Equation (6) is a convex programming problem, hence it can be solved efficiently using various optimization algorithms. We provide an algorithm for solving (6) using the alternating direction method of multiplier (ADMM) [49] algorithm (see Appendix), which will be used as a subroutine in the CS-SRR algorithm described in the next section.
3. Method
3.1. Modeling
First, we present a linear model where the LR dMRI volumes are considered as down-sampled versions of an underlying HR volume via suitable sampling operators. For this purpose, let Yk denote a collection of LR dMRI volumes for k = 1, . . . , K. Each Yk is a set of LR dMRI volumes acquired using the same spatial sampling scheme but with different gradient directions. It can be considered as a matrix of size with and being the number of voxels and the number of gradient directions, respectively. We assume that the K sets of gradient directions for the Yk's do not overlap with each other. Moreover, the LR acquisition Yk's are considered as low-pass filtered versions of an underlying true HR volume, denoted by S, which has nx × ny × nz voxels and gradient directions. The acquisition model for each of the LR scans Yk can be written as
| (7) |
where Dk denotes the down-sampling matrix that averages neighboring slices, Bk denotes the blurring operator (or point-spread function), Qk is the sub-sampling matrix in q-space and μk denotes the measurement noise. This model is a generalization of the image formation model used in [13, 17] where Qk's were assumed to have the same value in all Yk's enforcing each set of LR dMRI volumes to have the same gradient directions. In the proposed model (7), the Yk's are allowed to have different sets of gradient directions by using different Qk's, which reduces the total acquisition time.
We further use the spherical ridgelets to model the diffusion signal at each voxel of S. Hence, S can be written as S = VAT with A being the basis matrix introduced in Section 2.3 and each row vector of V being the representation coefficients at the corresponding voxel. Each row of V is sparse, so is the whole matrix V.
Following (6), we estimate S by solving
| (8) |
where W is a weighting matrix to adjust the penalty for selecting the isotropic element in A at each voxel based on using prior information regarding the tissue type (gray, white or CSF). The quadratic term in (8) corresponds to the assumption that the noise components in Yk's follow Gaussian distributions which is usually assumed in SRR methods, see e.g. [17, 21]. For other type of distributions, such as Rician distribution, the quadratic term can be replaced by the corresponding log-likelihood functions as was done in [50]. However, the Gaussian assumption is valid for high SNR (SNR>5) [21, 51]. Moreover, using a quadratic term in (8) usually leads to computationally efficient algorithms which is preferred in solving large scale optimization problems.
We note that the -norm regularization in (8) is carried out at each individual voxel. Therefore, the correlation between the diffusion signal at neighboring voxels is not considered. This prior knowledge can be incorporated in the CS-SRR method by adding a spatial-regularization term which is described in the next section.
3.2. Total-variation (TV) regularization
Let sr(un) denote the diffusion signal along the direction un at the voxel indexed by r ∈ Ω with Ω being the set of coordinates of all voxels. The diffusion signal at all voxels along the gradient un forms a 3D image volume denoted by Sn. Due to the correlation of diffusion signal in neighboring voxels, Sn can be assumed to have a spatially smooth structure. Taking advantage of this information helps in improving the performance of the CS-SRR method. A standard technique to achieve this is using the TV semi-norm of Sn defined as
where N(r) denotes the set of neighbors of r. In this paper, we follow a standard way to define N(r) with r = [i, j, k] as
For a collection of image volumes , the TV semi-norm of S is defined as the sum of the TV semi-norm of each individual volume Sn:
By adding this regularization term in (8), the optimization problem can be rewritten as
| (9) |
where the positive parameters λ1, λ2 determine the relative importance of the data fitting terms versus the sparsity and the TV regularization terms. Next, we introduce an efficient algorithm for solving (8) based on the alternating direction method of multipliers (ADMM) algorithm [49].
3.3. Optimization algorithm
The optimization problem (9) typically involves high dimensional optimization variables. A suitable implementation of the ADMM algorithm distributes the computational cost and decomposes the optimization into a sequence of simpler problems. First, we note that (9) can be equivalently written as
| (10) |
where Z is an auxiliary variable that equals to S, and the augmented terms with ρ1, ρ2 ≥ 0 do not change the optimal value. Let Λ1, Λ2 be the multipliers for S–VAT = 0 and S–Z = 0, respectively. Then, each iteration of the ADMM algorithm consists of several steps of alternately minimizing the augmented Lagrangian
over S, V, Z and one step of updating Λ1, Λ2. More specifically, let Vt, St, Zt and denote the values of these variables at iteration t. Then, iteration (t + 1) consists of two steps of estimating {Vt+1, Zt+1} and Ht+1 by solving
| (11) |
| (12) |
and one step of updating the multipliers as
A typical stopping criteria is to check if and have “stopped changing”, i.e. and for some user defined choice of ε1, ε2.
We point out some important notes for the above iterative algorithm: (1) Problem (11) can be decomposed into two independent optimization problems to solve V and Z. The update for Vt is obtained by solving an -minimization problem with non-negative constraints using the algorithm in appendix. In particular, the solution for each voxel can be obtained independently (in parallel). (2) The update for Zt is a standard TV denoising problem, which can be efficiently solved using [52]. (3) Problem (12) is a least-squared problem which needs a matrix inversion to compute the closed-form solution. In particular, we note that [Q1, . . . , QK] is a permutation matrix since the sets of gradient directions for the LR Yk's are not overlapping. Let for k = 1, . . . , K. Hence, the update procedure for each are independent with each other. The value of at iteration (t + 1) is the solution of the least-squares problem
which is given by
We note that the down-sampling operator DkBk determines the dimension of matrices to be inverted in the above equation. In this particular situation where Dk and Bk down-samples and blurs the image along the z direction, we only need to invert a matrix of size nz × nz, which can be easily done on a standard workstation. We also note that in a more general situation when the matrix size is too large, an alternative method is to use the steepest descent iterative method [17].
4. Experiments
We tested the performance of the proposed method using three experiments. In the first one, we artificially generated (by slice averaging and blurring) thick-slice acquisitions based on the high resolution data set from the Human Connectome Project (HCP) [53]. The second and the third experiments consisted of actual validation setups where data was acquired from a healthy human subject using a 3T Siemens clinical scanner. We compared the recovered CS-SRR result with the corresponding gold-standard (GS) HR data and the LR data using the following metrics:
Percentage of FA di erence: Whole brain multi-tensor tractography [38] was computed on the GS and the reconstructed data, and several fiber bundles were extracted. The average fractional anisotropy (FA) and trace for tensors along the fiber bundles were computed. The percentage of FA difference was computed using |FACS–SRR–FAGS|/FAGS. The percentage of Trace difference was defined in an analogous fashion.
- Error in long-range fiber connectivity using tractography: Tractography is a useful tool to study brain connectivity and network layout. Any reconstruction method should be able to produce similar white matter tracts as one would expect from the actual ground truth data. In our experiments, we used the multi-tensor tractography algorithm of [38] to trace fiber bundles for the GS and the CS-SRR data sets. For quantitative comparison between the obtained tracts, we use the following comparison metric based on the probability distribution function (pdf) of the physical coordinates of the tracts. In particular, let px, py and pz be the pdf of the x, y, z coordinates of the fiber tracts obtained from the GS data set. Let and be the corresponding pdfs for the CS-SRR data set. Then, the similarity between two fiber bundles can be computed using the following:
which is the average Bhattacharyya coefficient between the three pairs of marginal pdfs and takes value in the interval [0, 1]. A value of 1 indicates exact match between the fiber bundles, whereas a value of 0 indicates complete mismatch between the two set of tracts. We note that a similar metric was also used in [54] to compare fiber bundles.
4.1. Evaluation on HCP data
In this experiment, we used HCP data, which has spatial resolution of 1.25 × 1.25 × 1.25 mm3 with 90 gradient directions at b = 2000 s/mm2. To construct LR images, we first artificially blurred the DWI volumes along the slice direction using a Gaussian kernel with full width at half maximum (FWHM) of 1.25 mm. Then the data was down-sampled by averaging three contiguous slices to obtain a single thick-slice volume with spatial resolution of 1.25 × 1.25 × 3.75 mm3. Similarly, two additional LR volumes were obtained so that all the three LR volumes were slice-shifted in physical space (see Figure 1). The thick-slice volumes were also sub-sampled in q-space so that each set had 30 unique gradient directions. We also obtained a segmentation of the brain into three tissue types, namely, gray, white and CSF, from the T1-weighted (T1w) MR images using the method in [55]. This tissue classification was used as a prior to set w = 10−4 in CSF and w = 1 in gray and white matter areas. The regularization parameter was λ1 = 0.01. The auxiliary parameter was set to ρ1 = 1. Since the measurement model is known perfectly in this example, we did not use any total-variation denoising term in the algorithm by setting the parameter λ2 = 0. Hence, the reconstruction results manifest the effectiveness of the spherical ridgelets and the regularization terms.
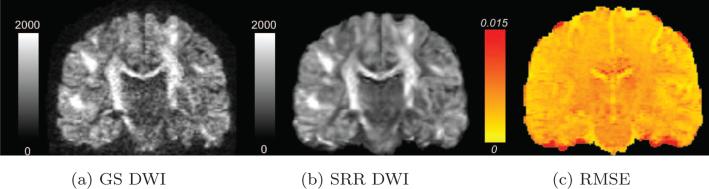
Figures 2a and 2b show a coronal slice of the diffusion-weighted image along the same gradient direction in the GS and SRR data sets, respectively. To quantitatively assess the difference between the two data sets, we computed the root-mean-square error (RMSE) between the two data sets with the RMSE in the i-th voxel being defined as
where and denote the diffusion-weighted signal in the i-th voxel of the SRR and GS data volumes, respectively. RMSE reflects the average difference of the diffusion signal along each gradient directions. Figure 2c shows the RMSE in the same coronal slice. We note that RMSE is below 1% in most of the brain regions.
Figure 2.
(a), (b) shows a coronal slice of an arbitrarily chosen gradient direction in the GS and SRR dMRI data sets respectively. (c) shows the RMSE between the GS and SRR data sets computed for all gradient directions of the same slice. Note that the error is less than 3% in most of the white and gray matter regions.
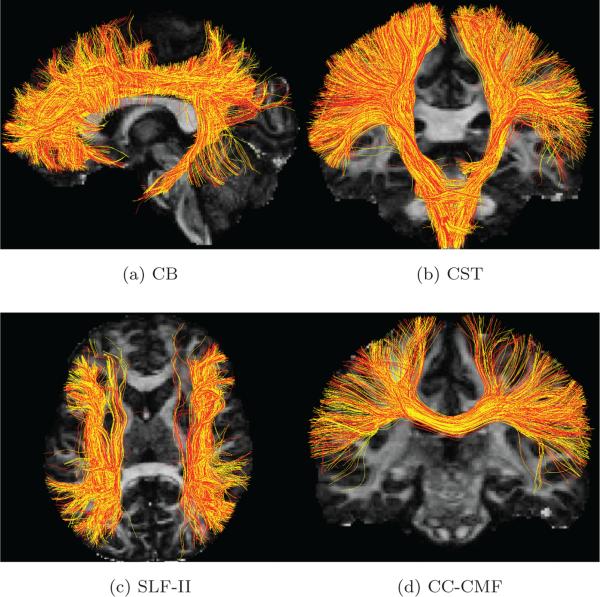
To compare the tractography results, we traced all fiber bundles using whole-brain tractography [38] for the GS and the reconstructed data sets, respectively. Next, we extracted the cingulum bundle (CB), the corticospinal tract (CST), the superior longitudinal fasiculus II (SLF-II) and a sub-part of the corpus callosum called caudal middle frontal bundle (CC-CMF), respectively, using the white matter query language (WMQL) [56] which uses Freesurfer cortical parcellations. The four pairs of fiber bundles are shown in Figure 3a to 3d where the red and yellows tracts are results from the GS and CS-SRR data sets, respectively. The comparison metrics between the fiber bundles is summarized in Table 1. The fiber-bundle overlap measure is very close to one, indicating a significant overlap between the fiber bundles obtained using the GS and CS-SRR data. Further, the estimated average FA and trace are very similar for both data sets. The percentage error for FA and trace are within the typical range of variations from different acquisitions [57]. We also note that CC-CMF has higher trace error and lower fiber-bundler overlap compared with other fiber bundles, which may be caused by the downsampling operator that mixes the voxels in corpus callous and the CSF areas. However, in the true scenarios in the following examples, the tractography results for the fibers bundles in corpus callosum turn out to have better performance than in this example.
Figure 3.
(a), (b) (c) and (d) are the tractography results for the cingulum bundle (CB), the corticospinal tract (CST), the superior longitudinal fasciculus II (SLF-II) and the corpus callosum caudal middle frontal (CC-CMF) bundle (with red and yellow tracts obtained using the GS data set (with 90 directions) and CS-SRR data set (using 30 directions for thick-slice acquisitions), respectively. The comparison metrics for the fiber bundles are shown in Table 1.
Table 1.
Comparison metrics for the fiber bundles in Figure 3.
| FA difference | Trace difference | Fiber-bundle overlap | |
|---|---|---|---|
| CB | 2.8% | 1.8% | 0.97 |
| CST | 4.0% | 1.2% | 0.98 |
| SLF-II | 3.6% | 1.6% | 0.95 |
| CC-CMF | 3.1% | 3.2% | 0.95 |
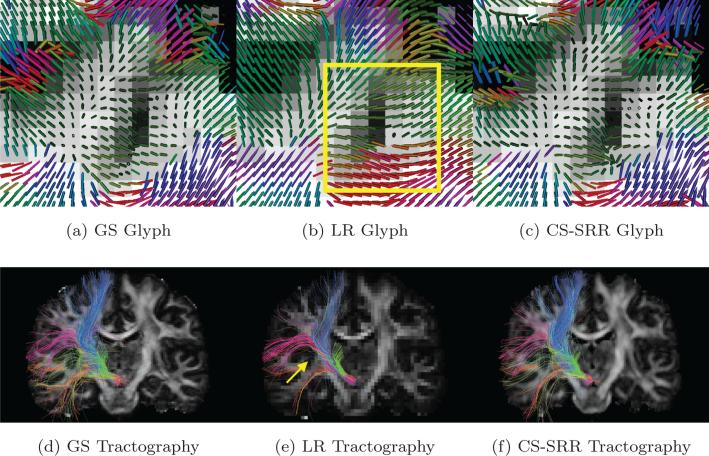
An important goal of this work is to demonstrate the advantage of using high-resolution DWI image in studying small white-matter fascicles. For this purpose, we also generated a low-resolution DWI volume by averaging every 2 × 2 × 2 neighboring voxels from the GS data to obtain LR dMRI data with isotropic voxel size of 2.53 mm3. Figure 4a-4c shows the single-tensor glyphs color coded by the direction of the dominant eigenvector of the diffusion tensors for the GS, LR and SRR data sets in the same brain region from a coronal slice. The glyphs were estimated on the same spacial resolution by using trilinear interpolation methods. The background of the glyphs is the corresponding T1w image. As pointed out in the rectangular area in Figure 4b, due to partial-volume effects, the LR image was not able to capture the fine curvature of the fiber bundles near the gray matter areas. Figure 4d-4f show the tractography results for tracts originating from the sub-thalamic nucleus with fibers being color-coded by orientation. As pointed out by the arrow in Figure 4e, most of the green fibers are missing in the LR image, though the number of seeds in each voxel of the LR image is 8 times higher than the HR images. On the other hand, the tracts obtained from the GS and CS-SRR data are very similar.
Figure 4.
(a), (b) and (c) show the single tensor glyphs for the GS data set (1.253 mm3 isotropic voxels), LR data set (2.53 mm3 isotropic voxels) and the CS-SRR HCP data sets (1.253 mm3 isotropic voxels), respectively. The rectangle in (b) shows the partial-volume effects in the LR image where the orientations of the glyphs are not estimated correctly. (d), (e) and (f) are the fiber tracts, color-coded with tract orientation for the three data sets with seeds in sub-thalamic nucleus. The arrow points out some missing fiber tracts in the LR image.
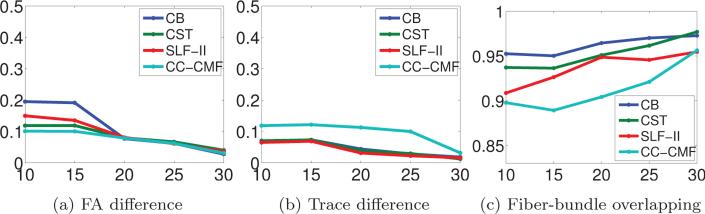
A significant advantage of the proposed method is that the acquisition time is reduced by using subsampled thick-slice acquisitions. In the above experiment, we have shown that using 30 diffusion gradients for each of the thick-slice acquisitions provides satisfying results that are similar to the gold-standard data. From a practical viewpoint, it is interesting and important to investigate the performance limit in reducing the number of samples. To this end, we have tested our method in 4 additional scenarios where we use 10, 15, 20 and 25 gradient directions for each thick-slice acquisition. In order to create these thick-slice data sets with measurements uniformly spread over the sphere for each LR image, we used spherical harmonics of order 8 to interpolate the signal on a dense grid followed by subsampling along the desired gradient directions. Each of the four sets of gradient directions were chosen so that they were quasi-uniformly distributed on the hemisphere. Following the same procedure as in the previous experiment, we reconstructed the HR images using the proposed algorithm, computed the whole-brain tractography results and extracted the CB, CST, SLF-II and CC-CMF tractography results using WMQL [56]. For comparison, we also computed the normalized FA error, normalized trace error and the fiber-bundle overlap compared to the gold standard results. In particular, the normalized FA error was defined as |FAGS – FACS–SRR|/FAGS where FAGS and FACS–SRR are the FA values of the GS and the CS-SRR tractography results, respectively.
Figure 5a, 5b and 5c show the normalized difference in FA, trace and fiber-bundle overlap for the four sets of tractography results versus the number of gradient directions used for the thick-slice images. The normalized FA error and Trace error monotonically decrease with increasing number of gradient directions. In particular, using 20 gradient directions, the normalized FA error for all tracts was about 0.08 and the normalized trace error was about 0.04 which are similar to typical range of variations expected with different scans of varying spatial resolutions. On the other hand, the fiber-bundle overlap in Figure 5c monotonically increases with increasing number of samples. For only 10 gradient directions, the fiber-bundle overlap for all the tracts was about 0.9 or higher.
Figure 5.
(a), (b) and (c) show the percentage of FA difference, percentage of Trace difference and fiber-bundle overlapping for the reconstructed CB, CST, SLF-II and CC-CMF bundles versus the number of gradient directions in the thick-slice acquisitions.
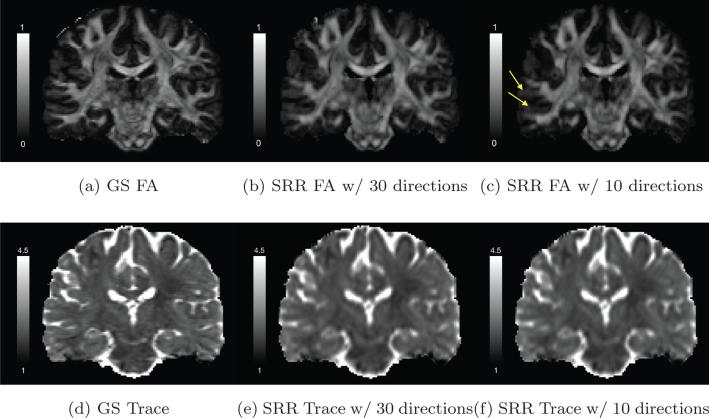
For qualitative assessment of the reconstruction algorithm in different brain regions, Figures 6a, 6b and 6c illustrate the FA images of a coronal slice in the GS data set and the SRR data sets obtained using 30 and 10 gradient directions respectively. The three images show similar values in most white-matter areas. As indicated by the yellow arrows in Figure 6c, the SRR result obtained using only 10 gradient directions slightly underestimates the FA value in regions near the cortical areas. Figures 6d to 6f are the corresponding trace images in the same slices. The three images have similar values in all brain regions though the SRR results are smoother than the GS result. Though the differences in FA and trace images may not seem to be as significant as the results shown in Figure 5, it should not be surprising since the tractography results were obtained using a multi-tensor model which typically needs more measurements than the single-tensor model in order to resolve crossing fibers.
Figure 6.
(a), (b) and (c) show the FA image of a coronal slice of the diffusion-weighted image in the GS data set, the SRR results using 30 and 10 gradient directions, respectively. (d), (e) and (f) show the corresponding Trace image for the same slice with the unit of Trace being μm2/ms.
4.2. True CS-SRR scenario using clinical 3T scanner
The second experiment was based on a data set acquired on a 3T Siemens Trio clinical scanner (maximum gradient strength of 40 mT/m). We acquired three overlapping thick-slice scans with spatial resolution of 1.2 × 1.2 × 3.6 mm3. The DWI volumes were sub-pixel shifted by 1.2 mm along the slice-select direction. Each LR DWI had a set of 30 unique gradient directions with b = 1000 and TE = 89, TR = 6300 ms. For comparison, we also acquired 9 acquisitions (with 90 gradient directions each) of the same subject with a spatial resolution of 1.2 × 1.2 × 1.2 mm3, which was used as the “gold standard” data. Due to time limitations, these high resolution scans had partial brain coverage (it took more than 1.5 hours to obtain these 9 scans). The average of these 9 scans (after motion correction) was considered as the gold standard. We also acquired a high resolution b0 and T1w image to obtain tissue classification for prior-information used in our algorithm. To ensure that the LR DWI's were in the same spatial co-ordinate system, we first down-sampled the whole-brain b0 image to produce, three thick-slice volumes which were considered as the reference images. These images were only used for spatial normalization and not in the actual reconstruction algorithm. Then, the three acquired thick-slice LR DWI scans were registered to the corresponding reference volumes. The T1w was registered to the whole-brain b0 image using a nonlinear transformation. The registered T1w image was then segmented into different tissue types using the method of [55]. We set the FWHM of the blurring kernel to 1.2 mm, λ1 = 0.005, λ2 = 0.05, ρ1 = ρ2 = 1 and w = 0.01 in CSF area and w = 1 in gray and white matters. These parameters were learned using exhaustive search experiments based on one slice of the image so that the reconstruction error was small compared with the gold-standard. For computing quantitative metrics, we registered the reconstructed whole-brain data to the partial-brain GS data set.
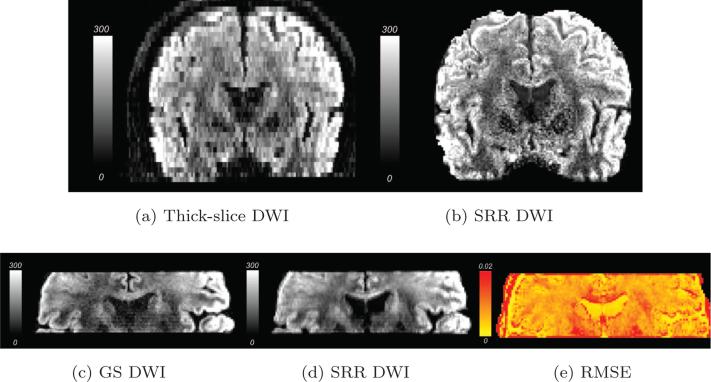
Figures 7a and 7b shows a coronal slice along the same gradient direction with thick-slice and the SRR data set respectively. Clearly, Figure 7b shows better finer details than the acquired thick-slice data set. The reconstructed whole-brain SRR data set was registered to a partial-brain field of view for quantitative comparisons with the GS data set. Figures 7c and 7d show a coronal slice of the partial-brain GS and SRR data set, respectively. Figure 7d is smoother than Figure 7c due to the combined effects of image registration, regularization and total-variation denoising. As shown in (7e), the RMSE is lower in the CSF areas while it is slightly higher near the image boundary, which may be caused by imperfect alignments between the two data sets. In most white and gray-matter areas, the RMSE is about 0.02 or less implying that the SRR reconstruction is close to the GS data set.
Figure 7.
(a) is a coronal slice of a thick-slice dMRI volume. (b) is the corresponding slice from the SRR dMRI volume. (c) and (d) are the partial-brain coronal slice of the same diffusion-weighted dMRI volume in the GS and the SRR data sets, respectively. (e) shows the RMSE between the GS and SRR dMRI volumes.
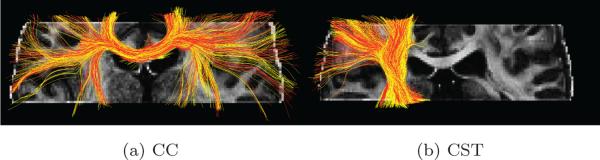
For more detailed comparisons, we first obtained the tractography results from the reconstructed (CS-SRR) and GS partial-brain data sets using the method in [38]. Since whole-brain FreeSurfer cortical parcellation was not available, we could not employ WMQL for specific fiber bundle extraction. Consequently, we used manually selected ROI's to extract fiber bundles in the corpus callosum (CC) and the corticospinal tract (CST), respectively. The extracted fiber bundles are shown in Figure 8a and 8b, respectively. Quantitative comparison metrics for the two pairs of fiber bundles are shown in Table 2. We note that the difference between FA and Trace obtained from both the data sets is similar to those reported for test-retest reliability studies. The Hellinger distance between the tracts indicates a significant overlap between the fiber bundles.
Figure 8.
(a), (b) are the tractography results with manually selected seeds in corpus callosum (CC) and the corticospinal tract (CST) (with red and yellow tracts obtained using the GS and CS-SRR data sets (both with 1.23 mm3 isotropic voxels), respectively). The comparison metrics for the fiber bundles are shown in Table 2.
Table 2.
Comparison metrics for the fiber bundles in Figure 8.
| FA difference | Trace difference | Fiber-bundle overlap | |
|---|---|---|---|
| CC | 1.6% | 9.1% | 0.96 |
| CST | 3.2% | 10% | 0.94 |
To demonstrate the difference between HR and LR images, we also generated a LR image by averaging every 2 × 2 × 2 neighboring voxel in the GS data set to obtain a LR dMRI data set with isotropic voxel size of 2.43 mm3. Figure 9 shows the single tensor glyphs color coded by direction for the GS, LR and the CS-SRR data sets in the same brain region from a coronal slice. The background of the glyphs is the corresponding T1w image. As pointed out in the rectangular region in Figure 9b, due to partial-volume effects, the LR image was not able to capture the correct fiber orientations near the gray matter areas. Figure 9c is similar to Figure 9a, indicating that the proposed method was able to correctly reconstruct the fiber orientations near gray-matter areas.
Figure 9.
(a), (b) and (c) show the single tensor glyphs colored coded by fiber orientation for the GS data set (1.23 mm3 isotropic voxels with 90 gradient directions), LR data set (2.43 mm3 isotropic voxels with 90 gradient directions), and CS-SRR data sets (1.23 mm3 isotropic voxels with 90 gradient directions), respectively. The rectangle in (b) points out the partial-volume effects in the LR image where the directions of the glyphs are not estimated correctly (shown by different colors from the GS glyphs).
4.3. A whole-brain true CS-SRR scenario
The third experiment was based on whole-brain data sets acquired using a 3T scanner with a maximum magnetic gradient at 300 mT/m (the MGH connectome scanner). The strong magnetic gradients allowed us to acquire high in-plane resolution thick-slice DWI volumes with a voxel size of 0.9 × 0.9×2.7 mm3 and TE/TR = 84/7600 ms. Each LR DWI had a set of 20 unique gradient directions at b = 2000 s/mm2. We also acquired one acquisition of isotropic LR DWI with a spatial resolution of 1.83 mm3 and with 60 gradient directions at b = 2000 s/mm2, which is the spatial typical resolution for many clinical neuroimaging studies. High-resolution T1w and a T2w images with 0.9 mm3 isotropic voxels were also acquired. For this experiment, we set the FWHM of the blurring kernel to 0.9 mm, λ1 = λ2 = 0.02, ρ1 = ρ2 = 1, and w = 0.01 in CSF area and w = 1 in gray and white matters.
Figures 10a to 10i show coronal, sagittal and axial slices from the isotropic LR, the thick-slice and the SRR dMRI data sets respectively. Due to the larger voxel size, the isotropic LR dMRI volume has higher SNR than the thick-slice and the SRR data sets. The SRR result increases the spatial resolution of the thick-slice data set and also decreases the noise level due to the regularization terms.
Figure 10.
First row: coronal slices, Second row: Sagittal slices, Third row: Axial slices, show raw dMRI data obtained from the isotropic LR, the thick-slice and the SRR dMRI data sets respectively.
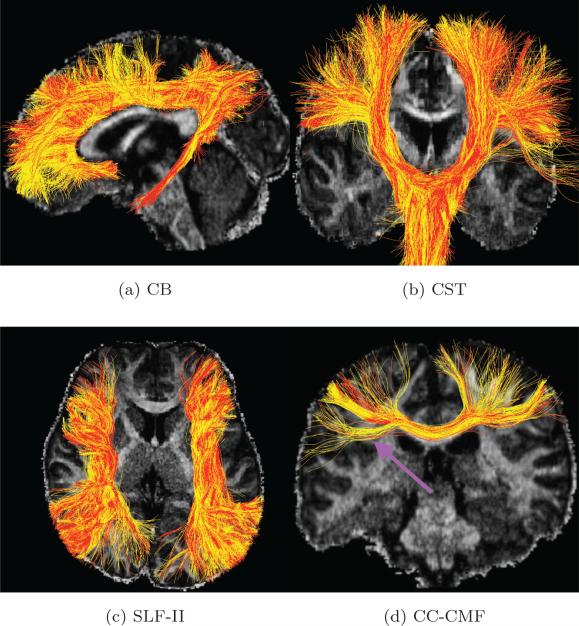
Whole brain tractography was computed for the LR data set (with 1.83 mm3 isotropic voxels) and the CS-SRR data set (with 0.93 mm3 isotropic voxels) using the multi-tensor tractography algorithm [38]. The number of seeds for the LR isotropic data was set to eight times higher than that for the CS-SRR data (for proper comparison). Figure 11a to 11d show the cingulum bundle (CB), the corticospinal tract (CST), the superior longitudinal fasiculus II (SLF-II) and the caudal middle bundle of the corpus callosum (CC-CMF) of the LR and CS-SRR data sets in red and yellow, respectively. The comparison metrics between the fiber bundles are summarized in Table 3. The FA and trace for all the bundles have similar values. We note that the fiber-bundle overlap for the CC-CMF is lower than the values of the other bundles which was caused by the fact that LR tractography failed in detecting some fibers as indicated by the arrow in Figure 11d.
Figure 11.
(a), (b) (c) and (d) are the tractography results for the cingulum bundle (CB), the corticospinal tract (CST), the superior longitudinal fasciculus II (SLF-II) and the corpus callosum caudal middle frontal (CC-CMF) bundle (with red and yellow tracts obtained using the LR data set (with 1.83 mm3 isotropic voxels) and CS-SRR data set (with 0.93 mm3 isotropic voxels), respectively. The arrow in (d) points out some fiber bundles (yellow) that were missing in the LR results (red). The comparison metrics for the fiber bundles are shown in Table 3.
Table 3.
Comparison metrics for the fiber bundles in Figure 11.
| FA difference | Trace difference | Fiber-bundle overlap | |
|---|---|---|---|
| CB | 1.2% | 1.7% | 0.94 |
| CST | 1.4% | 4.1% | 0.92 |
| SLF-II | 5.6% | 1.8% | 0.92 |
| CC-CMF | 0.5% | 1.1% | 0.85 |
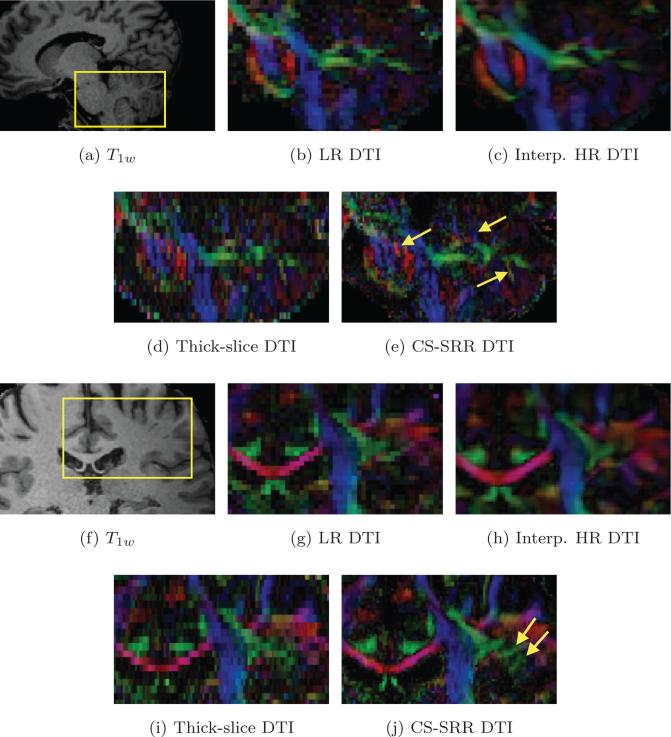
To further demonstrate that the proposed scheme recovers important spatial details of the anatomy, which cannot be obtained by simply interpolating the low-resolution data, we show some results from interpolated data in Figures 12c and 12h. We created a high-resolution dMRI data set by interpolating the acquired isotropic LR data set into a small-voxel volume with voxel size reduced to 0.9 × 0.9 × 0.9 mm3 using the trilinear interpolation method. Figures 12b to 12e show the color-coded DTI images of the LR, the interpolated-HR, the thick-slice and the CS-SRR data sets for the pons and parietal region as indicated by the rectangle in Figure 12a. Though the interpolated HR DTI is much smoother (as expected) than the other two images due to interpolation, it is still very similar to the LR image as no new “information” is available about the fine structures in the LR data. A similar result was also reported in [11]. On the other hand, the CS-SRR result shows clear demarcation between the fine laminar oriented structure (indicated by the left arrow in Figure 12e) in the pons and the cerebellum (indicated by the middle and right arrow in Figure 12e). Similar observations have also been reported for the pons area in [58]. These features are missed in the LR and the interpolated-HR images as seen in Figures 12b and 12c. On the other hand, these features are revealed in the thick-slice images shown in Figure 12d. This observation shows that thick-slice acquisitions with high in-plane resolution helps to reconstruct structures that are aligned inferior-superior. Figures 12g to 12j are the color-coded DTI images of the four data sets for the region shown in Figure 12f. The yellow arrows in Figure 12j point out some structures recovered in the CS-SRR data sets that are not seen in the other three data sets, including the acquired thick-slice images. This result demonstrates the capability of our algorithm in recovering fine structures from the overlapping thick-slice acquisitions.
Figure 12.
(b) to (e) are the colored DTI images for the LR (with 1.83 mm3 isotropic voxels), the interpolated-HR, the thick-slice and the CS-SRR data sets (with 0.93 mm3 isotropic voxels), respectively, for the rectangle region in the T1w image in (a). (g) and (j) are colored DIT images from the four data sets for the rectangle region in (f), respectively. The yellow arrows in (e) point out the fine details in the CS-SRR results while these details are missing in the LR and the interpolated-HR results. The yellow arrows in (j) point out some structures in white matters of the CS-SRR data sets while these structures are not shown in the other three data sets.
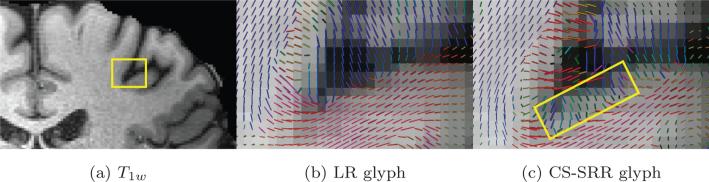
Figure 13b and 13c show the single-tensor glyph results color coded by orientations of the LR and CS-SRR results for the rectangle region in Figure 13a. As seen in the rectangular region in Figure 13c, the CS-SRR data shows details of the fiber orientation near a sulci which is completely missing from the LR resolution images.
Figure 13.
(b) and (c) are the single-tensor glyphs with color-coded by orientations for the LR data set (with 1.83 mm3 isotropic voxels) and the CS-SRR data set (with 0.93 mm3 isotropic voxels), respectively, for the rectangle region in the T1w image in (a). The glyphs in (b) and (c) have the same size and are interpolated to the same spacing. The rectangle in (c) shows the glyphs in a gray-matter region that were missing in the LR results shown in (b).
5. Discussion and conclusion
In this work, we demonstrated using several in-vivo human experiments that improving the spatial resolution for dMRI data is critical for determining accurate tracing of white matter fibers as well as gray matter topography. We combined the twin concepts of compressed sensing and super-resolution to propose a practical diffusion acquisition and reconstruction scheme that allows for obtaining very high spatial resolution dMRI data. In particular, we showed the ability of the proposed method to obtain high resolution dMRI data with isotropic voxels of size 0.93 mm3 along 60 directions using three overlapping thick-slice acquisitions with anisotropic voxels of size 0.9 × 0.9 × 2.7 mm3 along 20 directions. Note that, the proposed method is not limited to this spatial resolution and can be used to obtain even higher spatial resolution if an MRI scanner can afford to acquire such data with reasonable SNR. The proposed technique is independent of scanner type and can be implemented on any clinical scanner. Further, an important contribution of this work is the ability to obtain such high resolution scans within a clinically feasible scan time. For example, from our experiments, we can conclude that a total of 60 gradient directions on a single b-shell is enough to obtain very high spatial resolution images. This is in contrast to standard techniques which would require several hours of scanning to obtain equivalent results. Moreover, if one uses the standard super-resolution setting, the scan time would still be at-least 3 times longer than the one for the proposed method. Thus, the proposed CS-SRR method allows for obtaining very high resolution scans in about the same time as a standard dMRI scan. Note that, the acquisition time can be further reduced by a straightforward use of multi-band (or multi-slice) acquisition sequences [59, 60].
Before we conclude, we note some practical points regarding thick-slice acquisitions. Since diffusion images are usually acquired using echo planar imaging (EPI), overlapping thick-slice acquisitions not only improve SNR but also provide some extra information about the underlying tissue than a thin-slice acquisition. For example, figure 14a and 14b illustrate the magnetization of three contiguous slices (in red, black and blue) for thin-slice acquisitions and overlapping thick-slice acquisitions, respectively. Since the slice selection is usually not perfect (its a sinc function), the signal contribution from the tissue near the edge and between two slices is usually very small. On the other hand, overlapping measurements have signal contribution from all regions of the tissue, which is not obtained in non-overlapping thin-slice images. In this aspect, thick-slice acquisitions may have some added value.
Figure 14.
(a) and (b) are illustrations for the magnetizations for three contiguous slices (in red, black and blue) for thin-slice acquisitions and overlapping thick-slice acquisitions, respectively.
We also note some limitations of the proposed method. In particular, large motion between the shifted LR acquisitions can result in very little or no overlap between contiguous regions. Thus, if large head motion is expected, it might be better to acquire several overlapping acquisitions (and not just 3) to ensure good data reconstruction quality. Our future work will focus on this aspect of the algorithm. We should however note that, problems related to large head motion is a limitation not just of the proposed method, but any technique that uses super-resolution reconstruction.
In the proposed method, one has to set parameters such as λ1, λ2, which are related to SNR of the LR scans. For example, higher noise would require more spatial regularization and consequently higher λ2. Automatically determining these parameters based on the estimated noise in the data is part of our future work. We should note that small differences in these parameter settings will not significantly change the results. Hence, the parameter settings in this paper can be applied to any other data sets acquired using similar setups. Moreover, the total-variation denoising method was used in this paper to regularize the spatial smoothness of the data mainly due to its simplicity in implementation. Though it provides satisfactory results in the experiments done in this paper, other advanced methods such as [61] can be expected to provide more robust performance when pursuing higher resolutions.
Highlights.
High---resolution dMRI is reconstructed using multiple thick---slice acquisitions.
Our approach combines super---resolution reconstruction and compressed sensing.
The total acquisition time and noise can be simultaneously reduced.
The proposed method can accurately recover complex and small tissue structures.
Acknowledgement
The authors would like to acknowledge the following grants which supported this work: R01MH099797 (PI: Rathi), R00EB012107 (PI: Setsompop), P41RR14075 (PI: Rosen), R01MH074794 (PI: Westin), P41EB015902 (PI: Kikinis), Swedish Research Council (VR) grant 2012-3682, Swedish Foundation for Strategic Research (SSF) grant AM13-0090, VA Merit (PI: Shenton) and W81XWH-08-2-0159 (Imaging Core PI: Shenton).
Appendix
We present an algorithm for solving (6) using the alternating direction method of multipliers (ADMM) for a given basis matrix A, a positive weighting vector w and λ > 0. First, we introduce an auxiliary variable z and rewrite (6) as follows
| (13) |
where with Ind+(·) be an indicator function defined as
The ADMM algorithm is an iterative procedure to solve (13) with each iteration consists of three steps of updating c, z and a dual variable p based on their values in the previous step. In particular, let
denote the augmented Lagrangian for some ρ > 0. Then, starting from an arbitrary c0, z0 and p0 for iteration t = 0, the (t + 1)th iteration consists three steps of updating c, z and p given by
| (14) |
| (15) |
| (16) |
In particular, the update equation (14) equals to
which has a closed-form expression given by
where diag(w) denotes a diagonal matrix with w as the diagonal elements. The update equation (15) is equal to
and the mth element of zt+1 is given by
A stopping criteria is to check if pt has reached a stationary point, i.e. for some given εp > 0.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Thomason ME, Thompson PM. Diffusion imaging, white matter, and psychopathology. Clinical Psychology. 2011;7(1):63. doi: 10.1146/annurev-clinpsy-032210-104507. [DOI] [PubMed] [Google Scholar]
- 2.Shenton M, Hamoda H, Schneiderman J, Bouix S, Pasternak O, Rathi Y, Vu M-A, Purohit M, Helmer K, Koerte I, et al. A review of magnetic resonance imaging and diffusion tensor imaging findings in mild traumatic brain injury. Brain imaging and behavior. 2012;6(2):137–192. doi: 10.1007/s11682-012-9156-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Berlot R, Metzler-Baddeley C, Jones DK, O'Sullivan MJ. CSF contamination contributes to apparent microstructural alterations in mild cognitive impairment. NeuroImage. 2014;92:27–35. doi: 10.1016/j.neuroimage.2014.01.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Alexander AL, Hasan KM, Lazar M, Tsuruda JS, Parker DL. Analysis of partial volume effects in diffusion-tensor MRI. Magnetic Resonance in Medicine. 2001;45(5):770–780. doi: 10.1002/mrm.1105. [DOI] [PubMed] [Google Scholar]
- 5.Metzler-Baddeley C, O'Sullivan MJ, Bells S, Pasternak O, Jones DK. How and how not to correct for CSF-contamination in diffusion MRI. NeuroImage. 2012;59(2):1394–1403. doi: 10.1016/j.neuroimage.2011.08.043. [DOI] [PubMed] [Google Scholar]
- 6.Nishimura DG. Principles of magnetic resonance imaging. Stanford University; 1996. [Google Scholar]
- 7.van Ouwerkerk J. Image super-resolution survey. Image and Vision Computing. 2006;24(10):1039–1052. [Google Scholar]
- 8.Manjón JV, Coupé P, Buades A, Fonov V, Louis Collins D, Robles M. Non-local MRI upsampling. Medical Image Analysis. 2010;14(6):784–792. doi: 10.1016/j.media.2010.05.010. [DOI] [PubMed] [Google Scholar]
- 9.Rousseau F. A non-local approach for image super-resolution using inter-modality priors. Medical Image Analysis. 2010;14(4):594–605. doi: 10.1016/j.media.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Coupé P, Manjón JV, Chamberland M, Descoteaux M, Hiba B. Collaborative patch-based super-resolution for diffusion-weighted images. NeuroImage. 2013;83:245–261. doi: 10.1016/j.neuroimage.2013.06.030. [DOI] [PubMed] [Google Scholar]
- 11.Dyrby TB, Lundell H, Burke MW, Reislev NL, Paulson OB, Ptito M, Siebner HR. Interpolation of diffusion weighted imaging datasets. NeuroImage. 2014;103:202–213. doi: 10.1016/j.neuroimage.2014.09.005. [DOI] [PubMed] [Google Scholar]
- 12.Irani M, Peleg S. Motion analysis for image enhancement: resolution, occlusion, and transparency. Journal of Visual Communication and Image Representation. 1993;4(4):324–335. [Google Scholar]
- 13.Greenspan H, Oz G, Kiryati N, Peled S. MRI inter-slice reconstruction using super-resolution. Magnetic Resonance Imaging. 2002;20(5):437–446. doi: 10.1016/s0730-725x(02)00511-8. [DOI] [PubMed] [Google Scholar]
- 14.Greenspan H. Super-resolution in medical imaging. The Computer Journal. 2009;52(1):43–63. [Google Scholar]
- 15.Gholipour A, Estroff JA, Warfield SK. Robust super-resolution volume reconstruction from slice acquisitions: application to fetal brain MRI. IEEE Transactions on Medical Imaging. 2010;29(10):1739–1758. doi: 10.1109/TMI.2010.2051680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Peled S, Yeshurun Y. Superresolution in MRI: application to human white matter fiber tract visualization by diffusion tensor imaging. Magnetic Resonance in Medicine. 2001;45(1):29–35. doi: 10.1002/1522-2594(200101)45:1<29::aid-mrm1005>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 17.Scherrer B, Gholipour A, Warfield SK. Super-resolution reconstruction to increase the spatial resolution of diffusion weighted images from orthogonal anisotropic acquisitions. Medical Image Analysis. 2012;16(7):1465–1476. doi: 10.1016/j.media.2012.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Poot DH, Van Meir V, Sijbers J. General and efficient super-resolution method for multi-slice mri. Medical Image Computing and Computer-Assisted Intervention–MICCAI. Springer. 20102010:615–622. doi: 10.1007/978-3-642-15705-9_75. [DOI] [PubMed] [Google Scholar]
- 19.Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, Feinberg DA, Yacoub E, Lenglet C, Van Essen DC, Ugurbil K, Behrens TEJ. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. NeuroImage. 2013;80:125–143. doi: 10.1016/j.neuroimage.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Van Steenkiste G, Jeurissen B, Sijbers J, Poot D. Super resolution reconstruction from differently oriented diffusion tensor data sets. ISMRM 21th Annual Meeting and Exhibition. 2013:3186. [Google Scholar]
- 21.Van Steenkiste G, Jeurissen B, Parizel PM, Poot DHJ, Sijbers J. Super-resolution reconstruction of diffusion parameters from multi-oriented diffusion weighted images. ISMRM 22th Annual Meeting and Exhibition. 2014:2572. [Google Scholar]
- 22.Van Steenkiste G, Jeurissen B, Veraart J, den Dekker AJ, Parizel PM, Poot DHJ, Sijbers J. Super-resolution reconstruction of diffusion parameters from diffusion-weighted images with di erent slice orientations. Magn Reson Med. doi: 10.1002/mrm.25597. http://dx.doi.org/10.1002/mrm.25597 doi:10.1002/mrm.25597. [DOI] [PubMed]
- 23.Tuch DS. Q-ball imaging. Magnetic Resonance in Medicine. 2004;52(6):1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- 24.Alexander DC. Multiple-fiber reconstruction algorithms for diffusion MRI. Annals of the New York Academy of Sciences. 2005;1064(1):113–133. doi: 10.1196/annals.1340.018. [DOI] [PubMed] [Google Scholar]
- 25.Michailovich O, Rathi Y, Dolui S. Spatially regularized compressed sensing for high angular resolution diffusion imaging. IEEE Transactions on Medical Imaging. 2011;30(5):1100–1115. doi: 10.1109/TMI.2011.2142189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stejskal E, Tanner J. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. The Journal of Chemical Physics. 1965;42(1):288–292. [Google Scholar]
- 27.Wedeen VJ, Hagmann P, Tseng W-YI, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magnetic Resonance in Medicine. 2005;54(6):1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- 28.Descoteaux M, Deriche R, Le Bihan D, Mangin J-F, Poupon C. Multiple q-shell diffusion propagator imaging. Medical Image Analysis. 2011;15(4):603–621. doi: 10.1016/j.media.2010.07.001. [DOI] [PubMed] [Google Scholar]
- 29.Özarslan E, Koay C, Shepherd T, Blackb S, Basser P. Simple harmonic oscillator based reconstruction and estimation for three-dimensional q-space MRI, in: ISMRM 17th Annual Meeting and Exhibition. Honolulu. 2009:1396. [Google Scholar]
- 30.Merlet SL, Deriche R. Continuous diffusion signal, EAP and ODF estimation via compressive sensing in diffusion MRI. Medical Image Analysis. 2013;17(5):556–572. doi: 10.1016/j.media.2013.02.010. [DOI] [PubMed] [Google Scholar]
- 31.Hosseinbor AP, Chung MK, Wu Y-C, Alexander AL. Bessel fourier orientation reconstruction (BFOR): An analytical diffusion propagator reconstruction for hybrid diffusion imaging and computation of q-space indices. NeuroImage. doi: 10.1016/j.neuroimage.2012.08.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Assemlal H-E, Tschumperlé D, Brun L. Efficient and robust computation of PDF features from diffusion MR signal. Medical Image Analysis. 2009;13(5):715–729. doi: 10.1016/j.media.2009.06.004. [DOI] [PubMed] [Google Scholar]
- 33.Basser P, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance, Series B. 1994;103(3):247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- 34.Tuch D, Reese T, Wiegell M, Makris N, Belliveau J, Wedeen V. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magnetic Resonance in Medicine. 2002;48(4):577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
- 35.Jian B, Vemuri BC. A unified computational framework for deconvolution to reconstruct multiple fibers from diffusion weighted mri. IEEE Transactions on Medical Imaging. 2007;26(11):1464–1471. doi: 10.1109/TMI.2007.907552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ghosh A, Deriche R. Fast and closed-form ensemble-average-propagator approximation from the 4th-order diffusion tensor. Biomedical Imaging: From Nano to Macro; 2010 IEEE International Symposium on; IEEE; 2010. pp. 1105–1108. [Google Scholar]
- 37.Michailovich O, Rathi Y. On approximation of orientation distributions by means of spherical ridgelets. IEEE Transactions on Image Processing. 2010;19(2):461–477. doi: 10.1109/TIP.2009.2035886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Malcolm JG, Shenton ME, Rathi Y. Filtered multi-tensor tractography. IEEE Transactions on Medical Imaging. 2010;29:1664–1675. doi: 10.1109/TMI.2010.2048121. http://dx.doi.org/10.1109/TMI.2010.2048121 doi:10.1109/TMI.2010.2048121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang JC, Papadimitriou G, Eckbo R, Yeterian EH, Liang L, Dougherty DD, Bouix S, Rathi Y, Shenton M, Kubicki M, Eskandar EN, Makris N. Multi-tensor investigation of orbitofrontal cortex tracts affected in subcaudate tractotomy. Brain Imaging and Behavior. 2014:1–11. doi: 10.1007/s11682-014-9314-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rathi Y, Michailovich O, Setsompop K, Bouix S, Shenton ME, Westin C-F. Medical Image Computing and Computer-Assisted Intervention–MICCAI. Springer; 2011. 2011. Sparse multi-shell diffusion imaging; pp. 58–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Candès EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory. 2006;52(2):489–509. [Google Scholar]
- 42.Donoho DL. Compressed sensing. IEEE Transactions on Information Theory. 2006;52(4):1289–1306. [Google Scholar]
- 43.Bruckstein AM, Donoho DL, Elad M. From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Review. 2009;51(1):34–81. [Google Scholar]
- 44.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine. 2007;58(6):1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 45.Asif MS, Romberg J. Dynamic updating for ℓ1 minimization. IEEE Journal of Selected Topics in Signal Processing. 2010;4(2):421. [Google Scholar]
- 46.Becker S, Bobin J, Candès EJ. NESTA: a fast and accurate first-order method for sparse recovery. SIAM Journal on Imaging Sciences. 2011;4(1):1–39. [Google Scholar]
- 47.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences. 2009;2(1):183–202. [Google Scholar]
- 48.Candès EJ, Wakin MB, Boyd SP. Enhancing sparsity by reweighted ℓ1 minimization. Journal of Fourier analysis and applications. 2008;14(5-6):877–905. [Google Scholar]
- 49.Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning. 2011;3(1):1–122. [Google Scholar]
- 50.Dolui S, Patarroyo ICS, Michailovich OV, Rathi Y. IEEE Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA) IEEE; 2012. Reconstruction of HARDI using compressed sensing and its application to contrast HARDI; pp. 17–23. [Google Scholar]
- 51.den Dekker AJ, Sijbers J. Data distributions in magnetic resonance images: A review. Physica Medica. 2014;30(7):725–741. doi: 10.1016/j.ejmp.2014.05.002. [DOI] [PubMed] [Google Scholar]
- 52.Bresson X, Chan TF. Fast dual minimization of the vectorial total variation norm and applications to color image processing. Inverse Problems and Imaging. 2008;2(4):455–484. [Google Scholar]
- 53.Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K. The WU-Minn human connectome project: an overview. Neuroimage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rathi Y, Gagoski B, Setsompop K, Michailovich O, Grant PE, Westin C-F. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2013. Springer; 2013. Diffusion propagator estimation from sparse measurements in a tractography framework; pp. 510–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Transactions on Medical Imaging. 2001;20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- 56.Wassermann D, Makris N, Rathi Y, Shenton M, Kikinis R, Kubicki M, Westin C-F. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2013. Springer; 2013. On describing human white matter anatomy: The white matter query language; pp. 647–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Vollmar C, O'Muircheartaigh J, Barker GJ, Symms MR, Thompson P, Kumari V, Duncan JS, Richardson MP, Koepp MJ. Identical, but not the same: intra-site and inter-site reproducibility of fractional anisotropy measures on two 3.0 T scanners. NeuroImage. 2010;51(4):1384–1394. doi: 10.1016/j.neuroimage.2010.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Heidemann RM, Anwander A, Feiweier T, Knösche TR, Turner R. k-space and q-space: combining ultra-high spatial and angular resolution in diffusion imaging using ZOOPPA at 7T. NeuroImage. 2012;60(2):967–978. doi: 10.1016/j.neuroimage.2011.12.081. [DOI] [PubMed] [Google Scholar]
- 59.Feinberg DA, Setsompop K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. Journal of magnetic resonance. 2013;229:90–100. doi: 10.1016/j.jmr.2013.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SP, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. NeuroImage. 2013;80:220–233. doi: 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Bredies K, Kunisch K, Pock T. Total generalized variation. SIAM Journal on Imaging Sciences. 2010;3(3):492–526. [Google Scholar]