Comparison of cortical folding measures for evaluation of developing human brain

Abstract

We evaluated 22 measures of cortical folding, 20 derived from local curvature (curvature-based measures) and two based on other features (sulcal depth and gyrification index), for their capacity to distinguish between normal and aberrant cortical development. Cortical surfaces were reconstructed from 12 term-born control and 63 prematurely-born infants. Preterm infants underwent 2–4 MR imaging sessions between 27 and 42 weeks postmenstrual age (PMA). Term infants underwent a single MR imaging session during the first postnatal week. Preterm infants were divided into two groups. One group (38 infants) had no/minimal abnormalities on qualitative assessment of conventional MR images. The second group (25 infants) consisted of infants with injury on conventional MRI at term equivalent PMA. For both preterm infant groups, all folding measures increased or decreased monotonically with increasing PMA, but only sulcal depth and gyrification index differentiated preterm infants with brain injury from those without. We also compared scans obtained at term equivalent PMA (36–42 weeks) for all three groups. No curvature-based measured distinguished between the groups, whereas sulcal depth distinguished term control from injured preterm infants and gyrification index distinguished all three groups. When incorporating total cerebral volume into the statistical model, sulcal depth no longer distinguished between the groups, though gyrification index distinguished between all three groups and positive shape index distinguished between the term control and uninjured preterm groups. We also analyzed folding measures averaged over brain lobes separately. These results demonstrated similar patterns to those obtained from the whole brain analyses. Overall, though the curvature-based measures changed during this period of rapid cerebral development, they were not sensitive for detecting the differences in folding associated with brain injury and/or preterm birth. In contrast, gyrification index was effective in differentiating these groups.

Introduction

The mammalian cerebral cortex is characterized by complex folding that varies strikingly across species (Welker, 1990). During human brain development, this folding occurs mainly during the third trimester of gestation (Kostovic and Vasung, 2009), as the lissencephalic cortex is transformed into a structure whose folding complexity rivals that of an adult brain (Hill et al., 2010). Gross developmental abnormalities of folding have been associated with premature birth (Dubois et al., 2008a; Ment et al., 2009). For preterminfants, extensive cortical folding occurs ex utero, at a time during which these infants face the challenges of the neonatal intensive care unit (NICU) environment. During this period, cortical folding patterns may be adversely affected by numerous medical and/or environmental factors (Engle, 2004).

The optimum means by which to quantify cortical folding during early brain development has yet to be determined, though a variety of qualitative and quantitative methods have been applied. Qualitative studies can provide a score based on visual inspection of MR images that take into account depth/height, width, branching complexity, location and density of sulci and gyri (Childs et al., 2001; Ramenghi et al., 2007; van der Knaap et al., 1996). In contrast, quantitative estimates of cortical folding have been proposed that use approaches based on local geometric features (e.g. curvature-based measures) and are integrated across a brain region or entire hemisphere. A subset of these measures is dependent on cortical surface area (Ajayi-Obe et al., 2000; van der Knaap et al., 1996; Van Essen and Drury, 1997), and thereby may be disadvantageous for developmental studies insofar as brain size varies greatly with gestational age and between clinically distinct populations. A set of measures of global curvature that were developed to be independent of surface area has also been proposed to study cortical folding in infants (Awate et al., 2010; Rodriguez-Carranza et al., 2008). In addition, a spectral analysis of the variation of curvature measures across the cortical surface of adult brains has also been undertaken (Germanaud et al., 2012).

We evaluated 20 curvature-based measures plus two measures not based on curvature – sulcal depth and gyrification index (GI) – using cortical surface reconstructions in infants. This dataset included three populations of infants studied as part of a larger investigation of the effects of premature birth on cerebral development. One group includes healthy, term-born control infants, hereafter referred to as “term” infants. The second and third groups include prematurely-born infants further subdivided based on an assessment of brain injury on conventional MRI at term equivalent postmenstrual age (PMA) (Kidokoro et al., 2013). One group includes infants with no or minimal brain abnormalities on MRI, hereafter referred to as “uninjured preterm” infants. The other includes infants with brain injury on conventional MRI, hereafter referred to as “injured preterm” infants.

Background

Curvature is a well-defined geometrical property that quantifies the nature and degree to which a surface deviates from being flat. For one-dimensional contours in two-dimensional space (Fig. 1A), the curvature of point P on curve C is the inverse of the radius of the osculating circle at P (the largest circle that touches curve C only at point P). As the curve becomes more creased, the osculating circle becomes smaller and the curvature greater.

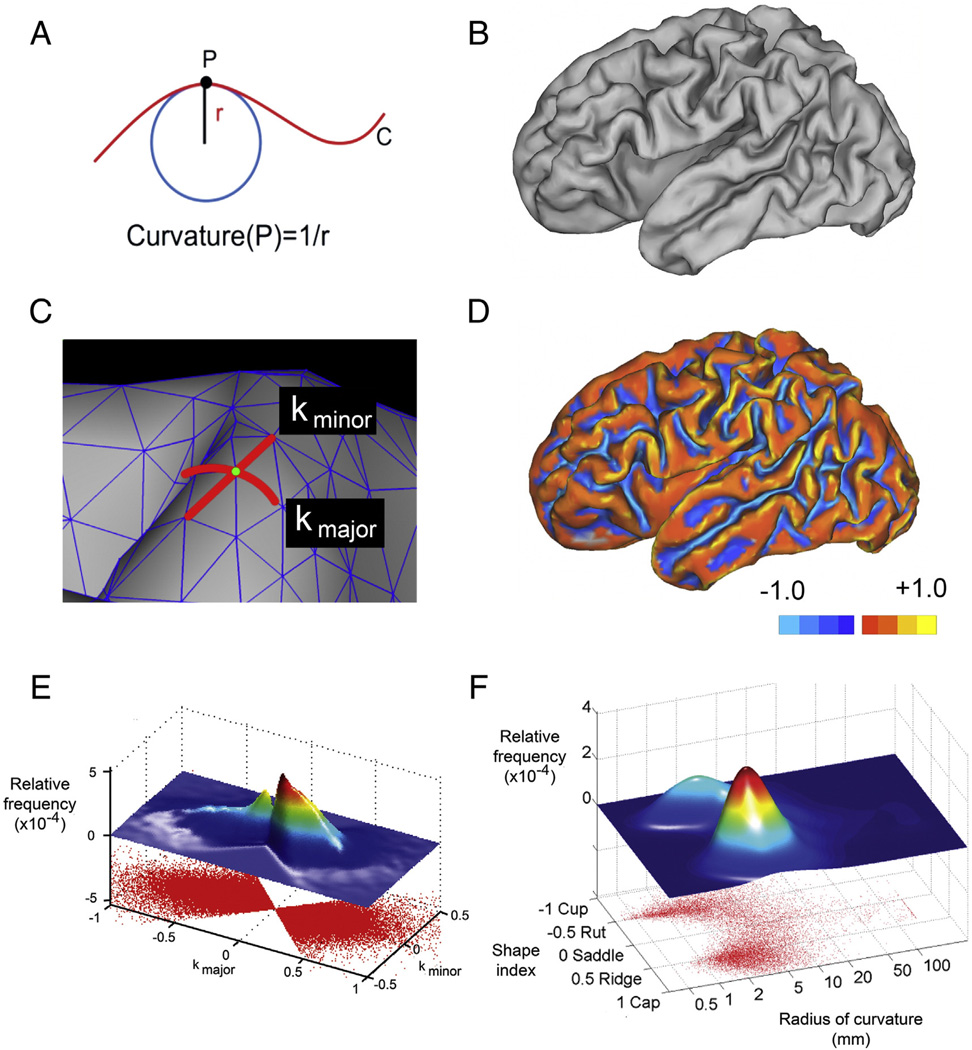
Fig. 1.

(A) An example of measuring curvature at point P on a line. The curvature of point P is determined by the radius of the osculating circle at P. (B) A mid-cortical surface generated using Caret software. (C) An enlargement of the surface showing the surface mesh. The vertices of the mesh are the node points. Note the designation of k_major and k_minor for one of the node points. (D) A mid-cortical surface upon which a color scale representing k_major is shown. Note that values on gyri are positive while those on sulci are negative. (E) A scatter plot displaying each vertex of a cerebral hemisphere at its k_major, k_minor location. Above that is shown a two-dimensional histogram of the joint frequency distribution — a surface whose z value corresponds to the density of k_major, k_minor points on the scatter plot. (F) A plot of the radius of curvature (on a log scale) vs. shape index. Above that is shown a two-dimensional histogram of the joint frequency distribution.

For two-dimensional surfaces in three-dimensional space, the concept becomes more complicated. At any point on a surface, there are two principal curvatures which represent the extremes of curvature at that point (Fig. 1B–C). The directions on the surface along which these principal curvatures occur are perpendicular to each other (Euler, 1767; Kreyszig, 1991), so the curvatures are measured along curves that are orthogonal to one another at their intersection. Historically, these curvatures have been designated, and defined, in various ways. The most common designations are k₁ and k₂ or k_max and k_min. These parameters have been assigned different definitions in different publications, either k₁ ≥ k₂ or |k₁| ≥ |k₂|, which can lead to confusion.

Using the surface of a brain as an example and following the convention that the curvature of a convex surface is positive and that of a concave surface is negative, the values of k that best characterize a given point on the surface of the brain are a relatively large positive number along the crown of a gyrus and a relatively large negative number along the fundus of a sulcus. As a result, the choice of definition for k₁ and k₂ influences how these important positive and negative values are assigned to k₁ and k₂. If k₁ ≥ k₂ is used, the sharpest (and, in this case, defining) curvature for a gyrus will be found in k₁, and the sharpest curvature for the base of a sulcus, which is a negative number, will be found in k₂. If instead |k₁| ≥ |k₂| is used, then the sharpest curvature for both gyrus and sulcus will be k₁. With this second definition, k₂ is useful for calculating some curvature measures such as the shape index (vide infra), but it is k₁ which indicates whether a point is on a gyrus or a sulcus and how tightly curved it is. While k₁ ≥ k₂ is widely used in geometry, we prefer the simplicity resulting from the |k₁| ≥ |k₂| definition, as do the two major surface-deriving software packages, Freesurfer and Caret. To avoid ambiguity, we reserve the use of k₁ and k₂ for the definition k₁ ≥ k₂ and use k_major and k_minor for the principal curvatures, using the definition |k_major| ≥ |k_minor|. The distribution of k_major across the surface of a typical brain is shown in Fig. 1D.

Using these measures, the two most commonly derived curvature-based measures are the mean curvature (H), which is the average of k_major and k_minor, and the Gaussian curvature (K), which is k_major · k_minor. Various other curvature-based measures can be derived for each point on a surface from the principal curvatures, possibly using H or K as intermediate variables. Here, we evaluated a modified set of published curvature-based measures, primarily from Rodriguez-Carranza et al. (Rodriguez-Carranza et al., 2008) and also from (Batchelor et al., 2002; Koenderink and van Doorn, 1992; Van Essen and Drury, 1997) (Table 1). Many of these curvature-based measures are a direct function of the previously introduced measures k_major and k_minor, and thus can generically be represented as a function of these parameters, f(k_major, k_minor). A list of such measures is provided in the top section of Table 1. There are also several derived measures (lower section of Table 1) that deviate from the formula above. These include the area fraction measures and ratios of other curvature-based measures as defined by Rodriguez-Carranza et al. (Rodriguez-Carranza et al., 2008).

Table 1.

Measures of local curvature^a.

Name	Symbol	Definition	Reference
Principal curvatures	kmajor, kminor	|kmajor| ≥ |kminor|	See Background
Principal curvatures (alternate definition)	k1, k2	k1 ≥ k2	See Background
Gaussian curvature (GC)	K	kmajor · kminor
Positive Gaussian curvature (PGC)	K+	$\{\begin{array}{cc}\hfill K,\hfill & \hfill K>0\hfill \\ \hfill 0,\hfill & \hfill K\le 0\hfill \end{array}$	Van Essen and Drury (1997)
Negative Gaussian curvature (NGC)	K−	$\{\begin{array}{cc}\hfill 0,\hfill & \hfill K>0\hfill \\ \hfill K,\hfill & \hfill K\le 0\hfill \end{array}$	Modified from Rodriguez-Carranza et al. (2008)
Squared Gaussian curvature (SGC)	K2	K2	Batchelor et al. (2002)
Mean curvature (MC)	H	$\frac{(k_{\text{major}}+k_{\text{minor}})}{2}$
Positive mean curvature (PMC)	H+	$\{\begin{array}{cc}\hfill H,\hfill & \hfill H>0\hfill \\ \hfill 0,\hfill & \hfill H\le 0\hfill \end{array}$	Modified from Rodriguez-Carranza et al. (2008)
Negative mean curvature (NMC)	H−	$\{\begin{array}{cc}\hfill 0,\hfill & \hfill H>0\hfill \\ \hfill H,\hfill & \hfill H\le 0\hfill \end{array}$	Modified from Rodriguez-Carranza et al. (2008)
Squared mean curvature (SMC)	H2	H2	Batchelor et al. (2002)
Folding index (FI)	FI	|kmajor|(|kmajor| − |kminor|)	Van Essen and Drury (1997)
Curvedness index (CI)	CI	$\sqrt{\frac{(k_{\text{major}}^2+k_{\text{minor}}^2)}{2}}$	Koenderink and van Doorn (1992)
Shape index (SI)b	SI	$-\frac{2}{\pi }\mathit{\text{arctan}}(\frac{k_2+k_1}{k_2-k_1})$	Modified from Koenderink and van Doorn (1992)
Shape index positive (SIP)	Si+	$\{\begin{array}{cc}\hfill SI,\hfill & \hfill SI>0\hfill \\ \hfill 0,\hfill & \hfill SI\le 0\hfill \end{array}$
Shape index negative (SIN)	Si−	$\{\begin{array}{cc}\hfill 0,\hfill & \hfill SI>0\hfill \\ \hfill SI,\hfill & \hfill SI\le 0\hfill \end{array}$
Area fraction of PGC	A(K+)	AK +/A	Rodriguez-Carranza et al. (2008)
Area fraction of NGC	A(K−)	AK −/A
Area fraction of PMC	A(H+)	AH +/A	Rodriguez-Carranza et al. (2008)
Area fraction of NMC	A(H−)	AH −/A	Rodriguez-Carranza et al. (2008)
Ratio of mean curvatures	SH2SH	ΣAH2ΔA/ΣAHΔA	Rodriguez-Carranza et al. (2008)
Ratio of Gaussian curvatures	SK2SK	ΣAK2ΔA/ΣAKΔA	Rodriguez-Carranza et al. (2008)

^aGyri have been defined as having positive curvature and sulci negative curvature.

^bFor simplicity of representation, the Shape Index is defined using k₁ and k₂ where k₁ ≥ k₂.

Examining the distribution of two-variable data (e.g., k_major and k_minor) is often done using a joint probability distribution. In this approach (Fig. 1E), the lower part of the figure shows raw data points, while the upper part displays the joint frequency distribution created using a Gaussian kernel distribution function with points weighted according to their local area of mesh. A more easily interpreted distribution results from showing the radius of curvature (on a log scale) on one axis and the shape index on the other axis, as shown in Fig. 1F. We remind the reader that a shape index value of −1 corresponds to a cup, −0.5 to a sulcus, +0.5 to a gyrus, and +1 to a cap (Koenderink and van Doorn, 1992).

One additional concept, especially in relation to the rapidly growing brain, is scaling. As discussed by others (Rodriguez-Carranza et al., 2008), it may be desirable that global curvature-based measures be independent of size. In other words, if the brain increases in size without adding new sulci or gyri, the global curvature-based measure should remain constant. A variety of approaches have been suggested to achieve isometric scaling (Batchelor et al., 2002; Rodriguez-Carranza et al., 2008), one of which is that of Knutsen et al. (Knutsen et al., 2013), in which the principal curvature values are multiplied by the “characteristic length” of the structure being evaluated. This approach is appealing, in part because multiplying curvature-based measures by characteristic length gives a unitless number, thereby appearing to compensate for differences in scale. However, in the case of comparing term infants with preterm infants, the characteristic length, which may be approximated by biparietal diameter (BPD, maximal width of the parietal cortex on a coronal image at the level of the third ventricle, cochlea and basilar truncus), is significantly smaller in preterm than term infants. As a result, multiplying the curvature measures by BPD leads to widespread, but spurious, differences in curvature measures between groups in the same way that multiplying random values by BPD would introduce differences between these populations (data not shown). Thus, we did not scale the data using BPD. Alternatively, to account for differences in brain size in our analysis, we chose to evaluate the data with and without incorporating total cerebral volume into the statistical model.

A second form of scaling, allometric scaling, was also considered. In the context of brain development, allometric scaling refers to the power relationship between brain surface area and volume. If the brain was a sphere, the power relationship between volume and surface area would have an exponent of 2/3. Due to increases in folding, and hence surface area, associated with growth of the developing brain, this exponent is on the order of 1.3 (Kapellou et al., 2006; Paul et al., 2014). However, because of this interrelationship between brain surface area, volume and folding, incorporation of this scaling coefficient would also confound investigations of the curvature measures and was not performed.

For comparison purposes, we also included the two well-known, non-curvature-based measures of GI and sulcal depth (Hill et al., 2010) in the analysis. A more detailed description of GI and sulcal depth in this cohort,with emphasis on the influence of perinatal factors, has been published (Engelhardt et al., 2015).

Finally, since the changes in cortical topography associated with preterm birth may vary regionally (with the inferior frontal and temporal lobes appearing most affected on visual inspection), we also evaluated the curvature-based measures on a lobar basis.

Methods

Participants

Sixty-three prematurely-born infants (born before 30 weeks gestation) were recruited from the St. Louis Children's Hospital NICU as part of a larger study of the effects of preterm birth on cerebral development. Infants were imaged at b30, 30–31, 34–35 and 38–40 weeks postmenstrual age (PMA). However, not all infants were imaged at each time point because the patient's clinical status sometimes precluded moving him/her from the NICU for an imaging session. All infants were imaged at term equivalent (36–42 weeks PMA), as this was approximately when they were discharged from the hospital. A total of 114 scans were collected across all time points. Of the studied infants, 38 had no/limited brain injury on MRI at term equivalent PMA using a standardized scoring system (Kidokoro et al., 2013). The remaining 25 infants had injury on MRI at term equivalent PMA. Volume data were not available for 3 of the 22 infants in the injured group, and these subjects were excluded from the analysis incorporating total cerebral volume. Demographic and clinical information for the preterm cohort are provided in Table 2.

Table 2.

Characteristics of preterm infants.

Clinical variable	Number of infants (n = 63)
Gestational age at birth (weeks) — mean (SD)	27 (1.9)
Male — n (%)	34 (54)
White — n (%)	35 (56)
Birthweight (g) — mean (SD)	943 (254)
Intrauterine growth restriction — n (%)	3 (5)
Antenatal steroids — n (%)	57 (90)
Inotropic support — n (%)	22 (35)
Postnatal steroids — n (%)	20 (32)
Positive pressure ventilation — n (%)	51 (81)
Total positive pressure ventilation days — mean (SD)	7 (11)
Total ventilator days — mean (SD)	14 (22)
Total parenteral nutrition (days) — mean (SD)	25 (22)
Patent ductus arteriosus treated medically — n (%)	26 (41)
Intraventricular hemorrhage, grades II–IV — n (%)	16 (25)
Periventricular leukomalacia, mod-severe — n (%)	6 (10)
Cerebellar hemorrhage, mod-severe — n (%)	9 (14)

Twelve term-born control infants without cerebral injury on MRI scans were also recruited from the Barnes Jewish Hospital Newborn Nursery. Inclusion criteria included no maternal history of major illness, no maternal medication use or substance abuse during pregnancy, gestation >37 weeks, good prenatal care (>5 visits), 5-minute APGAR score ≥8, no admission to a neonatal or special care nursing unit and no known risk for neurological abnormality (no antenatal cerebral abnormality on ultrasound, no concerns for chromosomal abnormality or congenital or acquired infection and no neonatal encephalopathy). Volume data were not available for 2 of the 12 term control infants, and these subjects were excluded from the analysis incorporating total cerebral volume. Demographic and clinical information for the term cohort are provided in Table 3.

Table 3.

Characteristics of Term Infants.

Clinical variable	Number of infants (n = 12)
Gestational age at birth (weeks) — mean (SD)	39 (0.9)
Male — n (%)	6 (50)
White — n (%)	5 (42)
Birthweight (g) — mean (SD)	3345 (476)
Postmenstrual age at scan (weeks) — mean (SD)	39.3 (0.9)

The Washington University Institutional Review Board approved all procedures related to the study. Parents or legal guardians provided informed, written consent.

Image acquisition and analysis

As described previously (Hill et al., 2010), T2-weighted images were acquired and cortical surfaces were generated using the semi-automated LIGASE segmentation method. T2-weighted sequence acquisition parameters included TR = 8600 ms, TE = 161 ms and 1 × 1 × 1 mm³ voxels. Images were acquired on a 3 T Tim Trio system (Siemens, Erlangen, Germany). All studies were performed without sedating medications and were obtained during natural sleep or while the infant rested quietly.

Computation of folding measures

Mid-cortical segmentation volumes were generated using the semiautomated LIGASE method (Hill et al., 2010). Caret was used to manually correct topological errors and to generate surfaces for each hemisphere under study using Caret software (Van Essen et al., 2001). Principal curvatures (k_major and k_minor) and the derived curvature-based measures shown in Table 1 were computed for each node on the corresponding surface mesh (Fig. 1C).

The majority of the principal curvatures and curvature-based measures were then weighted by the area of the cortical surface to which they corresponded using Eq. (1):

$$\mathit{\text{Area Averaged Measure}}=\frac{1}{\mathit{A}}\sum \mathit{f}({\mathit{k}}_{\text{major}},{\mathit{k}}_{\text{minor}})\Delta \mathit{A}$$ (1)

where A represents the surface area of the entire cerebral hemisphere (excluding the non-cortical medial wall) or the surface area of the different lobes, and ΔA represents the surface area corresponding to the node of interest. ΔA was calculated by averaging the areas of the tiles abutting the node of interest (i.e., each tile having the node as one of its vertices). Note that the exceptions to this equation were SH2SH and SK2SK, which are ratios of measures defined in Table 1.

In addition, sulcal depth was determined for each node as the distance from the node to the nearest point on a convex hull of the hemisphere and this was also averaged across the surface of the cortex. (Though often used in maps as a vertex-wise measure, here we sum across the hemisphere and normalize as in Eq. (1) above.) Finally, GI was calculated as the ratio of the area of the mid-thickness cortical surface to the surface area of the cerebral hull (Van Essen, 2005). The non-cortical medial wall was excluded from all measures. For the majority of the infants, data were available for both the left and right hemispheres, and the results were statistically indistinguishable for the two hemispheres. For some infants, only data for the left hemisphere was available, and thus for consistency we only used data fromthe left hemisphere for all infants.

Fig. 2 shows representative brain surfaces from term, uninjured preterm and injured preterm infants. An identical set of folding measures was also calculated for the brain areas shown. For this analysis, the different lobes (temporal, frontal, parietal, occipital and limbic) were identified using versions of the lobar parcellations from Van Essen et al. (Van Essen, 2005), which was based upon Ono et al. (Ono et al., 1990). The temporal lobe was delineated by the Sylvian fissure, temporo-occipital line, lateral and basal parietotemporal lines and collateral and rhinal sulci. It was selected after trimming so that it did not extend beyond the collateral sulcus medially, nor the inferior branch of the circular sulcus laterally. The frontal lobe extended laterally from the frontal pole to the central sulcus, separated from the temporal lobe by the Sylvian fissure, the limbic lobe medially by the cingulate sulcus and the parietal lobe by a line extending from the marginal end of the central sulcus to the cingulate sulcus. The parietal lobe was bounded laterally by the central sulcus, parietotemporal line and posterior Sylvian fissure, and medially by the parieto-occipital sulcus, subparietal sulcus, and marginal end of the central and cingulate sulcus. The occipital lobe lies posterior to the parieto-occipital sulcus medially, and posterior to the lateral parieto-occipital line. Finally, the limbic lobe includes cingulate and parahippocampal gyri.

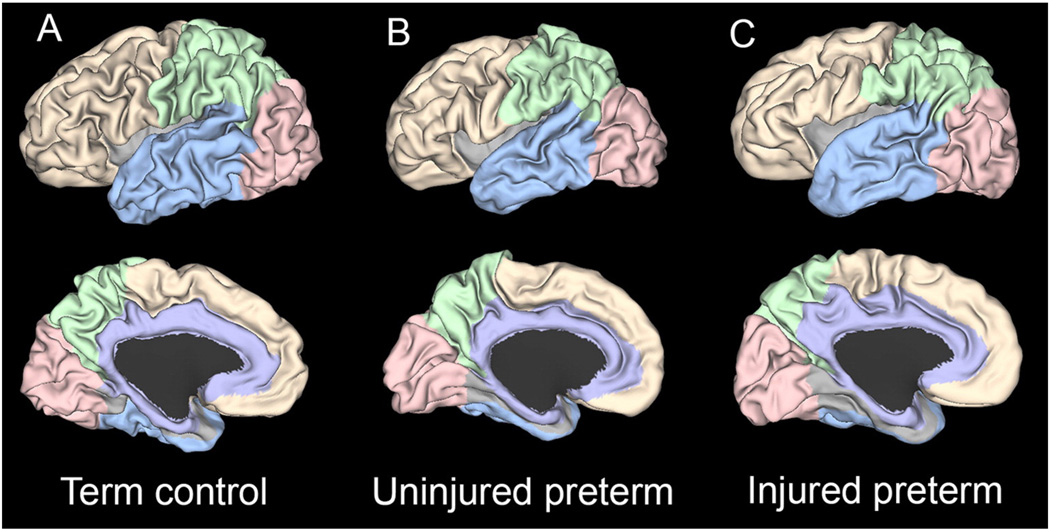
Fig. 2.

Representative left hemispheres at term equivalent PMA from (A) term, (B) uninjured preterm and (C) injured preterm infants. Note the decrease in sulcal depth and complexity of the temporal lobe surface from term through injured preterm. Each example was chosen because it provided the result closest to the mean sulcal depth value for each group. The area corresponding to the temporal lobe is shown in light blue, the occipital lobe in rose, the parietal lobe in green, the frontal lobe in yellow and the limbic area in purple.

Folding measure plots

The capacity of each folding measure to distinguish term, uninjured preterm and injured preterm infants was evaluated. For the curvature-based measures, scaled and non-scaled parameter values for the whole-hemisphere mesh were plotted versus PMA at time of MR image acquisition. Plots for sulcal depth and GI were created in a similar fashion. All results were fit using a linear model. Using measures calculated from only scans obtained at term equivalent PMA (36–42 weeks), folding measures were compared for term and preterm (uninjured and injured) subjects using both the whole-hemisphere mesh and lobe-specific meshes. Finally, two-dimensional joint-probability Gaussian kernel density plots of Principal Curvatures vs. Shape Index, as described above, were generated for all MRI scans across each subject.

Total cerebral volume

Volumetric data were generated using an imaging pipeline that combines high-dimensional template construction, diffeomorphic registration and expectation-maximization segmentation (Avants et al., 2011a). The Advanced Normalization Tools (ANTs) software package (http://www.picsl.upenn.edu/ANTS) and segmentation algorithm Atropos (Avants et al., 2011b) were used to generate cerebrospinal fluid, gray matter, white matter, deep gray matter and cerebellum segmentations. Segmentations were then manually corrected using ITK-Snap software tools to ensure accuracy and fidelity of measurements (Yushkevich et al., 2006).

Statistical analyses

We employed a general linear model, with each folding measure as the dependent variable, group (term, uninjured preterm, injured preterm) as the independent variable, and PMA as a covariate. An additional analysis was performed with total cerebral volume added to the model as a covariate. Post-hoc univariate general linear models were used to compare group pairs. For these analyses, comparisons between preterm groups were performed using results obtained for the full-hemisphere mesh across all PMA. Comparison between the term group and both preterm groups were performed using both the full-hemisphere mesh and each lobe-specific mesh at term equivalent PMA only. Since we principally evaluated 22 folding measures, p values were considered significant after Bonferroni correction at a value of 0.05/22 = 0.0023. Uncorrected p values for all analyses are shown in Supplemental Tables 1–12.

Results

Cerebral volume

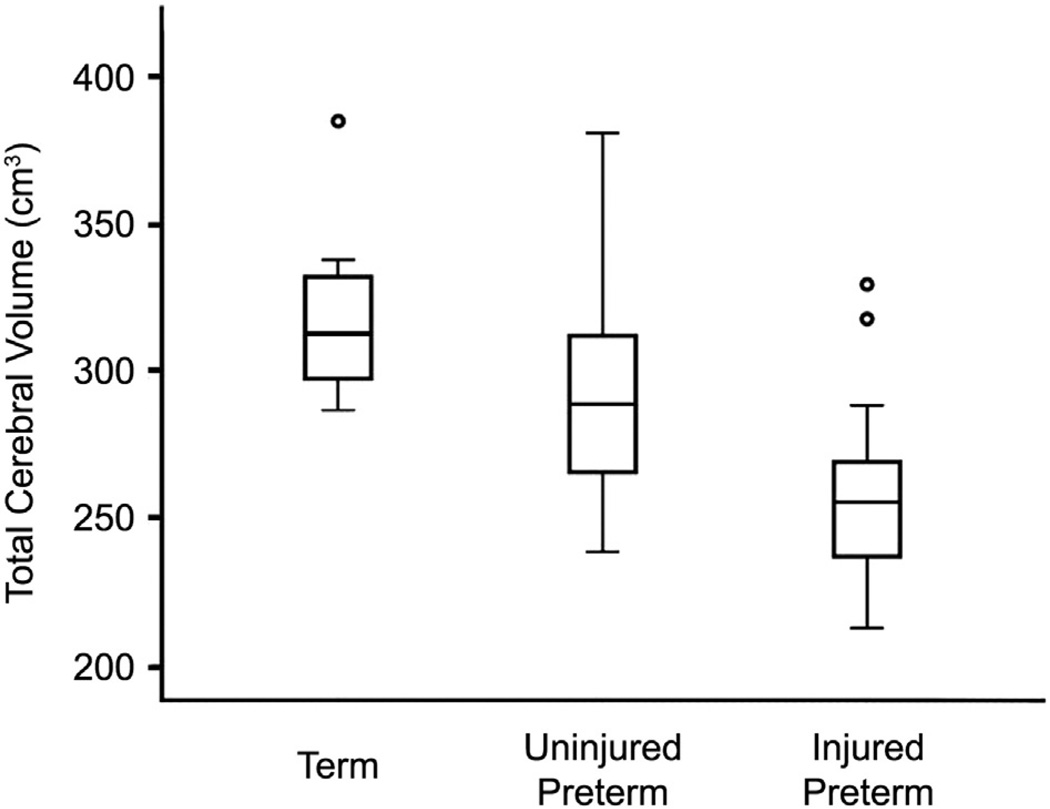
As shown in Fig. 3, cerebral volumes were lower in preterm than term infants (280.6 vs. 318.4 cm³, p = .003). Further, they were lower still in injured compared to uninjured preterm infants (258.1 vs. 293.7 cm³, p=.0001). Finally, standard deviations were larger for preterm than term infants (37.7 vs. 29.2 cm³).

Fig. 3.

Box plot demonstrating mean total cerebral volume values for term, uninjured preterm and injured preterm subjects at 36–42 weeks PMA. Note differences in results between groups.

Folding measures and PMA

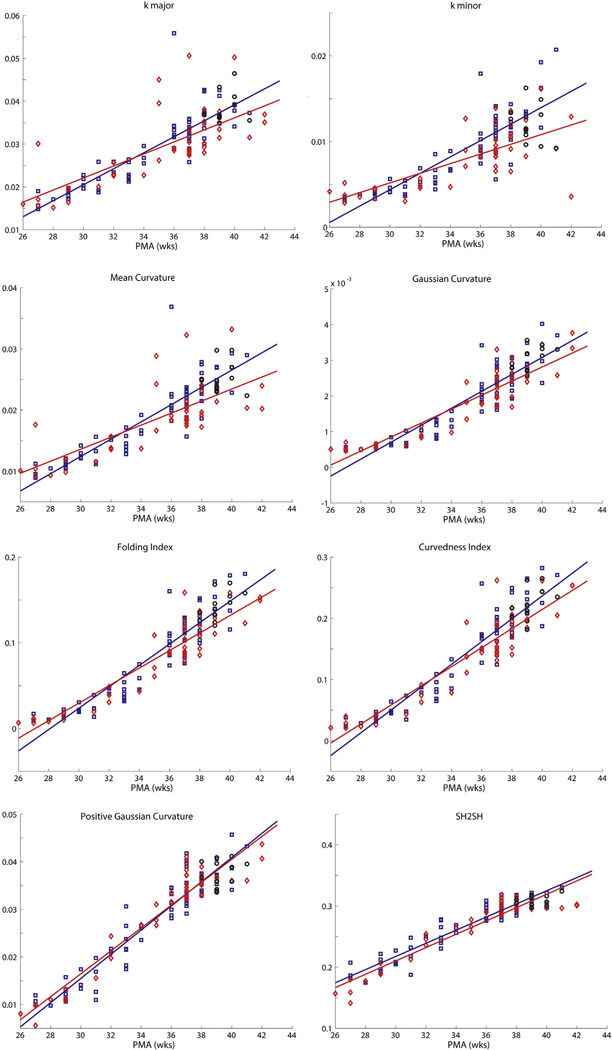
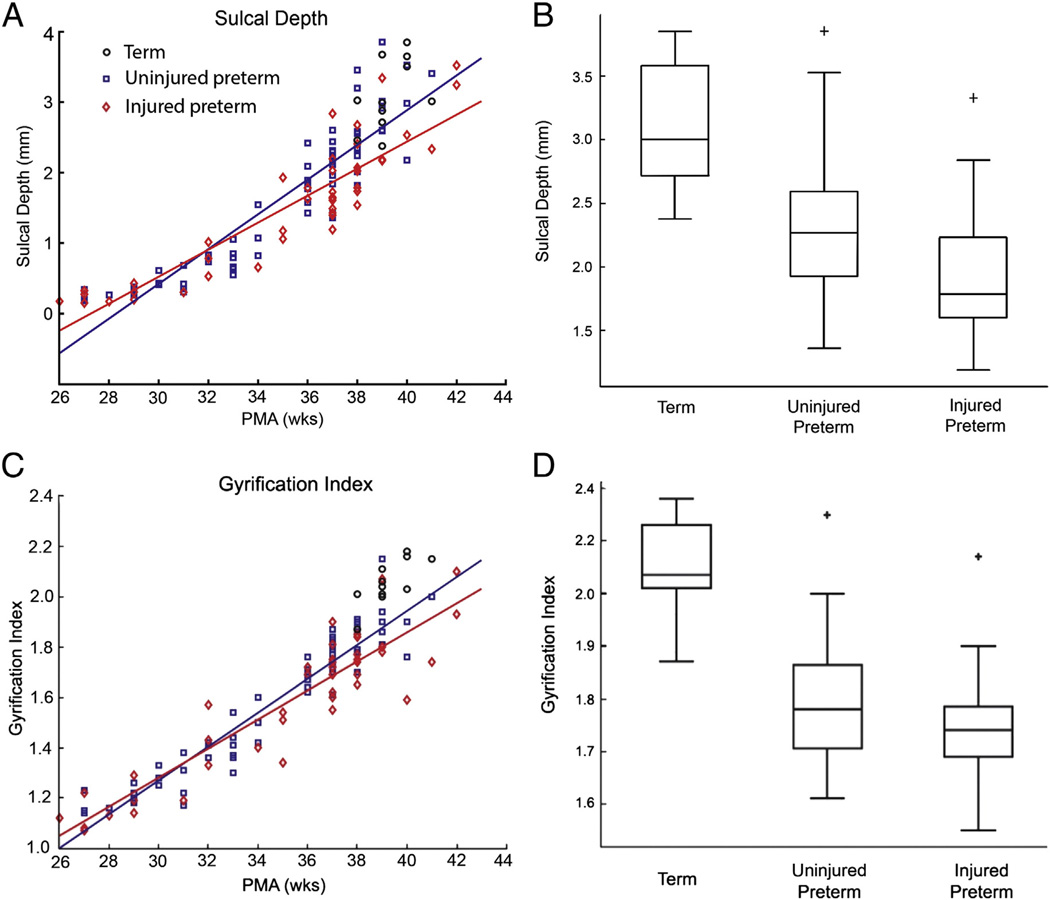
Fig. 4 shows results for representative folding measures from Table 1 plotted versus PMA at time of scan (the remaining measures are shown in Supplemental Figs. 1 and 2). All measures change monotonically with PMA, and correlations between each measure and PMA were highly significant (all p values <10⁻²¹). The two measures that distinguish between term control and uninjured and injured preterm infants were sulcal depth (p = 0.00068 and p < 10⁻⁴, respectively) and GI (p < 10⁻⁷ and p < 10⁻⁹, respectively) (Fig. 5A and C).

Fig. 4.

Plots demonstrating a representative group of the folding measures listed in Table 1 versus PMA for term, uninjured preterm and injured preterminfants. Note the similarity of the plots across measures. In each plot, black circles represent terminfants, blue squares represent uninjured preterminfants and red diamonds represent injured preterminfants. Solid lines denote results from linear fits of data, with blue lines representing results from uninjured preterm infants and red lines representing results from injured preterm infants.

Fig. 5.

(A) Plot of individual mean sulcal depth versus PMA for term(black circles), uninjured preterm(blue squares) and injured preterminfants (red diamonds). Solid lines denote results from linear fits of data, with the blue line representing the results from uninjured preterm and the red line representing the results from injured preterm infants. (B) Box plot demonstrating mean sulcal depth values for term, uninjured preterm and injured preterm subjects at 36–42 weeks PMA for the whole hemisphere. (C) and (D) show results from comparable analyses performed using the gyrification index.

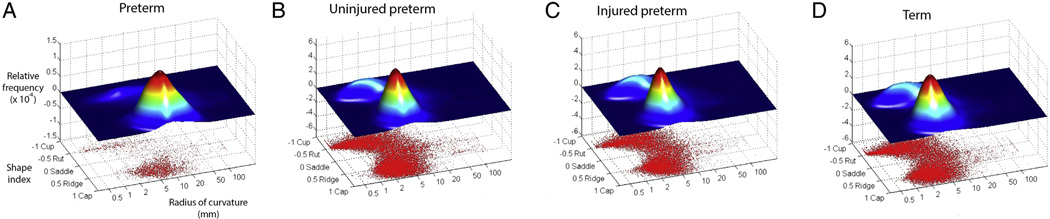
Fig. 6 shows plots of the relative frequency of values for shape index and radius of curvature [log(1/k_major)] for all vertices of representative infants from each group, illustrating the changes in cortical surface that accompany brain development. For the exemplar preterm infant scanned at 27 weeks PMA (Fig. 6A), the shape index of the majority of the surface vertices corresponds to a ridge, while their radius of curvature is relatively large. This is consistent with a hemisphere that is comparatively smooth with few sulci and broad gyri. For the three representative infants at term equivalent PMA (Fig. 6B–D), there are a substantial number of vertices with negative shape index, corresponding to the development of sulci. In addition, the positive shape index vertices cluster around a radius of curvature smaller than for 27 weeks as a result of the development of narrower gyri. Note also that the plots for the three groups at term equivalent PMA are quite similar.

Fig. 6.

Scatter plots showing shape index vs. radius of curvature (1/|k_major|) for each vertex of a representative cerebral hemisphere. Above the scatter plot is a two-dimensional joint frequency distribution histogramin which the z values correspond to the relative frequency of values on the scatter plot. Note the use of log scale for radius of curvature. The taller of the two data peaks centers on ridge shape, implying that these data points are located on gyri. The smaller peak is centered on rut shape, reflecting data points located at the bottom of sulci. Each plot corresponds to the data from a single representative subject. (A) shows data from a preterm infant scanned at 27 weeks postmenstrual age. (B–D) show data from three infants at term equivalent PMA.

Folding measures at term equivalent PMA

We evaluated the capacity of each measure to distinguish between term and uninjured preterm infants, and between term and injured preterm infants, based on scans obtained at term equivalent PMA. Similar to the results for the entire age range, a strong correlation between most measures and PMA at time of term equivalent scan was evident.

When folding measures were evaluated without inclusion of total cerebral volume in the model (Supplemental Tables 1–6), differences between groups were seen with sulcal depth, which distinguished between term control and injured preterm infants (p = 0.0002) and GI, which distinguished between term control and uninjured and injured preterm infants (p < 10⁻⁶ and p < 10⁻⁸, respectively) (Fig. 5B and 5D). Evaluating the data by lobe, sulcal depth distinguished the term control and injured preterm groups for all regions except the occipital lobe and limbic system(note that GI was not tested by lobe). In addition, some curvature-based measures differentiated groups in the frontal lobe. These were the positive shape index for term control vs. uninjured preterm infants (p = 0.001) and squared mean curvature (p =0.002) and folding index (p = 0.001) for term control vs. injured preterm infants.

When total cerebral volume was included in the statistical model used for analysis (Supplemental Tables 7–12), GI remained able to distinguish between term control and uninjured and injured preterm infants (p < 10⁻⁶ and 10⁻⁷, respectively). In contrast, sulcal depth no longer differentiated groups for any comparison, either globally or by lobe. With regards to the curvature-based measures, positive shape index demonstrated a difference between term and uninjured preterm subjects on both the whole-hemisphere (p = 0.0004) and frontal lobe (p = 0.0004) comparisons.

Discussion

We evaluated 22 curvature-based measurements in three ways. In the first, we evaluated their change in association with the marked increase in cortical folding that accompanies brain development in preterm infants between 27 weeks and term equivalent PMA. Overall, the measures performed similarly and, as expected, demonstrated increasing (or decreasing) values in association with increasing PMA. Notably, they did not appreciably distinguish between the uninjured and injured preterm groups. In contrast, the non-curvature-based measures of sulcal depth and GI did. In the second evaluation, we addressed the sensitivity of these measures to alterations in folding after it is well established – at term equivalent PMA – for the two preterm groups in comparison to a term control group without including total cerebral volume in the statistical model. Again, sulcal depth and GI were more effective than curvature measures in differentiating between groups, with sulcal depth distinguishing between control and injured preterm infants and GI distinguishing between all three groups. While the multiple comparisons correction for number of measures evaluated increased the standard for any measure to reach significance, both sulcal depth and GI outperformed the curvature-based measures. In the third evaluation, we again compared these measures at term equivalent PMA, but this time included total cerebral volume in the statistical model. GI was once again effective in differentiating groups, but sulcal depth was not. Of the curvature-based measures, positive shape index performed better than other measures, distinguishing the term and uninjured preterm groups in the whole-hemisphere and frontal lobe analyses.

While alterations in curvature-based measures have been detected in adult populations in association with dementia (Yin et al., 2014), genetic disorders (Manara et al., 2014), and degree of myelination (Shafee et al., 2015), we found only one curvature-based measure (positive shape index) associated with preterm birth despite differences in cortical folding visible on qualitative inspection of cortical surfaces. This may be related to the nature of the abnormality in preterminfants. The cortex of preterm infants at term equivalent PMA has shallower sulci than term infants, as indicated by the smaller sulcal depth values in the present study, and as has been shown by our group and others (Engelhardt et al., 2015; Ramenghi et al., 2007). These shallower sulci retain areas of high curvature at the bottom of sulci and the edges of gyri, but are missing areas of low curvature in the sulcal walls. The effect on curvature-based measures would be to give higher values when averaged over the cortical surface (in the sense of showing greater average overall curvature). However, this effect may be offset by the existence of fewer/shorter sulci in preterm infants (compare the temporal lobes in Fig. 2A with 2B and 2C). The presence of fewer/shorter sulci would decrease the values of averaged curvature-based measures. Overall, these offsetting influences could make the curvature-based measures insensitive to the effects of preterm birth.

Of note, positive shape index showed differences between the term and uninjured preterm groups on some term equivalent analyses. However, positive shape index did not distinguish between term and injured preterm infants even though the average values were similar for injured and uninjured preterminfants. This is likely due to the smaller standard deviation of the values from uninjured preterm infants, which may be a consequence of a larger number of infants in this group (38 uninjured vs. 25 injured) and/or lower biologic variability in the uninjured group. This curvature-based measure should be strongly influenced by areas of positive curvature, which lie mainly at the edges of gyri, though the index is the average of all areas of positive curvature, including the gyral crowns. Its ability to distinguish groups suggests the edges of gyri are less sharply folded in preterm than term infants, but not appreciably different between injured and uninjured preterm infants.

While the factors of having fewer/shorter sulci and shallower sulci in preterm infants have offsetting effects for the curvature-based measures, they do not for sulcal depth and GI. Sulcal depth measurements are designed to detect shallower sulci. GI, in contrast, is reduced both by having fewer/shorter sulci and by having shallower sulci. This may explain its high sensitivity to the effects of preterm birth in the present study, in which it outperformed even sulcal depth by distinguishing between term and preterm infants at term equivalent PMA. It should be noted that sulcal depth and GI have been shown to be sensitive to the effects of preterm birth in other studies (Dubois et al., 2008b; Engelhardt et al., 2015; Ramenghi et al., 2007).While this classification of curvature-based measures, sulcal depth and GI is an oversimplification, it provides a conceptual framework from which to consider which measures are most likely to be useful under different conditions. The effect of incorporating brain volumes in the comparisons of measures at term equivalent PMA also deserves mention. In the case of GI, there was little statistical effect. This is, perhaps, not surprising because the GI intrinsically takes brain size into account by including hull surface area in its denominator. Notably, GI may be measured regionally (Li et al., 2014; Schaer et al., 2008), though it was used only globally for the study under consideration. Sulcal depth, in contrast, no longer showed differences between populations after total cerebral volume was taken into account. This is presumably due to the strong correlation between sulcal depth and total cerebral volume (r²=0.87 for all PMA's, r² = 0.61 for term equivalent surfaces only, data not shown).

Finally, it is important to consider that we have assessed these measures in a single patient population, albeit one with rapidly-changing cortical folding. The curvature-based measures may have utility in circumstances other than brain development in premature infants. For example, in one recent study (Lefevre et al., 2015), some measures of cortical folding were found to be greater in preterminfants than fetuses studied at comparable postmenstrual/gestational age.

Conclusion

In summary, we investigated 22 cortical curvature-based measures averaged over a brain hemisphere across a large cohort of prematurely-born infants, with and without brain injury, and compared them to a group of term control infants. For both preterm groups, all folding measures increased or decreased monotonically with increasing PMA, but the curvature-based measures did not distinguish between them. With few exceptions, the curvature-based measures did not distinguish between the three groups at term equivalent PMA, though the non-curvature-based measure GI did differentiate groups. Positive shape index outperformed other curvature-based measures in differentiating groups on some analyses. Overall, though the measures of cortical folding changed during this period of rapid cerebral development, none of the curvature-based measures was consistently effective in identifying the effects of pretermbirth or brain injury in preterminfants on cortical folding.