Abstract
RNA transcripts that include expanded CCUG repeats are associated with myotonic dystrophy type 2. Crystal structures of two CCUG-containing oligomers show that the RNA strands associate into slipped duplexes that contain noncanonical C–U pairs that have apparently undergone tautomeric transition or protonation resulting in an unusual Watson–Crick-like pairing. The overhanging ends of the duplexes interact forming U–U pairs, which also show tautomerism. Duplexes consisting of CCUG repeats are thermodynamically less stable than the trinucleotide repeats involved in the TRED genetic disorders, but introducing LNA residues increases their stability and raises the melting temperature of the studied oligomers by ∼10°C, allowing detailed crystallographic studies. Quantum mechanical calculations were performed to test the possibility of the tautomeric transitions or protonation within the noncanonical pairs. The results indicate that tautomeric or ionic shifts of nucleobases can manifest themselves in biological systems, supplementing the canonical “rules of engagement.”
Keywords: CCUG repeats, myotonic dystrophy type 2, X-ray crystallography, thermodynamics, tautomerism
INTRODUCTION
Myotonic dystrophy type 2 (DM2) belongs to a family of neurodegenerative diseases associated with an expansion of specific microsatellite sequences located in certain genes (Mirkin 2007). Among the various microsatellite sequences found in the human genome, most consist of trinucleotide repeats such as CNG (N stands for any nucleotide residue) but there are also tetra-, penta-, and hexa-repeats. They all have the ability to undergo an abnormal multiplication resulting in disease. In the case of DM2, disorder occurs because of an expansion of CCTG repeats present in intron 1 of the ZNF9 (zinc finger protein 9) gene also known as the cellular nucleic acid-binding protein (CNBP) gene (Liquori et al. 2001).
The CCTG repeats within the ZNF9 gene are usually interrupted by one or more (TCTG) or (GCTG) motifs whose probable role is to stabilize the poly-CCTG tract, and when they are lost an expansion can occur. The number of extended repeats can reach 11,000 units but usually is ∼5000 (Bachinski et al. 2003). The mutated gene is transcribed into pre-mRNA that includes the expanded CCUG repeats, which are then spliced out (Margolis et al. 2006) and accumulate in the nucleus. They have an ability to bind many proteins, thus forming nuclear foci and causing a depletion of these proteins elsewhere in the nucleus (Mankodi et al. 2003; Wojciechowska and Krzyzosiak 2011). The most crucial of the sequestered proteins is MBNL1, the regulator of alternative splicing (Mankodi et al. 2001; Fardaei et al. 2002). Its ablation disrupts the equilibrium between MBNL1 and the antagonistically acting CUG-BP1 protein, causing a misregulation of alternative splicing of numerous developmentally regulated transcripts (Ranum and Cooper 2006).
DM2 has common features with dystrophy type 1 (DM1), which is caused by an expansion of CTG tracts in the 3′ UTR of the DMPK gene (Aslanidis et al. 1992; Brook et al. 1992; Harley et al. 1992). Both DM1 and DM2 exhibit similar symptoms and pathomechanism resulting in an aberrant splicing pattern (Ranum and Cooper 2006; Sicot et al. 2011). However, DM2 is usually less severe and develops only in adults, which sometimes makes it difficult to distinguish from normal aging. The mutated alleles containing CCTG repeats are considerably larger than CTG tracts in DM1, but the size of the expansion does not correlate with the age of onset or the severity of the phenotype (Udd and Krahe 2012). The reason for the diverse manifestations of mytonic dystrophies has not been identified. The effect could be due to differences in expression levels of the DMPK and ZNF9 genes or varied composition of proteins interfering with the pathogenic RNA and with other important molecules (Sicot et al. 2011).
RNA containing an extended number of CCUG repeats folds into a characteristic hairpin structure also observed in CUG and other types of CNG repeats (Sobczak et al. 2003). The stem of the hairpin consists of a repeated pattern of C–G and G–C pairs interrupted by two noncanonical C–U and U–C pairs. A number of RNA structures of CNG repeats have been determined by crystallography (for review, see Kiliszek and Rypniewski 2014). All the RNA structures adopt the A-form and contain noncanonical N–N pairs. The bases within each type of the N–N pair interact in a specific way and the pairs are accommodated within the helix in a characteristic manner. Recently, a structure of CCUG repeats was published by Childs-Disney et al. (2014). The model consists of three CCUG repeats attached to an RNA motif containing a tetraloop and a tetraloop receptor. Elements of the tetraloop system associate in solution, facilitating crystallization (Coonrod et al. 2012).
We have solved two crystal structures of RNA containing CCUG repeats: GCCUGLCCUGC and GCCUGLCCUG (GL is an LNA modified guanosine). They form slippery duplexes in which the noncanonical base pairs are apparently stabilized by a shift to uncommon tautomeric or ionic forms. The possibility of tautomeric transitions of the common nucleobases has long been recognized but only recently has their role in biological processes been demonstrated (Demeshkina et al. 2012, 2013; Singh et al. 2015). Tautomeric and anionic forms of the bases are believed to contribute to DNA mutagenesis, errors during translation, nucleic acid catalysis, and RNA–ligand recognition (Bevilacqua and Yajima 2006; Weixlbaumer et al. 2007; Gilbert et al. 2009; Wang et al. 2011). Despite growing evidence for the biological role of the rare tautomers or anionic forms, they have been very difficult to observe. Very recently, a sophisticated NMR study has pinpointed rare tautomeric species in noncanonical base pairs (Kimsey et al. 2015). Some X-ray studies also revealed unusual inter-base interactions that were interpreted in terms of tautomeric shifts (Weixlbaumer et al. 2007; Wang et al. 2011; Demeshkina et al. 2012, 2013).
In the results presented in this article, we would like to emphasize the apparent tautomeric or anionic forms of the nucleic bases, as they have not been considered before in studies of expanded RNA repeats. The crystallographic, thermodynamic, and quantum mechanical analyses are consistent, reveal new biochemical properties of the molecules and should be useful in the search for drugs against DM2.
RESULTS
Overall structure and duplex conformation
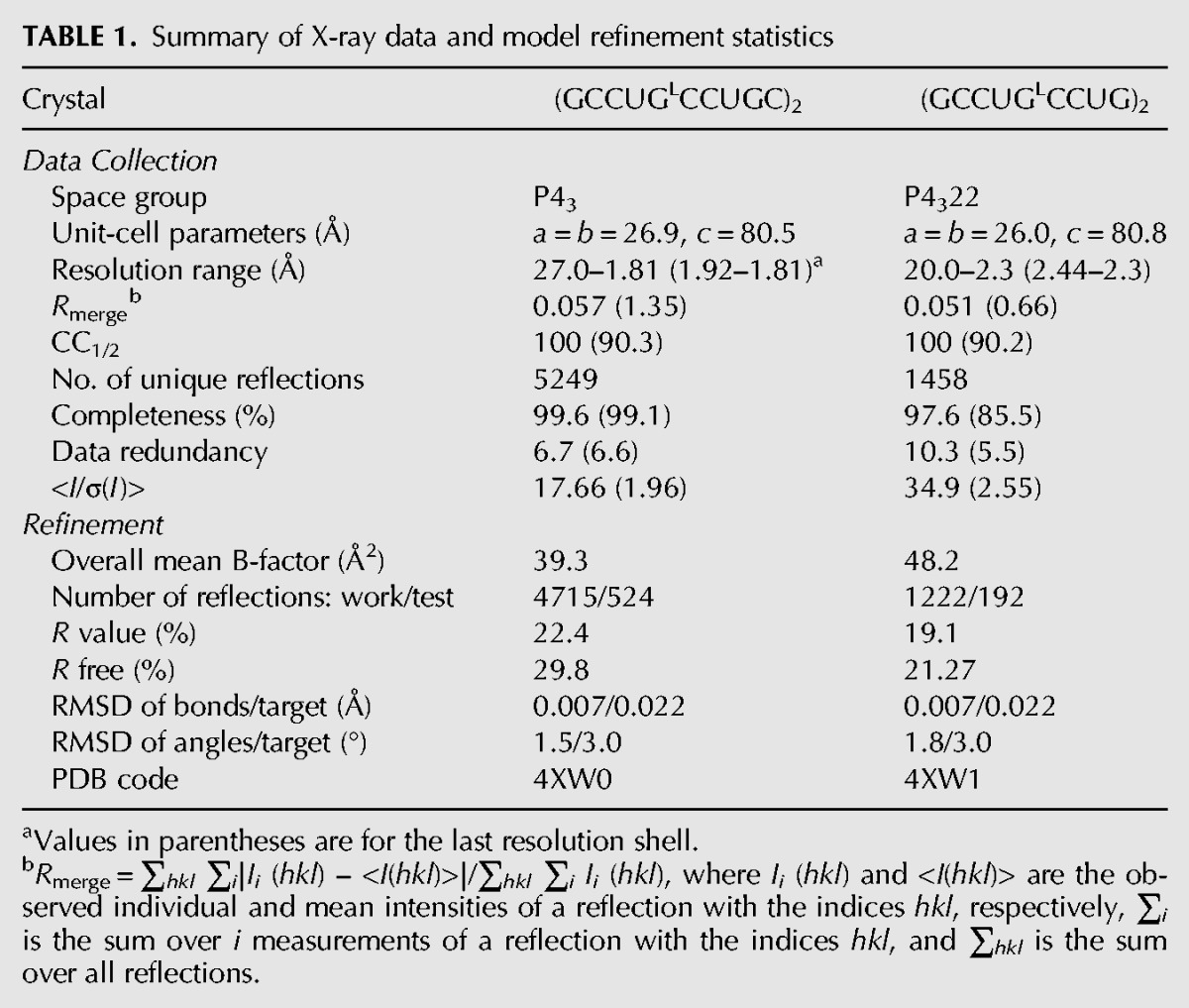
Crystals of GCCUGLCCUGC were analyzed first. The space group was initially assigned as P4322 with a single RNA strand in the asymmetric unit, but an inspection of electron density maps revealed merohedral twinning manifest in an apparent overlapping of the terminal 10C residue with its symmetry-related mate. The calculated twining fraction was close to 0.5. Subsequently, the data were reprocessed in space group P43 and the twinning operator -k, h, -l was used in the refinement. Twinned data with the twinning fraction of 0.5 cannot be “detwinned” algebraically, which makes the refinement cumbersome. Nevertheless, with proper care, an unambiguous model can be obtained even though the final statistics are usually worse than in the case of untwinned data. The final model was a duplex (chains A and B). The second oligomer, synthesized without residue 10C (the cause of the twinning), crystallized in the space group P4322 with similar cell parameters, but no sign of twinning. A duplex was formed by strand C and a symmetric-related strand C′. The X-ray data and refinement statistics are summarized in Table 1.
TABLE 1.
Summary of X-ray data and model refinement statistics
Both RNA oligomers formed a slippery duplex with four 3′-overhanging nucleotides in the longer duplex and three in the shorter structure. The three common overhanging residues were paired with the symmetry-related strand, forming pairs: C–G, a noncanonical U–U, and G–C (Fig. 1). The overlapping oligomers formed semi-infinite helices parallel to the c unit cell edge (Supplemental Fig. S1). In the longer oligomer, the fourth overhanging residue, 10C, from strand A was folded back, whereas in strand B it was completely disordered and was not modeled.
FIGURE 1.
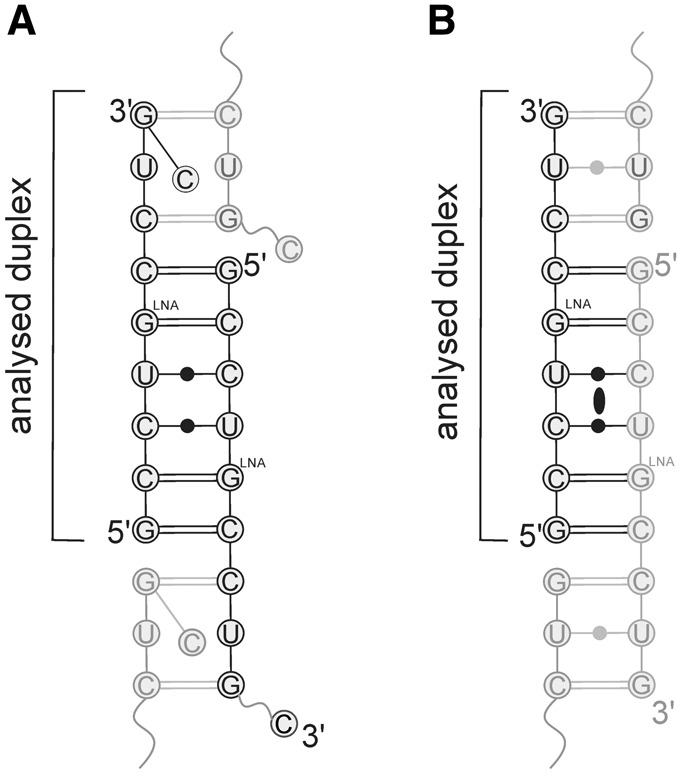
The secondary structure of (GCCUGLCCUGC)2 (A) and (GCCUGLCCUG)2 (B). The ellipse indicates a crystallographic twofold axis.
Although the oligomers differ in length by one residue, both structures are very similar. The root-mean-square-deviation (RMSD) between atomic positions of the superimposed duplexes is only 0.67 Å. The main discrepancies between the RNA chains are at the 3′ ends, because of the presence of the folded back 10C residue in the longer oligomer. Each helix contains nine base pairs, including two noncanonical C–U pairs and one U–U pair (in the overlap region). The remaining residues form Watson–Crick G–C pairs. The part of the duplexes with continuous backbone (i.e., excluding interactions between the sticky ends) consist of one CCUG repeat flanked by G–C and C–G pairs (Fig. 1). In both cases the oligomers form A-RNA with the sugar rings in the C3′-endo conformation, except 9G in strand A which has the C2′-endo pucker. The helical parameters show some deviations from values typical of A-RNA (Supplemental Table S1). One is the helical twist whose values range between 26° and 40°, although the average is typical: 32° for the A+B and C+C′ duplexes. Angle—a parameter related to inclination, defined as the angle between the C1′–C1′ vector and the helix axis, subtracted from 90—is relatively high: 19°–20°. The average rise is only 2.3 Å, compared with the typical value for A-RNA of 2.8 Å. In each structure, the smallest rise is 1.5 Å, observed between 6C–4G and 7C–3G pairs. Roll shows elevated values for the base pairs located in the middle part of the helix (Supplemental Table S2). Together, the latter two parameters indicate bending of the helix axis (∼44°), which in the crystal structure is C-shaped. Thus, in the crystal lattice, the pseudo-infinitive helix formed by symmetry-related molecules is not straight but sinuous (Supplemental Fig. S1). The bending of the duplex restricts access to the major groove in the middle of the helix. The duplex opens up at the ends, in the contact area between symmetry-related molecules (Supplemental Fig. S2).
Two sulfate ions are observed in the major groove of the longer helix. Each anion interacts with two adjacent cytosine residues forming H-bonds with their exo-amino groups. One sulfate is located near the 2C and 3C residues, whereas the second is close to 6C and 7C.
In both structures the stacking interactions are similar (Supplemental Fig. S3). The most extensive overlaps of base rings are observed between the GL–C and C–G pairs, and stacking between the C–U pairs is limited. The sole difference between the two duplexes is observed in the U–U pairs because of the different conformation of the base pairs. Also, the pattern of electrostatic potential surface is similar in both structures (Supplemental Fig. S4). The minor groove has a regular and characteristic distribution: The G–C pairs generate alternating strips of positive and negative potential, similar to the pattern observed in CNG repeats (Kiliszek and Rypniewski 2014), whereas the noncanonical base pairs show only a negative potential. The potential in the major groove is distributed more evenly. Areas of positive potential are mixed with areas of negative potential.
Noncanonical base pairs
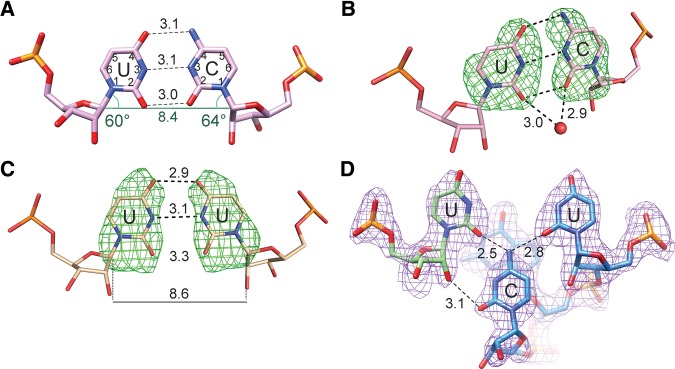
Each duplex contains three noncanonical base pairs: two C–U pairs, formed within the CCUG motif, and a U–U pair formed between the 3′ dangling ends of consecutive helices. Altogether, the two crystals forms contain three independent C–U pairs: two in the longer duplex and one in the shorter duplex (the other pair being symmetry-related). All the C–U pairs show similar conformations. The C and U residues are relatively close to each other and are almost co-planar. The C1′–C1′ distance is only 8.4 Å compared with the average distance of the flanking G–C pairs of 10.6 Å. The pair forms two clear hydrogen bonds: between the N4 exo-amino group and the O4 carbonyl atom and between the N3 imino group and the N3 amino group (Fig. 2A). The remaining two carbonyl O2 atoms are also close (2.9–3.0 Å). Positions of hydrogen atoms are not resolved at this resolution, but such a close contact between potential donor/acceptor atoms indicates a hydrogen bond, which in turn implies a tautomeric or ionic transition. Each C–U pair interacts with at least one water molecule in the minor groove. All the solvent peaks are located out of the plane of the pyrimidine bases, interacting with the carbonyl atoms of both C and U residues (Fig. 2B). The noncanonical pairs are also characterized by unusual values of the helical twist (Supplemental Table S1). The lowest value, 27°, is observed for the CC/UGL and UGL/CC steps (i.e., between the C–U and C–GL pairs), while the highest value, 40°, is between two neighboring C–U pairs. The perturbation can be described as alternating unwinding and twisting of the CCUG segment (Supplemental Table S1). Narrowing of the helix at the C–U pair (8.4 Å between the C1′ atoms) is accommodated by local changes in torsion angles: ε (rotation about the C3′–O3′ bond) in U and β (O5′–C5′) in GL residues. The value of ε is −118°, compared with the typical value of −153°, and β = 140° (typical value is 178°). The decrease of β reduces the distance between the P and C4′ atoms from 3.9 to 3.6 Å, whereas increasing ε pushes the phosphate group outward, enabling a widening of the helix (Supplemental Fig. S5).
FIGURE 2.
The noncanonical base pairs. (A) C and U interact via their Watson–Crick edges; the distances are shown in Å. The alignment of functional groups of the Watson–Crick edges of the C–U pairs corresponds with relatively high values of the λ angles (green), compared with the typical value of 55°. This indicates that the residues are inclined toward the major groove. The distance between the C1′ atoms is also shown. (B,C) Fo–Fc omit maps calculated for the nucleobases of pairs C–U and U–U in the shorter duplex. Contours mark the 3σ level. Red sphere represents a water molecule in the major groove. (D) 2Fo–Fc map of the U–U pair in the longer duplex.
The noncanonical U–U pairs in the two crystal structures show different conformations. In the shorter duplex, there is a close interaction between the uracil moieties. The C1′–C1′ distance is 8.6 Å and the functional groups of their Watson–Crick edges are symmetrically counterpoised (Fig. 2C). The O4 carbonyl atoms, N3 and O2 of each U are close: 2.9, 3.1, and 3.3 Å, respectively. Again, the distances of ∼3 Å between the juxtaposed atoms indicate H-bonding, which would necessitate a tautomeric transition. The uracil rings are significantly twisted with respect to one another (propeller = 21°). Elevated values of the helical twist are observed between the U–U and neighboring G–C pairs (twist ∼ 35°). In the longer duplex, the U residues are more separated (C1′–C1′ = 9.7 Å) than in the shorter duplex. The bases are nearly parallel and the functional groups of their Watson–Crick edges are too far apart (>4.7 Å) to interact (Fig. 2D). The unusual conformation of the U–U pair in the longer duplex is stabilized by the folded back 10C residue, absent in the shorter duplex. In the minor groove, the cytosine residue is wedged between the pair of uridines. A bifurcated H-bond is formed between the exo-amino group and the O2 carbonyl atoms of each U. A second hydrogen bond is observed between the O2 atom of the cytosine and the hydroxyl group of one of the uridine residues.
In both structures, high values of roll are associated with each nucleotide step involving the noncanonical pairs.
Thermodynamics
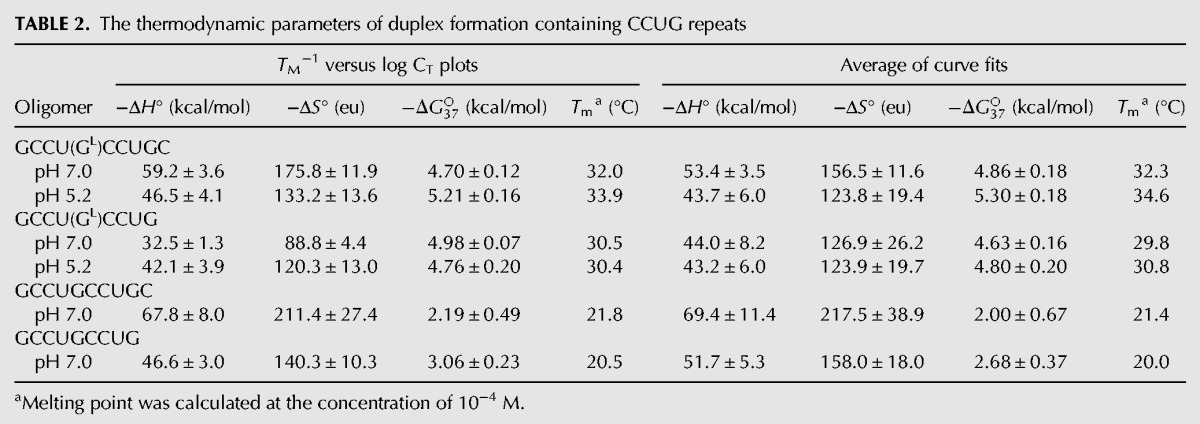
Thermodynamic stability of both duplexes was measured by the UV melting method. In addition, two analogous oligomers of the same sequence but with no modification were measured for comparison (Table 2). The enthalpy (ΔH), entropy (ΔS), and free energy (ΔG37), for 37°C, were calculated by two methods: fitting the experimental and theoretical melting curves and linear correlation of the melting temperature 1/TM and concentration of RNA (log CT). Overall, the oligomers melt in a two-state manner with the exception of the shorter duplex containing LNA, (GCCUGLCCUG)2. The two modified oligomers show similar thermodynamic stability, with ΔG37 approximately −4.7 kcal/mol. In the case of the unmodified oligomers, the longer one is less stable than the shorter. A comparison of the obtained parameters indicates that introducing one LNA guanosine residue in the middle of the duplex decreases ΔG37 by at least 2 kcal/mol. Thus, the modified duplexes are more stable and have melting temperature higher by 10°C. Additionally, UV melting was performed for the modified duplexes at pH 5.2. The value of ΔG37 for the longer oligomer decreased by ∼0.5 kcal/mol. For the shorter oligomer, the dependence between 1/TM and log CT was linear, indicating a two-state melting manner, which was not observed at pH 7.0. The absorbance curves obtained at various pH appear similar (Supplemental Fig. S6).
TABLE 2.
The thermodynamic parameters of duplex formation containing CCUG repeats
Quantum mechanical calculations
Calculations were carried out to determine the structural stability and relative energies of the noncanonical pairs C–U and U–U in their different possible tautomeric or protonated forms (Fig. 3).
FIGURE 3.
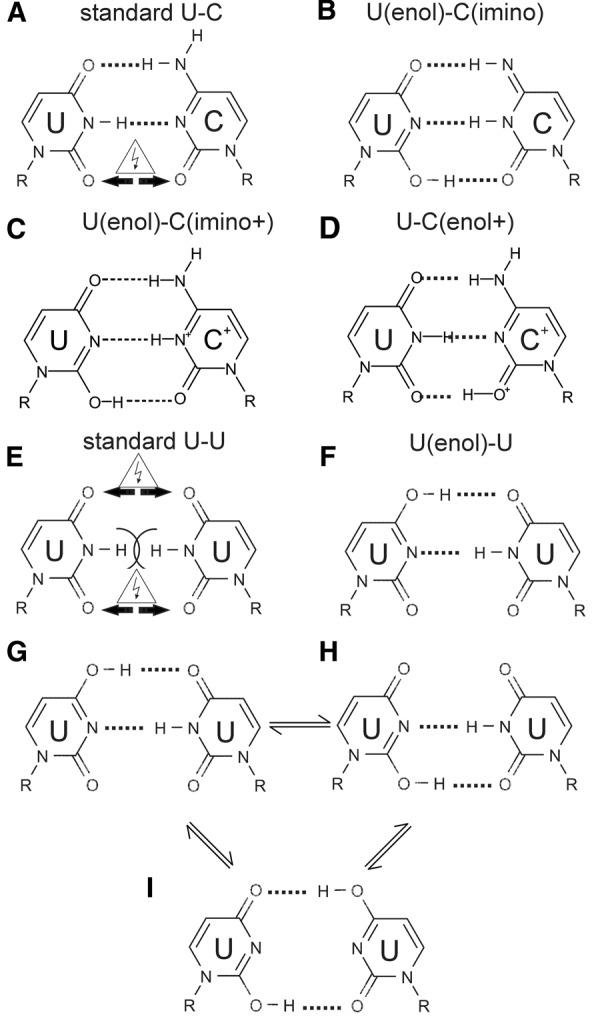
Standard and tautomeric or protonated forms within the C–U (A–D) and U–U pairs (E,F). A balance between three tautomeric forms is also possible in the U–U pair (G–I).
The C–U base pair observed in the crystal was modeled using the standard forms of C and U (Fig. 3A), the enol tautomer of U with imino C (Fig. 3B), enol U with imino+ C (Fig. 3C), and standard U with enol+ C (Fig. 3D). The C–U pair in the crystal was nearly planar, with the O atoms juxtaposed 3.0–3.1 Å apart. Optimized QM models of standard C and U are characterized by the RMSD between 0.16 and 0.33 Å from the crystal structure, depending on the imposed constrains. The pair in the standard form was unstable during the calculation, because of a repulsion between the opposite O2 atoms, which tended to shift sideways up to 0.8 Å, leading to an increase of the O–O distance to 3.4 Å. The pair that diverged the least from the crystallographic structure was the C(imino)-U(enol) tautomeric pair. It deviated from the X-ray coordinates by RMSD of 0.13 Å and was stabilized by three hydrogen bonds. However, its calculated free energy was higher by 15.0 kcal/mol than the energy estimated for the standard C–U. A similar consistency with the X-ray coordinates was observed for the optimized models of U–C(enol+) and U(enol)–C(imino+) pairs (RMSD of 0.12 Å and 0.14 Å, respectively), characterized by small free energy difference of 3 kcal/mol in favor of U–C(enol+). In the two models, the coplanarity of bases is also maintained by three hydrogen bonds.
The noncanonical U–U base pair found in the crystal was highly unstable in the calculation when it was modeled using the standard form (Fig. 3E). The U bases were pushed away and rotated during the optimization because of the repulsion between the carbonyl O atoms and clashing H atoms. The resulting minimized model deviated highly from the crystal structure, indicating that such an arrangement of the U bases was not acceptable. The most stable model that corresponded to the crystallographic structure was the U–U(enol) tautomeric base pair (Fig. 3F). It deviated from the crystal structure by RMSD of 0.21 Å and was stabilized by two hydrogen bonds. The alternative U–U(enol) pair (Fig. 3H) was also stabilized by two H-bonds, diverged from the crystal structure by RMSD of 0.20 Å and its relative energy was higher by 10 kcal/mol than for the aforementioned U–U(enol) pair. The third possible tautomeric base pair U(enol)–U(enol) (Fig. 3I) deviated from initial crystal structure by RMSD of 0.31 Å and its energy was higher by 17 kcal/mol compared with the optimal U–U(enol).
DISCUSSION
Characteristic features of the helix
Inspection of the helix reveals bending in addition to twisting, which amounts to supercoiling (Supplemental Fig. S1). This is manifest in widening of the central hole observed in an A-helix along the helical axis. Another effect of this is an apparent shrinking of the rise parameter (Supplemental Table S1; average value = 2.2 Å). The bending takes place at the CU/UC step and is accompanied by closing of the major groove over this step. A bending of the CCUG helix was also reported by Childs-Disney et al. (2014). The bending/coiling effect was not observed in any of the tri-nucleotide repeats analyzed before (Kiliszek et al. 2009, 2010, 2011, 2012).
Strand slippage
The oligomer was designed to form two double-stranded CCUG repeats, but this was reduced to one because of strand slippage. This is reminiscent of the two known crystal structures of CCG repeats: one containing an LNA residue and the other unmodified (Kiliszek et al. 2012). In both structures strand slippage was observed, reducing the number of CCG repeats from two to one. That was interpreted as a sign of instability of C–C pairs. In this report, the strand slippage can be interpreted as a result of instability of C–U pairs. It is unlikely that LNA induces the strands to slip. LNA is known to stabilize A-RNA duplexes by locking the ribose ring in the C3′-endo conformation. We have demonstrated the stabilizing effect also in this article (see Thermodynamics section). The structure reported by Childs-Disney et al. (2014) does not show strand slippage, which could be the result of embedding the CCUG repeats within a larger molecule.
Thermodynamics
CCUG repeats are markedly less stable than any of the CNG repeats (Broda et al. 2005). The melting temperature of an unmodified oligomer is close to room temperature, whereas including a “locked” residue stabilizes it by ∼10°C. This explains its better crystallization properties. Removing the terminal C, which was disordered in the crystal structure, also reduces entropy in solution. One could ask if the molecule in solution, used in the thermodynamic measurement, had a similar form to the crystal structure (i.e., with strand slippage)? The thermodynamic behavior was consistent with a homogenous population, and it is reasonable to propose that this corresponded to the slipped duplexes. This could explain the low stability, as only a part of the molecule participates in base-pairing. This would not be the first example of a system acting, through strand slipping, to reduce the number of destabilizing base pairs.
In previous thermodynamic studies, it was observed that C–C pairs can undergo protonation (Romby et al. 1986; SantaLucia et al. 1991). The UV melting experiments conducted at low pH showed an increase in thermal stability of a duplex. In the present case of CCUG repeats, the duplexes do not show a pH dependence upon melting. A similar result was obtained for an RNA oligomer CGCCUGCG containing two noncanonical C–U base pairs, which showed a pH dependence only at low temperatures (SantaLucia et al. 1991). This suggests that in the structure of CCUG repeats protonation of the N1 atom of the cytosine does not take place readily, although it cannot be definitely excluded. One possibility is that pKa could be shifted in the local environment above the pH range of the measurements. In that case, no change would be detected because protonation would be always present.
Nature of C–U interactions
The C–U interactions are puzzling because of the close distance between the O2 atoms: 2.9–3.0 Å. C and U, in their classical forms, have carbonyl O atoms in position 2 and their close proximity would give rise to substantial repulsive interactions between them unless a hydrogen atom is present in between. Hydrogen atoms cannot be observed at this resolution but hydrogen bonds in crystal structures are inferred readily on the basis of distance and spatial criteria. These are easily satisfied in this case, but to interpret this interaction as H-bonded, one would need to postulate a tautomeric transition of both bases (Fig. 3B) or a protonation of C (Fig. 3C,D). Minor tautomeric forms are rarely observed but they could be stabilized under favorable conditions (Singh et al. 2015) and captured in a crystal structure. It has been proposed that tautomerization in DNA contributes to mutations during polymerization (Wang et al. 2011). In RNA, tautomerization has been postulated to play a role in ribozymes (Singh et al. 2015) and in proofreading tRNA during translation (Weixlbaumer et al. 2007; Westhof 2014).
In the structure containing CCUG repeats by Childs-Disney et al. (2014), in two of the three CCUG motifs, the four C–U pairs also interact vis à vis, although the distance between the O atoms is somewhat larger (3.2 Å) and the authors did not invoke tautomerization to explain this interaction. Instead they proposed that the hydrogen bond between the N3 atoms overcame the repulsive interactions between the neighboring carbonyl O atoms. Three further examples of C–U pairs can be found in databases (Sarver et al. 2008; Popenda et al. 2010). In the 16S RNA of Thermus thermophilus, the U244 residue forms a vis-à-vis pair with C893. Besides the two expected H-bonds, the O2 atoms are 2.9 Å apart. The other two examples come from a domain of IRES HCV structure. In the two crystallographically independent pairs C63A:U104B, the distances between the O2 atoms are 3.0 and 3.1 Å.
The close proximity of the two carbonyl oxygen atoms observed in this study cannot be easily explained by local factors compensating their repulsive interactions, because we do not see any compensation, such as intercalating cations or a large propeller twist. One could argue that the adjacent water molecule is in fact a potassium cation, but potassium would give rise to a peak heavier than water and anyway we did not add any potassium to the crystallization solution. On balance, it is easier to admit a possibility that tautomerization or protonation has taken place and in consequence we observe three hydrogen bonds instead of two H-bonds and one repulsive close interaction. Tautomeric or ionic nucleobases are rare in isolation but could be more common in the context of nucleic acids and could play important roles in biological processes (Gottstein-Schmidtke et al. 2014; Kimsey et al. 2015).
Nature of U–U interaction
A well-defined U–U pair is observed (Fig. 2C) in the overhang region of the shorter duplex, involving U8 and its symmetric equivalent from the next molecule in the pseudo-infinite column. The mutual orientation of the bases and short distances between the O4 atoms and the N3 atoms are difficult to explain without invoking tautomerism. A shift of one of the uracil rings to an enolo state allows two hydrogen bonds to form within the pair: between the N atoms and one pair of the O atoms (Fig. 3F). The second pair of O atoms would remain mutually repulsive (the O2 atoms are 3.3 Å apart, compared with 2.9 Å for the pair of O4 atoms; with the propeller twist of −21.3° between the uracil rings), or the system could undergo resonance, which would result in a balance between the attraction and repulsion (Fig. 3G–I). The U–U(enol) pair appears to be a previously unobserved form of U–U interaction.
Significance of quantum mechanical calculations
We decided to augment the experimental data with quantum mechanical (QM) calculations because they allow an implicit modeling of hydrogen atoms and give a measure of energies involved. The QM computation, carried out on isolated bases and base pairs in vacuo, was meant as a simple evaluation of the tautomeric model rather than a comprehensive assessment of the overall structure. The calculated energies indicated clearly that in this crystal structure the U–U(enol) is favored over the standard U–U form, whereas the tautomerized C–U pair has higher energy than the standard form but not to the point of excluding it. In recent studies, the tautomeric properties of nucleic acid bases and base pairs have been investigated using diverse approaches to the calculation and different models of the environment (Shukla and Leszczynski 2013). Application of modern high-level quantum chemistry computational algorithms implemented on state-of-the-art hardware makes possible a rigorous analysis of complex systems, and the results approximate well the experimental data. An earlier comprehensive QM study of possible tautomeric forms in nucleotide base pairs (Rejnek and Hobza 2007) demonstrated that the calculated energy depended strongly on the complexity of the approach and the accuracy of the model. When more aspects were included, such as tautomeric penalization, solvent effect and other environmental factors, the energies of the two possible tautomeric forms of C–G base pairs decreased from 19 and 15 kcal/mol to 6 and 5 kcal/mol above the canonical form. The authors concluded that the experimental detection of such tautomers could not be excluded. Those results suggest that also in our study the calculated energy differences for the tautomerized C–U pair could be lower if the computation was carried out on a deeper level of theory (Singh et al. 2015).
DM2 versus DM1
Similarities between myotonic dystrophies of type 1 (associated with CUG repeats) and type 2 (CCUG repeats) include common symptoms, tissue specificity and general pathomechanism, but they are clearly different disorders (Udd and Krahe 2012). Both involve splicing misregulation (Savkur et al. 2004; Ranum and Cooper 2006), but there are indications that this does not account fully for the symptoms (Udd and Krahe 2012). The cause of pathogenicity is also to be found at the post-transcriptional level, when the mutant RNA accumulates in the nucleus and interacts with other molecules, such as MBNL1 (Miller et al. 2000; Fardaei et al. 2002; Mankodi et al. 2003), PKR (Huichalaf et al. 2010), or PKC (Kuyumcu-Martinez et al. 2007). These proteins interact differently with the expanded CUG and CCUG repeats. For instance, MBNL1 is always found in the CUG-containing nuclear foci but not always in the CCUG-containing foci (Wojciechowska and Krzyzosiak 2011). Also, PKC is activated in the presence of CUG repeats, with the resulting hyperphosphorylation of CUG-BP1 (Kuyumcu-Martinez et al. 2007). On the other hand, there is a controversy as to whether CUG-BP1 is hyperphosphorylated in the presence of CCUG repeats, so it remains to be determined if PKC is activated by CCUG. When we consider specificity of interactions, the question comes down to differences between the structures of the CCUG and CUG repeats. The main difference is the presence of the C–U pairs in the CCUG repeats. The special characteristics of the C–U pairing also have to be taken into account, which in effect allow them to form Watson–Crick-like interactions. The other significant features are the observed supercoiling of the CCUG duplex, differences in accessibility to the helical grooves or different spacing between the CG steps in the two repeats. The latter could be important in interactions with MBNL1, which is thought to contact several CG steps simultaneously. Perhaps a parallel can be drawn also between the relative thermodynamic instability of CCUG repeats relative to CUG runs, and the relatively mild and indistinct course of DM2 compared to DM1.
MATERIALS AND METHODS
Synthesis, purification, and crystallization of the CCUG oligomers
All oligomers were synthesized commercially (future Synthesis sp. z o.o.). Desalted oligomers were purified using the TLC method on silica gel plates with ammonia/1-propanol/water solvent. The oligomers were eluted with water and lyophilized under vacuum using Speed-Vac. Before crystallization, the RNA was dissolved in 200 mM ammonium acetate to the final concentration of 1 mM and annealed for 5 min at 95°C, then cooled to ambient temperature within 2–3 h. Crystals were grown by the sitting drop method at 19°C. The crystallization medium of the GCCUGLCCUGC oligomer contained 40 mM magnesium sulfate, 40 mM HEPES pH 7.0 and 1.3 M lithium sulfate. Crystals of the second oligomer, GCCUGLCCUG, grew in 10 mM magnesium acetate, sodium cacodylate pH 6.5 and 1.3 M Li2SO4. The RNA was mixed with the crystallization solution in the ratio 3:1.
UV melting of oligonucleotides
UV thermal melting studies were performed according to Pasternak and Wengel (2010) on a Beckman DU 640 spectrometer with a thermoprogrammer. The RNA oligomers were dissolved in a buffer containing 1 M sodium chloride, 20 mM sodium cacodylate, and 0.5 mM Na2EDTA, pH 7.0 and 5.2. Each duplex was prepared in nine different concentrations in the range 10−5 to 10−6 M. The concentrations of single strand oligomers were calculated from a high-temperature (>80°C) absorbance and single strand extinction coefficients approximated by the nearest-neighbor model. The UV absorption versus temperature was measured at 260 nm at the heating rate of 1°C/min in the range 5°C–95°C. The melting curves were analyzed and the thermodynamic parameters calculated using MeltWin 3.5.
X-ray data collection, structure solution, and refinement
X-ray diffraction data were collected on the BL 14.2 beam line at the BESSY synchrotron in Berlin. The resolution for the GCCUGLCCUGC crystal was 1.8 Å and for GCCUGLCCUG it was 2.3 Å. Both crystals were cryoprotected by 20%–30% glycerol (v/v) in the mother liquor. The data were integrated and scaled using XDS (Kabsch 2010). The space group was assigned as P43 for the longer oligomer and P4322 for the shorter RNA. The X-ray data are summarized in Table 1. The structures were solved by molecular replacement with PHASER (McCoy et al. 2007) using one strand of the CCG repeat structure (PDB code 4E58) as the search model. Early stages of the refinement were carried out using Refmac5 (Murshudov et al. 1997) from the CCP4 program suite (Winn et al. 2011), and then refinement was continued with PHENIX (Afonine et al. 2012). The longer oligomer was refined against the twinned data, using the least-squares method rather than the more powerful maximum likelihood method. This was due to the impossibility of “detwinning” the data algebraically when the twin fraction is 0.5 (Dauter 2003). The program Coot (Emsley et al. 2010) was used for visualization of electron density maps, calculated with the coefficients 2Fo–Fc and Fo–Fc, and for manual rebuilding of the atomic model. The last few cycles were performed using all data, including the Rfree set. The models are summarized in Table 1. The helical parameters were calculated with 3DNA (Lu and Olson 2003) using a sequence-independent method based on vectors connecting the C1′ atoms of the paired residues, to avoid computational artefacts arising from noncanonical base-pairing. Program PBEQ-Solver (Jo et al. 2008) was used to calculate the electrostatic potential map. All pictures were drawn using UCSF Chimera (Pettersen et al. 2004) and PyMOL v0.99rc6 (DeLano 2002). Atomic coordinates of the crystallographic models have been deposited with the Protein Data Bank (accession codes 4XW0 and 4XW1).
Quantum mechanical calculations
The presence of possible tautomeric forms of U and C has been evaluated by computational chemistry methods. Optimized noncanonical base pairs were obtained at the B3LYP hybrid functional level with the aug-cc-pVTZ basis set (Dunning 1989; Kendall et al. 1992). All calculations were carried out with the Gaussian 09 suite of programs (Frisch et al. 2009) and the geometry of the structures were handled and visualized with the Molden (Schaftenaar and Noordik 2000) and Accelrys Discovery Studio packages (Accelrys 2007). The model structures for the calculations were obtained from the crystallographic atomic coordinates of the C–U and U–U base pairs. The base pairs were modeled using Molden by appropriate placing of hydrogen atoms for the standard and tautomeric forms; each base was terminated by replacing the C1′ atom with a methyl group. The resulting structures were then optimized to determine the possible location of hydrogen atoms while keeping still the nonhydrogen atoms. Further optimization was performed with a gradual release of the constrains. Several approaches were used to obtain a model that is optimized for the calculation and close to the crystal structure. In all the presented calculations, the methyl groups mimicking the attachment of the bases to the RNA backbone were used as anchor points and the distance between them was kept close to the C1′–C1′ distance determined in the crystal structure. In the cases where the repulsive forces disturbed substantially the initial positions, the orientation of the bases was additionally maintained by constraining the N1 or C6 atoms.
SUPPLEMENTAL MATERIAL
Supplemental material is available for this article.
Supplementary Material
ACKNOWLEDGMENTS
We thank the National Science Centre (Poland, UMO-2011/01/B/NZ1/04429), the Ministry of Science and Higher Education (Poland, NN519405037, 01/KNOW2/2014), the European Commission (the Seventh Framework Programme), the BioStruct-X project (contract No. 283570), and the Poznan Supercomputing and Networking Center.
Footnotes
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.052399.115.
REFERENCES
- Accelrys. 2007. Discovery studio modeling environment, release 3.5. Accelrys Software Inc. [Google Scholar]
- Afonine PV, Grosse-Kunstleve RW, Echols N, Headd JJ, Moriarty NW, Mustyakimov M, Terwilliger TC, Urzhumtsev A, Zwart PH, Adams PD. 2012. Towards automated crystallographic structure refinement with phenix.refine. Acta Crystallogr D Biol Crystallogr 68: 352–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aslanidis C, Jansen G, Amemiya C, Shutler G, Mahadevan M, Tsilfidis C, Chen C, Alleman J, Wormskamp NG, Vooijs M, et al. 1992. Cloning of the essential myotonic dystrophy region and mapping of the putative defect. Nature 355: 548–551. [DOI] [PubMed] [Google Scholar]
- Bachinski LL, Udd B, Meola G, Sansone V, Bassez G, Eymard B, Thornton CA, Moxley RT, Harper PS, Rogers MT, et al. 2003. Confirmation of the type 2 myotonic dystrophy (CCTG)n expansion mutation in patients with proximal myotonic myopathy/proximal myotonic dystrophy of different European origins: a single shared haplotype indicates an ancestral founder effect. Am J Hum Genet 73: 835–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevilacqua PC, Yajima R. 2006. Nucleobase catalysis in ribozyme mechanism. Curr Opin Chem Biol 10: 455–464. [DOI] [PubMed] [Google Scholar]
- Broda M, Kierzek E, Gdaniec Z, Kulinski T, Kierzek R. 2005. Thermodynamic stability of RNA structures formed by CNG trinucleotide repeats. Implication for prediction of RNA structure. Biochemistry 44: 10873–10882. [DOI] [PubMed] [Google Scholar]
- Brook JD, McCurrach ME, Harley HG, Buckler AJ, Church D, Aburatani H, Hunter K, Stanton VP, Thirion JP, Hudson T, et al. 1992. Molecular basis of myotonic dystrophy: expansion of a trinucleotide (CTG) repeat at the 3′ end of a transcript encoding a protein kinase family member. Cell 69: 799–808. [DOI] [PubMed] [Google Scholar]
- Childs-Disney JL, Yildirim I, Park H, Lohman JR, Guan L, Tran T, Sarkar P, Schatz GC, Disney MD. 2014. Structure of the myotonic dystrophy type 2 RNA and designed small molecules that reduce toxicity. ACS Chem Biol 9: 538–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coonrod LA, Lohman JR, Berglund JA. 2012. Utilizing the GAAA tetraloop/receptor to facilitate crystal packing and determination of the structure of a CUG RNA helix. Biochemistry 51: 8330–8337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dauter Z. 2003. Twinned crystals and anomalous phasing. Acta Crystallogr D Biol Crystallogr 59: 2004–2016. [DOI] [PubMed] [Google Scholar]
- DeLano WL. 2002. The PyMOL molecular graphics system. DeLano Scientific, Palo Alto, CA. [Google Scholar]
- Demeshkina N, Jenner L, Westhof E, Yusupov M, Yusupova G. 2012. A new understanding of the decoding principle on the ribosome. Nature 484: 256–259. [DOI] [PubMed] [Google Scholar]
- Demeshkina N, Jenner L, Westhof E, Yusupov M, Yusupova G. 2013. New structural insights into the decoding mechanism: translation infidelity via a G.U pair with Watson–Crick geometry. FEBS Lett 587: 1848–1857. [DOI] [PubMed] [Google Scholar]
- Dunning TH. 1989. Gaussian-basis sets for use in correlated molecular calculations.1. The atoms boron through neon and hydrogen. J Chem Phys 90: 1007–1023. [Google Scholar]
- Emsley P, Lohkamp B, Scott WG, Cowtan K. 2010. Features and development of Coot. Acta Crystallogr D Biol Crystallogr 66: 486–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fardaei M, Rogers MT, Thorpe HM, Larkin K, Hamshere MG, Harper PS, Brook JD. 2002. Three proteins, MBNL, MBLL and MBXL, co-localize in vivo with nuclear foci of expanded-repeat transcripts in DM1 and DM2 cells. Hum Mol Genet 11: 805–814. [DOI] [PubMed] [Google Scholar]
- Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, et al. 2009. Gaussian 09. Gaussian Inc, Wallingford, CT. [Google Scholar]
- Gilbert SD, Reyes FE, Edwards AL, Batey RT. 2009. Adaptive ligand binding by the purine riboswitch in the recognition of guanine and adenine analogs. Structure 17: 857–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottstein-Schmidtke SR, Duchardt-Ferner E, Groher F, Weigand JE, Gottstein D, Suess B, Wohnert J. 2014. Building a stable RNA U-turn with a protonated cytidine. RNA 20: 1163–1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harley HG, Brook JD, Rundle SA, Crow S, Reardon W, Buckler AJ, Harper PS, Housman DE, Shaw DJ. 1992. Expansion of an unstable DNA region and phenotypic variation in myotonic dystrophy. Nature 355: 545–546. [DOI] [PubMed] [Google Scholar]
- Huichalaf C, Sakai K, Jin B, Jones K, Wang GL, Schoser B, Schneider-Gold C, Sarkar P, Pereira-Smith OM, Timchenko N, et al. 2010. Expansion of CUG RNA repeats causes stress and inhibition of translation in myotonic dystrophy 1 (DM1) cells. FASEB J 24: 3706–3719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo S, Vargyas M, Vasko-Szedlar J, Roux B, Im W. 2008. PBEQ-Solver for online visualization of electrostatic potential of biomolecules. Nucleic Acids Res 36: W270–W275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabsch W. 2010. Xds. Acta Crystallogr D Biol Crystallogr 66: 125–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendall RA, Dunning TH, Harrison RJ. 1992. Electron-affinities of the 1st-row atoms revisited—systematic basis-sets and wave-functions. J Chem Phys 96: 6796–6806. [Google Scholar]
- Kiliszek A, Rypniewski W. 2014. Structural studies of CNG repeats. Nucleic Acids Res 42: 8189–8199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiliszek A, Kierzek R, Krzyzosiak WJ, Rypniewski W. 2009. Structural insights into CUG repeats containing the ‘stretched U-U wobble’: implications for myotonic dystrophy. Nucleic Acids Res 37: 4149–4156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiliszek A, Kierzek R, Krzyzosiak WJ, Rypniewski W. 2010. Atomic resolution structure of CAG RNA repeats: structural insights and implications for the trinucleotide repeat expansion diseases. Nucleic Acids Res 38: 8370–8376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiliszek A, Kierzek R, Krzyzosiak WJ, Rypniewski W. 2011. Crystal structures of CGG RNA repeats with implications for fragile X-associated tremor ataxia syndrome. Nucleic Acids Res 39: 7308–7315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiliszek A, Kierzek R, Krzyzosiak WJ, Rypniewski W. 2012. Crystallographic characterization of CCG repeats. Nucleic Acids Res 40: 8155–8162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimsey IJ, Petzold K, Sathyamoorthy B, Stein ZW, Al-Hashimi HM. 2015. Visualizing transient Watson–Crick-like mispairs in DNA and RNA duplexes. Nature 519: 315–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuyumcu-Martinez NM, Wang GS, Cooper TA. 2007. Increased steady-state levels of CUGBP1 in myotonic dystrophy 1 are due to PKC-mediated hyperphosphorylation. Mol Cell 28: 68–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liquori CL, Ricker K, Moseley ML, Jacobsen JF, Kress W, Naylor SL, Day JW, Ranum LP. 2001. Myotonic dystrophy type 2 caused by a CCTG expansion in intron 1 of ZNF9. Science 293: 864–867. [DOI] [PubMed] [Google Scholar]
- Lu XJ, Olson WK. 2003. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res 31: 5108–5121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mankodi A, Urbinati CR, Yuan QP, Moxley RT, Sansone V, Krym M, Henderson D, Schalling M, Swanson MS, Thornton CA. 2001. Muscleblind localizes to nuclear foci of aberrant RNA in myotonic dystrophy types 1 and 2. Hum Mol Genet 10: 2165–2170. [DOI] [PubMed] [Google Scholar]
- Mankodi A, Teng-Umnuay P, Krym M, Henderson D, Swanson M, Thornton CA. 2003. Ribonuclear inclusions in skeletal muscle in myotonic dystrophy types 1 and 2. Ann Neurol 54: 760–768. [DOI] [PubMed] [Google Scholar]
- Margolis JM, Schoser BG, Moseley ML, Day JW, Ranum LP. 2006. DM2 intronic expansions: evidence for CCUG accumulation without flanking sequence or effects on ZNF9 mRNA processing or protein expression. Hum Mol Genet 15: 1808–1815. [DOI] [PubMed] [Google Scholar]
- McCoy AJ, Grosse-Kunstleve RW, Adams PD, Winn MD, Storoni LC, Read RJ. 2007. Phaser crystallographic software. J Appl Crystallogr 40: 658–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JW, Urbinati CR, Teng-Umnuay P, Stenberg MG, Byrne BJ, Thornton CA, Swanson MS. 2000. Recruitment of human muscleblind proteins to (CUG)(n) expansions associated with myotonic dystrophy. EMBO J 19: 4439–4448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirkin SM. 2007. Expandable DNA repeats and human disease. Nature 447: 932–940. [DOI] [PubMed] [Google Scholar]
- Murshudov GN, Vagin AA, Dodson EJ. 1997. Refinement of macromolecular structures by the maximum-likelihood method. Acta Crystallogr D Biol Crystallogr 53: 240–255. [DOI] [PubMed] [Google Scholar]
- Pasternak A, Wengel J. 2010. Thermodynamics of RNA duplexes modified with unlocked nucleic acid nucleotides. Nucleic Acids Res 38: 6697–6706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. 2004. UCSF Chimera--a visualization system for exploratory research and analysis. J Comput Chem 25: 1605–1612. [DOI] [PubMed] [Google Scholar]
- Popenda M, Szachniuk M, Blazewicz M, Wasik S, Burke EK, Blazewicz J, Adamiak RW. 2010. RNA FRABASE 2.0: an advanced web-accessible database with the capacity to search the three-dimensional fragments within RNA structures. BMC Bioinformatics 11: 231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranum LP, Cooper TA. 2006. RNA-mediated neuromuscular disorders. Annu Rev Neurosci 29: 259–277. [DOI] [PubMed] [Google Scholar]
- Rejnek J, Hobza P. 2007. Hydrogen-bonded nucleic acid base pairs containing unusual base tautomers: complete basis set calculations at the MP2 and CCSD(T) levels. J Phys Chem B 111: 641–645. [DOI] [PubMed] [Google Scholar]
- Romby P, Westhof E, Moras D, Giege R, Houssier C, Grosjean H. 1986. Studies on anticodon-anticodon interactions: hemi-protonation of cytosines induces self-pairing through the GCC anticodon of E. coli tRNA-Gly. J Biomol Struct Dyn 4: 193–203. [DOI] [PubMed] [Google Scholar]
- SantaLucia J Jr, Kierzek R, Turner DH. 1991. Stabilities of consecutive A.C, C.C, G.G, U.C, and U.U mismatches in RNA internal loops: evidence for stable hydrogen-bonded U.U and C.C.+ pairs. Biochemistry 30: 8242–8251. [DOI] [PubMed] [Google Scholar]
- Sarver M, Zirbel CL, Stombaugh J, Mokdad A, Leontis NB. 2008. FR3D: finding local and composite recurrent structural motifs in RNA 3D structures. J Math Biol 56: 215–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savkur RS, Philips AV, Cooper TA, Dalton JC, Moseley ML, Ranum LP, Day JW. 2004. Insulin receptor splicing alteration in myotonic dystrophy type 2. Am J Hum Genet 74: 1309–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaftenaar G, Noordik JH. 2000. Molden: a pre- and post-processing program for molecular and electronic structures. J Comput Aided Mol Des 14: 123–134. [DOI] [PubMed] [Google Scholar]
- Shukla MK, Leszczynski J. 2013. Tautomerism in nucleic acid bases and base pairs: a brief overview. Wiley Interdiscip Rev Comput Mol Sci 3: 637–649. [Google Scholar]
- Sicot G, Gourdon G, Gomes-Pereira M. 2011. Myotonic dystrophy, when simple repeats reveal complex pathogenic entities: new findings and future challenges. Hum Mol Genet 20: R116–123. [DOI] [PubMed] [Google Scholar]
- Singh V, Fedeles BI, Essigmann JM. 2015. Role of tautomerism in RNA biochemistry. RNA 21: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobczak K, de Mezer M, Michlewski G, Krol J, Krzyzosiak WJ. 2003. RNA structure of trinucleotide repeats associated with human neurological diseases. Nucleic Acids Res 31: 5469–5482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Udd B, Krahe R. 2012. The myotonic dystrophies: molecular, clinical, and therapeutic challenges. Lancet Neurol 11: 891–905. [DOI] [PubMed] [Google Scholar]
- Wang W, Hellinga HW, Beese LS. 2011. Structural evidence for the rare tautomer hypothesis of spontaneous mutagenesis. Proc Natl Acad Sci 108: 17644–17648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weixlbaumer A, Murphy FVt, Dziergowska A, Malkiewicz A, Vendeix FA, Agris PF, Ramakrishnan V. 2007. Mechanism for expanding the decoding capacity of transfer RNAs by modification of uridines. Nat Struct Mol Biol 14: 498–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westhof E. 2014. Isostericity and tautomerism of base pairs in nucleic acids. FEBS Lett 588: 2464–2469. [DOI] [PubMed] [Google Scholar]
- Winn MD, Ballard CC, Cowtan KD, Dodson EJ, Emsley P, Evans PR, Keegan RM, Krissinel EB, Leslie AG, McCoy A, et al. 2011. Overview of the CCP4 suite and current developments. Acta Crystallogr D Biol Crystallogr 67: 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wojciechowska M, Krzyzosiak WJ. 2011. Cellular toxicity of expanded RNA repeats: focus on RNA foci. Hum Mol Genet 20: 3811–3821. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.