A Local and Global Function Model of the Liver

Abstract

Purposes

To develop a local and global function model in the liver based upon regional and organ function measurements to support individualized adaptive radiation therapy (RT).

Methods and Materials

A local and global model for liver function was developed to include both functional volume and the effect of functional variation of subunits. Adopting the assumption of parallel architecture in the liver, the global function was composed of a sum of local function probabilities of subunits, varying between 0 and 1. The model was fit to 59 datasets of liver regional and organ function measures from 23 patients obtained prior to, during and 1 month after RT. The local function probabilities of subunits were modeled by a sigmoid function in relating to MRI-derived portal venous perfusion values. The global function was fitted to a logarithm of an indocyanine green retention rate at 15 min (an overall liver function measure). Cross-validation was performed by leave-m-out tests. The model was further evaluated by fitting to the data divided based upon whether the patients had hepatocellular carcinoma (HCC) or not.

Results

The liver function model showed that 1) a perfusion value of 68.6 ml/(100g·min) yielded a local function probability of 0.5; 2) the probability reached 0.9 at a perfusion value of 98 ml/(100g·min), and 3) at a probability of 0.03 (corresponding perfusion of 38 ml/(100g·min)) or lower, the contribution to global function was lost. Cross-validations showed that the model parameters were stable. The model fitted to the data from the patients with HCC indicated that the same amount of portal venous perfusion was translated into less local function probability than the patients with non-HCC tumors.

Conclusions

The developed liver function model could provide a means to better assess individual and regional dose responses of hepatic functions, and provide guidance for individualized treatment planning of RT.

Introduction

High dose radiation therapy (RT) can control intrahepatic cancer.[1,2] However, high-dose RT in intrahepatic tumors is limited by the development of radiation-induced liver disease (RILD).[3–5] RILD typically occurs within a few months of completion of RT, and can lead to liver failure and death in severe cases. Currently, there is no established therapy for RILD.

Normal tissue complication probability (NTCP) models have been developed to enable physicians and radiation treatment planners to minimize the risk of RILD in intrahepatic cancers.[6–10] These models fit complication probabilities to observed frequencies of RILD in the patient population to determine tolerable normal liver doses. Although some recent studies consider the effects of pathological and clinical factors on radiation sensitivities in the subgroups,[6,9] variation of liver function within the population is generally neglected. Another approach to modeling liver injury is to explicitly assume that it is due to the accumulated damage of functional subunits (FSU), assumed to be liver lobules and organized in a parallel structure.[7,11] Due to lack of functional measurements for the FSUs, the previous local-damage global-injury models[7,11] neglect function variations of the subunits over the liver volume. The over-simplifications in the models potentially decrease their predictive ability, particularly in the patients in whom local hepatic function has been compromised (due to either underlying diseases, e.g., cirrhosis, or previous liver-directed treatments). A new model that builds upon global and local function of the liver using functional measurements is needed.

Total liver function and local function distributions can be measured quantitatively in individual patients by indocyanine green (ICG) clearance and functional imaging, respectively.[12–18] The ICG clearance test, a well-established overall liver function test, has been used to guide liver resection and RT to avoid post-therapy liver dysfunction.[12,13,18] Portal venous perfusion imaging, quantified from dynamic contrast enhanced (DCE) CT/MRI, is an imaging biomarker for local liver function.[15,16] In this study, we developed a local-and-global function model of the liver based upon ICG clearance and portal venous perfusion imaging data. The model considered individual variations of the organ function as well as the local distribution of function of the subunits. Finally, we explored the utility of the model for investigating individual dose-response of the local function in the liver after irradiation.

Materials and Methods

Patients and RT

Twenty-three patients (6 females and 17 males, age range: 43 to 81 years) receiving RT for intrahepatic cancer were enrolled in an institutional review board-approved, prospective, imaging study (Table 1). As clinically indicated, twelve patients received stereotactic body RT (SBRT) (median dose: 50 Gy, range: 22.8–60 Gy), and the other 11 patients were treated by 3-dimensional conformal RT or intensity modulated RT (median dose: 59 Gy, range: 48–82 Gy), with fractionation as given in Table 1. Treatment was planned on CT scans obtained at the end of normal exhalation. The dose prescription was given to have 10% or less risk for the development of RILD, assessed by a population-based NTCP model,[8] but none of the patients developed RILD.

Table 1.

Patients and Treatment Information

Patient No.	Gender/age (y)	Cancer	pre-RT ICG-R15	post-RT ICG-R15	Total dose (Gy)	Fraction Dose (Gy)
1	M/55	HCC	16.26	30.3	62	2
2	M/65	HCC	23.2	27.53	50	10
3	M/77	Cholangiocarcinoma	8.29	13.2	48	2
4	M/54	HCC	48.1	48.7	50	10
5	F/45	Colorectal metastases	13.4	14	63	3
6	M/62	Anal metastases	11.5	16.6	52.5	2.5
7	M/43	HCC	35	53.18	64	2
8	M/58	Colon metastases	6.72	NA	82	2
9	M/72	Colon metastases	19.79	21.98	75	3
10	M/65	HCC	44.15	44.09	30	10
11	M/80	Neuroendocrine metastases	9.63	21.33	55	2.5
12	F/76	Cholangiocarcinoma	41.83	41.27	70	2
13	M/72	HCC	13	22.31	50	2.5
14	M/58	HCC	38.87	39.46	30	10
15	F/74	Cholangiocarcinoma	9.93	13.81	48.4	2.2
16	F/79	HCC	11.53	14.23	50	10
17	F/51	Rectal meatstases	10.38	NA	55	11
18	M/71	HCC	10.08	11.88	55	11
19	M/56	HCC	27.94	31.98	48.6	11/7.8*
20	M/76	HCC	41.27	45.16	33	11
21	M/81	HCC	51.69	64.73	22.8	7.6
22	F/54	HCC	11.71	13.2	60	12
23	M/60	HCC	13.6	14.2	60	12

R15: ICG retention rate 15 min after administration; HCC: hepatocellular carcinoma; NA: data not available;

^*First three fractions: 11Gy/fraction, remaining: 7.8Gy/fraction

DCE-MRI and ICG Test

DCE-MRI scans were acquired within 2 weeks prior to RT (pre-RT), after delivery of ~60% of the planned dose, and 1 month after completion of RT (post-RT). Within ±2 days of each scan, an ICG clearance test was performed. The retention rate of ICG 15 min after administration (ICG-R15), a ratio of the ICG concentration at 15 min to its initial concentration in the blood, was used as a measurement of overall liver function[13,19,20], with a higher retention rate indicating a worse liver function.

Patients #1–16 had liver DCE-MRI scans on a 3T Philip scanner (Achieva, Philips Healthcare) with a 3D gradient echo (GRE) pulse sequence, and patients #17–23 were scanned on a 3T Siemens scanner (Skyra, Siemens) using a time-resolved angiography sequence with interleaved stochastic trajectories (TWIST). The DCE scans had a total of 60 dynamic volumes in a coronal or oblique-coronal orientation with 2.4 – 3.0 sec per volume. A breath-control paradigm was used for the scans to mitigate respiration motion effects.[21] Hepatic arterial and portal venous perfusion maps were quantified by fitting the DCE data to a dual-input single-compartment model.[22]

Considering that the patients were scanned on two different scanners, we assessed the possible systematic difference of computed liver perfusion[23] between the two scanners using data from pre-RT normal liver tissue regions (the volumes of interest range: 4.5 - 9.8 cc). We found a systematic difference in the normal portal venous perfusion values between the Philips and Siemens scanners (96.1 ± 7.0 and 67.1 ± 4.1 ml/(100g·min), respectively). To overcome this systematic difference, we normalized the portal venous perfusion values to 100 ml/(100g·min) by using 100/96.1 and 100/67.1 for the Philips and Siemens scans, respectively.

Liver Local-and-Global Function Model

Model Description

We adopted the parallel-structure concept used in the local-damage global-injury liver NTCP models [7,11] and assumed that the global function of a liver (P̄) is composed of the functions of all its subunits. Here, we consider the effective volume of subunits contributing to the global function as well as the function variation by allowing the local function probability to vary as a continuous variable. Therefore, we have:

$$\overline{P}={\sum }_{p_{i=0}}^1{\nu }_i{p}_i$$ [1]

where p_i is the probability of function of a subunit (varying between 0 and 1), and v_i is the fraction of the subunits with the function probability between p_i and p_i+Δp. If the minimal physical volume within which the local function is measured, e.g., the voxel size of the functional images, is greater than the physical size of a subunit (lobule), p_i can be considered as the mean probability of subunit function within a voxel. Thus, Eq.1 can be interpreted as a summation of a normalized histogram of p_i over the liver volume.

To model the function probability of a subunit using portal venous perfusion images, there were several issues to be considered. Portal-venous perfusion has been observed to increase locally after partial liver irradiation in low dose regions that are well perfused pre-RT.[16] This phenomenon is most likely due to hemodynamic compensation, which has a limited effect on the overall hepatic function once the local function saturates. In addition, a previous study indicates that local tissue regions with low portal venous perfusion contribute little to the global liver function.[15] Between the two extremes, a monotonic relationship between the portal venous perfusion value and local function probability is expected. Thus, a sigmoid function was selected to model the function probability of the subunit from the portal venous perfusion value (F) in a voxel as:

$$p(F)=\frac{1}{1+(\frac{F_{0.5}}{F})n}$$ [2]

where F_0.5 is the perfusion value corresponding to the function probability of 0.5, and n determines the steepness of the function probability change with perfusion. Substituting Eq.2 into Eq.1 and considering that liver global function only has contributions from the subunits that have local function probabilities greater than a threshold (τ), the global liver function is given by:

$$\overline{P}={\sum }_{i\in (p_i(F)>\tau )}{\nu }_i\frac{1}{1+(\frac{F_{0.5}}{F_i})n}$$ [3]

now ν_i is the liver fractional volume with portal venous perfusion values between F_i and F_i + Δ F_i. The three free parameters (F_0.5, n, τ) in Eq.3 were determined by fitting the model to both the overall liver function and portal venous perfusion data.

Model Fitting

We fitted the liver global function P̄ in Eq.3 to the ICG retention in the blood measured at 15 minutes (ICG-R15), a metric of the overall liver function commonly used by physicians. Previous studies have shown a linear correlation between the mean portal venous perfusion in the liver and the ICG clearance rate.[15,16] We therefore related the liver global function to a logarithm of ICG-R15 (R = log(ICG-R15)) as:

$$R=\alpha \overline{P}(F_{0.5},n,\tau )$$ [4]

where α is a constant. The zero intercept in Eq.4 was set by assuming that 100% of ICG-R15 (i.e., R=0) implied zero liver global function. Using data pairs of perfusion images and ICG-R15 scores, the three parameters were determined by minimizing a sum of squared errors (SSE):

$$E={\sum }_m{(R_m-\alpha {\overline{P}}_m(F_{0.5},n,\tau ))}^2$$ [5]

where m is an index of the data pairs. To minimize E, first, a least-squares solution of slope α was analytically computed as α = Σ_m(R_mP̄)/Σ_mP̄_m², and substituted into Eq.5, resulting in E as a function of parameters (F_0.5,n,τ) only. Then, a grid of parameters that spanned F_0.5 from 10 to 110 ml/(100g·min), n from 1 to 11, and τ from 0 to 0.08 was generated. After that, a nonlinear least squares (NLS) fitting initialized with the parameters of a grid point was performed at each grid point. Finally, the optimal solution of (F_0.5, n, τ) was determined as the minimum of the minima from all grid points. Leave-m-out cross-validations were performed by repeating the model fitting after randomly leaving one dataset out (leave-1-out, 59 times) or leaving 10% of the data out (10-fold, 400 times). Means and standard errors (SEs) of the fitted parameters from the leave-m-out tests were calculated.

Factors affecting the Model

To evaluate whether SBRT vs conventional fractionated RT had an effect on the fitted parameters of the model, the models were re-fitted by dividing the data into the two groups based upon the fraction size (> vs < 6 Gy) that a patient received. Similarly, whether tumor types affected the fitted parameters was evaluated by fitting the model using the data from the patients had HCC vs other non-HCC tumors. The estimated parameters of (F_0.5,n,τ) and the related 95% Confidence Intervals (CI) were compared between the models fitted by all the data and subgroup data.

Results

Liver Local-and-Global Function Model

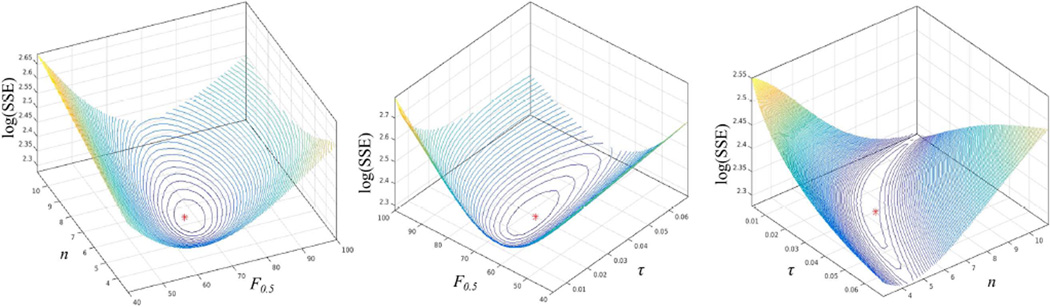
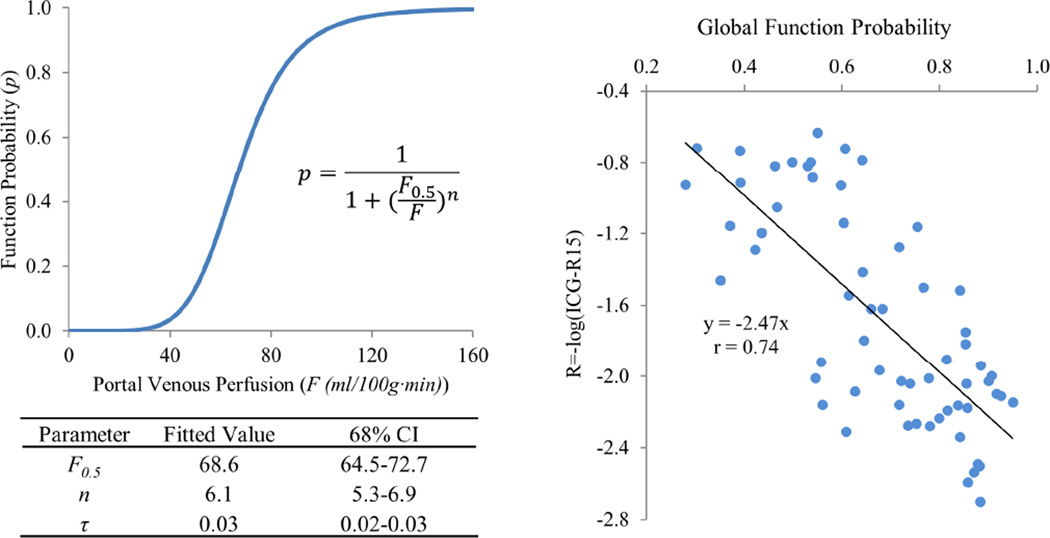
The local-and-global function model of the liver was fitted to 59 pairs of ICG-R15 and liver perfusion image datasets from the 23 patients. The best fit in the parameter space was found, as shown by iso-SSE curves of estimates illustrated in Fig. 1. The best fitted parameters were F_0.5 = 68.6 ml/(100g·min) (68% CI: 64.5–72.7), n = 6.1 (5.3–6.9), and τ = 0.03 (0.02–0.03). Note that, denotes the function probability threshold, at which the subunits have meaningful contributions to the liver global function, and 0.03 of the function probability is corresponding to a portal venous perfusion value of 38 ml/(100g·min), which is consistent with the previous finding.[15] The local function probability is plotted as a function of portal venous perfusion with the best fitted parameters of (F_0.5, n, τ) in Fig. 2. The model shows that a subunit has 0.5 of function probability at a perfusion value of 68.6 ml/(100g·min). Also, at a perfusion value of 98 ml/(100g·min) or greater, the function probability is 0.9 and approaching saturation, with limited room to further increase the function probability. The global liver function values as derived from the probabilities of the local function of the subunits, with the best fitted parameters, and as measured by ICG scores were significantly correlated (r=0.74, P<.000001), as shown in Fig. 2.

Figure 1.

Iso-SSE surfaces on planes of τ=0.03 (left), n=6.4 (middle), and F_0.5=67.4 ml/(100g·min) (right) in the space of parameters of (F_0.5, n, τ). *: the best fitting parameters. SSE: sum of squared errors.

Figure 2.

(Left) The local function probability as a function of portal venous perfusion value with the best fitted parameters; (Right) scatter plot of the global liver functions derived from the local function probabilities of the subunits and measured by log(ICG-R15). The solid line represents the fitted line with a slope of −2.47 and r=0.74.

The leave-1-out and 10-fold cross validations resulted in respective 6.1 ± 0.1 (mean ± SE) and 6.9 ± 0.1 for n, 67.7 ± 0.2 and 68.2 ± 0.2 ml/(100g·min) for F_0.5, and same mean of 0.03 ± 0.001 for τ, suggesting the model is stable.

Effects of Fraction Dose and Tumor Type

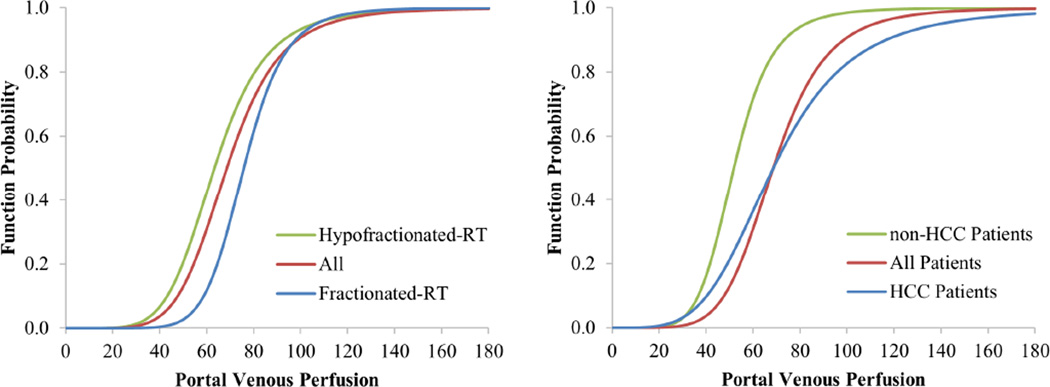
The models were fitted by 30 and 29 paired datasets of ICG-R15 and liver perfusion images from 12 and 11 patients treated by SBRT and fractionated RT, respectively. There were no significant differences in the fitted parameters between the patient subgroups, see Table 2 and Figure 4a.

Table 2.

The local-and-global function probability model with 95% Confident Interval (95% CI) from different patient groups

	All Patients	Fractionated-RT	Hypofractionated-RT	non-HCC	HCC
F0.5	68.6 (60.3–76.8)	75.8 (62.7–88.9)	63.3 (49.7–76.9)	51.9 (41.1–62.6)	68.6 (54.1–83.1)
n	6.1 (4.5–7.7)	8.6 (6.1–11.2)	5.8 (3.5–8.0)	6.4 (4.4–8.4)	4.2 (2.4–6.0)
τ	0.03 (0.02–0.04)	0.02 (0.02–0.03)	0.02 (0.01–0.03)	0.03 (0.01–0.05)	0.08 (0.03–0.12)

Figure 4.

The local and global liver function models fitted to the data divided based upon fractionated vs hypofractionated RT (left panel), and the data divided based upon the patients who had HCC vs non-HCC tumors (right panel). Red curves represent the model fitted to all the data.

The models were fitted by 38 and 21 paired datasets of ICG-R15 and liver perfusion images from 14 and 9 patients with HCC and non-HCC tumors, respectively. There were no significant differences of the fitted parameters between the patient subgroups (Tale 2 and Figure 4b). F_0.5 and n in the HCC subgroup, as respective 69 ml/(100g·min) and 4.2, were slightly, but not significantly (p>0.05), greater than respective fitted parameters in the non-HCC subgroup, suggesting the same amount of portal venous perfusion translating into greater local function probability in the non-HCC subgroup than the HCC subgroup, which could be due to the cirrhotic liver in the latter subgroup.

Discussion

In this study, we developed a local-and-global model of liver function by incorporating local and organ function measurements of the patients. This model considers both the volume effect and function distributions of the subunits. This study models the organ function as a continuous variable, which differs from considering only the complication frequency in the previous NTCP models.[7,8,25] Our model provides a better means to understand the dose-response of the local function post-RT, particularly in the situation with the pre-RT local function compromised by either previous liver-directed therapy or cirrhosis. This model has the potential to be a tool to support adaptive radiation therapy and dose rearrangement for individualized intrahepatic cancer treatment.

In our model, we adopt the basic concepts of the local-damage organ-injury NTCP models in parallel-structured organs, such as lung and liver.[7,11,26] In the previous models, the functional subunits are assumed to be normal before RT, and the complication occurs after RT only if the number of damaged “normal” functional subunits is large enough to break the limit of the organ functional reserve. The assumption of “normal” functional subunits before RT does not hold in the patients who have either a previous liver-directed therapy or a underlying disease, e.g., cirrhosis,[6,9,10,15–17,25] who are seen more often in the clinic today. With advances in physiological and functional imaging techniques, it is feasible to map regional function distributions in the individual livers, thereby incorporating them in the model. Also, we model the organ function by incorporating an overall liver function measure from the individual patients, rather than simply using the binary outcome of complication and no-complication. Thus, the development and validation of this model does not depend upon the number of complications in the data, which is often a limitation for the development of a model.

This study derived the liver local function probabilities from portal venous perfusion images. Previous studies have demonstrated that portal venous perfusion is a biomarker of regional liver function after irradiation,[15,16] and indicated that there is an associative relationship between the two. In addition, a previous study suggests that the region with low portal venous perfusion may have little contribution to the global function.[15] Post-RT hyperperfusion in the pre-RT well-perfused regions that received low doses (~10 Gy or less) has been observed,[16] for which hemodynamic compensation is most likely the primary cause rather than an increase in local function. This is supported by the observation of no meaningful increase in hepatic extraction fraction (HEF) in the liver regions that received low doses post-RT compared to pre-RT, except a portal-vein thrombosis case in which the post-RT HEF increase was associated with a globally suppressed HEF pre-RT.[17] Therefore, we elect a sigmoid function to phenomenologically describe the behavior of the local function probability as a function of portal venous perfusion.

In this study, we evaluated whether the liver with HCC had a different conversion curve from portal venous perfusion to the local function probability, possibly affected by cirrhotic liver or other mechanisms, compared to non-HCC tumors. Although the fitted parameters have overlaps between 95% confidence intervals of the two subgroups, it seems that the same amount of portal venous perfusion in the liver with HCC is translated into local function probability less than the one with other tumors. This suggests that the liver for the patients with HCC is less functional than those with non-HCC tumors. Also, we divided the patients into two subgroups based upon the fractionated and hypofractioned RT to fit the local function probability, which yields very similar results. This does not mean that the dose-response of the local function probability is the same for fractionated and hypofractioned RT, which requires to correct the fraction size of the liver dose distribution carefully.[36] Nevertheless, the findings in this study are needed to be further validated in a larger sample in the future.

The function models for all patients and the patient subgroups are determined by a NLS fitting initialized with a grid-search scheme. Conventional NLS fitting finds only a local minimum from a starting point. To obtain a global solution, we created a grid of parameters that covered the space of possible parameter values, and performed NLS fitting at each grid point to determine a minimum over the parameter space. The NLS cost function Eq.[5] is non-differentiable due to the threshold behavior of parameter τ. Therefore, we used the Nelder-Mead Simplex minimization instead of a gradient-based method for the NLS fitting.

In this study, we tested the systematic difference in the normal portal venous perfusion values from different scanners. The data collected on different scanners have the potential to increase variations and reduce statistical power of the study.[23] In this study, each patient was scanned on the same scanner. Furthermore, standardization of quantitative perfusion is a task to integrate the quantitative data from multi-centers or even in a single institute when the imaging technology is evolving over time. We found that standardization of the perfusion data improved the correlation result in Fig. 2 by approximately 8% compared to that without standardization.[37]

Our approach is different from the conventional NTCP model. The NTCP model is based upon fitting the frequency of RILD events in relating to mean live doses. Our model is based upon measured global and local liver functions. Two models have complementary contributions. The NTCP model can estimate the complication-risk based upon the population data with a single dosimentric parameter of mean liver dose. The liver functional model is based upon the individual liver functional measurements, locally and globally. Individual liver functional measures can provide information for precision medicine. It is also worthwhile to point out that the patients who come to radiation oncology clinic toady either have previous liver-directed treatments or will receive repeated treatments. The clinical question becomes whether we can maximize liver function reserves in the patients after this treatment and so have adequate hepatic function for the future treatments. This requires liver function measurements, both locally and globally. Meanwhile, redistributing high doses to poorly-functional regions has the potential to increase doses to target volume without increasing the risk for complication. The function probability threshold τ could be chosen to define the poorly-functional “expendable” regions. Furthermore, the local function probability can be directly used to categorize the local function-risk, and thereby spatially weight dose planning.[38,39]

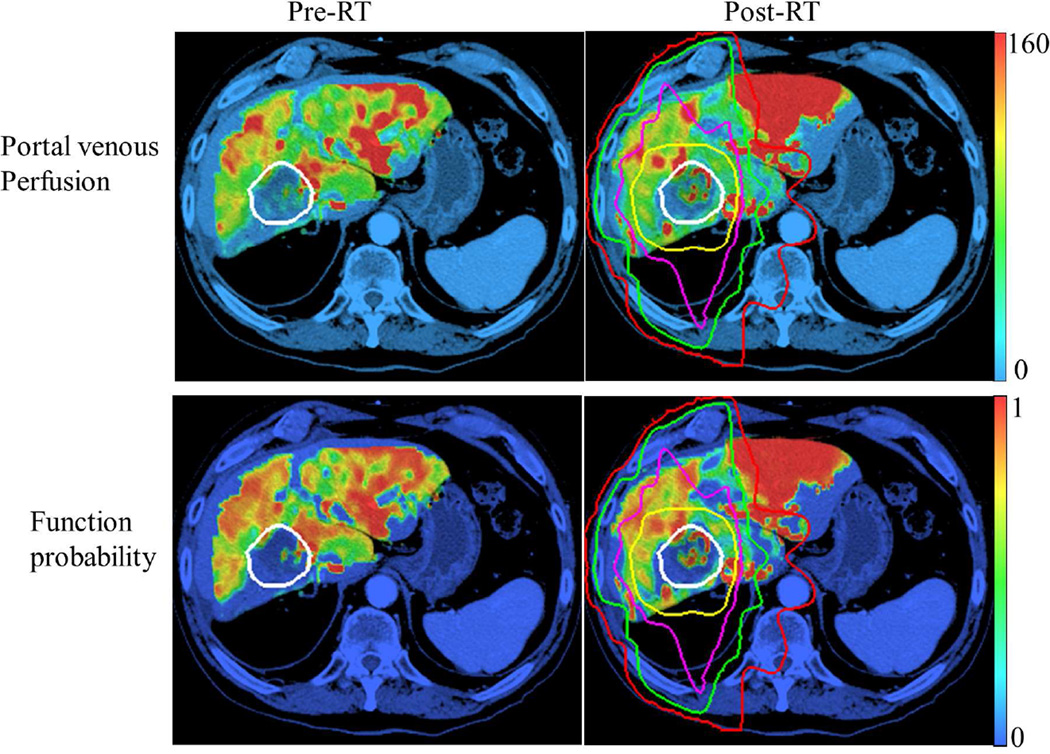
Figure 3.

Portal venous perfusion (top) and local function probability maps (bottom) at pre-RT (left column) and one month post-RT (right column). Perfusion unit: ml/(100g·min). White contour: gross tumor volume; Red, green, magenta and yellow contours: Isodose curves of 10, 20, 40 and 60 Gy, respectively.

Summary.

A local and global liver function model that accounts for regional and global function variations was developed. Applying this model, individual dose-response of the local function probability can be assessed, and could facilitate adaptive re-planning for individual patients.