The importance of distribution-choice in modeling substance use data: a comparison of negative binomial, beta binomial, and zero-inflated distributions

Abstract

Background

It is important to correctly understand the associations among addiction to multiple drugs and between co-occurring substance use and psychiatric disorders. Substance-specific outcomes (e.g. number of days used cannabis) have distributional characteristics which range widely depending on the substance and the sample being evaluated.

Objectives

We recommend a four-part strategy for determining the appropriate distribution for modeling substance use data. We demonstrate this strategy by comparing the model fit and resulting inferences from applying four different distributions to model use of substances that range greatly in the prevalence and frequency of their use.

Methods

Using timeline followback (TLFB) data from a previously-published study, we used negative binomial, beta-binomial and their zero-inflated counterparts to model proportion of days during treatment of cannabis, cigarettes, alcohol, and opioid use. The fit for each distribution was evaluated with statistical model selection criteria, visual plots and a comparison of the resulting inferences.

Results

We demonstrate the feasibility and utility of modeling each substance individually and show that no single distribution provides the best fit for all substances. Inferences regarding use of each substance and associations with important clinical variables were not consistent across models and differed by substance.

Conclusion

Thus, the distribution chosen for modeling substance use must be carefully selected and evaluated because it may impact the resulting conclusions. Furthermore, the common procedure of aggregating use across different substances may not be ideal.

1. INTRODUCTION

Of great importance in substance abuse research is to better understand the associations among addiction to different drugs and between co-occurring substance use and psychiatric disorders. Abundant substance use data exist and are currently being collected via Timeline Followback (TLFB), a semi-structured interview that retrospectively reconstructs daily use of each drug for the period of interest(1). Typical analyses of TLFB data often have one or more of the following problems.

Aggregating use across drugs

Studies of polysubstance users, such as adolescents in treatment, have collected daily use data during the period of interest (e.g., treatment) separately for both commonly used substances (e.g., cigarettes, cannabis) and for substances that are used by some participants but not used by a substantial portion of the sample (e.g., cocaine, opioids). Much of this detailed information is often ignored during analysis. Use information is typically either reported for only the drugs that are frequently and commonly used in the subset of regular users (e.g., cannabis and cigarettes)(2–4); or use information is collapsed across drugs into summary scores like number of days of use of any substance(5–9).

The summary score or “aggregate” outcome variable that counts days of use of any drug is dominated by the most commonly and most frequently used substance, obscuring potential changes in use of less common/frequent substances. By summarizing over various drugs, any information to be gained on rates or patterns of co-occurrence (poly-substance use) is lost. Moreover, different substances may have distinctive use patterns and it is possible that treatment and other variables of interest do not have similar associations with use of each drug.

Variations in length of observation/report

Commonly, substance related studies have incomplete TLFB data due to early participant drop-out, leading to variability in the number of TLFB days assessed. Previous solutions to this issue include excluding subjects with incomplete TLFB reports(10), imputation(2, 4) or modifying outcome variables depending on number of TLFB days assessed(6). Each of these solutions requires potentially inaccurate assumptions.

Non-normal distributions

Daily use TLFB data consist of either binary (yes/no) responses or counts of drug used (e.g., number of drinks per day) and common outcome variables are aggregates such as sum or percent of days used during treatment. There are natural limits imposed on these variables, for example the information consists of non-negative integer values. Data of this type are usually not normally distributed and the distributional characteristics of specific substances can vary widely. In general, the Poisson distribution is considered appropriate for unrestricted count data. For the case where the counts are restricted (e.g., there is a maximum on the counts due to observation time such as length of TLFB report) a binomial distribution should be considered. However, both the Poisson and binomial distributions make strong assumptions about the relationship between the mean and variance that are often violated by overdispersed clinical data, i.e., have greater variability than that assumed by these distributions. Extensions that incorporate overdispersion include the negative binomial and beta-binomial distributions. Often in clinical research, a larger number of zero counts are observed over what is expected by the chosen distribution. In this circumstance, a zero-inflated distribution should be considered.

Aggregates of use across drugs (e.g., number/percent days of drug use) have been reportedly non-normal(5, 6). More recent studies have attempted to address non-normally distributed data by applying the Poisson or the more general, zero-inflated Poisson distributions(11–15). Although this represents a step forward, the Poisson distribution has the aforementioned limiting assumptions. We recommend a four-part strategy to improve guidance around modeling these substance outcomes 1) considering the subset of distributions that are theoretically appropriate based on knowledge of the outcome’s characteristics, 2) visually inspecting the outcome data (i.e., histogram of percentage of subjects with each use-frequency) and comparing the fit of potential distributions to the outcome data using 3) statistical model selection criteria (described below) and 4) visual confirmation, by superimposing the model based on each distribution onto the histogram graphically.

Here, we discuss four theoretically appropriate distributions that one could use to model substances individually across the period of interest. We consider distributions which directly account for variation in the number of days with TLFB report and for a larger than expected proportion of zero values which may better characterize use of less common substances. We compare the model fit and the inferences from applying those distributions to four substances (cannabis, cigarettes, alcohol, and opioids) that range in the prevalence and frequency of their use to a previously-published sample of adolescents in treatment for ADHD and substance use(5). The application of the proposed four-part strategy is demonstrated and the importance of model selection criteria and visual inspection of plots of each distribution are exhibited. A brief review of the example dataset and statistical methods considered will be presented in sections 2 and 3, respectively. Section 4 contains the application of these methods to the example and section 5 provides a discussion of the findings.

2. EXAMPLE DATASET

Data to demonstrate this modelling strategy and results come from a multisite pharmacotherapy trial in which 303 adolescents with ADHD and at least one non-tobacco substance use disorder were randomized to a 16-week trial comparing OROS-MPH to placebo(5). Participants in both groups received cognitive behavioral therapy as standardized substance treatment. Self-reports of daily drug use were collected at weekly visits with Miller and Del Boca’s version of TLFB(16). Thirteen drug categories were assessed. Previously published study results evaluated counts of days used non-tobacco drugs in 28 day periods with linear mixed models and showed significant decreases in substance use, but no difference between groups(5). The authors acknowledge two problems with this analysis. First, the outcome did not satisfy the normality requirements assumed by the analysis. Second, TLFB reports were incomplete in over 50% of subjects due to study non-completion. Consequently, multiple additional analyses were necessary to confirm the reported results(5).

Using data from Riggs et al (5), we separately modeled use of: (1) cannabis, which is the most commonly and frequently used in this example, (2) cigarettes and (3) alcohol, which are also commonly and frequently used and conjectured associated with cannabis, and (4) opioid use, which is much rarer but has been increasingly used in adolescents. As described below, we evaluated model fit of 4 different distributions and compared the inferences that resulted from each model regarding associations between use and clinical characteristics.

3. STATISTICAL MODELS

First, we consider the subset of distributions that are theoretically appropriate based on knowledge of the outcome’s characteristics. These outcomes are counts of days of use of each drug and have an upper limit (total number of days of each subject’s TLFB report).

Beta-Binomial (BB) and Negative Binomial (NB) Distributions

Restricted count data which are bounded by the total number of days observed (the variability in observation length) can be described using a binomial distribution. Estimation using the binomial distribution can be tedious, however, and is therefore often approximated with the Poisson distribution. The Poisson distribution can be used to model restricted counts by including the total observation length as an offset. Here, the offset is the log transformed variable of the total number of days of TLFB report constrained such that no parameter estimate is obtained for this term, i.e., the parameter estimate is constrained to equal 1. Inclusion of an offset transforms each outcome from a count into a proportion of days of use and accounts for differential days of TLFB report assessed for subjects who left treatment early. However, as stated before, both binomial and Poisson distributions make strong assumptions about the relationship between the mean and variance that clinical data often violate.

Overdispersion is common and occurs when patient variability results in data variance which is greater than that assumed by the distribution. Unaccounted for, overdispersion will result in incorrect predictions and will tend to overestimate standard errors increasing the type I error rate(17). Overdispersion can be addressed and tested by using a mixture of distributions in which the probability is not fixed but random and is generated from another distribution. These mixture distributions have potential for modeling substance use data well. Here, we evaluate the beta-binomial (beta-binomial mixture) and the negative binomial (gamma-Poisson mixture)(18) distributions.

Zero-Inflated Distributions

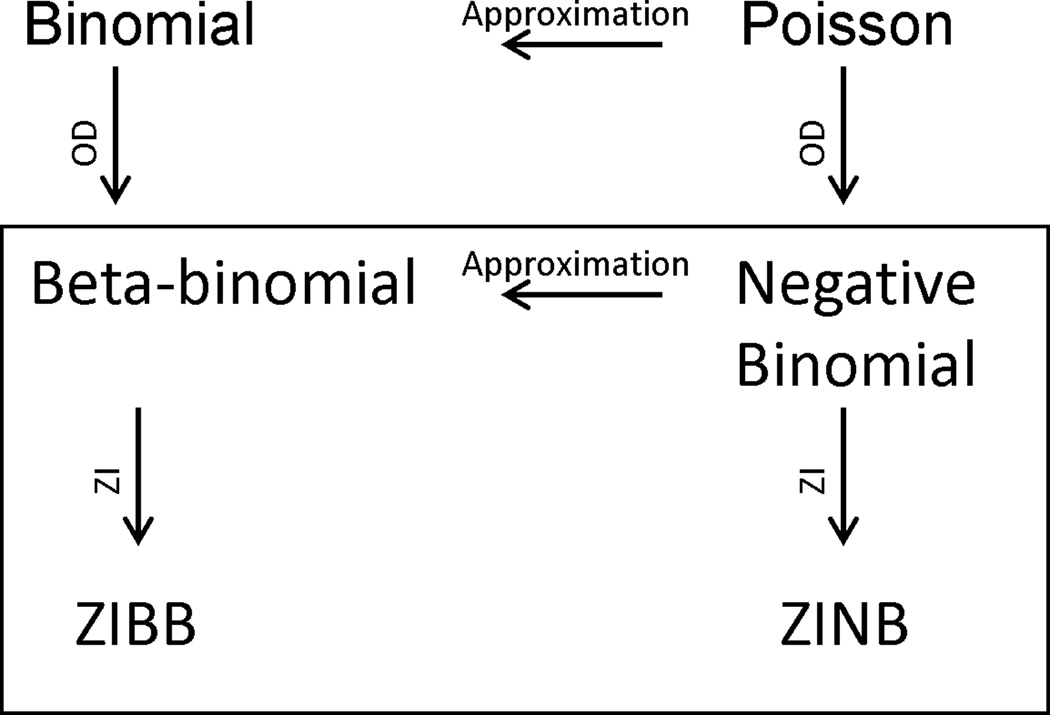
In clinical research, count data with a large proportion of zeros are routinely encountered(17, 19, 20). Substances of interest are characterized by different frequencies of use but many typically demonstrate a large number of patients reporting zero days of use during treatment. These zero counts are thought to occur for two reasons: 1) the subject does not use that particular drug (true zero) or 2) the subject does use the drug but did not report use during the time of observation (e.g., if the observation time was extended the subject may report use). To avoid problems from these two types of zeros, substance use research has commonly either restricted samples to those who use a substance of interest (e.g., evaluating cannabis use in those with cannabis use disorders(2, 21); evaluating alcohol use in alcoholics(10)) or has aggregated use across substances(5, 6). Alternatively, a zero-inflated (ZI) model is attractive in assuming that zero counts result from a mixture of two distributions, one where subjects always produce zero counts (non-users, where no variation in the predictor variables will change the expected number of days of drug use) and one where subjects who do use the drug produce zero counts (users who did not report using during the study period). The likelihood of being from either population (user or non-user) is estimated with a zero-inflation probability component, while the counts in the second population of those who likely use the substance are modeled with an ordinary count distribution such as the binomial or Poisson(22) or here, the negative binomial and beta-binomial distributions. Zero-inflated negative binomial (ZINB) and zero-inflated beta-binomial (ZIBB) distributions were therefore also considered as potential theoretically appropriate distributions for use of each substance. Figure 1 diagrams interrelationships among these distributions, i.e. how the negative binomial and beta-binomial distributions handle overdispersion in binomial and Poisson models, respectively, and how additional zero-inflation can be modeled with the corresponding ZINB and ZIBB models. The probability distribution functions along with more specific information for these distributions are included in the appendix.

Figure 1.

A graphical representation of the relationship between the distributions discussed, those inside the box are the distributions used in the analyses. OD: overdispersion; ZI: zero-inflation; NB: negative binomial; BB: beta-binomial.

Model Fitting and Comparisons

The four distributions were fit to use of each substance with SAS NLMIXED version 9.3 software (SAS Institute Inc., Cary, NC, 2011). Although NLMIXED is designed to handle repeated measures, we modeled use across the entire treatment period for each substance, i.e. one observation of proportion of days of drug use during treatment per subject. We chose NLMIXED because no other single SAS routine could fit all four distributions, which NLMIXED accomplishes by allowing a user-specified likelihood. Other SAS procedures such as COUNTREG and GENMOD can estimate the negative binomial and ZINB models, are easier to implement, and therefore recommended if the beta-binomial model is not a contender.

The model for each substance (e.g., cannabis) included the following as predictor variables: ADHD severity score prior to treatment(23), proportion of days of non-tobacco substance use in the 28 days prior to treatment, age, conduct disorder diagnosis (yes, no), medication group (OROS-MPH, Placebo), and the proportion of days of use of the other three substances during treatment (e.g., cigarettes, alcohol, opioids). Zero-inflated models can include the same or different covariates in their ZI-probability (predicting non-user) and count (predicting frequency of use) components; here, we included all predictors described above in both components. An offset was specified in the negative binomial models to account for differential days of use assessed so that all models were similarly evaluating proportion of days of use. We used a standard model selection criterion, Akaike Information Criterion (AIC). AIC is a likelihood statistic that compensates for artificial model improvement that may occur from including additional predictor variables with a penalty for the number of parameters in the model; smaller values indicate better model fit among competitors(24). When NLMIXED identified problems during the attempted application of a distribution to an outcome (e.g., warnings, errors, failure to converge on a solution), the corresponding models were excluded from the results. Supplementary material contains the SAS code.

4. RESULTS

Table 1 describes the median and range for each variable or alternatively, the number and percent with the characteristic on the 297 subjects with TLFB data. Outcome data characteristics were representative of those likely to be encountered in substance use data from adolescents in treatment (Figure 2). Cannabis and cigarettes had a large percentage of subjects who reported using and who used more days. A large percentage of patients reported not using opioids at any time during the study. Although more commonly used than opioids, alcohol also had a large percentage of patients with no use during the study.

Table 1.

Sample Characteristics in 297 Adolescent Patients

Characteristic		Median (Range) or Percent % (n)
Age in years		17 (13 – 19)
Male		79% (n=234)
ADHD severity score prior to treatment		39 (14 – 54)
Conduct Disorder		21% (n=96)
Randomized to OROS-MPHmedication		50% (n=149)
Pre-treatment substance use(proportion of days non-tobacco drug use in month prior to treatment)		0.46 (0.0 –1.00)
Days in treatment (by TLFB report)		112 (7 – 112)
Substances (Proportion of days of use during treatment)
Opioid		0.0 (0.0 – 0.28)
Alcohol		0.03 (0.0 – 0.90)
Cannabis		0.19 (0.0 – 1.00)
Cigarettes		0.63 (0.0 – 1.00)

Figure 2.

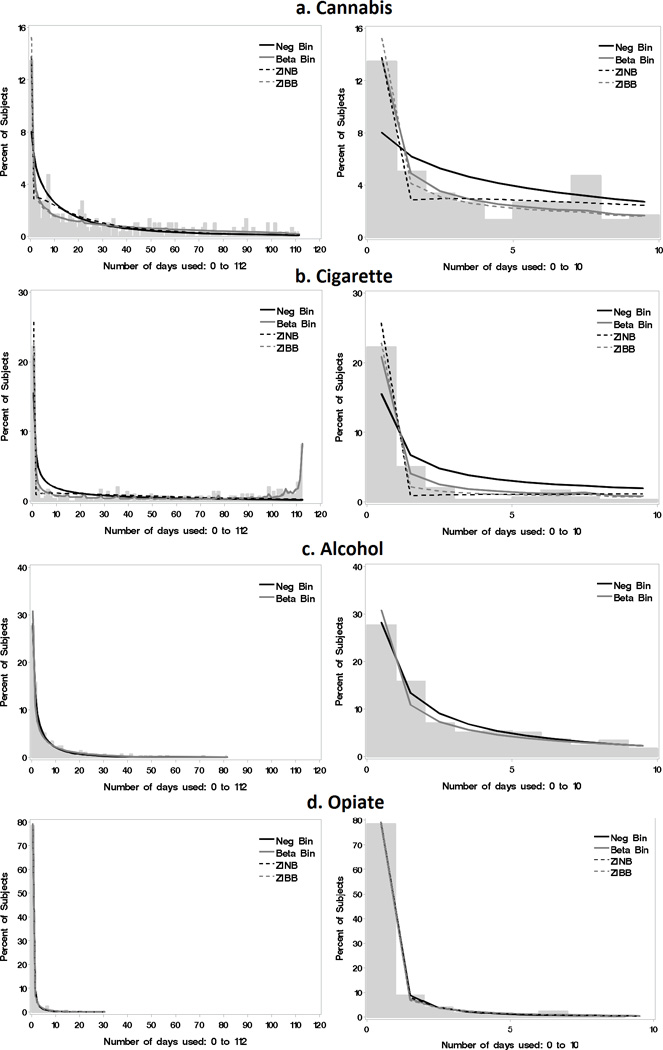
A graphical comparison of the model fits overlaid over histograms of percent of subjects using each number of days during treatment, illustrating the empirical probability distribution for Cannabis (a), Cigarettes (b), Alcohol (c) and Opioids (d). The plots on the left display the entire range of data while those on the right better display the smaller counts from 0 to 10 days of use.

Because they utilize different link functions, regression coefficient estimates from negative binomial (log link) and beta-binomial (logit link) models have different interpretations when exponentiated. For each variable in the negative binomial models, the log of the expected proportion of days of drug use (e.g. cannabis) changes by the amount of the regression coefficient estimate for each unit increase in the corresponding predictor (e.g. age), assuming other variables are held constant. For each variable in the beta-binomial models, the exponentiated regression coefficient estimate provides an adjusted odds ratio (OR) for a one unit increase of each predictor variable in regards to the proportion of days of drug use assuming other variables are held constant. Parameter estimates from all models are reported in the supplementary material.

Based on AIC (Table 2), no single model provided the best fit for all substances. The overdispersion parameter was significant in all models, indicating that a simpler Poisson or binomial model for these data would be inadequate. In modeling use of each substance, inferences regarding associations with other clinical variables changed depending on the distribution specified.

Table 2.

Model Selection Based on AIC Criterion

		Cannabis	Cigarettes	Alcohol	Opioids
AIC (smaller is better)	Negative Binomial	2448.8	2768.2	1647.3	565.1
	Beta Binomial	2329.1	2078.5	1664.1	564.8
	Zero-Inflated Negative Binomial	2412.6	2650.0	*	545.9
	Zero-Inflated Beta-Binomial	2328.4	2077.1	*	559.8

Models with AIC values within 2 units of the lowest AIC are evaluated further for model selection

^*Excluded models

Zero-inflated models have an additional set of parameters corresponding to each predictor that estimate the likelihood of being a non-user of the dependent variable while holding the other variables constant. The need for the added complexity of a ZI-model could be indicated by a smaller AIC or if visual comparison of model fit shows that the proportion of estimated zeros from a simpler model is lower than the observed proportion of zero counts. The preferred model and corresponding results for each substance are described next and compared with conflicting inferences that would result from selecting alternative models.

Cannabis: Beta-Binomial

Based on Jones’ (25) recommendation that models within 2 units of the lowest AIC be considered competitors for selection, both the beta-binomial and the ZIBB were further investigated for cannabis use (Table 2). Visual inspection of model fit (Figure 2a), showed that the beta-binomial better captured the counts represented by the observed distribution compared to the ZIBB model; furthermore, no variables in the ZI-probability component of the ZIBB model were significant. Therefore, the beta-binomial model was chosen. For this selected model, significant associations with cannabis use were as follows: a negative parameter estimate for ADHD score indicated each one unit increase in ADHD severity at baseline was associated with a lower proportion of days of cannabis use (OR=0.97; p <0.01). Cannabis use was also associated with having conduct disorder (OR=1.5, p <0.01), proportion of days of non-tobacco substance use before treatment (OR=7.7, p <0.01) and with co-occurring use of alcohol (OR=3.4, p=0.04) and cigarettes (OR=1.6, p <0.01).

For comparison, the negative binomial underestimated the percentage of subjects with zero counts and overestimated the percentage with smaller non-zero counts (Figure 2a). Had this negative binomial or the ZI-models been selected instead of the better-fitting beta-binomial model, the association between concurrent cannabis and alcohol use would have been identified as non-significant (Figure 3).

Figure 3.

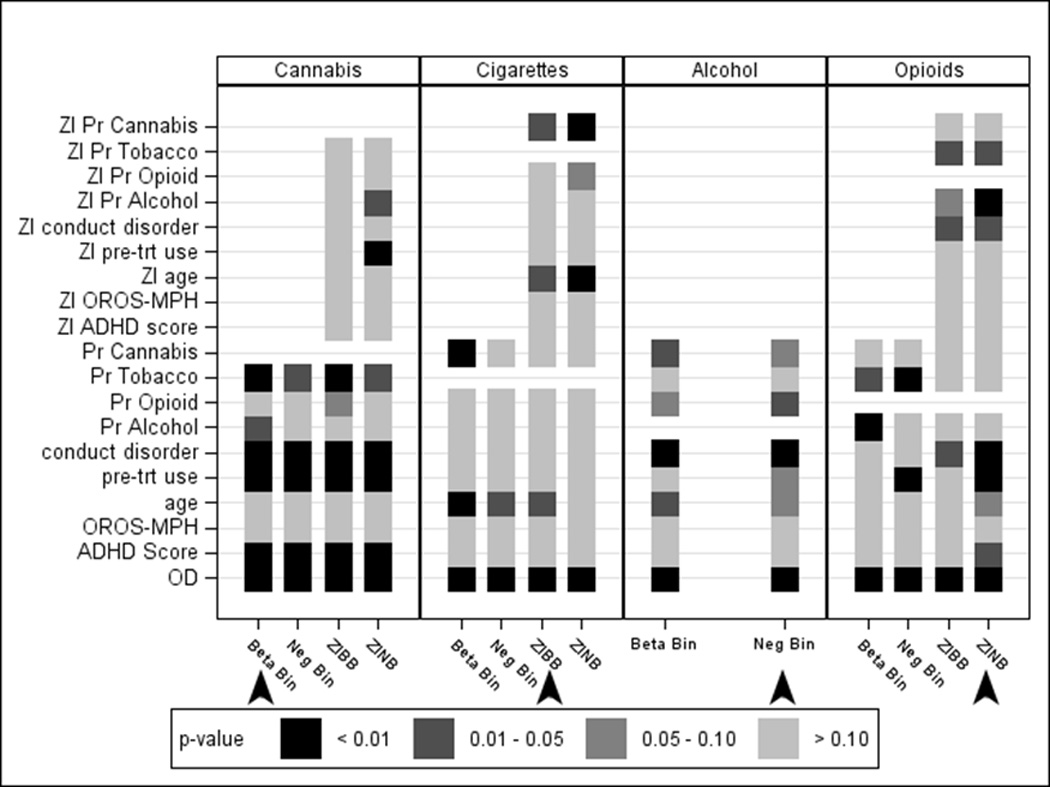
Significance (p-values) for each variable in each model for proportion of days of cannabis, cigarettes, alcohol and opioid use, illustrating that inferences regarding the predictors of use change depending on the model. Arrows indicate the best-fitting model for each substance. Variables with the ZI prefix correspond to variables included in the zero-inflation probability component of the zero-inflated models predicting non-users; OD = over dispersion parameter; Pr = proportion of days of use.

Cigarettes: Zero-Inflated Beta-Binomial (ZIBB)

The AIC values indicated that both beta-binomial and ZIBB models were competitors for modeling cigarette use (Table 2). The histogram was U-shaped with a concentration of observations at the boundaries corresponding to no cigarette use and near daily use. Both the beta-binomial and ZIBB models captured this second peak (Figure 2b) but further inspection of the model fit indicated that the ZIBB better estimated the number of zero and smaller counts and was therefore selected as the best fitting model for cigarette use. Significant associations with cigarette use are first described for those variables that predicted being a nonsmoker (ZI-probability component) and then for those variables that predicted proportion of days of cigarette use in those who are predicted to be smokers (beta-binomial count component). The distribution of predicted probabilities for being a nonsmoker based on the independent variables in the ZI-probability component for the 297 subjects showed a decreasing trend (Figure 4), with the majority of subjects at the lower probabilities (likely to be smokers). Two variables were significantly negatively associated with predicted probabilities for being a nonsmoker, age (OR=0.66, p=0.03) and cannabis use (OR=0.08, p=0.02). In other words, being older and increased proportion of days of cannabis use were associated with increased probability of being a smoker.

Figure 4.

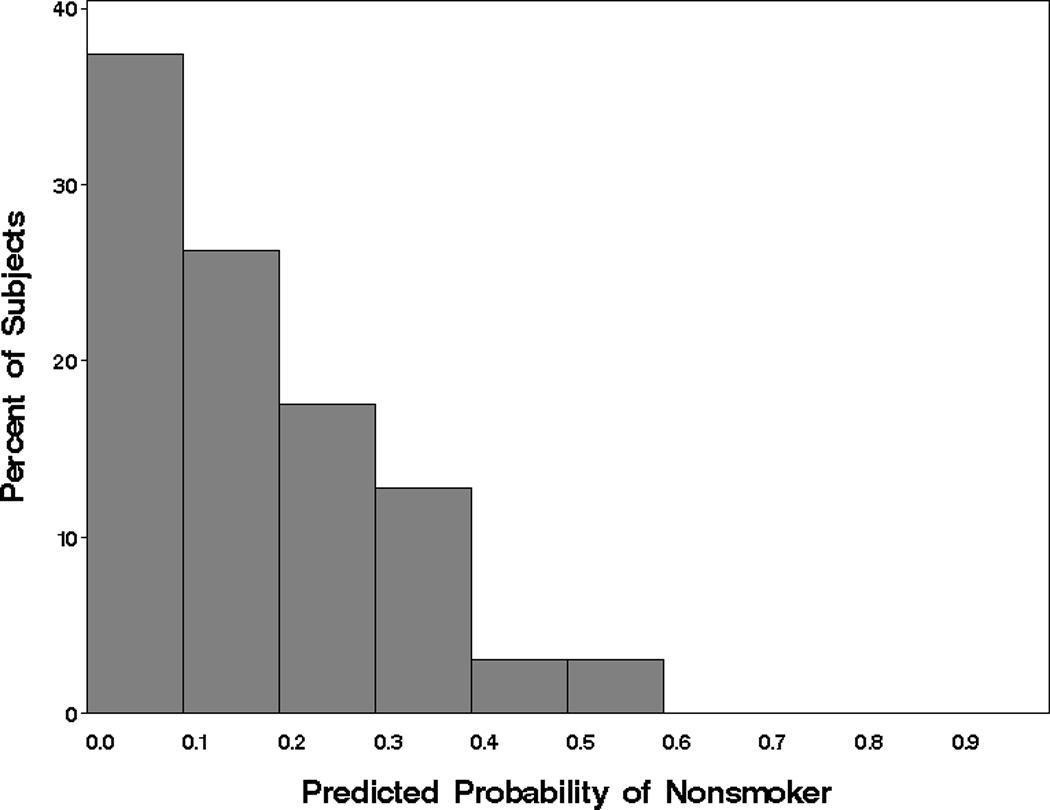
Distribution of the predicted zero-inflation probabilities for cigarette use from ZIBB model. Smaller probabilities indicate a subject that is more likely a smoker and larger probabilities indicate a subject that is more likely a non-smoker.

A one-year increase in age at baseline (OR=1.2, p <0.01) was associated with increased proportion of days of cigarette use during treatment in those who are predicted to be smokers. All other predictors, including variables describing concurrent use of other drugs during treatment (alcohol, cannabis, opioids) were not significant in the count component of the ZIBB. Thus, proportion of days of cannabis use is informative for identifying smokers versus nonsmokers, but not for determining cigarette use among expected smokers.

Figure 2b (right panel) shows that the beta-binomial and negative binomial models under-estimated the percentage of subjects with zero counts of days used and over-estimated the percentage in the lower counts. Whereas, the ZINB model over-estimated the percentage of subjects with zero counts and under-estimated the percentage in the lower counts. Additionally, both the negative binomial and the ZINB were unable to capture the second peak corresponding to near daily use. Had the ZINB model been selected, the association between cigarette use and age would have been identified as non-significant (Figure 3).

Alcohol: Negative Binomial

The negative binomial provided the best fit for proportion of days of alcohol use by AIC (Table 2) and by visual inspection of model fit (Figure 2c). A one year increase in age at baseline was associated with 1.2 times higher alcohol use (p=0.05) and having conduct disorder was associated with 1.8 times higher alcohol use (p <0.01). An increase of 10% in the proportion of days of opioid use corresponded to 2.1 times higher alcohol use (p=0.03).

Visual inspection indicated that zeros were adequately captured with both the beta-binomial and negative binomial models. Therefore, the added complexity of the ZI-models attempted to force a component that was not present, resulting in no solution as indicated in Table 2. In fact, the beta-binomial distribution overestimated the percentage of subjects with zero days of use (Figure 2c). Had this beta-binomial model been selected, the association between concurrent alcohol and opioid use would have been identified as non-significant (Figure 3).

Opioid: Zero-inflated Negative Binomial (ZINB)

Visual inspection suggested that the four models describe the proportion of days of opioid use equally (Figure 2d) but the ZINB model provided the best fit by AIC (Table 2). In this selected model, significant associations are first described for those variables that predicted being a non-opioid user (ZI-probability component) and then for those variables that predicted proportion of days of opioid use in those who are predicted to be users (count component). The distribution of predicted probabilities for being a non-user based on the independent variables in the ZI-probability component for the 297 subjects showed multiple peaks (Figure 5), one at the lower probabilities (patients likely to be users) and a second at the higher probabilities (patients not likely to be users). Three variables were significantly negatively associated with predicted probabilities for being a non-user, conduct disorder (OR=0.02, p=0.02), alcohol use (OR <0.01, p=0.01) and cigarette use (OR=0.06, p=0.01). In other words, having conduct disorder and increased proportions of days of alcohol and cigarette use were all associated with increased probability of being an opioid user.

Figure 5.

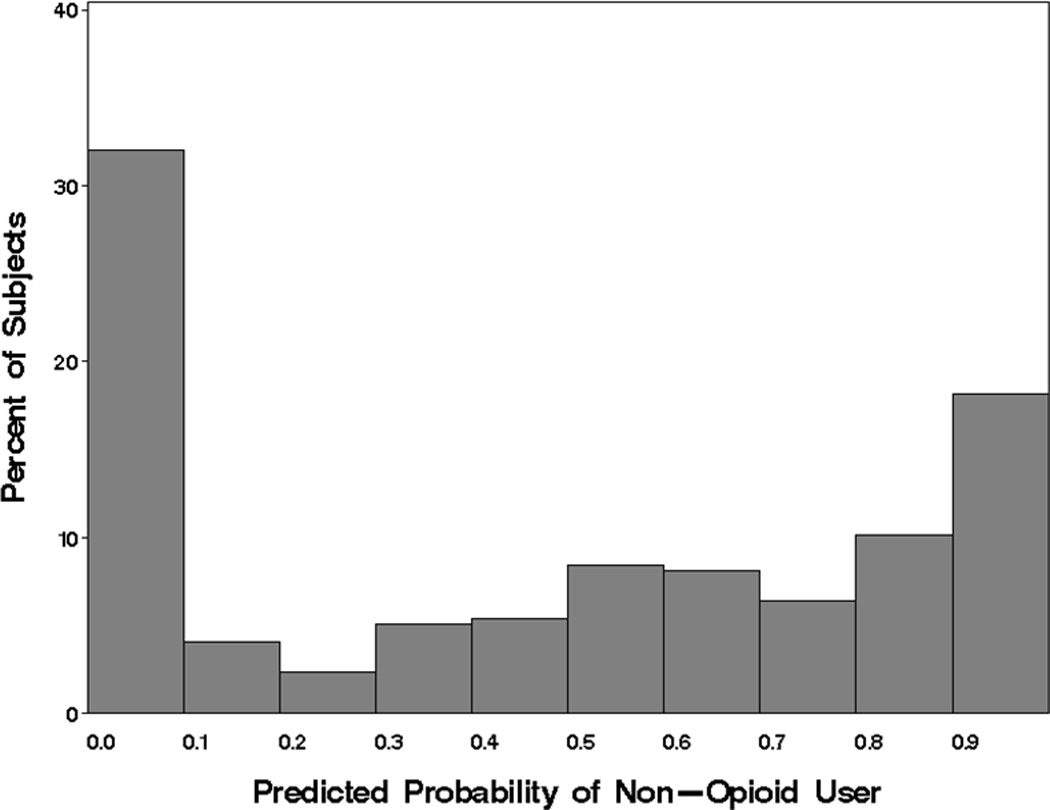
Distribution of the predicted zero-inflation probabilities for opioid use from ZINB model. Smaller probabilities indicate a subject that is more likely a user and larger probabilities indicate a subject that is more likely a non-user.

Variables describing concurrent use of other drugs during treatment (alcohol, cigarettes, cannabis) were not significant in the count component of the ZINB, indicating that proportion of days of alcohol and cigarette use are informative for distinguishing opioid users from non-users, but not for determining the proportion of days of opioid use among expected users. Three baseline variables were significant in the count component of the ZINB. Increased ADHD severity at baseline (p=0.01) and having conduct disorder (p <0.01) were both associated with lower opioid use. An increase of 10% in proportion of days of non-tobacco substance use prior to treatment corresponded to 1.2 times higher opioid use during treatment (p <0.01) in those predicted to be opioid users.

Had this best fitting ZINB model not been selected, the associations between opioid use with baseline ADHD severity and conduct disorder would have been identified as non-significant (Figure 3). Moreover, use of alcohol and cigarettes during treatment were positively associated with the proportion of days of opioid use in the non-ZI models, however, in the ZINB model these were identified as important distinguishing factors between non-users and likely users of opioids, rather than with the amount of opioid use.

5. DISCUSSION

We demonstrate the utility of a recommended strategy for modeling substance use outcomes, the importance of proper model selection, and potential benefits from modeling substance-specific use rather than aggregating use across substances. Four different distributions were evaluated in modeling four substances of interest. The distributions considered here were appropriate for overdispersed, restricted count data and took into account variations in the number of days of TLFB report, allowing all available data to be included. Although we fit all distributions to each substance for comparison purposes, a sequential process of applying the simpler models and evaluating their fit could have eliminated the need to fit all distributions to some of the substances. Inspection of the histogram for cigarette use alone would have provided enough evidence to exclude the negative binomial distribution from consideration given its U-shape, which has been reported elsewhere(14). The negative binomial provides a better approximation to the beta-binomial distribution when the proportion of days of drug use is small, as was the case with alcohol use. Beta-binomial models are more difficult to fit, often requiring specialized code, but were necessary to adequately model cannabis and cigarette use outcomes. Visual determination that zeros were adequately captured by non-ZI models with cannabis and alcohol use could also have ruled out the need for ZI-models prior to fitting them.

Importantly, results from models that were not indicated as best-fitting by AIC with visual inspection led to different inferences than those resulting from the chosen model, showing that inferences are not robust to model misspecification. Model selection should be considered an important part of any analysis and should start with the correct theoretical distribution. Simplified models relying on asymptotic normality (i.e., assuming that as the mean count increases the use distribution will be normal) should be evaluated prior to making inferences.

It is a common practice to aggregate across substances in studies of polysubstance users(5–9). In the selected model for each substance, the clinical variables of interest that were significantly associated with use differed for each substance. ADHD severity score at baseline was negatively associated with both cannabis and opioid use during treatment but not with cigarette and alcohol use. Whereas age was only associated with cigarette and alcohol use, pre-treatment drug use was only positively associated with cannabis and opioid use. Conduct disorder was positively associated with cannabis and alcohol but negatively associated with opioid use. The differences in these associations illustrates an advantage of modeling substance specific use rather than across substances to prevent obscuring or confounding relationships among variables.

Model selection should be considered an important part of any analysis and should start with the correct theoretical distribution. Simplified models relying on asymptotic normality (i.e., assuming that as the mean count increases the use distribution will be normal) should be evaluated prior to making inferences.

APPENDIX

Details of statistical distributions

The widely used Timeline Followback (TLFB) assessment is a semi-structured interview that retrospectively reconstructs use of each drug (yes, no) on each day for the period of interest. Thus, for each subject, counts of days used each drug during treatment can be generated. The binomial distribution is the discrete probability distribution of the number of successes/events (e.g. days used cannabis) in a sequence of n independent yes/no experiments (e.g. up to n=112 days assessed whether used cannabis during treatment), each of which yields success with probability p. The binomial distribution can be used to model count data but the variance (np(1−p)) is constrained in relation to the mean (np), which makes it inappropriate to apply to clinical data that are overdispersed, with a larger variance than expected.

There are several ways to address overdispersion which include the estimation of a scale parameter, inclusion of a random effect, or application of a more general version of the distribution that includes an overdispersion parameter. We chose the latter approach for two reasons: 1) so that we could test the amount of dispersion by evaluating the significance of this parameter and 2) so that these models could be more easily extended to include random effects when this characteristic is part of the study design.

In a standard binomial distribution, the binomial probability p is assumed to be fixed for successive trials. However, to account for overdispersion, we can assume that p comes from a beta distribution. Using this beta-binomial mixture distribution, the value of p changes for each subject, and is modeled as a random variable from a beta-distribution with shape parameters α > 0 and β > 0.

$$f(\mathrm{p}|\mathrm{\alpha },\mathrm{\beta })=\frac{p^{\alpha -1}{(1-p)}^{\beta -1}}{B(\alpha ,\beta )}$$

where B is the beta function. The marginal distribution of x = number of days used, is then the beta-binomial distribution,

$$f(x|\mathrm{\alpha },\mathrm{\beta },\mathrm{n})=(\begin{array}{c}n\hfill \\ x\hfill \end{array})\frac{B(\alpha +x,n+\beta -x)}{B(\alpha ,\beta )}$$

The binomial family of models are often approximated with the Poisson family of distributions. An offset can be included to account for differential days of use assessed to yield similar estimates of rates or proportions as those obtained by the binomial. Like the binomial, the Poisson constrains the mean (λ) and variance (also λ) relationship and the negative binomial distribution is often used as one approach for handling overdispersion.

The negative binomial distribution (18) can be derived by assuming the Poisson rate λ is from a gamma distribution. Because of this, the negative binomial distribution is also known as the gamma–Poisson (mixture) distribution, where k ≥ 0 is the dispersion parameter. As k becomes small, the variance of×approaches λ, that is, as k approaches 0 the negative binomial approaches the Poisson and the larger the k, the larger the overdispersion.

$$f(x)=\frac{\mathrm{\Gamma }(x+1/k)}{\mathrm{\Gamma }(x+1)\mathrm{\Gamma }(1/k)}\frac{{(k\lambda )}^x}{{(1+k\lambda )}^{x+1/k}}\text{for}x=0,1,2\dots$$

Note that for a small mean and large overdispersion, the value of 0 has by far the largest probability.

Zero-inflated (ZI) models assume the zero counts result from a mixture of two distributions, one where subjects always produce zero counts (non-users) and one where subjects produce zero counts by chance (users who did not report using during the study period). The likelihood of being from either population is estimated with a logistic regression model, while the counts in the second population are modeled with a count distribution. The following generally describes the ZI model:

$$f(Y=y|\pi )=\{\begin{array}{cc}\hfill (1-\pi )*\mathit{\text{pdf}}& \hfill y>0\hfill \\ \hfill \pi +(1-\pi )*\mathit{\text{pdf}}& \hfill y=0\hfill \end{array}$$

where π is the probability that only zero counts are possible and pdf refers to the distribution of the count data, which in this case is either beta-binomial or negative binomial. Note the negative binomial and beta-binomial models are nested within their ZI counterparts (i.e., ZINB and ZIBB, respectively).