Mg²⁺-induced Variations in the Conformation and Dynamics of HIV-1 TAR RNA Probed Using NMR Residual Dipolar Couplings

Abstract

The effects of divalent Mg²⁺ on the conformation and dynamics of the stem-loop transactivation response element (TAR) RNA from HIV-1 have been characterized using NMR residual dipolar couplings (RDCs). Order matrix analysis of one bond ¹³C–¹H RDCs measured in TAR at [Mg²⁺]:[TAR] stoichiometric ratios of ~3:1 (TAR(3.0 Mg)) and ~4.5:1 (TAR(4.5 Mg)) revealed that Mg²⁺ reduces the average inter-helical angle from 47(±5)° in TAR(free) to 5(±7)° in TAR(4.5 Mg). In contrast to the TAR(free) state, the generalized degree of order for the two stems in TAR(4.5 Mg) is found to be identical within experimental uncertainty, indicating that binding of Mg²⁺ leads to an arrest of inter-helical motions in TAR(free). Results demonstrate that RDC-NMR methodology can provide new insight into the effects of Mg²⁺ on both the conformation and dynamics of RNA.

By neutralizing backbone electrostatic repulsions, divalent ions such as Mg²⁺ can profoundly affect RNA average conformation and plasticity, and thus have important consequences on folding,^1–4 catalysis,^5,6 and recognition.⁷ Understanding how divalent ions affect RNA conformation and function at a molecular level requires not only the atomic characterization of typically folded divalent ion bound conformations, but also what is more often an ensemble of partially unfolded divalent ion free conformations.^1–4 However, elucidating high-resolution structures of dynamically inter-converting conformational substates poses significant challenges to techniques such as X-ray crystallography and NMR spectroscopy, which remain by and large, limited in applicability to “static” average structure determination of well folded conformations. While NMR relaxation measurements can probe “slow” (microseconds–milliseconds timescales) internal motions,^8–10 these methods provide limited information about motional amplitudes and directions. Fluorescence resonance energy transfer (FRET)¹¹ has emerged as a powerful alternative technique for measuring time-dependent changes in RNA global conformation,¹² but structural resolution also remains limited to distances separating pairs of donor and acceptor dye molecules. These experimental limitations have made it difficult to more directly investigate the effect of divalent ions on RNA structural dynamics.

By providing long-range angular sensitivity to both structure and dynamic fluctuations over a wide range of timescales (<ms), the measurement of residual dipolar couplings (RDCs) in partially oriented systems^13,14 has opened a new avenue for characterizing the conformational dynamics of flexible biomolecules using NMR.^15–20 We recently reported the RDC-NMR characterization of a divalent cation free transactivation response element (TAR) RNA variant (TAR(free)) (Figure 1(a)).²¹ The TAR domain has been the subject of intense structural studies,^22–25 both because its interaction with trans-activator protein Tat is critical for HIV-1 viral replication,²⁶ making it an attractive drug target,²⁷ and because it is a paradigm for studies of RNA–protein adaptive recognition.^28,29 Our RDC-NMR investigation unveiled a highly dynamic global TAR conformation, executing directionally unbiased collective helical excursions with amplitudes of 46(±4)° about an average inter-helical angle of 47(±5)°.²¹

Figure 1.

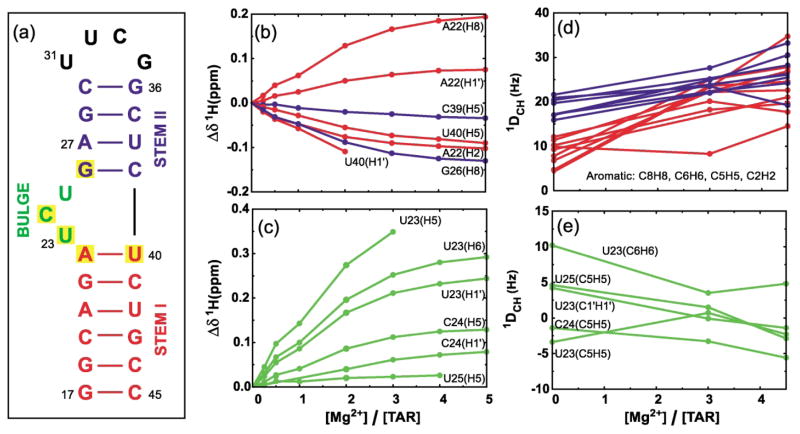
Secondary structure of the TAR RNA domain and variations in chemical shift and RDCs as a function of [Mg]:[TAR] stoichiometry. (a) The HIV-1 TAR analog used in this study. The six-residue hairpin loop in wt-TAR (CUGGGA) has been replaced with the more stable tetraloop (UUCG). Yellow boxes indicate residues having the largest Mg²⁺-induced ¹H chemical shift perturbations[(Δδ (ppm) = δ_TAR(Mg) – δ_TAR(free)) > 0.1 ppm, positive values imply downfield shifts]. Perturbations in ¹H chemical shifts for (b) residues in stem I (red) and II (blue) and, (c) bulge residues. RDC values measured between directly bonding C–H nuclei in (d) base moieties of residues in stems I (red) and II (blue) and (e) base and sugar moieties of bulge residues. Uniformly labeled ¹⁵N/¹³C-labeled TAR was prepared using standard procedures as described.²¹ NMR samples contained ~1.0 mM ¹⁵N/¹³C-labeled TAR, 15 mM sodium phosphate (pH 6.0–6.2), 25 mM sodium sulfate, 0.1 mM EDTA, and 3.0 and 4.5 mM Mg²⁺ for TAR(3.0 Mg) and TAR(4.5 Mg), respectively. An identical NMR sample also contained ~21 mg/ml of Pf1 phage.^34,35 All NMR data were acquired on Varian Inova spectrometers operating at ¹H frequencies of 500 and 600 MHz at 25 °C. Resonances were assigned by following incremental shifts upon addition of Mg²⁺. As described,²¹ splittings between [C8–H8, C6–H6, C2–H2], [C5–H5], [C1′ –H1′] were measured using ¹H and ¹³C IPAP-HSQC experiments⁴⁰ and between [C2′ –H2′, C3′ –H3′, C4′ –H4′] using the ¹J_CH-CT-CE-HSQC experiment.¹⁶ RDCs were calculated as the differences between splittings measured in the presence and absence of phage. The uncertainty in RDCs, estimated from measuring splittings in the ¹H and ¹³C dimension, was <3.5 Hz and <4.5 Hz for TAR(3.0 Mg) and TAR(4.5 Mg), respectively. The greater uncertainty in RDCs measured in the presence of Mg²⁺ relative to TAR(free)²¹ is attributed to increased line widths arising from greater degree of alignment as well as exchange broadening due to non-specific Mg²⁺ binding.

Although several studies have reported evidence for binding of divalent metal ions to TAR, discrepancies persist regarding the effects of divalent ions on the TAR average conformation while little is also known about the effects of divalent ions on TAR dynamics. Using electric birefringence, Zacharias and Hageraman previously reported that Mg²⁺ (~2 mM) induces ~50% reduction in the inter-helical angle of a 120 nt long RNA containing the bulge region of TAR. In contrast, a 1.3 Å X-ray structure of an RNA duplex comprising the bulge region of TAR determined in the presence of much higher divalent ion concentrations (100 mM CaCl₂) shows a coaxially aligned conformation with four Ca²⁺ bound to TAR. Three of these ions stabilize a looped out bulge conformation that is also distinct from previous solution NMR structures of TAR determined in the absence of divalent ions.^23,24,30 Fluorescence studies also provide evidence for Mg²⁺ destabilizing complexes of TAR with Tat-derived peptides.³¹ More recently, experiments employing ¹⁹F chemical shift perturbations in combination with Pb²⁺-induced RNA cleavage have more directly established that the bulge region of TAR binds $\text{Co}{({\text{NH}}_3)}_6^{3+}$, Mg²⁺, and Ca²⁺ with increasing specificity in solution.³² Here, we have employed RDC-NMR to investigate the effects of Mg²⁺ on both TAR average conformation and dynamics under solution conditions.

Binding of Mg²⁺ to TAR was initially examined by recording 2D ¹³C–¹H correlation spectra of TAR in the presence of increasing Mg²⁺ concentrations. Monotonous variations in ¹H and ¹³C chemical shifts were observed (Figure 1(b) and (c)), indicating rapid exchange (10⁵–10³ s⁻¹) between free and Mg²⁺ “bound” TAR conformations. In agreement with previous ¹⁹F NMR studies,³² the largest chemical shift perturbations (>0.1 ppm in ¹H) are observed in and around bulge residues (Figure 1(a), in yellow), while negligible shifts are observed for the UUCG tetraloop. Although it is not possible to distinguish contributions to chemical shift perturbations arising from conformational change and Mg²⁺ localization, these results indicate that Mg²⁺ primarily binds residues in and around the bulge, consistent with the previously reported X-ray structure of TAR bound to Ca^2+.33 Interestingly, while most of the stem resonances move downfield (Figure 1(b)), bulge resonances exclusively move upfield (Figure 1(c)). Modest line broadening was also observed with increasing Mg²⁺ concentrations, especially for the C8H8 resonances of guanine residues. This was attributed in part to exchange broadening due to non-specific Mg²⁺binding to TAR.

To investigate the effects of Mg²⁺ on the structure and dynamics of TAR, RDCs were measured between directly bonded ¹H–¹³C nuclei (¹D_CH) at [Mg²⁺]:[TAR] stoichiometric ratios of ~3:1 [TAR(3.0 Mg)] and ~4.5:1 [TAR(4.5 Mg)]. Based on a two-state interpretation of the chemical shift titrations (Figure 1(b) and (c)), the latter stoichiometries correspond to ~84% and ~94% of TAR existing in a Mg²⁺ bound conformation, respectively. Initial dissolution of TAR(3.0 Mg) in ~21 mg/ml Pf1 phage^34,35 yielded NMR spectra identical to those recorded for TAR(free). This effect was attributed to sequestering of Mg²⁺ by phage as spectra of TAR(3.0 Mg) and TAR(4.5 Mg) could be restored by incremental addition of Mg²⁺ to final concentrations of ~6.0 and ~7.5 mM, respectively. In all cases, the ²H splittings, and hence the apparent degree of phage alignment remained unchanged at ~21 Hz. Greater line broadening was also observed for TAR(3.0 Mg) and TAR(4.5 Mg) relative to TAR(free) when dissolved in phage. Although the resulting uncertainty in RDCs, estimated from measuring splittings in the ¹H and ¹³C dimension, was greater for TAR(3.0 Mg) (<3.5 Hz) and TAR(4.5 Mg) (<4.5 Hz) compared to TAR(free) (~1 Hz), this adverse effect was in part offset by an observed Mg²⁺-induced increase (~32%) in the total TAR alignment (see below). Hence, in addition to exchange broadening due to non-specific Mg²⁺ binding, the resonances in TAR(3.0 Mg) and TAR(4.5 Mg) likely experience additional line broadening relative to TAR(free) due to greater alignment and dipolar interactions. Due to the greater overlap observed in spectra of TAR in the presence of Mg²⁺, a smaller number of RDCs could on average be measured in TAR(3.0 Mg) and TAR(4.5 Mg) relative to TAR(free) (Table 1).

Table 1.

Statistics for order matrix analysis of RDCs measured in the two stems of TAR as a function of Mg²⁺ concentration

Stem	No. RDCs	CN	RMSD (Hz)	RMSDN (Hz) × 103	R
TAR(free)stem I	18	2.5	1.9	3.7	0.99
TAR(free)stem II	22	2.3	2.6	3.0	0.98
TAR(3.0 Mg)stem I	17	2.5	3.9	3.7	0.94
TAR(3.0 Mg)stem II	11	3.3	2.8	2.5	0.98
TAR(4.5 Mg)stem I	16	5.9	4.5	3.9	0.94
TAR(4.5 Mg)stem II	16	2.8	4.0	3.4	0.97

Shown are the total number of RDCs employed in the order matrix analysis (No. RDCs), resulting condition numbers (CN) defined as the ratio of the largest to smallest singular value in the singular value decomposition, root mean square deviation between experimental RDCs and values calculated using best fit order tensor parameters (RMSD), RMSD values normalized for degree of alignment (RMSD (Hz)/ϑ), and correlation coefficient between measured and predicted RDCs (R). Parameters are reported using input coordinates from idealized A-form RNA duplexes. Note that variations in stem-specific RMSD values correlate with the observed degree of alignment, such that RMSD^N values are more uniform across the stems.

The RDC values measured in TAR(3.0 Mg) and TAR(4.5 Mg) along with previous values measured for TAR(free)²¹ are compared in Figure 1 separately for stem (Figure 1(d)) and bulge residues (Figure 1(e)). Although Mg²⁺ leads to changes in almost all of the RDCs measured in TAR (Figure 1(d) and (e)), two variations are noteworthy. First, the pronounced difference between the magnitudes of RDCs measured in stems I and II in TAR(free), which was previously attributed to inter-helical kinking and dynamics,²¹ is diminished in TAR(3.0 Mg), and indiscernible in TAR(4.5 Mg) (Figure 1(d)). Second, whereas Mg²⁺ induces an increase in the absolute magnitude of stem RDCs (Figure 1(d)), a decrease is observed for RDCs measured in juxtaposed bulge residues (Figure 1(e)). This attenuation is particularly pronounced and uniform across three RDCs measured in residue U23. These results indicate the Mg²⁺ changes both the global inter-helical and local bulge structure and/or dynamics of TAR.

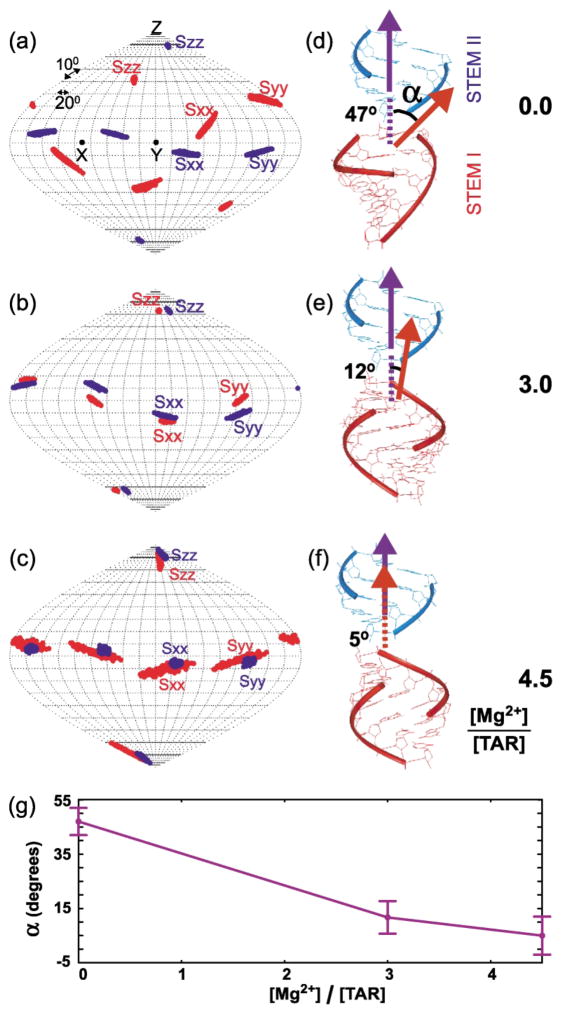
To examine the effects of Mg²⁺ on the global conformation of TAR, RDCs measured in Watson–Crick regions of stems I and II were used to solve for stem-specific order matrix elements using idealized A-form geometries as input coordinates.^36,37 This analysis revealed that Mg²⁺ induces a change in the global conformation of TAR. As now reported in a number of RDC-NMR studies of RNA,^{19–21,38,39} measured RDCs were found to agree within experimental uncertainty with local geometries for the stems derived from idealized A-form helices in all of TAR(free),²¹ TAR(3.0 Mg) and TAR(4.5 Mg) (Table 1). However, a change in the relative orientations of stem principal axes (S_zz, S_yy, S_xx), and hence stem alignment is observed with increasing Mg²⁺ concentrations. This can be visualized when stem-specific principal orientations (S_zz, S_yy, S_xx) are mapped relative to a continuous, coaxially aligned A-form helix (Figure 2(a)–(c)). Greater overlap between stem solutions and hence inter-helical straightening is observed in going from TAR(free) (Figure 2(a)),²¹ to TAR(3.0 Mg) (Figure 2(b)) and TAR(4.5 Mg) (Figure 2(c)). Correspondingly, TAR conformations determined by superimposing stem-centered principal axes exhibit a significant decrease in the average inter-helical angle (a) from 47(±5)° in TAR (free)²¹ (Figure 2(d)), to 12(±6)° in TAR(3.0 Mg) (Figure 2(e)), and 5(±7)° in TAR(4.5 Mg) (Figure 2(f)). Note that the conformation of TAR(3.0 Mg) should be interpreted with caution. In particular, it is difficult to decipher if the observed conformation corresponds to a population-weighted average of free and Mg²⁺-bound states or a state in which Mg²⁺ binding sites in TAR have not been completely occupied. It is nevertheless interesting to note that the observed inter-helical angle for TAR(3.0 Mg) can be reproduced based on a population weighted average of TAR(free) and TAR(4.5 Mg) states (84% × 5°(bound) + 16% × 47°(free) ≈12°). This is consistent with exchange of TAR between Mg²⁺ free and bound forms and hence cooperative Mg²⁺ binding. Although the relatively small number of RDCs measured in TAR(3.0 Mg)_stemII and TAR(4.5 Mg)_stemI resulted in higher condition number and consequently higher uncertainty in derived order matrix elements, the precision with which the TAR inter-helical angle is determined and the overall trend observed across TAR(free), TAR(3.0 Mg) and TAR(4.5 Mg) strongly suggest that Mg²⁺ induces complete coaxial alignment of the TAR conformation. The accuracy of derived principal orientational solutions is also supported by the fact that as expected for phage-induced alignment,³⁵ co-axial alignment of helices is accompanied by greater coincidence between the principal (S_zz) and helix (“z”) axes of TAR (Figure 2(a)–(c)). The effects of Mg²⁺ on the TAR global conformation observed here using RDC-NMR (Figure 2(g)) can reconcile the standing discrepancy between bent and linear TAR conformations determined by NMR^23,24,30 and X-ray crystallography,³³ respectively, which can be attributed to the absence of divalent ions in the former rather than crystal packing forces in the latter. Our results are also in qualitative agreement with transient electric birefringence studies,²⁵ which report ~50% reduction in the TAR inter-helical angle at lower Mg²⁺ concentrations (~2 mM), noting that the authors did not preclude the possibility for further inter-helical straightening at higher Mg²⁺ concentrations.

Figure 2.

TAR inter-helical conformation as a function of [Mg]:[TAR] stoichiometry. Order tensor orientations (S_xx, S_yy, S_zz) for stem I (red) and II (blue) in (a) TAR(free) (b) TAR(3.0 Mg) and (c) TAR(4.5 Mg). Ribbon representation of the relative orientation of stem I (in red) and II (in blue) determined by superimposing stem-specific principal axes for (d) TAR(free), (e) TAR(3.0 Mg) and (f) TAR(4.5 Mg), where the helix axis of stem I is oriented towards the reader. The helix axis of stem II is superimposed for all three conformations along the molecular z direction. (g) The average and allowed range of determined inter-helical angles (a). Order matrix analysis^36,37 was carried out independently for stems I and II for both TAR(3.0 Mg) and TAR(4.5 Mg), closely following the procedure previously described for TAR(free)²¹(see Table 1). In all cases, repeating order matrix analyses when excluding data measured in terminal residues in various permutations had a negligible effect on the average values of derived structural and dynamic parameters. Stems I and II were rotated into the principal axis system (PAS) using the program Insight II, and one orientation among four degenerate solutions could be selected based on linkage geometry considerations.²¹ In particular, the translational disposition of the two stems was determined by fixing the distance between atoms U40 (P) and C39(O3′) at 1.59 Å . With the latter translational constraint, two of the four inter-stem orientations generated through 180° rotations about the S_xx and S_yy directions could be discarded because they lead to anti-parallel stem alignments that is inconsistent with the secondary structure and sequence (terminal residues G17–C45 in stem I are oriented towards residues G26– C39 in stem II). Among the two remaining solutions involving180° rotation about S_zz, one of the solutions could be discarded because it lead to a considerable distance between A22(O3′) and G26(P) (~35 Å and 33 Å for TAR(3.5 Mg) and TAR(4.5 Mg), respectively) which cannot be connected using a three-residue bulge (the same distance in A-form helices is only ~17 Å).

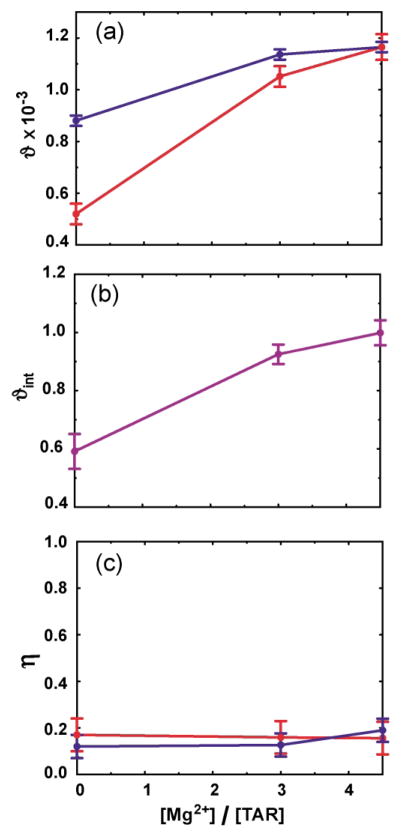
The generalized degree of order (ϑ)¹⁷ and asymmetry (η) are two additional stem-specific principal order parameters derived from the order matrix analysis,³⁶ which describe the degree and asymmetry of molecular alignment, respectively. While these values should be identical for rigidly connected helices, inter-helical motions can lead to differences in a manner dependent on both motional amplitudes and directions.^17,21 For TAR(free), inter-helical motions result in significant attenuation of ϑ_stemI relative to ϑ_stemII²¹ (Figure 3(a)). Remarkably, this difference, and hence the amount of inter-helical motions, is significantly diminished with increasing Mg²⁺ concentrations (Figure 3(a)). As can be seen in Figure 3(b), the internal generalized degree of order (ϑ_int = ϑ_stemI/ϑ_stemII) increases from 0.59(±0.06) in TAR(free) to 0.93(±0.03) in TAR(3.0 Mg), and 0.99(±0.03) in TAR(4.5 Mg) (Figure 3(b)). In contrast to the ϑ values, the computed stem-specific η values remain similar and only marginally change with increasing Mg²⁺ concentrations (Figure 3(c)). Once again, this overall trend provides strong evidence for a dramatic Mg²⁺-induced arrest of inter-helical motions in TAR(free).

Figure 3.

Principal order parameters and inter-helical dynamics in TAR as a function of [Mg]:[TAR] stoichiometry. (a) The generalized degree of order (ϑ) for stem I (red) and II (blue), (b) internal generalized degree of order (ϑ_int = ϑ_{stem I}/ϑ_{stem II}), (c) asymmetry parameter (η = (S_yy − S_xx)/S_zz).

As noted earlier, despite having almost identical ²H splittings and hence phage order in all of TAR(free), TAR(3.0 Mg) and TAR(4.5 Mg), Mg²⁺ induces an apparent ~32% increase in the total alignment of TAR. This can be seen as a Mg²⁺-induced increase in the ϑ value for the more ordered stem II (Figure 3(a)). A number of factors can give rise to this behavior. First, increase in the structural anisotropy of “linear” TAR(4.5 Mg) versus “bent” TAR(free) can result in an increase in molecular alignment. Second, and as discussed previously,²¹ motions of stem I in TAR(free) could in principle reduce the absolute alignment of stem II, an effect that is attenuated in the more rigid TAR(4.5 Mg). Finally, it is possible that quenching of electrostatic repulsions between TAR and phage through the observed Mg²⁺ binding to both phage and TAR allows for greater intermolecular proximity and hence greater TAR alignment.

In conclusion, we have described large Mg²⁺-induced variations in the structure and dynamics of TAR. Although the total number and coordination of bound Mg²⁺ along with the conformation of bulge residues remains to be investigated, our results show that Mg²⁺ significantly affects both the global conformation and dynamics of TAR, stabilizing a coaxially aligned conformation. It is noteworthy that based on our previous RDC study of TAR(free),²¹ this coaxially aligned conformation falls within the envelope of inter-helical conformations that are apparently sampled dynamically in TAR(free) (Figure 3(e)). We are now examining whether the Mg²⁺-induced changes in RDCs measured in the bulge residues correspond to changes in structure, dynamics, or both. The RDC-NMR approach outlined here should continue to illuminate the conformational transitions associated with RNA folding, catalysis, and recognition.

Abbreviations used

RDC

residual dipolar couplings

TAR

transactivation response element