Modelling hepatitis C therapy—predicting effects of treatment

Abstract

Mathematically modelling HCV RNA changes measured in patients who receive antiviral therapy has yielded many insights into the pathogenesis and effects of treatment on the virus. By determining how rapidly HCV is cleared when viral replication is interrupted by a therapy, one can deduce how rapidly the virus is produced in patients before treatment. This knowledge, coupled with estimates of the HCV mutation rate, enables one to estimate the frequency with which drug resistant variants arise. Modelling HCV also permits the deduction of antiviral agent effectiveness at blocking HCV replication from the magnitude of the initial viral decline. One can also estimate the lifespan of an HCV infected cell from the slope of the subsequent viral decline and, determine the duration of therapy needed to cure infection. Our understanding of HCV RNA decline under IFN-based therapies needs to be revised in order to understand the HCV RNA decline kinetics seen when using direct-acting antiviral agents (DAAs). In this Review, we also discuss the unresolved issues involving understanding therapies with combinations of DAAs, such as whether a sustained virological response necessarily involves elimination of all infected cells

Introduction

HCV research and treatment has entered a new era with the advent of direct acting antivirals (DAAs) that are safe, orally deliverable, and have a short treatment duration to cure HCV infection in nearly every patient¹ Some of the rapid advances in bringing new therapeutics to the clinic have their basis in mathematical modelling, which provided tools to rapidly assess the in vivo effects of new antivirals. Terms that were originally used as mathematical characterizations of viral kinetics, such as the first and second phase of viral decline, have become phrases familiar to almost all researchers and clinicians in the field. In this Review we provide insights into these developments and show how the early concepts in HCV viral dynamics developed from the study of patient responses to IFN-based therapies to understand the effects of DAA-based therapies. Furthermore, we as clinicians want to know how short the period of treatment can be made when DAA combinations are used. Can we cure individuals with 4 weeks or 2 weeks of treatment? What are the barriers to rapid cure? How can we evaluate if a patient can be cured rapidly or if longer treatment durations are needed? In this Review we will also discuss the mathematical models and concepts required to answer such questions.

Modelling IFN-based therapy

Dynamic equilibrium in absence of treatment

One of the most important insights into viral kinetic modelling has its origins in work that modelled the effects of antiretroviral treatment for HIV.^2–5 This insight is based on the simple heuristic argument that a change in viral load reflects an imbalance between the antagonistic processes of viral production and clearance and can be mathematically written as

$$\frac{dV}{dt}=pI-cV$$ (1)

where V is the viral load, dV/dt is rate of viral load change, p is the rate of virus production per infected cell, I, and c is the per virion rate of viral clearance (that is, the virion half-life: ln(2)/c). During chronic infection, the viral load is stable and remains roughly equal to a set-point level denoted V₀. At the set-point, the rates of viral production and viral elimination balance so that pI₀ = cV₀, where the set-point number of infected cells is I₀.

The first phase of viral decline

The initiation of anti-HCV treatment disrupts the equilibrium between virus and host. Most antivirals (such as IFN or DAAs) block viral production and, therefore, reduce p, by a factor of (1-ε), where ε is the effectiveness of therapy that varies between 0 and 1, and 1 represents a 100% effective therapy. Neumann et al.⁶ showed that Equation 1, with p replaced by (1 − ε)p, predicted that the viral load will fall according to Equation 2

$$V(t)=V_0(1-\epsilon +\epsilon e^{-ct})$$ (2)

for a short period of time after the initiation of therapy, during which the viral production rate pI remains approximately constant and equal to pI₀. The exponential term in Equation 2 approaches 0 as time proceeds, therefore, the viral load will decline to the value V₀(1-ε), reflecting that treatment leads to lower levels of viral production. This assertion implies, that if a drug is 99% effective then the viral load should fall to 0.01 V₀. Consequently, one can calculate the effectiveness of a drug that blocks viral production by the log₁₀ viral decline it causes, that is, if a drug results in a 2 log₁₀ decline then it is 99% effective

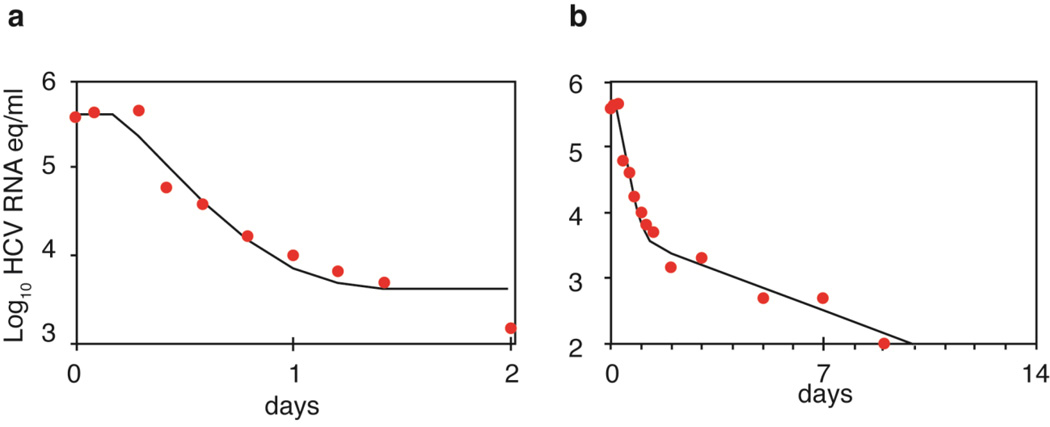
This model has been used to fit viral load data obtained from patients infected with genotype 1 HCV who were treated with different doses of IFN-α and sampled every few hours during the first two days and daily for two weeks after drug therapy was started.⁶ After a delay of ~8 h, which reflected the time for IFN to bind to cellular receptors and lead to upregulation of IFN-stimulated genes⁷ HCV RNA declined rapidly for the first day (Figure 1a), with a clearance rate c ~6 d⁻¹ corresponding to a half-life of HCV in the circulation of ~2.7 h.⁶ Furthermore, the extent of decline was dependent on IFN dose corresponding to a dose-dependent effectiveness in blocking viral production.⁶ Importantly, if HCV is rapidly eliminated from serum it implies that large quantities of virus need to be produced every day (about 10¹¹ to 10¹² virions) to maintain set-point viral levels of 10⁶ to 10⁷ HCV RNA copies/ml in the absence of treatment.

Figure 1.

Viral load decay in a patient with genotype 1 HCV treated with 15 MIU daily of IFN-α. a) Viral decline during the first 2 days of therapy as predicted by Equation 2 (solid line) plotted alongside actual data (solid circles). b) Viral decline in the same patient over the first 10 days of therapy (solid circles) and the best-fit of the Neumann et al. model⁶ that incorporates a second phase decline and the death of infected cells (solid line). Adapted from Neumann et al. Science 282: 103–107 (1998).

The second phase of viral decline

After day 2, the viral load does not plateau, as predicted by Equation 2, but rather continues to decline, albeit with a slower rate (Figure 1b). This failure of Equation 2 to continue to correctly predict the kinetics of viral decline reflects the fact the rate of viral production begins to decline as infected cells die and are not efficiently replaced due to the fact that the viral load has declined during the first phase.⁸As the number of newly infected cells decline, overall viral production is further reduced. Consequently, the effect of treatment, even if modest, triggers a circle of events that leads to a continuous decline of virus and infected cells, called the second phase, which continues as long as treatment is maintained. Mathematical analysis reveals that the rate of this decline is approximately equal to δε, where δ is the loss rate of infected cells.⁶ Thus, for potent drugs, where ε~1, the second phase slope is approximately δ.

[H2] Extended models

Although the biphasic model provides the basic foundation for understanding the determinants of early viral decline, more complex models have been introduced to understand the role of liver regeneration and the effects of ribavirin [and drug pharmacokinetics.^9–24 The putative effects of ribavirin have been extensively reviewed elsewhere and will not be discussed here.^{10,11,25–29}

Liver regeneration

An important prediction of models that take into account hepatocyte proliferation is the existence of a threshold, called the ‘critical drug effectiveness’ (ε_c).¹⁶ If ε <ε_c, the virus is not eradicated sufficiently rapidly and the progressive replenishment of target cells over time enables the remaining virus to infect new cells and establish a new, lower, set-point despite ongoing therapy.¹⁶ Interestingly, mathematical analysis of these models reveals that the value of ε_c depends on and increases with parameters that determine the baseline HCV RNA and the proportion of infected cells,¹⁸ and therefore possibly explains why high baseline viral loads and presence of advanced fibrosis are negatively correlated with sustained virologic response (SVR).³⁰

Drug pharmacokinetics

Viral rebound can occur because of a loss of drug effectiveness over time as the result of lower drug concentrations towards the end of the dosing period, and is sometimes seen with weekly administration of PEG-IFN.^9,13,19 The relationship between drug concentration and antiviral effectiveness in blocking viral production can be described by an E-max model (Equation 3)

$$\epsilon (t)=\frac{E_{\mathit{\text{max}}}C{(t)}^n}{E{C}_{50}^n+C{(t)}^n}$$ (3)

where C(t) is the drug concentration at time t; EC₅₀ is the drug concentration needed to achieve an effectiveness of 50% of the maximum effect, E_max; and n is the Hill coefficient, a constant that determines the steepness of the drug concentration–effect curve.^22,31 Because drug concentrations are sometimes unavailable, empirical models have also been proposed to describe the patterns of change in drug effectiveness over time,^32,33 such as an exponential model for drugs whose concentrations decay or build up over time (Equation 4)

$$\epsilon (t)={\epsilon }_1+({\epsilon }_2-{\epsilon }_1)(1-e^{-k_{\epsilon }t})$$ (4)

where the treatment effectiveness starts from an initial level, ε₁, changes to a final level, ε₂, with k_ε representing the rate of change of effectiveness. Therefore, if ε₂ is < ε₁ the model can mimic the effect of a decrease in drug effectiveness over time, as observed for example near the end of the dosing interval with weekly PEG-IFN.^32,34 Conversely, if ε₂ > ε₁ the model can mimic the effect of an increase in drug effectiveness over time, as is the case with some DAAs where the short half-life or the time to achieve high levels of active metabolites might induce a delay until the drug is fully effective.^{31,35–38,24,39}

Although the models described above have been useful to analyze early changes in viral load with IFN and some DAAs, they are limited by the fact that the models assume treatment simply blocks production of drug-sensitive virus. To understand the patterns observed during DAA treatment, such as the origin of the accelerated viral decay, one needs more complex models that account the various stages of viral replication targeted by DAAs.

Viral kinetics of DAAs

Blocking virion assembly and secretion

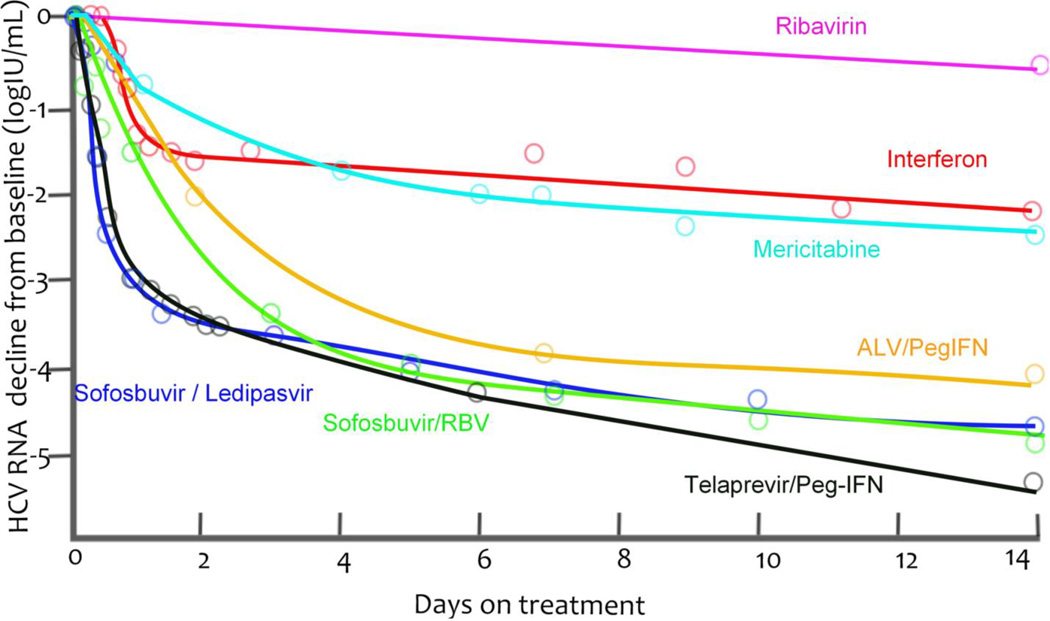
Because NS5A, which has a central function in HCV replication and has been targeted by DAAs, has no enzymatic functions, the effect of blocking this protein has been poorly understood. Using an innovative screening approach that focused on identifying compounds that were functionally distinct from those acting on the NS3 protease and the NS5B RNA-dependent RNA-polymerase, investigators identified that the NS5A inhibitor daclatasvir could be an important target for anti-HCV treatment.⁴⁰ The viral kinetics observed when a patient receives daclatasvir reveal a first phase of viral decline that is much faster than that seen with other treatments⁴⁰, such as with IFN⁶, Peg-IFN plus ribavirin⁴¹, the protease inhibitor telaprevir^35,41, and the polymerase inhibitors mericitabine⁴² and sofosbuvir³⁷ (Fig. 3a).^40,43 In fact, HCV RNA can decline by 3 logs 12 h after a single dose of daclatasvir,⁴⁰ from which it was deduced that HCV RNA was cleared from the circulation with a half-life of 45 min⁴³ and not with the previously estimated 2–3 h half-life estimated based on the response to IFN-based therapy.^6,44 Other investigators have hypothesized that if NS5A inhibitors potently block both viral secretion and viral replication, then viral load will fall more rapidly than with therapies that only block viral replication.⁴³ If a therapy inhibits viral replication, then viral RNA present within infected cells when therapy is started can continue to be packaged into virions and exported after drug therapy was initiated. If this situation arises, then viral production continues and results in an underestimate of the viral clearance rate.⁴³

Figure 3.

Median viral load decays from baseline (points) and nonparametric kinetic fitting (line) caused by agents belonging to different therapeutic classes during (A) short-term monotherapy or (B) combination therapy. (A). IFN 10 or 15 MIU QD⁶ (black), mericitabine 1500 mg BID⁴⁴ (green), sofosbuvir 400 mg QD³⁷ (red), telaprevir 750 mg q8h³⁵ (blue) and a single dose of daclatasvir (10 or 100 mg, purple)43. (B). IFN 10 or 15 MIU QD6 (black), sofosbuvir 400 mg QD + RBV (red)⁵⁷, telaprevir 750 mg q8h + Peg-IFN³⁵ (blue) and sofosbuvir 400 mg QD + ledipasvir 90 mg QD⁶¹ (purple).

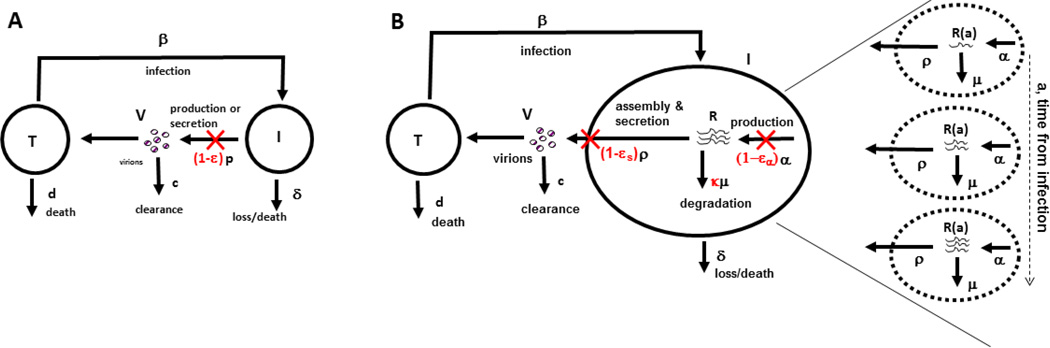
To precisely characterize the effect of daclatasvir, a multiscale model to analyze clinical data has been developed (Figure 2).⁴³ An important feature of this model was that the number of viral RNA molecules, R(a,t), within an infected cell were modelled as a function of the length of time, a, the cell had been infected and the time t the patient had been exposed to therapy. Within an infected cell, viral RNAs accumulate as they are synthesized and decrease in number as they are degraded or assembled into virions, which are then secreted. The multiscale model, therefore, includes the drug effectiveness in blocking viral RNA production, ε_α, the drug effectiveness in blocking viral assembly/secretion, ε_s and its effectiveness in modulating the rate of viral RNA degradation, κ (that is, κ >1 if a drug enhances the rate of viral RNA degradation).⁴³ Converting the multiscale model into a set of equations is complicated and beyond the scope of this Review; however, for interested readers the mathematical formulation and analysis of the model can be found in a number of publications.^8,43,45

Figure 2.

Comparison of the standard viral dynamic model and a multiscale model. a) In the standard model target cells, T, are produced at rate s (not shown) and become infected with rate constant β by interacting with virus and die at per capita rate d. Infected cells, I, produce virus at rate p per cell and die at per capita rate δ. Finally, virus, V, in addition to being produced is cleared at rate c per virion. Treatment reduces the average number of virions produced by an infected cell from p to p(1 − ε). The effectiveness of a drug, ε, represents a global measure of antiviral effectiveness that does not distinguish between the stages of intracellular viral replication, assembly and release that are blocked by treatment. b) The multiscale model accounts for intracellular processes involving HCV RNA (vRNA), R, that is, production, degradation and assembly and secretion with rate parameters α, μ, and ρ, respectively. The vRNA level within an infected cell (dashed circle) is assumed to increase with time since the first infection, that is, the age of an infected cell, a, and ultimately reaches a steady state. Treatment (parameters in red) can block vRNA production with effectiveness ε_±, and/or virion assembly and secretion with effectiveness ε_s, and/or enhance the degradation rate of vRNA by a factor κ. Reproduced with permission from Guedj et al. Proc. Natl. Acad. Sci. USA 110: 3991–3996 (2013).

Using this multiscale model to fit the viral decline during the first 2 days of IFN and daclatasvir treatment, led to the conclusion that daclatasvir has a dual mode of action and efficiently blocked viral RNA production (ε_α = 0.99), and profoundly inhibited virus assembly and secretion (ε_s = 0.998).⁴³ Daily IFN was predicted to have a small effect on assembly and secretion (ε_s = 0.39) and its main effect at doses of 10 and 15 million IU was on viral replication (ε_α = 0.96). Because the first phase declines observed with the protease inhibitors telaprevir and danoprevir were also faster than those observed during IFN-based therapy (Figure 3a), it was then asked whether protease inhibitors may also have an affect on virion assembly/secretion. Although telaprevir and danoprevir were found to have an inhibitory effect on virion assembly and secretion (ε_s = 0.95 and 0.56, respectively)^43,45 the effect was not as profound as that of daclatasvir.^43,45 This finding might explain why the virion clearance rate estimated for patients treated with telaprevir (c=12 d⁻¹)^34,44 was higher that of patients treated with IFN (c=6 d⁻¹)^35,41 but not as high as for those treated with daclatasvir (c=22 d⁻¹.⁴³ Interestingly, the predictions that NS5A inhibitors and protease inhibitors affect both viral replication and virion assembly and secretion are now supported by in vitro experiments.^43,46,47 Furthermore, IFN has been shown to rapidly affect infectious particle genesis.⁴⁸

The intracellular model used in the multiscale model is simplistic in that only positive strand HCV RNA is described (Figure 2). More complex models of intracellular replication that include many more features such as the replication complex, HCV RNA proteins and the membraneous web, have been developed;^49,50 however, using such models to fit clinical data within the context of a multiscale model remains challenging as there are too many unknown parameters to reliably estimate from the available data.

Curing infected cells

Although standard dynamic models initially attributed the second phase of viral decline to the death of infected cells,^6,44,51 the fast second phase decline seen with many DAAs, and particularly protease inhibitors,^35,41,45,52 has questioned this assumption. A plausible assumption, therefore, is that intracellular penetration of highly effective drugs leads to the cure of infected cells, that is, the treatment causes the loss of intracellular viral RNA. This was shown for self-replicating subgenomic HCV RNA in Huh-7 clones after prolonged treatment with IFN-α and for 5 genotype 1a H77 replicon cell lines treated with a combination of IFN-α the NS3 protease inhibitor BILN-2061, and the NS5B polymerase inhibitor GS-9190.^53,54 In addition, some DAAs, in particular protease inhibitors, might also restore innate immune responses within infected cells and these responses can contribute to a faster loss of intracellular viral RNA.⁵⁵ However, whether their in vivo concentrations are high enough to generate this affect has been questioned by some investigators.⁵⁶

Interestingly, nucleoside and nucleotide polymerase inhibitors have so far not led to as fast second phase declines as the HCV protease inhibitors.^37,42 For example, the viral declines induced by the HCV polymerase inhibitor sofosbuvir alone or in combination with ribavirin or another nucleotide analogue have been modelled, and the second phase decline slope δ was estimated to be 0.2–0.3 d⁻¹ in treatment naïve patients.^37,57 This decline is faster than the average 0.14 d⁻¹ decline seen using IFN-based therapies,^6,51 but slower than the 0.5–0.6 d⁻¹ observed with telaprevir monotherapy or in combination with PEG-IFN, again in treatment naïve patients (Figure 3).³⁵

The possibility that the rapid second phase viral declines seen in response to protease inhibitors might be the result of infected cells being cured led to a proposed model that included the effect of DAAs on intracellular viral replication [.⁵⁸ In this model, called the intracellular and cellular infection model, both positive strand HCV RNA and replication complexes within infected cells were incorporated. Using this model, the investigators showed that drugs resulting in a continuous loss of replication complexes at rate γ, can generate an accelerated second phase of viral decline with slope δ+ γ.⁵⁸ The model, therefore, predicted that the second phase viral decline was the result of a combined effect of infected cell death and reduced levels of viral replication in the remaining infected cells.

The majority of viral kinetic analyses of DAA-based treatments have been performed for treatment naïve patients who do not have.^{35,37,41–43} Results obtained in studies involving small patient populations found a much slower second phase of viral decline in cirrhotic or treatment experienced patients, than non-cirrhotic treatment naive patients].^59,60 More data are now needed to precisely evaluate the second phase of viral kinetics with DAAs in “real life” where the proportion of patients with unfavorable characteristics (cirrhosis or treatment experienced) is often larger than in clinical trials.[

Implications for treatment duration

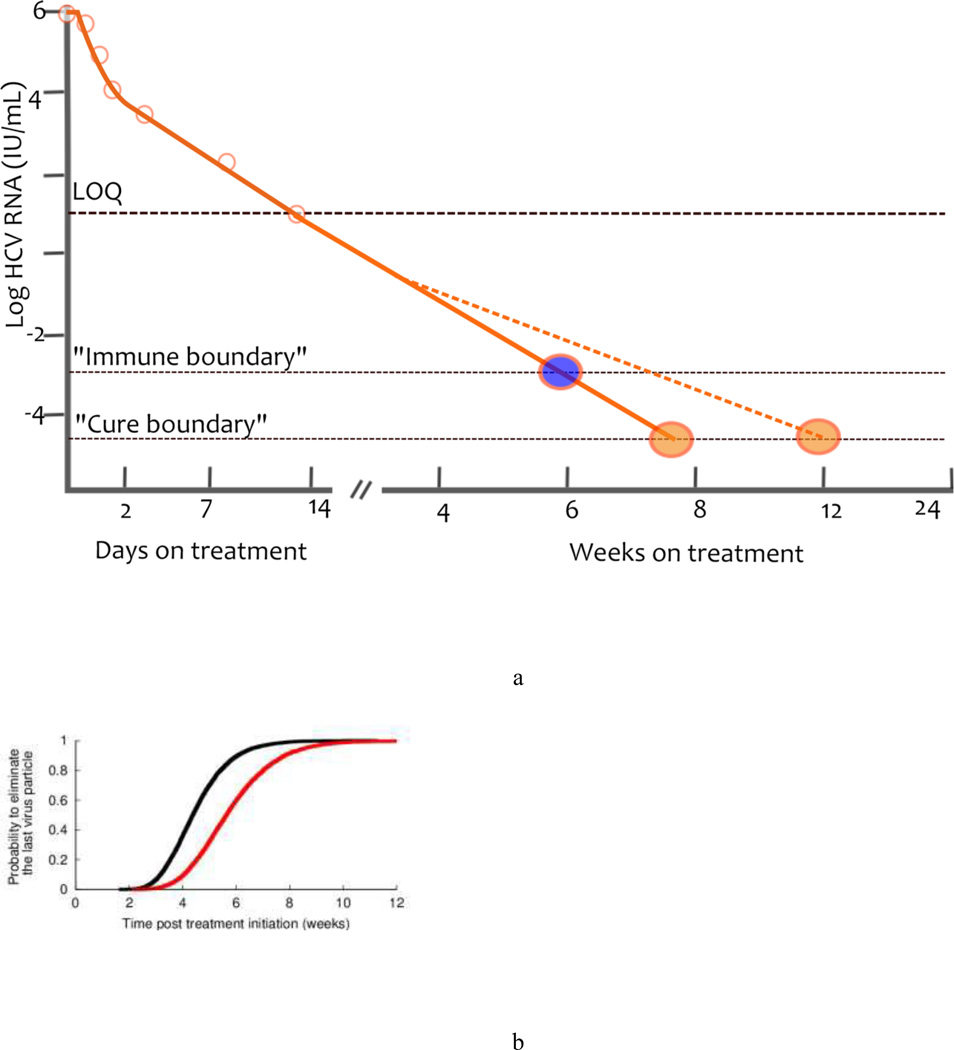
Regardless of its origin, a rapid second phase should allow for shorter treatment duration. To predict the time needed to eradicate HCV, a theoretical threshold, now known as a ‘cure boundary’ has been introduced into mathematical models.^11,51 The cure boundary is defined as having less than one viral particle in the extracellular body fluid, this is in 15 l, and corresponds to the unobservable concentration of 10^−4.22 IU/ml.¹¹ Using this cure boundary, eradication requires the viral load to decline >10 log₁₀ from a typical baseline of 10⁶ IU/ml.¹¹ With current assay limits of detection of about 10 IU/ml^61,62 there is still approximately another 5 logs of viral decline needed before the viral load hits the cure boundary (Figure 4a). Other investigators have defined the cure boundary as having fewer than one infected cell, which is a conservative assumption and delays the predicted time to eradication by 2–3 weeks using standard parameter values.^35,51

Figure 4.

Curing viral infection a) A schematic of the cure boundary. The cure boundary can be based on eliminating the last virus particle (orange circle), eliminating the last infected cell (not shown) or be a threshold beyond which the immune system can contain the infection (blue circle). In addition, when the viral load falls below the LOQ, the rate of viral decay can no longer be observed and might change in response to missed drug doses, emergence of drug resistance, viral reservoirs or other factors. Consequently the time needed to hit the cure boundary might be extended (blue dashed line). b) Estimated cumulative probability distribution function for the treatment duration needed to eliminate the last remaining virus particle. The black line corresponds to perfect treatment adherence, while the red line represents the case of partial adherence to a regime of three doses per day, where one dose is randomly missed every 2 days. Abbreviations: LOQ, limit of quantification. Reproduced with permission from Guedj et al. Hepatology 53: 1801–1808 (2011).

Treatment duration can easily be predicted from the first and second phases of viral decline using the cure boundary concept. Using the rapid viral decline in patients treated with danoprevir, a protease inhibitor, and mericitabine, a polymerase inhibitor, this approach led to the prediction that between 8 and 12 weeks of treatment should be sufficient to cure patients treated with DAAs.⁶³ Furthermore, in a study simulating a clinical trial in which the first and second phase declines of patients were chosen at random from the parameter distributions estimated in patients treated with telaprevir, 95% of patients could obtain SVR (defined as having less than one virion remaining) in 7 weeks, assuming that the patients complied with their therapy and that the predicted second phase decline continued unchanged when it is below the limit of detection (Figure 4b).³⁵ This situation could occur only if the treatment has a sufficiently high genetic barrier to resistance and there are no viral reservoirs. In fact, SVR rates obtained after 12 or 24 weeks of treatment with danoprevir and mericitabine are low, and virologic breakthrough or relapse were associated with danoprevir-resistant virus in most cases.⁶⁴ Similarly, the prediction of 7 weeks of therapy to obtain 95% SVR would not apply to telaprevir monotherapy but rather to some combination DAA therapy, which would prevent resistance development, and which had the kinetic characteristics observed during short-term telaprevir therapy.

Interestingly, the results of several clinical trials have now validated the prediction that SVR can be achieved in a large fraction of treatment naive patients without cirrhosis who received 8 weeks of treatment or fewer with some DAA combinations.^61,65,66 For example, in the ION-3 trial,⁶⁵ among previously untreated patients with HCV genotype 1 but without cirrhosis SVR12 was 94% after 8 weeks of treatment with sofosobuvir and ledipasvir. In the C-WORTHY trial,⁶⁶ among patients with previously untreated HCV genotype 1a who received grazoprevir and elbasvir for 8 weeks, SVR12 was 80%. Finally, in the SYNERGY trial,⁶¹ among treatment naïve HCV genotype 1 patients who received sofosobuvir, ledipasvir and either GS-9669 (a non-nucleoside NS5B inhibitor) or GS-9451 (an NS3/4A protease inhibitor) SVR12 was 95% after 6 week treatment.

The prediction of treatment outcome can be further improved by including pharmacokinetic data to account for the effect of drug exposure on the response to treatment and predict the effect of different dosing regimens.^51,67–69 For example, the viral kinetics observed in patients treated for 4 weeks with various doses of alisporivir (a cyclophilin inhibitor) or alisporivir/PEG-IFN have been modelled.^23,69 The investigators used what has been called a PK-VK model, i.e. a standard viral kinetic (VK) model⁶ in which the drug effectiveness depends on drug concentration, which in turn is determined by a pharmacokinetic (PK) model, to accurately predict the SVR rate of a subsequent clinical study with a 24 week treatment duration and different doses of alisporivir.²³ These results highlight how modelling of short-term data can be used to anticipate the outcome in a complex clinical trial.

Modelling drug resistance

The emergence of drug resistant HCV variants can mean that the second phase of viral decline might not be sustained and the treatment duration predicted from the second phase might be inaccurate.^35,70,71 In fact, viral breakthrough owing to drug resistance was shown to occur as early as 2 days after initiation of telaprevir monotherapy, with 5–20% of clones sequenced found to carry known resistance mutations.⁷⁰ Furthermore, the virus rapidly rebounded and by the end of therapy (day 14) almost all virus was drug resistant.⁷⁰ Given that HCV has a high daily production rate⁶ and a high error rate during replication,^72,73 all viable single and double mutant resistant viruses might exist before treatment and compete with wild-type virus during therapy.⁷⁴ This calculation led to the prediction that only treatments with a high genetic barrier to resistance can lead to SVR.⁷⁴ Viral competition has a crucial role in determining long-term viral decline, mathematical models have, therefore, been expanded to include both drug-sensitive and drug-resistant virus,⁷⁴ or wild-type plus multiple viral strains as well as cell infected with these various viral strains.^68,71,75,76 In the framework of these models, viral eradication can be achieved only if the different variants are sufficiently sensitive to treatment or have a low fitness, i.e., a low capability to grow.

However, the mechanism underlying the rapid rebound of resistant virus is not fully understood. A resistant virus needs ‘replication space’ to grow in. In some models the rapid expansion of a mutant, drug-resistant, virus is supported by the infection of newly produced hepatocytes.^71,74 However, this assumption has not been validated because there is little quantitative data regarding hepatocyte kinetics in HCV-infected livers. The replication space might also be supplied by other mechanisms, such as ‘superinfection’, i.e., reinfection of cells previously infected with wild-type virus or the loss of an antiviral state due to lower viral levels. Although for the most part, in vitro experiments support the notion of superinfection exclusion, some superinfection has been observed in vitro.^77–79 Further, in order for recombination of HCV genomes to occur, multiple viruses must infect a single cell. Recombinant forms of HCV have recently been identified⁸⁰ providing support for superinfection occurring in vivo. The loss of IFN-induced antiviral states has been included in a viral kinetic model of influenza infection⁸¹, but not in HCV models to our knowledge. Understanding the mechanism of drug-resistant virus expansion and subsequent treatment failure might enable the design of improved combination therapies that target both the virus and its host.

Predicting future treatments effects

Modelling potent drug combination in vivo

In the future, most treatments for HCV will involve IFN-free combinations of DAAs. Standard or multiscale models can be expanded to account for drug combinations using pharmacological concepts of drug additivity and synergy^82,83 or by simply analyzing the HCV RNA decline kinetics and estimating the overall effectiveness of the combination therapy. From a mathematical modelling perspective, two interesting clinical trials of DAAs have been the SPARE⁵⁷ and SYNERGY trials.⁶¹ In SPARE, 60 treatment naïve patients infected with genotype 1 HCV were given 400 mg daily of sofosbuvir plus ribavirin for 24 weeks. In the SYNERGY trial,⁶¹ 60 treatment naïve HCV genotype 1 infected patients were randomly assigned (1:1:1) to sofosbuvir and ledipasvir for 12 weeks (arm A), sofosbuvir and ledipasvir plus the non-nucleoside polymerase inhibitor GS-9669 for 6 weeks (arm B) or sofosbuvir and ledipasvir plus polymerase inhibitor GS-9451 for 6 weeks (arm C). The viral load decline in all three arms of the SYNERGY trial was initially more rapid than in patients treated with sofosbuvir plus ribavirin, which can be attributed to a high effectiveness of the NS5A inhibitor ledipasvir in blocking viral assembly and secretion.⁴⁶ [However, by day 3, patients treated with sofosbuvir plus ribavirin achieved largely comparable levels of virus as the patients in all arms of SYNERGY, which suggest two possibilities: firstly, in spite of an additive effect in vitro⁸⁴, sofosbuvir and ledipasvir did not have a larger effect in blocking viral RNA production in vivo than sofosbuvir plus ribavirin; and secondly, that the possibility of shorter treatment with sofosbuvir and ledipasvir was not due to faster kinetics of viral decline. Furthermore, based on the observed viral decline kinetics in arms B and C of SYNERGY, one would predict an SVR rate between 7% and 26% (based on eliminating the last virus particle after 6 weeks of treatment) and not the 95% observed.⁶¹

Is HCV RNA still a reliable biomarker?

Another unexpected finding in arms B and C of the SYNERGY trial was that at the end of treatment at week 6, 12 of 20 patients (60%) in arm B and 10 of 20 (50%) in arm C, had detectable HCV RNA levels, that is over the 3 IU/ml detection limit of the highly sensitive Abbott real-time HCV assay.⁶¹ Having HCV RNA close to the detection limit implies that viral eradication is still far off; in fact, standard mathematical modelling tools predict that ~1 million virions are still produced each day.⁶ Consequently, all existing mathematical models of HCV would predict that patients with detectable viraemia will progressively rebound as active intracellular drug decayed after the end of treatment (EOT). But in SYNERGY one patient in arm B had a viral rebound (and one patient in arm C was lost to follow-up after reaching SVR4).⁶¹ Consequently, the notion of a cure boundary corresponding to the loss of the last viral particle or last infected cell at the EOT does not appear to be a valid criterion for cure with these DAAs. This situation in the SYNERGY trial is not an isolated incident. For example, in a phase 2a trial (PILOT study) in which 11 patients received a NS3A protease inhibitor co-dosed with low dose ritonavir, a non-nucleoside NS5B polymerase inhibitor and ribavirin for 12 weeks, residual viremia was detected by the Abbott real time HCV assay in three patients who ultimately achieved SVR at therapy weeks 9, 10 and 12.⁶² These observations, as well as the observation that among five participants in the SYNERGY trial who achieved SVR12, 4 had quantifiable HCV RNA measured two weeks after completing therapy (range 15–57 IU/ml) and another participant had 14 IU/ml of HCV RNA measured 4 weeks after EOT,⁸⁵ also raise the possibility that HCV RNA levels post-treatment might not be useful in clinical decision making. For example, currently no proven explanation has been presented for the lack of viral rebound in patients with detectable HCV RNA at EOT in the SYNERGY and PILOT studies. However, two obvious possibilities exist: the immune system controls the virus, which results in a functional cure, as reported in rare instances in patients with HIV who ceased therapy;^86,87 or that the HCV RNA detected by the high sensitivity assay was not infectious.⁸⁸

A related concern has been the phenomenon of late viral relapse. In a small phase 2a trial involving 11 patients given two DAAs (ABT-450/r and ABT-072) plus ribavirin for 12 weeks, one patient relapsed at post-treatment week 36 with a virus that was most likely the baseline strain determined by sequence analysis.⁸⁹ Other cases of very late relapse have also been published,^90,91 which might support the idea of breakthrough from immune control or the existence of viral reservoirs, i.e., infected cells that are not eradicated by treatment and may activate after the end of treatment. Consistent with an important role of immune system suppression of HC], trace amounts of HCV RNA were sporadically found in plasma up to 8 years after successful therapy.⁹²

More data are needed to assess whether other DAA combinations give rise to the same phenomenon and if clinical treatment algorithms duration based on the time to achieve undetectable viremia need to be revisited for new treatments. Given the potential importance of the immune system in the controlling viral infection, immunological data, such as l\anti-HCV antibodies, or cytokines, such as interferon γ–induced protein 10 (IP-10) levels,⁹³ might be correlated to the long-term rate of viral decline and thus help improve SVR prediction.

Conclusions

The use of mathematical models has had an important role in deciphering the kinetics of viral decline during anti-HCV drug therapy, leading the FDA to recommend its use during drug development.⁹⁴ The magnitude of the first phase of viral decline has been used to determine the antiviral effectiveness of drugs that block HCV replication in very short-term clinical trials. New developments, such as the multiscale model, can be used to provide a novel understanding of the origin of the early rapid viral decline with DAAs and gain further information into the modes of action of new antivirals Mathematical models have also led to the concept of a cure boundary, which can help determine the length of IFN-based therapies. With some new DAA combinations, high SVR rates have been obtained after 6–12 weeks of therapy. However, some patients on this short duration therapy have a slow viral decline and detectable HCV RNA at the end of therapy or very late relapses, which suggests that new models are needed to understand the in vivo interactions between DAAs and their effect on viral eradication.

Key Points.

1. After patients receive therapy for hepatitis C infection, HCV RNA declines in a biphasic manner, the first phase reflects viral clearance, the second phase the loss of infected cells.

2. Modeling has revealed that viral production is so large that all single or double mutant variants are produced daily allowing resistance to emerge during therapies with low genetic barriers.

3. Modeling the HCV RNA kinetics has allowed researchers to estimate the effectiveness of therapy and the optimal treatment duration to achieve a sustained virologic response.

4. Multiscale models that include intracellular viral replication and extracellular spread indicate that NS5A and protease inhibitors can inhibit both viral replication and viral assembly or release.

5. IFN-free combination therapies are available now, show little resistance and can generate sustained virologic responses after treatments as short as 6 weeks.

6. HCV RNA has been detected after treatment with some DAA combinations in patients who develop a sustained virologic response, but viral kinetic theory cannot currently explain this phenomenon.

Review criteria.

We searched PubMed for English-language articles that focused on hepatitis C viral kinetics, estimating effectiveness of therapy and determining the duration of therapy using HCV and kinetics as key words.

Biographies

Jeremie Guedj is a research fellow at the French National Institute of Health and Medical Research (INSERM), Paris, France. During his PhD from 2003 to 2006 with Dr Rodolphe Thiébaut at Université Bordeaux 2, he worked on the statistical issues of parameter estimation in viral dynamic models. As a postdoctoral fellow between 2007 and 2012 with Avidan Neumann at Bar-Ilan University, Tel Aviv, Israel and then with Alan Perelson at Los Alamos National Laboratory, NM, USA he specialized in modeling HCV viral dynamics. His research has theoretical and clinical objectives, including understanding the determinants of response to anti-infective agents for HIV, HCV, and Ebola and improving individualization of therapy.

Alan S. Perelson has B.S. degrees in Life Sciences and in Electrical Engineering from MIT, Boston, MA, USA and a Ph.D. in Biophysics from University of California, Berkeley, CA, USA. Dr Perelson has held faculty positions at UC Berkeley and Brown University, RI, USA, and is now a Senior Fellow at Los Alamos National Laboratory, NM, USA. He is also an external professor at the Santa Fe Institute, Santa Fe, NM, USA and holds Adjunct Professorships at Boston University, MA, the University of New Mexico, and the University of Rochester School of Medicine all in the USA. He is a member of the American Academy of Arts and Sciences and has published >500 articles. His research focuses on developing models of the immune system and infectious diseases such as HCV and HIV.