Statistical controversies in clinical research: an initial evaluation of a surrogate end point using a single randomized clinical trial and the Prentice criteria

The Prentice criteria, although often misapplied, may be used to provide initial insight into the quality of a surrogate biomarker. This paper demonstrates appropriate measures to assess the four Prentice criteria. In particular, a novel statistic is provided to determine the adequacy of Prentice criterion 4, the most difficult of the four criteria to evaluate.

Abstract

Surrogate end point research has grown in recent years with the increasing development and usage of biomarkers in clinical research. Surrogacy analysis is derived through randomized clinical trial data and it is carried out at the individual level and at the trial level. A common surrogate analysis at the individual level is the application of the Prentice criteria. An approach for the evaluation of the Prentice criteria is discussed, with a focus on its most difficult component, the determination of whether the treatment effect is captured by the surrogate. An interpretation of this criterion is illustrated using data from a randomized clinical trial in prostate cancer.

introduction

The definitive end point for randomized phase III clinical trials in oncology is survival time. The use of survival time as an end point is unambiguous and easily ascertained. There are some drawbacks, however, as these trials require larger sample sizes, longer follow-up times, greater cost, and are compromised by patient cross-over to alternative therapies. Consequently, current clinical research is focused on the development of surrogate end points, which shorten the time-span for their realization, while retaining the information derived from survival time.

Examining a potential surrogate end point requires embedding the end point within randomized clinical trials. Simply finding an end point that is highly correlated with survival time in an observational study is not sufficient, since it is unlikely to account for all confounding factors, which may influence the treatment the patient is assigned to, the potential surrogate outcome, and the survival time of the patient. The classic example of this confounder effect is the patient's baseline health, which may be a factor in the physician's choice of treatment, as well as the surrogate and survival outcomes.

Utilization of a randomized clinical trial, where treatment assignment is accomplished via a ‘coin flip’, removes the potential for unobserved confounders; the randomization framework is crucial in the assessment of surrogacy. Ideally, this assessment should take place across multiple randomized clinical trials [1, 2]. The advantages include: (i) replication of scientific observations, (ii) a level of robustness for the surrogacy analysis, provided by testing across multiple patient populations, (iii) a framework for trial-level analysis by simultaneously delivering the randomized treatment effects on the surrogate end point and the survival end point. An important statistical methodology used to determine surrogacy from multiple randomized trials is known as a meta-analysis [1].

Although comprehensive surrogacy analysis dictates multiple randomized clinical trials, the initial surrogate evaluation may be constrained by the availability of a single randomized clinical trial. The lack of trials may be due to a number of factors including: (i) the limited number of patients within a population that enter clinical trials, (ii) randomized studies that are either planned or underway may not reach completion for a number of years, (iii) the requirement of a common treatment mechanism, for example a specific molecular target, limiting the available pool of patients available for a surrogate analysis.

methods

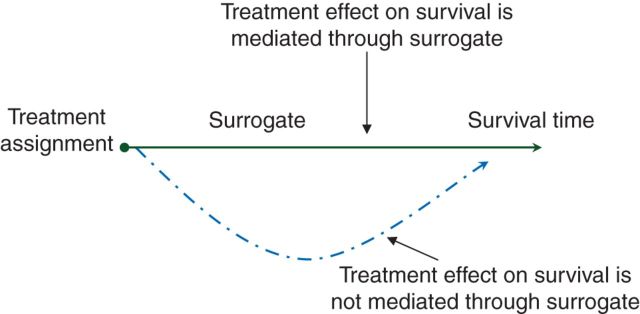
The most popular surrogacy assessment approach in the single randomized trial setting was developed by Prentice [3]. Prentice's definition of a surrogate in this setting is that the null hypothesis of no treatment effect on the surrogate is equivalent to the null hypothesis of no treatment effect on survival time. This is often depicted using the causal graph shown in Figure 1, where the surrogate end point mediates the treatment effect on survival.

Figure 1.

Causal graph demonstrating surrogacy.

The determination of this causal relationship requires additional information that is external to the randomized trial and is usually neither obtainable nor testable. As a result, a set of operational characteristics, known as the Prentice criteria, are utilized to assess surrogacy. The four Prentice criteria are:

1. The treatment has an effect on survival time.

2. The treatment has an effect on the surrogate.

3. The surrogate is associated with survival time.

4. The treatment effect on survival is captured by the surrogate.

The first three criteria, which explore whether pairwise relationships exist between the treatment assignment, surrogate end point, and survival time, may be evaluated empirically using straightforward statistical hypothesis testing procedures. The fourth criterion, however, is the most difficult to satisfy, since it requires a demonstration of no relationship between treatment and survival after accounting for the surrogate outcome.

A common error is to perform a statistical significance test for the treatment effect on survival conditional on the surrogate, and if this significance test produces a P value >0.05, then it is wrongly interpreted that the surrogate satisfies Prentice criterion 4. An illustration of this misapplication can be found in an analysis using the prostate specific antigen (PSA) as a surrogate within a randomized clinical trial, designed to test the efficacy of docetaxel + estramustine relative to mitoxantrone + prednisone, for patients with metastatic castration-resistant prostate cancer [4]. The surrogate end point was defined as a PSA decline by at least 30% within 3 months from the start of treatment. The surrogacy evaluation noted that although there was a treatment effect on survival, after adjusting for a post-treatment decline in PSA of 30%, the treatment effect was no longer significant. This assessment is problematic because the authors used a significance testing approach for finding the difference between treatments, rather than establishing an equivalence relationship between treatments. Importantly, the inability to reject the null hypothesis that the treatments have equal survival rates is not the same as the acceptance of the null hypothesis of equal survival rates between treatments. As succinctly stated by Altman and Bland [5], ‘the absence of evidence is not evidence of absence.’

The inability to utilize significance testing has resulted in multiple measures to assess Prentice Criterion 4. Freedman et al. [6] proposed a measure of the proportion of the treatment effect explained by the surrogate. The interpretation of this measure, however, is problematic because although it is called a proportion it is not bounded between zero and one. Alonso et al. [7] and Qu and Case [8] developed measures that reflect the correlation between two statistical models: one model containing both the surrogate and treatment assignment variables and the other model containing only one of these factors. Although these correlation measures are bounded between zero and one, they may be sensitive to the rate of censoring in a randomized clinical trial [9].

In this paper, the evaluation of Prentice criterion 4 is based on a test for the equivalence of the treatment-specific survival rates conditional on the surrogate factor. An example of this equivalence testing approach is provided using a randomized clinical trial for patients with metastatic castration-resistant prostate cancer [10]. Initially, the single biomarker circulating tumor cells (CTCs) was examined as a surrogate end point. However, this end point did not satisfy the Prentice criteria. As a result of further exploration, a surrogate marker was developed using CTCs and lactate dehydrogenase (LDH) evaluated at 12 weeks. Guidance for the choice of these biomarkers was based on previous clinical research in this patient population [11]. CTC is a blood-based assay that provides information on the accumulation of tumor cells in the peripheral blood. LDH is a marker of cellularity and cell turnover, and in prostate cancer it is considered an indirect marker of tumor burden. The data were derived from the 711 patients with 12-week marker values. The surrogate end point was defined as the disease control rate at 12 weeks, and was categorized as

Disease controlled at 12 weeks	CTC < 5
Disease moderately controlled at 12 weeks	CTC ≥ 5 and LDH ≤ 250
Disease uncontrolled at 12 weeks	CTC ≥ 5 and LDH > 250

The finding that five or more CTCs are associated with shorter survival times has been found in multiple metastatic solid tumor populations [12]. The upper limit of normal for LDH was defined as 250 units per liter as determined by the central laboratory used for this study. These previously determined normal/abnormal ranges were used to define the disease control surrogate marker.

Two applications of the log-rank test demonstrate that the survival rates differ by treatment (Figure 2A, P = 0.034) and the survival rates vary by surrogate level (P < 0.001). These hypothesis tests indicate that Prentice criteria 1 and 3 are satisfied. In addition, a χ² test to assess whether the surrogate distribution differed by treatment generated a P value <0.001, and so Prentice criterion 2 was satisfied.

Figure 2.

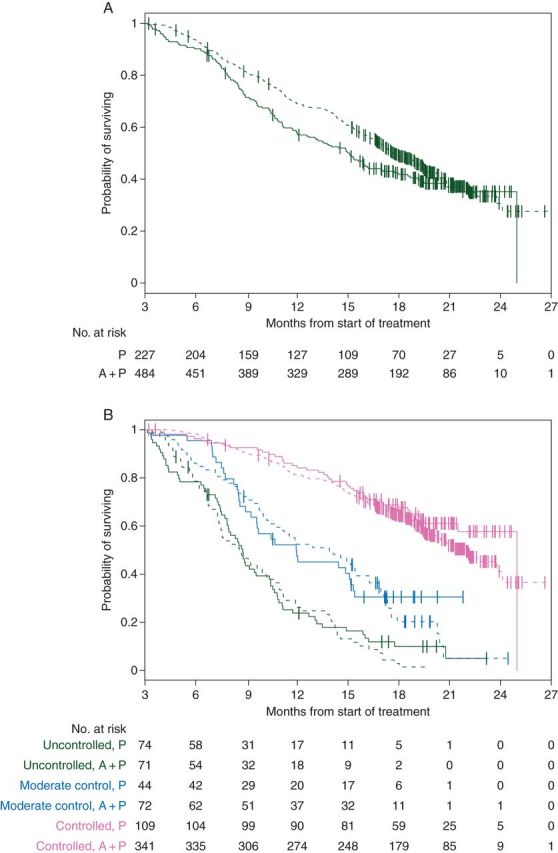
(A) Kaplan–Meier estimates by treatment. (B) Kaplan–Meier estimates by treatment and risk group. Credit line: Scher HI, et al. Circulating tumor cell biomarker panel as an individual-level surrogate for survival in metastatic castration-resistant prostate cancer. J Clin Oncol 2015 Apr 20; 33(12): 1348–1355. Reprinted with permission. © 2015 American Society of Clinical Oncology. All rights reserved.

One cannot, however, use significance testing to evaluate Prentice criterion 4. The key concept for Prentice criterion 4 is that the surrogate captures the treatment effect on survival. For survival analysis, this may be visualized using Kaplan–Meier estimates. Figure 2A is a demonstration that there is an overall treatment effect on survival; abiraterone + prednisone extends survival relative to prednisone alone. However, when the survival rates between treatments are compared within each of the three disease control surrogate groups, Figure 2B provides a clear depiction that the survival advantage for abiraterone + prednisone no longer exists. This is what is meant by the condition—the treatment effect is captured by the surrogate.

A rigorous assessment of Prentice criterion 4 is obtained by computing the distance between the treatment-specific survival probabilities within each disease control surrogate group. This distance measure is derived from survival estimates, from a proportional hazards model, for patients treated with abiraterone + prednisone (a + p) or prednisone alone (p). The goodness of fit of the proportional hazards model to the data was tested and found acceptable. The survival estimates produced from the model are:

1. The probability of surviving beyond t months given the patient's surrogate level is s and the patient's randomized treatment assignment is a + p. This probability is denoted as Pr(T > t |s, a + p).

2. The probability of surviving beyond t months given the patient's surrogate level is s and the patient's randomized treatment assignment is p. This probability is denoted as Pr(T > t |s, p).

The distance measure used to determine Prentice Criterion 4 is the weighted average distance of these two probabilities across the three surrogate levels, where the weight is a function of the number of patients within each surrogate level. The distance measure is represented as

$$D(t)=\sum w_s|Pr(T>t|s,a+p)-\text{Pr}(T>t|s,p)|$$

where the summation is over the three surrogate levels (s).

The statistic D(t) provides an estimate of its population counterpart—the weighted average treatment effect in the population, which is denoted by Δ(t). The population parameter Δ(t) may be interpreted as the weighted average treatment effect if one were to randomize all patients diagnosed with metastatic castration-resistant prostate cancer to either abiraterone + prednisone or prednisone alone.

Prentice criterion 4 implies that the population value Δ(t) = 0 at any follow-up time point t. It is clear that requiring identical population survival probabilities for the two treatments under study is an almost impossible task to achieve, and this issue has been the subject of much debate in the surrogacy literature [13]. In order to relax this condition, for this study, equivalence was generalized to Δ(t) < 0.05 at any time point t. In order for Δ(t) to be small, the difference in the population survival rates between treatments must be small for each surrogate level.

At a technical level, an approach to determining if the Prentice criterion 4 is satisfied is to use the randomized clinical trial data to compute the statistic D(t) and its standard error (se[D(t)]), at specified time points over the study. To account for the multiple time points under evaluation, Bonferroni adjusted 95% upper confidence bounds are computed from these estimates. If each Bonferonni adjusted 95% upper confidence bound indicates Δ(t) < 0.05, then our finding is that the treatment population survival rates do not differ at each surrogate level. As a result of this equivalence between survival rates, we would find that the data satisfy the Prentice criterion 4.

For the CTC/LDH disease control surrogacy data, the distance measure D(t) and its standard error were evaluated at monthly intervals from 6 to 24 months after the start of treatment. The estimated distance and the 95% Bonferonni upper confidence bounds are provided in Table 1. The upper confidence bounds all fall below 0.034, and so it is determined that Δ(t) < 0.05 for all time points t, validating this generalized definition of equivalence. As a result, it is found that the surrogate CTC + LDH, used as a measure of disease control at 12 weeks after the start of treatment satisfies Prentice criterion 4, and along with the other three criteria, indicates that this surrogate biomarker is worthy of further surrogacy research at the trial level.

Table 1.

Equivalence test for Prentice criterion 4.

Month	D(t): estimate of Δ(t)	Bonferroni 95% upper confidence bound for Δ(t)
6	0.0027	0.0090
7	0.0040	0.0134
8	0.0055	0.0182
9	0.0068	0.0226
10	0.0075	0.0252
11	0.0083	0.0278
12	0.0091	0.0305
13	0.0093	0.0309
14	0.0095	0.0318
15	0.0099	0.0330
16	0.0101	0.0337
17	0.0101	0.0338
18	0.0100	0.0336
19	0.0099	0.0332
20	0.0098	0.0329
21	0.0097	0.0326
22	0.0089	0.0301
23	0.0087	0.0292
24	0.0086	0.0260

discussion

A proposal for the evaluation of Prentice criterion 4 was developed to directly address the stated criterion: the treatment effect on survival is captured by the surrogate. This condition is difficult to satisfy and has resulted in the development of alternative measures of surrogacy. In this study, the concept of equivalence was generalized to indicate that after controlling for the surrogate, the difference in treatment-specific survival probabilities lie within 0.05 throughout all the follow-up times of the study. The 0.05 equivalence threshold was derived from discussions among the investigators involved in the metastatic prostate cancer trial as to what would be considered a clinically relevant difference in the survival rates between treatments.

A limitation of the Prentice criteria is that its assessment is derived from a single large-scale randomized phase III study. As a result, the utilization of the surrogate in future randomized phase III studies may not be appropriate unless the mechanisms of action for the treatments on the new studies are similar to the treatments where the surrogate was developed. This point was also made by Fleming [14], who noted that the Prentice criteria (and its quantitative derivatives) are necessary but not sufficient conditions for surrogacy.

The single-trial Prentice criteria evaluation could, however, be used as an exploratory tool to evaluate potential surrogates. If a functional form of the surrogate satisfying the Prentice criteria is found, then validation should be achieved through the use of independent multiple randomized clinical trials.

funding

This research was supported by the MSKCC SPORE in Prostate Cancer (P50 CA92629) and the Department of Defense Prostate Cancer Research Program (PC051382).

disclosure

The author has declared no conflicts of interest.