Abstract
Motivation: There is a need for effective automated methods for profiling dynamic cell–cell interactions with single-cell resolution from high-throughput time-lapse imaging data, especially, the interactions between immune effector cells and tumor cells in adoptive immunotherapy.
Results: Fluorescently labeled human T cells, natural killer cells (NK), and various target cells (NALM6, K562, EL4) were co-incubated on polydimethylsiloxane arrays of sub-nanoliter wells (nanowells), and imaged using multi-channel time-lapse microscopy. The proposed cell segmentation and tracking algorithms account for cell variability and exploit the nanowell confinement property to increase the yield of correctly analyzed nanowells from 45% (existing algorithms) to 98% for wells containing one effector and a single target, enabling automated quantification of cell locations, morphologies, movements, interactions, and deaths without the need for manual proofreading. Automated analysis of recordings from 12 different experiments demonstrated automated nanowell delineation accuracy >99%, automated cell segmentation accuracy >95%, and automated cell tracking accuracy of 90%, with default parameters, despite variations in illumination, staining, imaging noise, cell morphology, and cell clustering. An example analysis revealed that NK cells efficiently discriminate between live and dead targets by altering the duration of conjugation. The data also demonstrated that cytotoxic cells display higher motility than non-killers, both before and during contact.
Contact: broysam@central.uh.edu or nvaradar@central.uh.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
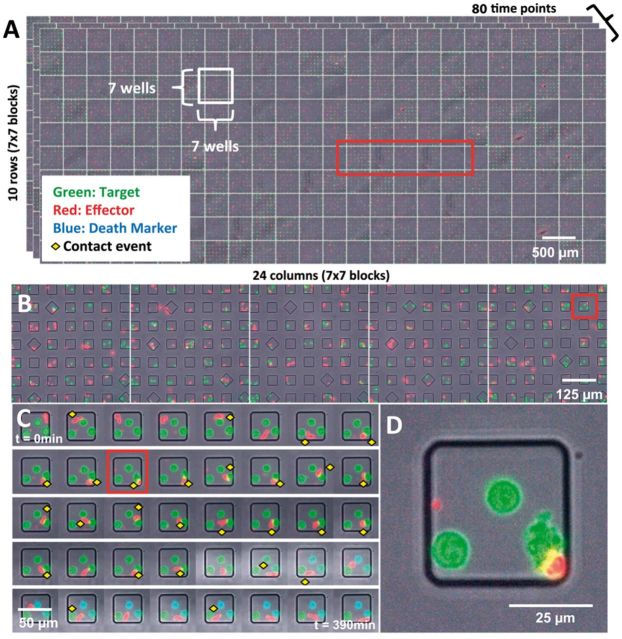
Dynamic cell behaviors, especially cell–cell interactions, are of vital interest in immunology (Romain et al., 2014; Vanherberghen et al., 2013; Varadarajan et al., 2012; Zaretsky et al., 2012), cancer biology (Wang et al., 2012; Yin et al., 2008; Zheng et al., 2012) and stem cell engineering (Ma et al., 2013; Zhao et al., 2011). Automated time-lapse microscopy of live cells in vitro is a well-established method for spatiotemporal recording of cells and biomolecules, and tracking multi-cellular interactions. Unfortunately, most conventional methods assess limited numbers (10–100) of manually sampled ‘representative’ cell pairs, leading to subjective bias and therefore lack the ability to quantify the behaviors of statistically under-represented cells reliably. This is significant since many biologically significant cellular subpopulations like tumor stem cells, multi-killer immune cells and biotechnologically relevant protein secreting cells, are rare. There is a need for methods to sample cell–cell interaction events on a larger scale to investigate such cellular phenomena. Recent advances have enabled the fabrication of large arrays of sub-nanoliter wells (nanowells) cast onto transparent biocompatible polydimethylsiloxane substrates (Forslund et al. 2012; Ostuni et al., 2001; Rettig and Folch, 2005; Whitesides and Stroock, 2001). Small groups of living cells from clinical samples, and laboratory-engineered cells can be confined to nanowells, and imaged over extended durations by multi-channel time-lapse microscopy, allowing thousands of controlled cellular events to be recorded as an array of multi-channel movies (Liadi et al., 2013; Varadarajan et al., 2012). We refer to this method as Time-lapse Imaging Microscopy In Nanowell Grids (TIMING). The spatial confinement can enable a rich sampling of localized cellular phenomena, including cell movements, cellular alterations, and cell–cell interaction patterns, along with the relevant intra-cellular event markers (Pham et al., 2013). TIMING is thus ideally suited for tracking cell migration and interactions at short distances but if cell migratory patterns over larger distances are of interest, arrays with larger wells can be fabricated. Similarly, if unconfined migratory behavior of cells is desired, other methods have been described (Sackmann et al., 2014). The promise and challenge of nanowell arrays, is high throughput, eliminating the need for user selection of events of interest, and the ability to repeatedly follow the same cell(s) over time. Figure 1 illustrates a TIMING dataset consisting of >11 000 nanowells containing fluorescently tagged human CAR+ T-cells (red) and NALM-6 tumor cells (green) that were imaged by time-lapse microscopy over 80 time points at 5-min intervals to yield an array of 4-channel movies, one per nanowell. The border nanowells from each block are discarded, yielding 25 usable nanowells/block. TIMING datasets vary in size between 200 GB and 1.5 TB depending upon the array size, and the number of time points. A sample TIMING dataset corresponding to one block is provided as Supplementary Material A. Production datasets are often of lower quality than the example in Figure 1, for example, see (Figs 2–4) and exhibit natural cellular variability, variations in signal to noise ratio (SNR), staining variations, focus drift, spectral overlap between fluorochromes and photobleaching.
Fig. 1.
Illustrating a small TIMING dataset. (A) An array of 168 × 70 nanowells arranged in blocks of 7 × 7 (with 5 × 5 usable inner nanowells/block). (B) Enlarged views of five blocks highlighted by the red box in Panel A. (C) Time-series data at 5-min intervals for the nanowell highlighted by the red box in Panel B. (D) Enlargement of a single frame of the time-lapse series for the nanowell shown in Panel C, showing 3 NALM-6 target cells (green), one CD19-specific CAR+ T-cell (red, lower right) in contact with a target cell (contact region appears yellow) and a red fluorescent debris particle that is rejected in the analysis (left edge) (Color version of this figure is available at Bioinformatics online.)
Fig. 2.
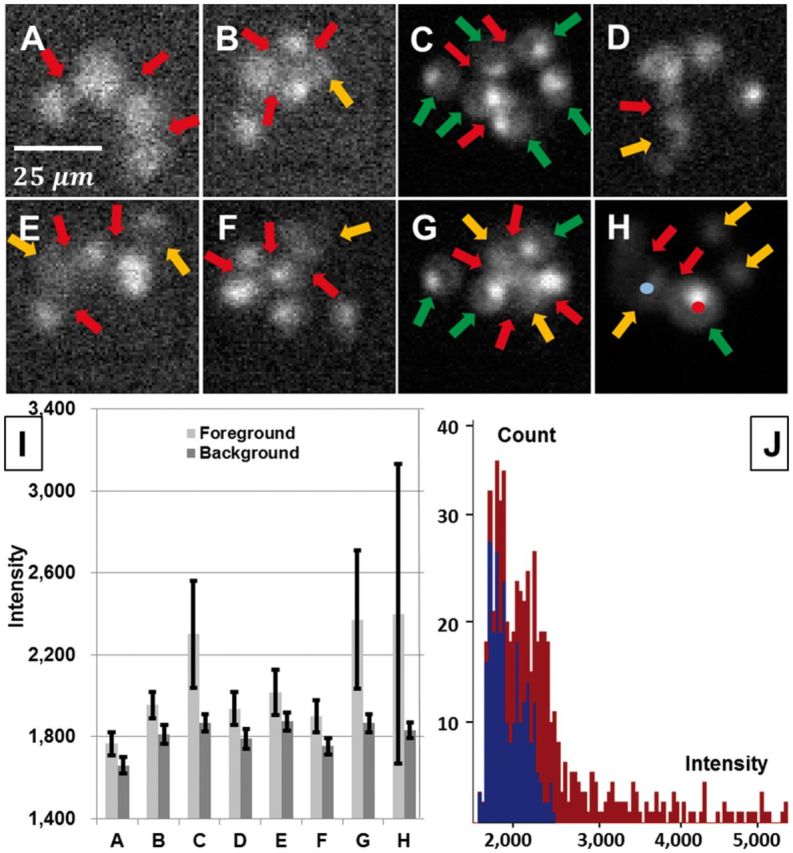
Illustrating automated image analysis challenges. (A–H) Sample image frames. The red arrows indicate unclear boundaries between adjacent cells. The yellow arrows highlight low-intensity cells that are difficult to detect. The green arrows highlight cells that are difficult to segment due to non-uniform fluorescence. Panels A, B, D, E and F exemplify frames with low contrast and SNR. (I) Mean and standard deviation (error bars) of the background intensity (dark gray) and the foreground intensity (light gray) for the panels A–H. (J) Variation in fluorescence distribution both across the pixels associated with one cell, and across cells. The red and blue histograms correspond to the cell indicated by the red and blue dots, respectively, in Panel H (Color version of this figure is available at Bioinformatics online.)
Our goal is to develop highly automated pipeline of algorithms that can reliably segment and track the cells in TIMING datasets with minimal parameter tuning, and yield a sufficiently rich set of cellular-scale measurements for statistical profiling, without the need for manual proofreading (Supplementary Material B). A direct application of general-purpose segmentation and tracking algorithms is not a viable strategy since their yield (the number of correctly analyzed nanowells) is surprisingly low, and their parameter tuning needs are high. For example, a direct application of Al-Kofahi et al. (2010) segmentation algorithm with a reported accuracy >95% that is the core of the open-source FARSIGHT toolkit (farsight-toolkit.org) to the dataset in Figure 1 produces an error-free yield of only 43% of the nanowells for the basic case when a nanowell contains one effector and one target (Table 1). The situation with tracking algorithms is similar. For example, in analyzing one sample block containing 36 nanowells, out of which 21 contained at least one cell, a state-of-the art algorithm (Magnusson et al., 2015) accurately tracked only six nanowells with zero errors (yield of 28%) (Supplementary Material C). When the yield falls below 90%, manual proofreading is essential to identify the nanowells that were tracked accurately. If on the other hand, when the automated accuracy exceeds 90%, the user can simply accept the automated results, and the modest error that they entail. General-purpose segmentation and tracking algorithms are inadequate because they do not exploit the powerful constraints that are germane to TIMING datasets, specifically, the spatial confinement of cells and rarity of cell divisions. They also lack mechanisms to cope with the higher morphological variability and non-uniform fluorescence of cell bodies compared with cell nuclei that were heavily studied in the prior literature (Al-Kofahi et al., 2010; Arslan et al. 2013; Couprie et al., 2011; Lin et al., 2007; Meijering et al., 2012; Parvin et al., 2007; Yang et al., 2006). In this article, we present algorithms that exploit the confinement and cell-cycle constraints, and utilize novel segmentation approaches to increase the yield to 98% for the basic case noted above (Results section, compare Table 1 versus Table 2), and deliver high tracking accuracies (Table 3). At this level of performance, the quantitative measurements derived from automated segmentation and tracking can be directly utilized for statistical studies without the need for manual proofreading. The following sections describe our methodology.
Table 1.
Summary of yield from traditional automated segmentation (Al-Kofahi et al., 2010)
| No. of targets |
||||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| Effectors | 0 | 160/59.4% | 128/56.2% | 80/51.2% | 69/47.8% | 19/31.6% |
| 1 | 165/54.6% | 174/45.9% | 98/40.8% | 60/41.7% | 32/15.6% | |
| 2 | 148/47.3% | 111/43.2% | 93/37.6% | 56/35.7% | 21/14.2% | |
| 3 | 57/37.4% | 74/37.8% | 73/35.6% | 29/34.5% | 16/12.5% | |
| 4 | 39/25.6% | 43/13.9% | 29/10.3% | 19/10.5% | 10/0.0% | |
The first entry indicates the number of nanowells containing the corresponding cell distribution (manually verified), and the second entry indicates the corresponding yield.
Table 2.
Summary of error-free nanowell yield using the confinement constrained cell detection method
| No. of Targets |
||||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| Effectors | 0 | 160/99.4% | 128/98.4% | 80/97.5% | 69/92.8% | 19/89.5% |
| 1 | 165/98.7% | 174/98.3% | 98/97.9% | 60/91.7% | 32/78.1% | |
| 2 | 148/97.9% | 111/97.3% | 93/96.8% | 56/91.1% | 21/80.9% | |
| 3 | 57/94.7% | 74/94.6% | 73/91.8% | 29/89.7% | 16/81.2% | |
| 4 | 39/87.1% | 43/88.4% | 29/86.2% | 19/84.2% | 10/80.0% | |
Table 3.
Frequency of cell segmentation and tracking errors
| Number of cells | 2 targets | 3 targets | 4 targets |
|---|---|---|---|
| Under-segmentation | 1.2% | 1.4% | 0.1% |
| Over-segmentation | 1.3% | 0.6% | 4.2% |
| Incorrect-correspondence | 0.9% | 0.8% | 3.6% |
| Total cells validated | 816 | 636 | 168 |
2 Methods
2.1 Specimen preparation and imaging
The TIMING datasets were derived from ongoing studies in which human T cells (genetically engineered to express chimeric antigen receptor CAR) and natural killer (NK) cells were used as effectors. Antibodies for phenotyping of T cells were purchased from Biolegend (CA, USA). Human leukemic lines NALM6, K562 or mouse EL4 cells expressing the appropriate ligands were used as targets (T). Both cell types were washed once in serum-free medium, suspended to ∼2 million/mL and labeled with PKH67 Green and PKH26 Red dyes respectively, as directed by the manufacturer (Sigma-Aldrich). Approximately 100 000 effector (E) cells were loaded onto the nanowell array, followed by ∼200 000 target cells. Cells were allowed to settle into the nanowells for 5 min, and excess cells were washed away. Next, 50 µL of Annexin V-Alexa Fluor 647 (AnnV-AF647, Life Technologies) was mixed in 3 mL of complete culture medium (RPMI-1640 + 10% FBS, containing no phenol red, Cellgro) and pipetted onto the nanowell array plate, thus immersing the array in the medium throughout the image acquisition while allowing for nutrition and gas exchange (37°C, 5% CO2). The nanowell array is much wider than the field of view of the microscope, so a computer-controlled microscope stage (AxioObserver Z1, Carl Zeiss) was used to scan the array spatially. Images were collected over 12-13 hr periods at 5-10 min intervals. This temporal sampling rate is in the range of times described between first contact and killing in previous in vitro observations (Deguine et al., 2012; Yamanaka et al., 2012). The stage movements from one block to the next require ∼100 ms, negligible compared with the sampling interval. We used an LD Plan Neofluar 20×/0.4 NA Korr Ph1 Ph2 M27 (Carl Zeiss) objective lens combined with an optovar of 1× Tubulens, yielding a total magnification of 200×, and a resolution of 0.325 µm/pixel (pixel size). A Peltier-cooled (−10°C) digital scientific CMOS camera (ORCA-Flash 4.0 V2 C11440-22CU), or Hamamatsu EM-CCD camera were used for recording the images.
2.2 Automatic nanowell localization
Automatic localization of nanowells is necessary for delineating the cell confinement regions, correcting for stage re-positioning errors, and breaking up the overall TIMING dataset into a large number of motion-corrected video sequences, one per nanowell. This operation must be reliable since a single well-detection error can render the nanowell unusable for analysis, reducing the experimental yield. It must be robust to focus drift (accounting for shrinkage/swelling/irregularity of the polymer substrate), wells with compromised geometry, illumination variations, ringing artifacts and debris or air bubbles that may move, and abruptly appear/disappear from the camera view over time (Fig. 3A ).
Fig. 3.

Illustrating automated localization of nanowells. (A) Examples of nanowells showing artifacts. (B) NCC for the best-fitting template. (C) Estimated nanowell cropping regions (Color version of this figure is available at Bioinformatics online.)
Content-independent image registration methods like SIFT matching (Li et al., 2010) were neither sufficiently reliable nor practical for TIMING data. They required multiple parameter adjustments, and failed in the presence of artifacts. Therefore, we adopted a normalized cross-correlation (NCC) based template fitting method that is robust to illumination variations and artifacts (Yoo and Han, 2009). We exploited the fact that the geometry of nanowells is known from the fabrication process, and they are always visible in the phase-contrast channel. Note in Figure 1B that some of the nanowells are intentionally rotated by 45° for implementing a coding strategy designed to uniquely locate individual wells in an array. Therefore, we select two empty wells (regular and rotated by 45°) from the dataset being analyzed and use them as templates that are fitted to the image data. The NCC responses are in the range of (−1, +1), with −1 indicating a poor match, and +1 a perfect match. To speed up NCC, we used a Fourier implementation, and performed the normalization in the spatial domain. Figure 3B shows the NCC responses of the example wells in Figure 3A to the best-fitting (of the two) templates in Figure 3A. We used the local maximum clustering algorithm (Wu et al., 2004) on the best-fitting NCC response to detect well centers, and used the known spacing between nanowells to filter out invalid responses, yielding a robust localization of wells with >99% accuracy (Section 3). To cope with artifacts, we discard the nanowell videos whose maximum NCC response falls below a predefined threshold (typ. 0.75). The resulting rigid spatial transformation estimates (Fig. 3C) are used to generate cropped motion-corrected nanowell video recordings.
2.3 Image pre-processing
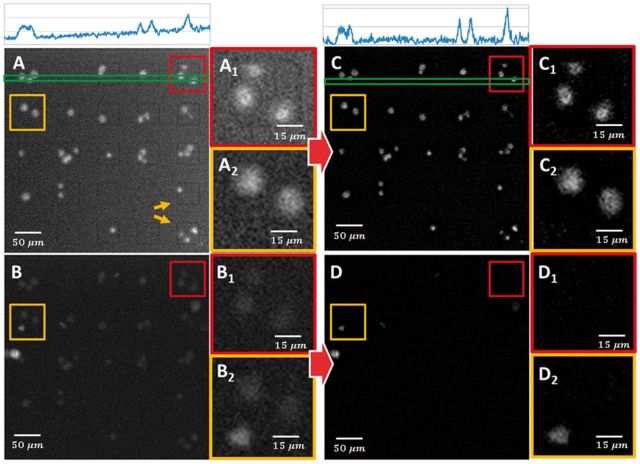
Each image frame of every video sequence is leveled to correct illumination variations by subtracting the local background estimated at each pixel using a Gaussian kernel with σ = 15 (Fig. 4 ). Next, we correct for spectral overlap between the emission spectra of the PKH67 and PKH26 dyes used to label the effector and target cells. The columns of the mixing matrix are estimated offline using principal component analysis for a 7 × 7 block of nanowell videos, and then re-used across the rest of the array. The unmixing was performed by the linear inverse method (Keshava and Mustard, 2002). Finally, we smooth the images using a median filter with radius rm = 3 while preserving cell boundaries. As noted by other authors, such pre-processing is essential for reducing high-throughput cell segmentation errors (Singh et al., 2014).
Fig. 4.
Illustrating the pre-processing (leveling, smoothing, unmixing, illumination correction) for a sample 5 × 5 nanowell block. (A) Shows the presence of well outlines in the target (NALM-6 cells) channel. Panels A1 and A2 show close-up views of two selected nanowells. (B) The corresponding effector (CAR+ T cells) channel. Panels B1 and B2 correspond to the same nanowells highlighted in A1 and A2, respectively. Panels C and D show the target and effector channels after pre-processing. The histograms of pixel intensities in the green boxes on top of the images show the uneven illumination in the raw image that is corrected by the pre-processing (Color version of this figure is available at Bioinformatics online.)
Even after pre-processing, cells exhibit variability in shape and intra-cellular fluorescence (Fig 5A), and this is a challenge for cell detection and separation of touching/overlapping cell bodies. The widely used multi-scale Laplacian of Gaussian (LoG) map (Al-Kofahi et al., 2010) misses the dim cell indicated by the red arrow, and is unable to separate the pair of cells indicated by the yellow arrow that exhibit non-round shapes and non-uniform intensities (Fig. 5C). Gradient-weighted watershed algorithms (e.g. Lin et al., 2007) have difficulty separating cells with weak edges. In order to overcome these limitations, we propose a normalized multi-threshold distance map (NMTDM) (Fig. 5C) that is designed to detect cell bodies, and it works by averaging distance maps corresponding to multiple thresholds, as follows. First, the normalized pixel intensity distributions p (i) of our pre-processed images are modeled by a mixture of 3 Gaussian distributions , with parameters and weights , that capture the dim background, intermediate foreground, and hyper-fluorescent foreground pixels, respectively. We use the k-means algorithm with deterministic seeding for estimating the mixture weights since it is fast, requires few initialization parameters, converges reliably, and produces comparable results to expensive expectation maximization algorithms, making it ideal for our high-throughput analysis. Clusters 2 and 3 together capture the image foreground. This foreground is divided into a set of connected components denoted . Next, let Lmin and Lmax denote the minimum and maximum pixel intensity values for this foreground. We define a series of M threshold levels (typ. 20) denoted l between Lmin and Lmax separated by , so . Each of these thresholds is used to generate a corresponding binary mask denoted and a corresponding Euclidean distance map . We then normalize the Euclidean distance maps for each connected component by the corresponding maximum value within each connected component , to ensure that the distance maps at different levels contribute equally to the final response. With this, the NMTDM for each connected component Rh can be written as the following pixel-level average of normalized distances across the thresholding levels l:
| (1) |
Note that the NMTDM computation is only performed for the foreground pixels, and can be carried out efficiently in parallel for different connected components. This map exhibits much clearer peaks compared with the multi-scale LoG (Fig. 5B versus C), and allows reliable cell detection.
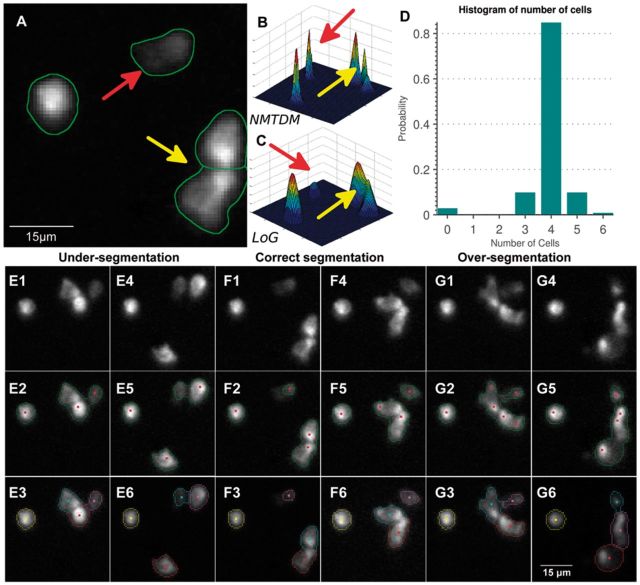
Fig. 5.
Illustrating the ability of the confinement-constrained cell segmentation method to recover a nanowell movie that cannot be segmented by conventional methods. (A) A sample image frame for a single nanowell containing four effector (NK) cells. The red arrow points to a cell with very low contrast that is missed by conventional algorithms. The yellow arrow points to two cells that are difficult to separate due to non-uniform fluorescence. (B) The proposed NMTDM improves upon the Log response in (C). (D) Histogram of cell counts shows a variable number of cells, implying that this nanowell cannot be automatically segmented without error. The confinement-constrained algorithm uses the peak of this histogram (correctly at 4) to re-segment the entire movie correctly. (E–G) Examples of re-segmentation results for under-, correct, and over segmentation scenarios (Color version of this figure is available at Bioinformatics online.)
Individual cells are detected using local maxima clustering over the NMTDM (Wu et al., 2004). This step requires only two parameter settings: the number of levels M, and the clustering radius r for selecting the peaks. Using this, we estimate the number of cells independently for each frame, and compute a histogram over the time series (Fig. 5D). Knowing that the number of cells in a nanowell stays constant (cell divisions are rare within the observation period), the presence of more than one non-zero entry in this histogram implies that conventional segmentation and tracking results would be error prone for this nanowell, and require proofreading. However, the histogram exhibits a peak at the correct cell count (4). We found that the histogram peak is a reliable indicator of cell counts over a time-lapse sequence despite errors in individual frames, and the height of the peak of the normalized histogram is a reliable measure of our confidence in the cell count. For this illustration, the peak reaches 82%. We discard nanowells for which the peak falls below 75%.
2.4 Confinement constrained cell re-segmentation
Although the above-described method is effective for estimating the correct number of cell bodies, it does not yield precise cell location estimates and cell segmentations, because it assumes that the cells are brighter closer to their centers. Our strategy to overcome this limitation is to use the histogram-based cell count estimate to re-segment the cells de novo by a normalized spectral clustering of image pixels (Shi and Malik, 2000). This method can detect cells of diverse shapes, and tends to estimate clusters (cells) with similar sizes—a reasonable assumption when handling ambiguous images. Given N foreground pixel coordinates, we compute a similarity matrix as follows:
| (2) |
where ε is a user-defined constant representing the maximum distance between a pixel and its neighbors, is the Euclidean norm, and σ controls the neighborhood width. Next, we compute the degree matrix D and the un-normalized graph Laplacian matrix L = D − W where D is a diagonal matrix defined as:
| (3) |
From this, we form the matrix by computing the first eigenvectors of the generalized eigenvalue problem . Finally, we cluster the points corresponding to the rows of into clusters , and re-label the foreground pixels accordingly. This method (Fig. 5E–G) enables cells in video sequences to be re-segmented accurately despite errors on individual frames. We are guaranteed to obtain a fixed number of cells across each movie, and this simplifies cell tracking. Interestingly, the confinement constrained cell re-segmentation algorithm also enables efficient editing of incorrect segmentation and tracking results. If needed, a user can re-run the spectral clustering based re-segmentation with the corrected cell count, and this yields the correct results in most cases.
2.5 Confinement-constrained cell tracking
Reliable cell tracking is needed to quantify the complex motile behaviors of cells at high throughput. The low temporal sampling rate (5–10 min/frame) implies that cells can undergo significant displacements and shape changes between frames. In addition, the effect of the nanowell walls makes it difficult to predict cell movements. Importantly, we wish to avoid the need for manual proofreading. With these considerations in mind, we propose a confinement-constrained tracking method that is fast, fully automated, and reliable. It is formulated globally over the entire movie, rather than on a successive frame-by-frame basis. It does not require any initialization, and requires only three parameters. Note that our algorithm is not proposed for general-purpose cell tracking problems. It is designed specifically for confinement-constrained TIMING data with no cell divisions and sparse temporal sampling. For general problems, sophisticated cell-tracking methods have been described and compared in the literature (Chenouard et al., 2013; Magnusson et al. 2015; Maska et al. 2014; Narayanaswamy et al., 2012). The approaches include particle filtering (Smal et al., 2008), Kalman filtering (Genovesio et al., 2006) that require a motion model and an observation model, but do not need prior segmentations. Contour based (Mukherjee et al., 2004), mean-shift (Comaniciu et al., 2000) and level-set methods (Dzyubachyk et al., 2010), are preferable when high-temporal resolution data are available, and some can handle merging and splitting of cells implicitly (Dufour et al., 2011). Optimization-based approaches (Al-Kofahi et al., 2006; Li et al., 2010; Magnusson and Jaldén, 2012; Morefield, 1977; Padfield et al., 2011) require objects to be detected/segmented a priori and are preferred for low temporal resolution data. When objects can enter/exit the field, cells divide or die, or when the segmentation is unreliable, elaborate methods are described to handle appearance, disappearance, merge and split and automatic correction of segmentation errors (Held et al. 2010; Li et al. 2008; Magnusson et al., 2015; Narayanaswamy et al., 2012; Padfield et al., 2011; Zhou et al. 2009). For TIMING data, we are unconcerned with such complications because of the nanowell confinement property, so our formulation is a streamlined one.
We formulate the tracking of K cells over T frames as a globally optimal edge selection problem on a directed graph. A node in the graph represents cell j at frame t, and is described by an attribute vector , where is the centroid; is the area of the cell; and denotes the pixels defining cell j. An edge associates cell i at frame t − 1 to cell at frame , and we compute an association cost that measures the dissimilarity between cell regions i and j. An edge selection variable indicates if a given edge is selected in the final solution. Using integer programming, we seek the solution , where that minimizes the following sum of association costs over each nanowell:
| (4) |
The cell confinement constraint is implicit in this formulation. The inequality constraints ensure that each node is associated with a maximum of one node in the previous frame, and the next frame, respectively. In computing , we ignore shape and texture features since cell morphologies and intensity profiles vary over time. We compute a weighted sum of the Euclidean distance between cell centroids , the area difference between cells , and the following set-theoretic distance between the pixels for the two cells:
| (5) |
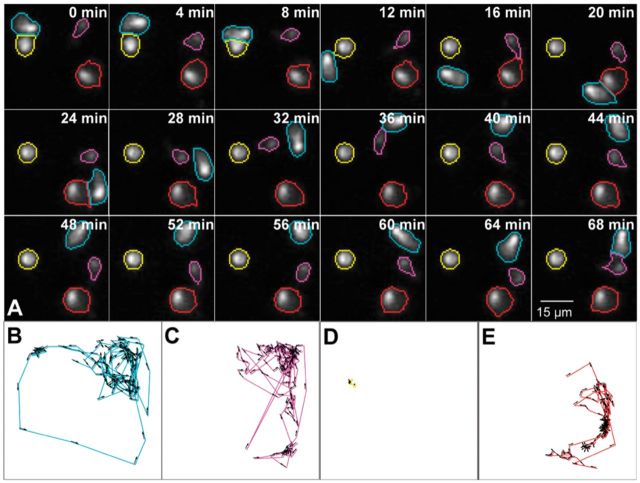
where is the overlapping area, and is the shortest distance between the cells’ pixels. The overall cost is written as , where the weights w1, w2 and w3 can be adjusted if needed. We used the default values , , and . One can increase when high temporal resolution data and good segmentation results are available. We solve the integer program in Equation (4) using the branch-and-bound algorithm (Schrijver, 1998). Although the theoretical worst-case running time can grow exponentially, this is not a concern since we are processing small cohorts of cells in each nanowell. Figure 6A illustrates the results of automated tracking for a nanowell containing only effector cells, showing our ability to cope with large inter-frame movements. Panels B–E depict sample cell trajectories for effector and target cells with diverse motion patterns. Additional examples are presented in Figure 8.
Fig. 6.
Illustrating confinement-constrained cell tracking. (A) Sample tracking of NK cells in a nanowell. The cell outlines are colored by cell identity. (B–E) Color-coded sample cell movement paths illustrating the ability to track effector and target cells with diverse movement patterns (Color version of this figure is available at Bioinformatics online.)
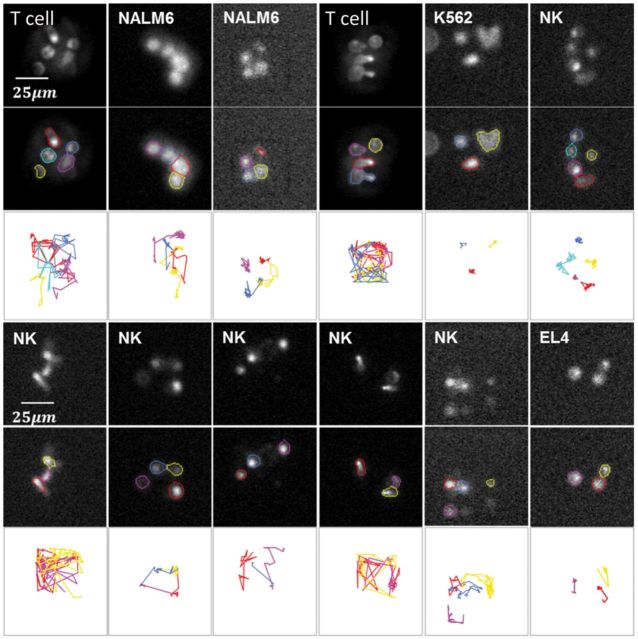
Fig. 8.
Visual summary of segmentation and tracking results involving various target cells (NALM6, K562 and EL4) and effector cells (NK cell or CAR+ T cell) from 12 TIMING experiments, all run with identical parameter settings (Table 4). The upper rows show sample frames. The middle rows show segmentations. The bottom rows show the cell tracks (Color version of this figure is available at Bioinformatics online.)
2.6 Detection and quantification of cell–cell contacts
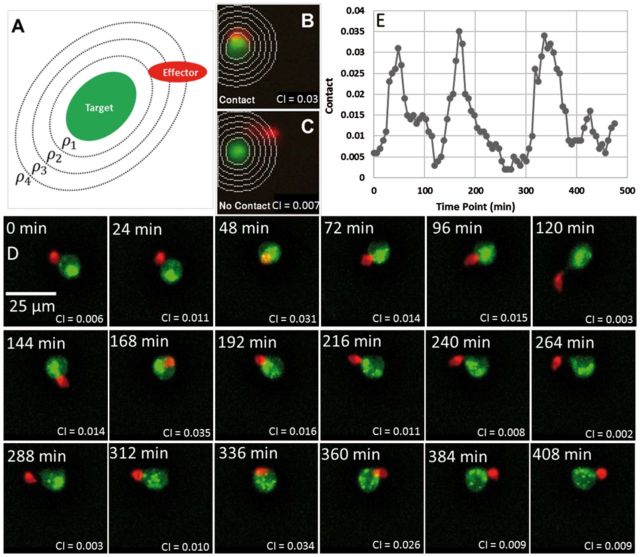
Detecting contacts between effectors and targets, and measuring the contact parameters (e.g. onset time, duration, frequency, extent) is needed for understanding how cell behaviors predict subsequent events of interest, especially the killing of targets by effectors. Approaches using the spatial proximity of cell segmentations (Chen et al., 2009; Klauschen et al., 2009) can be unreliable for TIMING data since they require much higher resolution imaging, and are sensitive to segmentation errors. With this in mind, we define a soft cell interaction measure CI for quantifying the interaction of a cell with its surrounding cells, as follows. First, we compute the normalized effector fluorescence signal in each nanowell j. Next, we define a series of ring-like compartments using a Euclidean distance map with respect to the segmented target cells as illustrated in Figure 7. Pixels with distances between and pixels form compartments with inner radii , where is the maximum distance needed to cover the complete nanowell. We sum the fluorescence intensities over each compartment, and normalize them by their radii that are proportional to the compartment areas. With this, the cell interaction measure is the following weighted intensity summation:
| (6) |
Fig. 7.
Illustration of cell interaction analysis using the CI measure. (A) Spatial regions used to compute CI for a target cell (K562 cell, green) and effector (NK cell, red); (B) Contact event for which CI = 0.03; (C) Non-contact for which CI = 0.007; (D) Sample frames over 5 h every 24 min. (E) The contact measure CI variation over time for target cells (Color version of this figure is available at Bioinformatics online.)
Figure 7 shows how CI (t) captures contacts between NK cells and K562 cells in a graded manner over an image sequence. This measure can be thresholded to detect contact events with a desired sensitivity. The threshold is set and verified manually by an immunologist based on visual verification of at least 30 nanowells for each TIMING dataset, starting with a default value (typ. 0.01). We consider this visual verification to be valuable due diligence. A full manual annotation of the contacts by five independent observers over 156 nanowell videos showed a 90.4% concordance with the default threshold. In order to definitely assign contact, it is defined to occur when the threshold criterion is met for two successive frames. The measure is defined above for a single cell and its neighbors. It can be extended to handle multiple cells by using the segmentation masks.
2.7 Feature computation
For each cell, the automated segmentation and tracking operations produce multiple time series of primary features including cell location , area , instantaneous speed , cell shape as measured by the eccentricity of the best-fitting ellipse , and the contact measure . In addition, target cell death events (apoptosis) are detected using Annexin V whose summed fluorescence intensity , is measured as another primary feature. Next, we compute cellular features at the scale of each nanowell, specifically, the number of effector cells , target cells , dead effectors , contacted targets , and killed targets . These measurements can be used to profile the nanowells.
The primary cellular features capture essential aspects of the cellular activities within each nanowell, but they have two disadvantages. First, they have a variable dimensionality, since the number of time points varies across TIMING experiments. Second, a long experiment can result in unnecessarily high-dimensional feature data. With the intent of deriving meaningful lower-dimensional representations of cellular events independent of the number of time points, we derive a set of eight secondary features for each cell. For each cell, we compute the average speed prior to first contact , average speed during the contact phase , average cell eccentricity prior to first contact , average eccentricity during the contact phase , time elapsed between first contact and death , total contact duration between first contact and death , time duration before first contact , the number of conjugations prior to target cell death .
3 Experimental results
The proposed method was evaluated on 12 TIMING experiments involving combinations of target cells (NALM6, K562 and EL4) and effector cells (NK cells or CAR+T cells), to evaluate its ability to cope with biological and imaging variability, different cell types, and varying experimental conditions. All the datasets were analyzed using the parameter settings summarized in Table 4. Given the sheer volume of the data, we start by presenting a visual summary of sample segmentation and tracking results in Figure 8. Overall, the algorithms and parameter settings proved reliable for automated analysis. As a detailed example, we present results of manually validating the segmentation and tracking on a small dataset with 2000 nanowells containing CAR+T cells and NALM6 cells imaged over 70–80 time points. Of these, 157 nanowells had more than four effectors or targets. These larger cohorts are irrelevant for the current biological study of interest, so they were omitted from further analysis. An additional 33 wells (1.7%) were discarded because the confidence in cell counts (histogram peak) was below 75%. Of the remaining 1803 nanowells, only 7 were not detected accurately due to air bubbles, so our overall nanowell detection accuracy exceeds 99%.
Table 4.
List of parameter settings
| Parameter | Processing step | Value (units) |
|---|---|---|
| Median filter size rm | Pre-processing | 3–5 (pixels) |
| Local maximum clustering r | Nanowell detection | Well width (pixels) |
| NCC response threshold | Nanowell detection | 0.75 (on 0–1 scale) |
| Number of mixtures K | Binarization | 3 |
| Thresholding Levels M | Seed detection | 20 (levels) |
| Local maximum clustering r | Seed detection | 8–15 (pixels) |
| Neighborhood | Spectral clustering | 2 (pixels) |
| Shape parameter σ | Spectral clustering | 2 (pixels) |
| Cost weights w1, w2, w3 | Cell tracking | 1, 10 and 100 |
| CI threshold | Contact analysis | 0.01 |
| Death marker threshold | Cell death analysis | 150 |
3. 1 Improvement in yield
In order to assess the fraction of wells with zero cell detection errors, we manually validated the results over the 1803 remaining nanowells using the proposed method and the (Al-Kofahi et al., 2010) algorithm was used as a benchmark. The results are summarized in Table 2. For the table entries with >90 wells, we manually validated 40% of wells, and the full set of wells for the remaining entries. Comparing the corresponding entries in Tables 1 and 2 show that the proposed method dramatically increased the number of usable wells. The few errors were due to persistently dim fluorescent cells that were missed, or because a cell was persistently occluded by another cell for >80% of the recording duration. For perspective, yield rates <90% render the automated image analysis results unusable, since the user has to manually analyze an excessive number of nanowells. With a yield close to 98%, the user can simply accept the automated results, and the modest error that they entail.
3.2 Cell segmentation and tracking performance
A total of 5061 cells were segmented and tracked in this dataset. The automated segmentation and tracking results were overlaid on the movies and presented to an immunologist, and the errors were scored as: under-segmentation, over-segmentation and incorrect association. Over-segmentation errors appear when a cell is identified as two or more objects. Under-segmentation occurs when the same label is assigned to multiple cells. Both of these errors can occur if the cell count is incorrect. Incorrect correspondence occurs when the tracking fails, usually due to segmentation errors. We consider a single association error sufficient to render the tracking results for a nanowell movie unusable. Despite this stringent requirement and the high volume of data, the algorithm is extremely accurate (Table 3). We next compared automatic segmentations of 30 randomly selected target and effector cells against manual segmentations. The Jaccard similarity index for target cells was 0.86 ± 0.12 (mean ± SD.) and 0.78 ± 0.17 for effector cells, indicating good segmentation accuracy.
3.3 Data analysis
We analyzed a TIMING dataset containing 11 520 nanowells (320 blocks of 6 × 6 wells) in which we imaged the dynamics of killing of K562 cells by in-vitro expanded NK cells for 8 h at 6-min intervals. From the automatically extracted features, we selected only the nanowells containing exactly one effector and one target cell, showing a stable effector-target contact of at least 6 min (two successive frames), and in the case of target death, contact by effector prior to death. This resulted in a cohort of 552 nanowells that is ideal for analyzing the dynamic behaviors of effectors, without the confounds associated with multi-effector cooperation or serial killing. Comparisons of the out-of-contact motility and the velocity during tumor cell conjugation demonstrated that NK cells that participated in killing displayed higher motility during both phases (Fig. 9A), consistent with our recent report that demonstrated that motility might be a biomarker for activated immune cells (Liadi et al., 2015). Furthermore, for NK cells the change in speed and arrest upon target cell ligation is well documented (Beuneu et al., 2009). Second, we were also interested in quantifying differences in NK cell behavior in interacting with live or dead cells. Of all the NK cells that participated in killing, only 18% re-conjugated to target cells subsequent to apoptosis, and when they did, their duration of conjugation 18 ± 14 min was significantly shorter than conjugations mediated by the same NK cells to live tumor cells (52 ± 72 min) (Fig. 9B). These results suggest that NK cells largely avoided conjugating to dead target cells, and even when they did, made an early decision to terminate the conjugation.
Fig. 9.
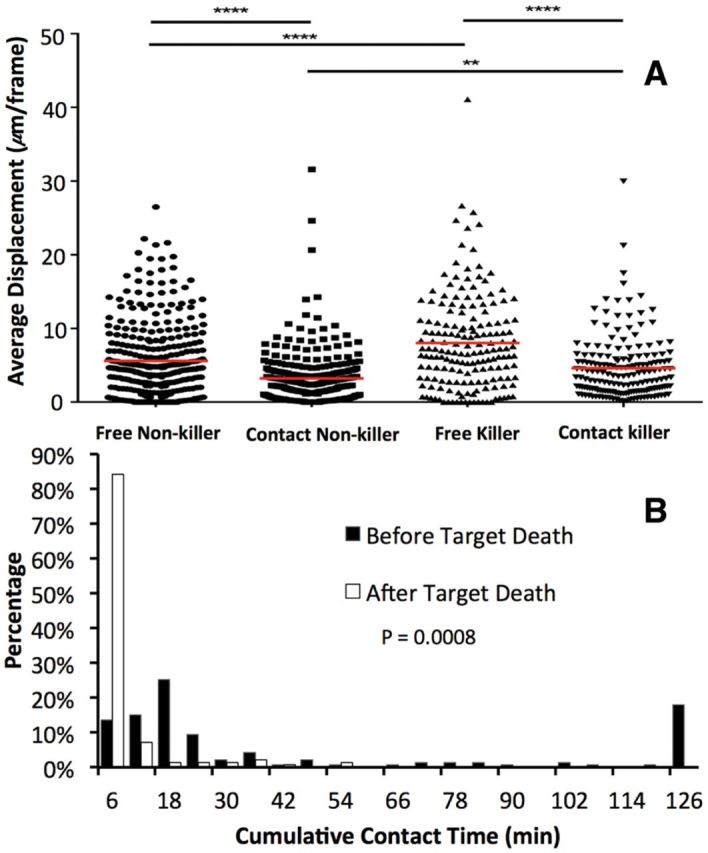
Illustrating TIMING feature analysis. (A) Distribution of Cumulative time in contact between effector cells and target cell, before and after cell death. (B) Distributions of displacements of NK cells before (free) or during contact with their target. The bars indicate comparisons, along with their significance (*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001) (Color version of this figure is available at Bioinformatics online.)
3.4 Implementation
For a block with 36 wells and 60 cells, the processing time is 9–10 s/block per time point on a Dell 910 PowerEdge server with 40 CPU cores, 1 TB of RAM, and a RAID 5 storage system. The cell tracking took 1.1 s/block; segmentation took 3.1 s/block; well detection took 1.5 s/block; and feature computation took 3.5 s/block. Various portions of the software were implemented in Python and C++, and MATLAB (Supplementary Material D).
4 Conclusions
The combined TIMING system consisting of the nanowell arrays and the proposed confinement-constrained image analysis methods enables a far more comprehensive sampling of cellular events than is possible manually. The proposed algorithms dramatically improved the yield and accuracy of the automated analysis to a level at which the automatically generated cellular measurements can be utilized for biological studies directly, with little/no editing. Most segmentation and/or tracking errors (mostly due to persistently low fluorescence (dim cells), or persistent cell occlusion over extended durations) can be detected based on the histogram threshold method, and the corresponding nanowells can either be ignored or edited. Our pipeline is now in active use in several biological studies being reported separately (e.g. Liadi et al., 2015; Romain et al., 2014). It is scalable to multi-terabyte datasets, and does not require elaborate initialization or careful parameter tuning. Supplementary Material D includes the software for the computational pipeline that enables routine, accurate, comprehensive, high-throughput, and high-yield analysis of TIMING datasets on multi-core computers.
Supplementary Material
Acknowledgements
We thank Dr Vladimir Senyukov and Dr Dean Lee for providing cells, and Dr Arvind Rao and Dr Joon Sang for informatics advice. This work was supported by the National Institutes of Health [R01CA174385]; the Cancer Prevention Research Institute of Texas [RP130570]; Welch Foundation [E1774] and the Melanoma Research Alliance Stewart-Rahr Young Investigator Award (NV). We thank Dr Magnusson for sharing his code and providing guidance.
Conflict of Interest: Dr. Cooper founded and owns InCellerate, Inc. He has patents with Sangamo BioSciences with artificial nucleases. he consults with Targazye, Inc (American Stem cells, Inc.), GE Healthcare, Ferring Pharmaceuticals Inc., Bristol-Myers Squibb. None of these activities had any influence on any part of this study.
References
- Al-Kofahi O., et al. (2006) Automated cell lineage construction: a rapid method to analyze clonal development established with murine neural progenitor cells. Cell Cycle, 5, 327–335. [DOI] [PubMed] [Google Scholar]
- Al-Kofahi Y., et al. (2010) Improved automatic detection and segmentation of cell nuclei in histopathology images. IEEE Trans. Biomed. Eng., 57, 841–852. [DOI] [PubMed] [Google Scholar]
- Arslan S., et al. (2013) Attributed relational graphs for cell nucleus segmentation in fluorescence microscopy images. IEEE Trans. Med. Imaging, 32, 1121–1131. [DOI] [PubMed] [Google Scholar]
- Beuneu H., et al. (2009) Dynamic behavior of NK cells during activation in lymph nodes. Blood, 114, 3227–3234. [DOI] [PubMed] [Google Scholar]
- Chen Y., et al. (2009) Automated 5-D analysis of cell migration and interaction in the thymic cortex from time-lapse sequences of 3-D multi-channel multi-photon images. J Immunol. Methods, 340, 65–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chenouard N., et al. (2013) Multiple hypothesis tracking for cluttered biological image sequences. IEEE Trans. Pattern Anal. Mach. Intell., 35, 2736–3750. [DOI] [PubMed] [Google Scholar]
- Comaniciu D., et al. (2000) Real-time tracking of non-rigid objects using mean shift. In: Proceedings of the Computer Vision and Pattern Recognition, vol. 2 pp. 142–149. [Google Scholar]
- Couprie C., et al. (2011) Power watershed: A unifying graph-based optimization framework. IEEE Trans. Pattern Anal. Mach. Intell., 33, 1384–1399. [DOI] [PubMed] [Google Scholar]
- Deguine J., et al. (2012) Cutting edge: tumor-targeting antibodies enhance NKG2D-mediated NK cell cytotoxicity by stabilizing NK cell-tumor cell interactions. J. Immunol., 189, 5493–5497. [DOI] [PubMed] [Google Scholar]
- Dufour A., et al. (2011) 3-D active meshes: Fast discrete deformable models for cell tracking in 3-D time-lapse microscopy. IEEE Trans. Image Process., 20, 1925–1937. [DOI] [PubMed] [Google Scholar]
- Dzyubachyk O., et al. (2010) Advanced level-set-based cell tracking in time-lapse fluorescence microscopy. IEEE Trans. Med. Imaging, 29, 852–867. [DOI] [PubMed] [Google Scholar]
- Forslund E., et al. (2012) Novel microchip-based tools facilitating live cell imaging and assessment of functional heterogeneity within NK cell populations. Front. Immunol., 3, 300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genovesio A., et al. (2006) Multiple particle tracking in 3D+t microscopy: method and application to the tracking of endocytosed quantum dots. IEEE Trans. Image Process., 15, 1062–1070. [DOI] [PubMed] [Google Scholar]
- Held M., et al. (2010) CellCognition: time-resolved phenotype annotation in high-throughput live cell imaging. Nat. Methods, 7, 747–754. [DOI] [PubMed] [Google Scholar]
- Keshava N., Mustard J. (2002) Spectral unmixing. IEEE Signal Process. Mag., 19, 44–57. [Google Scholar]
- Klauschen F., et al. (2009) Quantifying cellular interaction dynamics in 3D fluorescence microscopy data. Nat. Protoc., 4, 1305–1311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F., et al. (2010) Multiple nuclei tracking using integer programming for quantitative cancer cell cycle analysis. IEEE Trans. Med. Imaging, 29, 96–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K., et al. (2008) Cell population tracking and lineage construction with spatiotemporal context. Med. Image Anal., 12, 546–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liadi I., et al. (2013) Quantitative high-throughput single-cell cytotoxicity assay for T cells. J. Vis. Exp., e50058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liadi I., et al. (2015) Individual motile CD4+ T cells can participate in efficient multi-killing through conjugation to multiple tumor cells. Cancer Immunol. Res., 3, 473–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin G., et al. (2007) A multi-model approach to simultaneous segmentation and classification of heterogeneous populations of cell nuclei in 3D confocal microscope images. Cytometry, 71, 724–736. [DOI] [PubMed] [Google Scholar]
- Ma Z., et al. (2013) Mesenchymal stem cell-cardiomyocyte interactions under defined contact modes on laser-patterned biochips. PLoS One, 8, e56554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnusson K., Jaldén J. (2012) A batch algorithm using iterative application of the Viterbi algorithm to track cells and construct cell lineages. In: Proceedings of the IEEE 9th Symposium on Biomedical Imaging (ISBI), pp. 382–385. [Google Scholar]
- Magnusson K., et al. (2015) Global linking of cell tracks using the viterbi algorithm. IEEE Trans. Med, Imaging, 34, 911–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maska M., et al. (2014) A benchmark for comparison of cell tracking algorithms. Bioinformatics, 30, 1609–1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meijering E., et al. (2012) Methods for cell and particle tracking. Methods Enzymol., 504, 183–200. [DOI] [PubMed] [Google Scholar]
- Morefield C. (1977) Application of 0–1 integer programming to multitarget tracking problems. IEEE Trans. Automat. Control, 22, 302–312. [Google Scholar]
- Mukherjee D., et al. (2004) Level set analysis for leukocyte detection and tracking. IEEE Trans. Image Process., 13, 562–572. [DOI] [PubMed] [Google Scholar]
- Narayanaswamy A., et al. (2012) Multi-temporal globally-optimal dense 3-D cell segmentation and tracking from multi-photon time-lapse movies of live tissue microenvironments. Spring. Lect. Notes Comp. Sci., 7570, 147–162. [Google Scholar]
- Ostuni E., et al. (2001) Selective deposition of proteins and cells in arrays of microwells. Langmuir, 17, 2828–2834. [Google Scholar]
- Padfield D., et al. (2011) Coupled minimum-cost flow cell tracking for high-throughput quantitative analysis. Med. Image Anal., 15, 650–668. [DOI] [PubMed] [Google Scholar]
- Parvin B., et al. (2007) Iterative voting for inference of structural saliency and characterization of subcellular events. IEEE Trans. Image Process., 16, 615–623. [DOI] [PubMed] [Google Scholar]
- Pham K., et al. (2013) Divergent lymphocyte signalling revealed by a powerful new tool for analysis of time-lapse microscopy. Immunol. Cell Biol., 91, 70–81. [DOI] [PubMed] [Google Scholar]
- Rettig J.R., Folch A. (2005) Large-scale single-cell trapping and imaging using microwell arrays. Anal. Chem., 77, 5628–5634. [DOI] [PubMed] [Google Scholar]
- Romain G., et al. (2014) Antibody Fc engineering improves frequency and promotes kinetic boosting of serial killing mediated by NK cells. Blood, 124, 3241–3249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sackmann E.K., et al. (2014) Characterizing asthma from a drop of blood using neutrophil chemotaxis. Proc. Natl. Acad. Sci. USA, 111, 5813–5818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrijver A. (1998) Theory of Linear and Integer Programming. John Wiley & Sons. [Google Scholar]
- Shi J., Malik J. (2000) Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell., 22, 888–905. [Google Scholar]
- Singh S., et al. (2014) Pipeline for illumination correction of images for high-throughput microscopy. J. Microsc., 256, 231–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smal I., et al. (2008) Particle filtering for multiple object tracking in dynamic fluorescence microscopy images: Application to microtubule growth analysis. IEEE Trans. Med. Imaging, 27, 789–804. [DOI] [PubMed] [Google Scholar]
- Vanherberghen B., et al. (2013) Classification of human natural killer cells based on migration behavior and cytotoxic response. Blood, 121, 1326–1334. [DOI] [PubMed] [Google Scholar]
- Varadarajan N., et al. (2012) Rapid, efficient functional characterization and recovery of HIV-specific human CD8+ T cells using microengraving. Proc. Natl. Acad. Sci. USA, 109, 3885–3890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., et al. (2012) Quantitating cell-cell interaction functions with applications to glioblastoma multiforme cancer cells. Nano Lett., 12, 6101–6106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitesides G.M., Stroock A.D. (2001) Flexible methods for microfluidics. Phys. Today, 54, 42–48. [Google Scholar]
- Wu X., et al. (2004) The local maximum clustering method and its application in microarray gene expression data analysis. EURASIP J. Adv. Signal Process., 2004, 53–63. [Google Scholar]
- Yamanaka Y.J., et al. (2012) Single-cell analysis of the dynamics and functional outcomes of interactions between human natural killer cells and target cells. Integr. Biol. (Camb), 4, 1175–1184. [DOI] [PubMed] [Google Scholar]
- Yang X., et al. (2006) Nuclei segmentation using marker-controlled watershed, tracking using mean-shift, and Kalman filter in time-lapse microscopy. IEEE Trans. Circuits Syst., 53, 2405–2414. [Google Scholar]
- Yin Z., et al. (2008) Analysis of pairwise cell interactions using an integrated dielectrophoretic-microfluidic system. Mol. Syst. Biol., 4, 232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoo J.-C., Han T.H. (2009) Fast normalized cross-correlation. Circuits, Syst. Signal Process., 28, 819–843. [Google Scholar]
- Zaretsky I., et al. (2012) Monitoring the dynamics of primary T cell activation and differentiation using long term live cell imaging in microwell arrays. Lab. Chip., 12, 5007–15. [DOI] [PubMed] [Google Scholar]
- Zhao W., et al. (2011) Cell-surface sensors for real-time probing of cellular environments. Nat. Nanotechnol., 6, 524–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng C., et al. (2012) Quantitative study of the dynamic tumor-endothelial cell interactions through an integrated microfluidic co-culture system. Anal. Chem., 84, 2088–2093. [DOI] [PubMed] [Google Scholar]
- Zhou X., et al. (2009) A novel cell segmentation method and cell phase identification using Markov model. IEEE Trans. Inf. Technol. Biomed., 13, 152–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.