Abstract
While advances in genomics have enabled sensitive and highly parallel detection of nucleic acid targets, the isolation and extraction of the nucleic acids remain a critical bottleneck in the workflow. We present here a simple 3D printed microfluidic chip that allows for the vortex and centrifugation free extraction of nucleic acids. This novel microfluidic chip utilizes the presence of a water and oil interface to filter out the lysate contaminants. The pure nucleic acids, while bound on cellulose particles, are magnetically moved across the oil layer. We demonstrated efficient and rapid extraction of spiked Human Papillomavirus (HPV) 18 plasmids in specimen transport medium, in under 15 min. An overall extraction efficiency of 61% is observed across a range of HPV plasmid concentrations (5 × 101 to 5 × 106 copies/100 μl). The magnetic, interfacial, and viscous drag forces inside the microgeometries of the chip are modeled. We have also developed a kinetics model for the adsorption of nucleic acids on cellulose functionalized superparamagnetic beads. We also clarify here the role of carrier nucleic acids in the adsorption and isolation of nucleic acids. Based on the various mechanistic insights detailed here, customized microfluidic devices can be designed to meet the range of current and emerging point of care diagnostics needs.
INTRODUCTION
Sample preparation is a crucial part of rapid molecular assays and remains to be a bottleneck in the field of diagnostics.1,2 To date, the most commonly used methods for the extraction of nucleic acids are spin column based purification and magnetic bead based immobilization purification. While those are proven and established methods that have demonstrated good rate of recovery of nucleic acids, they require multiple steps of washing and exchanges of fluids. These procedures often require multiple instruments such as high speed centrifuges and vortexers. As a result, although many downstream isothermal assays already have the potential be performed in point of care settings, most nucleic acid extraction workload are sent to specialized labs.3 The inability to quickly and easily extract nucleic acids at the point of sample collection greatly hinders the progress of point of care diagnostics.
Microfluidics devices can be applied to streamline sample extraction steps. We evaluate here the efficacy of microfluidic chip fabrication using stereolithographic (SLA) 3D printing. In this work, we develop a novel 3D printed microfluidic chip design and used it to perform extraction of Human Papillomavirus (HPV) type 18 DNA, a potential oncogenic marker. In this microfluidic chip, two wells are connected by a microchannel containing a hydrophobic oil phase. Since the two wells contain hydrophilic fluids, two oil and water interfaces are formed at the microchannel and well junctions. Cellulose functionalized super-paramagnetic beads are used to capture and magnetically transport bound nucleic acid from one (sample well (SW)) well to the other (elution well (EW)). Due to the hydrophobic barrier, organic cellular contaminants and carryover lysis buffer salts are effectively left behind, and purified nucleic acids are transported to the elution well.
Although researchers have attempted to convert tube-based extraction kits to microfluidic platforms, the fundamental modeling to explain the designs of the microfluidic chips is largely missing.4–6 We detail here a quantitative model of the three main forces in a typical two phase microgeometry: the interfacial tension, the magnetic, and the viscous drag forces. While the adsorption of nucleic acids on silica surfaces has been studied,7,8 the adsorption kinetics on cellulose functionalized magnetic particles is not well understood. We also present here a kinetics model for the adsorption characteristics of nucleic acids on cellulose functionalized surfaces.
MATERIALS AND METHODS
3D microfluidic chip design
The microfluidic chip consists of three wells, an SW, an EW, and an oil chamber (OC). A rectangular microchannel connects the sample and elution wells and hosts the hydrophobic oil layer (Figure 1). The OC extends from the top of the mid-point of the microchannel and served as the oil loading platform. An oil chamber cap is designed to be snapped off from the microfluidic chip and inserted into the oil chamber after the microchannel is filled. The closed microchannel is designed with a number of fluid displacement windows that can be opened or closed during various stages of the operations of the chip (Figure 1(a)). Four displacement windows are designed into the top of the microchannel. The two windows closest to the oil chamber are 1 mm in diameter, and the two opening further away are 0.6 mm in diameter. Right next to the oil chamber are four plugs that can be snapped off, to close the four displacement windows during the operations of the chip. Two uni-directional valves are designed into the geometry of the microchannel. They are located near the channel and well junctions to prevent the magnetic particles from moving backwards. A magnetic bead reservoir (BW) is designed into the bottom of the EW. The bead reservoir aids the collection of magnetic beads after the bound nucleic acid is elution.
FIG. 1.
Illustrations of the overall shape and dimensions of the microfluidic chip. (a) A 3D mockup of the microfluidic chip from the top. The sample well (SW) and elution well (EW) are connected by a microfluidic channel. An oil chamber (OC) sits on top at the middle of the microchannel. Along with four openings, a removable oil chamber cap is designed into the top of the channel. (b) Cut-away side view of the microfluidic chip illustrating the dimensions of the chip features. (c) Profile view of the microfluidic chip in operation with the oil chamber closed off. The green dyed solution in the SW simulates the sample lysate solution, the blue dyed solution simulates the elution buffer, and the pink dyed oil simulates the hydrophobic oil layer. (d) Light microscopy image of chip microchannel. The designed width is 2 mm and the measured width is 2.04 mm. (e) Illustration of the cross section of the microchannel. The channel is 1 mm high and 2 mm wide.
3D microfluidic extraction chip fabrication
The microfluidic chip architecture (Figure 1) is designed in house using AutoCAD 2015 (Autodesk) and fabricated using an SLA 3D printing process by Quickparts (Atlanta, GA). The microfluidic chip was 3D printed using the Accura ClearVue resin on a high resolution SLA process. The chips were removed from any support material and polished with 200 grit sandpaper. Microscopic inspection of the microfluidic chips was performed before any experiments. The microchannel's dimensional accuracy was verified under a microscope.
3D microfluidic extraction chip operation
The microfluidic chip is designed to be used without powered tools. First, a lysis solution containing propan-2-ol, chaotropic salts, and carrier RNA is made using the supplied reagents from the MagMax Viral RNA kit (Thermo Fisher Scientific, Waltham, MA). The lysis solution is then added to the sample at a ratio of two to one. 10 μl of superparamagnetic bead solution (MagMax) is then added to lysed sample and pipette mixed for 4 min. To form the hydrophobic oil layer, 60 μl of castor oil from Sigma-Aldrich (St. Louis, MO) is loaded into the oil chamber, and the oil chamber is then capped. The bead and sample lysate solution are then loaded into the sample well (Figure 1) and the elution buffer (MagMAX) is added to the elution well. After the beads are collected at the bottom of the sample well using a D8C neodymium permanent magnet (K&J Magnets, Jamison, PA), they are moved across the water and oil interphase. As the magnetic beads are moved into the oil filled channel, the majority of the hydrophilic protein and salt contaminants are filtered out. As the bead cluster moves pasts each fluid displacement windows, the respective plugs are inserted into the windows to close them off. After the beads are transported into the elution well, the elution buffer containing the magnetic beads is pipette-mixed for 2 min to elute the purified nucleic acids. A neodymium permanent magnetic is then placed directly under the bead reservoir and the bead free supernatant is collected.
Extraction of spiked HPV-18 plasmid in specimen transport medium (STM)
The spiked HPV samples were prepared by serially diluting HPV-18 plasmids in Sigma Virocult Specimen Transport Medium from Medical Wire and Equipment (MWE) (Wiltshire, England). The Sigma Virocult specimen transport medium contains hydrolyzed bovine milk albumin (lactalbumin hydrolysate) at 3 mg/ml, as well as glucose at 1 mg/ml. Lyophilized full length HPV-18 plasmids were obtained from the American Type Culture Collection (ATCC, Manassas, VA). A range of concentrations from 5 × 101 to 5 × 106 per 100 μl of spiked HPV samples were made. 100 μl of each concentration of spiked sample was used for the positive extraction runs. Nuclease free water was used for negative control runs. Eluted nucleic acids were quality checked using nanodrop spectrophotometer (Thermo Fisher Scientific, Waltham, MA) before quantitative Polymerase Chain Reaction (PCR) quantitation.
Quantitation of HPV-18 plasmid extraction efficiency
Real time quantitative PCR was performed on all extracted HPV DNA. 5 μl of eluted nucleic acid was used in the PCR mix for each concentration. Reactions were performed in 20 μl volumes using the Rotor Gene SYBR Green PCR Kit (Qiagen, Valencia, CA) on a PikoReal 24 real time PCR machine (Thermo Scientific, Waltham, MA). Primers were designed in house. 4 pmol of each forward (5′ CGAACCACAACGTCACACAA) and reverse (5′ ACGGACACACAAAGGACAGG) primers was used. Reactions were run in duplicates. A positive control reaction using 5 × 108 copies of HPV plasmids was performed along with a no template control (NTC) reaction using nuclease free water. The percentage recovery of nucleic acid was calculated from the difference in threshold values between recovered nucleic acid from each extraction reaction and the positive control.
Evaluation of nucleic acid adsorption kinetics
For the calculation of the maximum binding capacity of the beads, the mass of nucleic acid adsorbed was approximated to be the same as the amount of nucleic acid eluted from the beads. The mass of eluted nucleic acid was quantified using a UV-vis nanodrop spectrophotometer (Thermo Fisher Scientific, Waltham, MA). The number of magnetic beads used for the experiments was estimated by performing a one thousand fold dilution of the stock concentration of magnetic beads, and then calculating the number of beads per unit volume under light microscopy. 2 μg of carrier RNA was incubated with 1 μl and 2.5 μl of stock bead solution for 240 s to measure the maximum binding capacity of the beads. To determine the binding kinetics of nucleic acid on cellulose surfaces, 1 μg of carrier RNA was incubated with 10 μl of stock concentration of magnetic bead solution (7.2 ± 0.5 × 107 beads) for 10, 20, 30, 100, and 240 s.
RESULTS AND DISCUSSION
3D printing for microfluidics
Due to the applications required, microfluidic chips have to be water tight, chemically inert, dimensionally accurate, and optically transparent. With the increasing availability of high resolution stereolithographic 3D printing, simple additive manufactured microfluidic devices are now possible. Here, we report a microfluidic chip fabricated using a watertight and transparent resin, Accura ClearVue. The various dimensions of the microfluidic chip features are illustrated in Figure 1. The high resolution SLA process we used has a specified x-y resolution of 75 μm and a z resolution of 50 μm. The dimensional accuracy of the microchannel is evaluated under light microscopy (Fig. 1(d)). The designed channel width is 2 mm, and the measured width is 2.04 ± 0.005 mm. This is within the acceptable range for dimensional tolerances.
Magnetic particle motion inside a microchannel
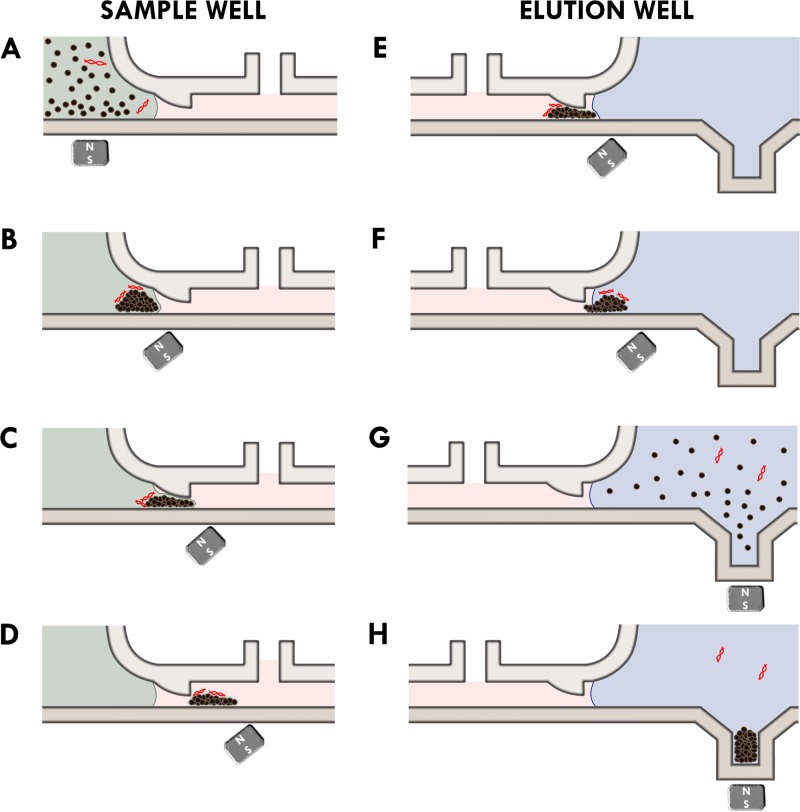
We visually observed the movement of the magnetic beads through the microchannel. Figure 2 schematically shows the bead transport process as observed during the experiments. First, the beads along with the HPV plasmids were loaded into the SW as shown in Figure 2(a). The beads were then collected at the bottom of the SW (Figure 2(b)). As the magnet was moved towards the right (elution well), beads were observed to break through the oil water interface as shown in Figure 2(c). As the beads moved into the oil phase, some of the oil was displaced, and the oil level in the fluid displacement window rose. The magnetic bead clump retains an outer aqueous layer as it is moved into the oil layer (Figure 2(d)). When the beads reached the end of the microchannel, they broke into the oil-water interface again (Figure 2(e)) and are moved into the EW (Figure 2(e)). As expected, when the beads entered the elution well, it lowered the oil level in the nearest fluid displacement window (Figures 2(e) and 2(f)). Finally, the beads were collected at the bottom of the elution well, inside the bead reservoir (Figures 2(g) and 2(h)). The entire process takes less than 5 min to complete. Very little visible bead loss was observed. A video of the motion of the bead plug is included in the supplementary material (Supplementary Media File 1).9 Another video documenting the entire bead transfer process is included as well (Supplementary Media File 2).9 The magnetic beads (approximately 7.2 ± 0.5 × 107) moved as a randomly distributed “marching band” and was approximately 300 ± 50 μm in height and approximately 1–2 mm in length. The width of the beads band spanned the entire width of the channel. The height was governed by the entrance height of the channel as shown in Figure 2.
FIG. 2.
Schematic overview of the changes (a)–(h) in the oil and water interface as beads are magnetically moved across the microchannel. The lysis buffer is shown in green. The oil layer is shown in pink. The elution buffer is shown in blue.
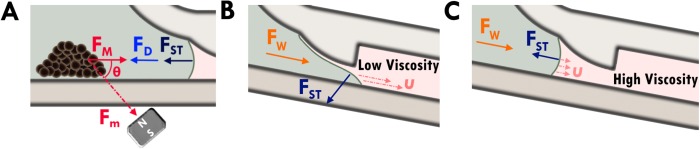
Dominating forces on the magnetic particles
The size and shape of bead clusters, as observed in experiments, depend on the quantity of beads used for a chosen magnet. As super-paramagnetic beads are moved from the aqueous lysis buffer into the oil channel (Figure 3), it experiences a set of forces: the magnetic driving force FM, the hydrodynamic drag force FD, the gravitational force Fg, and the interfacial tension force FST. The short-ranged inter-particle surface forces and random Brownian forces can be neglected to develop some basic understanding of the force balance. The gravitational force is also ignored as it is negligible compared to the other dominating forces. The magnetic beads can be modeled as spherical particles with a mean diameter of . The horizontal component of magnetic force on beads, under strong magnetic field, can be estimated using10
| (1) |
where is the mass of bead, is the saturated mass magnetization of the bead, is the magnetic field intensity, and . The magnet specifications as given by the manufacturer are used to plot the magnetic field gradient, dBx/dx (Figure 4(a)). Hence, when the distance between the magnet and the magnetic beads is 7.5 mm (), the force acting on each magnetic bead is approximately 5.62 pN (Figure 4(b)). Here, we used the mass of the bead m = 8.24 × 10−12 g, the mass magnetization M0 = 23.5 A m2/kg, and θ = 45°. The horizontal component of the force (FM) is about 3.97 pN. The density and the diameter of the magnetic beads in the MagMax kit were not given by the manufacturer; hence, for the purpose of calculations, we used the specifications of a similar type of magnetic bead (Dynabeads MyOne by the same manufacturer).11 The densities and mass magnetizations of the MagMax and the Dynabead MyOne magnetic beads were approximated to be the same. The viscous stokes drag force, experienced by each magnetic bead, is given by
| (2) |
where is the viscosity of the castor oil at room temperature and is the average velocity of magnetic beads. Hence, the drag force on the bead is as it moves through castor oil and as it moves through buffer. For a single magnetic bead, the viscous drag in oil is higher than the horizontal component of the driving force (FM), and the bead will not move when they are in the oil phase. The driving force increases linearly with the number of magnetic beads (n), and the viscous drag force increases by a factor of n1/3. Therefore, as the number of magnetic beads in formed clump increases, the driving force will eventually exceed the viscous force. Assuming that the magnetic beads form a spherical coagulate, a minimum of 3800 ± 50 beads are required to be moved in the oil phase (Figure 4(c)). The gravitational force on the beads is negligible in comparison to the drag and magnetic forces on the bead. As beads are moved towards the oil–water interface (as shown in Figure 2(c)), they must overcome surface tension forces before breaking into the oil and water interface. The surface tension force can be approximated as
| (3) |
where is the surface tension, is the curvature of the deformed oil and water interface created by the penetrating magnetic bead blob, and θST is the angle between the oil-water interface and the microchannel wall. The surface tension () of castor oil in water was measured to be 14.28 mN m−1 at room temperature. The maximum force of curvature due to surface tension for one magnetic bead is 4.7 × 104 pN. For a single magnetic bead, this force (FST) is much larger than both the driving force and the viscous drag force. Similar to the viscous drag, the surface tension force increases at a rate of n1/3 as the number of magnetic beads increases. A much larger number of beads, 1.3 ± 0.05 × 106, are required to be magnetically moved across the center of water and oil interphase (Figure 4(d)). Due to the curvature of the oil meniscus, the horizontal component of the force due to surface tension near the sides of the microchannel is lower than that at the center of the interphase. The angle of the meniscus is measured to be approximately 45°, and the force (FST) near the bottom of the microchannel per one magnetic bead is 3.3 × 104 pN. The number of beads required to be moved magnetically across the oil and water interphase near the bottom of the channel is therefore 7.7 ± 0.05 × 105 (Figure 4(d)). In addition to the vertical component of the driving force provided by the magnet, the lower FST near the side of the microchannel also causes the beads to break through the interphase near the bottom of the channel. The number of magnetic beads used in all experiments is much larger than the numbers required to overcome both the drag and interfacial tension forces.
FIG. 3.
Overview of the resultant forces acting on the magnetic beads and oil/water interface. (a) The resultant forces on the clump of magnetic beads. (b) The effect of a low viscosity oil phase on the retention of the water and oil interface. (c) The effect of a high viscosity oil phase on the retention of the oil and water interface.
FIG. 4.
Overview of the magnetic, hydrodynamic drag and surface tension forces acting on the magnetic beads. The magnet is at a 45° angle to the direction of motion, and the separation between the magnet and the bead is . (a) The change in dB/dx as the distance between the magnet and bead increases. (b) The change in the magnetic force as the distance between the magnet and the bead increases. (c) The minimum number of magnetic beads in a clump required for the magnetic driving force FM to overcome the viscous drag force in the microchannel. (d) The minimum number of magnetic beads required for the driving force to overcome the surface tension at the center and at the peripheral of the water and oil interphase. The angle, θ, of the interface is approximated to be 45°.
Stability of water and oil interphases
The water and oil interface is kept in place by both the interfacial tension and the viscous drag forces. The viscosity of the oil phase is very important in keeping the interface stable (Figures 3(b) and 3(c)). As illustrated in Figure 3(b), when the viscosity of the hydrophobic phase is low, any disturbances caused by the handling of the microchip will disrupt the water and oil interface. Before standardizing on using castor oil, we tried olive oil for the hydrophobic phase and the interface was not stable.
Recovery efficiency of HIV-18 plasmids
The extraction efficiency of our microfluidic chip was evaluated using real time qPCR. Eight different concentrations of spiked plasmid samples were used for extraction. Figure 5(a) shows fluorescence signal as function of cycle number for the eight serially diluted samples. A positive control using 5 × 108 copies of HPV plasmids and a NTC using water were included. 5 μl of extracted DNA from each sample was used in the PCR reaction mixture, meaning that only 1/20th of the actual number of recovered plasmids is represented in the PCR results. The initial concentration of the spiked samples ranged from 5 × 101 to 5 × 106 copies. The Ct values are plotted (Figure 5(b)) against the starting number of copies of plasmids. Across the range of concentrations, an overall recovery rate of 61% was achieved. The recovery rate is comparable to that achieved using conventional in tube extraction methods (data not shown). The real time q-PCR results demonstrate that this microfluidic chip is capable of achieving high extraction efficiencies across a large range of HPV plasmid concentrations. The lactalbumin hydrolysate in the specimen transport medium served as a mock protein contaminant for the HPV plasmid isolation experiments. Therefore, the q-PCR results also illustrate the efficacy of the microfluidic chip in filtering out any protein contaminants.
FIG. 5.
Real time q-PCR curves of extracted nucleic acids from spiked HPV samples. (a) The positive control reaction has 5 × 108 copies of stock HPV plasmid. The starting number of HPV plasmids in each sample is shown. For each sample, one twentieth of the extracted amount of HPV plasmid is used in the real time PCR mixture. The number of copies used in real time PCR is shown in brackets. (b) The calculated recovered number of HPV plasmids is plotted against the actual input number of HPV plasmids. The R2 value is 0.999 and one error bar denotes 1 standard deviation (s.d.).
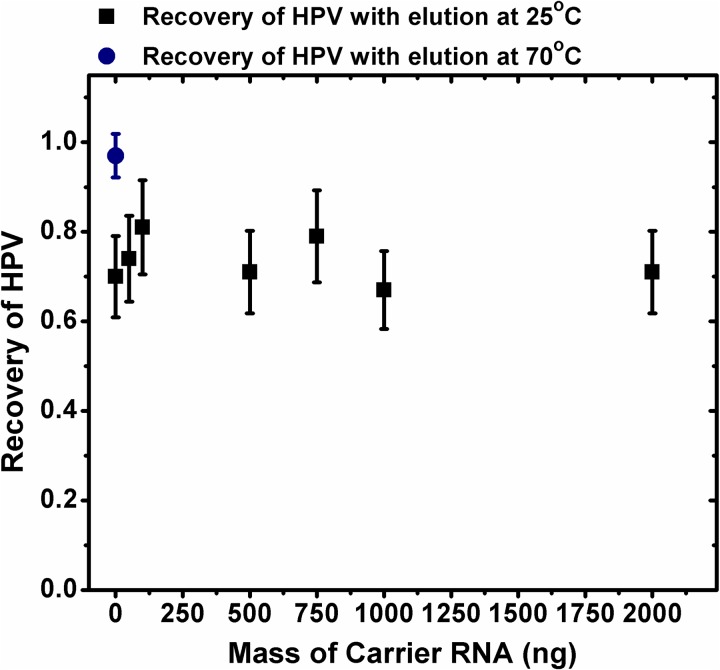
Effect of carrier RNA on the recovery of target nucleic acid
Some literature12,13 suggest that the inclusion of carrier RNA in the binding buffer can increase the nucleic acid extraction efficiency. The exact reason for such an increase is not clear; however, it has been hypothesized that on the bead surface, there are always a certain number of sites which will irreversibly bind nucleic acids. By including carrier RNA in the binding buffer, it can sacrificially bind to these sites, minimizing the loss of target DNA. We performed extraction of HPV plasmids using different concentrations of carrier RNA in the binding buffer. Figure 6 shows that, at least in our experiments, the HPV recovery rate (number of copies recovered/starting number of copies of plasmids) does not change with inclusion of carrier RNA in the binding buffer. For these runs, 5 × 106 copies of HPV plasmids were spiked in the samples. Even as the carrier RNA concentration was varied from zero to 2 μg, the recovery rate of HPV plasmid stayed at around 60%–70%. This suggests that perhaps the carrier RNA does not occupy the irreversible sites on the beads' surfaces. This would imply that 30%–40% of HPV DNA was lost to these higher affinity binding sites. Indeed, when we increased the temperature to 70 °C during the elution step, the recovery rate for when no carrier RNA was used jumped to close to 95% (as can be seen from Figure 6). This would suggest that, for our experiments, carrier RNA plays no role in the binding events of the target nucleic acids and does not influence the recovery rate.
FIG. 6.
The effect of the mass of carrier RNA on the recovery of target nucleic acid. The recovery efficiency of when the elution of captured HPV plasmids was performed at 25 °C is denoted by black squares, and the recovery efficiency of when elution was performed at 70 °C is shown by the navy circle. Error bars denote 1 s.d.
Model of binding kinetics of nucleic acids on cellulose beads
Although adsorption-desorption kinetics of nucleic acids onto various functionalized surfaces is a complex process, some broad stroke experimental time scales can be established using Langmuir kinetics. To quantify adsorbed concentration of nucleic acids onto the bead surface, cellulose functionalized magnetic beads were incubated in 1 μg of carrier RNA solution for various times. The adsorption rate is proportional to the number of available sites and the bulk solute concentration in the buffer. The desorption rate can be assumed to be proportional to . Hence, the rate of surface accumulation of nucleic acids can be written as
| (4) |
Here and denote adsorption and desorption rate constants and denotes total number of sites available on the bead surfaces. The concentration of nucleic acids in buffer can be estimated via mass balance
| (5) |
where , A, and V are initial concentration of nucleic acids in buffer, total available area on the beads, and volume of the buffer, respectively. Assuming negligible desorption rates (), we can combine Equations (4) and (5) and non-dimensionalize it to obtain
| (6) |
where is the fraction of available occupied sites on the beads, is the dimensionless time, and is the ratio of the available nucleic acids sites on the bead surface and the mass of nucleic acid available in the bulk fluid. This suggests that if , then a number of nucleic acid sites are limited and the adsorption will be governed by exponential decrease of the time of incubation. However, , then the number of nucleic acids in the bulk are limited, and adsorption follows second order kinetics. A close form analytical solution of Equation (6) can be obtained as
| (7) |
In the limit , that is when nucleic acids sites on the bead surface are equal to the nucleic acid available in the bulk fluid, the fraction of occupied sites approaches
| (8) |
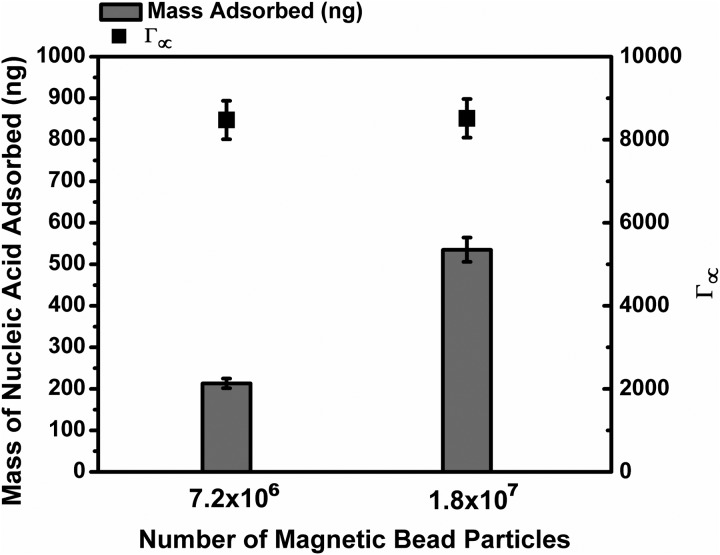
Maximum binding capacity of cellulose functionalized magnetic beads
As shown in Figure 7, the mass of adsorbed nucleic acid is measured for two different concentrations of magnetic beads. Since the mass of nucleic acid used is known to be in a great excess compared to the number of binding site available, the bead surface should be saturated at equilibrium. The maximum binding capacity for these beads is calculated to be, .
FIG. 7.
The mass of adsorbed nucleic acid for different concentrations of magnetic beads. The bulk concentration of nucleic acid used is in an excess compared to the maximum number of binding sites. The error bars denote 1 s.d.
Time based adsorption kinetics of nucleic acid on cellulose beads
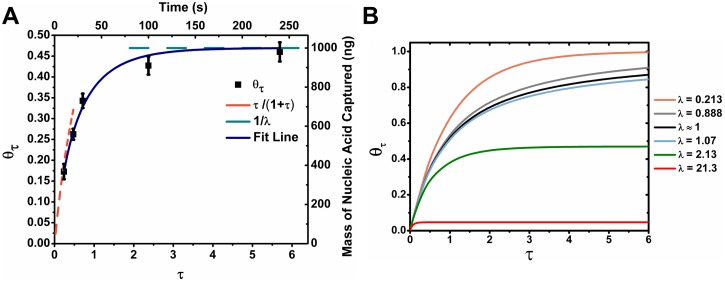
Figure 8(a) shows a plot of measured values of at different incubation times. The maximum number of available binding sites was determined from Figure 7. The experimental data are fitted using our binding kinetics model, which fits well with our data. There is no free parameter used in our model. This fit not only establishes that the desorption rate for these nucleic acid is negligible, but also that simple Langmuir kinetics works well to describe our system. In the limits , and as , . As shown in Figure 8(a), these limits agree well with our experimental data. Figure 8(b) shows the modeled for different values of λ. As can be seen in Figure 8(b), as the value of λ approaches 1, the adsorption rate slows down drastically due to the depletion of both substrate and binding sites as it approaches equilibrium. When λ ≫ 1 or λ ≪ 1, either the bulk nucleic acid or the binding sites available will always be in an excess even when the adsorption approaches equilibrium.
FIG. 8.
The effect of incubation time on the recovery of nucleic acids. (a) The effect of increasing the time of incubation on mass of nucleic acid adsorbed. Error bars denote 1 s.d. (b) Model of the effect of different bulk concentration of nucleic acids on the fraction of binding sites occupied as a function of time.
As the amount of nucleic acid adsorbed approaches equilibrium, approaches . The time taken for to reach can be obtained from the following equation:
| (9) |
where is , the fraction of the bulk concentration of nucleic acid in solution at time . Figure 9 models the timed require for different values of α across a range of λ. As can be expected, τ increases exponentially as α decreases. For large λ, or small α, the ratio between two and is .
FIG. 9.
The time required for different degrees of adsorption completion. The time required is modeled for 50%, 90%, 99%, and 99.9% completion of adsorption (α of 0.5, 0.1, 0.01, and 0.001, respectively).
For the concentrations of HPV plasmids attempted in this study, λ is on the order of magnitude of 104–109. As shown in Figure 9, the time required to reach completion of adsorption is very small for values of λ greater than 104. Therefore, at clinically relevant viral loads of HPV, adsorption will reach completion very quickly.
CONCLUSION
We demonstrated a novel 3D printed microfluidics chip can rapidly and efficiently extract nucleic acids in a power free environment. Utilizing a water and oil interfacial barrier, the filtering of contaminants in the sample and purification of the target nucleic acid are performed with just a simple magnetic motion. This microfluidic chip can be further integrated with various downstream assays to perform on-site diagnostic tests. We modeled the fundamental magnetic, interfacial, and viscous drag forces inside a microfluidic channel and calculated the required number of magnetic particles to enable transport of beads across a water and oil interface. In addition, we developed a model for the adsorption kinetics of nucleic acids on cellulose functionalized magnetic beads and demonstrated that carrier RNA played no role in the adsorption of target DNA.
ACKNOWLEDGMENTS
This work was supported in part by a Seed Award for Translational Research from Brown University. Lei Zhang is supported by a Graduate Fellowship from Brown University. The authors thank Dr. Mark Bobrow and Richard Joseph at PerkinElmer for their technical support. The authors also thank Dr. Susan Cu-Uvin at Miriam Hospital for insightful discussions on HPV typing in resource limited settings. Anubhav Tripathi oversaw the project and provided technical advice. Lei Zhang designed the microfluidic chip, performed the experiments, and analyzed the data. Lei Zhang and Anubhav Tripathi developed the models and wrote the manuscript. Rachel Deraney provided the oil viscosity measurement. The authors declare that they have no competing interests.
References
- 1. Cui F., Rhee M., Singh A., and Tripathi A., Annu. Rev. Biomed. Eng. 17, 267–286 (2015). 10.1146/annurev-bioeng-071114-040538 [DOI] [PubMed] [Google Scholar]
- 2. Weidemaier K., Carrino J., Curry A., Connor J. H., and Liebmann-Vinson A., Future Virol. 10(3), 313–328 (2015). 10.2217/fvl.14.117 [DOI] [Google Scholar]
- 3. Notomi T., Mori Y., Tomita N., and Kanda H., J. Microbiol. 53(1), 1–5 (2015). 10.1007/s12275-015-4656-9 [DOI] [PubMed] [Google Scholar]
- 4. Berry S. M., Alarid E. T., and Beebe D. J., Lab Chip 11(10), 1747–1753 (2011). 10.1039/c1lc00004g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Sur K., McFall S. M., Yeh E. T., Jangam S. R., Hayden M. A., Stroupe S. D., and Kelso D. M., J. Mol. Diagn. 12(5), 620–628 (2010). 10.2353/jmoldx.2010.090190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. den Dulk R. C., Schmidt K. A., Sabatte G., Liebana S., and Prins M. W. J., Lab Chip 13(1), 106–118 (2013). 10.1039/C2LC40929A [DOI] [PubMed] [Google Scholar]
- 7. Nguyen T. H., Chen K. L., and Elimelech M., Biomacromolecules 11(5), 1225–1230 (2010). 10.1021/bm901427n [DOI] [PubMed] [Google Scholar]
- 8. Nguyen T. H. and Elimelech M., Langmuir 23(6), 3273–3279 (2007). 10.1021/la0622525 [DOI] [PubMed] [Google Scholar]
- 9.See supplementary material at http://dx.doi.org/10.1063/1.4938559E-BIOMGB-9-023506 for videos of the transfer of magnetic beads inside the microfluidic chip.
- 10. Smistrup K., Bu M. Q., Wolff A., Bruus H., and Hansen M. F., Microfluid. Nanofluid. 4(6), 565–573 (2008). 10.1007/s10404-007-0213-0 [DOI] [Google Scholar]
- 11. Fonnum G., Johansson C., Molteberg A., Morup S., and Aksnes E., J. Magn. Magn. Mater. 293(1), 41–47 (2005). 10.1016/j.jmmm.2005.01.041 [DOI] [Google Scholar]
- 12. Read S. J., J. Clin. Pathol.-Mol. Pathol. 54(2), 86–90 (2001). 10.1136/mp.54.2.86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Shaw K. J., Thain L., Docker P. T., Dyer C. E., Greenman J., Greenway G. M., and Haswell S. J., Anal. Chim. Acta 652(1–2), 231–233 (2009). 10.1016/j.aca.2009.03.038 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4938559E-BIOMGB-9-023506 for videos of the transfer of magnetic beads inside the microfluidic chip.