Summary of Recent Advances
Current multiscale simulation approaches for membrane protein systems vary depending on their degree of connection to the underlying molecular scale interactions. Various approaches have been developed that include such information into coarse-grained models of both the membrane and the proteins. By contrast, other approaches employ parameterizations obtained from experimental data. Mesoscopic models operate at larger scales and have also been employed to examine membrane remodeling, protein inclusions, and ion channel gating. When bridged together such that molecular level information is propagated between the different scales, a systematic multiscale methodology for membrane protein systems can be achieved.
Introduction
Biomolecular systems consisting of membranes interacting with either embedded or bound proteins (which, from this point forward, will be referred to as membrane protein systems) represent an important challenge in the field of biomolecular simulation. The large length and time scales involved in these systems has motivated the development of novel coarse-grained (CG) and mesoscopic simulation approaches [1] to complement all-atom molecular dynamics (MD) simulation. Previous reviews in this journal have examined aspects of multiscale simulation in complex biomolecular systems [2-5], while other articles have reviewed the current state of large scale MD and CG simulations of self assembly [6], and the upper length scale limits of all atom MD simulation [7]. Excellent reviews examining the overall challenge of simulating membrane proteins can be found in Refs. [8,9], and a review of current MD protein and lipid force fields has recently appeared [10].
The focus of this review is on the ways in which molecular-level interactions can be incorporated into the systematic multiscale modeling of membrane protein systems. This focus is different from approaches based on parameterization of CG or mesoscopic models from experimental or other “knowledge-based” modeling concepts. The next section will describe, in a general context, how molecular level information can be incorporated and bridged into multiscale descriptions of membrane protein systems. Subsequent sections in this review will describe various recent CG and mesoscopic approaches, and how they each incorporate this important concept into their underlying methodologies.
Systematic multiscale simulation of membrane protein systems
The two main components of a multiscale simulation methodology for membrane protein systems are CG simulation (see Refs. [1-5] for examples and reviews) and mesoscopic and/or continuum approaches [11-17]. A CG model is one where at least three heavy atoms are combined into one single CG site and, as a result, some degree of molecular-level structure is retained. With CG simulation, the typical computational speedup can be from 10 to 1000 times faster than all-atom MD, depending on the complexity of the CG modeling and the size of the system. Mesoscopic models share with continuum approaches length scales and resolutions such that individual molecules are not explicitly defined. These approaches are closer to field theoretic models.
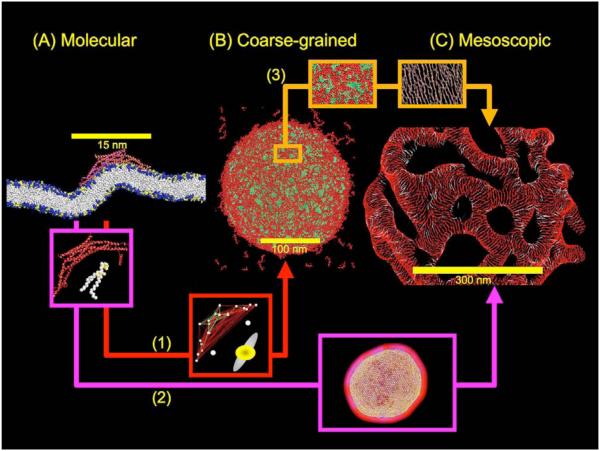
A working definition of a systematic multiscale simulation of a membrane protein system is one where the different spatial domains are bridged such that molecular scale information is somehow incorporated into the description at the lower resolution and therefore to higher length scales. Incorporating molecular scale information at higher scales allows for the emergent behavior at these scales to be traced back to the original molecular level detail. This scenario is shown in Fig. 1 using recent results from atomic (A)[18,19•], CG (B)[20,21] and mesoscopic (C)[12] simulations of N-BAR protein mediated membrane remodeling as a demonstration; however, this scenario is general and could be applied to a wide variety of membrane protein systems. Beginning with image (A), molecular scale information is employed in path (1) to develop CG models of both the protein and lipids (and possibly non-lipid molecules such as cholesterol). In this example, a heterogeneous elastic network (HeteroENM) model of the N-BAR protein [20] and a Hybrid Analytic-Systematic (HAS) model [21] for the lipid are then employed; however, other coarse-graining methodologies might also be used. In image (B), the resulting CG simulation accesses longer length and time scales than the original atomistic MD simulation; this example shows the early stages of liposome remodeling at length scales of 200 nm. In path (2), atomic level information is used to both guide in the development and then the subsequent parameterization of a mesoscopic (field theory-based) model [12], where proteins are not explicitly modeled, but rather their average behavior is incorporated into new collective variables (a spontaneous curvature field is used here and is depicted by the red/purple zone surrounding the inset mesoscopic liposome) [12]. This is shown in image (C) where an entire liposome has been remodeled by a mesoscopic N-BAR protein spontaneous curvature field. Path (3) instead bridges information obtained from the CG model in image (B) (e.g., local spatial correlations in N-BAR proteins as shown as the boxed images along the path) to a mesoscopic model capable of describing mesoscopic behavior at very large length and time scales. It should be noted that all of the CG paths (1-3) bridging the molecular, CG, and mesoscopic scale can be categorized as “serial” multiscale approaches [3].
Fig. 1.
A schematic showing the multiscale simulation methodology for a membrane protein system. The specific example of N-BAR domain protein mediated membrane remodeling is considered, but this approach can in principle be applied to a wide variety of membrane protein systems. The three main scales of the multiscale methodology are the molecular (A), coarse-grained (CG) (B) and mesoscopic (C). These scales are bridged by paths (1-3). Paths (1) and (3) connects the molecular to the mesoscopic via the CG scale, while path (2) directly connects the molecular to the mesoscopic regime. The image in path (2) shows how the N-BAR protein is directly transformed into a mesoscopic spontaneous curvature field (red/purple border surrounding the liposome in the inset), which combines with the elastic membrane (the liposome in the inset). Path (3) instead first describes emergent mesoscopic behavior at the CG level and then employs it in the development of new mesoscopic models. This approach utilizing CG simulation provides a more refined level of detail in the final mesoscopic model than could be obtained along path (2). For example, the spatial correlations shown in the orange box can be employed to derive new phenomenological mesoscopic field based descriptions of the system that capture the behavior beyond what could be accessed with even very large scale MD simulation.
Two main approaches for coarse-graining membrane protein systems (image (B) in Fig. 1) will be considered in this review: (1) CG membrane protein models arising from the “bottom-up” Multiscale Coarse-graining (MS-CG) methodology [22-26], and (2) CG membrane protein models developed from the “top-down” MARTINI (and related) CG force-fields [27-32]. It is important for the reader to distinguish between these two coarse-graining philosophies. A number of current mesoscopic approaches will also be described [11-16].
The Multiscale Coarse-graining Methodology
The MS-CG methodology [22-26] provides a rigorous bottom-up theoretical framework in which to construct CG models from the underlying molecular scale forces, and thus it provides a direct route for path (1) in Fig. 1. It shares with other complementary inverse CG approaches [33,34] the ability to directly incorporate atomistic MD simulation data into the resultant CG force field. Further development of the MS-CG method has formalized the variational aspect of the approach and proven that the method yields the optimum CG force field relative to the exact many-body potential of mean force (PMF) that rigorously governs the system at the CG scale for a given set of thermodynamic conditions [24••,25]. The quality of the MS-CG force field is dependent on the choice of CG basis set (i.e., what kinds of CG interactions are required to model the system), the choice of location and number of CG sites (the CG “resolution”), and the degree of MD sampling used in constructing the MS-CG model.
If one believes that specific molecular-scale interactions are important for the behavior of biomolecular systems at the CG scale and beyond, then the MS-CG approach provides a means to develop such CG models. In terms of biomolecular systems, the MS-CG method has been applied to develop new CG representations for lipids and lipid mixtures [22,23,35], solvent-free model lipid bilayers [36], peptides [37], and mixed resolution models containing all-atom proteins in CG lipids [38]. The MS-CG approach can also be applied to develop hybrid schemes that combine the MS-CG information with analytic models for configurations that are not well sampled in the MS-CG procedure. This hybrid approach has been used, for example, to model a 200 nm diameter liposome at a very low resolution CG level [21]. Extensions of the MS-CG approach to large proteins can yield a Heterogeneous Elastic Network (HeteroENM) protein model [20]. This approach has been employed, for example, to construct a HeteroENM model for an N-BAR protein [20], as shown in path (1) of Fig. 1. When combined with single site lipid models using the HAS CG approach [21], simulations of the early stages of membrane remodeling can be explored (image (B) in Fig. 1). In all of these approaches, molecular scale information obtained from all-atom MD forces provides the starting point for the development of the subsequent CG model.
The variational character of MS-CG [24••-26], combined with the formal result that, strictly speaking, the MS-CG force field is not only a function of the CG site positions but also the temperature and volume, can mean that MS-CG force fields may need to be determined separately for different thermodynamic states. The approach does guarantee that the resulting CG force field will be the closest to the exact many-body PMF for the CG variables (in a variational sense). However, there are likely to be more advanced MS-CG representations of the system that will improve the transferability of the force field by including three body interactions. The current research focus of the MS-CG methodology for membrane protein systems is also directed at two key topics: (1) determining the optimal location and number of CG sites, and (2) specifying the degree of MS-CG force field complexity required to provide the most accurate and transferable CG force field possible.
Parameterized “top-down” CG force fields for membrane protein systems
Force fields such as the MARTINI CG force field [27-31] were originally designed for CG simulations of lipid bilayers [27] and have recently been extended to proteins [28••]. Variants by Sansom and co-workers [29,30•] and Schulten and co-workers [31] have also been developed. The philosophy of the MARTINI approach differs substantially from the MS-CG method [24••-26] and inverse coarse-graining techniques [33,34] in that the parameterization of the model employs certain bulk thermodynamic data, in particular experimentally determined oil/water partitioning coefficients. In the case of proteins, the partitioning free energy of amino acid side chains between oil and water phases were employed [28••,30•].
This top-down approach to membrane protein CG models does not incorporate molecular scale information as depicted by path (1) in Fig. 1. However, the approach employed with the MARTINI force field and some of its variants may incorporate molecular information in an implicit way. For example, the location, size, and number of CG sites selected for the lipids and proteins are chosen to mirror the structure of their atomistic counterparts. In the case of proteins, the focus on a parameterization based amino acid partitioning in lipid bilayers (which has been found to be an important property in these systems [39]) appears to at least indirectly incorporate some degree of molecular scale information onto the CG representation. The MARTINI approach can also provide valuable insight into the gross features that define transferability of CG models.
A number of current CG membrane protein simulations are worth noting. The MARTINI CG [27,28••] model has been used to examine gating motions in voltage-gated potassium channels [40], tension driven gating in the mechanosensitive channel of small conductance (MscL) [41], BAR domain induced membrane sculpting [32], and self assembly of G protein-coupled receptors in model lipid bilayers [42]. However, as previously noted [43••], CG approaches along these lines can underestimate hydration free energies of charged residues (e.g., Arg [27]). An important issue is the choice of the effective dielectric constant for the electrostatic interactions in these models [28••,32,43••] and no clearly systematic procedure has yet been developed to address this challenge. Another feature of the MARTINI model is that the water solvent is represented by CG spherical particles each effectively representing four water molecules and interacting with one other through a Lennard-Jones interaction [27].
A variant of the MARTINI force field developed by Sansom and coworkers [29,30•] has been used to examine the one-dimensional PMF (free energy profile) governing a gated potassium channel and gating modifier toxin (VSTx1) [44]. The binding constants were significantly larger than those reported experimentally for VSTx1, and the source of this discrepancy has not been resolved. Microsecond long CG MD simulations of zwitterionic vesicles (composed of 877 palmitoyloeoylphosphatidylethanolamine (POPE) lipids) with multiple Maculatin 1.1 antimicrobial peptides have revealed spontaneous adsorption of the peptides into the vesicle [45]. In this work, Bond et al., [45] noted that this CG approach would not be able to fully model peptide-water-ion and lipid-water-ion interactions during membrane permeation and lysis, and that the long term solution to addressing the limitations of this CG approach might be to combine CG and all atom models together in a unified approach [22,38], or by coupling atomic and continuum membrane models using Multiscale Coupling [46] and inverse techniques [33]. Other CG simulations of an arylamide antimicrobial agent in a DMPC bilayer (using a different CG model [34]) suggested interesting collective behavior of these agents while also emphasizing that making direct quantitative conclusions about water-passage through the membranes could not be made [47]. An important modification of the MARTINI approach by the Sansom group has been developed [30•] which employs modified amino acid parameters and protein secondary structure restraints. Ring-based side chains employ two CG particles (in contrast to 3-4 particles employed in the MARTINI force field [28••]). The resulting free energy barrier height for bilayer insertion of the Arg side chain is found to be about 50% of that estimated from atomistic MD simulation [48].
As an alternative step towards bridging CG simulations with molecular scale phenomena, a combined atomic-CG methodology has been developed [49,50] wherein a CG membrane protein self assembly simulation is used to generate a starting configuration for a conventional atomistic MD simulation. In this approach, the final configuration of the CG simulation is converted to an atomistic model, which is then used as the initial configuration for a conventional atomic MD simulation. This approach was applied to phospholipase A2 [49] and a hydrated influenza M2 channel–dipalmitoylphosphatidylcholine (DPPC) lipid bilayer system [50]. Within the context of Fig. 1, this particular CG approach offers a route back to the molecular scale system, and thus could form a key alternative approach to an overall multiscale methodology for membrane protein systems.
Mesoscopic simulation
In Fig. 1 the important endpoint of the overall multiscale simulation approach for membrane protein systems is the mesoscopic model (image (C)). The work of Brown and co-workers involving the development of consistent elastic theories for membrane protein inclusions [13,14••] are important in this regard. In this approach [13,14••] a generic CG membrane simulation is used in order to validate various advanced continuum elastic membrane models; a distinct Gaussian curvature contribution for small inclusions was found. It would be of great interest to use this approach in conjunction with atomistically determined parameterizations, and then “activate” the elastic model via the Fourier-based approach as was previously done [15]. This could potentially offer a direct systematic route along path (2) in Fig. 1 to develop rigorous mesoscopic models of complex membrane protein systems.
The Elastic Membrane Version 2 (EM2) approach gives a discretized solution to continuum elastic membrane models [11,12] and has been used to examine N-BAR protein mediated membrane remodeling [12], as shown in Fig. 1, image (C). Molecular scale information can be directly input into the mesoscopic EM2 model (path 2), e.g., in this example the curvature induced by a single N-BAR protein as calculated from atomistic MD simulation [18] provides the maximum possible local spontaneous curvature on the membrane, or via an intermediate route (path 1 to 3) using a CG model to provide a bridge to the mesoscopic scale. Recasting the final continuum mesoscopic model in a discrete representation circumvents the need to solve complex integrals with pre-specified boundary conditions. The range of accessible structures and/or topologies is thereby greatly increased, such that even membrane remodeling from liposomes to tubules or small vesicles can be examined within this approach [12] (e.g., Fig. 1, image (C)).
Mechanosensitive channel gating for the mechanosensitive channel of large conductance (MscL) has also been examined at the continuum-level using the “MD-decorated finite element method” (MDeFEM) [16]. Equibiaxial tension and torsion were applied to the channel and an iris-like opening was observed. The authors note that this continuum-level framework might be more tightly coupled to atomic level information. A similar coupling scheme has been developed by Schulten and co-workers [32].
Conclusions and outlook
This article has described strategies to develop a systematic multiscale simulation methodology for membrane protein simulations (cf. Fig. 1). A number of current and promising CG and mesoscopic approaches have been surveyed. In terms of CG methods, the MS-CG approach offers a systematic and rigorous route to develop the critical CG component of membrane protein systems where detailed molecular level information is propagated from bottom-up in scale to the CG level. However, the MS-CG approach as presently formulated can sometimes result in complex CG interactions that may have limited transferability to other thermodynamic conditions and/or physical systems. Complementary methodologies, e.g., the MARTINI model, treat the multiscale problem from the top down. In the latter approach, molecular level information may still be implicitly included via a careful choice of CG representations and parameterizations. However, current applications of the MARTINI methodology suggest that some key physical interactions are difficult to account for via simple reparameterizations of the model, and as a result the quantitative predictive power of the method is reduced. Somewhere in the middle between fully systematic and top-down CG approaches is one that may provide an optimum strategy that contains systematically determined molecular level information, but is also computationally efficient and reasonably transferable across different systems and thermodynamic conditions.
In terms of membrane protein systems, a clear set of criteria are still needed to determine when a high degree of resolution (i.e., approaching a fully atomistic model) is required, versus when a low resolution CG model is sufficient in order to model the system. Comparing CG local structure (e.g., CG radial distribution functions), as well as partitioning free energies, are two popular diagnostics to determine whether or not the CG resolution is adequate. Current experience suggests that highly charged species (e.g., charged residues), along with aromatic rings, may require a higher degree of resolution in order for the CG model to give quantitative predictive power. This observation is tied with both the complexity of the charge distributions, as well as the excluded volume, and this trend may carry over to similar systems. Intrinsically coupled with the degree of resolution is the length scale where the emergent behavior of the CG system can give meaningful insights and results. Indeed, the structure in a highly CG system could be quite far off what would be expected in a fully molecular level model, for example, in terms of molecular radial distribution functions. However, the behavior at longer length-scales may be accurate; for example in the bending modulus of a lipid bilayer or the size of domain structures in CG mixtures of lipids and proteins.
Systematically determined mesoscopic models that clearly connect to molecular scale interactions are still in their infancy relative to the CG approaches, but current work has shown that mesoscopic models allow very long time and length scales to be reached. Given that many experimental membrane protein systems operate at such length and time scales, it is this upper end of the multiscale simulation methodology that may best connect with experimental results, and thus bridge the overall multiscale simulation approach with real biological phenomena. It is possible to speculate on the future directions of multiscale membrane protein simulations and the problems that may be solved by such approaches. Experimental techniques such as fluorescence microscopy and electron (cryo)microscopy have provided a wealth of information into protein mediated membrane remodeling (e.g., the endocytotic pathway); however, the resolution of these methods requires a degree of inference into the molecular-level details. A systematic multiscale simulation methodology that is able to directly make contact with experimental results, yet also connect to molecular-level information, has the potential to become a key tool in understanding protein-mediated membrane remodeling phenomena. Indeed, it can certainly be anticipated that this novel approach will soon be utilized for a number of membrane protein systems to help interpret and even predict experimental observations.
Acknowledgments
This research was supported by the National Institutes of Health (R01-GM063796).
Contributor Information
Gary S. Ayton, Center for Biological Modeling and Simulation, University of Utah, 315 S. 1400 E. Rm 2020, Salt Lake City, Utah 84112-0850, gazz@hec.utah.edu
Gregory A. Voth, Center for Biological Modeling and Simulation, University of Utah, 315 S. 1400 E. Rm 2020, Salt Lake City, Utah 84112-0850
References
- 1.Voth GA, editor. Coarse-graining of condensed phase and biomolecular systems. CRC Press/Taylor and Francis Group; Boca Raton: 2009. [Google Scholar]
- 2.Tozzini V. Coarse-grained models for proteins. Curr Opin Struc Bio. 2005;15:144–150. doi: 10.1016/j.sbi.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 3.Ayton GS, Noid WG, Voth GA. Multiscale modeling of biomolecular systems. In serial and in parallel. Curr Opin Struct Bio. 2007;17:192–198. doi: 10.1016/j.sbi.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 4.Lindahl E, Sansom MSP. Membrane proteins: molecular dynamics simulations. Curr Opin Struct Biol. 2008;18:425–431. doi: 10.1016/j.sbi.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 5.Sherwood P, Brooks BR, Sansom MSP. Multiscale methods for macromolecular simulations. Curr Opin Struct Biol. 2008;18:630–640. doi: 10.1016/j.sbi.2008.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Klein ML, Shinoda W. Large-scale molecular dynamics simulations of self-assembling systems. Science. 2008;321:798–800. doi: 10.1126/science.1157834. [DOI] [PubMed] [Google Scholar]
- 7.Sanbonmatsu KY, Tung CS. High performance computing in biology: Multimillion atom simulations of nanoscale systems. J Struct Biol. 2007;157:470–480. doi: 10.1016/j.jsb.2006.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ash WL, Zlomislic MR, Oloo EO, Tieleman DP. Computer simulations of membrane proteins. Biochem et Biophys Acta. 2004;1666:158–189. doi: 10.1016/j.bbamem.2004.04.012. [DOI] [PubMed] [Google Scholar]
- 9.Marrink SJ, de Vries AH, Tieleman DP. Lipids on the move: Simulations of membrane pores, domains, stalks and curves. Biochimica et Biophysica Acta (BBA) - Biomembranes. 2009;1788:149–168. doi: 10.1016/j.bbamem.2008.10.006. [DOI] [PubMed] [Google Scholar]
- 10.Kandt C, Ash WL, Peter Tieleman D. Setting up and running molecular dynamics simulations of membrane proteins. Methods. 2007;41:475–488. doi: 10.1016/j.ymeth.2006.08.006. [DOI] [PubMed] [Google Scholar]
- 11.Ayton GS, McWhirter JL, Voth GA. A second generation mesoscopic lipid bilayer model: Connections to field-theory descriptions of membranes and nonlocal hydrodynamics. J Chem Phys. 2006;124:064906. doi: 10.1063/1.2165194. [DOI] [PubMed] [Google Scholar]
- 12.Ayton GS, Blood PD, Voth GA. Membrane remodeling from N-BAR domain interactions: Insights from multiscale simulation. Biophys J. 2007;92:3595–3602. doi: 10.1529/biophysj.106.101709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brannigan G, Brown FLH. A consistent model for thermal fluctuations and protein-induced deformations in lipid bilayers. Biophys J. 2006;90:1501–1520. doi: 10.1529/biophysj.105.075838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ••14.West B, Brown FL, Schmid F. Membrane-protein interactions in a generic coarse-grained model for lipid bilayers. Biophys J. 2009;96:101–115. doi: 10.1529/biophysj.108.138677. A generic coarse-grained lipid bilayer model is used to compare two analytic theories for membranes. The elastic theory successfully models deformation profiles of the membrane around single proteins. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lin LCL, Gov N, Brown FLH. Nonequilibrium membrane fluctuations driven by active proteins. J Chem Phys. 2006;124:074903. doi: 10.1063/1.2166383. [DOI] [PubMed] [Google Scholar]
- 16.Tang Y, Yoo J, Yethiraj A, Cui Q, Chen X. Mechanosensitive channels: Insights from continuum-based simulations. Cell Biochem Biophys. 2008;52:1–18. doi: 10.1007/s12013-008-9024-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reynwar BJ, Illya G, Harmandaris VA, Muller MM, Kremer K, Deserno M. Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature. 2007;447:461–464. doi: 10.1038/nature05840. [DOI] [PubMed] [Google Scholar]
- 18.Blood PD, Voth GA. Direct observation of Bin/amphiphysin/Rvs (BAR) domain-induced membrane curvature by means of molecular dynamics simulations. Proc Nat Acad Sci. 2006;103:15068–15072. doi: 10.1073/pnas.0603917103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- •19.Blood PD, Swenson RD, Voth GA. Factors influencing local membrane curvature induction by N-BAR domains as revealed by molecular dynamics simulations. Biophys J. 2008;95:1866–1876. doi: 10.1529/biophysj.107.121160. Results for large scale MD simulations of N-BAR mediated membrane remodeling are presented. Results examining the effect of the charged BAR surface, N-BAR binding without N-terminal helices, and the behavior of the N-terminal helices alone have been examined. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lyman E, Pfaendtner J, Voth GA. Systematic multiscale parameterization of heterogeneous elastic network models of proteins. Biophys J. 2008;95:4183–4192. doi: 10.1529/biophysj.108.139733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ayton GS, Voth GA. A hybrid coarse-graining approach for lipid bilayers at large length and time scales. J Phys Chem B (in press) 2009 doi: 10.1021/jp8087868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Izvekov S, Voth GA. A multiscale coarse-graining method for biomolecular systems. J Phys Chem B. 2005;109:2469–2473. doi: 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- 23.Izvekov S, Voth GA. Multiscale coarse-graining of mixed phospholipid/cholesterol bilayers. J Chem Theor Comp. 2006;2:637–648. doi: 10.1021/ct050300c. [DOI] [PubMed] [Google Scholar]
- ••24.Noid WG, Chu JW, Ayton GS, Krishna V, Izvekov S, Voth GA, Das A, Anderson HC. The multiscale coarse-graining method I: A rigorous bridge between atomistic and coarse-grained models. J Chem Phys. 2008;128:244114. doi: 10.1063/1.2938860. The overall theoretical framework for the Multiscale Coarse-graining (MS-CG) methodology is given. The formal link between atomistic and coarse-grained representations is derived using the consistency principle for the atomistic and coarse-grained distribution functions. The MS-CG methodology guarantees that the resulting MS-CG force field will be the closest, in a variational sense, to the exact force field as found from the many body potential of mean force. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Noid WG, Liu P, Wang Y, Chu J-W, Ayton GS, Izvekov S, Andersen HC, Voth GA. The multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models. J Chem Phys. 2008;128:244115. doi: 10.1063/1.2938857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Noid WG, Chu J-W, Ayton GS, Voth GA. Multiscale coarse-graining and structural correlations: Connections to liquid state theory. J Phys Chem B. 2007;111:4116–4127. doi: 10.1021/jp068549t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, deVries AH. The MARTINI force field: Coarse grained model for biomolecular simulations. J Phys Chem B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- ••28.Monticelli L, Kandasamy SK, Periole X, Larson RG, Tieleman DP, Marrink S-J. The MARTINI coarse-grained force field: Extension to proteins. J Chem Theory Comput. 2008;4:819–834. doi: 10.1021/ct700324x. An extension to the MARTINI CG force field for proteins is presented. The model is validated by calculating the potential of mean force for each amino acid as it is removed from a dioleoylphosphatidylcholine bilayer. The model is computationally efficient and can represent CG peptide lipid interactions, along with the partitioning of amino acids and peptides in lipid bilayers. [DOI] [PubMed] [Google Scholar]
- 29.Bond PJ, Holyoake J, Ivetac A, Khalid S, Sansom MS. Coarse-grained molecular dynamics simulations of membrane proteins and peptides. J Struct Biol. 2007;157:593–605. doi: 10.1016/j.jsb.2006.10.004. [DOI] [PubMed] [Google Scholar]
- •30.Bond PJ, Wee CL, Sansom MS. Coarse-grained molecular dynamics simulations of the energetics of helix insertion into a lipid bilayer. Biochemistry. 2008;47:11321–11331. doi: 10.1021/bi800642m. A modified CG model for proteins and membranes is presented. The secondary structure of the protein employs harmonic bonds. An iterative process is used to parameterize the model to give good agreement with experimental measurements of oil/water partition free energies. [DOI] [PubMed] [Google Scholar]
- 31.Shih AY, Arkhipov A, Freddolino PL, Schulten K. Coarse grained protein-lipid model with applications to lipoprotein particles. J Phys Chem B. 2006;110:3674–3684. doi: 10.1021/jp0550816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Arkhipov A, Yin Y, Schulten K. Four-scale description of membrane sculpting by BAR domains. Biophys J. 2008;95:2806–2821. doi: 10.1529/biophysj.108.132563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lyubartsev AP. Multiscale modeling of lipids and lipid bilayers. European Journal of Biophysics. 2005;35:53–61. doi: 10.1007/s00249-005-0005-y. [DOI] [PubMed] [Google Scholar]
- 34.Shelley JC, Shelley MY, Reeder RC, Bandyopadhyay S, Klein ML. A coarse grain model for phospholipid simulation. J Phys Chem B. 2001;105:4464–4470. [Google Scholar]
- 35.Lu L, Voth GA. Systematic coarse-graining of a multi-component lipid bilayer. J Phys Chem B. 2009 doi: 10.1021/jp809604k. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Izvekov S, Voth GA. A solvent free lipid bilayer model using multiscale coarse-graining. J Phys Chem B. 2008 doi: 10.1021/jp810440c. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Thorpe I, Zhou J, Voth GA. Peptide folding using multiscale coarse-grained models. J Phys Chem B. 2008;112:13079–13090. doi: 10.1021/jp8015968. [DOI] [PubMed] [Google Scholar]
- 38.Shi Q, Izvekov S, Voth GA. Mixed atomistic and coarse-grained molecular dynamics: Simulation of a membrane bound ion channel. J Phys Chem B. 2006;110:15045–15048. doi: 10.1021/jp062700h. [DOI] [PubMed] [Google Scholar]
- 39.MacCallum JL, Bennett WFD, Tieleman DP. Partitioning of amino acid side chains into lipid bilayers: Results from computer simulations and comparison to experiment. J Gen Physiol. 2007;129:371–377. doi: 10.1085/jgp.200709745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Treptow W, Marrink S-J, Tarek M. Gating motions in voltage-gated potassium channels revealed by coarse-grained molecular dynamics simulations. J Phys Chem B. 2008;112:3277–3282. doi: 10.1021/jp709675e. [DOI] [PubMed] [Google Scholar]
- 41.Yefimov S, van der Giessen E, Onck PR, Marrink S. Mechanosensitive membrane channels in action. Biophys J. 2008;94:2994–3002. doi: 10.1529/biophysj.107.119966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Periole X, Huber T, Marrink SJ, Sakmar TP. G protein-coupled receptors self-assemble in dynamics simulations of model bilayers. J Am Chem Soc. 2007;129:10126–10132. doi: 10.1021/ja0706246. [DOI] [PubMed] [Google Scholar]
- ••43.Allen TW. Modeling charged protein side chains in lipid membranes. J Gen Physiol. 2007;130:237–240. doi: 10.1085/jgp.200709850. The general challenge of modeling membrane protein insertion and protein-bilayer interactions is discussed. The important role of partitioning experiments on understanding the thermodynamics of protein insertion in to membranes is presented. The role of CG models in examining this kind of phenomena is given, with an emphasis on the need for careful parameterization and correct physical behavior of the model. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wee CL, Gavaghan D, Sansom MS. Lipid bilayer deformation and the free energy of interaction of a Kv channel gating-modifier toxin. Biophys J. 2008;95:3816–3826. doi: 10.1529/biophysj.108.130971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bond PJ, Parton DL, Clark JF, Sansom MS. Coarse-grained simulations of the membrane-active antimicrobial Peptide maculatin 1.1. Biophys J. 2008;95:3802–3815. doi: 10.1529/biophysj.108.128686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chang R, Ayton GS, Voth GA. Multiscale coupling of mesoscopic and atomistic-level lipid bilayer simulations. J Chem Phys. 2005;122:244716. doi: 10.1063/1.1931651. [DOI] [PubMed] [Google Scholar]
- 47.Lopez CF, Nielsen SO, Srinivas G, DeGrado WF. Probing membrane insertion activity of antimicrobial polymers via coarse-grain molecular dynamics. J Chem Theory Comput. 2006;2:649–655. doi: 10.1021/ct050298p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Dorairaj S, Allen TW. On the thermodynamic stability of a charged arginine side chain in a transmembrane helix. Proc Natl Acad Sci. 2007;104:4943–4948. doi: 10.1073/pnas.0610470104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wee CL, Balali-Mood K, Gavaghan D, Sansom MS. The interaction of phospholipase A2 with a phospholipid bilayer: Coarse-grained molecular dynamics simulations. Biophys J. 2008;95:1649–1657. doi: 10.1529/biophysj.107.123190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Carpenter T, Bond PJ, Khalid S, Sansom MS. Self-assembly of a simple membrane protein: Coarse-grained molecular dynamics simulations of the influenza M2 channel. Biophys J. 2008;95:3790–3801. doi: 10.1529/biophysj.108.131078. [DOI] [PMC free article] [PubMed] [Google Scholar]