Top-down formation of fullerenes in the interstellar medium

Abstract

Fullerenes have been recently detected in various circumstellar and interstellar environments, raising the question of their formation pathway. It has been proposed that they can form at the low densities found in the interstellar medium by the photo-chemical processing of large polycyclic aromatic hydrocarbons (PAHs). Following our previous work on the evolution of PAHs in the NGC 7023 reflection nebula, we evaluate, using photochemical modeling, the possibility that the PAH C₆₆H₂₀ (i.e. circumovalene) can lead to the formation of C₆₀ upon irradiation by ultraviolet photons. The chemical pathway involves full dehydrogenation of C₆₆H₂₀, folding into a floppy closed cage and shrinking of the cage by loss of C₂ units until it reaches the symmetric C₆₀ molecule. At 10” from the illuminating star and with realistic molecular parameters, the model predicts that 100% of C₆₆H₂₀ is converted into C₆₀ in ~ 10⁵ years, a timescale comparable to the age of the nebula. Shrinking appears to be the kinetically limiting step of the whole process. Hence, PAHs larger than C₆₆H₂₀ are unlikely to contribute significantly to the formation of C₆₀, while PAHs containing between 60 and 66 C atoms should contribute to the formation of C₆₀ with shorter timescales, and PAHs containing less than 60 C atoms will be destroyed. Assuming a classical size distribution for the PAH precursors, our model predicts absolute abundances of C₆₀ are up to several 10⁻⁴ of the elemental carbon, i.e. less than a percent of the typical interstellar PAH abundance, which is consistent with observational studies. According to our model, once formed, C₆₀ can survive much longer (> 10⁷ years for radiation fields below G₀ = 10⁴) than other fullerenes because of the remarkable stability of the C₆₀ molecule at high internal energies. Hence, a natural consequence is that C₆₀ is more abundant than other fullerenes in highly irradiated environments.

1. Introduction

The mid-infrared (mid-IR) spectrum of galactic and extragalactic objects exhibits emission in bands (strongest at 3.3, 6.2, 7.7, 8.6, and 11.2 μm) attributed to carbonaceous macromolecules, more specifically to polycyclic aromatic hydrocarbons (PAHs, Tielens 2008). In addition to PAH bands, IR emission bands at 7.0, 8.5, 17.4, and 19.0 μm have been reported (Cami et al. 2010; Sellgren et al. 2010), and found to match quite closely the IR active bands of neutral buckminsterfullerene (C₆₀, Kroto et al. 1985), a cage-like carbon molecule. Additional bands at 6.4, 7.1, 8.2, and 10.5 μm were observed in the NGC 7023 reflection nebula and attributed to the ${\mathrm{C}}_{60}^{+}$ cation (Berné et al. 2013). Carbonaceous macromolecules, especially PAHs, are believed to play a fundamental role in the physics and chemistry of the interstellar medium (ISM), and their infrared signatures are commonly used as a tracer of physical conditions (especially the UV radiation field). PAHs are believed to lock up between 5 and 20% of the elemental carbon (Joblin & Tielens 2011), while C₆₀ and ${\mathrm{C}}_{60}^{+}$are found in small abundances in the ISM (at most 5.6×10⁻⁴ of the elemental carbon for the neutral form according to Castellanos et al. 2014, and at most 10⁻⁴ of the elemental carbon for the cation according to Berné et al. 2013). Nevertheless, C₆₀ and ${\mathrm{C}}_{60}^{+}$ are the only species belonging to the family of carbonaceous macromolecules which have been specifically identified in the ISM, and therefore these molecules have attracted considerable interest because they open a new possibility to probe carbon chemistry and physical conditions in the ISM.

One question related to fullerenes, and in particular C₆₀ , concerns their formation pathway. Recently, “top-down” schemes where larger carbon clusters shrink to reach C₆₀ have been proposed (Chuvilin et al. 2010; Zhang et al. 2013; Pietrucci & Andreoni 2014), and can be opposed to the traditional “bottom-up” approach where C₆₀ is built up from small compounds (Kroto & McKay 1988; Heath 1992; Hunter et al. 1994; Dunk et al. 2013). Using infrared observations of the NGC 7023 nebula, Berné & Tielens (2012) found evidence of an increase of the abundance of C₆₀ with increasing UV field, while the abundance of PAHs decreases. This was interpreted by these authors as evidence for the formation of C₆₀ from large PAHs (N_C > 60) under UV irradiation, a top down mechanism similar to the one observed by Chuvilin et al. (2010). García-Hernández et al. (2010, 2011) and Micelotta et al. (2012) proposed a similar mechanism where the starting materials are more complex, such as hydrogenated amorphous carbon instead of PAHs. Top-down scenarios are particularly appealing, given that the densities prevailing in the ISM are many orders of magnitude too low to allow for a “bottom-up” formation (i.e. starting from small compounds) over reasonable timescales¹. In this paper, we use a detailed photochemical model coupled to a description of the physical conditions in the NGC 7023 nebula. We demonstrate that the formation of C₆₀ by UV processing of large PAH molecules is a plausible mechanism to account for astronomical observations.

2. Model for the formation of C₆₀ from PAHs

2.1. Description of the proposed scenario

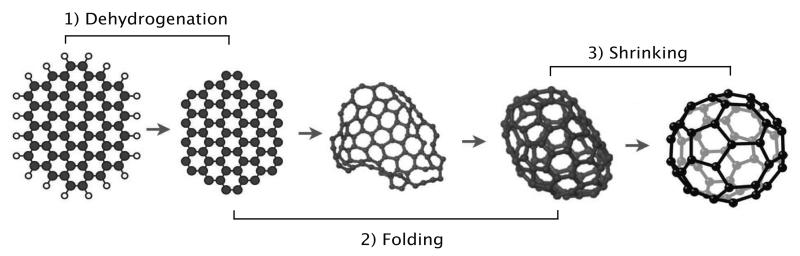
The proposed scenario of formation is inspired by the one described in Berné & Tielens (2012) and is represented schematically in Fig. 1. PAHs are assumed to be formed in the envelopes of evolved stars (Frenklach & Feigelson 1989; Cherchneff et al. 1992; Merino et al. 2014), and then injected in the ISM. Under UV irradiation, large PAHs, (N_C > 60) are first fully dehydrogenated into small graphene flakes, dehydrogenation being by far the dominant dissociation channel (see Montillaud et al. 2013, and references therein). Further UV irradiation enables these flakes to fold into closed cages. Once the cages are closed, they can loose C₂ units if they continue absorbing energy (Irle et al. 2006). Because of the low densities prevailing in the considered regions (n_H < 10⁴cm⁻³), the reverse reaction, i.e. addition of C₂ is too slow to balance photodissociation. Once a system has reached C₆₀ it will remain in this form for a very long period of time, because of its remarkable stability.

Fig. 1.

Schematic representation of the evolutionary scenario for the formation of fullerenes from PAHs under UV irradiation.

2.2. The specific case of the transformation of C₆₆H₂₀ into C₆₀

In this paper we consider the evolution of circumovalene, C₆₆H₂₀ (first molecule in Fig. 1), for the physical conditions of NGC 7023 (see Sect. 3). We restrict ourselves to a single molecule as a starting point, for simplicity, and because modeling a complete population would introduce many free parameters that would be irrelevant in this proof of concept study. C₆₆H₂₀ is selected as a test case because it gathers the typical properties expected for an interstellar PAH (N_C ≳ 50, compactness), it can be considered as a potential precursor of C₆₀ and its spectroscopic properties are available in the Cagliari Theoretical spectral database of PAHs² (Malloci et al. 2007, hereafter Cagliari database). The photophysical modeling relies on several key processes: 1) UV absorption which brings the molecules to high temperatures, 2) radiative cooling, 3) unimolecular dissociation, 4) isomerization and more specifically folding of the graphene flakes and 5) reactions with electrons, H atoms or C⁺. In the following sections, we present the adopted methods to describe these processes which were then implemented in the photochemical model developed by Montillaud et al. (2013).

2.2.1. UV absorption

UV absorption is the first step in the photophysical evolution of the considered species. The efficiency of this process in a given radiation field depends on the UV absorption cross-section. The UV absorption cross-section of C₆₆H₂₀ used here is taken from the Cagliari database. The same value is used for dehydrogenated PAHs C₆₆H_n as well as for planar C₆₆, considering that the UV absorption cross-section in a PAH is, in first approximation, proportional to the number of carbon atoms. For C₆₀ , we adopt the UV absorption cross-section from Berkowitz (1999). The same absorption cross-section is used for the other cages, but with a scaling proportional to the number of C atoms (Joblin et al. 1992). The impact of the chosen UV absorption cross-sections on the results is discussed in Sect. 4.3.

2.2.2. Ionization

In the frame of our interstellar model, two ionization processes should be considered: direct photoionization and thermionic emission. Direct ionization occurs after the absorption of a single UV photon with an energy above the ionization threshold. In the case of thermoionic emission, the successive absorption of several UV photons brings the molecule to high temperatures and can lead to delayed electron emission.

For the hydrogenated and dehydrogenated PAHs, the direct photoionization process is included, following Montillaud et al. (2013). For the cages, including C₆₀ , we do not include direct photoionization. This assumption relies on the fact that observations indicate that this species is mostly in the neutral form in NGC 7023, ${\mathrm{C}}_{60}^{+}$being localized only very close to the star (Berné et al. 2013). It cannot be excluded that this is due to an efficient recombination of C₆₀ with electrons from the ambient medium, and hence ionization could still be efficient as a sink of energy for relaxation. Since the ionization potential of C₆₀ is 7.5 eV, only photons with energies 7.5 < hν < 13.6 eV can contribute to ionization. Given the spectral profile of the radiation field in NGC 7023 (see Montillaud et al. 2013) and the fact that in this range the ionization yield is low compared to the total photo-absorption (Berkowitz 1999), only a small fraction of the energy from absorbed UV photons will be lost in photoelectrons, and most of it will be converted into vibrational energy that can eventually be used for dissociation. The other cages have similar ionization potentials (Seifert et al. 1996) and are therefore assumed to behave like C₆₀ . Hence, we have neglected direct photoionizaiton for the cages in the photo-chemical model.

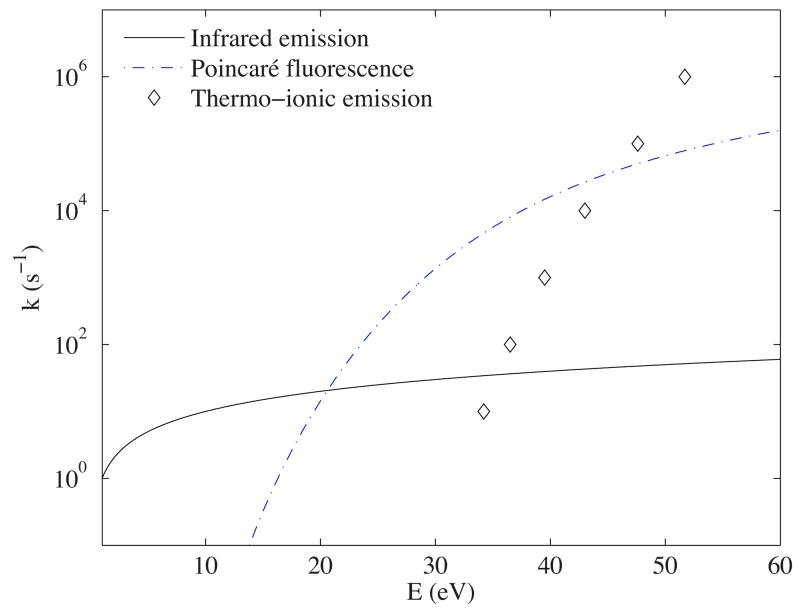
Thermoionic emission becomes efficient only at internal energies higher than ~ 30 eV (Hansen et al. 2003). It could therefore be an efficient relaxation process, competing with photodissociation (Sect. 2.2.4) and cooling by fluorescence from thermally excited electronic states (Sect. 2.2.3). As can be seen in Fig. 2, the termoionic emission rate becomes larger than fluorescence from thermally excited electronic states only for internal energies above ~ 45 eV. This is well above the internal energies of dissociation (see Sect. 4.1) and therefore relaxation through thermionic emission can be neglected since it will always be dominated by fluorescence from thermally excited electronic states.

Fig. 2.

Cooling rates for C₆₀ as a function of the internal energy of the molecule. The infrared emission and cooling by fluorescence from thermally excited electronic states are calculated (labelled Poincaré in the figure) following the formalism described in this paper. The thermionic emission rates are taken from Hansen et al. (2003).

2.2.3. Radiative cooling

Radiative cooling can occur through emission of photons in the infrared, but when the molecules reach high enough temperatures, it has been shown that fluorescence from thermally excited electronic states becomes the dominant cooling mechanism (see Léger et al. 1988, who called this mechanism Poincaré fluorescence). This process has been observed for internal energies of ~ 7 eV for the anthracene cation, ${\mathrm{C}}_{14}{\mathrm{H}}_{10}^{+}$, (Martin et al. 2013) and internal energies of ~ 13 eV for the C₆₀ anion (Andersen et al. 2001).

The infrared cooling rates are calculated using the microcanonical formalism of Joblin et al. (2002). This requires the full knowledge of the vibrational properties of the considered species. For C₆₆H₂₀, we use the spectroscopic properties from the Cagliari database as in Montillaud et al. (2013). For C₆₀ , they are taken from Schettino et al. (2001). For dehydrogenated PAHs C₆₆H_n and cages, we use the DFT vibrational frequencies of C₆₆H₂₀ from the Cagliari database, after removing the C-H vibrational modes and 3 modes per missing C atom. The cooling rates calculated with this approach for C₆₀ are reported in Fig. 2.

Cooling by fluorescence from thermally excited electronic states is calculated using the formalism described in Chupka & Klots (1997). The cooling rate is given by:

$$k\left(T\right)=(2c∕a_0)\sum f_i{({\mathit{hv}}_i∕{\mathit{mc}}^2)}^2\mathit{exp}(-{\mathit{hv}}_i∕k_{B}T)$$ (1)

where a₀ is the Bohr radius, f_i and _i are respectively the oscillator strengths and frequencies of the electronic transitions and T is the temperature of the molecule. For C₆₆H₂₀ and for the dehydrogenated PAHs we use the ν_i and f_i values for C₆₆H₂₀ from the Cagliari database (Table 1). For the cages, we use the energies and oscillator strengths of C₆₀ taken from Chupka & Klots 1997, reproduced in Table 1. Note that these oscillator strengths are a convenient approximation to calculate the radiative cooling but are not true oscillator strengths. Nevertheless, Chupka & Klots (1997) have shown that this approximation is in very good agreement with rate calculations including detailed molecular property information. Using the microcanonical formalism described above for the calculation of the IR cooling rates, we derived the relation between internal energy E and temperature T for the different species. Using Eq. 1, this allowed us to derive the radiative cooling rates as a function of E. For the case of C₆₀ these rates are shown in Fig. 2) and are in good agreement with the earlier work models of Tomita et al. (2003).

Table 1.

Frequencies and oscillator strengths adopted in the approximation to calculate the cooling by fluorescence from thermally excited electronic states (see text for details).

λ(Å)	νi (Hz)	fi
C66H20
5470	5.48 × 1014	0.72
4980	6.02 × 1014	0.24
C60
4540	6.60 × 1014	0.214
3485	8.60 × 1014	1.17
2725	1.10 × 1015	2.02
2240	1.34 × 1015	1.30

2.2.4. Photodissociation: dehydrogenation and shrinking by loss of C₂

Photodissociation is treated using the statistical approach, and based on the inverse Laplace transform of the Arrhenius equation (see details in Montillaud et al. 2013 and references therein). The parameters involved in this calculation are the activation energy E₀, the pre-exponential factor A, and the vibrational densities of states that are computed using the vibrational frequencies. For PAH dehydrogenation (first step in Fig. 1), we use the parameters given in Montillaud et al. (2013). For the shrinking of cages by loss of C₂ molecules (step 3 in Fig. 1), experimental and theoretical results are scarce, except in the case of C₆₀ and C₆₀⁺ for which published molecular data have a large scatter, as noticed by Matt et al. (2001). These authors reanalyzed published experiments of C₆₀⁺ dissociation and showed that when using similar and consistent sets of molecular data, most experiments lead to similar results, with a pre-exponential factor of 5 × 10¹⁹s⁻¹ and a dissociation energy of 10.0 ± 0.2 eV. The activation energy should be equal to the dissociation energy if there is no barrier for the reverse reaction, i.e. C₂ addition. Experimental (Laskin et al. 1997) and theoretical (Yi & Bernholc 1993) studies indeed indicate the absence of such a barrier. More recent studies are generally in line with these results (Diaz-Tendero et al. 2003; Gluch et al. 2004, among others). We consider each shrinking step from C₆₆ to C₅₈ individually (Eqs. 2 to 6 in Table 2). Dissociation energies have been determined theoretically (Zhang et al. 1992) and the values differ significantly from experimental data (Gluch et al. 2004). The theoretical values were computed directly for neutral cages in a consistent manner for all species. In contrast, the experimental values were derived from measurements on fullerene cations. We used the theoretical values in our standard model (Table 2). This choice has the advantage of providing consistent energies for all cages in this study, but with a relatively high value for C₆₀ (11.1 eV), compared to the results of Matt et al. (2001) (10.0 eV). To reconcile our choice of binding energies with the results of Matt et al. (2001), we adopted a pre-exponential factor of $2\times {10}^{20}{\mathrm{s}}^{-1}$ which leads to a dissociation rate comparable to that of Matt et al. (1999) (their Fig. 8). We used the same factor for the C₂ loss of all cages. The impact of all these assumptions is discussed in Sect. 4.3.

Table 2.

Activation energy and pre-exponential factors for the key reactions considered in the model

		Act. energy Ea (eV)	Pre-exp. factor A (s−1)
(1)	${\mathrm{C}}_{66}^{\mathit{planar}}\to {\mathrm{C}}_{66}^{\mathit{cage}}$	4.0	1 × 1015
(2)	${\mathrm{C}}_{66}^{\mathit{cage}}\to {\mathrm{C}}_{64}^{\mathit{cage}}+{\mathrm{C}}_2$	8.1a / 9.4b	2 × 1020
(3)	${\mathrm{C}}_{64}^{\mathit{cage}}\to {\mathrm{C}}_{62}^{\mathit{cage}}+{\mathrm{C}}_2$	9.4a / 9.0b	2 × 1020
(4)	${\mathrm{C}}_{62}^{\mathit{cage}}\to {\mathrm{C}}_{60}^{\mathit{cage}}+{\mathrm{C}}_2$	6.0a / 8.1b	2 × 1020
(5)	${\mathrm{C}}_{60}^{\mathit{cage}}\to {\mathrm{C}}_{58}^{\mathit{cage}}+{\mathrm{C}}_2$	11.1a / 11.2b	2 × 1020
(6)	${\mathrm{C}}_{58}^{\mathit{cage}}\to {\mathrm{C}}_{56}^{\mathit{cage}}+{\mathrm{C}}_2$	8.7a / 9.7b	2 × 1020

^aNotes. Using activation energies of Zhang et al. (1992);

^bUsing activation energies of Gluch et al. (2004).

2.2.5. Folding

For the folding of the carbon flakes (step 2 in Fig. 1), there are, to our knowledge, no experimental data to constrain the activation energy and pre-exponential factors. Recently, Lebedeva et al. (2012) conducted molecular dynamics simulations of the folding of the C₉₆ and C₃₈₄ graphene nanoflakes. For these two systems, they ran simulations at several temperatures and found that the rates follow an Arrhenius law from which they were able to derive the effective activation energies and pre-exponential factors. They show that these parameters do not vary significantly with size³, hence we adopt their values reported for C₉₆ to describe the folding (see Table 2).

2.2.6. Reaction with electrons, H atoms or C⁺

The other processes of interest include the recombination with electrons and the reaction with H atoms. During the dehydrogenation step all these processes are included, following Montillaud et al. (2013). We do not include the addition of C₂, because the abundance of this species is expected to be very low in the cavity of NGC 7023. The C⁺ cation is however abundant, and could react efficiently with cages. There are to our knowledge no studies of the kinetics of this reaction. We estimated the maximum contribution of this process in the case of C₆₀ using the Langevin rate. A polarizability of ~ 80 ų for C₆₀ (Zope et al. 2008) leads to k_Langevin ~ 6 × 10⁻⁹ cm³s⁻¹, and assuming a high abundance of C⁺ of 3 × 10⁻⁴ n_H, one gets an effective C⁺ addition rate of ~ 2 × 10⁻¹² n_H s⁻¹ (that is < 4 × 10⁻⁸ s⁻¹ for n_H < 2×10⁴cm⁻³). This rate must be compared to the rate of the reverse process, i.e. photodissociation of ${\mathrm{C}}_{61}^{+}$. We modeled this latter process with the same formalism as described in Sect. 3, using a dissociation energy of 4 eV (Slanina & Lee 1994) and a pre-exponential factor of 1.6 × 10¹⁵ s⁻¹ (Klots 1991). We find photodissociation rates from ~ 7 × 10⁻⁸ s⁻¹ to ~ 2×10⁻⁵ s⁻¹ for the various astrophysical conditions considered in Sect. 4.2. Therefore, the photodissociation of C₆₁ is estimated to be generally much faster than C⁺ addition in the regions of interest, and we do not include this latter process in our study.

3. Astrophysical environment: NGC 7023

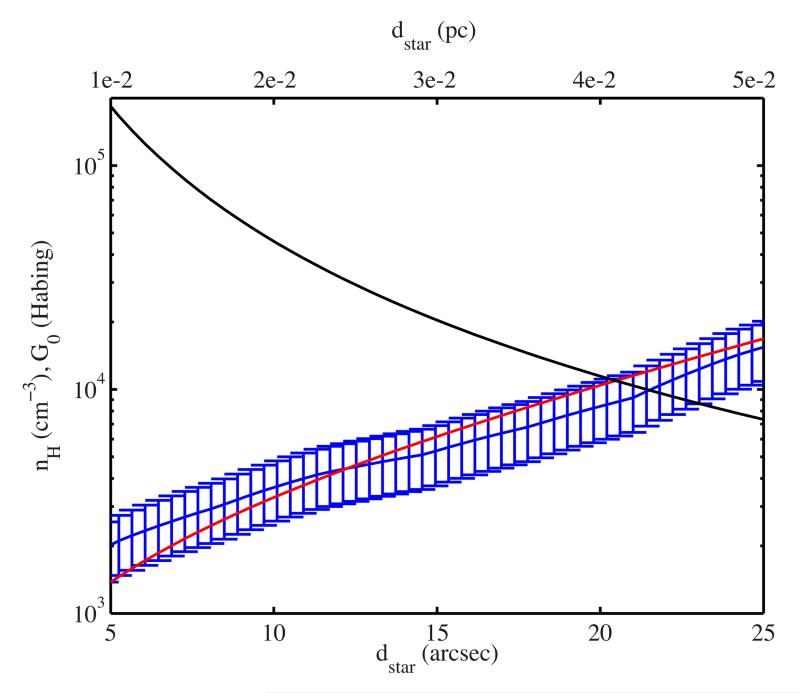
Since NGC 7023 is the template interstellar source for the study of fullerene formation (Sellgren et al. 2010; Berné & Tielens 2012; Montillaud et al. 2013), we will model the photochemical evolution of C₆₆H₂₀ for conditions found in this nebula. The formation of C₆₀ is thought to occur inside the cavity between the star HD 200775 and the PDR situated 40” at the North-West of the star. Here, we study five positions at 5, 10, 15, 20 and 25” from the star, situated on a cross-cut (see Fig. 1 in Montillaud et al. 2013) that goes from the star to the PDR. On the same cross-cut, we derive the spectral energy distribution of dust emission using archival data from the Herschel space telescope (see Abergel et al. 2010). Using these SEDs, we derive the column density on the line of sight using a value for dust opacity at 250 μm of 1.14×10⁻²⁵cm² per H atom (see details on the method in Planck Collaboration XXV 2011). This yields a column density profile, which we divide by the thickness of the region derived by Pilleri et al. (2012) based on the modeling of the PAH emission profile, i.e. 0.13 pc. The resulting density profile is shown in Fig. 3. To obtain an analytical description of this profile, we fit it with an exponential law (see Fig. 3). The intensities of the radiation field at 5, 10, 15, 20 and 25” from the star are derived as in Montillaud et al. (2013) and the corresponding profile of G₀ (UV field intensity in terms of the Habing field, which corresponds to 1.6 × 10⁻³ erg cm⁻² s⁻¹ when integrated between 91.2 and 240 nm, Habing 1968) as a function of distance to the star is presented in Fig. 3. In order to derive the temperature of the gas at these positions PDR modeling is required. For the conditions described above the gas temperature derived by the Meudon PDR model typically ranges between a few 100 and 1000 K. Here we adopt a characteristic temperature of 300 K for the photochemical model but the exact value is not critical (see Sect. 4.3). Finally, a parameter that is key when comparing the results of the model with observations is the age of the nebula, i.e. the time from when the cloud started to receive UV photons. This number cannot be derived directly and hence other indicators have to be used. One is the age of the illuminating star HD 200775. It is difficult to give a precise “age” for such a young and massive star, however, it is most likely ranging between 10⁴ and 5 × 10⁵ years (Alecian et al. 2008, 2013 and Alecian 2014 priv. comm.). Berné & Tielens (2012) adopted a value for the age of the nebula ranging from a few 10⁴ to 1 × 10⁵ years. The analysis of the dynamical properties of the warm neutral gas traced by the C⁺ line with Herschel indicate an age of ~ 0.5 Myrs (Berné et al. 2012). However, more recent calculations focusing on the photo-evaporation flow in the NGC 7023 North PDR indicate ages as low as 1.6×10⁴ years (Berné et al. in prep). We will use 10⁵ years as the reference age, but we will consider a range between 10⁴ and 5 × 10⁵ as an age uncertainty range.

Fig. 3.

Physical conditions in NGC 7023. Density profile derived from observations of the far-infrared dust emission in the cavity of NGC 7023 (blue with error-bars) and exponential fit to this profile used in the photochemical model (red line). The black line shows the adopted profile for the intensity of the radiation field G₀.

4. Results

4.1. Internal energies

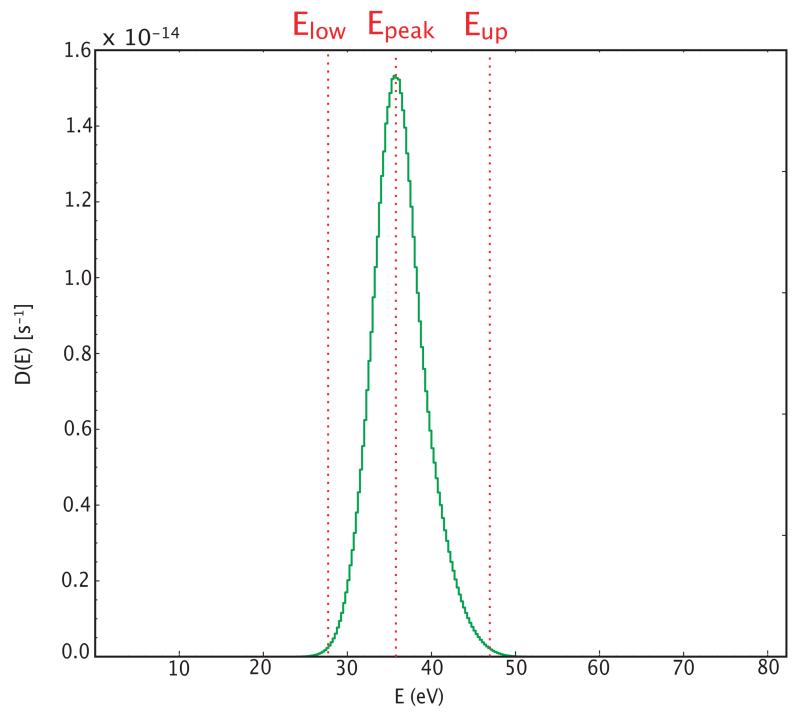
In order to understand the processes at play in the photochemistry, it is useful to evaluate the probability density functions (PDFs) of the internal energies of the species that photodissociate with the model. Fig. 4, shows such a PDF for C₆₀ at a distance of 5” from the star. In Table 3, we report the main characteristics of these PDFs for all the cages considered in the model: the peak energy E_peak i.e. the energy of maximum dissociation rate D(E) expressed in s⁻¹, and the lower and upper bounds E_low and E_up defined by D(E_up) = D(E_low) = D(E_peak)/100 with E_up > E_low (see Fig. 4 for a graphical definition of these parameters). These values are calculated using the activation energies of Zhang et al. (1992), and those of Gluch et al. (2004) (Table 2). The results presented in Table 3 indicate that the internal energies required to dissociate the molecules are high, i.e. > 15 eV. Photons in the NGC 7023 nebula have a maximum energy set by the Lyman limit, i.e. 13.6 eV. Hence, the molecules that dissociate must have absorbed multiple photons, and therefore the photochemistry of these species is completely governed by these multiple-photon absorptions. In the specific case of C₆₀ , the energy needed is at least 27 eV, i.e. requiring the absorption of at least three photons in order to dissociate.

Fig. 4.

Probability density function of dissociation of the C₆₀ molecule as a function of internal energy, at a distance of 5” from the star (G₀ ~ 2 × 10⁵). Energies E_peak at maximum dissociation rate (D(E) = k_diss(E) × n(E)), E_low and E_up (where D(E_up) = D(E_low) = D(E_peak)/100 and E_up > E_low) are depicted. The values of E_peak, E_low and E_up for all cages are given in Table 3.

Table 3.

Properties of the probability density functions of dissociation of cages (see example of such a function in Fig. 4) : E_peak, E_low and E_up. All values in eV and derived for a distance of 5” from the star (G₀ ~ 2 × 10⁵).

	a.			b.
Species*	Elow	Epeak	Eup	Elow	Epeak	Eup
C66	22	32	39	26	35	43
C64	24	35	43	24	34	41
C62	15	20	28	22	30	36
C60	27	36	47	27	36	47
C58	22	30	37	24	33	41

^*Notes. Cages only are presented in this table.

^aUsing activation energies of Zhang et al. (1992);

^bUsing activation energies of Gluch et al. (2004).

4.2. Abundances

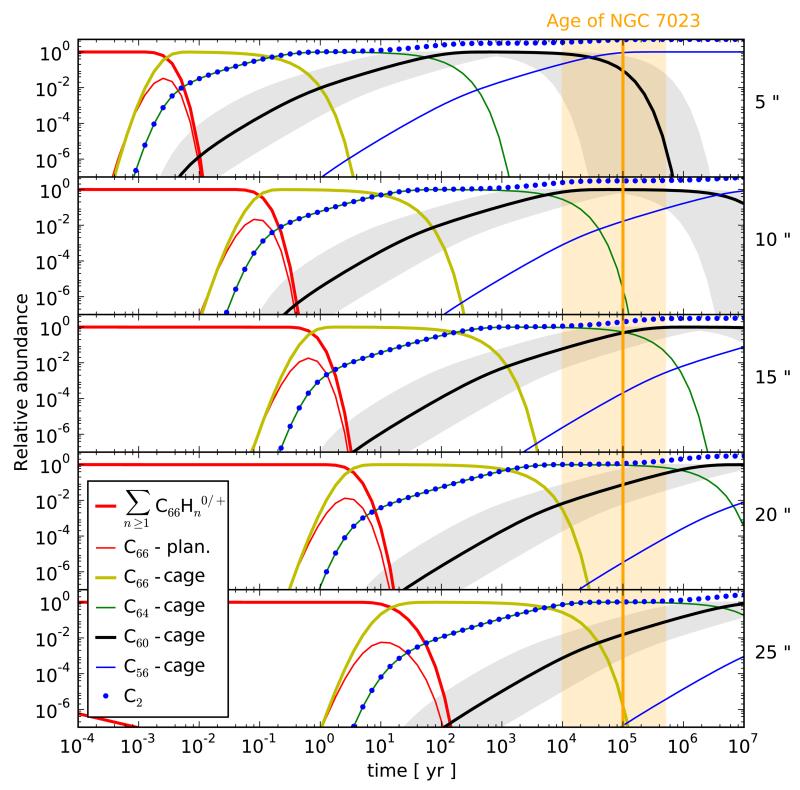
The results of the model are given in Fig. 5 which presents the 20 time-evolution of the abundance of PAHs $(\sum _{n=1}^{20}{\mathrm{C}}_{66}{\mathrm{H}}_n)$, and cages $({\mathrm{C}}_{66}^{\mathit{planar}},{\mathrm{C}}_{66}^{\mathit{cage}},{\mathrm{C}}_{64}^{\mathit{cage}},{\mathrm{C}}_{62}^{\mathit{cage}},{\mathrm{C}}_{60}^{\mathit{cage}},{\mathrm{C}}_{58}^{\mathit{cage}})$ and C₂, at distances of 5, 10, 15, 20 and 25” from the star HD 200775 in NGC 7023. For these five positions, full dehydrogenation occurs very quickly (a few 10s of years at 25” and a few days at 5” from the star). This implies that C₆₆H₂₀ is quickly destroyed in NGC 7023, however larger PAHs could survive over longer timescales. Once the planar C₆₆ is formed, it immediately folds and forms a cage. This implies that graphene flakes are only transient species and therefore unlikely to be detected in the ISM. The C₆₄ cage, instead, can survive for a relatively long period of time (few 10s of years at 5” from the star and up to several 10⁵ years at 25” from the star). It is therefore the shrinking step, where cages loose C₂ units, that limits the efficiency of the C₆₀ formation process in this model. Since each of the C₂ loss process is time consuming, it appears unlikely that PAHs with sizes N_C ≳ 66 C atoms will contribute significantly to the formation of C₆₀ . At distances shorter than 10” from the star the cages can shrink to C₆₀ and after 10⁵ years all the C₆₆H₂₀ has been converted to C₆₀ . Once the molecules have reached C₆₀, it takes a very long time to destroy them: C₆₀ survives for 10’s of Myrs at distance larger than 10” to the star (radiation fields below G₀ of a few 10⁴). Only at the closest position to the star (5”, G₀ ~ 2 × 10⁵) is C₆₀ destroyed efficiently and hence it is predicted that its abundance will decrease after a few 10⁴ years.

Fig. 5.

Model results for the time-evolution of the abundance of PAHs $(\sum _{n=1}^{20}{\mathrm{C}}_{66}{\mathrm{H}}_n)$, and cages $({\mathrm{C}}_{66}^{\mathit{planar}},{\mathrm{C}}_{66}^{\mathit{cage}},{\mathrm{C}}_{64}^{\mathit{cage}},{\mathrm{C}}_{62}^{\mathit{cage}},{\mathrm{C}}_{60}^{\mathit{cage}},{\mathrm{C}}_{58}^{\mathit{cage}})$ and C₂. These are normalized to the abundance of C₆₆H₂₀ at t = 0. The model calculations are done for distances of 5, 10, 15, 20 and 25” from the star HD 200775 in NGC 7023. Note that the dissociation of C₂ is not treated in our model, hence the C₂ abundances reported are only provided as an indication of how much C₂ is formed from the dissociation of cages. Similarly, the dissociation of the ${\mathrm{C}}_{56}^{\mathit{cage}}$ is not included in the model and therefore its abundance is provided as an indication of how much C₆₀ is being destroyed. The gray shadowed regions indicate the uncertainty range implied by uncertainties of a factor of 10 on the rates of C₂ loss (see Sect. 4.3 for details). The approximate age of NGC 7023 is given, with orange shadowed regions representing the uncertainty on this value (see Sect. 3 for details).

4.3. Sensitivity of model results

Is the model very sensitive to the adopted parameters, and if so, which are the critical parameters ?

First, we have checked that the dehydrogenation timescale is always much smaller than the cage formation plus shrinking timescale for the physical conditions of the considered positions. Therefore, it is equivalent to start our calculations with the planar C₆₆ rather than with C₆₆H₂₀. All the following tests have been conducted with the above assumption, except for the gas temperature test. We first test the choice in the vibrational frequencies for the system. We find the exact values of the frequencies to have a negligible impact on the results, as long as the number of vibrational degrees of freedom and the orders of magnitude of the frequencies are correct. We have varied the gas temperature in the model from 100, to 300 and 1000 K and found that this has a negligible impact on the C₆₀ formation timescale. The UV-visible absorption cross section of the cages, which is not well known, has a somewhat larger impact on the results. For instance, if for the cages we use the cross section per C atom of C₆₆H₂₀ (Malloci et al. 2007) instead of the one of C₆₀ (Berkowitz 1999), we obtain a variation by a factor of three in the timescale of formation of C₆₀. Multiplying the pre-exponential factors of C₂ loss by 0.1 or 10 simultaneously for all cages we observe an inversely proportional variation of the C₆₀ formation timescale. This effect in the abundance of C₆₀ is illustrated by the shadowed region in Fig. 5. When varying individually these coefficients, we find that the results are impacted mainly by the value for C₆₆ → C₆₄ + C₂, and marginally for C₆₄ → C₆₂ + C₂, while changes for the two other shrinking reactions do not impact the results. We compared our standard results (i.e. using the activation energies from Zhang et al. 1992) with the results obtained when using the experimental dissociation energies of Gluch et al. (2004). The C₆₀ formation timescales is slightly increased, mainly due to the higher stability of ${\mathrm{C}}_{66}^{\mathit{cage}}$ in the experimental data set. Overall, the effect does not affect the comparison with observations and discussion which follow. Hence from now on we only consider the results of the model using the activation energies from Zhang et al. 1992. The main source of uncertainty appears to arise from the pre-exponetial factors chosen for the shrinking steps. We will therefore consider their effect in the comparison with observations.

5. Comparison with observations

In this section we compare the results of our model with the observation of C₆₀ formation in NGC 7023. To be completely accurate, this comparison would require that the model contains a whole size distribution of PAHs in agreement with observations. This requirement is beyond the scope of this paper, but the agreement between the observations and the model can be tested bearing this limitation in mind.

The comparison is primarily based on confronting the maximal abundance of C₆₀ observed in NGC 7023, at a distance of 11” from the star, with the value obtained in the model for a distance of 10”. Taking into account the uncertainty on the age of NGC 7023 and the uncertainty on the pre-exponential factors, the model-predicted abundances of C₆₀ ranges between a minimum value of 1.3×10⁻² and 0.98, relative to C₆₆H₂₀ (Fig. 5). To convert this into an absolute abundance of C₆₀ one needs to know the abundance of C₆₆H₂₀ relative to the total PAH population, and to know the total abundance PAHs in NGC 7023. The latter was estimated by Berné & Tielens (2012) to be $f_C^{\mathit{PAH}}=7\times {10}^{-2}$ expressed in fraction of carbon locked in PAHs. The maximum abundance of C₆₆H₂₀ relative to the total PAH population, α, can be estimated following Pilleri et al. (2009), using the PAH size distribution of Desert et al. (1990), which yields a value α = 5.3 × 10⁻³. Thus, the fraction of carbon locked in C₆₆H₂₀ is 5.3 × 10⁻³ × 7 × 10⁻² = 3.7 × 10⁻⁴. With this value, the fraction of carbon locked in C₆₀ predicted by the model at a distance of 10” from the star ranges between $f_C^{C_{60}}=4.8\times {10}^{-6}$ and $f_C^{C_{60}}=3.6\times {10}^{-4}$ (where the lower and upper limit of the range include the uncertainty on the pre-exponential factor and the age of the nebula). This range of values is in agreement with the one derived by Berné & Tielens (2012) of $f_C^{C_{60}}=1.7\times {10}^{-4}$. So far we have considered C₆₆H₂₀ as the only precursor of C₆₀ . As mentioned in Sec. 4.2, it is reasonable to expect that only PAHs bearing between 60 and 66 C-atoms will be able to form C₆₀, and hence can increase the final abundance of C₆₀. Hence, it is realistic to calculate α incorporating all the species bearing between 60 and ~66 C atoms, which yields α = 3.8 × 10⁻². With this value, the abundance of C₆₀ at 10” from the star is predicted to range between $f_C^{C_{60}}=3.5\times {10}^{-5}$ and $f_C^{C_{60}}=2.6\times {10}^{-3}$, in good agreement with the value derived by Berné & Tielens (2012) of $f_C^{C_{60}}=1.7\times {10}^{-4}$. The comparison can be extended to the other positions (15, 20 and 25”) where the abundance of C₆₀ has been measured. At these three positions, the model derived ranges of abundance are also in good agreement with the observed abundances. However, as the distance grows the range of acceptable values predicted by the model become broader and less constraining. Overall, the present comparison demonstrates that our scenario is compatible with observations within the uncertainties on the molecular parameters and the age of the nebula.

6. Discussion

6.1. Comparison to other models

Models of C₆₀ formation in a top-down mechanism were presented in Berné & Tielens (2012) and Micelotta et al. (2012). The scenarios in these papers are quite similar, the main difference being that Berné & Tielens (2012) consider PAHs as the starting ingredient while for Micelotta et al. (2012) it is nanometer-sized “arophatic” clusters. In both of these studies the evolution of the species is described by a “thermal model” (Arrhenius equation), where the driving parameter is the activation energy. For the loss of C atoms at the edge of graphene sheets, Berné & Tielens (2012) used a value tuned to 4.5 eV to obtain reasonable formation efficiencies. Yet, as noted by Micelotta et al. (2012) this value is somewhat arbitrary and the obtained C₆₀ formation efficiencies remain low. To explain the efficient formation of C₆₀ in evolved stars, Micelotta et al. (2012) used the results from the molecular dynamics simulations of Zheng et al. (2007), and extracted a unique activation energy of 0.35 eV for the shrinking reaction by loss of C₂. However, this value is a factor of ~ 20 smaller than what is generally accepted for this reaction (see Table 1), leading to over-estimations of the rates by many orders of magnitude, casting serious doubts on the conclusions of Micelotta et al. (2012). In summary, since these simple models do not allow the molecules to reach high internal energies through multiple photon absorptions, high formation rates of C₆₀ require activation energies tuned to values that are too low to be physical.

In summary, since these simple models do not consider multiple photon absorptions, the molecules never reach the high internal energies necessary to a high formation rate of C₆₀ . Therefore, they strongly underestimate the C₆₀ formation yields, unless one assumes activation energies that are too low to be physical. Instead, the approach presented here, including a complete description of the photochemical processes, allows, using realistic molecular parameters, to predict formation efficiencies that are in agreement with observations.

6.2. Comparison to experimental results of gas-phase cage formation

After we submitted the present paper, Zhen et al. (2014) reported experimental results in which they demonstrate that C₆₀ can be formed in the gas phase through laser irradiation of larger PAH molecules. These results support the idea put forward here that C₆₀ can be formed following a top-down scheme. However, Zhen et al. (2014) suggest that in some cases the conversion of graphene into cages could involve a prior step of C₂ loss. This is in contradiction with our photochemical model in which the dissociation by loss of C₂ is less efficient than the folding by many orders of magnitude, and therefore folding always precedes the loss of C₂. This is mainly because the activation energy for folding (which relies on molecular parameters derived from molecular dynamics simulations performed by Lebedeva et al. 2012) is a factor of ~ 2 smaller than the activation energy for C₂ loss. Further experimental investigation is necessary, in particular to quantify the activation energies involved in the folding and C₂ loss by flakes, so that they can be included in our model.

6.3. Stability of C₆₀

Table 3 demonstrates that C₆₀ can reach particularly high internal energies. In this state, fluorescence from thermally excited electronic states becomes a very efficient cooling channel, postponing the dissociation and conferring an increased stability to C₆₀⁴. Hence, in the frame of the top-down mechanism detailed here and because of its remarkable stability, C₆₀ is expected to be the most abundant of all fullerenes in highly UV irradiated environments in space. It is interesting to note that similar kinetic stability arguments have been put forward (Fedorov et al. 2011) to explain the high abundance of C₆₀ relative to other fullerenes observed in laboratory experiments (Kroto et al. 1985; Krätschmer et al. 1990). As discussed in Sect. 4.2, C₆₀ is expected to survive for 10s of Myrs in intense radiation fields. In the diffuse ISM, where the radiation field is several orders of magnitude smaller, C₆₀ is therefore expected to resist to radiation for even larger timescales. In such conditions, other energetic processes must be invoked to destroy C₆₀ , such as shocks or cosmic rays.

6.4. Isomerization of C₆₀

There exists a large number of C₆₀ isomers, and hence there is a-priori no reason for the icosahedral Ih-C₆₀ to be the one present in the ISM. Ih-C₆₀ has the lowest energy amongst all C₆₀ isomers and the closest isomers lie about 2 eV higher in energy (Raghavachari & Rohlfing 1992). Upon UV absorption, the isomerization reaction from any C₆₀ isomer towards Ih-C₆₀ requires only 5.4 eV of activation energy (Yi & Bernholc 1992), and is therefore expected be fast in the conditions investigated here. Conversely, the isomerization reaction from Ih-C₆₀ to another C₆₀ isomer requires ~ 5.4 + 2 = 7.4 eV, and will be much slower than the previous reaction. Therefore, relatively quickly, the population of C₆₀ molecules will be dominated by the icosahedral isomer.

7. Conclusions

We have presented the first detailed photochemical modeling of C₆₀ formation from PAHs in space following a top down scheme. This model is calculated for a single molecule (C₆₆H₂₀) as a starting point, and the key processes are explicitly described: UV photon absorption (including multiple photon events), radiative cooling and dissociation. Because the involved activation energies in this top-down mechanism are high (especially for the shrinking steps), multiple photon absorptions dominate the photochemistry. Using the physical conditions which prevail in the NGC 7023 reflection nebula, we find that C₆₀ can be formed from C₆₆H₂₀ over a timescale of about 10⁵ years with a high efficiency in highly irradiated regions. Assuming that only PAHs containing between 60 and 66 C atoms are precursors of C₆₀ and a classical size distribution for PAHs, the comparison between the modeled and observed abundances of C₆₀ shows a good agreement, within the uncertainties of the model. These uncertainties can be reduced once a better characterization of the reaction rates of the shrinking of cages is available. While developed for the physical conditions of NGC 7023 as representative of the interstellar medium, the scenario and model described in this paper could also be applied to the irradiated circumstellar gas of planetary nebulae, if the physical conditions in these environments can be characterized in detail.