Validity and sensitivity of a human cranial finite element model: implications for comparative studies of biting performance

Abstract

Finite element analysis (FEA) is a modelling technique increasingly used in anatomical studies investigating skeletal form and function. In the case of the cranium this approach has been applied to both living and fossil taxa to (for example) investigate how form relates to function or infer diet or behaviour. However, FE models of complex musculoskeletal structures always rely on simplified representations because it is impossible completely to image and represent every detail of skeletal morphology, variations in material properties and the complexities of loading at all spatial and temporal scales. The effects of necessary simplifications merit investigation. To this end, this study focuses on one aspect, model geometry, which is particularly pertinent to fossil material where taphonomic processes often destroy the finer details of anatomy or in models built from clinical CTs where the resolution is limited and anatomical details are lost. We manipulated the details of a finite element (FE) model of an adult human male cranium and examined the impact on model performance. First, using digital speckle interferometry, we directly measured strains from the infraorbital region and frontal process of the maxilla of the physical cranium under simplified loading conditions, simulating incisor biting. These measured strains were then compared with predicted values from FE models with simplified geometries that included modifications to model resolution, and how cancellous bone and the thin bones of the circum‐nasal and maxillary regions were represented. Distributions of regions of relatively high and low principal strains and principal strain vector magnitudes and directions, predicted by the most detailed FE model, are generally similar to those achieved in vitro. Representing cancellous bone as solid cortical bone lowers strain magnitudes substantially but the mode of deformation of the FE model is relatively constant. In contrast, omitting thin plates of bone in the circum‐nasal region affects both mode and magnitude of deformation. Our findings provide a useful frame of reference with regard to the effects of simplifications on the performance of FE models of the cranium and call for caution in the interpretation and comparison of FEA results.

Introduction

Finite element analysis (FEA) is increasingly applied in studies of skeletal form and function. A focus of interest is the craniofacial skeleton, where mechanical loading during ontogeny is important in ensuring balanced, normal growth and, therefore, normal adult form and function (Lieberman, 1996; Moss, 2007; Menegaz et al. 2010). Further, comparative analyses of craniofacial strains predicted by FEA are potentially informative in relation to ecology and diet in both living and fossil taxa (Rayfield, 2007; Kupczik et al. 2009; Strait et al. 2009; Wroe et al. 2010; Gröning et al. 2011b; Ross et al. 2011; O'Higgins et al. 2012; Smith et al. 2015b). However, the results of an FEA depend on model geometry, material properties, applied loads and kinematic constraints. Full reproduction of these characteristics in a model of a structure such as the human cranium is currently extremely difficult. Among model characteristics, detailed anatomy can be difficult to achieve because of limitations in imaging and thus reconstruction. Representation of anatomy is particularly error‐prone in the case of fossil material because of taphonomic alteration of bone internal anatomy (e.g. due to sediment deposition) and tissue characteristics (e.g. similar image characteristics of fossilised bone and sediments) (Turner‐Walker & Parry, 1995; Olesiak et al. 2010; Fitton et al. 2015), or in the case of models built from clinical computed tomograms where image resolution is limited (Toro‐Ibacache et al. 2015). Thus, simplification is inevitably necessary and it is important to assess the validity of FE models and, in particular, to understand how different modelling simplifications impact on performance.

Several studies have assessed FE model validity and sensitivity (Kupczik et al. 2007; Bright & Gröning, 2011; Ross et al. 2011; Fitton et al. 2012; Cox et al. 2015; Fitton et al. 2015; Smith et al. 2015a). Collecting in vivo strain measurements for validation is impossible in many cases (e.g. because of ethical constraints and in fossils) and, where it is practicable, strain data are usually limited to a few point locations where the siting of strain gauges is feasible. More detailed and comprehensive measurement of surface strains is possible using postmortem material (Gröning et al. 2009) but replicating physiological loading in vitro then becomes an issue. In any case, the gathering of experimental data against which FE model performance can be assessed is time‐consuming, often destructive, subject‐specific, error‐prone and only possible in extant, not fossil, specimens. A practical solution is to validate one or a limited number of FE models in detail and to base further models on what has been learnt from the validation and accompanying sensitivity analyses. The aim in this scenario is to validate the modelling approach and to understand the sensitivity of models to variants of this approach, in order to increase the accuracy of FE model behaviour and to know more about the limits of interpretation imposed by simplifications.

Several prior studies of FE models of the skull have compared predicted strains with those measured in vivo (Strait et al. 2005; Ross et al. 2011) or with strains resulting from loading of wet cadaveric or dried skeletal material (Marinescu et al. 2005; Kupczik et al. 2007; Gröning et al. 2009; Smith et al. 2015a). To our knowledge, only one study to date has validated a model of a human cranium. That study used 13 gauges to measure the strains over a cadaveric cranium that was loaded to perform a block‐bite using half the dental arch (Szwedowski et al. 2011). The model was built using area‐specific linearly elastic and isotropic material properties based on a map of bone density, as well as a hybrid solid‐shell mesh, representing cancellous and cortical bone respectively. Sensitivity analyses were performed by varying the elasticity modulus, Poisson's ratio and homogeneous cortical shell thicknesses. The authors showed that the model with the most detailed cortical bone reconstruction and material properties correlated best with the experimental data; however, the impact of different simplifications on strain contours and directions was not examined.

Among simplification approaches, it is common to omit structures that are very small and it is not feasible to reproduce them accurately at the given model resolution. Such structures include fine plates of bone, cancellous bone, sutures and the periodontal ligaments (Kupczik et al. 2007; Wood et al. 2011; Bright, 2012). Thus, cancellous bone is often modelled as a bulk material because even relatively large trabeculae are not always distinguishable in computed tomograms (Gröning et al. 2012). Further, in FEA studies of the skull and postcranial skeleton, bone is often allocated simplified homogeneous and isotropic material properties obtained either from the literature or from average values of the specimen itself, rather than by mapping directly measured, heterogeneous orthotropic material properties (Strait et al. 2005; Kupczik et al. 2007) which are often unavailable and, particularly in the case of fossils and living humans, impossible to obtain.

Given the need for simplifications in modelling (including the extent to which cortical and cancellous bone are differentiated), the aim of the present study is to provide a frame of reference for the construction of models of the human cranium and those of our anatomically close primate and fossil relatives. Five voxel‐based FE models of the same human cranium were built, varying their model geometry (anatomical detail and composition). Two manipulations are applied: the first involves changes in anatomical detail that are inevitable when finite element (voxel) sizes vary according to the typical limited range of resolution of primary CT data used in most studies to date, and the second represents or omits cancellous bone in the model. To assess the validity of the predictions of the FE models, strains were compared with those measured in vitro in the actual specimen.

In vitro strains were measured using an optical technique, digital speckle pattern interferometry (DSPI; Yang & Ettemeyer, 2003; Yang et al. 2007), which provides a full‐field surface measurement of microscopic deformation, from which the surface displacements and strains of an object under load can be calculated. This approach has been used previously to validate predicted stresses and strains from FE models of a human mandible (Gröning et al. 2009) and a pig cranium (Bright & Gröning, 2011). It offers several advantages over strain gauges; most notably, DSPI measures strains over the entire field of view, whereas strain gauges measure them at distinct points.

Model sensitivity was assessed by comparing the FEA results among models. In addition, larger, global changes in size and shape of the skull under loading can be compared among model variants using Procrustes size and shape analysis, from geometric morphometrics (Milne & O'Higgins, 2012; O'Higgins & Milne, 2013). This approach has been used previously in conjunction with strain maps from FEA of skeletal structures (Milne & O'Higgins, 2012; Fitton et al. 2015). It provides additional insights into modes of global deformation that are useful when assessing the impact of subtle differences among FE models in sensitivity analyses (Gröning et al. 2011a; Fitton et al. 2012, 2015).

The following null hypotheses (H0) were tested:

H01: There are no differences in distribution, magnitude and direction between the principal strains predicted by the different FE models, and between these and the principal strains measured in vitro.

H02: There are no differences in magnitudes and modes of global deformation among the different finite element models.

The testing of these hypotheses allows us to assess the magnitude and nature of any differences in performance among the models and between the models and the cadaveric cranium. This consideration leads to some important insights into sources of error and their impact on FEA studies of crania.

Materials and methods

Anatomical data

The cadaveric head of a 74‐year‐old man from the repository of the Centre for Anatomical and Human Sciences (Hull York Medical School, HYMS, UK) was used in this study. The subject signed consent for experimental anatomical studies in life when he donated his remains, and ethical approval was obtained from the HYMS Ethics Committee. All experimental work was carried out in accordance with the Human Tissue Act (available at www.hta.gov.uk) and HYMS protocols for the handling and storage of cadaveric material.

The cadaver had been embalmed 2 years prior to this study using a modified version of the University of Bristol embalming fluid formulation (1.4% formaldehyde and 70% ethanol; Vickers Laboratories Ltd., Pudsey, UK). The head was scanned using computed tomography (CT) at the York Teaching Hospital (York, UK) with a Siemens 16‐channel multidetector CT scanner equipped with a STRATON tube (Siemens Somatom Sensation 16; Siemens Healthcare, Erlangen, Germany) at 120 kV and 320 mA with an H60s edge‐enhancing kernel. Voxel size was 0.48 × 0.48 × 0.7 mm. Initial reconstruction of images was performed using a specialist system (Syngo Multimodality workplace; Siemens Healthcare) to ensure adequate field of view and image quality. The image stacks were then exported as DICOM files for detailed segmentation and reconstruction as described further below.

In vitro strain measurement

The head was skeletonised by dissection, removing the soft tissues and the periosteum, taking precautions not to damage the bone surface. The cranium was placed on the platform of a universal material testing machine with a 1‐kN load cell (Lloyd's EZ50; Ametek‐Lloyd Instruments Inc., Sussex, UK). The position and loading of the cranium was chosen as an easily replicable loading scenario; although the loading was not physiological, the loading at the teeth was comparable to the way a tooth is loaded during biting. Steel blocks were used to support the cranium at both mastoid processes and the left central incisor. Compressive vertical forces were applied to the midplane of the frontal squama, 13 mm anterior to bregma (see experimental setup in Fig. 1a). The load was applied in 11 steps of 50 N to achieve a final load of 550 N. The final arrangement of steel supports and load was arrived at by trial and error, with earlier runs of the loading experiment failing due to instability that was corrected by increasing friction between the steel blocks and platform using emery paper. Stability of the cranium after each step was assessed by repeatedly checking that increases in the reaction force at the constrained border of the left central incisor scaled linearly with increasing loads. Five successive and successful experimental rounds (i.e. with stability of the set up and replicable recording of strains and reaction force) for in vitro strain measurement in the infraorbital region and four for the frontal process of the maxilla were achieved. The position of the loading point on the cranium was marked to control the position of the load between loading experiments. Incisor reaction forces were measured using a strain meter equipped with a 5 kN load cell (Omega DP25B‐S; Omega Engineering Inc., Stamford, CT, USA) previously calibrated by applying known compressive loads with the Lloyd's testing machine described above.

Figure 1.

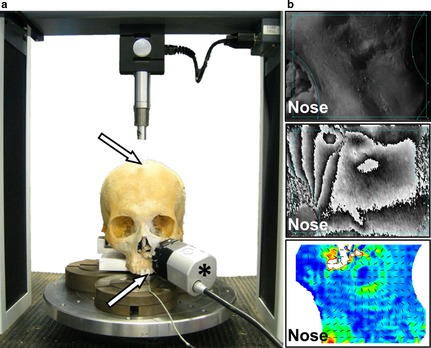
Experimental set up for in vitro strain measurement. (a) Vertical compressive load applied to the calvarium (upper arrow) simulating a left central incisor bite (lower arrow). The asterisk shows the DSPI sensor attached to the infraorbital region. (b) DSPI‐based surface strain measurement, where the unstrained surface (upper image) provides a speckle interferogram that changes under load. The change is quantified in a phase map (middle image). Surface strains are calculated from 3D displacements, and expressed as colour‐coded strain contour plots and strain vector orientations (lower image). The position of the nose is shown for reference.

Full‐field surface strains were measured using a Q‐100 DSPI system (DANTEC Dynamics GmbH, Ulm, Germany). The regions selected for strain measurement in this study were the left infraorbital area and the frontal process of the maxilla, as both show high strains in FEAs of simulated incisor bites in primates (Gross et al. 2001; Kupczik et al. 2009; Fitton et al. 2012). This system provides a maximum field of view (FOV) of 25 × 33 mm². The measured surfaces were covered with a thin layer of white spray (DIFFU‐THERM developer BAB‐BCB; Technische Chemie KG, Herten, Germany) to prevent surface reflection of ambient light. The Q‐100 sensor was glued using its three legs to the boundaries of the treated surface using an acrylic‐based adhesive (X60; HBM Inc., Darmstadt, Germany). Sensor attachment to the surface is standard procedure in using the Q‐100 system for safety critical engineering work. Although there is a theoretical impact on measured strains, in practice any effect is restricted to close to the points of attachment, which were not included in the analyses. This procedure was undertaken once for each surface, thus avoiding variations in the location of the measured surface between loading runs. Surface characterisation, phase calculation and deformation estimation (see steps in Fig. 1b) were carried out using the istra Q‐100 (v.2.7; DANTEC Dynamics GmbH). The primary strain data produced by the Q‐100 system, maximum (ε₁) and minimum (ε₃) principal strain magnitudes, plus 2D and 3D colour‐coded strain contour plots (representing strain distributions, i.e. relative locations of high and low strain) were exported and used for comparison of FEA results.

FE model construction

The cranium was reconstructed from the CT images through a combined approach of thresholding and manual segmentation of bone and teeth using the visualisation program avizo (v.7.0.1; Visualization Sciences Group, Burlington, MA, USA). Five different models were built (Table 1). To assess the impact of simplifying cancellous bone representation, in one model (model 1) cancellous bone was omitted, and hence all bone was modelled as a solid material with the Young's modulus of cortical bone. This approach has been used in previous studies of cranial FE models (Wroe et al. 2010; Bright & Gröning, 2011; Fitton et al. 2012; Jansen van Rensburg et al. 2012; Toro‐Ibacache et al. 2015) and is particularly relevant in cases where, because of model resolution, fossilisation and taphonomic processes, or in order to generate hypothetical model geometries via surface warping, modelling cancellous bone is impractical (Bright & Gröning, 2011; O'Higgins et al. 2011; Fitton et al. 2015). The remaining models (models 2–5) have a cortical shell with cancellous bone defined as a bulk material of much lower modulus than cortical bone, an approach also used in previous studies (Kupczik et al. 2009; Smith et al. 2015a). In these four remaining models, cancellous bone was represented as a bulk material in the regions normally strained during FE biting simulations, below the level of the fronto‐zygomatic suture, including the anterior and middle portions of the cranial base.

Table 1.

Characteristics of the finite element models. Young's modulus: Bone = 17 GPa; cortical bone = 17 GPa; cancellous bone = 56 MPa; teeth = 50 GPa

Model	Voxel size (mm)	No. of elements	Materials	Material volume		Features
				mm3	%
Model 1	0.48 × 0.48 × 0.48	4 028 280	Bone (cortical + cancellous)	448 472.94	97.96	Full manual reconstruction of sinus bony walls
			Teeth	9 316.41	2.04
Model 2	0.48 × 0.48 × × 0.48	3 326 922	Cortical bone	327 851.44	86.71	Partial (threshold‐based) reconstruction of inner sinus bony walls
			Cancellous bone	40 916.34	10.82
			Teeth	9 316.53	2.46
Model 3	0.48 × 0.48 × 0.48	3 504 595	Cortical bone	347 999.16	87.38	Full manual reconstruction of sinus bony walls
			Cancellous bone	40 960.09	10.28
			Teeth	9 316.53	2.34
Model 4	0.35 × 0.35 × 0.35	8 817 889	Cortical bone	327 113.15	86.74	Like model 2
			Cancellous bone	40 734.59	10.80
			Teeth	9 284.42	2.46
Model 5	0.35 × 0.35 × 0.35	9 241 525	Cortical bone	345 217.06	87.34	Like model 3
			Cancellous bone	40 749.30	10.31
			Teeth	9 284.29	2.35

The inner walls of the frontal, ethmoidal, sphenoidal and maxillary sinuses are often thinner than a single voxel and so are prone to being incompletely and poorly represented in the CT. In consequence, the question arose as to how best to represent them in an FE model. To assess the impact of omitting or including them in the model, their anatomies were either fully reconstructed manually, albeit using one or two voxels to represent their thickness, or left as assigned by grey‐level thresholding, resulting in thin plates of bone with irregular holes. Model resolution was varied via resampling by using two different voxel sizes (0.48 and 0.35 mm) to simulate the effect of typical differences in resolution in CT scans used in previous FE studies of crania. Reducing voxel size achieves a more accurate representation of the thin inner nasal walls compared with using the larger voxel size. It is of interest to assess the effect of such differences between corresponding models (models 2 vs. 4 and 3 vs. 5). We were unable to carry out a more detailed convergence analysis comparing a range of mesh resolutions because of limitations of resolution of the clinical CT scanner in relation to the finest details of bony anatomy.

Anatomical details were refined manually in each model where needed, thus varying the total number of voxels and so elements among models. In all cases, teeth were modelled as one material with a higher elastic modulus (E) than bone. The characteristics of each model are detailed in Table 1 and their features are depicted in Fig. 2a. Subsequently, data were exported as BMP stacks and converted into FE meshes of eight‐noded linear cubic elements by direct voxel conversion. Model pre‐ and post‐processing were performed using the custom FEA program vox‐fe (Fagan et al. 2007; Liu et al. 2012).

Figure 2.

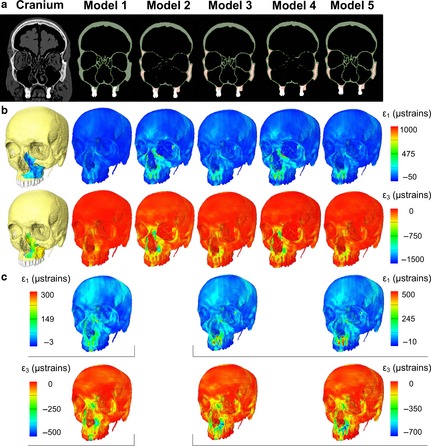
Cranium and finite element models. (a) Coronal section of the CT (cranium) and the five FE models showing the results produced by different segmentations; green represents cortical bone, red represents cancellous bone and white represents teeth. (b) Cranium with overlaid DSPI results, and FE models showing maximum principal strain ε₁ (upper row) and minimum principal strain ε₃ (lower row) strain contour plots. (c) Adjusted ranges of ε₁ (upper row) and ε₃ (lower row) contour plots for models 1, 3 and 5 to match the strain distributions of DSPI on the cranium, and models 2 and 4.

In all models, cortical bone, cancellous bone and teeth were allocated homogeneous linearly elastic and isotropic material properties (with Poisson's ratio = 0.3), following the approach used in previously validated models of human and macaque crania (Kupczik et al. 2007; Szwedowski et al. 2011) and the human mandible (Gröning et al. 2009). In models 2–5, cancellous bone was represented as a different material and was allocated an E of 56 MPa (Misch et al. 1999), and an E of 50 GPa was assigned to teeth, this being approximately the mean of the large range of values found in the literature for enamel and dentine (Meredith et al. 1996; Barak et al. 2009; Benazzi et al. 2012). The material properties of cortical bone are particularly important in relation to overall model stiffness (Marinescu et al. 2005; Strait et al. 2005) and these vary throughout the cranium. For this reason, material properties of the cadaveric cranium were measured directly from two different regions before settling on a suitable uniform value. A bone sample was collected from the maxillary tuberosity and from the zygomatic arch. E was measured using a nano‐hardness tester with a Berkovitch diamond indenter (CSM Instruments SA, Peseux, Switzerland) following the protocol in Kupczik et al. (2007). The average value was found to be 16.3 ± 3.7 GPa for the tuberosity and 21.9 ± 2.7 GPa for the zygomatic arch. As these values lie within the range used in the literature for models of the human cranium (Horgan & Gilchrist, 2003; Wroe et al. 2010; Jansen van Rensburg et al. 2012), a single E of 17 GPa, which has been used in previous models (Kupczik et al. 2009; Gröning et al. 2011b; Fitton et al. 2012), was assigned to all cortical bone.

The points of applied vertical load, the biting point and mastoid support were replicated in the model. The predicted bite force in model 5 was used to check the loading condition by confirming that this matched the reaction force measured in vitro at the left upper incisor. Based on the experimental setup and to simulate loading conditions (i.e. vertically loaded incisor and immobilised mastoids), a vertical kinematic constraint was applied to the tooth, and constraints in all three axes at each mastoid process. Loads and constraints were applied to the model in the form of selected nodes in the border of the incisor, and punctiform regions of nodes at the point of load application and tips of the mastoid processes.

Measured vs. predicted strains

The procedure to compare strains measured in vitro and those predicted by the FE models comprised three steps: (1) matching the FOV of the DSPI with the area of interest of the FE model, (2) data extraction and (3) data comparison.

To compare strain contours visually (representing strain distribution), similar colours were mapped to equivalent strain ranges from DSPI and FEA. The surface geometry of the region of the face measured by DSPI was exported as a Virtual Reality Modeling Language (VRML) file and visualised in 3D using avizo. The surface of the cranium extracted from the CT was loaded into the same scene as the DSPI surface. The DSPI surface was then manually positioned to obtain the best fit with the cranium surface guided by anatomical structures and high magnification photographs of the skull surface. Best‐fit was assessed by two observers (VT‐I and PO). Coordinates marking the location of the DSPI surface on the CT‐derived cranial surface were saved using avizo in order to match the positions of sampling points among models.

The strain magnitude outputs form DSPI and FEA are not the same in both dimensionality (2D for DSPI and 3D for FEA) and resolution, making one‐to‐one comparison impossible. We therefore used an approach that compares profiles of strain magnitudes along corresponding lines traced over the surfaces of the specimen and model. The DSPI computes strain magnitudes over a regular 2D grid in the plane of the lens. Two straight lines in this plane (lines 1 and 2) were traced across the infraorbital and two across the frontal process fields of view (FOV; lines 3 and 4) using the vertices of the FOVs to optimise replicability of measurement. Line correspondence between the models and the DSPI surfaces is shown in Fig. 3(a,b). Strain magnitudes at each point along the lines from DSPI were extracted and smoothed by once‐averaging of singe adjacent points on either side to reduce noise. To extract corresponding data from the 3D surface of the FE model, lines of landmarks were traced on the model surface forming equivalent straight lines to those used to extract strain magnitudes from the DSPI FOVs. Lines comprising 37 (line 1), 30 (line 2), 28 (line 3) and 33 (line 4) landmarks were traced over the model in avizo. These lines replicate those traced on the DSPI FOVs but they inscribe curves over the surface of the FE model. These curves have two dimensions, distance and depth, whereas DSPI traced lines have just one dimension, distance. The depth dimension was removed from each FE model curve by projecting it onto the plane described by its first two principal components. The first principal component, which represented distance rather than depth, was then rotated into the plane of the DSPI FOV to achieve best fit. The strain values were smoothed in vox‐fe by once‐averaging of neighbouring voxels to reduce strain fluctuations due to voxellation (Liu et al. 2012). After smoothing, predicted strain magnitudes at each of the landmarks were extracted for comparison against strains measured in vitro. The impact of simplifications of the model on relative (rather than absolute) strain magnitudes was assessed by calculating the correlation coefficient among models.

Figure 3.

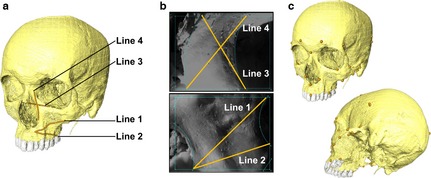
Lines for extracting strain magnitudes and landmarks for size and shape analysis. (a) Landmark lines on the FE model surface. (b) Corresponding lines in the DSPI outputs. (c) Landmarks for Procrustes size and shape analysis.

Both systems output surface strain magnitudes and vectors, the istra Q‐100 (DSPI) in 2D and vox‐fe in 3D. These software tools show vectors differently; with directions and magnitudes being represented in the vox‐fe output and directions alone in the istra Q‐100 outputs. Further, the densities and spacings of plotted vectors differ between the visualisations. Thus, to avoid crowding, in the visualisations from vox‐fe lines representing strain vectors were drawn at every fourth node in models 1, 2 and 3 and at every eighth node in the larger models, 4 and 5, over the areas of interest.

Global model deformation

It is important to note that there are two different definitions of the term ‘deformation’. In material science and in the context of morphometrics, ‘deformation’ refers to changes in size and shape (local or global). This is the definition followed here since it reflects the quantities measured by strains, i.e. how the finite elements deform under load. This differs from the definition of ‘deformation’ used occasionally in mechanics (see Truesdell & Noll, 2004, p. 48) where it may refer to the displacement of nodes of the FE model between unloaded and loaded states.

Global model deformations (changes in size and shape) resulting from applied loads were compared between FE models through Procrustes size and shape analyses based on 51 craniofacial landmarks (described in Supporting Information Table S1) and visualised in Fig. 3c). During size and shape analysis, coordinates are rotated and translated, thus preserving the changes in model size as well as shape due to loading. The resulting size and shape coordinates are then submitted to principal components analysis (PCA; O'Higgins et al. 2012; Fitton et al. 2015). Visualisations of predicted changes in cranial size and shape due to loading and the differences in modes of deformation among models used the surface corresponding to model 1, warped to the mean unloaded landmark configuration before further warping to represent model deformations. Two Cartesian transformation grids were drawn over the mean landmark configuration, and warped with the surface to facilitate interpretation of visualised deformations (Fitton et al. 2012; O'Higgins et al. 2012). As landmarks are placed only once on the CT‐derived surface representing all the models, there is no measurement error associated to the method.

Results

The experimental setup was replicated in vox‐fe for each of the models 1–5. The locations of each constrained point and applied load, plus the predicted vs. actual bite force measured in vitro were used to achieve accurate model and load orientation. The experimentally measured bite force in the most anatomically accurate model, 5, was 176.84 ± 9.44 N and the predicted bite force was 177.11 N. Repeating this setup, model 4 predicted 177.21 N of bite force, whereas low‐resolution models 1, 2 and 3 predicted 182, 182.54 and 182.55 N of bite force, respectively.

The results of the strain and global model deformation analyses are presented below.

Measured vs. predicted strains

In general, the strain contour plots predicted by the FEAs differ among models in magnitude but show similar distributions of regions of relatively high and low strain (Fig. 2b,c with adjusted strain ranges to improve visualisation). This is also evident from the plots of strain magnitudes (Figs 4 and 5) where strains from the FE simulations are compared with the in vitro ranges. The match is better for lines 1 and 2 than for lines 3 and 4. By comparing models 1, 2 and 4 with model 5, it appears that the main effect of representing regions of cancellous bone as solid cortical bone and reconstructing sinus and nasal walls was to increase model stiffness. Comparing FE models with each other and with the results from DSPI, the ‘solid’ model 1 shows strains three to four times lower than the in vitro results and the strains predicted for the other models (Figs 4 and 5). Overall, models 2–5 showed similar strain magnitudes. However, models 2 and 4 (with incompletely reconstructed sinus and nasal walls) show the largest discrepancy with the values measured in vitro (particularly ε₃ values; Fig. 5) and the lowest correlations (Table 2) with model 5 of strains traced along the lines drawn over the frontal process of the maxilla (see Fig. 3a,b). Model resolution (comparing models 2 vs. 4 and 3 vs. 5) over the limited range assessed in this study does not have an effect on strain magnitude.

Figure 4.

In vitro vs. predicted strain magnitudes across the infraorbital region. The grey area represents the mean measured (DSPI) strains ± 2 SD. The strain magnitudes predicted for model 1 multiplied by 3.5 were also plotted; this approximately corrects for increased model stiffness due to infilled cancellous bone.

Figure 5.

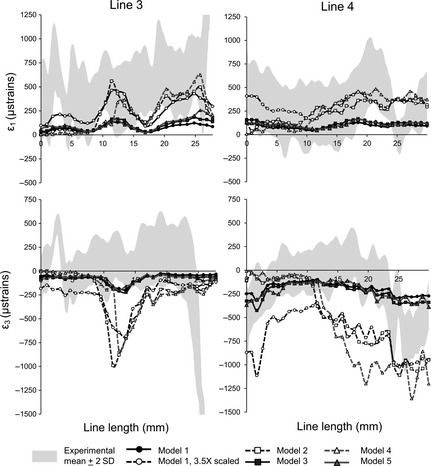
In vitro vs. predicted strain magnitudes across the frontal process of the maxilla. The grey area represents the mean measured (DSPI) strains ± 2 SD. The strain magnitudes predicted for model 1 multiplied by 3.5 were also plotted; this approximately corrects for increased model stiffness due to infilled cancellous bone.

Table 2.

Correlation of strain magnitudes between the most detailed model (5) and the other models

Model 5	Principal strains	Linear correlations (r)
		Model 1	Model 2	Model 3	Model 4
Line 1	ε1	0.91	0.83	0.97	0.90
	ε3	0.91	0.93	0.98	0.97
Line 2	ε1	0.98	0.96	0.97	0.99
	ε3	0.96	0.97	0.98	0.99
Line 3	ε1	0.80	0.71	0.88	0.75
	ε3	0.85	0.81	0.90	0.73
Line 4	ε1	0.85	0.25	0.85	0.36
	ε3	0.87	0.36	0.87	0.34

There are some differences in strain magnitudes between models and the experimentally measured strains, and between models 1, 2 and 4 compared with model 5 (the most accurate). However, the directions of the principal strain vectors are very consistent among models. These mainly consist of vertical compression and transverse tension of the nasal notch (Fig. 6) and of the infero‐medial margin of the orbital opening in the frontal process of the maxilla (Fig. 7). This is evident despite the differences described earlier in the ways strain vectors are displayed in the DSPI and vox‐fe outputs.

Figure 6.

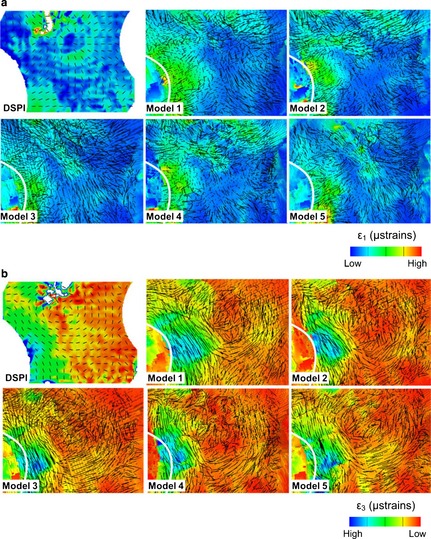
In vitro vs. predicted directions of strains in the infraorbital region. Black lines represent the vectors of strains in 2D (DSPI) and 3D (FE models). (a) Maximum principal strain ε₁ and (b) minimum principal strain ε₃. To best match contours and to facilitate the identification of corresponding regions, vector magnitudes in the FEA outputs and ranges of each strain contour plot have been adjusted independently.

Figure 7.

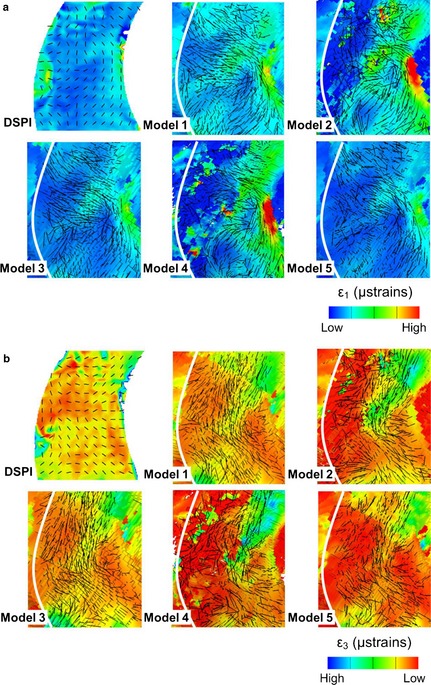
In vitro vs. predicted directions of strains in the frontal process of the maxilla. Black lines represent the vectors of strains in 2D (DSPI) and 3D (FE models). (a) Maximum principal strain ε₁ and (b) minimum principal strain ε₃. To best match contours and to facilitate the identification of corresponding regions, vector magnitudes in the FEA outputs and ranges of each strain contour plot have been adjusted independently.

Global model deformation

The PCA of size and shape variables confirms and clarifies the findings from the analyses of strains with regard to differences and similarities in modes of deformation. In the plots of principal components (PCs), model deformations are represented by lines connecting the loaded and unloaded models (Fig. 8). Global deformations generally consist of dorso‐ventral bending of the maxilla mainly at the level of the nasal notch. The deformations of models 1, 3 and 5 are virtually the same in direction (mode of deformation), varying only in magnitude, with model 1 deforming less. Models 2 and 4 deform to a greater degree and in subtly different ways from the others, with more vertical compression of the nasal aperture and lateral displacement of the mid to upper parts of the nasal margins. They also deform more asymmetrically than the other models. The magnitudes of model deformation due to loading are very small. As such, to aid visualisation the warpings in Fig. 8 were magnified 250 times.

Figure 8.

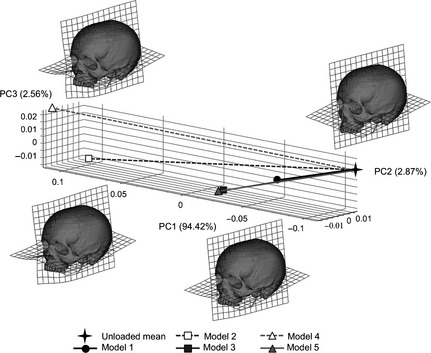
Principal components analysis of size and shape variables based on 51 landmarks representing deformation of models 1–5 under a simulated incisor bite with respect to the unloaded cranium. Deformations are magnified 250 times to facilitate visualisation.

Discussion

The aim of the present study was to validate the performance of FE models of a human cranium and to assess their sensitivity to variations in anatomical detail and, secondarily, in model resolution. This is important because finite element models of crania are increasingly used to assess and compare function.

For this, a wet cadaveric human cranium was loaded experimentally, simulating a bite at the left upper incisor, and the resulting strains and reaction force at the incisor were measured. These were then compared with the strains predicted by FE models built using two different simplification approaches: presence or absence of cancellous bone and inner sinus and nasal walls, and high or low resolution. It was hypothesised that there are no differences in distribution, magnitude or direction between the principal strains predicted by FE models built using different segmentation approaches, and between these and the principal strains measured in vitro.

Bite forces were measured during the loading experiments and the predicted bite force was obtained from each model after loading. The vector of the load applied to the neurocranium was adjusted until the bite force predicted in model 5 matched the force measured in vitro. A change in 0.1° in load orientation (or skull orientation) produced a difference of about 1 N in predicted bite force. The predicted bite forces from the lower resolution models were up to 3% higher when the same loads and constraints were applied to them, presumably reflecting subtle differences in how the applied load is transferred to the constraints when model resolution is reduced.

Model sensitivity to varying construction approaches was assessed in terms of strain magnitudes, contour plots and principal strain vector orientations. To date, this study presents the largest full field surface strain measurement and comparison carried out on a cranium. In addition, a Procrustes size and shape analysis compared global deformations among models.

The results of experiments conducted to test the hypotheses and considerations with regard to the use of simplifications when building FE models of the human cranium are discussed below.

Measured vs. predicted strains

This study used a voxel‐based approach for FE mesh generation that is fast and automated, facilitating the process of model construction (Keyak et al. 1990; Lengsfeld et al. 1998). The results show that, irrespective of model geometry and resolution, the FE models predict strain distributions (i.e. distribution of regions of relatively high or low strain) that are similar to those measured in the cranium under experimental loading. The main differences are in strain magnitudes, with the results from models with cortical and cancellous bone represented separately being closest to the values measured in vitro. Among these models, those with careful reconstruction of sinus and nasal walls showed the best overall fit to in vitro data. This is expected; anatomically more accurate FE models behave more similarly to the real cranium under experimental loadings than do simplified models (Marinescu et al. 2005; Strait et al. 2005; Kupczik et al. 2007). In the frontal process of the maxilla, ε₁ strains of models 2 and 4 better match the in vitro strain magnitudes than the remaining models, but only for a part of the traced line lengths. ε₃ strains in models 2 and 4 differ from the in vitro range (Fig. 5). The strain magnitudes along the traced lines (on Fig. 3a) show the lowest correlation with model 5 for models 2 and 4 (Table 2). These results reflect an issue in model building where the sinus and nasal walls are thinner than the width of a voxel. By excluding the walls, the model is more flexible; this results in a closer match in parts for ε₁ but a worse match for ε₃ than if the walls are reconstructed. This problem of how to represent very thin structures in low resolution models has no clear solution. However, the models with reconstructed sinus and nasal walls generally perform more reliably than those without, and hence reconstructing them, even though they appear thicker than they are in reality, would be a reasonable way to address this problem.

In model 1, where cancellous bone is represented as a solid material with properties of cortical bone, strains were on average about 3.5 times lower than in the more detailed models. Thus, not including cancellous bone as a low modulus distinct material produces a significant increase in model stiffness. However, surface strain distributions (rather than magnitudes) in the contour maps remain approximately consistent among all models (1, 3 and 5) with reconstructed sinus and nasal walls. This is more evident when the contour plots of these three models are scaled individually to use a similar range of the colour map (Fig. 2c). These results parallel those of Fitton et al. (2015) and support the use of the simplification approaches used here if relative rather than absolute magnitudes of strains are of interest, as they have limited local impacts on strain contours. The reduction in strains due to stiffening of the cancellous bone material between models reflects the findings of Renders et al. (2011), who noted a reduction in stresses with increasing trabecular mineral density heterogeneity in study of bone from the mandibular condyle. These findings are of importance in FEA studies where accurate representation of cancellous bone or sinus and nasal walls is not possible, such as in fossils or damaged archaeological material or where the construction of high resolution models is impractical. However, attention should be paid when comparison is made among individuals of significantly different sizes, where there is a possibility that the distribution of cancellous bone differs allometrically (i.e. larger individuals having disproportionately more extensive areas of cancellous bone and vice versa), potentially impacting on modes of deformation (Chamoli & Wroe, 2011).

Model resolution, over the limited range assessed here, has no appreciable effect on model performance and suggests that the model is close to convergence in the areas investigated. However, as there was no CT scan with a higher resolution available, increasing model resolution in this study was effected by increasing element number, and this may not accurately replicate the true differences in resolution of scan data.

The effect of another parameter of importance in FEA, material properties, was not considered in this study, although it is known that cranial skeletal material properties are heterogeneous (McElhaney et al. 1970; Dechow et al. 1993; Peterson & Dechow, 2003; Schwartz‐Dabney & Dechow, 2003). The use of linearly elastic, isotropic material properties of bone homogeneously throughout the skull is common in FEA (Kupczik et al. 2009; Wroe et al. 2010; Bright & Gröning, 2011; Gröning et al. 2012). Using heterogeneous material properties improved model accuracy in a study by Strait et al. (2005) but this required a large amount of preliminary work in mapping and representing heterogeneity and considerably increased model complexity to achieve solution. Moreover, determination of material properties is impossible in fossil material and impractical in studies based on medical CTs from living individuals, which are usually of too low a resolution to allow accurate material property determination based on Hounsfield units. However, several validation and sensitivity analyses support the use of simplified, homogeneous, material properties throughout the skull, as such models achieved results reasonably close to experimental data (Strait et al. 2005; Kupczik et al. 2007; Gröning et al. 2009; Szwedowski et al. 2011). The empirical findings of the present study indicate that using linearly elastic, isotropic and homogeneous material properties for the cranium and teeth, results in good concordance between predicted and measured strain contours when the sinus and nasal walls are represented in the model. However, this depends on accuracy in representing model geometry, in replicating the experimental loading conditions, and on the choices made with regard to material properties. In the present study we directly measured E in two locations, the maxillary tuberosity (E = 16.3 ± 3.7 GPa) and the zygomatic arch (E = 21.9 ± 2.7 GPa). It turned out that using an intermediate value, achieved strain magnitudes that reasonably matched measured ones, but other values for E could also have been chosen and the choice of homogeneous, isotropic material properties is arguably a source of error that would tend to make the model more or less flexible (affecting magnitude rather than mode of deformation). In this regard it is worth noting that in a study in which material properties of a macaque skull were varied, Berthaume et al. (2012), found that ‘large variations in modest‐to‐high strains and lower variations in modest‐to‐high stresses occur due to variation in material property values’. Thus, beyond the impact of simplifications of the FE model described here, errors in allocation of material properties also produce errors and so uncertainties with regard to estimated strains. The sum of such errors could potentially have a significant impact on, and limit, comparative studies of cranial biting performance. Further, Daegling et al. (2015) found that there is significant individual variation of material properties in the mandible, such that to incorporate them in a specific model, requires specimen‐specific measurement. However, we achieved a good match between strains in our most detailed homogeneous, isotropic model and those measured experimentally. Given that errors in material property allocation can have a marked effect, and that specimen‐specific data are not readily acquired (although they can be approximated directly from CT density) it seems reasonable to prefer simplified homogeneous, isotropic properties when accurate and detailed specimen specific data are not available.

Considering all of these results, model construction using simplification approaches that preserve sinus and nasal wall anatomy such as those described here (models 1, 3 and 5) does not appear to impact greatly on mode of deformation. However, variations in predicted strains among these models indicate that accurate estimates of strain magnitude are more difficult to achieve. It is only because we have experimental validation data that we have confidence in these predicted strain magnitudes. With fossils or in circumstances where experimental validation is impossible, predicted strain magnitudes will suffer from error of unknown degree. Does this mean that prediction of cranial deformation is not possible without prior validation? A consideration of global deformations is informative in this regard.

Global model deformation

In terms of global deformation, it is apparent that model sensitivity to how the internal sinus and nasal walls are reconstructed differs from and has greater overall impact than sensitivity to the presence of cancellous bone or variations in model resolution. Thus in the PC plot of Fig. 8 the three models (models 1, 3 and 5) with reconstructed sinus and nasal walls deform very similarly (direction of vector connecting unloaded and loaded models), differing mainly in the magnitude of deformation (length of vector connecting unloaded and loaded models). These deform differently (direction and magnitude) to models in which the sinus and nasal walls are omitted (models 2 and 4). These models manifest a higher degree and somewhat different modes of dorso‐ventral maxillary bending. This contrasts with the effects of not representing cancellous bone as a separate material (model 1 vs. models 3 and 5), where the major impact is on the magnitude (vector length) rather than mode (vector direction) of deformation. Model resolution when varied over the range assessed in this study has little effect between models 3 and 5, whereas between models 2 and 4, without inner sinus and nasal walls, the difference between models is comparatively larger.

It should be borne in mind that the PCA of size and shape offers quite a different insight into model performance than do analyses of stresses and strains. Thus, Procrustes size and shape analyses of global deformations describe general features of deformation such as dorso‐ventral bending or twisting (O'Higgins et al. 2012), whereas stresses and strains are relevant to prediction of failure/fracture and possibly, remodelling activity.

Wider considerations

It should be noted that the physical cranium was loaded non‐physiologically because of practical constraints, but the FE models were loaded identically to allow comparison. Of course, our findings may differ from those that would have arisen from physiological loading. For instance, the zygomatic region is relatively unstrained in our study, whereas it shows high strains in experimental and modelling studies (Strait et al. 2009; Bright & Gröning, 2011; Berthaume et al. 2012; Fitton et al. 2015) and lower strains when the masseter muscle is deactivated (Fitton et al. 2012). This said, the extent to which these findings of high zygomatic region strains reflect reality has been questioned by Curtis et al. (2011), who found that inclusion of temporal fascia in an FE model of a macaque greatly reduced strains in this region. Beyond this limitation, only one loading scenario, at a single bite point, has been assessed. Both the non‐physiological and limited loading scenarios used in this study may well mean that its findings do not reflect the full complexity and detail of differences among modelling approaches and between these and the physical cranium. This should be borne in mind when generalising from the present findings.

Using diverse approaches to comparing FE model performance (strain contour maps, strain vector magnitudes and directions, and global model deformation), we have demonstrated that simplifications in model geometry and material properties impact on the validity of FEA results. Some types of simplification, such as model 1 (one material), result in smaller degrees of deformation, a ‘stiffening of the cranium’ (Figs 2 and 8), whereas others (e.g. inaccurate lateral nasal wall reconstruction in models 3 and 4) impact on both mode and magnitude of deformation (Figs 2 and 8). Previous work has shown that other decisions in model construction, such as varying relative force magnitudes among jaw‐closing muscles, impact on both mode of deformation and strain contours, whereas total applied muscle force impacts more on magnitude of deformation and strains (Fitton et al. 2012).

This is important because it means that unless each model whose performance is to be compared has been separately refined using specimen‐specific validation data, there will always be a degree of uncertainty concerning differences in mode and degree of deformation which will impact strain contour maps, strain magnitudes and assessments of global deformation. Such validation is difficult in extant and impossible in living humans and fossil material.

However, through this and the many validation and sensitivity analyses cited above, we know that some types of error (material properties, muscle force vector magnitudes, simplifications in model geometry of certain types) will affect magnitude rather more than mode of deformation. Further, other types of error (e.g. in relative muscle activation, muscle force vector directions, simplifications in model geometry of certain types) will impact more on mode than magnitude of deformation. Thus carefully designed experiments that keep constant muscle vectors and relative activations and apply certain simplifications of model geometry (that do not affect, for example, nasal wall anatomy) and use the same degree of homogeneity and isotropy of material properties may produce reasonable results with regard to mode but not magnitude of deformation. In such cases, comparisons should cautiously be based on relative strains within models or the direction components of vectors of global deformation to minimise the risk of reaching erroneous conclusions. The validity of such analyses will, however, depend on the validity of the assumption of constant muscle load vectors and on how geometry has been simplified in each, as well as on the magnitude the biological signal (the true differences in performance) relative to the magnitude of error. Much is yet to be learned through careful sensitivity and validation studies before the impact of modelling and loading errors is fully understood and the field can be confident that differences in model performance reflect biological reality.

It may be more secure to adopt an explicitly experimental approach to the application of FEA to comparative cranial functional analyses, asking specific questions about the impact of particular aspects of morphology on cranial performance. This approach maintains all aspects of the model and loading constant except for the feature of interest (e.g. sutures, periodontal ligament; Moazen et al. 2009; Wood et al. 2011; Wang et al. 2012) which is modified and the impact on performance assessed.

The present study was limited by several factors. Significant but, we believe adequately corrected for (see Methods), is the issue of comparing surface strains projected onto a plane (DSPI output) with predicted strains over a 3D surface. Beyond this, the use of a single cadaveric specimen does not allow us to assess variation in the validity of outputs over a range of different morphologies. This is a limitation that is imposed by the complexity of obtaining human material for such work and the effort and resources required to carry out the detailed experimental and subsequent modelling work. Uniquely, in the present study we are able to present comprehensive sensitivity and validation using a single specimen and the largest and most directly measured map of surface strains to date. The findings indicate that a fairly simple model (model 5) is able to replicate the mode and magnitude of deformation of the physical cranium. However, the several sources of error in model building have different degrees of impact on mode and magnitude of deformation and hence on the strain contours and magnitudes. This calls for great care in the application of FEA in the wider, comparative context. Finally, all of the considerations we raise in this paper with regard to error in comparison of cranial performance are likely to also apply to a greater or lesser degree to other skeletal elements.

Conclusion

By comparing the strains predicted by a series of FE models of the human cranium with those measured in vitro in the actual specimen, the impacts of different modelling simplifications on predicted deformations were assessed. The hypothesis that there are no differences in strains predicted by the FE models and those measured in the cranium was falsified. Thus, the performance of all models differed to some degree from that of the experimentally loaded cranium. However, even though the model built with only cortical bone and teeth as distinct materials showed strain magnitudes that were about 3.5 times lower than the experimentally loaded cranium, the mode of deformation was very similar. Omitting internal sinus and nasal walls led to alterations in both modes and magnitudes of deformation.

The second hypothesis, that there are no differences in magnitudes and modes of deformation among finite element models of the same skull built using different approaches, was also falsified. Modes of deformation (as assessed by strain vectors, contour plots, and a size and shape analysis) are less sensitive to how cancellous bone is represented and to variations in model resolution, over the limited range examined here, than to variations in sinus and nasal wall representation. Thus, simplifications of cancellous bone anatomy have an impact on magnitude rather than mode of deformation, whereas under‐representation of very thin bony structures such as are found in the sinus and nasal walls impacts on both mode and magnitude of deformation. These differences suggest that comparative FEA studies of biting performance among crania will likely suffer from error due to uncertainty in the modelling process. The extent to which this error limits our ability to make ecological inferences from crania is likely significant but requires thorough investigation.

Authors' contributions

VT‐I, LCF and PO'H: study conception and design. VT‐I: FE model construction. VT‐I and PO'H: DSPI and FE data analysis. VT‐I, LCF, MJF and PO'H: DSPI experiments, interpretation of results and manuscript writing.

Supporting information

Table S1. Landmarks for Procrustes size and shape analysis.