Abstract
Noncompliance with study medications is an important issue in the design of endpoint clinical trials. Including noncompliant patient data in an intention-to-treat analysis could seriously decrease study power. Standard methods for calculating sample size account for noncompliance, but all assume that noncompliance is noninformative, i.e., that the risk of discontinuation is independent of the risk of experiencing a study endpoint. Using data from several published clinical trials (OPTIMAAL, LIFE, RENAAL, SOLVD-Prevention and SOLVD-Treatment), we demonstrate that this assumption is often untrue, and we discuss the effect of informative noncompliance on power and sample size.
Introduction
Endpoint trials follow patients over a pre-defined period of time, and the treatments are compared with respect to the incidence of some clinical endpoint. These trials typically require a great deal of resources. For example, the ISIS-IV trial [1] enrolled 58,050 patients with acute myocardial infarction, and the recently-completed ALLHAT trial [2] enrolled 33,357 patients with hypertension. For this reason, appropriate calculations of sample size and power are particularly important. If the sample size is too large, a great deal of resources may be wasted, but if it is too small then the entire effort may be in vain.
One issue in these trials is noncompliance with study drugs, or failure to follow the assigned treatment regimens (e.g., skipping doses and "drug holidays"). In this paper, we use the term noncompliance to refer solely to permanent discontinuation of study drug for any reason. We use the terms noncompliance and discontinuation interchangeably. We also assume that noncompliant patients, like compliant patients, continue in study follow-up for ascertainment of study endpoints. Noncompliance rates can be high in a lengthy trial. In the MRC trials [3,4] the rates exceeded 40%. While noncompliance cannot be avoided altogether, it can be minimized through diligent monitoring, and attention. In some respects, therefore, the compliance rate serves as an indicator for trial quality.
There can be many reasons for noncompliance, such as side effects in an actively treated group, lack of efficacy in a placebo group, or development of a new condition that makes continuation of the study treatment difficult. Regardless of the reasons, one concern is that study outcomes in noncompliant patients may not adequately reflect the effects of their randomized study therapies. For example, noncompliant patients in a placebo group might begin taking an effective therapy and experience clinical benefit, and a noncompliant patient in an experimental group might lose that treatment's benefit once the treatment is discontinued. In other circumstances, noncompliance might have little or no impact. For example, a treatment might have such a long-lasting effect that discontinuing it would have no discernable impact during the remainder of follow-up. It is also possible that noncompliance may increase study power, for example, if a treatment is actually inferior to the control. For most clinical trials, however, it seems considerably more likely that inclusion of noncompliant patients in the analysis will result in a decrease in the apparent effect of the treatment, and therefore will reduce statistical power.
Due to the potential reduction in power, a careful assessment of the expected rates of noncompliance is an important component of sample size calculation. We recently reviewed sample size methods for survival trials [5], including the following standard methods in common use: Halperin et al [6]; Wu, Fisher, and DeMets [7]; Freedman [8]; Lachin and Foulkes [9], and two methods by Lakatos [10,11]. The impact of noncompliance on sample size depends strongly on the assumptions made regarding event rates subsequent to discontinuation. The most common assumption is that patients switch to the opposite treatment, and that event rates in the two groups reverse. It is usually further assumed that the reversal is immediate, although some methods allow for the possibility of a delay or lag in the change in endpoint risk.
One assumption made by all the methods referenced above is that discontinuation is noninformative, i.e., that the risk of discontinuation is independent of the risk of an endpoint. If at some point in a trial, 10% of the patients in a treatment group have discontinued from study drug, this assumption suggests that these patients will contribute roughly 10% of future endpoints. In our experience, however, this assumption is seldom true – discontinued patients typically contribute a disproportionate share of future endpoints. Thus, we define "informative noncompliance" as the situation in which knowledge of whether or not a patient has discontinued from study medication provides information on how likely the patient is to experience a study endpoint in the future. In other words, the risk of noncompliance is dependent on the risk of an endpoint.
There are statistical methods for the analysis of clinical trials in the presence of informative noncompliance, including structural nested accelerated failure time models [12], the marginal structural proportional hazards approach [13], and the complier proportional hazards effect of treatment method [14]. Despite these methods, the standard approach in pharmaceutical trials is to include in an ITT analysis all patients, without regard to compliance[15]. The main disadvantage of this approach is that the true treatment effect may be underestimated and, thus, the power may be reduced.
The purpose of this paper is to illustrate the concept of informative noncompliance through analyses of several recent clinical trials and through hypothetical examples, and to discuss the potential impact of this phenomenon on sample size and power.
Measuring the degree of informative noncompliance
To illustrate the concept of informative noncompliance and to highlight the difficulty in measuring it, we start with a simple, hypothetical mortality trial. Since our purpose is to investigate informative noncompliance, not the effect of the treatment, we assume that the treatments are identical and we present only pooled-group results. Suppose a clinical trial has simultaneously enrolled 11,250 patients to be followed for three years. Further, suppose that among compliant patients, the risk of death is high immediately after randomization (10% over the first year), but low thereafter (1.25% during the 2nd year and 1% during the 3rd year). With respect to discontinuation, we assume that approximately 1 of every 9 patients is noncompliant at the start of the trial, and at the end of each of years 1 and 2, approximately 1 in 9 of the surviving compliant patients becomes noncompliant. We model informative noncompliance through the assumption that noncompliant patients have exactly twice the death rate of compliant patients: 20% during the first year, 2.5% during the 2nd year and 2% during the 3rd year.
Table 1 presents the results of this hypothetical trial. During the first year, 1,000 compliant patients and 250 noncompliant patients died. Between the end of the first year and the start of the 2nd year, 1,000 of the 9,000 surviving compliant patients became noncompliant, resulting in 8000 compliant patients and 1250-250+1000 = 2,000 noncompliant patients entering the 2nd year. During the 2nd year, 100 compliant patients and 50 noncompliant patients died. Between the end of the 2nd year and the start of the 3rd year, 878 of the surviving compliant patients became noncompliant, resulting in 7,022 compliant patients and 2,000-50+878 = 2,828 noncompliant patients entering the 3rd year.
Table 1.
Hypothetical Illustration of Informative Noncompliance
| Start of Study Year | Compliant Patients | Noncompliant Patients | |||||
| Number of Patients | Endpoint Rate | Number of Endpoints | New Noncompliant Patients | Number of Patients | Endpoint Rate | Number of Endpoints | |
| 1 | 10,000 | 0.1000 | 1,000 | 1,250 | 0.2000 | 250 | |
| 1000 | |||||||
| 2 | 8,000 | 0.0125 | 100 | 2,000 | 0.0250 | 50 | |
| 878 | |||||||
| 3 | 7,022 | 0.0100 | 70 | 2,828 | 0.0200 | 57 | |
| Total | 1,170 | 357 | |||||
One simple approach to evaluate the degree of informative noncompliance would be to calculate crude rates, based on compliance at the time of death or at the end of the trial. Using this approach, 1,170 patients were compliant at the time of death and 6,952 surviving patients were compliant at the end of the trial (the 7,022 who were compliant at the start of the 3rd year, minus the 70 who died), resulting in a crude rate of 14.4%. Similarly, 357 patients were noncompliant at the time of death and 2,771 surviving patients were noncompliant at the end of the trial (the 2,828 who were noncompliant at the start of the 3rd year, minus the 57 who died), resulting in a crude rate of 11.4%. Therefore, despite the fact that discontinuation was actually associated with twice the endpoint rate at any time during the trial, the crude rates would suggest that noncompliance was associated with relatively low risk. Clearly, the crude rates provide an inappropriate measure of the degree of informative noncompliance.
A second potential approach is to pick a point early in the trial, determine who is compliant and noncompliant at that time, and compare patients' crude endpoint rates. While this approach is reasonable, it has important drawbacks. 1) It is not clear what point in the trial to choose. Very early in the trial, the number of noncompliant patients might be too small to use as a reliable estimate, and later in the trial the number of future endpoints might be small. 2) It ignores important information prior to the chosen point in the trial. 3) Patients who are compliant at the chosen point in the trial may become noncompliant prior to having an endpoint.
Using this approach, one could calculate the mortality rates in the hypothetical example among patients who were compliant and noncompliant at the start of, say, the 2nd year. Among the 8,000 compliant patients, the number of deaths would be 100 during the 2nd year and approximately 88 during the 3rd year (including the 70 deaths among the patients who remained compliant, plus an expected 18 deaths among the 878 patients who became noncompliant at the start of the 3rd year), resulting in a crude rate of 2.35%. Among the 2,000 noncompliant patients, the total number of deaths would be approximately 89 (50 during the 2nd year plus approximately 39 during the 3rd year), leading to a crude rate 4.45%. While this method has correctly demonstrated that noncompliant patients have a higher mortality risk than compliant patients, it has underestimated the magnitude of the difference.
In this paper, we define a time-varying covariate, indicating whether or not the patient had discontinued by time t. For example, if a patient discontinues study medication on day 100, the covariate takes the value 0 for t < 100, and the value 1 for t ≥ 100. We calculate the hazard ratio associated with this covariate in a Cox regression model with time-to-event as the dependent variable. The assumption of noninformative noncompliance corresponds to the hazard ratio associated with this covariate being equal to 1. Note that in the hypothetical example above, if we assume that all deaths occur at the mid-point of the year, the Cox regression model appropriately calculates a hazard ratio of 2.00 associated with noncompliance.
When evaluating the association between discontinuation and endpoint risk, we need to be aware of a potential bias, which is described through the following example. Suppose the endpoint of interest is death. A patient is taking study drug when he suffers a stroke, is admitted to hospital, and is kept alive on life-support for four days before dying. Since the patient was not taking study drug during that 4-day period, it might appear that the patient was noncompliant at the time of death. This would be an incorrect interpretation, since the patient was compliant when suffering the event that led to death. Therefore, when evaluating the impact of compliance on endpoint risk, we use a 7-day rule, namely that the patient is considered to be compliant while taking study drug and for 7 days after permanent discontinuation of study drug. Since the choice of 7 days is somewhat arbitrary, it might be appropriate to investigate the sensitivity of the results to this choice.
The Cox model calculates a hazard ratio associated with noncompliance under the assumption that this hazard ratio is constant over time. In order to explore visually whether or not this assumption is true, we create extended Kaplan-Meier curves that compare endpoint rates for cohorts defined by time-varying covariates [16]. These curves are somewhat difficult to interpret but are consistent with the Cox regression method.
Examples of informative noncompliance in clinical trials
In this section we describe five examples of informative noncompliance, using databases from published endpoint trials. Although all the studies involve one of two drugs (enalapril and losartan) in closely related pharmacological classes, and all involve patients with or at high risk for cardiovascular disease, they cover a wide range of situations. The specific patient populations differ in all five trials, and the trials include various control groups and endpoints. In three of the trials, the hazard rate is roughly constant over time, in one trial it is clearly increasing and in another it is clearly decreasing.
In all examples, we present data for the pooled treatment groups. We have examined the results within treatment groups and have found them to be generally consistent with the overall results from that study. In addition, we have examined the sensitivity of the results to the choice of the 7-day window for determining the start of noncompliance, and have found little impact.
Below is a brief description of the studies. Their results with respect to informative noncompliance are summarized in Table 2 and are illustrated in Figures 1,2,3,4,5.
Table 2.
Results from Five Published Clinical Trials
| Trial Acronym | Experimental Treatment | Control Treatment | Patient Population | Endpoint | Sample Size | Endpoint Number and Rate |
Discontinuation Number and Rate |
Hazard Ratio Associated with Non-compliance | p-value |
| SOLVD-T | Enalapril | Placebo | Left Ventricular Dysfunction with Overt Heart Failure | Total Mortality | 2,569 | 961 (37.4%) | 839 (32.7%) | 2.7 | < 0.0001 |
| SOLVD-P | Enalapril | Placebo | Left Ventricular Dysfunction without Overt Heart Failure | Total Mortality | 4,228 | 638 (15.1%) | 987 (23.3%) | 3.2 | < 0.0001 |
| RENAAL | Losartan | Placebo | Type 2 Diabetes with Nephropathy | Doubling of Serum Creatinine, End-Stage Renal Disease or Death | 1,513 | 686 (45.3%) | 469 (31.0%) | 2.6 | < 0.0001 |
| LIFE | Losartan | Atenolol | Hypertension and Left Ventricular Hypertrophy | Myocardial Infarction, Stroke or Cardiovascular Death | 9,193 | 1096 (11.9%) | 2,273 (24.7%) | 2.6 | < 0.0001 |
| OPTIMAAL | Losartan | Captopril | High-Risk Acute Myocardial Infarction | Total Mortality | 5,477 | 946 (17.3%) | 1,156 (21.1%) | 5.0 | < 0.0001 |
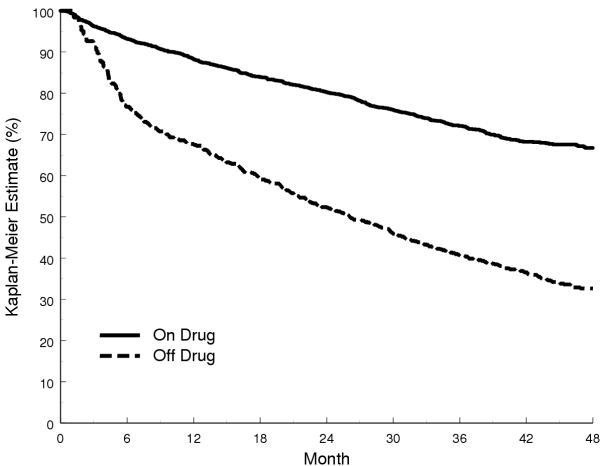
Figure 1.
Kaplan-Meier Estimates Stratified by Time-Varying Noncompliance in the SOLVD Treatment Trial
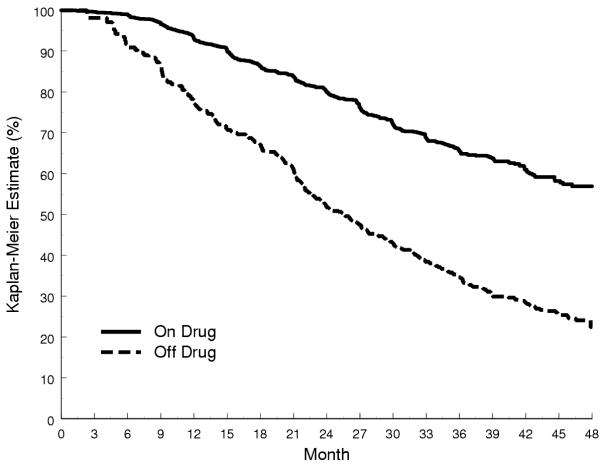
Figure 2.
Kaplan-Meier Estimates Stratified by Time-Varying Noncompliance in the SOLVD Prevention Trial
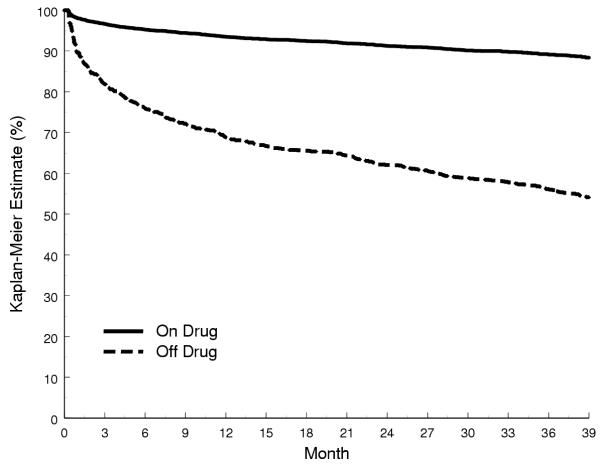
Figure 3.
Kaplan-Meier Estimates Stratified by Time-Varying Noncompliance in RENAAL
Figure 4.
Kaplan-Meier Estimates Stratified by Time-Varying Noncompliance in LIFE
Figure 5.
Kaplan-Meier Estimates Stratified by Time-Varying Noncompliance in OPTIMAAL
• The SOLVD Treatment Trial [17] randomized 2,569 patients with left ventricular dysfunction and overt heart failure to treatment with enalapril, an angiotensin converting-enzyme inhibitor, or to placebo (Figure 1).
• The SOLVD Prevention Trial [18] randomized 4,228 patients with left ventricular dysfunction but without symptoms of overt heart failure to treatment with enalapril or to placebo (Figure 2).
• The RENAAL Trial [19] randomized 1,513 patients with type 2 diabetes mellitus and nephropathy to treatment with losartan, an angiotensin II antagonist, or to placebo (Figure 3).
• The LIFE Trial [20] randomized 9,193 patients with hypertension and left ventricular hypertrophy to treatment with losartan or to atenolol, a beta-blocker (Figure 4).
• The OPTIMAAL Trial [21] randomized 5,477 patients with a high-risk of acute myocardial infarction to treatment with losartan or to captopril, an angiotensin converting-enzyme inhibitor (Figure 5).
In all of the trials presented here (Table 2), patients who discontinued from study drug were at higher risk of experiencing a study endpoint than patients remaining on study drug. The hazard ratio ranged from 2.6 to 5.0. While these examples do not prove that the phenomenon of informative noncompliance exists universally, it is important to note that these trials were not specifically chosen to illustrate the point, but rather are representative of real clinical trials in our experience.
Impact of informative noncompliance on sample size
Clearly, when patients are noncompliant with study medications, the ability to detect differences between treatment groups will be diminished. This is the reason that existing sample size methods account for the expected rate of noncompliance. However, it is not the rate of noncompliance per se that is important, but rather the proportion of endpoints that occur in noncompliant patients. Existing sample size methods, which assume noninformative noncompliance, can greatly underestimate this proportion, and therefore may greatly underestimate the required sample size.
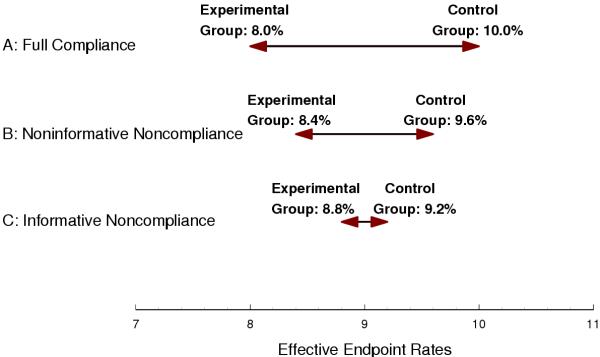
As an example, consider this relatively simple situation, which is illustrated in Figure 6. Patients are randomized simultaneously, and over the course of the study, the endpoint rates for the compliant patients are 10% and 8% in the control and experimental treatment groups, respectively. The discontinuation rates are 20% in each treatment group. For simplicity, assume that all noncompliance occurs immediately at the start of the trial and that endpoint rates in noncompliant patients correspond to those of compliant patients in the opposite treatment group. The impact of noncompliance is to reduce the difference between groups with respect to the effective endpoint rates (i.e., the rates that are estimated using an ITT analysis) relative to the difference with respect to the ideal endpoint rates (i.e., when patients are fully compliant).
Figure 6.
Difference between Effective Endpoint Rates in the Treatment (Left) and Control (Right) Groups. A: Full Compliance. B: Noninformative Noncompliance. C: Informative Noncompliance.
Take first the case of noninformative noncompliance. In the control group, the 80% of patients who are compliant have an endpoint rate of 10% and the 20% of patients who are noncompliant have an endpoint rate of 8%, for an overall effective endpoint rate of 9.6%. Similarly, in the experimental group the effective endpoint rate is 8.4%. Since the difference between 9.6% and 8.4% is smaller than the difference between 10% and 8%, sample size must be increased to account for noncompliance.
Now take the case of informative noncompliance. Noncompliance identifies a sicker subset of patients. For example, if they remained on the control therapy, noncompliant patients in the control group might be expected to have an endpoint rate of, say, 20%, and compliant patients might be expected to have an endpoint rate of, say, 7.5%. Note that this would result in an overall endpoint rate of 10%, as in the case of noninformative noncompliance. However, since the noncompliant patients become treated, their endpoint rate becomes 16%, and the effective endpoint rate in the control group is 9.2% (7.5% among the 80% of patients who are compliant and 16% among the 20% of patients who are noncompliant). By a similar argument, noncompliant patients in the treatment group have an endpoint rate of 20% (16% had they remained treated) and compliant patients have an endpoint rate of 6%, for an effective endpoint rate of 8.8% (6% among the 80% of patients who are compliant and 20% among the 20% of patients who are noncompliant). Therefore, informative noncompliance has further decreased the difference between the effective endpoint rates, which exacerbates the effect of noncompliance on power and sample size.
Now consider the impact of noncompliance on sample size. As above, assume that the endpoint rates in the two treatment groups are 8% and 10%, and ignore other factors that could influence sample size, such as staggered entry and treatment lag. Using the Lakatos method [11], the total sample size required for 90% power at a two-sided 5% significance level is 8,600 patients if we disregard noncompliance, and 11,890 patients if we account for noncompliance rates of 15% in each treatment group. If we further assume that noncompliance is informative and that the hazard ratio associated with noncompliance is 2, then using a modified version of the Lakatos method [22], the required sample size is 16,330 patients, and the power associated with a sample size of 11,890 patients is 79.0%. Based on this example, informative noncompliance is clearly an important factor in the calculation of sample size.
Conclusions
Noncompliance is present to some extent in virtually all clinical trials, but is typically a more serious concern in long-term endpoint trials of chronic therapies. While it is common to account for noncompliance in the calculation of sample size for these trials, existing methods assume that noncompliance is noninformative. In this paper we have shown that the assumption of noninformative noncompliance is often invalid, and that this can lead to incorrect sample size.
The presence of informative noncompliance can have two fundamentally different interpretations. First, it is possible that discontinuation from study drug is harmful to the patient, thereby causing the endpoint rate to increase. We believe that this interpretation is unlikely to be true in most cases. Of note, in the SOLVD and RENAAL trials, the risk of an endpoint was elevated to roughly the same degree in patients who discontinued from placebo as in patients who discontinued from active drug. It is more likely that noncompliance tends to occur in sicker patients who are at higher endpoint risk, regardless of discontinuation. For example, patients might experience severe symptoms of their condition, causing them to discontinue from study therapy and seek more effective therapies. This is supported by the observation that patients who discontinue often have high-risk characteristics at baseline. Regardless of the cause, however, the result of informative noncompliance is that an increased fraction of the study endpoints occur in patients who are no longer taking study drug. This, in turn, affects power.
Noncompliance can take many forms. Patients may take incorrect doses, miss doses, temporarily interrupt therapy, or permanently discontinue it. Temporary interruptions and permanent discontinuations can be initiated by the patient or the physician. Incorrect and missed doses are notoriously difficult to assess. Attempts to measure them by such methods as pill counts are easily thwarted by patients who want to appear to be compliant. Regardless of its form, noncompliance can have an important impact on power. In this paper, we have focused on permanent discontinuation, the form that is easiest to measure.
While informative noncompliance typically has not been considered with respect to sample size calculation, it has always been a consideration at the time of analysis. Although various analysis models exist, ITT has become the standard analysis approach for endpoint trials. If noncompliance could be assumed to be noninformative, we could obtain an unbiased estimate of the parameter of interest, the effect of the study treatment when patients are compliant, by censoring patients at the time of discontinuation (i.e., an "on treatment" analysis). In the presence of informative noncompliance, however, the "on treatment" analysis can be biased in either direction, depending on the levels of noncompliance and the relative degrees of informativeness in the two treatment groups. Although the ITT analysis will also give a biased estimate of the treatment effect, this approach is preferred, since noncompliance tends to diminish the difference between treatment groups, resulting in a conservative bias.
While noncompliance is an issue that can impact power in all types of clinical trials, informative noncompliance is of particular concern in endpoint trials, since information on the treatment effect comes primarily from the subset of patients experiencing endpoints. Thus, a particularly high noncompliance rate among patients who are most likely to experience an endpoint will have a considerably large impact on sample size and power. Conversely, in trials where the efficacy measure is a normally distributed variable, on the other hand, all patients contribute information and it makes little difference whether noncompliance occurs in patients with typical values or extreme values of the response variable.
As stated, the assumption of noninformative noncompliance implies that if they were to be treated identically, compliant and noncompliant patients would be at identical risk of experiencing a study endpoint. Compliant and noncompliant patients however are not treated identically. By definition, compliant patients remain on study therapy, while noncompliant patients do not. Therefore, the hazard ratio associated with noncompliance actually measures a combination of two factors: the inherent difference in risk between compliant and noncompliant patients (the factor of interest) and the impact of differential treatment between these patients. We do not believe that the latter factor had much practical impact in the examples presented here, the reasons being that 1) the magnitudes of the hazard ratios (2.6 to 5.0) far exceed the typical risk reductions due to therapies in these patients (on the order of 15–20%) and 2) when we examined the hazard ratios within each treatment group separately, the results were typically similar to those of the pooled groups.
In conclusion, informative noncompliance is a common phenomenon in endpoint trials that can have a dramatic impact on sample size and power. Appropriately accounting for informative noncompliance should become an important component of sample size planning.
Abbreviations
ALLHAT – Antihypertensive and Lipid-Lowering treatment to prevent Heart Attack Trial
ISIS – International Study of Infarct Survival
ITT – intention-to-treat
LIFE – Losartan Intervention For Endpoint reduction in hypertension trial
MRC – Medical Research Council
OPTIMAAL – Optimal Trial In Myocardial infarction with the Angiotensin II Antagonist Losartan
RENAAL – Reduction of Endpoints in NIDDM with the Angiotensin II Antagonist Losartan study
SOLVD – Studies Of Left Ventricular Dysfunction
Authors' Contributions
SS contributed to the study concept, performed all analyses of the clinical trial databases and wrote the first draft of the manuscript. QJ and BI contributed to the study concept and carefully reviewed all draft manuscripts. All authors read and approved the final manuscript.
Competing interests
SS and QJ were employees of Merck and Co., Inc., when that company sponsored some of the trials discussed here (RENAAL, LIFE, OPTIMAAL). They are now employees of competing pharmaceutical companies.
Acknowledgments
Acknowledgements
The work of BI was partially supported by a Study Leave from Temple University and by its Biostatistical Research Center.
Contributor Information
Steven M Snapinn, Email: ssnapinn@amgen.com.
Qi Jiang, Email: qi.jiang@pharma.novartis.com.
Boris Iglewicz, Email: boris.iglewicz@temple.edu.
References
- ISIS-4 Collaborative Group A randomized factorial trial assessing early oral captopril, oral mononitrate, and intravenous magnesium sulfate in 58,050 patients with suspected acute myocardial infarction. Lancet. 1995;345:669–685. doi: 10.1016/S0140-6736(95)90865-X. [DOI] [PubMed] [Google Scholar]
- The ALLHAT Officers and Coordinators for the ALLHAT Collaborative Research Group Major outcomes in high-risk hypertensive patients randomized to angiotensin-converting enzyme inhibitor or calcium channel blocker vs diuretic: The Antihypertensive and Lipid-Lowering treatment to prevent Heart Attack Trial (ALLHAT) JAMA. 2002;288:2981–2997. doi: 10.1001/jama.288.23.2981. [DOI] [PubMed] [Google Scholar]
- Medical Research Council Working Party MRC trial of treatment of mild hypertension: principal results. Br Med J. 1985;291:97–104. doi: 10.1136/bmj.291.6488.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MRC Working Party Medical research council trial of treatment of hypertension in older adults: principal results. Br Med J. 1992;304:405–412. doi: 10.1136/bmj.304.6824.405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Q, Snapinn S, Iglewicz B. In Encyclopedia of Biopharmaceutical Statistics. 2. New York: Marcel Dekker, Inc; 2003. Sample size adjustment in survival data; pp. 892–898. [Google Scholar]
- Halperin M, Rogot E, Gurian J, Ederer F. Sample sizes for medical trials with special reference to long-term therapy. J Chronic Dis. 1968;21:13–24. doi: 10.1016/0021-9681(68)90082-9. [DOI] [PubMed] [Google Scholar]
- Wu M, Fisher M, DeMets D. Sample sizes for long-term medical trial with time-dependent dropout and event rates. Control Clin Trials. 1980;1:111–123. doi: 10.1016/0197-2456(80)90014-8. [DOI] [PubMed] [Google Scholar]
- Freedman LS. Tables of the number of patients required in clinical trials using the logrank test. Stat Med. 1982;1:121–129. doi: 10.1002/sim.4780010204. [DOI] [PubMed] [Google Scholar]
- Lachin JM, Foulkes MA. Evaluation of sample size and power for analyses of survival with allowance for nonuniform patient entry, losses to follow-up, noncompliance, and stratification. Biometrics. 1986;42:507–519. [PubMed] [Google Scholar]
- Lakatos E. Sample size determination in clinical trials with time-dependent rates of losses and noncompliance. Control Clin Trials. 1986;7:189–199. doi: 10.1016/0197-2456(86)90047-4. [DOI] [PubMed] [Google Scholar]
- Lakatos E. Sample sizes based on the logrank statistic in complex clinical trials. Biometrics. 1988;44:229–241. [PubMed] [Google Scholar]
- Robins JM, Tsiatis AA. Correcting for noncompliance in randomized trials using rank preserving structural failure time models. Communications in Statistics A. 1991;20(8):2609–2631. [Google Scholar]
- Robins JM. Marginal structural models versus structural nested models as tools for causal inference. In: Halloran ME, Berry D, editor. In Statistical Models in Epidemiology: The Environment and Clinical Trials. New York: Springer-Verlag; 1999. [Google Scholar]
- Loeys T, Goetghebeur E. A causal proportional hazards estimator for the effect of treatment actually received in a randomized trial with all-or-nothing compliance. Biometrics. 2003;59:100–105. doi: 10.1111/1541-0420.00012. [DOI] [PubMed] [Google Scholar]
- Lachin JM. Statistical considerations in the intent-to-treat principle. Control Clin Trials. 2000;21:167–189. doi: 10.1016/S0197-2456(00)00046-5. [DOI] [PubMed] [Google Scholar]
- Snapinn SM, Jiang Q, Iglewicz B. Illustrating the impact of a time-varying covariate with an extended Kaplan-Meier estimator. unpublished manuscript.
- The SOLVD Investigators Effect of enalapril on survival in patients with reduced left ventricular ejection fractions and congestive heart failure. N Engl J Med. 1991;325:293–302. doi: 10.1056/NEJM199108013250501. [DOI] [PubMed] [Google Scholar]
- The SOLVD Investigators Effect of enalapril on mortality and the development of heart failure in asymptomatic patients with reduced left ventricular ejection fraction. N Engl J Med. 1992;327:685–691. doi: 10.1056/NEJM199209033271003. [DOI] [PubMed] [Google Scholar]
- Brenner BM, Cooper ME, de Zeeuw D, et al. Effects of losartan on renal and cardiovascular outcomes in patients type 2 diabetes and nephropathy. N Engl J Med. 2001;345:861–869. doi: 10.1056/NEJMoa011161. [DOI] [PubMed] [Google Scholar]
- Dahlöf B, Devereux RB, Kjeldsen SE, et al. Cardiovascular morbidity and mortality in the Losartan Intervention For Endpoint reduction in hypertension study (LIFE): a randomised trial against atenolol. Lancet. 2002;359:995–1003. doi: 10.1016/S0140-6736(02)08089-3. [DOI] [PubMed] [Google Scholar]
- Dickstein K, Kjekshus J, the OPTIMAAL Steering Committee, for the OPTIMAAL Study Group Effects of losartan and captopril on mortality and morbidity in high-risk patients after acute myocardial infarction: the OPTIMAAL randomised trial. Lancet. 2002;360:752–760. doi: 10.1016/S0140-6736(02)09895-1. [DOI] [PubMed] [Google Scholar]
- Jiang Q, Snapinn S, Iglewicz B. Calculation of sample size in survival trials: the impact of informative noncompliance. Biometrics. 2004;60:800–806. doi: 10.1111/j.0006-341X.2004.00231.x. [DOI] [PubMed] [Google Scholar]