The interaction of two oscillators (cell division cycle and yeast metabolic cycle) with different frequencies is studied. Cell cycle Start is coupled with the initiation of high oxygen consumption and breakdown of storage carbohydrates across diverse strains and different growth rates.
Abstract
Cells have evolved oscillators with different frequencies to coordinate periodic processes. Here we studied the interaction of two oscillators, the cell division cycle (CDC) and the yeast metabolic cycle (YMC), in budding yeast. Previous work suggested that the CDC and YMC interact to separate high oxygen consumption (HOC) from DNA replication to prevent genetic damage. To test this hypothesis, we grew diverse strains in chemostat and measured DNA replication and oxygen consumption with high temporal resolution at different growth rates. Our data showed that HOC is not strictly separated from DNA replication; rather, cell cycle Start is coupled with the initiation of HOC and catabolism of storage carbohydrates. The logic of this YMC–CDC coupling may be to ensure that DNA replication and cell division occur only when sufficient cellular energy reserves have accumulated. Our results also uncovered a quantitative relationship between CDC period and YMC period across different strains. More generally, our approach shows how studies in genetically diverse strains efficiently identify robust phenotypes and steer the experimentalist away from strain-specific idiosyncrasies.
INTRODUCTION
Biological oscillators such as the cell cycle, circadian clocks, and metabolic rhythms are ubiquitous across the domains of life. The cell division cycle (CDC) has a period that depends on nutrients and temperature, and the cell cycle regulatory network is strongly conserved across eukaryotes (Morgan, 2007). On the other hand, circadian clocks have a fixed ∼24-h period and are robust to changes to temperature, yet their regulatory networks have evolved independently in cyanobacteria, plants, and animals (Rosbash, 2009). These different biochemical oscillators coexist in the same cellular environment, sharing and competing for resources. It is well established that even weak coupling between oscillators can lead to their synchronization (Pikovsky et al., 2001). Thus, how do biochemical oscillators with different frequencies coexist in the same cell? Are there mechanisms and regulatory principles that ensure functional harmony between oscillators?
Quantitative analysis of circadian clocks and the CDC in cyanobacteria (Mori et al., 1996; Mori and Johnson, 2001), algae (Moulager et al., 2010; Miyagishima et al., 2014), fungi (Hong et al., 2014), and mammals (Nagoshi et al., 2004; Bieler et al., 2014; Feillet et al., 2014) have shown that the circadian clock gates the CDC, such that cell cycle events are halted at checkpoints during prohibitive circadian phases (Johnson, 2010). These oscillators appear to coexist through asymmetric coupling, whereby a slower, rigid circadian clock dominantly regulates a faster, flexible cell cycle. A related phenomenon occurs in the budding yeast, Saccharomyces cerevisiae, in which a well-studied metabolic cycle interacts with the cell cycle. In contrast to circadian clocks, the yeast metabolic cycle (YMC) is shorter than 24 h and shows a range of periods that depend both on the strain examined and growth conditions used.
The YMC was first observed as a synchronous oscillation in the pH and dissolved oxygen levels (pO2) in a population of budding yeast in low-glucose chemostat conditions (Finn and Wilson, 1954; Kaspar von Meyenburg, 1969). The population oscillated between a low oxygen consumption (LOC) phase and a high oxygen consumption (HOC) phase. During LOC, cells build and accumulate storage carbohydrates, such as trehalose and glycogen (Küenzi and Fiechter, 1969). On reaching some threshold, a fraction of cells commit to HOC and catabolize their storage carbohydrates to produce a pulse of energy for cell biosynthesis through aerobic fermentation (Futcher, 2006). These metabolically committed yeasts produce and secrete two-carbon products of fermentation (e.g., ethanol, acetaldehyde) and sulfur assimilation (e.g., dihydrogen sulfide) (Sohn and Kuriyama, 2001; Wolf et al., 2001), all of which can phase-shift the YMC of other cells. The population synchrony of the YMC in a chemostat is thought to arise from YMC-to-YMC coupling across cells via secreted metabolites (Robertson et al., 2008).
However, within each cell, the YMC also interacts with the CDC. The CDC and YMC periods range from 3 to 15 h and 0.4 to 15 h, respectively, in the literature, varying as a function of a dilution rate that sets the population growth rate in a chemostat; see Supplemental Table S1. The CDC and YMC periods do not appear to have a fixed relationship and, in fact, the ratio may change continuously with the dilution rate (Slavov and Botstein, 2011). Despite the seeming independence of these two oscillators, cell cycle events such as DNA replication occur once per YMC (Klevecz et al., 2004; Tu et al., 2005; Chen et al., 2007; Slavov and Botstein, 2011). The flexible coupling of these two oscillators resembles the gating observed between the circadian clock and CDC. On the basis of their work with the distiller’s strain IFO 0233, Klevecz and colleagues first suggested that the observed gating between YMC and CDC might be functionally important for the temporal separation of CDC events (i.e., DNA replication) that are incompatible with YMC events (i.e., HOC and aerobic respiration, which could lead to oxidative damage of DNA; Klevecz et al., 2004).
This was confirmed by subsequent work with a different laboratory strain, CEN.PK, which showed that DNA replication occurred toward the end of HOC as pO2 levels rise (Tu et al., 2005; Chen et al., 2007). The authors classified the end of HOC (when yeast oxygen consumption is still high) as a “reductive-building” phase, based on clustering of gene expression microarrays. However, later work with an S288C-derived laboratory strain (DBY12007) demonstrated that DNA replication could occur either in the middle of HOC or at the HOC/LOC boundary, depending on the underlying dilution rate (Slavov and Botstein, 2011). Thus strict separation of DNA replication and HOC does not appear to be a consistent feature of the YMC. These discrepancies have led to a debate on the fundamental frequency of the ultradian YMC, the definition of relevant metabolic phases, and the nature of YMC–CDC coupling (Lloyd, 2006; Murray, 2006; Tu et al., 2006; Slavov and Botstein, 2011). This raises the important question: Which YMC and CDC coupling phenotypes (e.g., gating and timing of CDC and YMC events, ratio of CDC and YMC periods at different dilution rates) are universally shared across all budding yeasts, and which might be strain-specific idiosyncrasies?
Growth medium and chemostat settings differed between previous YMC experiments, which confounds interpretations of YMC phenotype, because genotype (i.e., strains) and environment (i.e., chemostat settings) were uncontrolled; see Supplemental Table S1. Moreover, recent work on metabolic variation between a lab strain and a wild strain discovered genetic differences that affect sulfur assimilation, glucose uptake, and ethanol secretion (Breunig et al., 2014). These metabolic pathways are relevant to the YMC, which suggests that there could be profound differences between lab strains and wild isolates. To help untangle effects of genotype from those of environment, we first measured YMC–CDC coupling in lab strains, CEN.PK and DBY12007, and two wild strains, YJM128 (a clinical lung isolate) and YPS670 (an isolate from oak sap). These experiments were done in a chemostat environment with identical growth medium, oxygen flow, and pH. Growth rate is known to affect the timing of DNA replication with respect to HOC (Slavov and Botstein, 2011). Thus we also measured YMC–CDC coupling in these different strains over a range of dilution rates.
RESULTS
Quantitative measurement and analysis of strain-specific and universal YMC phenotypes
All strains were first grown to saturation in batch growth and starved for at least 6 h (Figure 1A). We then activated the chemostat feed pumps and added fresh medium at a constant dilution rate (D). The chemostat dilution rate sets the pace of glucose delivery and therefore sets the average yeast growth rate and cell division time. Yeasts grew more slowly at lower dilution rates and exhibited a longer population doubling time. After an interval of transient arrhythmic behavior, the dissolved oxygen levels (pO2) settled into a steady-state oscillation between HOC and LOC.
FIGURE 1:
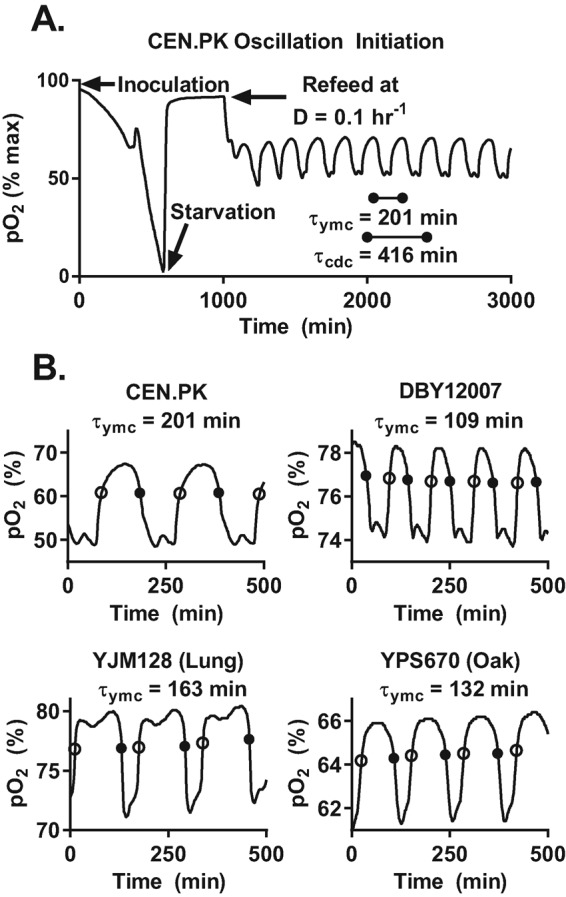
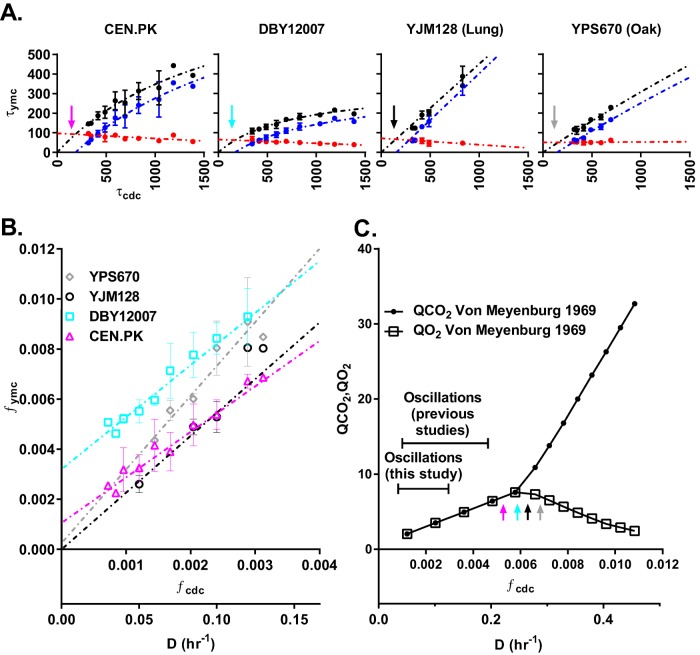
Measurement and analysis of the YMC across different strains. (A) Representative dissolved oxygen trace (pO2) after inoculation of chemostat with strain CEN.PK. Log phase yeasts first aerobically fermented the available glucose to produce ethanol; this was followed by a diauxic shift to pure respiration on ethanol. After a period of yeast starvation, we started the flow of fresh medium into the chemostat at a constant dilution rate (D = 0.1 h−1). The population began to exhibit clear oscillations in pO2 after refeeding. The period of the YMC (τymc) is the elapsed time from peak to peak in pO2 signal. At steady state, the average CDC period (τcdc) must be equal to the inverse of the dilution rate, or τcdc = ln (2)/D. (B) Sample pO2 traces of different yeasts at the same dilution rate. We used lab strains CEN.PK and DBY12007 and wild isolates YJM128 (lung) and YPS670 (oak). We developed an automated analysis pipeline to extract the YMC period, timing of entry into HOC (solid circle), and timing of entry into LOC (open circle) across different strains and dilution rates; see Materials and Methods.
We confirmed that the measured pO2 profile accurately tracks the steady-state oxygen level and is determined by the yeast oxygen uptake rate; see Materials and Methods and Supplemental Figure S1. Our measurements of gas transfer rates and pO2 probe behavior indicated that the pO2 measured in any given chemostat chamber reaches steady state after an abrupt change in oxygen uptake rate within 1–2 min. This is much shorter than the ∼15–30 min during which pO2 moves from low to high values between the HOC and LOC phases of the YMC. Thus the slow increase in pO2 after a local minimum in pO2 (“reductive-building” phase; Tu et al., 2005) corresponds to a high yeast oxygen uptake rate, wherein the rate of oxygen consumption is slowly decreasing. Similarly, the slow drawdown of pO2 after a local maximum in pO2 (“oxidative phase”; Tu et al., 2005) is due to a steady increase in the yeast oxygen uptake rate rather than the slow depletion of dissolved oxygen after a rapid increase in yeast respiration. Our controls show that we can classify oxygen consumption rate (HOC or LOC) on the basis of pO2 levels (low or high). We empirically defined the boundaries of HOC and LOC at 65% of local peak-to-trough pO2 levels, because 1) this threshold was robust to slow drifts in pO2 probe calibration, 2) it was independent of magnitude of pO2, and 3) entry into HOC was coincident with the onset of aerobic fermentation and acidification of the growth medium; see Supplemental Figure S1.
All tested strains were capable of synchronous metabolic cycles, including wild isolates from widely varying ecological contexts (Figure 1B). Thus the YMC appears to be robust to genetic variation in the sulfur assimilation, glucose uptake, and ethanol secretion pathways across our strains. However, this variation does affect the quantitative features of the YMC. For example, each strain had a different pO2 profile and YMC period (τymc = 110–200 min) at identical dilution rates. How does the pO2 profile and τymc of each strain change with growth rate?
To address this question, we first measured τymc as a function of the dilution rate for CEN.PK (Figure 2). As glucose became more limiting at lower dilution rates, the cells exhibited longer YMCs and CDCs. Strikingly, all of the increase in τymc occurred in the LOC interval (τloc), whereas the HOC interval (τhoc) stayed constant or actually decreased with increasing cell cycle period (τcdc). To better quantify this relationship, we plotted τymc, τhoc, and τloc as a function of τcdc across all strains (Figure 3A). These cross-strain data confirm that all of the increase in τymc occurred in the LOC interval (τloc). The LOC and HOC phases are associated with the anabolism and catabolism of storage carbohydrates, respectively. This suggests a simple model of how the YMC and CDC are related to metabolism: at lower dilution rates, cells spend more time in LOC accumulating storage carbohydrates because of the smaller glucose flux. Once these cells reach a metabolic threshold, they switch to HOC and catabolize their storage carbohydrates to provide biomass and energy for cell growth and division. Cell division and the subsequent switch back to LOC occur after a similar amount of time, regardless of the dilution rate.
FIGURE 2:
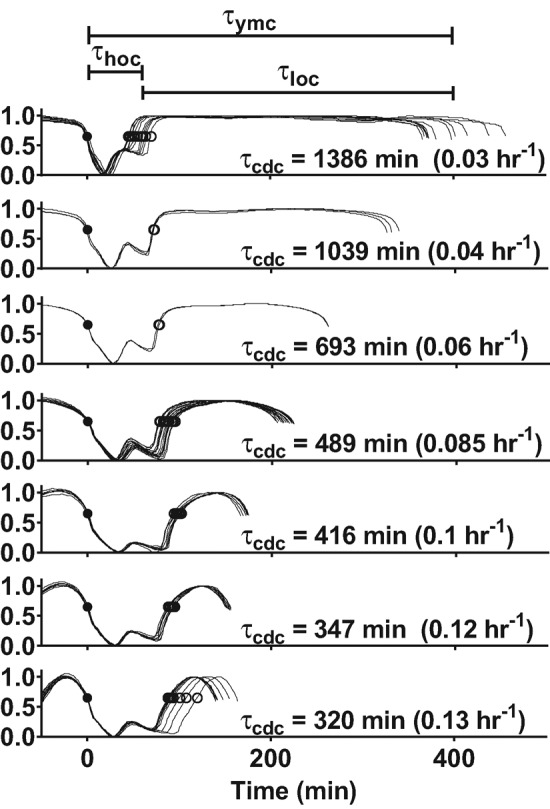
Increase in YMC period at slower dilution rates occurs in the LOC. The YMC of strain CEN.PK was analyzed over a range of dilutions rates (D = 0.03–0.13 h−1). All YMC oscillations in pO2 from a single chemostat run were overlaid according to their entry into HOC (solid circle, t = 0 min) and their amplitudes were normalized and arranged vertically by their dilution rates. As τcdc increased, both τymc and τloc increased, whereas τhoc slowly decreased.
FIGURE 3:
Quantitative relationship between the YMC and CDC. (A) Plots of YMC period (τymc; black dots), time spent in HOC (τhoc; red dots), and time spent in LOC (τloc; blue dots) as a function of CDC period (τcdc) for CEN.PK, DBY12007, YJM128 (lung), and YPS670 (oak). For clarity, we plot the mean and SD of time-series averages at identical dilution rates, which were measured during separate chemostat runs. We used nonlinear regression to best fit a mixed model to each data set; see Materials and Methods and Supplemental Figures S2 and S3. (B) Plot of YMC frequency (fymc = 1/τymc) and CDC frequency (fcdc = 1/τcdc) for all strains. (C) Metabolic profile of oxygen consumption (QO2) and carbon dioxide production (QCO2) of yeast strain LBGH1022 at different dilution rates from previous literature (Kaspar von Meyenburg, 1969). There is a transition from oxidative respiration (QCO2 is equal to QO2) to aerobic fermentation (QCO2 is greater than QO2) at a critical dilution rate, Dc ≈ 0.24 h−1, which corresponds to the dilution rates at which our tested strains are extrapolated to spend all their time in HOC phase (colored arrows) and not oscillate.
Recent observations in the common lab strain background S288C showed that τymc increases linearly with τcdc (Slavov and Botstein, 2011). To what extent does this quantitative relationship hold across multiple strains? Our analysis confirms that τymc initially increases linearly but slowly approaches a strain-specific maximum period at large τcdc (Figure 3A). This hyperbolic relationship was consistent across all strains, although each strain had a unique set of parameters (see Materials and Methods and Supplemental Table S2). Growth rate is often the relevant variable in microbial physiology. Thus we replotted our quantitative data in units of frequency, fymc = 1/τymc and fcdc = 1/τcdc, because fcdc is proportional to the average growth rate set by the dilution rate (D). The same data for each strain is now linear in frequency space with a unique slope and y-intercept (Figure 3B).
Extrapolation of the quantitative relationships in Figure 3A predicts a maximum growth rate at which yeasts spend all of their time in HOC and the YMC should disappear (i.e., vertical arrows, where τloc = 0). This maximum growth rate is strikingly close to the critical dilution rate Dc, at which yeast transitions from pure oxidative metabolism to aerobic fermentation (Figure 3C). This critical point is also where genes involved in mitochondrial respiration and catabolism of gluconeogenic carbon sources are repressed by glucose—the Crabtree effect (Cortassa and Aon, 1998). This suggests that fully respiratory carbon metabolism and the absence of glucose repression may play a role in the emergence of synchronous YMC in chemostat conditions.
How do the frequencies of the YMC and CDC oscillators vary relative to one another as a function of growth rate? The ratio of frequencies of simple coupled oscillators might be expected to hop discontinuously from one simple rational number to another (i.e., “Devil’s staircase”), as the frequency of one oscillator changes relative to the other (Pikovsky et al., 2001). Our data suggest that the ratio of YMC and CDC frequency (fymc/fcdc) stays constant in wild strains but varies continuously in laboratory strains as growth rate is adjusted (Figure 3B). The absence of discontinuous hopping indicates that the YMC and CDC oscillators across the population are not mode-locked in a simple and deterministic manner.
Cell division cycle and entry into HOC are tightly linked across different strains and growth rates
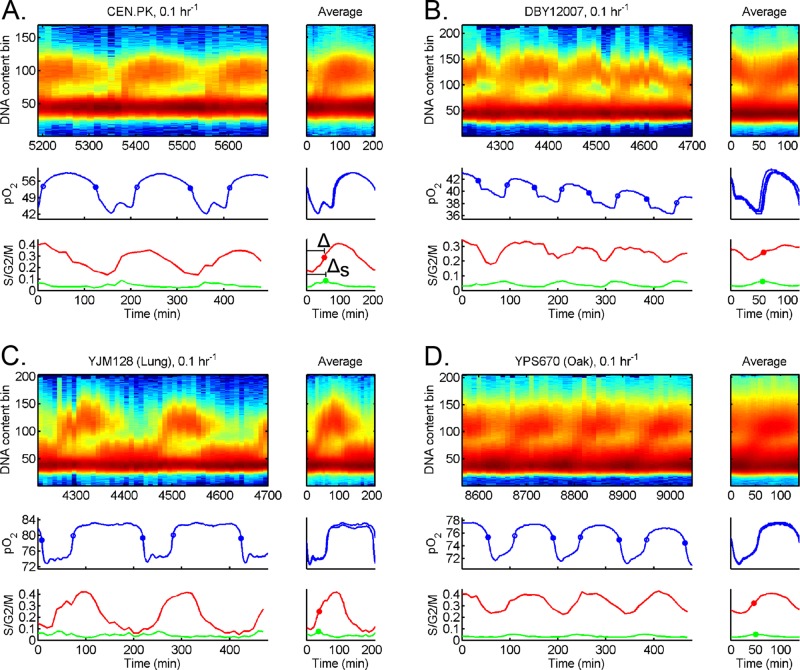
Budding yeast irreversibly commit to a CDC after passing a commitment threshold known as Start (Hartwell et al., 1974; Johnston et al., 1977). This triggers the expression of hundreds of G1/S genes, which is then followed by DNA replication. To quantify the timing of CDC relative to the YMC, we measured DNA replication of our different strains at high temporal resolution; see Figure 4. In agreement with previous studies, our cross-strain results showed that CDC events are gated such that all strains exhibit a single pulse of DNA replication per YMC. Moreover, only a fraction of cells commit to the CDC each YMC, that is, “one-to-some” coupling occurs. This coupling suggests a complicated subpopulation structure in the chemostat, in which staggered cohorts enter the CDC each YMC. It also explains how the YMC and CDC appear to be one-to-one coupled in bulk assays yet can have different periods.
FIGURE 4:
Timing of DNA replication relative to HOC across strains. Strains (A) CEN.PK, (B) DBY12007, (C) YJM128, and (D) YPS670 were cultured in chemostat at the same dilution rate (D = 0.1 h−1). We extracted samples every 10 min and measured CDC events (DNA content) and YMC events (pO2); see Materials and Methods. For each strain, the raw DNA content, pO2, S/G2/M fraction, and S fraction are plotted over several YMCs (left). The average over each YMC is plotted to the right of each full data set, where t = 0 corresponds to entry into HOC. We plot the 50% midpoint of S/G2/M fraction (solid red circle) and 100% peak of S fraction (solid green circle). The time of DNA replication (50% of S/G2/M fraction) after entry into HOC is defined as Δ, whereas time of DNA replication (100% of S fraction) is ΔS.
In contrast to one-to-some coupling, the timing of DNA replication relative to HOC showed strain variability (Figure 4). For example, CEN.PK replicated its DNA in the middle of HOC, whereas DBY12007 replicated its DNA near entry into LOC. These cross-strain data reinforce that the HOC phase is not strictly separated from DNA replication (Slavov and Botstein, 2011). If not strict separation, might there be other timing relationships that are universal or invariant across strains?
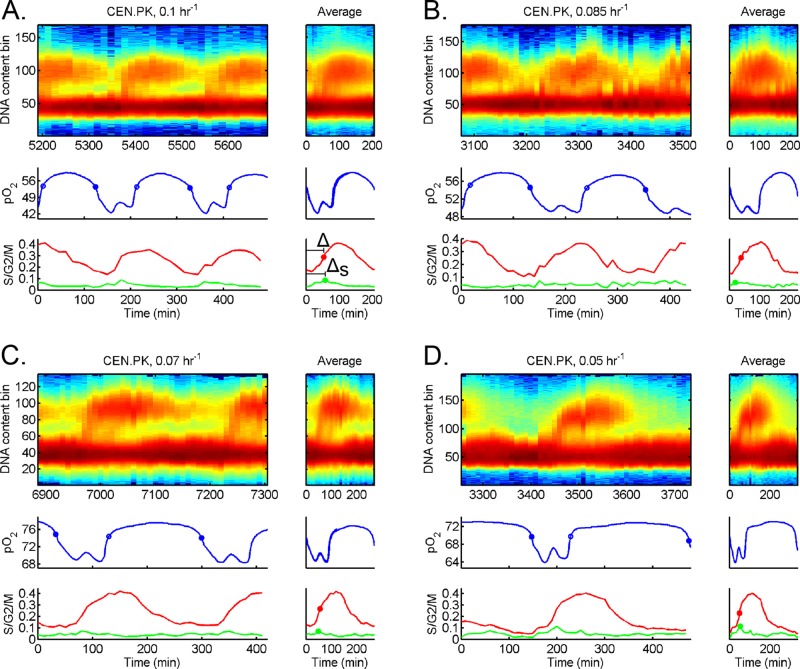
To address this question, we first analyzed DNA replication in a single strain (CEN.PK) at different dilution rates; see Figure 5. The YMC and CDC remained coupled one-to-some as we changed the dilution rate. We noticed that entry into HOC and onset of DNA replication was separated by a mostly invariant strain-specific time interval despite the longer periods of YMC, LOC, and CDC at lower dilution rates. Analysis of the separation between entry into HOC and DNA replication (ΔS) as a function of dilution rate across multiple chemostat runs supports a mostly invariant ΔS model; see Table 1. Strikingly, this invariant ΔS relationship extended to the other strains, DBY12007 and YPS670 (see Supplemental Figures S4 and S5 and Table 1), although each value of ΔS was strain specific.
FIGURE 5:
Timing of DNA replication relative to HOC in strain CEN.PK across growth rates. Additional cell cycle analysis for strain CEN.PK at different dilution rates: (A) 0.1 h−1, (B) 0.085 h−1, (C) 0.07 h−1, and (D) 0.05 h−1. The raw DNA content, pO2, S/G2/M fraction, and S fraction are plotted over several YMCs (left). The average over each YMC is plotted to the right of each full data set, where t = 0 corresponds to entry into HOC. We plot the 50% midpoint of S/G2/M fraction (solid red circle) and 100% peak of S fraction (solid green circle). The time of DNA replication (50% of S/G2/M fraction) after entry into HOC is defined as Δ, whereas time of DNA replication (100% of S fraction) is ΔS.
TABLE 1:
Timing of entry into HOC and DNA replication (ΔS) across strains and growth rates.
| D (h−1) | 0.1 | 0.085 | 0.07 | 0.05 |
|---|---|---|---|---|
| CEN.PK | 56.5 ± 0.7 | 53.7 ± 32.6 | 48.0 | 53.5 ± 0.7 |
| DBY12007 | 58.0 ± 2.0 | 59.0 ± 5.7 | 59.0 | 54.0 |
| YPS670 (oak) | 44.8 ± 8.5 | 58.0 | 44.0 | |
| YJM128 (lung) | 33.3 ± 3.8 |
The mean and SD of ΔS interval (min) of various strains at different growth rates. Mean and SD are for biological replicates of the same strains at identical growth rate on different days. YJM128 was unstable at lower dilution rates.
DISCUSSION
Our aim was to determine which behaviors of the YMC are universal. By studying multiple strains over a wide range of shared growth conditions, a number of key conclusions can be reached regarding the robustness of YMC–CDC phenotypes. First, all strains, including wild isolates, exhibited synchronous metabolic oscillations. Second, the increase in τymc across all strains resulted from an increase in the length of LOC, whereas the length of HOC remained approximately constant or actually decreased (Figures 2 and 3). Third, all strains exhibited a single pulse of DNA replication per YMC wherein only a fraction of cells commit to division each YMC, that is, one-to-some coupling occurs (Figure 4). Finally, all committed cells entered the cell cycle and replicated their DNA within a strain-specific interval (ΔS) regardless of the extended length of YMC, LOC, and CDC at different growth rates (Figure 5 and Table 1).
Population synchrony and structure of YMC–CDC coupling in a chemostat
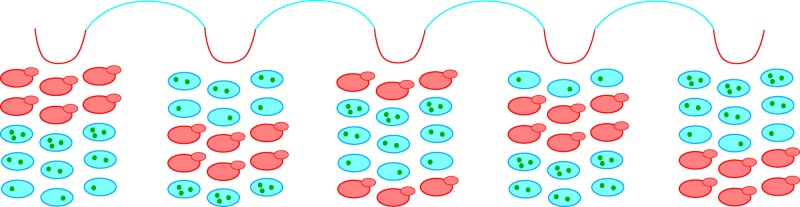
The universal features of YMC–CDC coupling observed in this work point to a simplified model of YMC–CDC coupling (Figure 6) in which cell cycle Start is intimately coupled to the catabolism of storage carbohydrates, as summarized in Futcher (2006). This connection between Start and metabolism is consistent with the known cell cycle literature, which reports that smaller yeasts (i.e., daughter cells) spend more time in G1 accumulating biomass until they have reached a critical size and can commit to the CDC (Hartwell et al., 1974). As the flux of glucose decreases at lower chemostat dilution rates, the yeasts spend more time in LOC, and presumably G1, accumulating sufficient biomass and storage carbohydrates. This would explain the increase in YMC, LOC, and CDC periods at lower dilution rates (Figures 2 and 3). When a cell has accumulated enough biomass and storage carbohydrates, it is able to enter HOC and consume its storage carbs.
FIGURE 6:
Simplified model of YMC–CDC coupling. The dissolved oxygen pO2 trace indicates LOC (blue line) and HOC (red line) over multiple YMCs. At the beginning of each YMC, a fraction of the population (red, budded cells) commits to catabolizing storage carbohydrates, entering HOC, and starting the CDC. These “committed” yeasts secrete metabolites, which trigger other “susceptible” yeasts with sufficient storage carbohydrates to catabolize their storage carbohydrates (Robertson et al., 2008). Such autocatalytic signaling through secreted metabolites causes an avalanche of susceptible yeasts to synchronously enter HOC and commit to the CDC. However, it is clear that not all yeasts commit to CDC each YMC. The rest of the yeast population in LOC (blue cells) is either refractory to metabolic signals, because the cells have not accumulated sufficient energy reserves (green dots) to commit to YMC, and/or has not accumulated sufficient biomass to initiate cell cycle Start upon entry to HOC. Over the coming YMC, these “refractory” yeasts in LOC continue to build up their reserves of storage carbohydrates and biomass, such that a new fraction of yeasts will be ready to spontaneously initiate and trigger other susceptible yeasts to commit to the next YMC. The yeast population in a low-glucose chemostat thus self-organizes into multiple staggered cohorts, such that only one cohort synchronously enters the CDC each YMC (i.e., one-to-some coupling). Cells likely migrate between cohorts over time due to cell-to-cell variability in both the YMC and CDC.
One-to-some coupling suggests that the population is likely composed of staggered cohorts that may differ in their degree of storage carbohydrate and/or biomass accumulation. Staggered cohorts could arise from and be maintained by the cell size asymmetry between mother and daughter cells (Hartwell and Unger, 1977) and/or secretion of different metabolites that advance or block different phases of the YMC and/or CDC (Young et al., 2012). Each YMC, a fraction of cells (usually less than a third) pass Start, enter the CDC, and replicate their DNA on schedule, that is, one-to-some coupling occurs (Figure 4). The temporal coordination of YMC events (i.e., burning storage carbohydrates and entering HOC) and CDC events (i.e., Start) would explain the mostly invariant ΔS across dilution rates. A biological rationale for coordinating cell cycle Start and carbohydrate catabolism in this cohort of committed cells may be to ensure that sufficient energy is available to complete biomass accumulation, DNA replication, and cell division in a timely manner. More work will be required to elucidate the complex population structure of the YMC and the nature of the cohorts initiating cell division each YMC. For example, what fraction of mother versus daughter cells (each having different CDC periods at the same population-doubling time) initiate cell division each YMC? Do all cells exhibit metabolic oscillations each YMC, or is it only the cohort that enters the CDC?
Strain-specific features
There were several notable YMC differences between strains. First, every strain had a distinct pO2 waveform and τymc when grown at the same dilution rate (see Figure 1). Second, the exact quantitative relationship between τymc, τloc, and τhoc as a function of τcdc varied across strains (Figure 3 and Supplemental Table S2). Third, the characteristic delay between entry into HOC and initiation of DNA replication (ΔS) varied between strains (Table 1), with wild strains having shorter delays than laboratory strains. Finally, the overlap between HOC and DNA replication depended on the strain and the dilution rate (Figure 4 and Supplemental Figure S6). Our results do not support the hypothesis that DNA replication is strictly segregated from aerobic respiration (Klevecz et al., 2004; Tu et al., 2005; Chen et al., 2007). Strain-to-strain variation in the length of HOC at a given growth rate can lead to DNA replication occurring in early HOC, late HOC, or early LOC (Figure 4). Changes in the length of HOC at different dilution rates can also lead to DNA replication occurring in HOC or LOC (Supplemental Figure S6).
Despite these strain differences, an unexpected regularity emerged when we examined the fraction of time spent in HOC (Φhoc) as a function of growth rate (Supplemental Figure S7). Φhoc is an approximately linear function of growth rate, such that all strains spent similar fractions of time in HOC at identical growth rates. This is reminiscent of bacterial growth laws in which the RNA/protein ratio increases linearly with growth rate, as bacteria grow faster and put more energy and biomass into growth and ribosome biosynthesis (Schaechter et al., 1958; Scott et al., 2010). Bacteria achieve this by smoothly ramping gene expression and metabolism in response to changes in growth rate. The YMC, in contrast, is associated with an oscillation in metabolic rate and expression levels of large fractions of the transcriptome. The early HOC phase (identified elsewhere as the “oxidative phase”) in particular is linked to a burst of expression of ribosome biosynthesis, amino acid biosynthesis, and RNA metabolism genes (Klevecz et al., 2004; Tu et al., 2005; Murray et al., 2007). Thus yeast appears to partition ribosome biosynthesis and carbon metabolism in time, using frequency modulation to smoothly tune the ratio of “productive” periods to “quiescent” periods with the growth rate.
Does the YMC occur outside particular chemostat conditions?
Historically, the YMC has been studied in low-glucose chemostats, because the budding yeast population self-synchronizes in these conditions. This synchrony is thought to arise from signaling between cells. The dispersal of secreted metabolites in a well-mixed bioreactor may help synchronize the oscillation across the population, allowing study at a bulk population level. However, mixing alone is insufficient to ensure synchrony, because the synchronous YMC disappears at different chemostat dilution rates, oxygen flow, and nutrient conditions in different strains. Loss of population synchrony could arise because 1) single cells no longer have an autonomous YMC oscillator, or 2) YMC oscillators in cells have lost their ability to entrain to other YMC oscillators. One could distinguish between these two cases by looking for evidence of the YMC in conditions under which population synchrony is lost.
Recent work suggests that the YMC may indeed occur in single cells in asynchronous populations. First, expression of genes known to oscillate across the YMC and CDC were measured in single cells using single-molecule RNA fluorescence in situ hybridization (FISH) (Silverman et al., 2010). These yeast cells, grown in chemostat in nutrient-starved conditions, did not exhibit synchronous YMC. The authors showed that different pairs of YMC and CDC transcripts, previously correlated and anticorrelated in populations undergoing synchronous YMC oscillations in chemostat, continued to be correlated and anticorrelated in single cells from an asynchronous chemostat. Second, the degree of stress resistance exhibited by yeasts was unimodal in a synchronized population, with all cells sensitive to heat shock during HOC and more resistant during LOC. However, stress resistance was bimodal in yeasts grown under similar but asynchronous conditions. The authors suggested that there was an asynchronous, biphasic mixture of cells in HOC and LOC—a large population dying rapidly, followed by a second population dying slowly during heat shock (Slavov et al., 2012).
Yeasts can also exhibit synchronous metabolic oscillations outside chemostat conditions. For example, oscillations were observed in batch growth upon diauxic shift to pure respiration on ethanol from aerobic fermentation (Mochan and Pye, 1973). More recently, the YMC was observed in batch-grown, phosphate-starved yeast with ethanol as a sole carbon source. These yeast remained blocked in the G1 phase of the cell cycle due to phosphate starvation, which suggests that the YMC can operate independent of the CDC (Slavov et al., 2011). Finally, respiratory oscillations have been observed in batch cultures of budding yeast (Saccharomyces), clinically significant yeasts (Candida), and fission yeast (Schizosaccharomyces pombe) synchronized at similar cell cycle stages through centrifugation; see review by (Lloyd, 2008). Strikingly, some of these respiratory oscillations persisted during a subsequent cell cycle block, which shows that respiration can oscillate autonomous of the CDC.
Coordinated cross-talk between YMC and CDC oscillators
There is evidence to support a bidirectional link between the YMC and CDC, in which both of these two oscillations are autonomous but mutually coupled. For example, induction of a premature HOC phase via addition of ethanol to a culture in LOC also triggers cell cycle entry (Robertson et al., 2008). Recent work has shown that increasing acetyl–coenzyme A levels during trehalose catabolism and glucose fermentation drives chromatin acetylation and increases the global expression of numerous genes, including the G1 cyclin CLN3 (a key regulator of the cell cycle Start; Shi and Tu, 2013). Other work strongly suggests that the ATP/ADP ratio (which oscillates with the YMC and peaks in HOC) directly regulates global gene expression via ISWI and RSC during the YMC (Machne and Murray, 2012; Amariei et al., 2014). Thus chromatin regulation may provide a generic mechanism by which the YMC can regulate the CDC.
A global survey of Cdk1 targets by the Morgan lab recently identified Nth1, a catabolic enzyme that degrades trehalose, as a likely target of Cdk1 (Holt et al., 2009). Unpublished work shows that Cdk1 phosphorylation of Nth1p can trigger the liquidation of stores of trehalose (JM Skotheim, personal communication). We speculate that these mechanisms create a positive-feedback loop (liquidation of storage carbohydrates can trigger cell cycle Start, and progress through cell cycle Start can trigger liquidation of storage carbs) that may be responsible for the strong coupling between the YMC and CDC. The bidirectional coupling may be a mechanism to ensure that these two oscillators with different average periods nonetheless maintain coordination between the production of energy and biomass and progress through the CDC.
MATERIALS AND METHODS
Yeast strains
We used diploid prototrophs in our experiments. Yeast strain DBY12007 was generously provided by the lab of David Botstein (Princeton University; Silverman et al., 2010). Haploid strains CEN.PK (MATa and MATα) were gifts from the lab of Benjamin Tu (UT Southwestern; Shi et al., 2010). We mated these haploids to produce diploid CEN.PK. Wild isolates YJM128 and YPS670 were chosen for their breadth of ecological niches and were gifts from the lab of Paul Magwene (Duke University). Strain YJM128 is a clinical isolate from the lung of an HIV patient (McCusker et al., 1994). YPS670 was originally isolated from oak sap exudate in the forests of Pennsylvania (Murphy et al., 2006).
Growth medium
We used minimal defined (MD) growth medium, which we adapted from several sources (Saldanha et al., 2004; Brauer et al., 2005; Tu et al., 2005). We first tested glucose concentrations between 0.1 and 2% mass/volume before choosing 0.25% for all subsequent experiments, due to the ability of all strains to oscillate at this concentration. MD medium was prepared by first autoclaving a base solution of 0.1 g/l CaCl2·2H2O, 0.5 g/l Mg2(SO4)2 ·7H2O, 2 g/l K2HPO4, 5 g/l (NH4)·2SO4, and 70 μl/l 96% H2SO4. After cooling, this autoclaved solution was supplemented with 1 ml/l 1000× vitamin solution, 100 μl/l, 10,000× trace salt solution, 0.02 g/l solid FeSO4·7H2O, 100 μl/l Sigma Antifoam 204, and 0.25% glucose mass/volume. The 10,000× trace salt solution consisted of 10 g ZnSO4·7H2O, 5 g CuSO4·5H2O, 1 g MnCl2·4H2O, and 100 ml filter sterilized H2O. The 1000× vitamin solution consisted of 1 mg biotin, 200 mg calcium pantothenate, 1 mg folic acid, 1000 mg inositol, 200 mg niacin, 100 mg p-aminobenzoic acid, 200 mg pyridoxine HCl, 100 mg riboflavin, 200 mg thiamine HCl, and 500 ml H2O, which was autoclaved for 40 min to dissolve vitamin powders and immediately cooled to 4°C. All chemicals were purchased from Sigma Aldrich (St. Louis, MO).
Continuous culture conditions
Continuous cultures were grown in a Multifors 6-vessel microbial system (Infors USA, Laurel, MD). All vessels had a 1000 ml working volume at 30°C. They were aerated with 1000 ml/min of filtered room air and stirred at 550 rpm. Dissolved oxygen (pO2) and pH were measured with OxyProbe and FermProbe (Broadley-James, Irvine CA). We recorded the pH, pO2, and pump flow rates every minute using IRIS V5 and V6 monitoring software (Infors USA). The pH was clamped by the chemostat control computer via the automatic addition of sterile 1 M phosphoric acid or 1 M sodium hydroxide, as necessary. Medium pH was maintained at 4.0 ± 0.1 for all strains, except YPS670, which was kept at 5.0 ± 0.1, because its growth was significantly diminished at a lower pH. Vessels containing 1000 ml of 1× base solution were autoclaved and cooled to a working temperature of 30°C. To prevent precipitation, sterile trace salts, vitamins, and glucose were added after cooling to working temperature, just before yeast inoculation. We calibrated feed pumps by measuring the volume of liquid dispensed before autoclaving when run at 100% speed. The pO2 sensors were calibrated by setting the probe to 100% at full oxygen saturation and 0% at full nitrogen gas in place of air. In the next section we outline how we verified that the measured pO2 profile reflects actual pO2 as well as the yeast oxygen uptake rate due to very rapid oxygen mass-transfer kinetics.
Measured pO2 reflects the actual pO2
We first measured the probe response time (τr) and the oxygen mass-transfer coefficient (k) of our chemostat using the dynamic method (Garcia-Ochoa and Gomez, 2009). The probe and oxygen dynamics are described by
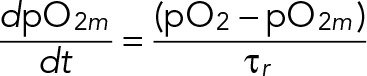 (1) (1)
|
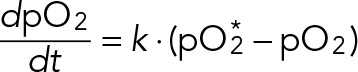 (2) (2)
|
where pO2m is the measured dissolved oxygen level, pO2 is the actual dissolved oxygen level, and pO2* is the target steady-state level that the system approaches. We determined τr and k by experimentally switching gas-line input from nitrogen gas (pO2* = 0%) to air (pO2* = 100%). The dynamics of reaching the new steady state is given by
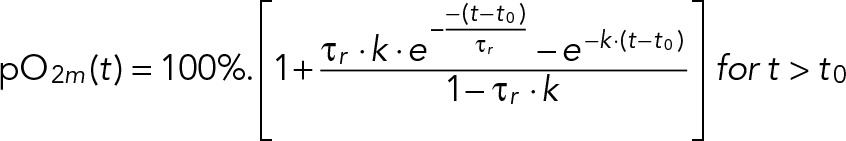 (3) (3)
|
where t0 is a variable time lag that arises from the manual switching of gas lines and adaptive temporal sampling of the recording software. The oxygen mass-transfer coefficient (k) in a chemostat depends on the rate of airflow, impeller type, rotation speed, and temperature. We fitted Eq. 3 to experimental pO2m from the same chemostat conditions used in our YMC experiments: airflow rate of 1000 ml/min mixed with a Rushton impeller at 550 RPM at 30°C. Our best fit to multiple data sets gives a response time τr ≈ 0.19 min and oxygen mass-transfer coefficient k ≈ 1.2 min−1; see Supplemental Figure S1A for one such fit.
By manipulating Eqs. 1 and 2, we can derive the time-varying steady-state level pO2*(t) from pO2m(t) (and associated first-derivative pO′2m(t) and second-derivative pO″2m(t)):
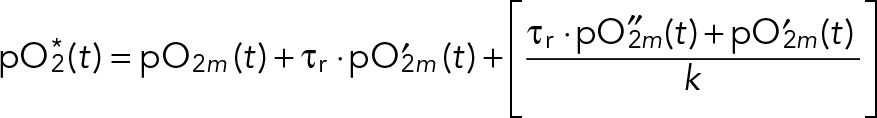 (4) (4)
|
The value of pO2*(t) represents what pO2m(t) would be if the chemostat had an infinite oxygen mass-transfer coefficient and zero probe-response time. We used Eq. 4 and our best-fit k and τr parameters to convert measured pO2m(t) into pO2*(t). The measured dissolved oxygen profile is nearly identical to steady-state oxygen levels; see Supplemental Figure S1B. Thus we will use pO2*, pO2, and pO2m interchangeably throughout our article.
Levels of pO2 are determined by the yeast oxygen uptake rate
It is important to clarify the relationship between high and low dissolved oxygen (pO2) and the rate of oxygen consumption by yeast in a bioreactor. Briefly, the pO2 is a balance between the rate of oxygen transfer from gas to liquid and the yeast oxygen uptake rate (OUR). Mathematically, the rate of change of pO2 is given by
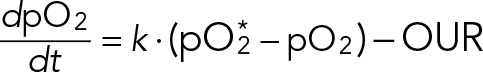 (5) (5)
|
where pO2* is the saturation level of dissolved oxygen (100%) that our chemostat would approach in the absence of any yeast respiration. The general solution to Eq. 5 is
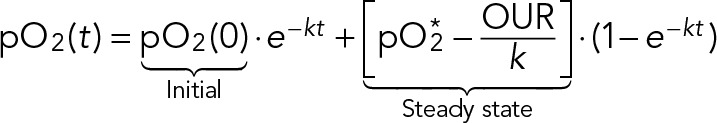 (6) (6)
|
The bioreactor oxygen mass-transfer coefficient (k) determines the timescale of how quickly an initial pO2 reaches its new steady state after a change in yeast OUR. Our calibration measurements showed that steady state is reached quickly (k ≈ 1.2 min−1). When the yeast OUR changes on a timescale that is slower than k, Eq. 6 is well described by the steady-state solution
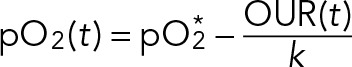 (7) (7)
|
If yeast OUR is high, then pO2 is low (or 0%, the absolute minimum). Conversely, if yeast OUR is low, then pO2 is high (or 100%, the absolute maximum). Our control experiments indicate that pO2 accurately reflects the yeast oxygen uptake rate in our chemostat.
Automated data analysis
Each chemostat run lasted from 1 to 3 wk. During each run, we scanned through different dilution rates. We allowed enough time to reach steady state after each change in the dilution rate. There were 16, 12, 9, and 10 chemostat runs, and we collected a total of 52, 50, 16, and 30 YMC time series over a range of different dilution rates for strains CEN.PK, DBY12007, YJM128 (lung), and YPS670 (oak), respectively. We discarded those parts of the time series that had not yet reached steady state by removing the first 1000 min after initiation of continuous growth and the first 250 min after each subsequent change in dilution rate. We applied a MATLAB-based peak-detection algorithm to these steady-state pO2 time series to identify local maxima and minima. We included a minimum peak size filter and a smaller local peak-exclusion size filter to ensure that only one local maximum and one local minimum per cycle were identified. Filter parameters had to be adjusted manually for each experiment to ensure that exactly one maximum and one minimum were identified per cycle. Entry into HOC was defined as the time at which pO2 drops to 65% of the span from a local maximum to the next local minimum, whereas entry into LOC was defined as the time at which the pO2 rises to 65% of the span from a local minimum to the next local maximum. Our definition of entry into HOC was coincident with the onset of aerobic fermentation and acidification of the medium; see Supplemental Figure S1C. For every time series at a fixed dilution rate, we recorded the time of each entry into HOC; minimum pO2; exit from HOC; maximum pO2; and the distribution of lengths of each YMC, HOC, and LOC. We discarded a time series if the coefficient of variation of τymc, τhoc, or τloc was >0.2. This stringent filter flagged and removed 19 YMC time series with stability problems (<9% of the data).
Quantitative relationship between YMC and CDC
The total YMC period (τymc) was split into a HOC interval (τhoc) and a LOC interval (τloc). Each strain data set {τ} contained average {τymc, τhoc, τloc} for each YMC time series at different dilution rates. For each strain, the {τ} at different dilution rates (τcdc) was best fitted using nonlinear least-squares fitting (nlinfit in MATLAB). We fitted these data in Supplemental Figure S2 to a linear model:
|
|
where b is the y-intercept and m is the relative slope. We also fitted these data in Supplemental Figure S2 to a hyperbolic model (i.e., Michaelis-Menten):
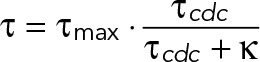 (9) (9)
|
where τmax is the maximum YMC and κ is the τcdc at which τ is half-maximum. The hyperbolic model becomes a linear model when the time variables τ are inverted to frequencies (f), such that
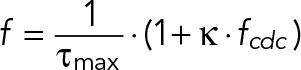 (10) (10)
|
where f = 1/τ and fcdc = 1/τcdc.
In the end, all data were best fitted by a mixed model, where τymc is hyperbolic, τhoc is linear, and τloc = τymc – τhoc; see Supplemental Figure S2 and the best-fit residuals of each model to different data sets in Supplemental Figure S3. The best-fit parameters of the mixed model to different data sets are listed in Supplemental Table S2.
Cell cycle analysis
Samples were taken from stably oscillating chambers at 10- or 15-min time intervals. These samples were immediately spun down and washed in distilled water, and cells were fixed in 70% ethanol at 4°C in 96-well plates. Our DNA-staining protocol was modified from Haase and Reed (2002) to handle reduced fluid volumes in 96-well plates: cells were first washed with 200 μl distilled water, resuspended in 100 μl RNase A solution (Qiagen) for 2–6 h, resuspended in 100 μl pepsin solution for 10–15 min, and then stored in 200 μl storage buffer. Before the final staining step, 30 μl of each sample was sonicated to separate cell clumps, using a medium setting (strains CEN.PK, DBY12007, YPS670) or high setting (YJM128) for 45 s in 3 × 8 strips of 96-well PCR plates floating in a Bioruptor water-bath sonicator (Diagenode, Denville, NJ). The sonicated cells were immediately added to 96-well plates containing 200 μl per well of 1 μM SYTOX Green (LifeTechnologies). The fluorescence of these stained cells was measured with a MACSQuant VYB (Miltenyi Biotech, Bergisch-Gladbach, Germany) using laser excitation at 488 nm and a 525/50 band-pass filter. We normalized the fluorescence distributions across all time samples by 1) shifting the fluorescence by a linear amount so that the maximum of all G1 peaks were aligned and 2) multiplying all frequencies with a scaling factor, such that each time point had the same rescaled cell count.
Dean-Jett-Fox and other cell cycle–parsing algorithms were unable to reliably identify the fraction of S-phase cells across all time points due to the width of G1 and G2/M distributions and asymmetrical G1 fluorescence peaks at slow growth rates. For each data set, we estimated two fluorescence thresholds that 1) separated G1 cells from S/ G2/M (i.e., G1 threshold) and 2) separated G2/M cells from G1/S (i.e., G2/M threshold). We determined G1 and G2/M thresholds by first averaging the fluorescence distribution across all time points, finding the local minimum between the G1 and G2 peaks, and choosing the G1 threshold such that it included 95% of cells with a DNA content below this local minimum. We chose the G2/M threshold such that it included 95% of the cells with DNA content above this local minimum. The fraction of cells above G1 threshold is the S/G2/M fraction, and the fraction between G1 and G2/M threshold is the S fraction.
For each 8-h time course, we also created an “average” YMC–CDC data set across a YMC. The start (t = 0 min) of each YMC was defined as entry into HOC. We partitioned the YMC into 1-min bins, and averaged DNA content, acidification, S/G2/M and S fraction across a window of 10 or 15 min centered on each bin. For each averaged YMC–CDC data set, we calculated Δ as the time at which the S/G2/M fraction reached 50% peak-to-trough and ΔS as the time at which S fraction reached 100% peak.
Supplementary Material
Acknowledgments
We thank Ryan Baugh, Philip Benfey, Stefano DiTalia, Xinnian Dong, Terry Hwa, Danny Lew, Rainer Machne, John Pringle, and Amy Schmid for helpful comments. This work was funded by Defense Advanced Research Projects Agency Biochronicity Grant DARPA-BAA-11-66, National Institutes of Health Director’s New Innovator Award DP2 OD008654-01, and Burroughs Wellcome Fund CASI Award BWF 1005769.01.
Abbreviations used:
- CDC
cell division cycle
- HOC
high oxygen consumption
- LOC
low oxygen consumption
- MD
minimal defined
- pO2
dissolved oxygen
- YMC
yeast metabolic cycle
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E15-07-0454) on November 4, 2015.
REFERENCES
- Amariei C, Machne R, Stolc V, Soga T, Tomita M, Murray DB. Time resolved DNA occupancy dynamics during the respiratory oscillation uncover a global reset point in the yeast growth program. Microbial Cell. 2014;1:279–288. doi: 10.15698/mic2014.09.166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bieler J, Cannavo R, Gustafson K, Gobet C, Gatfield D, Naef F. Robust synchronization of coupled circadian and cell cycle oscillators in single mammalian cells. Mol Syst Biol. 2014;10:739. doi: 10.15252/msb.20145218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brauer MJ, Saldanha AJ, Dolinski K, Botstein D. Homeostatic adjustment and metabolic remodeling in glucose-limited yeast cultures. Mol Biol Cell. 2005;16:2503–2517. doi: 10.1091/mbc.E04-11-0968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breunig JS, Hackett SR, Rabinowitz JD, Kruglyak L. Genetic basis of metabolome variation in yeast. PLoS Genet. 2014;10:e1004142. doi: 10.1371/journal.pgen.1004142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z, Odstrcil EA, Tu BP, McKnight SL. Restriction of DNA replication to the reductive phase of the metabolic cycle protects genome integrity. Science. 2007;316:1916–1919. doi: 10.1126/science.1140958. [DOI] [PubMed] [Google Scholar]
- Cortassa S, Aon MA. The onset of fermentative metabolism in continuous cultures depends on the catabolite repression properties of Saccharomyces cerevisiae. Enzyme Microbial Technol. 1998;22:705–712. [Google Scholar]
- Feillet C, Krusche P, Tamanini F, Janssens RC, Downey MJ, Martin P, Teboul M, Saito S, Lévi FA, Bretschneider T, et al. Phase locking and multiple oscillating attractors for the coupled mammalian clock and cell cycle. Proc Natl Acad Sci USA. 2014;111:9828–9833. doi: 10.1073/pnas.1320474111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn RK, Wilson RE. Fermentation process control, population dynamics of a continuous propagator for microorganisms. J Agricultural Food Chem. 1954;2:66–69. [Google Scholar]
- Futcher B. Metabolic cycle, cell cycle, and the finishing kick to Start. Genome Biol. 2006;7:107. doi: 10.1186/gb-2006-7-4-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Ochoa F, Gomez E. Bioreactor scale-up and oxygen transfer rate in microbial processes: an overview. Biotechnol Adv. 2009;27:153–176. doi: 10.1016/j.biotechadv.2008.10.006. [DOI] [PubMed] [Google Scholar]
- Haase SB, Reed SI. Improved flow cytometric analysis of the budding yeast cell cycle. Cell Cycle. 2002;1:132–136. [PubMed] [Google Scholar]
- Hartwell LH, Culotti J, Pringle JR, Reid BJ. Genetic control of the cell division cycle in yeast. Science. 1974;183:46–51. doi: 10.1126/science.183.4120.46. [DOI] [PubMed] [Google Scholar]
- Hartwell LH, Unger MW. Unequal division in Saccharomyces cerevisiae and its implications for the control of cell division. J Cell Biol. 1977;75:422–435. doi: 10.1083/jcb.75.2.422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt LJ, Tuch BB, Villén J, Johnson AD, Gygi SP, Morgan DO. Global analysis of Cdk1 substrate phosphorylation sites provides insights into evolution. Science. 2009;325:1682–1686. doi: 10.1126/science.1172867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong CI, Zámborszky J, Baek M, Labiscsak L, Ju K, Lee H, Larrondo LF, Goity A, Chong HS, Belden WJ, et al. Circadian rhythms synchronize mitosis in Neurospora crassa. Proc Natl Acad Sci USA. 2014;111:1397–1402. doi: 10.1073/pnas.1319399111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson CH. Circadian clocks and cell division: what’s the pacemaker? Cell Cycle. 2010;9:3864–3873. doi: 10.4161/cc.9.19.13205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston GC, Pringle JR, Hartwell LH. Coordination of growth with cell division in the yeast Saccharomyces cerevisiae. Exp Cell Res. 1977;105:79–98. doi: 10.1016/0014-4827(77)90154-9. [DOI] [PubMed] [Google Scholar]
- Kaspar von Meyenburg H. Energetics of the budding cycle of Saccharomyces cerevisiae during glucose limited aerobic growth. Arch Mikrobiol. 1969;66:289–303. doi: 10.1007/BF00414585. [DOI] [PubMed] [Google Scholar]
- Klevecz RR, Bolen J, Forrest G, Murray DB. A genomewide oscillation in transcription gates DNA replication and cell cycle. Proc Natl Acad Sci USA. 2004;101:1200–1205. doi: 10.1073/pnas.0306490101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Küenzi MT, Fiechter A. Changes in carbohydrate composition and trehalase-activity during the budding cycle of Saccharomyces cerevisiae. Arch Mikrobiol. 1969;64:396–407. doi: 10.1007/BF00417021. [DOI] [PubMed] [Google Scholar]
- Lloyd D. The ultradian clock: not to be confused with the cell cycle. Nat Rev Mol Cell Biol. 2006;7 DOI: 10.1038/nrm1980-c1. [Google Scholar]
- Lloyd D. Respiratory oscillations in yeasts. Adv Exp Med Biol. 2008;641:118–140. doi: 10.1007/978-0-387-09794-7_9. [DOI] [PubMed] [Google Scholar]
- Machne R, Murray DB. The yin and yang of yeast transcription: elements of a global feedback system between metabolism and chromatin. PLoS One. 2012;7:e37906. doi: 10.1371/journal.pone.0037906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCusker JH, Clemons KV, Stevens DA, Davis RW. Genetic characterization of pathogenic Saccharomyces cerevisiae isolates. Genetics. 1994;136:1261–1269. doi: 10.1093/genetics/136.4.1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyagishima S-Y, Fujiwara T, Sumiya N, Hirooka S, Nakano A, Kabeya Y, Nakamura M. Translation-independent circadian control of the cell cycle in a unicellular photosynthetic eukaryote. Nat Commun. 2014;5:3807. doi: 10.1038/ncomms4807. [DOI] [PubMed] [Google Scholar]
- Mochan E, Pye EK. Respiratory oscillations in adaptive yeast cultures. Nat New Biol. 1973;242:177–179. doi: 10.1038/newbio242177a0. [DOI] [PubMed] [Google Scholar]
- Morgan DO. The Cell Cycle: Principles of Control. London: New Science Press; 2007. [Google Scholar]
- Mori T, Binder B, Johnson CH. Circadian gating of cell division in cyanobacteria growing with average doubling times of less than 24 hours. Proc Natl Acad Sci USA. 1996;93:10183–10188. doi: 10.1073/pnas.93.19.10183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori T, Johnson CH. Independence of circadian timing from cell division in cyanobacteria. J Bacteriol. 2001;183:2439–2444. doi: 10.1128/JB.183.8.2439-2444.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moulager M, Corellou F, Vergé V, Escande M-L, Bouget F-Y. Integration of light signals by the retinoblastoma pathway in the control of S phase entry in the picophytoplanktonic cell Ostreococcus. PLoS Genet. 2010;6:e1000957. doi: 10.1371/journal.pgen.1000957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy HA, Kuehne HA, Francis CA, Sniegowski PD. Mate choice assays and mating propensity differences in natural yeast populations. Biol Lett. 2006;2:553–556. doi: 10.1098/rsbl.2006.0534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray DB. The respiratory oscillation in yeast phase definitions and periodicity. Nat Rev Mol Cell Biol. 2006;7 DOI: 10.1038/nrm1980-c2. [Google Scholar]
- Murray DB, Beckmann M, Kitano H. Regulation of yeast oscillatory dynamics. Proc Natl Acad Sci USA. 2007;104:2241–2246. doi: 10.1073/pnas.0606677104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagoshi E, Saini C, Bauer C, Laroche T, Naef F, Schibler U. Circadian gene expression in individual fibroblasts: cell-autonomous and self-sustained oscillators pass time to daughter cells. Cell. 2004;119:693–705. doi: 10.1016/j.cell.2004.11.015. [DOI] [PubMed] [Google Scholar]
- Pikovsky A, Rosenblum M, Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences. New York: Cambridge University Press; 2001. [Google Scholar]
- Robertson JB, Stowers CC, Boczko E, Johnson CH. Real-time luminescence monitoring of cell-cycle and respiratory oscillations in yeast. Proc Natl Acad Sci USA. 2008;105:17988–17993. doi: 10.1073/pnas.0809482105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosbash M. The implications of multiple circadian clock origins. PLoS Biol. 2009;7:e62. doi: 10.1371/journal.pbio.1000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saldanha AJ, Brauer MJ, Botstein D. Nutritional homeostasis in batch and steady-state culture of yeast. Mol Biol Cell. 2004;15:4089–4104. doi: 10.1091/mbc.E04-04-0306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaechter M, Maaløe O, Kjeldgaard NO. Dependency on medium and temperature of cell size and chemical composition during balanced growth of Salmonella typhimurium. Microbiology. 1958;19:592–606. doi: 10.1099/00221287-19-3-592. [DOI] [PubMed] [Google Scholar]
- Scott M, Gunderson CW, Mateescu EM, Zhang Z, Hwa T. Interdependence of cell growth and gene expression: origins and consequences. Science. 2010;330:1099–1102. doi: 10.1126/science.1192588. [DOI] [PubMed] [Google Scholar]
- Shi L, Sutter BM, Ye X, Tu BP. Trehalose is a key determinant of the quiescent metabolic state that fuels cell cycle progression upon return to growth. Mol Biol Cell. 2010;21:1982–1990. doi: 10.1091/mbc.E10-01-0056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi L, Tu BP. Acetyl-CoA induces transcription of the key G1 cyclin CLN3 to promote entry into the cell division cycle in Saccharomyces cerevisiae. Proc Natl Acad Sci USA. 2013;110:7318–7323. doi: 10.1073/pnas.1302490110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silverman SJ, Petti AA, Slavov N, Parsons L, Briehof R, Thiberge SY, Zenklusen D, Gandhi SJ, Larson DR, Singer RH, et al. Metabolic cycling in single yeast cells from unsynchronized steady-state populations limited on glucose or phosphate. Proc Natl Acad Sci USA. 2010;107:6946–6951. doi: 10.1073/pnas.1002422107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slavov N, Airoldi EM, van Oudenaarden A, Botstein D. A conserved cell growth cycle can account for the environmental stress responses of divergent eukaryotes. Mol Biol Cell. 2012;23:1986–1997. doi: 10.1091/mbc.E11-11-0961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slavov N, Botstein D. Coupling among growth rate response, metabolic cycle, and cell division cycle in yeast. Mol Biol Cell. 2011;22:1997–2009. doi: 10.1091/mbc.E11-02-0132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slavov N, Macinskas J, Caudy A, Botstein D. Metabolic cycling without cell division cycling in respiring yeast. Proc Natl Acad Sci USA. 2011;108:19090–19095. doi: 10.1073/pnas.1116998108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohn H-Y, Kuriyama H. Ultradian metabolic oscillation of Saccharomyces cerevisiae during aerobic continuous culture: hydrogen sulphide, a population synchronizer, is produced by sulphite reductase. Yeast. 2001;18:125–135. doi: 10.1002/1097-0061(20010130)18:2<125::AID-YEA655>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- Tu BP, Kudlicki A, Rowicka M, McKnight SL. Logic of the yeast metabolic cycle: temporal compartmentalization of cellular processes. Science. 2005;310:1152–1158. doi: 10.1126/science.1120499. [DOI] [PubMed] [Google Scholar]
- Tu BP, Kudlicki A, Rowicka M, McKnight SL. Let the data speak. Nat Rev Mol Cell Biol. 2006;7 doi: 10.1038/nrm1980. DOI: 10.1038/nrm1980-c3. [DOI] [PubMed] [Google Scholar]
- Wolf J, Sohn HY, Heinrich R, Kuriyama H. Mathematical analysis of a mechanism for autonomous metabolic oscillations in continuous culture of Saccharomyces cerevisiae. FEBS Lett. 2001;499:230–234. doi: 10.1016/s0014-5793(01)02562-5. [DOI] [PubMed] [Google Scholar]
- Young TR, Fernandez B, Buckalew R, Moses G, Boczko EM. Clustering in cell cycle dynamics with general response/signaling feedback. J Theor Biol. 2012;292:103–115. doi: 10.1016/j.jtbi.2011.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.