A Microstructurally Inspired Damage Model for Early Venous Thrombus

Abstract

Accumulative damage may be an important contributor to many cases of thrombotic disease progression. Thus, a complete understanding of the pathological role of thrombus requires an understanding of its mechanics and in particular mechanical consequences of damage. In the current study, we introduce a novel microstructurally inspired constitutive model for thrombus that considers a non-uniform distribution of microstructural fibers at various crimp levels and employs one of the distribution parameters to incorporate stretch-driven damage on the microscopic level. To demonstrate its ability to represent the mechanical behavior of thrombus, including a recently reported Mullins type damage phenomenon, we fit our model to uniaxial tensile test data of early venous thrombus. Our model shows an agreement with these data comparable to previous models for damage in elastomers with the added advantages of a microstructural basis and fewer model parameters. We submit that our novel approach marks another important step toward modeling the evolving mechanics of intraluminal thrombus, specifically its damage, and hope it will aid in the study of physiological and pathological thrombotic events.

1. Motivation

Thrombus plays crucial roles in physiology and pathology. It involves a complex interplay between platelet activity and coagulation, the latter of which depends on the conversion of fibrinogen to fibrin, which in turn is cross-linked by the serine protease thrombin to form a complex, three dimensional mesh. As the fibrin mesh forms, it traps cellular and non-cellular components of the blood that affect the structural integrity and biological activity of the thrombus [1]. If the thrombus is not proteolytically dissolved, it can be remodeled from a fibrin-dominated mesh to a collagen-dominated matrix [2].

Physiologically, formation of thrombus can be an essential step in the well-orchestrated healing response to internal and external insults; it is thus vital to reestablishing hemostasis after injury. Pathologically, thrombus plays a significant role in diseases of the arterial and venous circulation. On the arterial side, thrombus contributes to heart attacks and strokes, and it can be found in most abdominal aortic aneurysms [3, 4]. Of particular note on the venous side, thrombus contributes to deep vein thrombosis (DVT) [5]. In DVT, thrombus forms in the deep veins, usually of the legs, where it may embolize and lead to pulmonary embolism [6]. Embolization, the detachment of whole or partial thrombus, occurs when mechanical forces exceed the strength of the thrombus that in turn depends on its spatially and temporally varying histomechanical properties. Thus, pulmonary embolism, which is responsible for an estimated 60,000 to 100,000 deaths per year in the US alone [7], is at least in parts a mechanical phenomenon. Therefore, we suggest a critical role of thrombus mechanics, specifically thrombus damage mechanics, in the understanding and possibly prediction of DVT and its clinical sequelae.

Despite the important role of thrombus, both as an isolated pathological event and in conjunction with pathologic processes, thrombus mechanics has not received the attention one would expect (see section 2.1). Even more concerning is the lack of data on the failure mechanics of thrombus. Among the few data available, Gasser et al. [8] studied failure properties of intraluminal thrombus retrieved from human abdominal aortic aneurysms and subjected to static and cyclic mechanical loading. They found intraluminal thrombus to be susceptible to damage following repeated loading. They suggested a crucial role of intraluminal thrombus failure in aortic aneurysm rupture, hence emphasizing the broad roles played by thrombus in diverse pathologies.

The apparent lack of data on thrombus mechanics, especially thrombus damage, may be due in part to a lack of sample availability. Most studies have been reported on human thrombus which, for obvious reasons, is not readily available for mechanical testing [9, 10, 11, 12, 13]. Furthermore, human samples necessarily are from mature thrombus. Hence, past reports are limited in their mechanical and histological diversity, which makes the formulation of general models difficult. To overcome these shortcomings, we developed a mouse model to form suitably sized and shaped thrombus samples in vivo [14]. By ligating the inferior vena cava, we successfully created cylindrical samples of thrombus that lend themselves well for mechanical testing. During our first experiments, we explanted thrombi after 2 weeks and studied their mechanical and structural properties. We found that young venous thrombus exhibits distinctly different mechanical behavior from previous reports on mature thrombus, often retrieved from the arterial side [9, 10, 11, 13]. For example, our samples demonstrated a stretch driven failure behavior that has not been reported before.

The goal of this work is to develop a microstructurally inspired constitutive model that provides a flexible framework for the study of thrombus mechanics. We will employ our novel model to describe the mechanical behavior observed in our recent experimental study of early venous thrombus. Furthermore, due to the highlighted importance of thrombus damage mechanics, we will extend our material model to incorporate damage effects observed in the same experiments. Last, we will show that our novel model compares favorably to standard models of material damage developed by Simo and Ogden [15, 16], with the added advantage of fewer material parameters to estimate.

2. Thrombus Material Modeling

2.1. Previous Models of Thrombus Mechanics

One of the first studies on thrombus mechanics dates back to Di Martino and colleagues who performed uniaxial tensile tests on intraluminal thrombus from human abdominal aortic aneurysms [13]. They assumed that thrombus exhibits an isotropic linearly elastic behavior and identified a Young’s modulus and Poisson’s ratio. Since at least the study by Vorp et al. [17], however, we know that thrombus may exhibit a mildly nonlinear response over finite strains in vivo. To overcome limitations of Di Martino’s model, Wang et al. [18, 19] extended the description of thrombus to finite elasticity. Based again on uniaxial tensile data, they proposed a hyperelastic model for both the luminal and medial regions of human intraluminal thrombus retrieved from aortic aneurysms. Their isotropic strain energy is written as a linear function of the second invariant of the left Cauchy-Green tensor. Vande Geest et al. [11] further tested similar thrombus samples under biaxial extension. Based on their data, a hyperelastic constitutive relation was written as a second order polynomial, also of the first invariant of the left Cauchy-Green tensor. This model has since been used in finite element analyses of aneurysm mechanics [20]. One of the most comprehensive studies to date is that of Tong et al. [9]; they fit an anisotropic Fung-type hyperelastic model to biaxial data from the different layers of aneurysmal thrombus and suggested that such layers exhibit “aging” characteristics [21].

Thrombus has also been modeled using approaches other than linear and nonlinear elasticity. For example, Van Dam et al. [22, 23] modeled thrombus as viscoelastic based on shear experiments performed on samples from human aortic aneurysms. Thrombus has also been modeled as poroelastic; Polzer et al. [24] employed a poroelastic model to study the influence of intraluminal thrombus on wall stress in abdominal aortic aneurysms.

Whether modeled as elastic, viscoelastic, and poroelastic, of particular importance here is the need to account for the apparent cycle-dependent damage that could compromise the structural integrity of thrombus and lead to adverse mechanical and biological effects on the underlying vascular wall and downstream organs. Moreover, our review of the literature revealed that all prior models of thrombus have been phenomenological and, with the exception of Karsaj et al. [25], no attempts have been made to model thrombus at times prior to advanced maturity or during its “development”. Thus, there is a clear need for models that consider the microstructure and account for the evolving mechanical properties with age and damage; ultimately, there is also a need to characterize differences in thrombus mechanics depending on its source, arterial versus venous and intraluminal versus intramural or extravascular.

2.2. Experimental Methodology

We evaluate our new model using prior uniaxial tensile test data on early intraluminal venous thrombus [14]. The cylindrical samples were harvested from a mouse model and lend themselves well for mechanical testing. This section serves as a brief summary of the associated surgical and experimental procedures, but we refer the reader to the original paper for details.

Briefly, the inferior vena cava was isolated under sterile surgery in 8–16 week old C57BL/6J mice, and ligated just below the renal veins to initiate the formation of a cylindrical thrombus. We harvested five thrombi two weeks after the intervention by explanting the IVC and separating the vessel and thrombus. Length and diameter were measured before attaching the sample to the testing fixture. Using our custom, computer-controlled tensile testing system [26], each sample underwent a preconditioning cycle consisting of loading and unloading to 10g, after which the unloaded configuration was recorded. Following preconditioning, we loaded each sample twice to a load of 1g, then to 2g, and so forth up to a 10g maximum load.

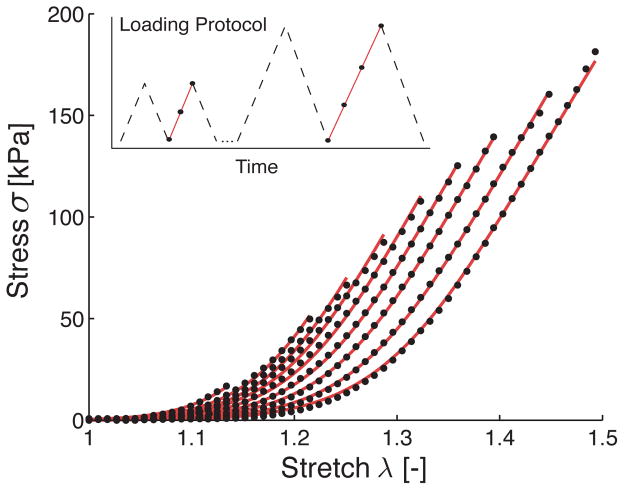
Both the loading protocol and the results for a representative sample are shown in Figure 1, which shows only the upstroke of the second cycle. Two particular characteristics of these uniaxial data stand out. First, early thrombus experience large deformations with a distinctly flat pre-toe region and a remarkably linear post-toe region. Second, the material response shifts along the λ-axis with each consecutive load cycle. The latter damage phenomenon will be discussed in detail in section 3.

Figure 1.

Data for a representative sample undergoing uniaxial extension (black circles) and fit of the proposed model for thrombus (continuous line). While fitting the model to all load curves simultaneously, the parameters μ₀, μ₁, β and γ were held constant for all load curves and only δ was allowed to change with each load curve. Only the second upstroke of the recorded data is shown as indicated in the loading protocol graph.

As in Figure 1, the subsequent mechanical analysis focuses on the upstroke of the second load cycle, at each loading increment, and we assume for modeling purposes that the material exhibits an elastic material behavior at each load level, thus ignoring hysteresis, cyclic softening, and permanent set.

2.3. Microstructurally Inspired Material Model for Thrombus

In the subsequent sections, we introduce a strain energy function and associated damage model to provide a flexible framework for studying thrombus mechanics. Based on its fibrous microstructure, we postulate the existence of a strain energy function 𝒲 of the general form:

$$\mathcal{W}={\mathcal{W}}_g(\mathit{C})+{\int }_S\phi (\mathrm{\Theta },\mathrm{\Phi }){\mathcal{W}}_f(\mathit{C},\mathit{N}(\mathrm{\Theta },\mathrm{\Phi }))\mathrm{d}A-p(J-1),$$ (1)

where C = F^TF is the right Cauchy-Green tensor and J the Jacobian, J = detF. 𝒲_g represents the material behavior of a ground substance matrix and 𝒲_f the behavior of fibers distributed according to the function φ(Θ, Φ) with orientation vectors N(Θ, Φ), where Θ, Φ are azimuthal and polar angles of a spherical coordinate system, respectively. The total strain energy is thus the sum of that for the ground substance and all fiber families integrated over the surface of the unit sphere, S. Furthermore, based on an ultrasonic study of thrombus [17], we assume incompressibility, enforced through the Lagrange multiplier p, which does not coincide with the hydrostatic pressure.

For the following analysis, we specialize 𝒲_f to be active only in the loading direction, N = [1, 0, 0]^T. Hence, the above equation simplifies to:

$$\mathcal{W}={\mathcal{W}}_g(\mathit{C})+{\mathcal{W}}_f(\mathit{C},\mathit{N})-p(J-1).$$ (2)

The specific form of 𝒲_f is based on the observation that individual microstructural fibers exist at various crimp levels. Thus, each fiber starts contributing to the stored energy at different recruitment stretches λ_s, whereby

$${\mathcal{W}}_f=\int \rho ({\lambda }_s){\mathcal{W}}_0(\mathit{C},\mathit{N},{\lambda }_s)\mathrm{d}{\lambda }_s.$$ (3)

Practically, equation (3) implies that the strain energy of the fibrous mesh is determined by the convolution of the distribution function of the fiber recruitment stretch ρ(λ_s) and the strain energy function 𝒲₀ of individual straight fibers. The distribution of the fiber recruitment stretch ρ(λ_s) is assumed as the well-known Weibull probability density function

$$\rho ({\lambda }_s)=\frac{\beta }{\delta }{\left(\frac{{\lambda }_s-\gamma }{\delta }\right)}^{\beta -1}exp\left[-{\left(\frac{{\lambda }_s-\gamma }{\delta }\right)}^{\beta }\right],$$ (4)

which is specified by a shape parameter β ∈ [1, ∞), a scale parameter δ ∈ (0, ∞) and a location parameter γ ∈ (0, ∞). For more information on the influence of these parameters, see [27, 28]. Here, we assume further that individual fibers behave elastically according to a neo-Hookean type relation:

$${\mathcal{W}}_0(\mathit{C})={\mu }_1({\overline{\lambda }}^2+2{\overline{\lambda }}^{-1}-3),\text{where}\overline{\lambda }=\lambda /{\lambda }_s,\text{and}\lambda =\sqrt{\mathit{C}:\mathit{N}\otimes \mathit{N}}.$$ (5)

In equation (5), the strain energy of the individual fiber is governed by the effective stretch λ̄, with 𝒲₀(λ̄ ≤ 1) = 0. Thus, each fiber only contributes to the strain energy when the material stretch exceeds the recruitment stretch of the individual fiber. This approach is consistent with multiplicative kinematics, where the total fiber stretch λ results from a sequential mapping from the crimped state to an uncrimped, stress free state according to λ_s and from the uncrimped state to the stretched state according to λ̄ [29, 30, 31].

Similar to the uncrimped fibers, we assume the ground substance behaves according to a neo-Hookean relation, but with a different shear modulus:

$${\mathcal{W}}_g(\mathit{C})={\mu }_0(I_1-3),\text{where}{I}_1=\text{tr}\mathit{C}.$$ (6)

The 2nd Piola-Kirchhoff stress tensor S follows from S = 2∂𝒲/∂C:

$$\mathit{S}=2{\mu }_0\mathit{I}+2{\mu }_1{\lambda }^{-2}{\int }_{\gamma }^{\lambda }\rho ({\lambda }_s)({\overline{\lambda }}^2-{\overline{\lambda }}^{-1})\mathrm{d}{\lambda }_s\mathit{N}\otimes \mathit{N}-p{\mathit{C}}^{-1},$$ (7)

where I is the identity tensor. Given the assumption of traction-free boundary conditions on the lateral surface of the sample under uniaxial tension, the stress in loading direction can be written as:

$$S=2{\mu }_0(1-{\lambda }^{-3})+2{\mu }_1{\lambda }^{-2}{\int }_{\gamma }^{\lambda }\rho ({\lambda }_s)({\overline{\lambda }}^2-{\overline{\lambda }}^{-1})\mathrm{d}{\lambda }_s.$$ (8)

Remark 1

In general, the spatial Cauchy stress may be obtained through the push-forward operation on S, σ = χ_*(S) = J⁻¹FSF^T. In the simple case of uniaxial extension of an incompressible material, the Cauchy stress in loading direction is defined through σ= λ²S.

3. Thrombus Damage Modeling

As can be observed for a representative sample in Figure 1, even after preconditioning, early venous thrombus undergoes progressive damage with increasing stretch, which was consistent among all five samples. While this behavior is, in the strict sense, not a Mullins effect, which describes damage accrued in elastomers during initial loading [32], these thrombus data are remarkably similar. In the following section we introduce a novel model for quantifying the damage phenomenon observed in our experimental data. Because of the similarity to Mullins effect, we will in the end compare our damage model to well-known models of Mullins effect in elastomers.

3.1. Experimental Observations

To model the progressive damage observed in our experimental data, we let one of the recruitment stretch distribution parameters capture the load history of the material. To test the scale parameter δ as a potential candidate, we fit our material model to all curves simultaneously holding μ₀, μ₁, β and γ constant, while δ was allowed to vary. With this constraint, we used nonlinear regression to identify an optimal parameter set to model the uniaxial tensile behavior of each thrombus sample. As illustrated in Figure 1, even under the given constraint, our proposed material model achieves excellent agreement between measured and predicted stresses. It is noted further that previously suggested polynomial and exponential hyperelastic material models for thrombus failed to reproduce the flat pre-toe region and the linear post-toe region of the individual load curves adequately (results not shown) [9, 11].

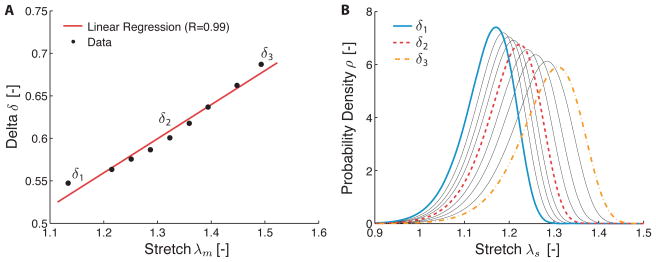
Figure 2A illustrates the “evolution” of the parameter δ with the previously experienced maximum stretch, that is, λ_m(t) = max_{s∈(−∞,t]} λ(s). As can be seen in the same figure, δ may be approximated linearly in terms of the experienced maximum stretch. The behavior shown was consistent across all samples, with an average R value for the linear fits of 0.99. Thus, δ captures well the load history of the material and we will take advantage of this property in the next section when we propose a microstructurally inspired damage model for thrombus. The recruitment stretch distribution function corresponding to the δ values are shown in Figure 2B. From a structural standpoint, it can be noted that with increasing damage, the recruitment stretch distribution shifted toward higher stretches, with a larger variance and a skew to the right.

Figure 2.

A) Evolution of the scale parameter δ of the recruitment stretch distribution function (cf. equation (4)), with the previously experienced maximum stretch λ_m. B) Recruitment stretch distribution functions corresponding to values of δ shown in A.

3.2. Microstructurally Inspired Damage Model for Thrombus

The damage model builds on the constitutive model introduced in section 2.3, but with an alternative strain energy function 𝒲(C, δ), where δ(λ_m) is the scale parameter of the Weibull function ρ(λ_s). Furthermore, we introduce the damage criterion Ψ(λ, λ_m) = λ − λ_m ≤ 0. Thus, as the current stretch λ achieves the previously experienced maximum stretch λ_m, we let λ_m = λ. Based on the behavior in Figure 1A, we further introduce an evolution equation for the damage parameter δ of the form:

$$\delta ({\lambda }_m)=c_1+c_2{\lambda }_m,$$ (9)

where c₁ and c₂ come directly from the observed linear relationship in Figure 1A.

To derive the expression for the 2nd Piola-Kirchhoff stress, we recall the isothermal Clausius-Duhem inequality [33]:

$$-{\rho }_0\stackrel{.}{\psi }+\mathit{S}:\frac{1}{2}\stackrel{.}{\mathit{C}}\ge 0.$$ (10)

Here ψ̇ is the material derivative of the Helmholtz potential per unit mass and the second term is the rate of internal mechanical work or “stress power”. Given that

$${\rho }_0\stackrel{.}{\psi }=\stackrel{.}{\mathcal{W}}(\mathit{C},\delta )=\frac{\partial \mathcal{W}(\delta )}{\partial \delta }\frac{\mathrm{d}\delta }{\mathrm{d}t}+\frac{\partial \mathcal{W}(\mathit{C})}{\partial \mathit{C}}:\frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}=\frac{\partial \mathcal{W}}{\partial \delta }\stackrel{.}{\delta }+2\frac{\partial \mathcal{W}(\mathit{C})}{\partial \mathit{C}}:\frac{1}{2}\stackrel{.}{\mathit{C}},$$ (11)

then (10) requires:

$$-\frac{\partial \mathcal{W}}{\partial \delta }\stackrel{.}{\delta }+\left(\mathit{S}-2\frac{\partial \mathcal{W}(\mathit{C})}{\partial \mathit{C}}\right):\frac{1}{2}\stackrel{.}{\mathit{C}}\ge 0.$$ (12)

Sufficient conditions for satisfying this relation for all δ and all C are:

$$-\frac{\partial \mathcal{W}}{\partial \delta }\stackrel{.}{\delta }\ge 0\text{and}\mathit{S}=2\frac{\partial \mathcal{W}(\mathit{C})}{\partial \mathit{C}}.$$ (13)

In the dissipation inequality, −part;𝒲/∂δ denotes the thermodynamic force that drives the damage evolution [34]. With the material model introduced in the previous section for the 2nd Piola-Kirchhoff stress for the uniaxial extension of an incompressible, anisotropic material, the uniaxial state of stress is given by:

$$S=2{\mu }_0(1-{\lambda }^{-3})+2{\mu }_1{\lambda }^{-2}{\int }_{\gamma }^{\lambda }\rho ({\lambda }_s,\delta ({\lambda }_m))({\overline{\lambda }}^2-{\overline{\lambda }}^{-1})\mathrm{d}{\lambda }_s.$$ (14)

Remark 2

For the explicit form of 𝒲 chosen in section 2.3, the condition 𝒟_int = −∂𝒲/∂δ δ̇ ≥ 0 is trivially satisfied within the integration limits, given a positive evolution of the damage parameter δ.

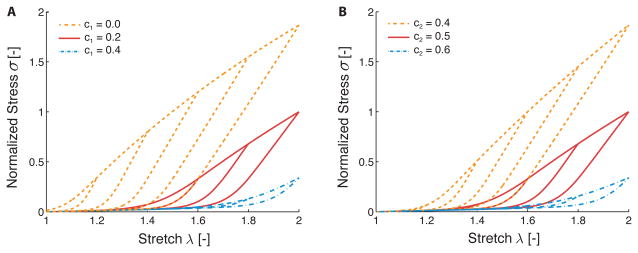
The sensitivity of the predicted response to the damage parameters c₁ and c₂, equation (9), is demonstrated in Figure 3A and 3B, respectively. Damage parameter c₁ shifts the stress response along the λ-axis; damage parameter c₂ changes the slope of the stress response during primary loading. These differences are subtle, however.

Figure 3.

A) Effect of varying damage parameter c₁. Increasing c₁ shifts the predicted stress response along the λ-axis to the right, while decreasing c₁ shifts the stress response along the λ-axis to the left. B) Effect of varying damage parameter c₂. Increasing c₂ decreases the stiffness of the material during primary loading, while decreasing c₂ increases the stiffness of the material during primary loading.

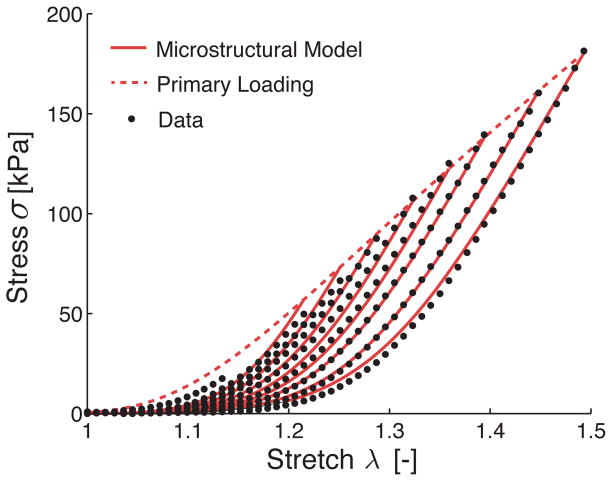
To test the damage model, we used the same experimental data for the uniaxial extension of early venous thrombus, see Figure 1A. Hence, we determined simultaneously, via nonlinear regression of the data, the remaining baseline model parameters μ₀, μ₁, β, γ and the newly introduced damage parameters c₁, c₂. As can be seen in Figure 4 the damage model predicted the evolving stress well, with the exception of stresses at low stretch during the primary loading, where the damage model overestimated the material response. The good agreement between predicted stresses and experimental stresses observed in Figure 4 was consistent across all samples as reflected in an average adjusted R² of 0.997, see Table 1.

Figure 4.

Fit of the proposed microstructurally inspired damage model to experimental data on the uniaxial extension of early venous thrombus. Shown here is the representative data set introduced earlier. The proposed model shows a good qualitative fit with the experimental data (μ₀ = 0.0037 kPa, μ₁ = 180.59 kPa, β = 5.27, γ = 0.92, c₁ = −0.34, c₂ = 0.50).

Table 1.

Identified material parameters, adjusted R² and residual norms for the proposed microstructurally inspired damage model (Micro), the Simo damage model (Simo), and the Ogden damage model (Ogden). Values are arithmetic means for n = 5 samples. Note that the parameter δ in the microstructural model is represented by its damage parameters c₁ and c₂, through δ = c₁ + c₂λ_m.

Micro	μ0 [kPa]	μ1 [kPa]	β	δ	γ	c1	c2	R̃2	norm [MPa]
	0.41	225.93	5.53	-	0.97	−0.29	0.42	0.997	1.05
Simo	μ0 [kPa]	μ1 [kPa]	β	δ	γ	α1	α2	R̃2	norm [MPa]
	9.40	2529.37	3.93	0.44	0.96	1.48	0.05	0.996	1.30
Ogden	μ0 [kPa]	μ1 [kPa]	β	δ	γ	m	r	R̃2	norm [MPa]
	12.10	406.90	4.73	0.54	0.96	1.00	20.71	0.987	5.48

3.3. Comparison With Previous Damage Models

Since the load-induced damage of early venous thrombus resembled the well-known Mullins effect, we compared our model with two established models from the elastomer literature, both based upon phenomeno-logical approaches [15, 16]. First, we considered the Simo model, a continuous damage approach employing the concept of equivalent stress [35, 36, 37]. Second, we considered the Ogden model, which employs the concept of pseudoelasticity [38, 39, 40, 41]. For both approaches we list only the most fundamental equations; details on the origin and derivation of these equations can be found in the original publications.

Briefly, Simo proposed a damage model with a modified strain energy function 𝒲:

$$\mathcal{W}(\mathit{C},D)=(1-D){\mathcal{W}}^0(\mathit{C})=\overline{g}{\mathcal{W}}^0(\mathit{C}),$$ (15)

where D ∈ [0, 1] is referred to as a damage parameter. Following the same line of reasoning as in equation (12),

$$\mathit{S}=2\overline{g}\frac{\partial {\mathcal{W}}^0(\mathit{C})}{\partial \mathit{C}}.$$ (16)

Simo also introduced an “equivalent” strain Ξ_m and a particular form of the “reduction” function ḡ(Ξ_m):

$${\mathrm{\Xi }}_m=\underset{s\in (-\infty ,t]}{max}\sqrt{2{\mathcal{W}}^0(\mathit{C}(s))},\overline{g}({\mathrm{\Xi }}_m)={\alpha }_1+(1-{\alpha }_1)\frac{1-exp(-{\mathrm{\Xi }}_m/{\alpha }_2)}{{\mathrm{\Xi }}_m/{\alpha }_2},$$ (17)

where α₁ and α₂ are given parameters and we chose 𝒲 from equation (2) for 𝒲⁰.

In contrast, Ogden used the theory of pseudoelasticity, which is based on the existence of a pseudo-energy function:

$$\mathcal{W}(\mathit{C},\eta )=\eta \stackrel{\sim }{\mathcal{W}}(\mathit{C})+\varphi (\eta ),$$ (18)

where ϕ(η) is a damage function. The value of η is implicitly defined through the condition ∂𝒲/∂η = 0. In contrast to Simo, and the model proposed herein, the material is governed by the strain-energy function 𝒲̃ during the primary loading of the material, where η = 1. Once, the material is unloaded, η takes the alternative form:

$$\eta =1-\frac{1}{r}\text{erf}\left(\frac{1}{m}({\mathcal{W}}_m-\stackrel{\sim }{\mathcal{W}}(\mathit{C}))\right),$$ (19)

where r and m are given parameters and 𝒲_m is the largest previously experienced value of 𝒲̃. The stress simply follows from:

$$\mathit{S}=2\eta \frac{\partial \stackrel{\sim }{\mathcal{W}}(\mathit{C},\eta )}{\partial \mathit{C}}.$$ (20)

As for the Simo model, for the calculations herein we chose for 𝒲̃ to take the form of our material model.

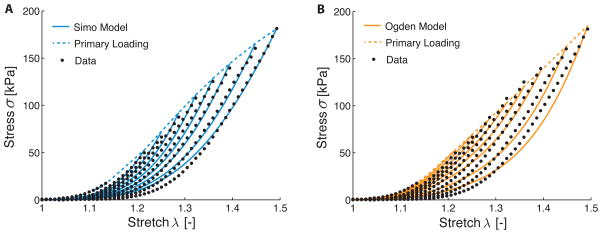
Figure 5A and 5B show the fit of both the Simo model and the Ogden model to the representative experimental data, respectively. Both models show excellent qualitative agreement. Quantitatively, we also compared the three damage models by fitting each to the uniaxial tensile data of all five available samples; average material parameters, average adjusted R² values, and residual norms are given in Table 1. As can be seen from the R̃², all three models represented the experimental data well (values of 0.997, 0.996, and 0.987 were obtained for our model, the Simo model, and the Ogden model, respectively). However, a comparison of the norm of the calculated residuals revealed that the model proposed herein gave the best fit, followed closely by the Simo model and the Ogden model.

Figure 5.

Fit of the phenomenological damage models proposed by Simo (A) and Ogden (B) to experimental data on the uniaxial extension of early venous thrombus (solid lines). Shown here is the representative data set introduced earlier (black circles). Both models show a good qualitative fit with the experimental data.

Note that the fitting procedure for the Ogden model differs from that of our model and the Simo model. Rather than finding all material parameters simultaneously, the unmodified strain energy function 𝒲̃ was fit to the primary loading curve first for the Ogden model, before the damage parameters m and r were fit to the individual load curves.

4. Discussion

We sought to develop a microstructurally inspired constitutive framework for studying the mechanics of damage evolution in early venous thrombus. Although we evaluated many different possible models and approaches, the model proposed herein was motivated by the observation that the microstructure of thrombus is dominated by fibers, both collagen and fibrin, at various levels of crimp or folding [42, 43]. Consequently, each fiber experiences an effective stretch that depends on the tissue-level stretch and its individual recruitment stretch. To incorporate this observation, we postulated the existence of a strain energy function that accounts for the energy stored in each fiber following its recruitment at an individual effective stretch. The distribution of fibers at various levels of crimp was described by a well-known Weibull distribution, while the strain energy of the individual fibers was modeled assuming a neo-Hookean behavior.

Similar models have been proposed for anisotropic soft tissues such as ligament, tendon, and skin [27, 28, 44]. In contrast to previous models, however, we employed an approach previously suggested by Gasser [45], in which one of the distribution parameters is used to describe the damage. The evolution equation of our damage parameter is based on our experimental observations and those by Münster et al. [42] on the damage of individual fibers in fibrin and collagen meshes. They found that each fiber exhibits a non-recoverable elongation upon loading on the microscopic level. The proposed damage model fit the experimental data well, comparable to that by previous models but with the added advantages of one less model parameter and a microstructural motivation [15, 16]. Specifically, in our model the scale parameter δ carries information on the load history of the material. Its evolution may therefore be interpreted as a shift of the recruitment stretch distribution toward higher values and increased dispersion reflecting damage on the individual fiber level.

There were few limitations associated with the current study. Even though the current model has been tested for early occlusive thrombus, there is no theoretical limitation for its general use in thrombus modeling. For the present purposes, however, we made one significant simplification. Rather than modeling the fiber orientation to be randomly distributed, we assumed that all fibers had a predominant direction. This assumption seems justified in the light of reports that the microstructure of fibrous meshes, even at very low strain, reorient readily toward the primary loading direction [43]. Furthermore, since we assumed that fibers can only resist tensile forces, and thus do not contribute to the total strain energy under compression, fibers orthogonal to the loading direction may be excluded from the strain energy calculation per se. Further generalizations are possible, as demanded by data. It is also worth noting that all thrombus samples underwent preconditioning before testing, as reported in section 2.2. Thus, the model parameters reported in Table 1 may be different for unconditioned samples. The goal of our preconditioning protocol was to minimize inconsistent load-history effects associated with excision and mounting of the sample and thereby to establish consistent in vivo-like conditions before testing. Thus, we believe the reported properties are more likely to represent the in vivo mechanical behavior of thrombus than non-preconditioned samples would have.

In conclusion, we emphasize that the data described herein on early venous thrombus (2 weeks of formation) differ significantly from the majority of related data in the literature, which stem from intraluminal thrombus harvested from human abdominal aortic aneurysms [13, 18, 11], which undoubtedly reflect years of development. In particular, our data show a flat pre-toe region and a distinct damage pattern with increasing stretch. Interestingly, both of these characteristics have been reported for non-cross-linked fibrin and collagen meshes [42]. Given the importance of deep vein thrombosis, and its devastating clinical sequelae, most notably pulmonary embolism, the present findings provide unique and potentially important insight. Nevertheless, there is a pressing need for future work to focus on detailed microstructural characterization, mechanical testing, and modeling of thrombus ranging from venous to arterial and early to aged so that damage models can be developed that have the widest range of applicability or intentional specificity possible.