GENESIS: a hybrid-parallel and multi-scale molecular dynamics simulator with enhanced sampling algorithms for biomolecular and cellular simulations

Abstract

GENESIS (Generalized-Ensemble Simulation System) is a new software package for molecular dynamics (MD) simulations of macromolecules. It has two MD simulators, called ATDYN and SPDYN. ATDYN is parallelized based on an atomic decomposition algorithm for the simulations of all-atom force-field models as well as coarse-grained Go-like models. SPDYN is highly parallelized based on a domain decomposition scheme, allowing large-scale MD simulations on supercomputers. Hybrid schemes combining OpenMP and MPI are used in both simulators to target modern multicore computer architectures. Key advantages of GENESIS are (1) the highly parallel performance of SPDYN for very large biological systems consisting of more than one million atoms and (2) the availability of various REMD algorithms (T-REMD, REUS, multi-dimensional REMD for both all-atom and Go-like models under the NVT, NPT, NPAT, and NPγT ensembles). The former is achieved by a combination of the midpoint cell method and the efficient three-dimensional Fast Fourier Transform algorithm, where the domain decomposition space is shared in real-space and reciprocal-space calculations. Other features in SPDYN, such as avoiding concurrent memory access, reducing communication times, and usage of parallel input/output files, also contribute to the performance. We show the REMD simulation results of a mixed (POPC/DMPC) lipid bilayer as a real application using GENESIS. GENESIS is released as free software under the GPLv2 licence and can be easily modified for the development of new algorithms and molecular models. WIREs Comput Mol Sci 2015, 5:310–323. doi: 10.1002/wcms.1220

INTRODUCTION

In 1977, McCammon, Gelin, and Karplus carried out the first molecular dynamics (MD) simulation of a protein.¹ Initially, simulations were carried out for a single protein in vacuum. Since the late 1980s, MD simulations of a protein in explicit water have been possible because of the speedup of computers and advances in MD methodologies.^2,3 Currently, not only soluble proteins but also membrane proteins in explicit lipid bilayers^4–6 and protein/nucleic acid complexes like ribosomes or RNA polymerases^7–9 are routinely subjected to MD simulations. Long MD simulations of various biomolecules are possible using highly optimized and parallelized MD software packages (like CHARMM,^10,11 AMBER,¹² NAMD,¹³ GROMACS,¹⁴ and others^15–17) on different computational platforms. However, on currently available general-purpose supercomputers¹⁸ or accelerators like graphics-processing units (GPUs),¹⁹ the MD simulation length is typically limited to 10–100 µs, which is shorter than many biologically relevant processes. The development of MD-special purpose computers such as MDGRAPE^20,21 or Anton/Anton 2^22,23 has allowed an expansion to miliseconds, although the maximum number of particles.²⁴ Note that reliable simulations require not only good sampling statistics but also accurate force field models, where much progress has been made recently as well.^25–27

In this Software Focus, we introduce a new package for MD simulations of biomolecules, which we call GENESIS (Generalized-Ensemble Simulation System). The main motivation for the development of GENESIS in spite of many already existing MD programs is to perform efficient all-atom MD simulation of very large biomolecular systems on general-purpose supercomputers. We believe that one of the future applications of MD simulations involves biomolecules under more realistic cellular environments, such as the cytoplasm, organelles, viruses, biological membranes, and nuclei. In the cytoplasm, a huge number of proteins, RNAs, other macromolecules as well as metabolites co-exist and function. To examine the effect of macromolecular crowding^28–30 on protein structures and dynamics with all-atom MD simulations, at least 10–100 million atoms in a simulation box are required. To make such large-scale all-atom MD simulations being available, we have developed several efficient computational schemes, namely, the inverse lookup table method,³¹ the midpoint cell method³² both for short-range real-space nonbonded calculations, and the efficient parallelization of three-dimensional (3D) Fast Fourier Transform (FFT)³³ for long-range reciprocal-space calculations (Jung et al., unpublished data) in the particle mesh Ewald (PME) method.^34,35 In addition, we utilized OpenMP thread-based parallelization for the communication within a multicore CPU and message-passing interface (MPI) for the communication between different CPUs. This hybrid (MPI + OpenMP) parallelization scheme has become more and more popular in high-performance computing software that runs on modern multicore architectures.

The second key motivation in GENESIS development is to provide a platform for testing new enhanced conformational sampling algorithms or multi-scale/multi-resolution models. To overcome the time-scale gap between MD simulations and experiments, these two have been widely recognized as important approaches in the community of computational biophysics and biochemistry.^36–46 Our own contributions consist of replica-exchange MD (REMD),⁴⁷ multi-canonical REM (MUCAREM),⁴⁸ replica-exchange umbrella sampling⁴⁹ (REUS, this method is also referred to as Hamiltonian REMD⁵⁰ or window-exchange REMD⁵¹), multi-dimensional REMD (MREMD),⁴⁹ and surface-tension REMD (γ-REMD and γT-REMD).⁵² Many of these methods were developed in collaboration with Yuko Okamoto. In GENESIS, these enhanced sampling simulations are available along with the high performance MD code based on all-atom/Go-like models^43,53–56 for standard NVT, NPT, NPAT, or NPγT ensembles.⁵⁷ The source code of GENESIS is written using the modern Fortran language and released to the community as free software under the GPLv2 licence. Therefore, new sampling methods and molecular models can be easily added by other users.

This paper as Software Focus is organized as follows. First, the software design of GENESIS package and the functions in the two MD simulators (ATDYN and SPDYN) are introduced. Second, high-performance aspects of GENESIS are described in detail. A key aspect is the combination of the midpoint cell method with an efficient parallelization of the 3D FFT method. The hybrid parallelization schemes in ATDYN and SPDYN are also outlined. The implementation of various REMD schemes for the NVT, NPT, NPAT, and NPγT ensembles in GENESIS is described next. Then, we briefly introduce the basic usage of GENESIS and the input/output files and their formats. One of special features in GENESIS is the option of parallel input/output files for simulations of extremely large systems (>10 million atoms). In the last section, we show performance benchmarks for all-atom MD simulations using GENESIS on a PC-cluster and K computer in RIKEN in comparison with other MD packages. Simulations of a mixed (POPC/DMPC) lipid bilayer using MD, REMD, γ-REMD, and γT-REMD methods are shown as an example of a real application with GENESIS.

SOFTWARE DESIGN OF GENESIS

Two MD Simulators: ATDYN and SPDYN

GENESIS consists of two MD simulators, namely ATDYN (ATomic decomposition DYNamics) and SPDYN (SPatial decomposition DYNamics), as well as various analysis and setup tools. ATDYN is designed for all-atom MD simulations based on molecular force-field parameters²⁶ and coarse-grained (CG) MD simulations based on Go-like models^43,53–56 under periodic and nonperiodic boundary conditions. ATDYN is parallelized based on an atomic decomposition scheme with hybrid parallelization using a replicated-data MD algorithm. Although this implementation is less efficient than SPDYN or other domain decomposition schemes, its advantages are (1) easy modification of source codes for testing new sampling methods and multi-scale models and (2) a good load balance for nonperiodic CG MD simulations. Unlike ATDYN, SPDYN uses a spatial decomposition scheme, where the simulation space is divided into subdomains and cells and a distributed-data MD algorithm is used. Each processor contains information on the atoms assigned to each subdomain. As this scheme requires less communication between processors, the parallel efficiency of SPDYN is much better than that of ATDYN.

Both simulators implement PME,^34,35 and we use FFTE⁵⁸ for the 3D FFT, which is also parallelized based on a hybrid parallelization scheme. In the current version of GENESIS, only the CHARMM force-fields²⁶ (CHARMM19,⁵⁹ CHARMM22/CMAP,^60,61 CHARMM27,⁶² CHARMM36,^63,64 and CHARMM37⁶⁵) are available in both simulators. The simulations based on Go-like models utilize the CHARMM input generated by the MMTSB web site.^66,67 Other force fields are now being implemented and will be available in the next version. As for enhanced conformational sampling methods, REMD simulations are available in both ATDYN and SPDYN. Analysis tools in GENESIS provide basic structural parameters such as distances, angles, RMSDs, and so on, as well as some advanced analysis functions like principal component analysis (PCA)⁶⁸. The usage of GENESIS for MD and REMD simulations is described in later sections and the users' manual.

Acceleration and Parallelization

Inverse Lookup Table

The major bottleneck in MD is the calculation of nonbonded interactions due to van der Waals (vdW) and electrostatic terms. In the PME method,^34,35 the most time-consuming calculations involve inverse square roots and complementary error functions. Various MD programs utilize lookup tables for energy and gradient evaluation instead of a direct calculation.^69,70 GENESIS employs a novel lookup table algorithm based on the inverse of the square distance, which we call “inverse lookup table”.³¹ In this approach, the spacing of table entries is decided from the inverse of the squared pair distances. Compared to the lookup table approach in other program,⁷⁰ the “inverse lookup table” approach makes use of larger number of table entries at short pair distances and less number of table entries for larger pair distances. Because the vdW energy changes rapidly at short pair distances, a lot of table entries at short distances improve the accuracy and allow fewer table entries to achieve the same accuracy as in other programs. The computation of nonbonded interactions based on our inverse lookup table is fast due to a small number of points used for 90% of nonbonded interactions in an MD simulation.³¹ For example, let us consider a system with 23,000 atoms and a 12 Å cutoff for nonbonded interactions. Under the assumption of the same total number of table entries, the inverse lookup table uses only 1/30 of the table points for the pairwise distance interval of [6 Å, 12 Å] compared to the lookup tables implemented in the CHARMM program.⁷⁰ Because the distance interval of [6 Å, 12 Å] includes 88% of nonbonded interactions, the inverse lookup table uses much fewer table entries for calculating short-range interactions. This results in fewer L1 cache misses. In benchmarks on K computer,⁷¹ the inverse lookup table improves the performance of nonbonded interactions by up to a 20% speed-up compared to a conventional distance-squared lookup table.³¹

Parallelization of ATDYN

The hybrid parallelization of ATDYN is based on the replicated-data MD algorithm where each MPI processor has a copy of atomic coordinates, velocities, atomic charges, and so on.^72,73 It starts from a proper distribution of do-loops according to MPI and OpenMP thread numbers. We first assign identification numbers (id) to MPI processors and OpenMP thread ranks. Let us assume that the total number of MPI process is N_MPI, and the number of OpenMP threads in one MPI process is N_THREAD. Here, N_MPI and N_THREAD are decided such that N_MPI × N_THREAD is identical to the total number of CPU cores used. In each core, id is defined as id = id_MPI × N_THREAD + id_THREAD where the MPI process rank (id_MPI) and the thread rank (id_THREAD) are automatically decided. Bonded indices are divided into N_MPI × N_THREAD blocks and each block is assigned to each CPU core. Nonbonded interactions are parallelized, distributing atom indices according to ids. For each i-th atom, we perform nonbonded calculations on each core only when the remainder after dividing i by N_MPI × N_THREAD is equal to id of the core. For the parallelization of reciprocal-space interaction in the PME method,^34,35 the pencil decomposition scheme of FFT is considered. For this purpose, we make use of the FFTE implementation⁵⁸ because of its efficient hybrid parallelization scheme. In the computation, potential energies in real space (bond, angle, dihedral angle, improper torsion angle, and nonbonded interactions terms) and in reciprocal space could be computed separately on different MPI processors to increase parallel efficiency. The basics of parallelization in the replicated-data MD with PME is described in Ref. 73. After calculating the real-space and reciprocal-space interactions, forces are accumulated by reduction communication. In ATDYN, increasing OpenMP threads within a CPU reduces the MPI communication time and thereby accelerates the MD simulations.

Parallelization of SPDYN

SPDYN is designed for large-scale MD simulations using an efficient hybrid parallelization scheme to match recent hardware trends toward multi-core architectures. In the spatial decomposition scheme, the simulation space is divided into subdomains according to the number of MPI processors (Figure 1(a)). Here, the subdomain size in each dimension is greater than or equal to the cutoff distance of nonbonded interactions. Subdomains are further divided into smaller cells. The cell size of each direction is greater than or equal to half of the cutoff distance. Interactions between particles are distributed over OpenMP threads according to cell pairs for shared-memory parallelization. For efficient cache usage, particle data are sorted according to cell indices. Unlike ATDYN, each processor only contains information of the corresponding subdomain and the buffer region surrounding the subdomain (distributed-data MD algorithm).

FIGURE 1.

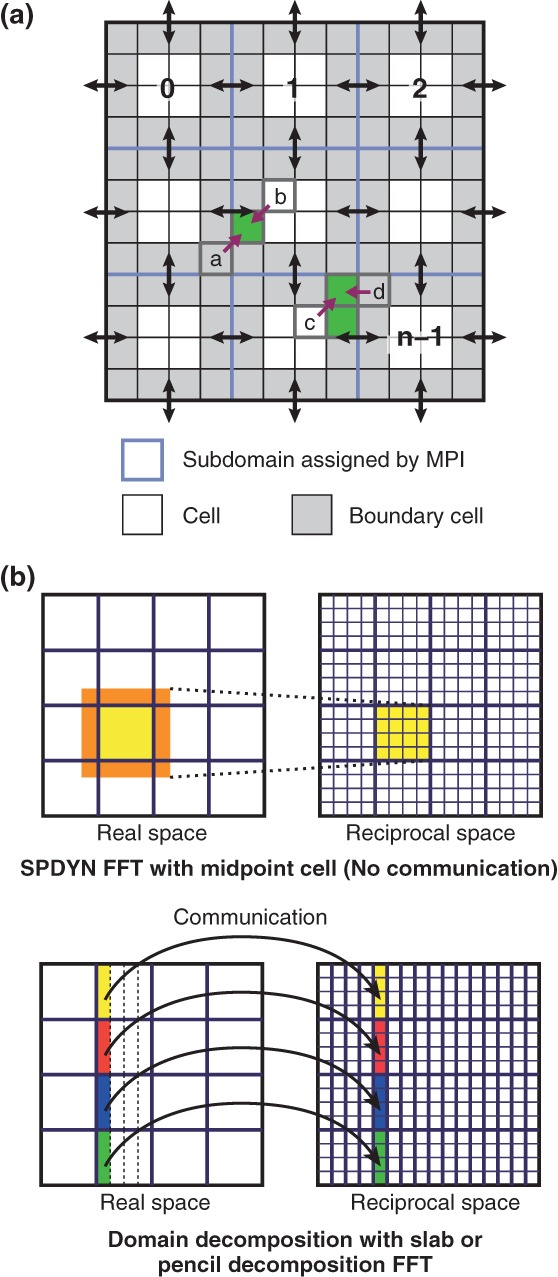
The hybrid (MPI + OpenMP) parallelization scheme in SPDYN. (a) Design of the hybrid parallelization of real space interaction in SPDYN. Adjacent cells for send/receive communication are colored by gray, and MPI communications are shown as black arrows. Midpoint candidate cells for cell pairs (a,b) and (c,d) are colored by green. (b) Two-dimensional views of charge-grid assignment in SPDYN and other MD programs using slab or pencil decomposition FFT.

The short-range nonbonded interactions in SPDYN are calculated via the midpoint cell method,³² which is an extension of the previously introduced midpoint method⁷⁴ for the hybrid parallelization. In the midpoint cell method, an interaction between two particles is computed in the subdomain containing the midpoint cell of the two cells where each particle resides. For example, interactions between particles in cell a and those in cell b are computed in the subdomain containing the midpoint cell of cell a and b (the midpoint cell is designated with a purple arrow in Figure 1(a)). This scheme improves the midpoint method by removing unnecessary calculations of midpoint checking for all of the particle pairs because the decision of which midpoint cell is appropriate for a given pair is made during the initial setup procedure. If the midpoint cell is not uniquely defined, the cell containing the minimum number of atoms is assigned as the final midpoint cell (the midpoint cell of cell c and d in Figure 1(a)). In the midpoint cell scheme, like midpoint method, sometimes interactions between a pair of particles on a processor on which neither particle resides are calculated (neutral territory method).⁷⁵ For interactions between particles in different subdomains, data of adjacent cells for each subdomain are communicated by MPI send/receive (black arrow in Figure 1(a)). This scheme is very effective in the context of a hybrid parallelization scheme because of the small amount of communication originating from the midpoint scheme and the efficient use of memory by grouping particles cell-wise. In a cutoff-based MD simulation of 1 million atoms, there is a speed up of 2000-fold with 32,768 cores compared to that achieved with 8 cores (parallel efficiency is 50%)³². The good shared-memory parallel efficiency is obtained by avoiding concurrent memory access in multi-thread calculations.

SPDYN also introduces good scalability for the reciprocal-space calculation by efficient parallelization of the 3D FFT. The 3D FFT is a key component of the PME scheme that reduces the computational cost of nonbonded interactions to O(NlogN).³⁴ Despite its usefulness, the 3D FFT is the main bottleneck in computation when using a large number of processors due to frequent communications. We developed a novel parallelization strategy in the 3D FFT using a volumetric decomposition scheme. In the midpoint cell method, each MPI processor contains data of its own subdomain and surrounding cells (yellow and orange in the upper panel of Figure 1(b), respectively), which are sufficient to compute charge data using B-spline functions in the subdomain. The communication of the charge data before the 3D FFT calculation is avoided due to the same volumetric decomposition between real and reciprocal spaces (upper panel of Figure 1(b)). In contrast, the slab or pencil decomposition 3D FFT schemes are often utilized in the distributed-data MD algorithms. In this case, all-to-all (or send/receive) communications of charge data between real and reciprocal space are required (bottom panel of Figure 1(b)). Our scheme, a combination between the midpoint cell method and the volumetric 3D FFT, is extremely useful for special network topologies such as torus networks because the number of processors involved in communication is minimized.

The benchmark performance of parallel FFT in SPDYN is as follows: for a 512 × 512 × 512 grid, it is scalable up to 131,076 cores with the sum of forward/backward FFT costing less than 4 ms on K computer, and, for a 1024 × 1024 × 1024 grid, it is scalable up to 262,152 cores with less than 10 ms execution time. As a result, for a 1 million atom system, the parallel efficiency of FFT in GENESIS provides a 890-fold speed-up on 32,768 cores relative to that achieved on 8 cores, even though the PME electrostatics is calculated at every step.

Replica-Exchange Simulations

Implementation of REMD

The REMD method is one of the enhanced conformational sampling methods widely used for systems with rugged free-energy landscapes.^47,76 In the original temperature-exchange (T-REMD) method, copies of the original system are prepared and different temperatures are assigned to each replica. Each replica is simulated in a canonical ensemble, and the target temperatures are exchanged between a pair of replicas during a simulation. Exchanging temperature enforces a random walk in temperature space, resulting in the simulation surmounting energy barriers. In the method, atomic momenta are rescaled after replica exchange to satisfy the detailed balance condition. If thermostat and barostat momenta are included in the equations of motion as in the Martyna-Tobias-Klein algorithm,⁷⁷ these variables should also be rescaled.^78,79 Recently, different types of replica exchanges schemes have been proposed.^80–83

In GENESIS, exchangeable parameters are temperature (T-REMD),⁴⁷ pressure (P-REMD),⁸⁴ surface tension (γ-REMD),⁵² and umbrella potentials⁴⁹ (REUS). The simulations can be performed in various ensembles such as NVT, NPT, NPAT, and NPγT.⁵⁷ For REUS simulations, umbrella potentials for distance, angle, dihedral angle, and positional restraints can be used. We can carry out not only one-dimensional but also multi-dimensional REMD simulations⁴⁹ without limitations on the number of dimensions. All combinations between exchangeable parameters (T, P, and γ), ensembles, and umbrella potentials are possible. For instance, in surface-tension REMD, not only surface tension (γ) but also temperature can be exchanged to enhance the conformational sampling of biological systems (γ-REMD and γT-REMD). In the current implementation, parameters are exchanged only between neighboring pairs. Let us consider that we have n different parameters assigned to each replica: λ₁, λ₂, …, λ_n (n is even). There are two patterns of parameter exchange: λ₁↔λ₂, λ₃↔λ₄, …, λ_{n − 1}↔λ_n (Pattern 1) and λ₂↔λ₃, λ₄↔λ₅, …, λ_{n − 2}↔λ_{n − 1} (Pattern 2). Exchanges using Patterns 1 and 2 are alternatively repeated during simulations. In the case of two-dimensional REMD simulation, parameters in the first and second dimensions are exchanged alternatively.

The REMD algorithm is suitable for parallel computation using MPI. In GENESIS, the global MPI communicator is split into subgroups, each of which is assigned to a replica. As mentioned above, the MD simulation of each replica is further parallelized using the hybrid parallelization scheme. The communication cost for the replica-exchange scheme is almost negligible, because only the value(s) of one or few variables instead of a set of coordinates is transferred among replicas. In T-REMD, P-REMD, γ-REMD, and REUS (H-REMD), the transferred variables are potential energy, volume, area, and restraint energy, respectively.

BASIC USAGE OF GENESIS

Input/Output for Standard MD

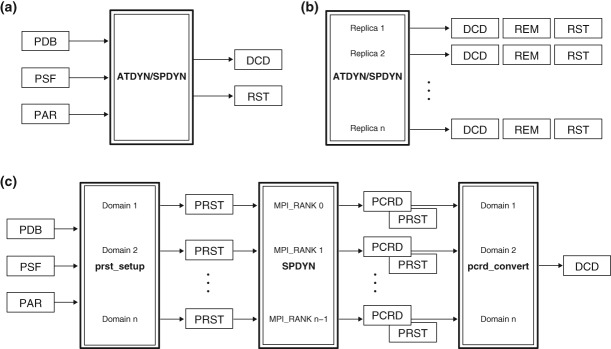
To perform simulations with GENESIS, users first prepare PDB (Protein Data Bank), PSF (Protein Structure File), and PAR (PARameter) files as input. The PSF file can be generated with PSFGEN supplied with NAMD,¹³ VMD,⁸⁵ CHARMM,¹¹ or with other tools. The PAR file is expected to be in standard CHARMM format. During simulations, trajectory files (coordinates and velocities) in standard DCD format are generated as output (Figure 2(a)). A restart file (RST) that contains atomic coordinates, velocities, box size, thermostat momenta, and barostat momenta is also written out.

FIGURE 2.

File input/output in GENESIS. (a) Scheme in standard MD simulations. PDB, Protein Data Bank; PSF, Protein Structure File; PAR, Parameter; RST, restart file. Coordinates and velocities are generated in the standard DCD file format. (b) Scheme in REMD simulations. REM, parameter index file. (c) Scheme in large-scale MD simulations. PRST, parallel restart files; PCRD, parallel coordinates files.

Input/Output for REMD

In REMD simulations, each replica generates individual trajectory data (energy, coordinates, velocities, and parameter index (REM file)) and restart files (Figure 2(b)). Because trajectory data are not sorted by replica condition (e.g., temperature in T-REMD), users have to convert trajectories to those sorted by a certain condition after the simulation using a trajectory converter tool (remd_convert).

Input/Output for Large-Scale MD

To perform MD simulations of a huge system (>10 million atoms) using SPDYN, the initial setup time may be substantial. Moreover, if single trajectory and restart files are generated during such a simulation, the communication time for gathering coordinates of all atoms on a specific CPU to write the output becomes very long, because each MPI processor has only local structure information in its domain. To avoid these problems, parallel input/output (I/O) function is available in SPDYN (Figure 2(c)). This function allows file I/O on each MPI processor. To use this feature, users first create parallel (or local) restart files (PRST files) from the initial PDB structure using a setup tool (prst_setup). The MD simulation is then performed using those PRST and PAR files as input. The output data are also written out in parallel with each file containing only local structural information such as coordinates (PCRD) and velocities. After the simulation is finished, users can combine the individual trajectory files into a single DCD file of the whole system or selected atoms by using a converter tool (pcrd_convert).

BENCHMARK PERFORMANCE OF GENESIS

Benchmark Performance on Conventional PC clusters: Comparison with Other MD Programs

Benchmark performance tests were carried out on our in-house PC cluster in which 32 nodes are connected with InfiniBand FDR. Each node has two Intel Xeon E5-2690 CPUs, each with eight 2.9 GHz cores. In total, up to 512 cores were utilized in the benchmark tests. Intel compilers (version 12.1) with OpenMPI (version 1.4.4) were used to compile the MD programs (GENESIS, NAMD version 2.9,¹³ and CHARMM c40a2⁸⁶). The performance was compared for three benchmark systems: DHFR (23,558 atoms in a 62.23 × 62.23 × 62.23 ų box), ApoA1 (92,224 atoms in a 108.86 × 108.86 × 77.76 ų box), and STMV (1,066,628 atoms in a 216.83 × 216.83 × 216.83 ų box). All input files were obtained from the NAMD webpage.⁸⁷ For the CHARMM program, we used domdec that implements a domain decomposition scheme and allows processors to be split between the calculation of real-space and reciprocal-space interactions.⁸⁶ In CHARMM, splitting processors shows better performance for small systems when increasing the number of processors. The processors are split according to a ratio of 3:1 (real-space:reciprocal-space). In the case of ATDYN, we use the ratio 1:1. In all systems, we tried to assign the same conditions: cutoff = 10 Å, pairlist cutoff = 11.5 Å, pairlist update every 10 steps, 2-fs time step with SHAKE/SETTLE^88,89 constraints with NVE ensemble. The PME grid sizes for DHFR, ApoA1, and STMV are 64 × 64 × 64, 128 × 128 × 96, and 256 × 256 × 256, respectively. In all cases, we used double precision arithmetic for real numbers. Multiple time-step integrators like r-RESPA⁹⁰ were not used. The performance shown in Figure 3(a–c) was evaluated as the CPU time difference between 1000 and 2000 integration steps. The best performance up to 512 cores is shown in Table 1. On the PC cluster, NAMD shows the best performance for all the three systems. The best performance of SPDYN lies between CHARMM and NAMD. For small numbers of processors, CHARMM shows better performance than SPDYN, but SPDYN scales better with an increasing number of cores. ATDYN shows the worst performance, which is due to an inefficient parallelization scheme, as expected.

FIGURE 3.

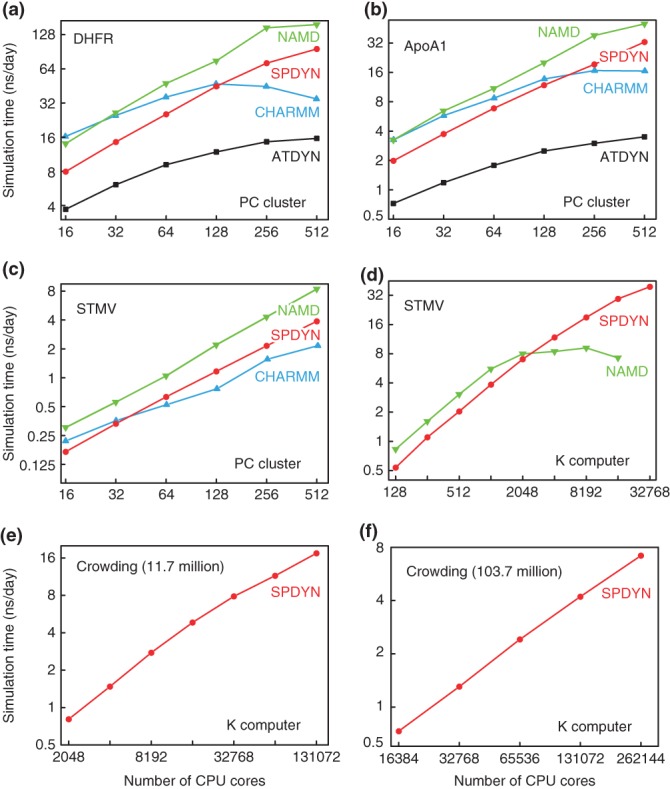
Benchmark performance of MD simulations of (a) DHFR, (b) ApoA1, and (c) STMV on PC clusters, and (d) STMV, macromolecular crowding systems consisting of (e) 11.7 million atoms and (f) 103.7 million atoms on K computer.

TABLE 1.

Best Benchmark Performance (ns/day) of DHFR and ApoA1 on PC Clusters and STMV on K Computer

System	DHFR	ApoA1	STMV
SPDYN (PC)	95.78 (512, 81)	32.74 (512, 41)	3.88 (512, 41)
ATDYN (PC)	15.60 (512, 81)	3.50 (512, 161)	—
NAMD (PC)	157.10 (512)	50.31 (512)	8.43 (512)
CHARMM(PC)	47.21 (128)	16.65 (512)	2.16 (512)
SPDYN (K)	—	—	39.17 (32,768)
NAMD (K)	—	—	9.18 (8,192)

Numbers in parentheses are number of CPU cores used to get the best performance.

¹Table 1Number of OpenMP threads used to get the best performance.

Benchmark Performance on K Computer: Comparison with NAMD

We also tested the benchmark performance for STMV on K computer⁷¹ by comparing with NAMD. K computer consists of over 80,000 SPARC64 VIIIfx processors. Each computing node contains a single processor (8 cores, 2.0 GHz), 6 MB L2 cache, 16 GB memory, and 64 GB/s memory throughput, providing 128 GFLOPS at peak performance. The total peak performance is 10.51 PFLOPS, making this system first in the Top500 of 2011. Each node is connected by a 6D mesh/torus interconnect (Tofu network), providing a logical 3D torus network for each job.

The simulation condition of the benchmark is identical to the tests on the PC cluster. However, we noticed that NAMD works better with multiple threads if a large number of processors is assigned. Because one CPU on K computer has eight cores, we assign seven worker threads combined with one communication thread in one MPI processor. In the case of SPDYN, we used eight OpenMP threads. The overall and best performance is described in Figure 3(d) and Table 1. In Figure 3(d), there is a noticeable difference between SPDYN and NAMD: up to 2048 cores, NAMD works better, which is consistent with the benchmark results on the PC cluster. NAMD does not show good scalability after 2048 cores while SPDYN shows good parallel scaling behaviour up to 32,768 cores. In other words, NAMD is more optimized for a small number of processors, whereas SPDYN has better parallel efficiency than NAMD. The benchmark result of STMV using SPDYN is very impressive considering that we calculated the PME reciprocal space interaction at every step.

Performance in Simulations of Large Systems

The larger systems that we used for further benchmark of SPDYN are all-atom models of the cytoplasm of the minimal bacterium Mycoplasma genitalium. In one system, 185 proteins, 28 RNAs, 3 ribosomes, 5005 metabolites, 23,049 ions, and 2,944,143 water molecules are included in a 50 × 50 × 50 nm³ box, and the resulting total number of atoms is 11,737,298 (11.7 million). In the second system, 103,708,785 atoms (103.7 million) with 1258 proteins, 284 RNAs, 31 ribosomes, 41,006 metabolites, 214,000 ions, and 26,263,505 water molecules are included in a 105 × 105 × 105 nm³ box. The systems were composed to be biochemically consistent following a metabolic network reconstruction. Molecular concentrations were estimated based on proteomic and metabolomic data for Mycoplasma pneumoniae,⁹¹ the closest relative of M. genitalium. Details of how the model was constructed are provided in Ref. 92. The two systems connect detailed structural views of biology to cellular levels and are attractive for investigating effects of macromolecular crowding on protein structures and dynamics in atomic detail. The benchmark MD simulations used CHARMM36⁶⁴ and CGenFF force field⁹³ parameters for proteins, RNAs, and metabolites, and the TIP3P model for water molecules. The PME method³⁵ was used for computing electrostatic interactions with a 12-Å real-space cutoff. SHAKE was applied to all bonds that connect hydrogen atoms and others, and SETTLE was used for treating TIP3P water as a rigid molecule. Due to the constraints, the time step for integrating the Newtonian equation of motion was 2 fs. PME grid sizes were 512 × 512 × 512 and 1024 × 1024 × 1024, for the 11.7 and 103.7 million atom systems, respectively. As a multiple time-step integrator like r-RESPA⁹⁰ was not used here, long-range electrostatics were evaluated at every step.

The benchmark results are shown in Figures 3(e) and 3(f). SPDYN shows scalability up to 130,000 and 260,000 cores for the systems consisting of 11.7 million atoms and 103.7 million atoms, respectively. The resulting simulation time is 17.5 and 6.5 ns/day for these two systems. Production runs of these two systems are now under way on K computer and results will be published elsewhere.

APPLICATION OF GENESIS

Finally, we show an MD simulation using GENESIS to demonstrate the usefulness. Mixed lipid systems are the major structural component of biological membranes. They are involved in a number of cellular processes such as signal transduction, membrane trafficking, and immune responses.⁹⁴ However, little is known about their structure. As such a complex system has many possible configurations, enhanced sampling is essential for reliable simulations. To examine the usefulness of REMD algorithms for mixed lipid bilayer systems, we carried out three different REMD simulations (T-REMD, γ-REMD, and two-dimensional γT-REMD). The target system contains 40 POPC lipids, 40 DMPC lipids, and 3680 TIP3P waters. In the initial structure, two lipid phases are completely separated. In T-REMD, we used 32 replicas, where temperatures are exponentially distributed between 303.15 and 373.74 K. In γ-REMD, we used four replicas (γ = 0, 6, 12, and 18 dyn/cm). In γT-REMD, temperatures are exponentially distributed between 303.15 and 318.01 K (8 temperatures) and surface tensions are set to 0, 6, 12, and 18 dyn/cm (8 × 4 = 32 replicas in total). We used CHARMM36 force field parameters for the lipids.⁶³ The SHAKE and SETTLE algorithms were applied for rigid bonds and waters, respectively. We carried out 100 ns simulation (time step = 2 fs) for each replica, and replica exchange was attempted at every 50 ps. We also carried out conventional MD at T = 303.15 K. All simulations were carried out in the NPT or NPγT ensemble at P = 1 atm.

In all simulations, the lipid bilayers maintained structural integrity, that is, there was no collapse in the bilayer structure, even at high temperature and under high surface tension. The acceptance ratio for the Metropolis criteria in all REMD simulations was about 0.3 in temperature space and 0.4 in surface-tension space, indicating frequent parameter exchanges between pairs of replicas. Figure 4(a) shows snapshots obtained from the MD and T-REMD simulations at T = 303.15 K. In T-REMD, the two lipid components are mixed more compared to MD, simply because high temperature accelerates lipid lateral diffusion. We analysed the mean-square displacement (MSD) of the centre of mass of lipid to examine lipid lateral diffusion (Figure 4(b)). All REMD simulations showed accelerated diffusion, where T-REMD was the most efficient and the order was T-REMD > γT-REMD > γ-REMD > MD. The enhanced lipid lateral diffusion observed in γ-REMD is due to free-area effects.^52,95 Note that diffusion and mixing are not identical in the lipid-bilayer systems. To quantify the degree of mixing of two lipid components, we analysed the number of contact pairs between POPC and DMPC. Contact pairs were defined based on the distance between the centres of mass of lipids with a cutoff distance of 10 Å. Figure 4(c) shows a histogram of the number of contact pairs obtained from the snapshots at T = 303.15 K and γ = 0 dyn/cm after 10 ns. We found that the mixing of the two components was enhanced in T-REMD compared to MD, while it was suppressed in γ-REMD. In γT-REMD, both enhancement and suppression were observed, presumably because diffusion is accelerated at high temperature while it is suppressed under high surface tension. There is a controversy about the effects of membrane tension on the phase formation in mixed lipid bilayers. Some studies suggest that membrane tension induces phase separation,^96–99 while others suggest mixing^100–102 or transition to other phases¹⁰³ would result. Our observation that γ-REMD and γT-REMD suppresses mixing agrees with the former studies. We suggest that REMD methods are useful for exploring structures at phase boundaries in mixed lipid bilayer systems.

FIGURE 4.

REMD simulations of POPC/DMPC mixed lipid bilayers. (a) Snapshots in the MD simulation at T = 303.15 K and P = 1 atm (upper panels), and snapshots in the T-REMD simulation at T = 303.15 K and P = 1 atm (lower panels). POPC and DMPC are coloured by blue and cyan, respectively. Structures in unit and image cells are shown together. (b) Mean-square displacements (MSD) of POPC lipids (left panel) and DMPC lipids (right panel) in MD, T-REMD, γ-REMD, and γT-REMD. MSD is computed for each replica and averaged over all replicas. (c) Histogram of degree of mixing (number of POPC–DMPC contact pairs) at T = 303.15 K and γ = 0 dyn/cm in MD, T-REMD, γ-REMD, and γT-REMD.

CONCLUSIONS

We have developed new MD software, which we call GENESIS. This contains two MD simulators, namely ATDYN and SPDYN, which are parallelized with hybrid (MPI + OpenMP) schemes based on the replicated-data and the distributed-data MD algorithms, respectively. GENESIS also allows various REMD simulations (T-REMD, REUS, and multi-dimensional REMD) both for all-atom and Go-like models in the NVT, NPT, NPAT, and NPγT ensembles. The benchmark performance tests suggest that the scalability of GENESIS in a PC-cluster is comparable to other existing MD programs. For very large biological systems containing more than one million atoms, the performance on K computer in RIKEN is better than other MD programs due to its good parallel efficiency. GENESIS allows high-performance MD simulations of large biological systems using the realistic representations on modern multicore architectures and advances biological sciences by rigorously connecting physical principles at the molecular level to biological phenotypes at the cellular level.