Benchmarks for Expected Annual Academic Growth for Students in the Bottom Quartile of the Normative Distribution

Abstract

Effect sizes are commonly reported for the results of educational interventions. However, researchers struggle with interpreting their magnitude in a way that transcends generic guidelines. Effect sizes can be interpreted in a meaningful context by benchmarking them against typical growth for students in the normative distribution. Such benchmarks are not currently available for students in the bottom quartile. This report remedies this by providing a comparative context for interventions involving these students. Annual growth effect sizes for K–12 students were computed from nationally normed assessments and a longitudinal study of students in special education. They reveal declining growth over time, especially for reading and math. These results allow researchers to better interpret the effects of their interventions and help practitioners by quantifying typical growth for struggling students. More longitudinal research is needed to show growth trajectories for students in the bottom quartile.

Effect sizes have become an increasingly important means of communicating the outcomes of education research. The American Psychological Association (APA) called the reporting of effect sizes for primary outcomes “essential to good research” in 1999 (Wilkinson & Task Force on Statistical Inference, 1999, p. 599). The APA Journal Article Reporting Standards (APA Publications and Communications Board Working Group, 2008), issued in 2008, require that effect sizes and their confidence intervals be reported in all manuscripts that include results from new data collection. The American Educational Research Association (2006) issued a similar requirement in their Standards for Reporting on Empirical Social Science Research in AERA Publications. A recent review of educational and psychological research publications found that rates of reporting of effect sizes increased from a mean of 29.6% of publications before 1999 to a mean of 54.7% of publications between 1999 and 2010 (Peng, Chen, Chiang, & Chiang, 2013). This review also determined that little had changed over time in the percentage of researchers who provided an interpretation of the magnitude of the effect along with the effect size. Authors provided an interpretation about 50% of the time, with the most frequent interpretation being a simple categorization of the effect size as small, medium, or large as measured against Cohen’s (1969, 1988) guidelines.

The limitations of relying solely on Cohen’s guidelines for interpreting effect sizes have been highlighted by a number of researchers (Bloom, Hill, Black, & Lipsey, 2008; Dunst & Hamby, 2012; Harrison, Thompson, & Vannest, 2009; Odgaard & Fowler, 2010; Sun, Pan, & Wang, 2010) and most notably in a report published by the Institute of Education Sciences (IES; Lipsey et al., 2012). In brief, Cohen’s guidelines were not intended to be applied broadly to all types of studies or to education research specifically, and there is little empirical support to suggest that they do. The IES report drew on Bloom et al.’s (2008) report to encourage education researchers to interpret effect sizes in a way that puts them into a meaningful context.

CREATING CONTEXTS FOR DETERMINING THE MAGNITUDE OF EFFECTS

One context for judging the magnitude of effects can be created by comparing effect sizes from an intervention to an effect size that represents the progress a student would be expected to make in a year’s time based on data from longitudinal studies and the norming samples of standardized tests. Bloom et al. (2008) calculated these annual growth effect sizes from seven standardized tests, using the mean scores from the norming sample for spring of one grade and the norming sample from spring of the following grade and the pooled standard deviations from the two samples. They provided this information for reading, mathematics, social studies, and science. These effect sizes for annual growth for students at the mean of the normative distribution showed a striking decline over time. For example, the mean effect size across seven reading tests dropped from 1.52 for the difference between spring of kinder-garten and spring of first grade to 0.36 for spring of third grade to spring of fourth grade to 0.19 for spring of ninth grade to spring of tenth grade. Similar downward trajectories were observed for math, social studies, and science as well. Bloom et al. also provided effect sizes calculated from extant longitudinal data from two school districts that showed effect sizes and trajectories over time that were very similar to the cross-sectional data from the norming samples.

The data provided by Bloom et al. (2008) highlight the need for context-sensitive guidance in interpreting effect sizes. Though Cohen’s generic guidelines may be burned into the minds of many education researchers, creating and using better tools for interpreting the effects of education research is critical. These tools, when built based on student characteristics, enhance our ability to determine which interventions are truly effective for which students.

Bloom et al. (2008) showed that grade level is one important student characteristic to consider in interpreting effect sizes. Another important variable that could influence the size of effects is the percentile rank in the normative distribution where the students who are the target of an intervention start out. Expected annual growth for students at or below the 25th percentile might differ from expected annual growth for students in the center of the distribution. Bloom et al. calculated effect sizes for students at the mean of the normative distribution only, and used SAT-9 reading scores for students who were in the bottom quartile in one school district to show that the overall trajectory of decline in effect sizes was similar to that of students near the center of the distribution. They do not provide the effect size values for these students and acknowledge that annual growth effect sizes may differ when data from a more representative sample of students in the bottom quartile of the normative distribution (rather than the bottom quartile of the scores from one district) are examined.

THIS STUDY

To date, no researchers have published data that provides benchmarks for annual gains for students in the bottom quartile of the normative distribution based on data from standardized assessments or longitudinal, nationally representative data sets. This study seeks to remedy this gap by replicating Bloom et al.’s (2008) methodology with scores for students at the 10th and 25th percentiles of the norming samples of standardized assessments in reading, math, social studies, and science. The resulting effect sizes can be used by future researchers as a comparative context for the effects they obtain from interventions aimed at struggling students who are in the bottom quartile on standardized measures at the beginning of the intervention. Additionally, this analysis will shed light on the relative trajectories of annual gains from kindergarten through grade 12 for struggling students compared to students with average achievement. Our research provides an important update to Bloom et al.’s findings by including data from more recent norming samples than those they included and reporting data for the median as well as the 10th and 25th percentiles, to allow for broader use of our results. We also report effect sizes from longitudinal data collected on a nationally representative sample of students receiving special education services to determine how the effect sizes from cross-sectional data compare to those collected on the same students over time.

METHOD

Participants

To calculate cross-sectional effect sizes for annual growth for students in the bottom quartile of the normative distribution, we extracted the relevant information from the technical reports, scoring manuals, and books of norms provided by the test publishers of six nationally normed tests that use vertically scaled scores. Information on participant characteristics for the norming samples is available in the technical reports for each assessment (MacGinitie, MacGinitie, Maria, & Dreyer, 2002, GMRT; MAT-8, 2002; SAT-10, 2004; TN-3, 2010; Williams, 2001, GRADE; Williams, 2004, GMADE).

Data used in calculating longitudinal effect sizes were collected by the Special Education Elementary Longitudinal Study (SEELS). SEELS was a longitudinal study of a national sample of students in special education conducted between 2000 and 2006 and funded by the U.S. Department of Education’s Office of Special Education Programs (OSEP). SEELS collected a wide range of data on these students over time. The data of interest to the present study were obtained from the only standardized math and reading tests given to students in two consecutive years of the study. Only students with data at both time points were included. SEELS data were collected on students in grades K–9, but too few students scored in the bottom quartile of the normative distribution on the standardized measures in grades K–2 to allow for the calculation of reliable effect sizes. See Table 1 for the number of students included by grade. Detailed information on characteristics of SEELS participants is available in Blackorby et al. (2004).

Table 1.

Number of SEELS students in each grade included in effect size calculation

	Math			Reading
	1st–10th	1st–25th	1st–50th	1st–10th	1st–25th	1st–50th
Grade	N	N	N	N	N	N
2	—	115	234	119	211	308
3	94	168	293	220	284	426
4	119	229	352	208	353	424
5	148	211	347	240	384	454
6	124	225	361	243	336	448
7	168	217	300	181	250	358
8	—	96	135	83	129	158
9	—	—	—	—	—	—

Note. Blank cells indicate grade levels where too few students scored at or below the 10th percentile to allow for calculation of a reliable effect size.

Measures

Cross-Sectional Estimates of Growth

Measures selected for inclusion in the computation of cross-sectional effect sizes for growth were those used in Bloom et al. (2008) that remained in publication at the time of this study and others that provided vertically scaled scores that allow for measuring growth on a continuous scale across all grade levels. Measures included in the longitudinal effect sizes were from the only measures of math and reading administered in consecutive years as part of the SEELS study.

Stanford Achievement Test (10th edition; SAT-10)

The SAT-10 is a multidisciplinary standardized assessment for students in grades K–12. The present study utilized the Total Reading, Total Mathematics, Science, and Social Studies subtest scores. Norming data were collected in 2002. Two parallel forms for all four subtests are available; Form A scores were used in the present report. Internal consistency reliabilities (KR-20) for spring scores ranged from .79 to .97.

Metropolitan Achievement Test (8th edition; MAT-8)

The MAT-8 is a standardized assessment of reading, mathematics, science, social studies, and language arts for students in kindergarten through grade 12. The Total Reading, Total Mathematics, Science, and Social Studies subtest scores were included in the present report. Norming data were collected in 1999–2000. Internal consistency reliabilities (KR-20) for spring scores ranged from .72 to .97.

TerraNova (3rd edition; TN-3)

The TN-3 assesses reading, language, mathematics, science, and social studies in students in kindergarten through grade 12. Form G of the Reading, Mathematics, Science, and Social Studies subtests were included in the present report. Norming data were collected in 2011. Internal consistency reliabilities (KR-20) for spring scores ranged from .78 to .93.

Gates-MacGinitie Reading Comprehension subtest (GMRT; 4th edition)

The Gates-MacGinitie Reading Test provides a standardized, group-administered measure of reading ability for students in spring of kindergarten through grade 12. Two equivalent forms are available; Form S scores were used in the present study. Norming data were collected in 2005–2006. Estimates of internal consistency reliabilities (KR-20) for Total Reading scores on Form S ranged from .93 to .97.

Group Reading Assessment and Diagnostic Evaluation (GRADE)

The GRADE is a group-administered, untimed assessment of reading ability for students in prekindergarten through postsecondary school. Two equivalent forms are available; Form A scores were used in the present report. Norming data were collected in 2000. Internal consistency reliabilities (KR-20) for spring Form A Total Reading scores ranged from .89 to .96. Split-half reliabilities ranged from .94 to .98.

Group Mathematics Assessment and Diagnostic Evaluation (GMADE)

The GMADE is a group-administered, untimed test of mathematics for students in kindergarten through grade 12. Two equivalent forms are available; Form A Total Math scores were used in the present report. Norming data were collected in 2002. Split-half reliabilities ranged from .91 to .96. KR-20 internal consistency reliabilities were not reported.

Longitudinal Estimates of Growth

Woodcock-Johnson Test of Achievement-III (WJ-III) Passage Comprehension Subtest

This individually administered, untimed assessment measures reading comprehension using a cloze procedure, in which students fill in missing words in passages of a text. The median split-half reliability is .88.

Woodcock-Johnson Test of Achievement-III Calculation Subtest

In this untimed subtest, students are presented with a worksheet of math problems to test their computation skills. The median split-half reliability is .86.

Effect Size Calculation

All effect sizes were calculated using the Hedges (1981) procedure (this statistic is also known as Hedges’ g). The longitudinal effect sizes were computed using the mean score for all SEELS students who scored at or below the 10th percentile, at or below the 25th percentile, and at or below the 50th percentile of the normative distribution of the WJ-III at the first data collection point in each grade level and the mean score for the same students at the second data collection point one year later. The standard deviations associated with the mean score at each time point for each group were pooled in calculating the effect size.

For the cross-sectional data, Hedges’ g was calculated using the spring norming sample’s data. The scaled scores provided in the test publishers’ books of norms at the 10th, 25th, and 50th percentile for each grade level and the next highest grade level, and the standard deviations and sample sizes for the overall norming sample for each grade (as reported in the test publishers’ technical reports) were used in computing each Hedges’ g. A sample-weighted average Hedges’ g for each grade-level comparison was computed to account for differences in sample sizes between tests. All mean effect sizes and their associated standard errors were computed using the Comprehensive Meta-Analysis (Version 2.2.064) software (Borenstein, Hedges, Higgins, & Rothstein, 2011).

RESULTS

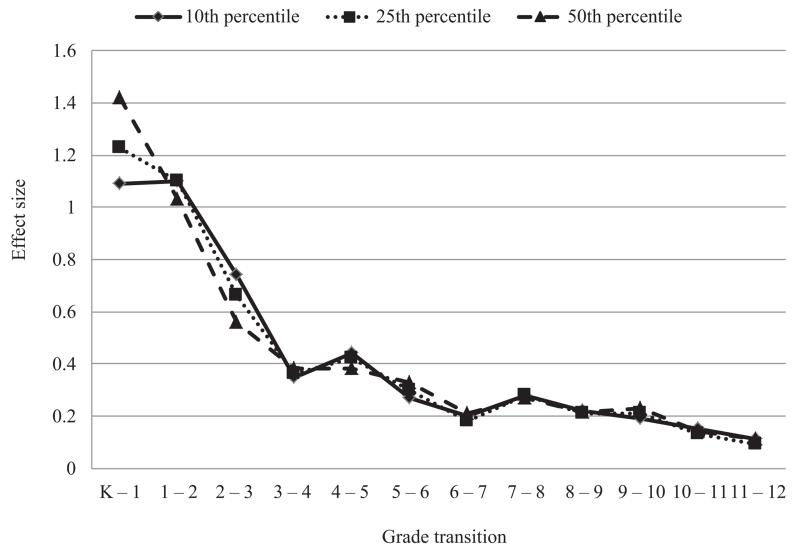
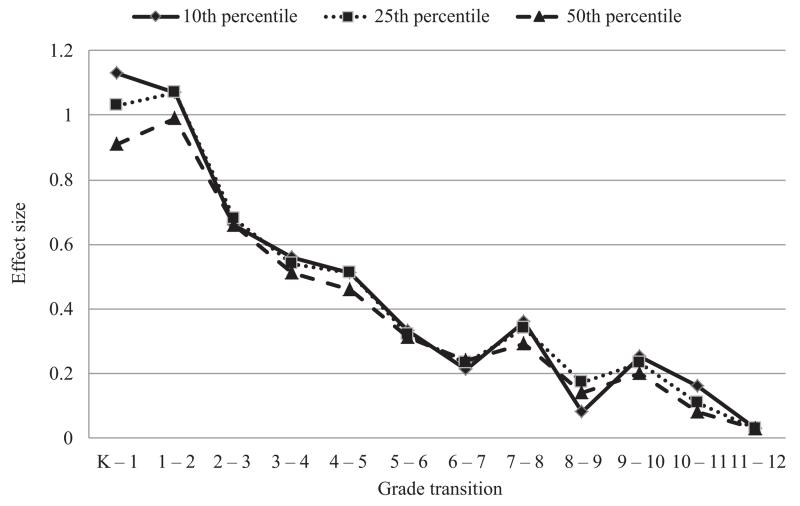
See Tables 2 through 5 for annual gains expressed as effect sizes in reading, mathematics, social studies, and science from the cross-sectional data from the nationally normed, standardized assessments. These effect sizes trend sharply downward as students progress through school. The drop in effect sizes is especially large in reading, where annual growth decreases from more than one standard deviation unit during first and second grade to less than half a standard deviation unit in fourth grade and beyond. Annual growth effect sizes for math show a similar trend. Figures 1 and 2 depict the trajectories for reading and math across grades K–12 using the cross-sectional data.

Table 2.

Annual gains in effect size for nationally normed reading tests

Grade (Spring)	Gates-MacGinitie			SAT-10			TerraNova 3			MAT-8			GRADE			Mean of Tests			SE of Mean
	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th
K–l	1.36	1.38	1.53	1.34	1.60	1.87	0.64	0.73	0.86	1.05	1.17	1.34	1.39	1.60	1.78	1.09	1.23	1.42	0.24	0.24	0.24
1–2	1.25	1.26	1.23	1.06	1.04	0.96	1.12	1.13	1.04	1.02	1.01	0.91	1.11	1.21	1.25	1.10	1.10	1.03	0.20	0.20	0.20
2–3	0.70	0.72	0.63	0.84	0.69	0.59	0.76	0.70	0.58	0.61	0.52	0.39	0.64	0.60	0.54	0.74	0.66	0.56	0.19	0.19	0.19
3–4	0.62	0.57	0.52	0.18	0.21	0.23	0.35	0.36	0.40	0.32	0.32	0.35	0.59	0.59	0.58	0.35	0.36	0.38	0.18	0.18	0.18
4–5	0.53	0.46	0.41	0.47	0.45	0.37	0.38	0.37	0.36	0.45	0.46	0.42	0.34	0.24	0.23	0.44	0.42	0.38	0.18	0.18	0.18
5–6	0.30	0.34	0.37	0.43	0.46	0.46	0.04	0.09	0.15	0.37	0.37	0.39	0.25	0.28	0.27	0.27	0.30	0.33	0.18	0.18	0.18
6–7	0.44	0.38	0.32	0.10	0.13	0.21	0.12	0.09	0.20	0.25	0.23	0.14	0.35	0.29	0.29	0.20	0.18	0.21	0.19	0.19	0.19
7–8	0.21	0.24	0.27	0.31	0.31	0.29	0.27	0.30	0.25	0.33	0.28	0.28	0.16	0.23	0.24	0.28	0.28	0.27	0.20	0.20	0.20
8–9	0.26	0.23	0.23	0.30	0.24	0.24	0.12	0.11	0.12	0.30	0.39	0.41	0.22	0.11	0.04	0.22	0.21	0.21	0.22	0.22	0.22
9–10	0.23	0.20	0.17	0.39	0.39	0.36	0.00	0.13	0.21	0.16	0.07	0.11	0.11	0.17	0.17	0.19	0.21	0.23	0.22	0.22	0.22
10–11	0.12	0.09	0.12	0.05	0.08	0.13	0.30	0.22	0.23	0.11	0.11	0.03	0.21	0.17	0.10	0.15	0.13	0.14	0.24	0.24	0.24
11–12	0.20	0.17	0.14	0.05	0.05	0.05	0.20	0.14	0.18	0.05	0.07	0.12	0.04	0.04	0.07	0.11	0.09	0.11	0.28	0.28	0.28

Figure 1.

Annual reading gains for students in grades K–12.

Figure 2.

Annual math gains for students in grades K–12.

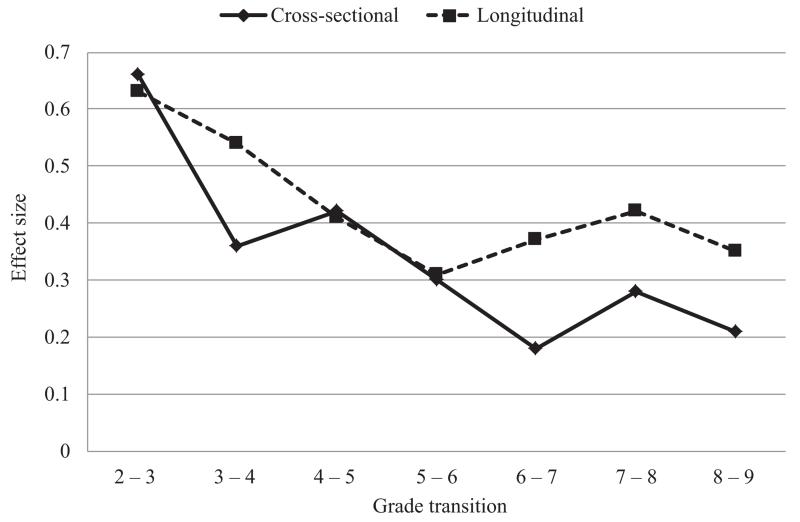
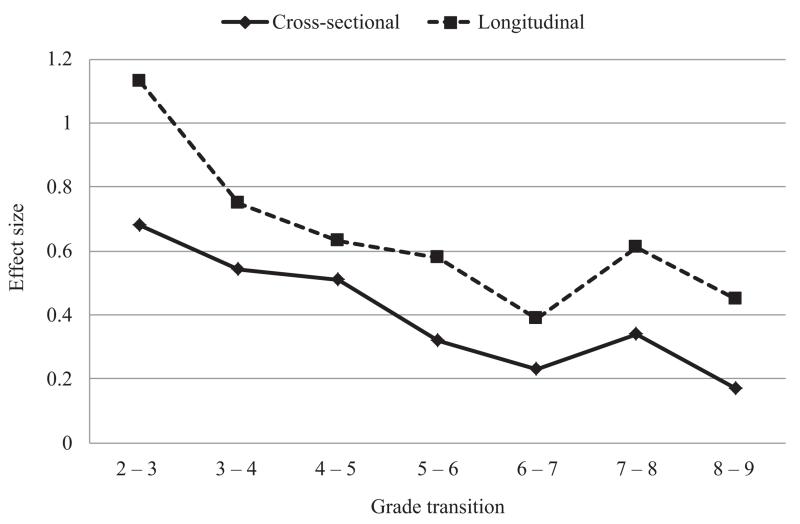
Tables 6 and 7 provide annual gains for reading and math based on the longitudinal data collected by SEELS. Figures 3 and 4 compare the trajectories for the longitudinal and cross-sectional data. As the graphs show, the downward trend over time is not as sharp for the longitudinal SEELS data as it is for the cross-sectional data. Because SEELS students were receiving special education services, it may be that they gained ground on the normative distribution, changing percentile ranks over time. To determine if this shifting occurred, the mean percentile rank change for students in each percentile group was calculated. As shown in Table 8, on average the students moved up the normative distribution between the two testing time points. However, the standard deviations all were quite large, indicating that there was a great deal of variation in movement over time for SEELS students.

Table 6.

Annual reading gain in effect size based on longitudinal SEELS data

	10th Percentile			25th Percentile			50th Percentile
Grade	Effect Size	L95% CI	U95% CI	Effect Size	L95% CI	U95% CI	Effect Size	L95% CI	U95% CI
2–3	0.78	−1.74	3.30	0.63	−1.43	2.68	0.48	−1.37	2.32
3–4	0.66	−1.41	2.73	0.54	−1.31	2.39	0.42	−1.21	2.04
4–5	0.51	−1.85	2.86	0.41	−1.40	2.22	0.36	−1.28	2.00
5–6	0.39	−1.60	2.37	0.31	−1.26	1.88	0.27	−1.2	1.75
6–7	0.44	−1.31	2.19	0.37	−1.11	1.85	0.23	−1.1	1.57
7–8	0.48	−1.44	2.39	0.42	−1.19	2.03	0.26	−1.15	1.66
8–9	0.46	−2.18	3.09	0.35	−1.69	2.39	0.26	−1.62	2.13

Note. L95% CI = lower 95% confidence interval; U95%CI = upper 95% confidence interval.

Table 7.

Annual math gain in effect size based on longitudinal SEELS data

	10th Percentile			25th Percentile			50th Percentile
Grade	Effect Size	L95% CI	U95% CI	Effect Size	L95% CI	U95% CI	Effect Size	L95% CI	U95% CI
2–3	—	—	—	1.13	−1.03	3.28	0.93	−0.55	2.42
3–4	0.91	−1.82	3.65	0.75	−1.30	2.83	0.62	−0.94	2.18
4–5	0.77	−1.49	3.03	0.63	−1.02	2.27	0.51	−0.86	1.88
5–6	0.75	−1.00	2.50	0.58	−0.88	2.05	0.43	−0.81	1.68
6–7	0.48	−1.79	2.74	0.39	−1.28	2.05	0.33	−1.04	1.70
7–8	0.66	−1.01	2.32	0.61	−0.92	2.13	0.45	−0.97	1.87
8–9	—	—	—	0.45	−1.91	2.81	0.34	−1.77	2.45

Note. L95% CI = lower 95% confidence interval; U95%CI = upper 95% confidence interval. Blank cells indicate grade levels where too few students scored at or below the 10th percentile to allow for calculation of a reliable effect size.

Figure 3.

Variations in the mean annual reading gains in the cross-sectional versus longitudinal data for the students at the 25th percentile.

Figure 4.

Variations in the mean annual math gains in the cross-sectional versus longitudinal data for the students at the 25th percentile.

Table 8.

Mean change in percentile rank from Year 1 to Year 2 by grade and subject area (SEELS data)

	Math			Reading
	1st–10th	1st–25th	1st–50th	1st–10th	1st–25th	1st–50th
Grade	M (SD)	M (SD)	M (SD)	M (SD)	M (SD)	M (SD)
2	—	11.98 (21.63)	7.15 (22.29)	3.03 (9.15)	2.32 (12.52)	.08 (15.22)
3	9.93 (18.02)	9.42 (20.37)	6.24 (21.34)	4.87 (11.68)	3.62 (12.84)	3.16 (16.04)
4	6.27 (14.81)	6.38 (17.68)	4.63 (20.42)	4.52 (10.07)	5.45 (13.69)	4.18 (15.40)
5	5.96 (12.02)	4.52 (15.11)	3.93 (18.87)	4.47 (11.37)	4.54 (14.61)	3.80 (15.53)
6	4.95 (11.60)	5.51 (17.09)	4.86 (19.90)	5.38 (11.96)	5.22 (13.36)	1.90 (17.06)
7	8.33 (16.42)	8.94 (18.15)	7.61 (21.03)	5.49 (12.12)	5.88 (13.11)	2.95 (16.45)
8	—	8.88 (20.38)	6.16 (21.08)	7.76 (16.71)	6.07 (17.10)	4.24 (18.44)

DISCUSSION

The results from the cross-sectional data analyses indicate that effect sizes for annual growth at the 10th, 25th, and 50th percentiles are very similar in magnitude and trend sharply downward across grade levels in a similar way. The downward trend in effect sizes over time is notable in the longitudinal data as well, although the decrease is not as sharp. These findings indicate that educational researchers would be wise to contextualize the effects of their interventions in comparison to typical annual growth seen for students at the grade level or levels of the students in their interventions, rather than rely on generic guidelines for assessing the magnitude of effects.

Using the Benchmarks

To understand how to use these annual growth effect sizes as benchmarks for comparing effects of interventions, consider the following example. Struggling readers at or below the 25th percentile in fourth grade are selected and randomly assigned to receive either a reading intervention or typical instruction for one semester. There are no significant differences between groups at pretest. The Hedges’ g effect size for the posttest difference in the groups’ scores on a standardized assessment is 0.40. Compare this value to 0.36, the weighted mean effect size in Table 2 for reading growth between spring of third grade and spring of fourth grade for students at the 25th percentile (which represents expected annual growth during fourth grade). The difference in growth between the treatment and comparison groups over one semester is roughly equal to one year of typical growth in reading for fourth graders at the 25th percentile. This effect of one year of growth is on top of the typical growth that would have occurred for these students during the semester. Typical growth is accounted for when the effect size is calculated for the treatment-comparison contrast, because the comparison group is experiencing typical growth in the absence of an intervention, assuming that the typical instruction that they receive is the school’s standard instruction provided to all students.

As this example shows, interpreting the magnitude of the effect of an intervention can be done with far greater precision when a benchmark for typical growth is available. The benchmarks also can be used in studies where a comparison group was not available and only a pre-post effect size for the treated group can be calculated. In this case, the normative effect sizes can be compared directly to those in the tables provided in this report if the effect size for the treated group is calculated using the standard deviations of the normative sample at each time point rather than the standard deviations of the treated group. The standard deviation for the norming sample is typically available at fall and spring of each grade level and can be found in a standardized assessment’s technical report, which can be obtained from the test publisher. To facilitate the use of our results for researchers conducting studies with a single-group design, we have created an online effect size calculator that uses the standard deviation of the normative sample to calculate a standardized mean difference when researchers input the means from each time point for one of the measures used in this report. The calculator can be accessed at http://www.texasldcenter.org/researchers/calculator.

Beyond their usefulness in benchmarking typical annual growth, the effect sizes reported here represent an interesting finding about what is required for students to maintain their position in the normative distribution over time. After third grade, annual growth of half a standard deviation or less in all four subject areas will keep a child at the same percentile rank regardless of whether that child is in the bottom decile, bottom quartile, or at the median. In high school, an annual gain of one-fourth of a standard deviation will maintain one’s standing in the distribution in all areas except for social studies, where a gain of about one-third of a standard deviation is required in tenth grade. This information can be used in planning interventions, as the goal of an intervention typically is to move struggling students up in the normative distribution. The benchmarks show researchers that gains that exceed the annual growth effect sizes are required to accomplish this goal.

Finally, the annual growth effect sizes also can be used in power calculations, where an estimate of the effect of an intervention is required to calculate the sample size needed for adequate power. Researchers who expect the effect of their intervention to exceed annual growth can use the tables in this report as a starting point for benchmarking the effect size their intervention will need to produce. This effect size can then be used to make a more accurate determination of the sample size required for acceptable power than would otherwise be possible.

Limitations and Suggestions for Future Research

A major limitation of the results presented here is that they rely mainly on cross-sectional comparisons. We made many attempts to locate usable longitudinal data, but met with no success on any front other than the SEELS project. Data from nationally representative longitudinal studies, including the Early Childhood Longitudinal Study (ECLS), did not include measurement points that were one academic year apart—making it impossible to compute annual gains. We requested longitudinal data sets from states that use vertically scaled standardized tests administered annually, but were denied access to them. Some extant data were located in an online data depository, but the data were collected so long ago that the testing manuals needed to define the bottom quartile and decile scores were no longer in print and could not be obtained.

Data from nationally representative longitudinal studies with annual measurement time points are sorely needed to determine if the cross-sectional effect sizes reported here will be replicated in longitudinal data. Such data also would allow researchers to understand better how students in the bottom quartile move over time relative to the normative distribution. ECLS:K 2011, the current longitudinal study sponsored by the National Center for Education Statistics (NCES), promises to be a valuable source of this information for students in kindergarten through fifth grade. Unfortunately, no data from this study were due to be released in time to be included in this report. Even when the ECLS:K 2011 data are available, annual growth will be able to be estimated only through fifth grade. Longitudinal studies that follow students through middle and high school are needed to provide a more complete picture of annual growth across the K–12 spectrum.

Table 3.

Annual gains in effect size for nationally normed math tests

Grade (Spring)	SAT-10			TerraNova 3			MAT-8			GMADE			Mean of Tests			SE of Mean
	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th
K–l	1.32	1.14	0.97	0.50	0.40	0.76	1.29	1.29	1.29	1.18	1.06	0.77	1.13	1.03	0.91	0.18	0.18	0.18
1–2	1.08	1.13	1.21	1.74	1.66	1.10	1.03	1.03	1.01	0.60	0.70	0.85	1.07	1.07	0.99	0.25	0.21	0.15
2–3	0.70	0.73	0.75	1.06	1.11	1.14	0.68	0.63	0.58	0.38	0.38	0.29	0.66	0.68	0.66	0.16	0.18	0.21
3–4	0.30	0.30	0.30	0.56	0.66	0.50	0.39	0.54	0.67	0.70	0.55	0.55	0.56	0.54	0.51	0.15	0.15	0.15
4–5	0.74	0.66	0.55	0.46	0.43	0.66	0.50	0.42	0.36	0.44	0.50	0.39	0.51	0.51	0.46	0.14	0.14	0.14
5–6	0.44	0.44	0.44	0.34	0.39	0.39	0.56	0.45	0.35	0.24	0.24	0.24	0.33	0.32	0.31	0.14	0.14	0.14
6–7	0.22	0.22	0.22	0.03	0.19	0.23	0.27	0.27	0.30	0.24	0.24	0.24	0.21	0.23	0.24	0.14	0.14	0.14
7–8	0.43	0.35	0.32	0.49	0.42	0.36	0.24	0.24	0.24	0.33	0.33	0.28	0.36	0.34	0.29	0.15	0.15	0.15
8–9	0.27	0.27	0.29	0.08	0.19	0.23	0.17	0.30	0.35	0.00	−0.11	0.00	0.08	0.17	0.14	0.18	0.18	0.18
9–10	0.75	0.67	0.50	0.15	0.22	0.29	0.17	0.17	0.17	0.00	0.00	0.00	0.25	0.23	0.20	0.18	0.18	0.18
10–11	0.34	0.27	0.14	0.35	0.14	0.22	0.05	0.05	0.05	0.00	0.00	0.00	0.16	0.11	0.08	0.18	0.18	0.18
11–12	0.07	0.07	0.07	0.06	0.08	0.09	0.05	0.05	0.05	0.00	0.00	0.00	0.03	0.03	0.03	0.18	0.18	0.18

Table 4.

Annual gains in effect size for nationally normed social studies tests

Grade (Spring)	SAT-10			TerraNova 3			MAT-8			Mean of Tests			SE of Mean
	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th
1–2	NA	NA	NA	0.59	0.53	0.48	0.71	0.77	0.77	0.66	0.66	0.63	0.24	0.24	0.24
2–3	NA	NA	NA	0.64	0.71	0.64	0.44	0.44	0.55	0.55	0.59	0.60	0.22	0.22	0.22
3–4	0.12	0.12	0.12	0.24	0.39	0.52	0.34	0.37	0.44	0.24	0.31	0.39	0.20	0.20	0.20
4–5	0.57	0.46	0.36	0.30	0.22	0.19	0.44	0.42	0.40	0.43	0.36	0.30	0.21	0.21	0.21
5–6	0.51	0.42	0.42	0.02	0.07	0.15	0.30	0.30	0.30	0.28	0.27	0.29	0.20	0.20	0.20
6–7	0.51	0.42	0.30	0.19	0.23	0.29	0.40	0.40	0.32	0.38	0.35	0.30	0.20	0.20	0.20
7–8	0.19	0.22	0.25	0.34	0.27	0.16	0.44	0.39	0.30	0.30	0.27	0.23	0.21	0.21	0.21
8–9	0.22	0.22	0.22	0.25	0.18	0.13	0.08	0.14	0.25	0.21	0.19	0.19	0.23	0.23	0.23
9–10	0.70	0.61	0.33	0.04	0.13	0.22	0.05	0.10	0.10	0.36	0.37	0.26	0.24	0.22	0.22
10–11	0.08	0.08	0.11	0.48	0.37	0.35	0.05	0.05	0.05	0.20	0.16	0.18	0.22	0.22	0.22
11–12	0.07	0.07	0.07	0.16	0.24	0.24	0.05	0.05	0.05	0.10	0.13	0.13	0.25	0.25	0.25

Table 5.

Annual gains in effect size for nationally normed science tests

Grade (Spring)	SAT-10			TerraNova 3			MAT-8			Mean of Tests			SE of Mean
	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th	10th	25th	50th
1–2	NA	NA	NA	0.56	0.55	0.58	0.61	0.58	0.52	0.59	0.57	0.54	0.25	0.25	0.25
2–3	NA	NA	NA	0.71	0.71	0.65	0.37	0.40	0.49	0.52	0.54	0.56	0.24	0.24	0.24
3–4	0.06	0.06	0.14	0.47	0.50	0.48	0.27	0.30	0.37	0.27	0.29	0.33	0.21	0.21	0.21
4–5	0.52	0.43	0.32	0.48	0.48	0.46	0.50	0.45	0.37	0.50	0.45	0.38	0.20	0.20	0.20
5–6	0.57	0.50	0.44	0.06	0.07	0.14	0.17	0.20	0.25	0.31	0.29	0.30	0.19	0.19	0.19
6–7	0.06	0.12	0.25	0.36	0.27	0.23	0.44	0.44	0.35	0.26	0.26	0.27	0.19	0.19	0.19
7–8	0.54	0.40	0.25	0.17	0.27	0.27	0.09	0.18	0.27	0.26	0.26	0.27	0.19	0.19	0.19
8–9	0.18	0.26	0.30	0.20	0.20	0.18	0.16	0.24	0.34	0.18	0.24	0.26	0.24	0.24	0.24
9–10	0.35	0.35	0.38	0.09	0.08	0.14	0.18	0.13	0.05	0.19	0.17	0.19	0.29	0.29	0.29
10–11	0.20	0.08	0.10	0.26	0.33	0.37	0.06	0.06	0.06	0.19	0.17	0.19	0.30	0.30	0.30
11–12	0.06	0.06	0.06	0.06	0.09	0.11	0.06	0.06	0.06	0.06	0.07	0.07	0.29	0.29	0.29