Global phosphorus retention by river damming

Significance

Phosphorus is an essential nutrient for life. Humans have massively altered the global phosphorus cycle by increasing loading to river systems through fertilizer use, soil erosion, and wastewater discharges. River damming interacts with anthropogenic phosphorus enrichment by trapping a fraction of the phosphorus in reservoir sediments. We estimate that in 2000, 12% of the global river phosphorus load was retained in dam reservoirs. This fraction could increase to 17% by 2030, because of the construction of over 3,700 new dams. Although reservoirs represent a huge phosphorus sink, rising anthropogenic phosphorus emissions continue to outpace the addition of new retention capacity by river damming. The resulting growth in riverine phosphorus export likely contributes to the expanding eutrophication of surface waters worldwide.

Abstract

More than 70,000 large dams have been built worldwide. With growing water stress and demand for energy, this number will continue to increase in the foreseeable future. Damming greatly modifies the ecological functioning of river systems. In particular, dam reservoirs sequester nutrient elements and, hence, reduce downstream transfer of nutrients to floodplains, lakes, wetlands, and coastal marine environments. Here, we quantify the global impact of dams on the riverine fluxes and speciation of the limiting nutrient phosphorus (P), using a mechanistic modeling approach that accounts for the in-reservoir biogeochemical transformations of P. According to the model calculations, the mass of total P (TP) trapped in reservoirs nearly doubled between 1970 and 2000, reaching 42 Gmol y⁻¹, or 12% of the global river TP load in 2000. Because of the current surge in dam building, we project that by 2030, about 17% of the global river TP load will be sequestered in reservoir sediments. The largest projected increases in TP and reactive P (RP) retention by damming will take place in Asia and South America, especially in the Yangtze, Mekong, and Amazon drainage basins. Despite the large P retention capacity of reservoirs, the export of RP from watersheds will continue to grow unless additional measures are taken to curb anthropogenic P emissions.

The systematic damming of rivers began with the onset of the Industrial Revolution and peaked in the period from 1950 to 1980 (1, 2). After slowing down during the 1990s, the pace of dam building has recently risen again sharply (3). As a consequence, the number of hydroelectric dams with generating capacity >1 MW is expected to nearly double over the next two decades (2). The current surge in dam construction will increase the proportion of rivers that are moderately to severely impacted by flow regulation from about 50% at the end of the 20th century to over 90% by 2030 (3). Homogenization of river flow regimes resulting from damming is a growing, worldwide phenomenon and has been invoked as one of the reasons for the decline in freshwater biodiversity (4).

Another major global driver of environmental change of river systems is enrichment by anthropogenic nutrients, in particular phosphorus (P) (5, 6). Fertilizer use, soil erosion, and the discharge of wastewater have more than doubled the global P load to watersheds compared with the inferred natural baseline (7–10). Because P limits or colimits primary productivity of many aquatic ecosystems, increased river fluxes of P have been identified as a main cause of eutrophication of surface water bodies, including lakes and coastal marine environments (6, 11, 12). River damming and P enrichment are interacting anthropogenic forcings, because sediments accumulating in reservoirs trap P and, thus, reduce the downstream transfer of P along the river continuum (13–15). This raises the question to what extent P retention by dams may offset anthropogenic P enrichment of rivers.

The number of published studies from which P retention efficiencies in dam reservoirs can be obtained is small: an extensive literature search only yields useable data for 155 reservoirs (Dataset S1), that is, less than 0.2% of the ∼75,000 dam reservoirs larger than 0.1 km² (16). The existing data nonetheless clearly show that even a single dam can significantly alter the flow of P along a river. For example, dam-impounded Lake Kariba (Zambezi River), Lake Diefenbaker (South Saskatchewan River), and Lac d’Orient (Seine River) sequester ∼87%, 94%, and 71% of their total P inflows, respectively (17–19). For the 1 million km² Lake Winnipeg watershed, 28 reservoirs and lakes accumulate over 90% of the total P load (18). The global retention of P by dams, however, remains poorly constrained (20, 21). Previous estimations have simply applied a correction factor to river P loads to represent retention by dams (22–24). This approach does not distinguish between the various chemical forms of P, nor does it account for differences in reservoir hydraulics or provide information about uncertainties on retention estimates.

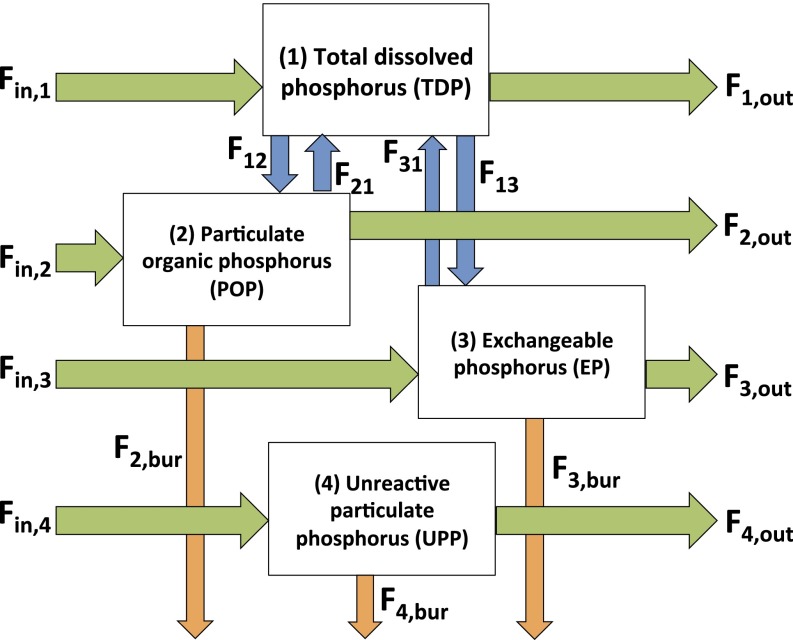
Here, we follow a mass balance modeling approach developed previously to calculate the global retention of nutrient silicon by dams (25). The mass balance model represents the key biogeochemical processes controlling P cycling in reservoirs (Fig. 1). The model separates total P (TP) into the following pools: total dissolved P (TDP); particulate organic P (POP); exchangeable P (EP); and unreactive particulate P (UPP). UPP consists mostly of crystalline phosphate minerals that are inert on reservoir-relevant timescales (≤100 y); TDP comprises inorganic and organic forms of P, whereas EP includes orthophosphate and organic P molecules sorbed to or coprecipitated with oxides, clay minerals, and organic matter. Reactive P (RP) is defined as the sum of TDP, EP, and POP; RP represents the potentially bioavailable fraction of TP.

Fig. 1.

Mass balance model used to estimate retention of P in reservoirs. F_in,i is the influx of the ith P pool into the reservoir, F_i,out is the corresponding efflux out of the reservoir, F₁₂ represents P fixation by primary productivity, F₂₁ represents mineralization of POP, F₁₃ and F₃₁ are the sorption and desorption rates of dissolved P, and F_i,bur is the permanent burial flux of the ith particulate P pool in the reservoir’s sediments.

Global predictive relationships for the retention of TP and RP in reservoirs are derived from a Monte Carlo analysis of the model, which accounts for parameter variability within expected ranges. The relationships are applied to the reservoirs in the Global Reservoirs and Dams (GRanD) database (16), to estimate the sequestration of TP and RP by dams in each of the major river basins of the world. Throughout, P retention efficiencies in a reservoir are defined as

$$R_X=\frac{X_{in}-X_{out}}{X_{in}},$$ [1]

where R_X is the fractional retention of TP or RP, and X_in and X_out are the input and output fluxes of TP or RP in units of mass per unit time. Annual amounts of TP and RP retained in a reservoir are then calculated by multiplying the R_X values with the corresponding TP and RP input fluxes from the dam’s upstream watershed. The latter are obtained from the Global-NEWS-HD model, which estimates emission yields for dissolved inorganic P (DIP), dissolved organic P (DOP), and particulate P (PP), of which 20% is assumed to be reactive (7, 26). The Global-NEWS-HD yield estimates are based on the biogeophysical characteristics, population density, socioeconomic status, land use, and climatic conditions within the drainage basin (20).

Because the biogeochemical mass balance model explicitly represents the in-reservoir transformations between the different forms of P, it allows us to estimate how dams modify both the total and reactive fluxes of P along rivers. With the proposed approach, we reconstruct global TP and RP retentions by dams in 1970 and 2000 and make projections for 2030. For the latter, we apply the nutrient P loading trends developed for the four Millennium Ecosystem Assessment (MEA) scenarios (27). The results illustrate the evolving role of damming in the continental P cycle and, in particular, the ongoing geographical shift in P retention resulting from the current boom in dam construction.

Results

P Retention in Dam Reservoirs.

P retention in lakes and reservoirs correlates with the hydraulic residence time (${\tau }_r$) (28–30). Accordingly, ${\tau }_r$ explains more than 45% of the variability of the R_TP and R_RP values generated by 6,000 Monte Carlo iterations of the P mass balance model. The model-derived R_TP and R_RP values follow the equation originally proposed by Vollenweider (31) for P retention in natural lakes:

$$R_X=1-\frac{1}{1+\sigma \times {\tau }_r},$$ [2]

where σ is a first-order rate constant describing P loss from the water column (see Supporting Information, section 4, for a derivation of Eq. 2). For TP retention in lakes, σ has been related to the relative thickness of the photic zone and the average particle settling velocity (30, 32, 33). Nonlinear least squares regressions yield the following statistically significant average values of σ: 0.801 y⁻¹ for R_TP (P < 0.05) and 0.754 y⁻¹ for R_RP (P < 0.05). The higher σ value for TP reflects the more efficient retention of UPP delivered to reservoirs, compared with the reactive P pools. The resulting difference between R_TP and R_RP is highest for hydraulic residence times between 0.5 and 1 y.

Preferential accumulation of UPP in reservoirs or, conversely, enhanced relative export of RP from reservoirs, is supported by observations. Salvia-Castellvi et al. (34) found that cascades of small dams in Luxembourg exhibit higher TP retention efficiencies than soluble reactive P, leading to the stepwise increase in TP reactivity after each consecutive dam passage. For 11 out of 16 reservoirs in the Lake Winnipeg drainage basin, Donald et al. (18) similarly found that retention of TP exceeded that of TDP, suggesting that the presence of dams increases the reactive fraction of the riverine P flux.

Global P Retention by Dams: 1970 to 2000.

The global, model-predicted retention of TP for 2000 is 42 Gmol y⁻¹, equivalent to 12% of the worldwide river TP load of 349 Gmol y⁻¹ (Table 1). The corresponding retention of RP amounts to 18 Gmol y⁻¹. The global annual mass of TP retained in 2000 is almost double that in 1970 (22 Gmol TP y⁻¹), although global TP loading to rivers only increased by 12% over the same time interval. Thus, the growth in TP (and RP) retention during the last three decades of the 20th century primarily reflects the increasing number of dams. The volume of dam reservoirs rose from about 3,000 in 1970 to almost 6,000 km³ in 2000 (16), whereas the mean reservoir retention efficiencies stayed nearly constant (R_TP, ∼44%; R_RP, ∼43%).

Table 1.

Global retentions of TP and RP by dams, in years 1970, 2000, and 2030

Global estimates	1970	2000	2030AM	2030GO	2030OS	2030TG
Global river TP load, Gmol y−1	312	349	366	384	372	380
Global river RP load, Gmol y−1	113	133	151	175	159	169
TP retained, Gmol y−1	22	42	61	67	62	66
RP retained, Gmol y−1	9	18	29	36	31	35
Fraction of global TP load retained, %	7	12	17	17	17	17
Fraction of global RP load retained, %	8	14	19	21	19	21

The 2030 retentions are calculated by including the new hydraulic dams (>1-MW generating capacity) planned to be completed by 2030 and using the projected 2030 TP and RP river loads for the four MEA scenarios: Adapting Mosaic (AM), Order through Strength (OS), Global Orchestration (GO), and TechnoGarden (TG).

During the period from 1970 to 2000, the 3.2 million km² drainage basin of the Mississippi River remained the top P-retaining catchment in the world (Fig. 2 A and B, Table 2, and Dataset S2). In 2000, the 700 reservoirs of the Mississippi River watershed accounted for 5.2% and 5.4% of the global amounts of TP and RP retention by dams, respectively. Other drainage basins with high TP and RP retentions included those of the Zambezi, Nile, Yangtze (Chang Jiang), Volga, and Paraná rivers. The high retentions in the drainage basins of the Zambezi and Volga are explained by a relatively small number of large reservoirs, including the 180-km³ Lake Kariba along the Zambezi River, and the cascade of reservoirs on the Volga River, including the Volgograd, Rybinsk, and Kuybyshev Reservoirs, each exceeding 25 km³ in volume.

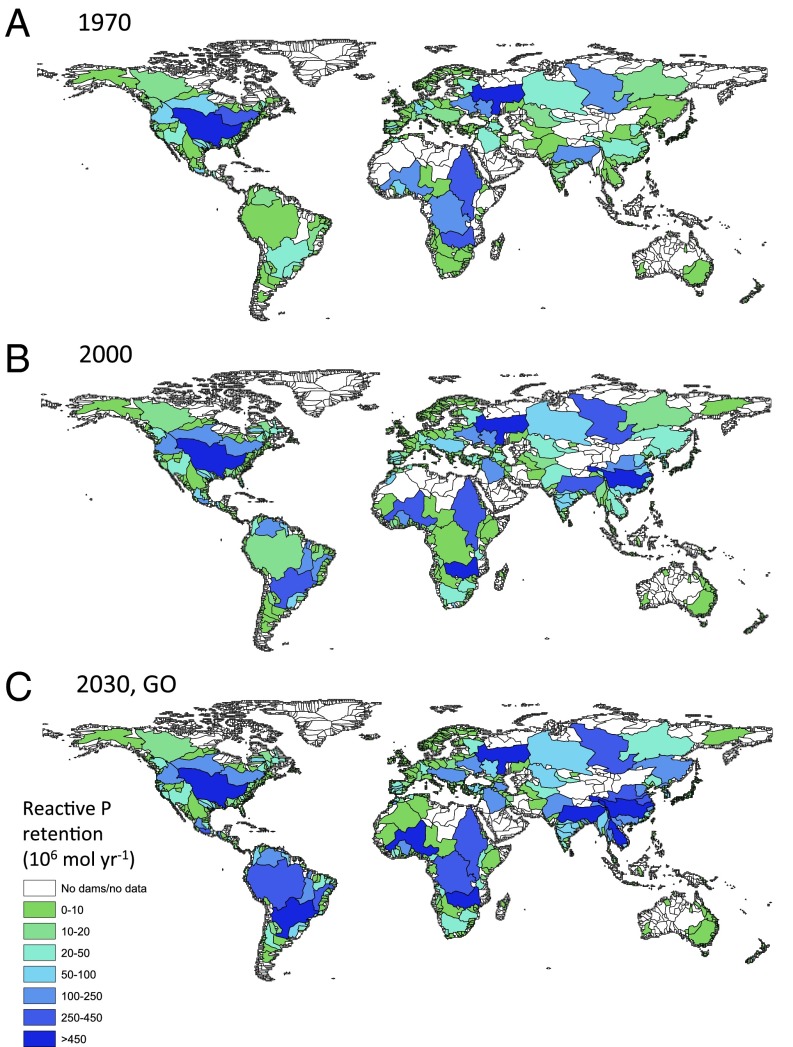
Fig. 2.

RP retention by dams in individual watersheds in 1970 (A), 2000 (B), and 2030 under the GO scenario (C). The 2030 RP retentions assume that all dams currently planned or under construction will be completed by 2030 (2). The GO scenario predicts the highest global river P load by 2030 and, hence, yields the largest relative changes in P retention.

Table 2.

Top 10 watersheds ranked according to the annual mass of RP retained in their dam reservoirs, for 1970, 2000, and 2030 (GO scenario)

Rank	Watershed	No. of reservoirs	RP load, 106 mol/y	RP retained, 106 mol/y	Retention, %
1970
1	Mississippi	546	2,700	1,805	66.9
2	Volga	15	1,423	676	47.5
3	Zambezi	13	734	390	53.1
4	Nile	7	581	376	64.7
5	St. Lawrence	162	1,896	337	17.8
6	Dnepr	5	466	298	63.9
7	Yenisei	3	773	280	36.2
8	Niger	17	602	247	41.0
9	Zaire	6	2,574	221	8.6
10	Ganges-Brahmaputra	43	6,044	152	2.5
2000
1	Mississippi	700	1,880	920	48.9
2	Zambezi	50	863	531	61.5
3	Volga	17	1,320	500	37.9
4	Yangtze	358	3,758	480	12.8
5	Paraná	70	2,410	357	14.8
6	Ganges-Brahmaputra	83	8,961	322	3.6
7	Yenisei	6	840	267	31.8
8	Niger	52	687	262	38.1
9	Nile	10	624	239	38.3
10	Dnepr	6	438	202	46.1
2030 (GO scenario)
1	Yangtze	500	8,327	2,898	34.8
2	Mississippi	700	2,294	1,124	49.0
3	Paraná	418	3,912	676	17.3
4	Mekong	140	3,283	650	19.8
5	Zambezi	65	884	649	73.4
6	Ganges-Brahmaputra	483	10,006	621	6.2
7	Niger	74	1,422	568	39.9
8	Volga	17	1,334	506	37.9
9	Zaire	20	2,462	417	16.9
10	Huang He	51	1,033	402	38.9

Nos. of reservoirs, river RP load, and RP retention are provided. An expanded list with the top 150 watersheds for year 2000 can be found in Dataset S2. Only reservoirs listed in the GRanD database and, for 2030, also reservoirs under construction or planned for completion by 2030 are included.

Projected P Retention by Dams: 2030.

Estimates of retention of P in dam reservoirs in 2030 are calculated by combining the four MEA scenarios (27) with the added retention capacity of new hydroelectric dams with generation capacities ≥1 MW that are projected to be completed by 2030 (2). The corresponding global TP retentions fall between 61 and 67 Gmol y⁻¹, or 17% of the global riverine TP loads (Table 1). The RP retentions are in the range 29–36 Gmol y⁻¹. Currently available global projections of river damming do not include smaller reservoirs or reservoirs whose main function is not electricity production. Our projections are therefore likely at the lower end of the potential increase in P retention by 2030.

Over the next 15 y, South America, central Africa, and Southeast Asia will experience the greatest growth in P retention by river damming (Fig. 2C and Table 2). By 2030, the largest single increase in dam P retention will occur in the Yangtze basin, with up to 2.6 Gmol y⁻¹ more RP retained behind 142 new dams. The Yangtze alone will then account for roughly a quarter of the additional mass of RP retained globally. Large increases in TP and RP are also projected for the drainage basins of the Mekong, Salween, and Ganges-Brahmaputra Rivers. In the Mekong River basin, 121 new dams will increase RP retention by 0.7 Gmol y⁻¹. Together, the basins of the Amazon, Paraná, and Tocantins Rivers in South America will retain an additional 0.7 Gmol y⁻¹ RP because of the construction of 616 new dams. In Africa, the Zaire and Zambezi river basins will experience significant increases in P retention attributable to the construction of 30 new dams. The retention of RP by dams in the basin of the Kura River, which empties into the Caspian Sea, should increase by 0.2 Gmol y⁻¹ upon completion of 14 new dams.

Discussion

Nutrient enrichment and damming are major anthropogenic pressures on river–floodplain systems and receiving water bodies. By building dams, humans further modify the fluxes and speciation of nutrients along the river continuum (15, 25). In particular, retention in reservoirs can greatly reduce the delivery of P to downstream areas and the coastal zone, influencing regional nutrient limitation patterns, trophic conditions, and food web dynamics (14, 15, 35). For example, the drop in primary production attributable to the near-complete cessation of P supply to the offshore Nile delta region, following the completion of the Aswan High Dam in 1964, is believed to be at the origin of the collapse of the local fishery industry (35). Here, we extend the existing studies on individual reservoirs and watersheds by performing spatially explicit assessments of the global impacts of damming on the riverine P fluxes for the period from 1970 to 2030.

Post-World War II dam construction was particularly intense in North America and Europe, with more than one-third of all dams globally located in the United States by 1970 (16). The geographical hub of dam construction started to shift during the last 30 y of the 20th century. This trend continues to the present day, as new regional economies develop and the need for nonfossil fuel-based energy sources becomes more critical. Current and near-future damming hotspots include western China, the Himalayas and Andes, Brazil, Southeast Asia, and the Balkans, where collectively more than 3,000 major hydropower dams (>1-MW generating capacity) are under construction or planned (2, 3). As a consequence, the global distribution of TP and RP retention by dams in the 21st century will depart significantly from that of the second half of the 20th century.

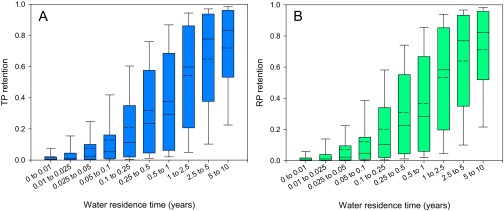
The global river TP load has at least doubled since prehuman times (7, 8, 26). That is, 50% or more of the average TP flux in rivers is now of anthropogenic origin. In addition, anthropogenic sources deliver relatively more RP to rivers than natural sources (7). From an ecological health perspective, riverine RP is more relevant than TP, because RP represents the P pool that is potentially available for biological assimilation. Although on average individual dam reservoirs retain more than 40% of the inflowing TP and RP, river damming itself had not offset global anthropogenic P enrichment of rivers by the end of the last century. In 2000, the model-predicted worldwide retention of TP by dam reservoirs only represented 12% of the global riverine TP load (Table 1), because (i) not all TP entering rivers passes through dam reservoirs and (ii) the majority of TP retention currently occurs in smaller reservoirs characterized by relatively short water residence times (≤0.5 y) and, correspondingly, relatively low retention efficiencies (Fig. S1).

Fig. S1.

Box plots for R_TP (A) and R_RP (B) predicted by 6,000 Monte Carlo simulations of the mass balance P model, plotted against the hydraulic residence time. The solid line within boxes indicates median, the dashed line indicates mean, edges of boxes indicate first and third quartiles, and whiskers are SDs.

From 1970 to 2000, the fraction of the global river TP load sequestered in reservoirs increased from 7% to 12% (Table 1). This increase is attributed to the construction of about 2,500 new dams during the last three decades of the 20th century, 65% of which have water residence times greater than 6 mo (16) and corresponding average TP retentions in excess of 25% (Fig. S1). By 2030, the retained TP fraction is projected to rise to 17% of the global river TP load, notwithstanding the much higher number of dams (3,782) projected to be built between 2000 and 2030. The more modest increase in post-2000 TP retention per dam, compared with the previous 30-y period, reflects the predominance of hydroelectric dams currently under construction or planned. Hydropower reservoirs generally have shorter water residence times, and correspondingly lower retention efficiencies, than reservoirs of similar size that are primarily used for irrigation or flood control. Of the dams under construction or planned, 63% have reservoirs with water residence times ≤0.1 y (2). In comparison, only 13% of the reservoirs currently included in the GRanD database have water residence times ≤0.1 y.

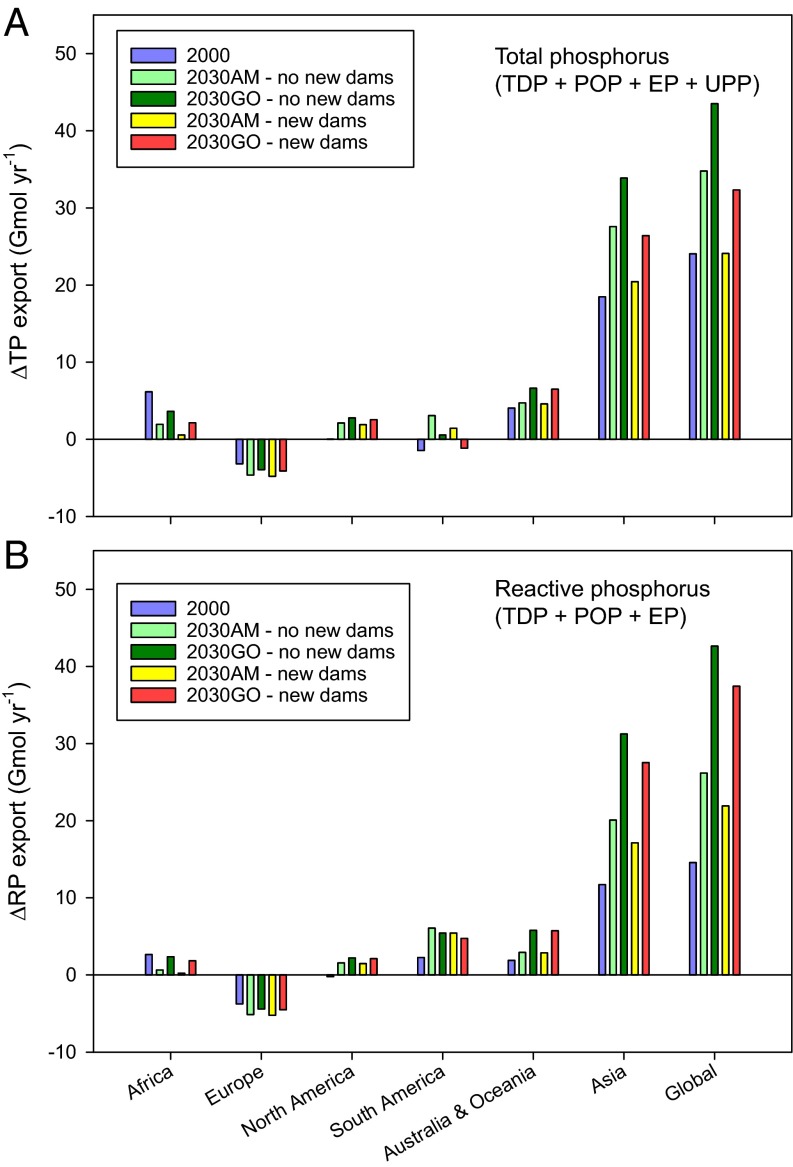
The combined effects of anthropogenic nutrient enrichment and damming on P export fluxes to the coastal zone are illustrated in Fig. 3 and Fig. S2. The decreases in TP and RP export between 1970 and 2000 observed for Europe are mainly attributable to the ∼10% drop in river TP loading following legislation to curb phosphate use in detergents and upgrades to wastewater treatment plants (36, 37). For the same time period, TP export in South America also decreased. However, in this case, damming caused the decline in TP export, as anthropogenic TP loading actually increased. In contrast to TP, RP export in South America increased from 1970 to 2000, because (i) RP made up much of the additional anthropogenic P released to rivers and (ii) RP tends to be retained less efficiently than UPP in reservoirs. Little change in TP and RP export fluxes are observed for North America, whereas in all other cases, TP and RP exports increased from 1970 to 2000. Thus, at the global scale, the accelerating anthropogenic P release to rivers during the last decades of the 20th century exceeded the added retention capacity of new dams.

Fig. 3.

Changes in riverine export fluxes of TP (A) and RP (B) to the coastal zone, relative to the corresponding 1970 values. Export fluxes are calculated by subtracting P retained by dam reservoirs in a watershed from the no-dam river P load predicted by the Global-NEWS-HD model. The 2030 scenarios with “no new dams” only account for retention by dams currently in the GRanD database, whereas the 2030 scenarios with “new dams” include the GRanD dams plus those planned to be completed by 2030, as compiled by Zarfl et al. (2).

Fig. S2.

Changes in net river export of TP (A) and RP (B) from the continents, normalized by the continental surface areas, relative to the corresponding 1970 values. Net export is defined as the difference between P loads to watersheds and P retained in reservoirs. The 2030 scenarios with “no new dams” consider only retention behind the GRanD database dams in the year 2000, whereas the 2030 scenarios with “new dams” consider both GRanD database dams (year 2000) plus new dams projected to be completed by 2030 (2).

Among the four MEA scenarios, the GO and AM yield the largest and lowest riverine TP and RP loads in 2030, respectively (Table 1). Assuming that either (i) no new dam construction takes place after 2000 or (ii) all dams under construction or planned will be completed by 2030, export fluxes calculated using the GO and AM river loads show that, with the exception of Europe, North America and Australia plus Oceania, the building of new dams in the period from 2000 to 2030 should reduce the export of TP (Fig. 3 and Fig. S2). For Africa and Europe, TP export fluxes are predicted to be lower than in 2000, whereas for Asia, North America, and South America TP, export fluxes under the AM scenario would remain close to their 2000 values. The current surge in dam construction would therefore appear to be able to largely offset the ongoing and future increases in anthropogenic TP inputs to river systems.

The global export of RP follows a different trajectory, however (Fig. 3B). In contrast to TP, even with the construction of new dams, the 2030 export fluxes of RP for South America, Asia, and Australia and Oceania are predicted to substantially exceed the corresponding fluxes in 2000, even under the AM scenario. These upward trends for RP are attributable principally to the fact that anthropogenic sources are mostly delivering reactive P phases to river systems. Hence, for South America, Asia, and Australia and Oceania combined, the RP fraction of the river TP load is estimated to grow from 34% in 2000 to 43% in 2030. Therefore, despite the massive dam-building activity now and in the near future, global anthropogenic RP loading is projected to continue to outpace RP retention until at least 2030. Under the GO scenario, global RP export is expected to be 21% higher in 2030 than in 2000. Such a large global increase in RP export would likely further exacerbate cultural eutrophication of surface water bodies.

Our estimations of TP and RP retention in reservoirs imply that global river damming represents a major anthropogenic perturbation of the continental P cycle. Dams also influence river fluxes of other nutrients, including nitrogen (N) and silicon (Si) (25, 38). Because retention efficiencies by reservoirs differ from one nutrient element to another (18, 25, 39), the presence of dams may modify nutrient stoichiometry along rivers and thereby affect nutrient limitation and food-web dynamics in river-fed aquatic ecosystems (40). The existing evidence suggests dams generally remove P more efficiently than N and Si (18, 39). Damming could therefore be one factor explaining the trend toward more widespread P limitation of coastal waters (41, 42). Given the importance of P as a key, and often limiting, nutrient, as well as the rapid pace of global damming, there is an urgent need to better understand the effects of dams on riverine P fluxes and to fully determine the associated environmental impacts.

Materials and Methods

The biogeochemical processes controlling P cycling in surface water bodies are relatively well understood. The existing knowledge base is thus used to build a P mass balance model that captures the key transformations responsible for changes in P speciation between river inflow and dam outflow (Fig. 1). Note that the model does not account for spatial trends within a reservoir or for subannual variability in P dynamics. The model is not designed to provide a detailed representation of any particular reservoir but rather to perform first-order estimations of annual P sequestration by dams at the river basin scale or higher.

The model assumes that P is supplied to a reservoir via river inflow. For each of the P pools considered in the model (TDP, POP, EP, and UPP), the input is computed as $F_i^{\text{in}}\mathrm{=}Q\mathrm{\cdot }{\left[TP\right]}_{\text{in}}\mathrm{\cdot }{\mathit{\alpha }}_i^{\text{in}}$, where Q is the volumetric river discharge, [TP]_in is the TP concentration of the inflow, and ${\mathit{\alpha }}_i^{\text{in}}$ is the fraction of species i in inflowing TP. The fluxes redistributing P between the TDP, POP, and EP pools, the burial fluxes of the particulate forms of POP, EP, and UPP, and the outflow fluxes of the four pools of P are all assumed to obey first-order kinetics with respect to the corresponding source pool mass. We define burial as the transfer of P below the topmost, active surface layer of sediment, where mineralization and desorption processes remobilize part of the deposited POP and EP. The pools in Fig. 1 are therefore partly located within the water column and partly within the upper, active sediment layer.

The P mass balance model contains 13 adjustable parameters (Table S1). Based on the available literature, probability density functions (PDFs) are assigned to 11 parameters, whereas fixed values are imposed to the remaining two (Table S1). Monte Carlo simulations are carried out by randomly generating 6,000 different parameter combinations from the imposed PDFs. Each individual model run is performed with Runge-Kutta 4 integration and 0.01-y time steps, for the length of time elapsed since dam closure (i.e., if the dam is 20 y old, the model is run for 2,000 time steps). As shown in Fig. S1, the model-predicted R_TP and R_RP values exhibit positive trends with the hydraulic residence time, τ_r, as expected from the literature (28–30). The trends are fitted to the classic Vollenweider model for P sequestration in lakes (Eq. 2).

Table S1.

Parameter ranges and distributions used in Monte Carlo analysis

Parameter	Range	Accuracy	PDF equation	PDF parameters	Assumptions/notes	Source
Volume	0.001–180 km3	High	Pareto: $y=\left(\frac{1}{\sigma }\right){\left(1+k\frac{x-\theta }{\sigma }\right)}^{-1-\frac{1}{k}}$	σ = 0.0556487	PDF fitted to GRanD database reservoir volume distribution, binned according to Freedman-Diaconis rule.	Ref. 16
				k = 1.39388
				θ = 0
Discharge	0.01–150 km3 y−1	High	Pareto: $y=\left(\frac{1}{\sigma }\right){\left(1+k\frac{x-\theta }{\sigma }\right)}^{-1-\frac{1}{k}}$	σ = 0.0511971	PDF fitted to GRanD database reservoir discharge distribution, binned according to Freedman–Diaconis rule.	Ref. 16
				k = 2.12464
				θ = 0
Inflowing TP concentration	0.001–800 μM (1,000 to 8 × 108 mol km−3)	High	Lognormal: $y=\frac{1}{x\sigma \sqrt{2\pi }}exp\left\{\frac{-{(\ln x-\mu )}^2}{2{\sigma }^2}\right\}$	μ = 15.148	PDF fitted to reservoir P budget database according to Freedman–Diaconis rule.	Dataset S1
				σ = 1.24707
Proportion TDP (αinTDP)	0–1	Moderate	Gamma: $y=\frac{\left(\frac{1}{b^a\text{Γ}\left(a\right)}{x}^{a-1}{e}^{\frac{-x}{b}}\right)}{20}$	a = 1.2, b = 1.5	Gamma PDF constrained using world average proportions of each species (TDP = 0.09, POP = 0.04, EP = 0.15, UPP = 0.72). Mean of Monte Carlo outputs will equal these constrained means, but the full range of proportions is possible in the outcome of each Monte Carlo iteration.	Refs. 7, 9, 26, and 53
Proportion POP (αinPOP)				a = 0.8, b = 1.0
Proportion EP (αinEP)				a = 3.0, b = 1.0
Proportion UPP (αinUPP)			αinUPP = 1 – (αinTDP + αinPOP + αinEP)	NA
kdesorb	0.01–2 y−1	Low	Uniform	NA	Sorption is held constant, whereas desorption can vary. ksorb is 1.5 y−1 if reservoir depth is ≤7m and 0.5 y−1 if >7m.	Ref. 52
ksorb	0.5 or 1.5 y−1	Low	NA	NA
kburial	0.01–60 y−1	Moderate	Gamma: $y=\frac{1}{b^a\text{Γ}\left(a\right)}{x}^{a-1}{e}^{\frac{-x}{b}}$	a = 0.2, b = 13	61 values, binned according to Freedman–Diaconis rule, cross-checked for suitability of range against Dataset S1 data.	Refs. 43–45 and 56–60
kup	0.08–200 y−1	Moderate	Uniform	NA	Range constrained using literature values, checked against Dataset S1 data.	Refs. 25 and 43–45
Reservoir age (i.e., model run-time)	0.05–1,000 y	High	Lognormal: $y=\frac{1}{x\sigma \sqrt{2\pi }}exp\left\{\frac{-{(\ln x-\mu )}^2}{2{\sigma }^2}\right\}$	μ = 3.88106	PDF fitted to GRanD database reservoir age distribution, binned according to Freedman–Diaconis rule.	Ref. 16
				σ = 0.46671
kminer	7 y−1	Moderate	NA	NA	Model insensitive to changes in this parameter.	Refs. 48–51

See the text for details. Note that σ values listed in the PDF parameter column are unrelated to the nutrient loss parameter σ in Eq. 2. NA, not applicable.

The TP and RP retention relationships (i.e., Eq. 2) are applied to the dams included in the GRanD database (16). For 1970 and 2000, only dams in operation in those years are considered in the calculations. For the 2030 scenarios, the GRanD database is augmented with the new hydroelectric dams (>1-MW generating capacity) projected to be completed by 2030 (2). Inputs of TP and RP to the reservoirs are obtained by overlaying the year-specific TP and RP watershed yields from the Global-NEWS-HD model (20) onto the GRanD reservoirs in 1970, 2000, and 2030. The yields are then multiplied by the surface areas of the reservoirs’ drainage basins to derive the loads in mass per unit time. The 2030 yields used for the individual MEA scenarios are taken from Seitzinger et al. (27). Note that the global estimations of the annual amounts of TP and RP retention by dams at the time points considered include a correction to account for the reservoirs not included in the GRanD database (∼24% of total reservoirs in 2000, predominantly those <0.1 km²). See the Supporting Information for full details, including model sensitivity analysis (Supporting Information, section 3 and Table S2).

Table S2.

Summary of the sensitivity analysis of the mass balance P model

Parameter	Default parameter	Adjustment	TP response, %	RP response, %
Inflow TP concentration	7.4 μM (GloRiCh average)	±10%	<±0.1	<±0.1
kdesorb	1 y−1	±10%	±0.2	±1
ksorb	1 y−1	±10%	±0.1	±1
kup	4 y−1	±10%	±0.5	±2
kburial	2.6 y−1	±10%	±10	±9
kminer	7 y−1	±10%	±0.1	±0.5
Reservoir age	40 y	10 y	<±0.1	<±0.1
Species inflow proportions, ${\alpha }_i^{\text{in}}$	POP = 0.04, TDP = 0.09, UPP = 0.72, EP = 0.15	All species = 0.25	+14	+0.4
		POP = 0.04, TDP = 0.05, UPP = 0.73, EP = 0.18	−2.7	−9
Initial conditions	0 μM	= GloRiCh averages	<±0.1	+0.2
		= Influx	<±0.1	+0.4

The calculated responses refer to the relative change in the rate constant σ in Eq. 2.

To approximate the uncertainties on global dam P retention estimates associated with the mechanistic modeling approach, we fitted gamma functions to the R_TP and R_RP distributions produced by the 6,000 Monte Carlo simulations of the model (Fig. S1). A second Monte Carlo analysis was then carried out to calculate global P retentions in which, for each reservoir in GRanD, R_TP and R_RP values were randomly selected from the corresponding gamma distributions. A total of 20 simulations were carried out, yielding ±7% SDs on the average global TP and RP retentions. Note that these relatively modest uncertainties do not account for the errors associated with the model structure, the Global-NEWS-HD output, and the GRanD database. Model uncertainties on the global TP and RP retentions of the 2030 MEA scenarios are ±20% higher than those of 1970 and 2000, because dams added between 2000 and 2030 tend to have shorter water residence times (95% have τ_r ≤ 2 y) than dams built before 2000. The ±20% error estimate is based on the drop in goodness-of-fit of Eq. 2 when only using the results of the Monte Carlo analysis for τ_r between 0 and 2 y.

1. Monte Carlo Analysis: Model Parameters

The ranges and distributions of parameter values used in the Monte Carlo analysis of the P mass balance model (Fig. 1) are given in Table S1. Details on how the parameter ranges and distributions are selected are given below. It is important to emphasize that sections 1.1, 1.2, 1.3, and 1.4 of the Supporting Information deal with assigning values to the rate constants (in y⁻¹) of the processes controlling the cycling of P in reservoirs, not to the corresponding fluxes (in mol y⁻¹). In the model, the effluxes out of the reservoir are inversely related to the water residence time, that is, in-reservoir fluxes (or rates) increase with water residence time as the corresponding processes act over longer time scales. In turn, we assume that the rate constants are independent of the water residence time, to avoid duplication of the water residence time effect on the rates/fluxes.

1.1. Permanent Burial.

The rate constant for burial of PP, k_burial, is the most sensitive parameter governing model-predicted TP retentions (Supporting Information, section 3). The probability function assigned to k_burial is obtained by fitting a gamma function to burial rate constants reported for 61 lakes and reservoirs gathered from literature sources (Table S1). The resulting gamma distribution reproduces the observed range of R_TP values of the reservoirs included in Dataset S1.

1.2. Primary Productivity.

P uptake and assimilation via primary productivity (F₁₂) is, in general, the main in-reservoir process leading to RP retention. The imposed range of k_up is based on annually averaged, whole-reservoir primary production rates reported in the literature (25, 43–45). Note that these rates are typically lower than those derived from short-term microcosm incubations (46, 47). The k_up range reproduces the TDP retentions and their corresponding TP retentions calculated for the 16 reservoirs with available TDP budgets of Dataset S1.

1.3. Mineralization.

Mineralization of organic P (F₂₁) is modeled using a fixed value of 7 y⁻¹ for the rate constant, k_miner, based on the references in Table S1 (48–51). Results of the model sensitivity analysis (Supporting Information, section 3 and Table S2) show no change (<0.1% difference) in model outcome for variations in k_miner of ±10%.

1.4. Sorption.

Sorption and desorption cover a wide range of processes with widely different kinetics. The sensitivity analysis indicates that R_TP and R_RP are relatively insensitive to the absolute values assigned to the rate constants k_sorb and k_desorb (Table S2) but rather depend on their ratio. Hence, the sorption rate constant is fixed, whereas the desorption rate constant is varied over a sufficiently broad range to simulate conditions ranging from net P sorption (k_sorb > k_desorb) to net desorption (k_sorb < k_desorb).

In general, phosphate sorption is stronger under oxygenated conditions than in the absence of oxygen (51). As a first order approach to determine the likelihood that the bottom waters of a reservoir become anoxic, we use the average water depth: in analogy with lakes (52), we assume that reservoirs with average water depth >7 m are more prone to undergo stratification and, hence, have a higher potential for anoxia than shallower reservoirs. A lower k_sorb value (0.5 y⁻¹) is assigned when water depth is >7 m and a higher value (1.5 y⁻¹) when water depth is ≤7m.

1.5. Riverine P Inputs.

The distribution of TP in world average river water is (7, 9, 26, 53): 9% TDP, 4% POP, 72% UPP, and 15% EP. These proportions imply that, on average, about 20% of PP is reactive. Gamma probability functions are used to represent the proportions of the reactive pools of P delivered by rivers into reservoirs (αⁱⁿ_i): αⁱⁿ_i values vary between 0 and 1, with mean values equal to the world average values given above.

2. Global P Retention Estimates

2.1. 1970 and 2000 Retentions.

To generate the 1970 and 2000 global TP and RP retentions in reservoirs, Eqs. 1 and 2 are scaled up by spatially intersecting the GRanD database (16) with the 1970 and 2000 P river loads calculated by the Global-NEWS-HD model (13, 20, 24). For the 1970 calculations, all dams built in 1971 and later are removed from the GRanD database. For each reservoir, the TP and RP inputs from the reservoir’s watershed are computed as

$$X_{\text{in,i}}=W\times Y,$$ [S1]

where X_in,i is the TP or RP influx to reservoir i in units of mol y⁻¹, W is the upstream watershed area (km²) listed in the GRanD database, and Y is the RP or TP yield of the watershed in units of mol P km⁻² y⁻¹. Note that the Y values in Eq. S1 are obtained after inactivating the Global-NEWS-HD model’s built-in damming function.

Eq. S1 assumes uniform RP and TP yields throughout a given catchment (54, 55). The amounts of TP or RP retained annually in the reservoir are then calculated as

$$X_{\text{ret,i}}=X_{\text{in,i}}\mathrm{-}{X}_{\text{out,i}}=R_X\mathrm{\times }{X}_{\text{in,i}},$$ [S2]

where R_X is defined by Eq. 1. Because Global-NEWS-HD estimates the yields of DOP, DIP, and PP, the corresponding RP yield is calculated as the sum of DOP and DIP, plus 20% of PP (7, 26).

The GRanD database accounts for ≥76% of the estimated global volume of reservoirs worldwide. The bulk of the reservoirs not included in the GRanD database are relatively small, <1 km² in size (16). Those reservoirs in the GRanD database that are smaller than 1 km² have a median water residence time of 0.6 y. We therefore assume that the missing reservoirs receive ∼24% of the global riverine TP and RP inputs and have water residence times of 0.6 y. The missing reservoirs then account for an additional 14 Gmol TP y⁻¹ and 6 Gmol RP y⁻¹ retained in 2000. For the 1970 calculations, we assume the number of missing reservoirs is half that in 2000, because 1970 was roughly midway through the first post-WWII boom in dam construction (2, 3). We thus estimate that in 1970, the missing reservoirs account for an additional 7 Gmol TP y⁻¹ and 3 Gmol RP y⁻¹.

2.2. 2030 Retentions.

With the recently published database of hydroelectric dams under construction or planned (2, 3), it is possible to estimate the projected increases in TP and RP retentions by the year 2030, under the assumption that all planned dams will be completed (3). The database contains 3,782 dams with hydropower production capacities of 1 MW or greater. Projected hydropower production capacities and dam discharges are given in Zarfl et al. (2), whereas reservoir volumes are estimated using a linear regression between hydroelectric capacity and reservoir volume established by Grill et al. (3). We overlay the global map of new reservoirs with the Global-NEWS-HD model output to estimate nutrient retention by the new dams constructed between 2000 and 2030, as done for existing reservoirs using the GRanD database.

We use the four MEA scenarios as incorporated into the Global-NEWS model by Seitzinger et al. (27). As before, the Global-NEWS-HD model is run after turning off the built-in damming function. The four scenarios, TG, GO, AM, and OS, yield different river P loads depending on whether society follows a proactive approach to environmental management (TG and AM) or a reactive approach (OS and GO) and whether the world becomes increasingly globalized (GO and OS) or regionalized (AM and TG) (27).

The 3,782 dams planned or under construction will be built on 344 rivers; that is, dam cascades are the norm for the current surge in damming. The effects of dam cascades are accounted for in the retention estimates by applying the following equation to all dam reservoirs in a watershed, except the most upstream one (for which Eq. S1 is used),

$$X_{\text{in,i}}=\left[\left(W_i-W_{i-1}\right)\times Y\right]+X_{i-1,out},$$ [S3]

where W_i−1 is the catchment surface area of the reservoir immediately upstream of reservoir i, and X_i−1,out is the TP or RP flux out of the reservoir immediately upstream of reservoir i.

3. Sensitivity Analysis

A sensitivity analysis is performed by varying the “default” parameter values listed in Table S2 by ±10% and running 150 model iterations per parameter value. Discharge and volume (and therefore surface area and depth) vary according to the ranges and distributions described in Table S1, to quantify parameter sensitivity over a range of hydraulic residence times. The sensitivity to the proportions of the different pools making up the total river P load is assessed using variable αⁱⁿ_i values reflecting the range of uncertainty in global river P export to the oceans (Table S2). To test the model’s sensitivity to initial conditions, the output using initial species concentrations of 0 mol km⁻³ are compared with the global averages for rivers from the Global River Chemistry Database (GloRiCh).

For each set of 150 iterations, R_TP and R_RP are plotted against the hydraulic residence time and fitted to Eq. 2 to determine the corresponding changes in σ. Results show that k_burial and the αⁱⁿ_i values are the most sensitive model parameters. The imposed variations in initial conditions, reservoir age, inflowing TP concentration and the other rate constants have little or no effects on R_TP and generally somewhat larger effects on R_RP (Table S2).

4. Derivation of Nutrient Loss Parameter (σ)

The following is an abbreviated derivation of that originally provided by Vollenweider (1975) (31), used to predict nutrient retention in lakes. The mass balance for a (nonvolatile) substance in a lake or reservoir is

$${\displaystyle \sum }_{i=1}^i{m}_i-m_w-{\displaystyle \sum }_{s=1}^s{m}_s-\frac{d{M}_w}{dt}=0,$$ [S4]

where M_w is the total mass of the substance in the lake/reservoir of volume V, m_i is the inflow flux of the substance to the lake/reservoir via the ith river, m_w is the outflow flux of the substance, and ${\sum }_{s=1}^s{m}_s$ = S represents all processes removing the substance from the lake/reservoir water column, other than through the outflowing river.

In the case of P, Eq. S4 applies to the total mass, or to the mass of any given compound or pool of compounds. Vollenweider (31) explicitly states that, “if, e.g. the substances in question would be ortho-phosphate only, then ${\sum }_{s=1}^s{m}_s$ would contain also all transformations of PO₄ to other P-compounds.” Thus, for TP in our mechanistic model (Fig. 1), the ${\sum }_{s=1}^s{m}_s$ = S term includes the burial fluxes of POP, EP, and UPP. For RP, the term includes the same burial fluxes, with the exception of burial of UPP (F_4,bur). Thus, we can expect numerically different ${\sum }_{s=1}^s{m}_s$ = S terms for TP and RP.

Assuming a first-order dependence, as in our model, S = σ × M_w, Vollenweider then obtains

$$\frac{d{M}_w}{dt}={\displaystyle \sum }_{i=1}^i{q}_i\left[m_i\right]-q_w\left[m_w\right]-\sigma \times M_w\hspace{0.17em}\hspace{0.17em},$$ [S5]

where q_i is the inflow to the lake/reservoir via the ith river, q_w is the outflow from the lake/reservoir, and [m_i] and [m_w] are the inflow and outflow concentrations of the substance of interest. For a perfectly mixed lake/reservoir, [m_w] is equal to the average water column concentration, or [m_w] = M_w/V. In Eq. S5, σ is the first-order rate constant for the total in-lake/in-reservoir removal flux S. In other words, σ accounts for all in-reservoir processes that remove the substance of interest from the water column.

By dividing all terms by V and solving the ordinary differential equation for steady state, we have

$$m_w=\frac{m_i}{1+\sigma \times {\tau }_r},$$ [S6]

where τ_r is the water residence time. Defining nutrient retention as

$$R_m=\frac{m_i-m_w}{m_i}$$ [S7]

and substituting Eqs. S6 into S7, we arrive at

$$R_m=1-\frac{1}{1+\sigma \times {\tau }_r},$$ [S8]

which is Eq. 2. The equation applies to both RP and TP, but with σ values that are specific for RP and TP.