Predicting experimentally stable allotropes: Instability of penta-graphene

Significance

We describe criteria that should be applied when evaluating whether theoretically proposed carbon allotropes may be experimentally isolated. We discuss the importance of energetic isomeric “funnels” centered on a stable allotropic form, the role of defects in catalyzing structural transformations to lower energy isomers, and chemical stability. This is demonstrated with literature examples such as C60 and B80. We apply these criteria to a recently proposed carbon allotrope, penta-graphene, demonstrating with the aid of density functional calculations that it will not be experimentally attainable. A second example, Haeckelites, are unlikely to be experimentally achievable when neutral but may be stabilized through significant charge transfer. The principals discussed here are general and can be applied to any theoretically proposed materials.

Abstract

In recent years, a plethora of theoretical carbon allotropes have been proposed, none of which has been experimentally isolated. We discuss here criteria that should be met for a new phase to be potentially experimentally viable. We take as examples Haeckelites, 2D networks of sp²-carbon–containing pentagons and heptagons, and “penta-graphene,” consisting of a layer of pentagons constructed from a mixture of sp²- and sp³-coordinated carbon atoms. In 2D projection appearing as the “Cairo pattern,” penta-graphene is elegant and aesthetically pleasing. However, we dispute the author’s claims of its potential stability and experimental relevance.

One of the joys of carbon research is the huge flexibility of carbon bonding (1–4), resulting in many varied allotropes that have already been experimentally identified. Computational modeling opens the floor to predicting many more, and tools such as graph theory (5) and evolutionary algorithms (6) allow systematic exploration of potential bonding networks. New computationally proposed phases are typically identified as metastable via positive phonon modes, and sometimes via molecular-dynamics (MD) simulations showing lattice coherence at experimental operating temperatures. However, there are common criteria beyond these two tests that link those allotropes that have been experimentally isolated.

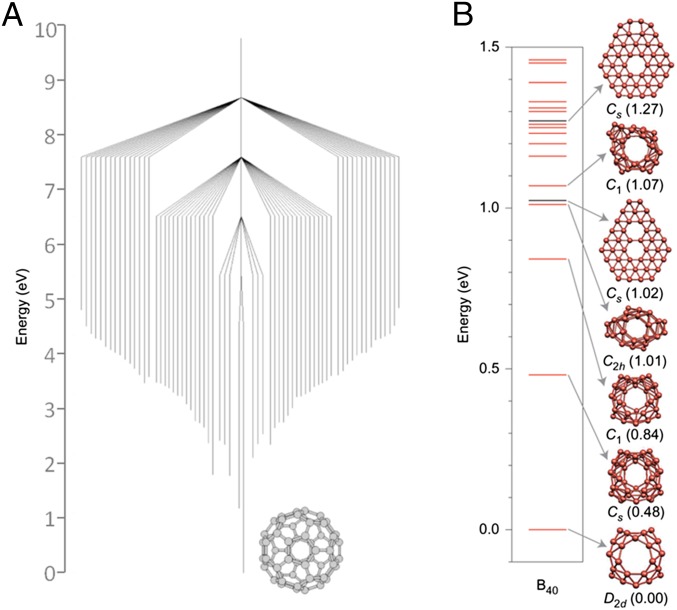
First, they occupy deep potential wells in the surrounding energetic landscape. Additionally, the surrounding energy wells are all higher in energy, “funneling” toward the stable structural form. Finally, barriers to subsequent conversion to alternative structures are typically high. Buckminsterfullerene, I_h-C₆₀, is a good example. The disconnectivity graph for C₆₀ connecting the 1,812 isomers with pentagonal and hexagonal faces via branches whose height indicates the transformation barrier has a “willow tree pattern,” with a gentle funnel running toward the stable I_h-C₆₀ isomer (7) (Fig. 1A). The relatively high barriers are accessible during high-temperature growth and alternatively can be catalyzed via the presence of impurities or carbon interstitial atoms (8–10).

Fig. 1.

(A) “Willow tree” pattern of different C₆₀ isomers, with the lower points of each vertical bar representing the calculated formation enthalpy relative to I_h-C₆₀, and bar heights representing the calculated barrier to transformation. This shows that I_h-C₆₀ is significantly more stable than other isomers and lies at the center of an “energetic funnel.” Adapted from ref. 7, with permission from Macmillan Publishers Ltd.: Nature, copyright 1998. (B) Calculated formation enthalpies of B₄₀, showing the D_2d cage structure is significantly more stable than alternative isomers. Reproduced from ref. 12, with permission from Macmillan Publishers: Nature Chemistry, copyright 2014.

In contrast, attempts to experimentally isolate higher-order boron fullerenes have been largely unsuccessful to date. For the proposed fullerene B₈₀, this can be understood because the energy landscape was shown to feature many closely related isomers with similar (and sometimes lower) energies (11). In contrast, calculations for B₄₀, for which there are first experimental indications (12), show a single (D_2d, 1A1) cage isomer, energetically well separated from alternative isomers (Fig. 1B). This behavior is consistent with the rules discussed above.

We apply here a similar analysis for experimental viability to other proposed phases, starting with “penta-graphene,” a 2D carbon allotrope proposed by Zhang et al. (4). The structure can be viewed as a series of out-of-plane distorted ethylene units connected via tetrahedral sp³-carbon linkers. The result is a corrugated layer that in projection matches the “Cairo pattern” of distorted pentagons (Fig. 2A).

Fig. 2.

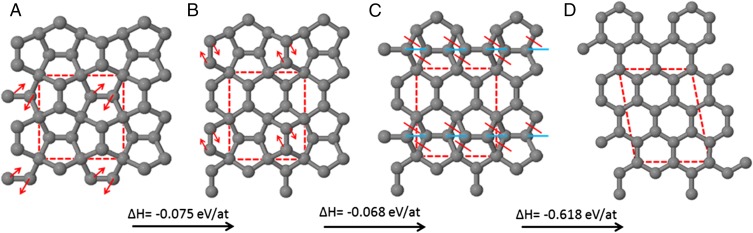
A calculated structural transformation route from (A) penta-graphene to (D) graphene; each step is exothermic. Red arrows indicate direction of motion of atoms for 90° rotation of carbon–carbon bonds. Red (blue) lines indicate C–C bonds that are broken (formed). Note that structures A–C were constrained within orthogonal unit cells; this constraint was lifted for step C to D. The final structure, graphene, is 0.761 eV per atom more stable than A. Unit cells are marked with dotted lines; calculated cell dimensions are (A) 5.095 × 5.095 Å, (B) 4.769 × 5.510 Å, (C) 4.888 × 5.318 Å, and (D) 4.883 × 6.476 Å, α = 100.88°.

Results and Discussion

Thermodynamic Stability: Relative Energy.

The first test of any new proposed structure is of its thermodynamic stability. Considering penta-graphene, although real phonon energies (positive eigenvalues from the Hessian matrix) indicate that it is at least a local structural minimum (4), its formation enthalpy shows that it is a very high-energy structure. We have performed a number of calculations on penta-graphene and structural derivatives, using density functional theory (DFT) (Methods). Penta-graphene is 0.761 eV per atom less stable than graphene. This is significantly less stable than amorphous carbons (0.16 eV) (13), most nanotubes, and I_h-C₆₀ (0.39 eV) (14), and places it in a similar energy range to experimentally unconfirmed isomers such as R3-carbon (15).

Transforming to Graphene.

Second, penta-graphene is not the stable center of a “funnel” of isomeric structures, but instead forms part of an energetic funnel of structures centered on graphene. Fig. 2 shows an example sequence of bond rotations and bond breakages by which penta-graphene can be transformed directly to graphene. Each step is exothermic, but only if the unit cell vectors are allowed to geometrically relax along with all atoms. This does not appear to have been done in the original paper by Zhang et al. The unit cell area increases 19.6% from penta-graphene (25.96 Ų) to graphene (31.05 Ų). This is because the sp³ bonding and corresponding nonplanarity in penta-graphene give it a relatively dense 2D projected basal plane compared with graphene. Constraining the unit cell dimensions to those of penta-graphene therefore energetically disadvantages planar sp² restructuring.

The periodic boundary conditions for the calculations necessarily require that the set of rotations at each step, e.g., from A to B, be simultaneous as shown, and this may be argued to be improbable. However, we have also tested the equivalent single isolated bond rotation for a 2 × 2 repeated supercell of penta-graphene. Rotating just one of the C–C bonds marked in Fig. 2A releases 0.812 eV, showing that transformation from penta-graphene to graphene could occur stepwise.

Thus, because penta-graphene forms part of a continuous energetic funnel toward graphene, it will not be possible to isolate experimentally on thermodynamic grounds.

The above analysis is consistent with MD simulations that have been used to map out carbon energy landscapes in terms of structural crystallinity and density, as a function of applied pressure and temperature (16). Consistent with experiment, these landscapes predict that stable crystalline carbon polytypes contain only one hybridization state of carbon (either sp² or sp³), with mixed phases stable in amorphous configurations. They also show energy funneling toward fully sp² or sp³ phases, depending on system pressure.

Metastable structures may still nonetheless be isolated if their conversion to stable phases is kinetically inhibited due to high interconversion barriers, so we next consider kinetic stability criteria.

Kinetic Stability and the Importance of Defects.

A classical stability test is the use of MD simulations at experimental temperatures. Penta-graphene was shown in this way to maintain its structure for 1 ps at 300 K (4). However, this is not sufficient to demonstrate kinetic stability.

Structural distortion in materials is typically a localized process commencing at defective sites, often catalyzed by impurities and defects. The 90° carbon–carbon bond rotation processes shown in Fig. 2A are an example of this. Each bond rotation step represents the annihilation of a dislocation dipole in the underlying graphene lattice and requires the simultaneous breaking and reformation of two carbon bonds. Similar carbon–carbon bond rotation in graphene has an extremely high calculated enthalpy barrier of 8.99 eV (9). For the single bond rotation step in penta-graphene discussed above, we have calculated the reaction barrier to be in the range 2.33–3.04 eV. (Because we are not able to simultaneously relax the unit cell dimensions with the atom positions within the nudged elastic band calculations, the two quoted values are calculated with the unit cell parameter fixed at the start and end structure values, respectively. Simultaneous unit cell and position relaxation may lower this barrier further.) This is already significantly lower than that of graphene.

However, the C–C bond rotation barrier in graphene is reduced by a factor of 4 in the presence of defects such as carbon adatoms (9), and similarly introducing a carbon adatom to penta-graphene also drops the calculated barrier by 35% to only 1.51 eV. Additionally, the local energy release associated with this restructuring will also likely render the process autocatalytic. Thus, in the presence of any defects, penta-graphene is unlikely to be stable. We note that the authors did indeed run MD simulations for point defects in penta-graphene (4), but these were for only 5 ps and with fixed lattice constants as discussed above.

Chemical Stability and Oxidation.

Although chemical stability is not strictly a criterion for experimental viability, it is nonetheless an important indicator. To examine potential environmental stability of penta-graphene, we calculated its reaction with O₂. In the triplet state, O₂ oxidation of the surface is highly exothermic, releasing 2.24 eV per O₂ molecule, with a barrier to chemisorption of only 0.16 eV. Accounting for spin conversion to an eventual singlet state (surface crossing) releases a further 2.34 eV. Oxygen forms epoxides at the distorted localized surface C=C bonds. Thus, penta-graphene would undergo highly exothermic spontaneous oxidation on the slightest exposure to air.

Haeckelites and Related sp²-Layered Structures.

Our next example is the Haeckelites (1–3), a family of layered sp²-carbon structures constructed from pentagons, heptagons, and optionally hexagons. Despite extensive theoretical investigation since their first proposition nearly 20 y ago (1), these structures have never been unambiguously experimentally isolated.

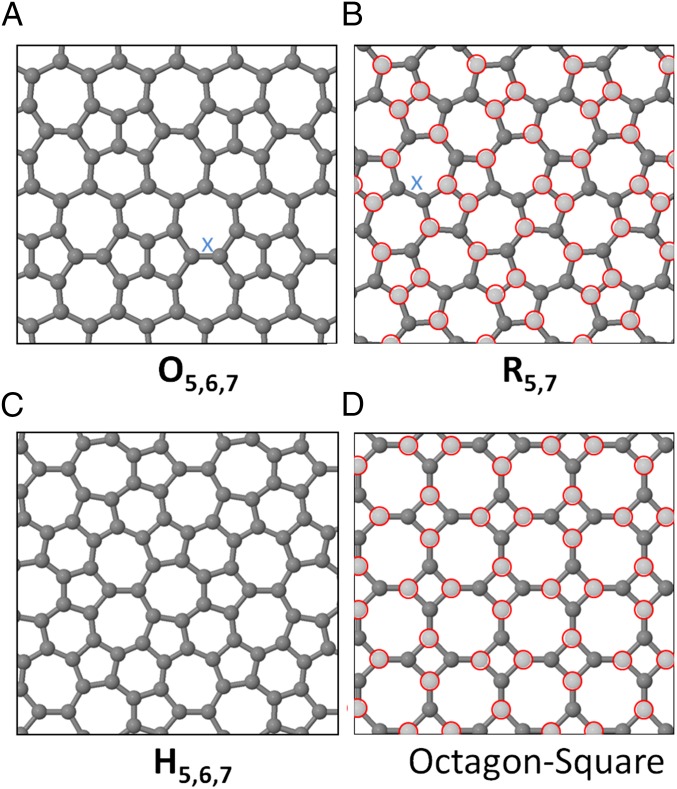
Fig. 3 A–C shows three Haeckelite structures. In terms of thermodynamic stability, all three are less stable than graphene, oblique O_5,6,7 by 0.377 eV/C (Fig. 3A), rectangular R_5,7 by 0.244 eV/C (Fig. 3B), and hexagonal H_5,6,7 by 0.251 eV/C (Fig. 3C), although the energies relative to graphene are significantly lower than that of penta-graphene. Structures in Fig. 3A and Fig. 3B can both be converted to graphene via 90° bond rotations of the bonds labeled “X” in Fig. 3, and hence lie on the thermodynamic funnel terminating at graphene. As discussed previously, the bond rotation barrier can also be lowered through the presence of defects. The structure in Fig. 3C cannot reconstruct via bond rotations to graphene but, if produced through a sequential edge growth process, could still be replaced by thermodynamically preferable graphene. Thus, from the arguments above, we would not expect these structures to be experimentally viable.

Fig. 3.

Three Haeckelite structures. (A) Oblique O_5,6,7, (B) a rectangular R_5,7, and (C) hexagonal H_5,6,7 (nomenclature from ref. 2), and (D) octagon-square structure. In MC₂B₂ borocarbides, lighter carbon atoms marked with red circles are replaced with boron in (B) M = Sc and (D) M = Ce, Y, Ca, Ln (metal ions located above the center of heptagons and octagons, respectively). Bonds marked “x,” when rotated, convert a 5–7–7–5 patch into four hexagons.

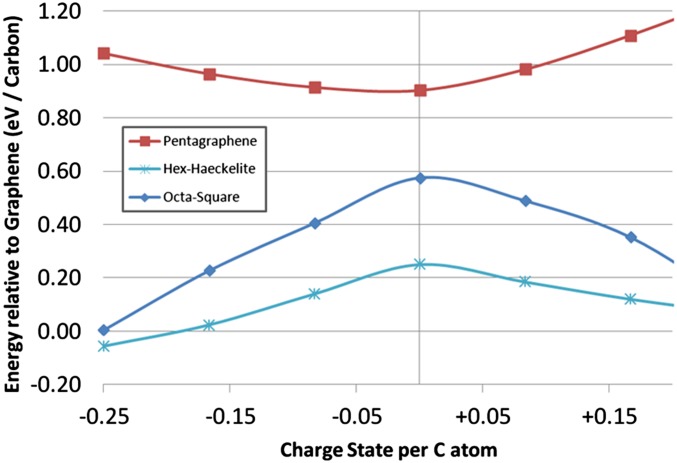
If the system is charged, however, the thermodynamic picture changes. Fig. 4 shows the energy of Haeckelite-H_5,6,7 and penta-graphene relative to graphene at different charge states. Although penta-graphene becomes increasingly unstable with charging, the Haeckelites become increasingly stable, and for high charge accumulation, Haeckelite-H_5,6,7 becomes more stable than graphene. The effect is even more marked for the octahedral-square structure (Fig. 3D), which shifts from 0.57 eV/C less stable than neutral graphene, to comparable energy when charged 0.25e/C.

Fig. 4.

Relative stability of penta-graphene (Fig. 2A) and hex-Haeckelite (Fig. 3A) compared with graphene, as a function of charge state per C atom. Although penta-graphene is increasingly unstable with charging, Haeckelites and square-octahedral structures are increasingly stabilized, becoming comparable with graphene or even thermodynamically favored at 0.25e per carbon.

Structural analogs that have indeed been experimentally isolated are metal borocarbides MB₂C₂, where M = Mg, Sc, Ce, Ca, Y, La, and Lu (17, 18). These are layered B₂C₂ structures intercalated with metal ions (Fig. 3). Hexagon, pentagon-heptagon (Fig. 3B), and octagon-square lattices (Fig. 3D) have been experimentally identified depending on the metal cation (18). Among these phases, MgB₂C₂ exhibits a stable hexagonal graphene-like lattice. This can be understood because the Mg²⁺ cation donates sufficient electrons to compensate the electron deficiency of boron with respect to carbon, i.e., two electrons for each B₂C₂ motif. In contrast, M³⁺ cations (La³⁺, Ce³⁺, Y³⁺, Sc³⁺, Lu³⁺) donate one extra electron compared with Mg²⁺, leading to an extra charge of 0.25e per lattice atom. These cations form nonhexagonal borocarbide lattices, in agreement with our analysis of thermal stability vs. charge state for carbon sheets, where at 0.25e per carbon atom Haeckelite and octahedron-square lattices become thermodynamically competitive with graphene. [The exception is Ca²⁺, which also favors a square-octahedral lattice; however, this is because of additional effects (ionic radius).]

Thus, although the calculations suggest that isolated Haeckelites are unlikely to be formed experimentally, in situations of heavy doping, such as metal–ion intercalation in layered crystals, or ion overlayers on surfaces, experimental isolation of Haeckelites may be possible.

Conclusions

The calculations presented here strongly suggest that penta-graphene will not be an experimentally achievable allotrope of carbon. Not only would penta-graphene be difficult to isolate from the plethora of alternative isomers with similar energies, it should rapidly restructure toward graphene in the presence of even a few catalytic impurities. Even were it to form, it would not be environmentally stable. Haeckelites, although unlikely to be experimentally attainable in isolation, may still be experimentally achievable in the presence of charge transfer ions.

In general, when determining the experimental feasibility of synthesizing new carbon phases, it is not sufficient to establish the pristine material as a metastable minimum on a local energy surface. We have highlighted here the importance that the structure lie at the apex of a disconnectivity graph of related isomers, occupying a unique energetically isolated position. Chemical and kinetic stability, notably in the presence of catalytic defects (both intrinsic and extrinsic) are also critical. This analysis could easily be extended to other proposed carbon allotropes, such as the various graphyne phases (19), and indeed is general beyond its simple application to carbon.

Methods

DFT calculations under the local density approximation were performed using the AIMPRO code (20), with a basis set containing 22 independent Gaussian-based functions per carbon atom and 40 per oxygen atom. Hartwigsen–Goedecker–Hutter relativistic pseudopotentials were used (21). Finite temperature smearing was used for the electronic state population with temperature kT = 0.01 eV. Lattice vectors were relaxed simultaneously with atom positions and lattice symmetry broken. For penta-graphene and related 12-atom unit cells, a 4 × 4 Monkhorst–Pack (22) k-point grid was used; for the 2 × 2 48-atom cell, a 2 × 2 k-point grid was used. Saddle points were determined using the climbing nudged elastic band algorithm (23). Orthorhombic octahedron-square cells contained 4 atoms, 8 × 8 × 1 k-points; hexagonal H₅₆₇ cells had 16 atoms, 4 × 4 × 1 k-points; R_5,7 cells contained 48 atoms, 2 × 2 × 1 k-point grid; and O_5,6,7 cells had 12 atoms, 4 × 4 × 1 k-point grid.