Cell membrane deformation and bioeffects produced by tandem bubble-induced jetting flow

Significance

Cavitation plays a pivotal role in ultrasound-generated bioeffects. Here, we report the design of an experimental system based on laser-generated tandem bubbles in a microfluidic chip and surface patterning to investigate the causal relationship between cavitation jetting-induced cell membrane deformation and resultant bioeffects. We have demonstrated that pinpoint membrane poration produced at the cell’s leading edge correlates with area strain integral, which varies significantly with standoff distance to the tandem bubble. By adjusting the standoff distance, distinctly different bioeffects (necrosis, repairable poration, or nonporation) could be produced in individual cells, providing the opportunity to probe mechanotransduction at single cell level with potential applications in disease diagnosis and treatment monitoring based on mechanical characterization of the cell.

Abstract

Cavitation with bubble–bubble interaction is a fundamental feature in therapeutic ultrasound. However, the causal relationships between bubble dynamics, associated flow motion, cell deformation, and resultant bioeffects are not well elucidated. Here, we report an experimental system for tandem bubble (TB; maximum diameter = 50 ± 2 μm) generation, jet formation, and subsequent interaction with single HeLa cells patterned on fibronectin-coated islands (32 × 32 μm) in a microfluidic chip. We have demonstrated that pinpoint membrane poration can be produced at the leading edge of the HeLa cell in standoff distance S_d ≤ 30 μm, driven by the transient shear stress associated with TB-induced jetting flow. The cell membrane deformation associated with a maximum strain rate on the order of 10⁴ s⁻¹ was heterogeneous. The maximum area strain (${\epsilon }_{A,M}$) decreased exponentially with S_d (also influenced by adhesion pattern), a feature that allows us to create distinctly different treatment outcome (i.e., necrosis, repairable poration, or nonporation) in individual cells. More importantly, our results suggest that membrane poration and cell survival are better correlated with area strain integral (${{\displaystyle \int }}^{}{\epsilon }_A^{2}dt$) instead of ${\epsilon }_{A,M}$, which is characteristic of the response of materials under high strain-rate loadings. For 50% cell survival the corresponding area strain integral was found to vary in the range of 56 ∼ 123 μs with ${\epsilon }_{A,M}$ in the range of 57 ∼ 87%. Finally, significant variations in individual cell’s response were observed at the same S_d, indicating the potential for using this method to probe mechanotransduction at the single cell level.

Cavitation-induced bioeffects (1–3) have been well recognized to play a pivotal role in a broad range of biomedical applications, including blood–brain barrier opening by focused ultrasound (4), shock wave lithotripsy (5), histotripsy (6), sonoporation (7), laser surgery (8), characterization (9, 10), and manipulation of single cells (11). Despite this, the dynamic processes of cavitation bubble(s) interaction with biological tissue and cells are not well understood, primarily due to the lack of enabling techniques and experimental systems to resolve such inherently complex and fast responses, especially at the cellular level. Although progress has been made in better control of cavitation–cell interaction, and characterization of bubble dynamics, associated flow field, and bioeffects (7, 12–14), a quantitative assessment of the cell membrane deformation produced by cavitation bubbles is still lacking. Without this knowledge, a disconnect exists between bubble-generated mechanical stress and the resultant cell response that may initiate calcium transients (15, 16), membrane poration (17, 18) that may eventually lead to necrosis, survival, gene expression, or proliferation of the cells following cavitation exposure (2).

The unique combination of high strain rate and large deformation of a cell produced by impulsive stretches from bubble oscillation (10, 19) presents a significant challenge to understanding the mechanism of action. Although cell mechanics have been extensively investigated under quasi-static and dynamic loading conditions with low strain rates (20, 21), recent evidence suggests that the classical area strain threshold under quasi-static loading conditions (about 3%; ref. 22) is not applicable to cavitation-produced membrane rupture (10, 23, 24). Considering the importance of mechanical stress in the growth and repair of cells and tissue to maintain their physiological functions (25–27), knowledge about cell mechanoresponse under high strain-rate loading is essential for understanding cavitation-produced bioeffects, and furthermore, for exploring viable biomedical applications by harnessing the beneficial potential of cavitation.

In addition to high-strain rate and large membrane deformation, other technical challenges exist in dissecting the complex bubble(s)–cell interaction. Recent studies have used ultrasound-activated microbubbles (7, 15, 17, 18) and laser-generated bubbles in microfluidic systems (13, 28) to reduce the randomness in cavitation initiation and bubble dynamics. Even so, significant variations in cell shape, size, growth adhesion environment (29), and heterogeneity in cell population (30) may also alter the bioeffects produced, hindering efforts to identify the most critical factor responsible for the treatment outcome. All these challenges motivate us to develop new technologies and experimental systems to investigate and better understand cavitation-induced bioeffects, especially at the single cell level.

In this study, we developed a versatile experimental system to investigate cell membrane deformation and bioeffects produced by laser-induced tandem bubbles (TBs) and resultant jetting flow at the single cell level. We characterized the heterogeneous deformation of the cell membrane produced by the jetting flow at different standoff distances and with different adhesion patterns. We further analyzed the correlations between the maximum area strain or area strain integral imposed on the cell membrane with cell viability following the TB treatment. The results provide insights into the mechanism responsible for the pinpoint membrane rupture produced by tandem bubbles and inertial cavitation-induced bioeffects under high strain-rate load conditions.

Results

Control of Bubble Generation and Cell Growth by Surface Patterning.

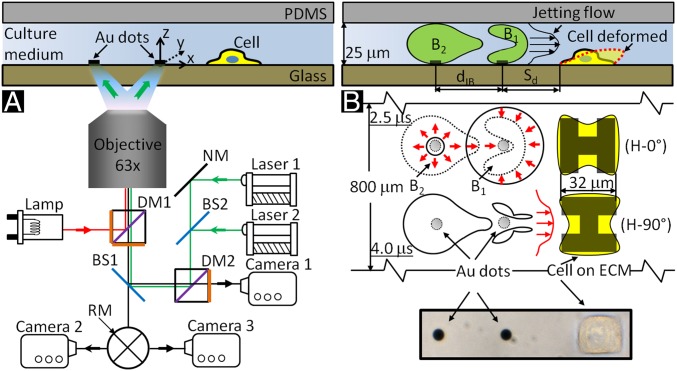
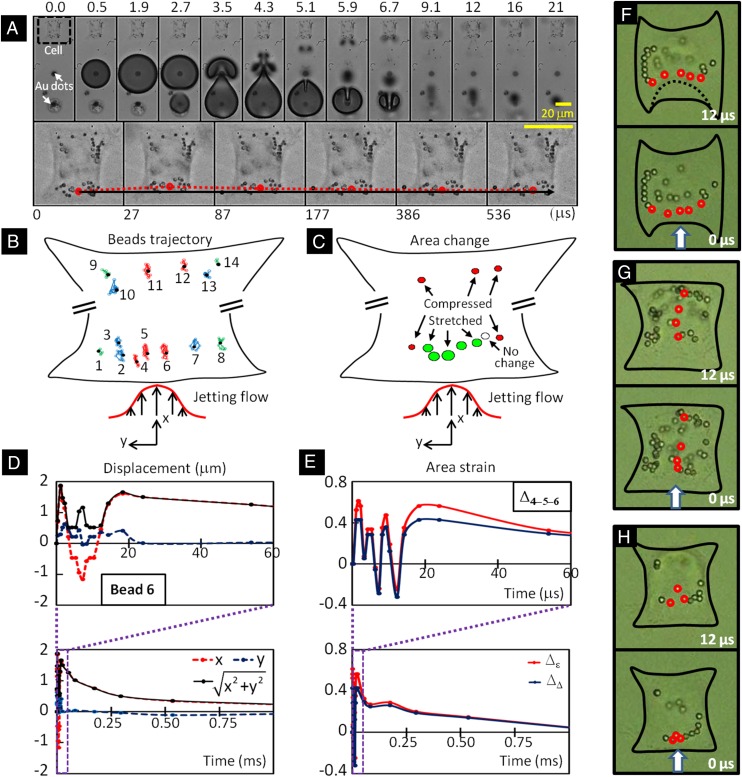
We have developed a unique experimental system to produce TBs with precise control of bubble location, size, and phase relationship, as well as its orientation and standoff distance (S_d) to a single cell grown nearby in a microfluidic channel (Fig. 1A). Cavitation bubbles (maximum diameter = 50 ± 2 μm) were generated by illuminating two pulsed Nd:YAG lasers (λ = 521 nm, 5-ns duration) on a pair of gold dots (15-nm thick and 6 μm in diameter, separated by an interbubble distance d_IB = 40 μm), patterned on the glass substrate of the microfluidic channel (31). Individual HeLa cells were captured nearby and grew on a square island (32 × 32 μm) coated with fibronectin in the shape of either “H-0°” or “H-90°” at various S_d from 10 to 40 μm (Fig. 1B and Fig. S1). This experimental design allows us to minimize the influence of cell size and adhesion characteristics on bubble(s)–cell interaction so that bubble dynamics and associated flow field can be better correlated with cell membrane deformation and resultant bioeffects.

Fig. 1.

Schematic diagrams of tandem bubble generation, jet formation, and resultant flow interaction with a single cell grown nearby in a microfluidic channels. (A) Experimental setup. Two Nd:YAG lasers (laser 1 and laser 2) are projected through a 63X objective (path shown in green) and focused onto a pair of gold dots (6 µm in diameter and 15 nm in thickness) coated on the glass substrate of the microchannel, separated by an interbubble distance (d_IB) of 40 µm. Two high-speed video cameras: a Shimadzu HPV-X (camera 1) and a Phantom v7.3 (camera 2) are used to record bubble–bubble–cell interaction when the fluorophore cube with a dichroic mirror (DM1) is off the light path and the beam splitter (BS1) is at 80/20 position. Thereafter, the fluorophore cube is switched back with BS1 at 0/100 position for fluorescent imaging (path shown in red) using a Zeiss AxioCam MRc 5 (camera 3) and a Xenon light source (Lamp). Imaging acquisition with camera 2 or 3 (path shown in black) is controlled by a rotating mirror (RM) underneath BS1. (B) Illustration of the dynamic interaction of tandem bubbles and the resultant deformation of a target cell (shown in dashed line). Bubble–bubble–cell interaction is conducted in the microchannel with dimension of 800 × 25 µm. Single HeLa cells are confined and grown within a 32 × 32 µm island coated with fibronectin. Two fibronectin coated patterns are used, namely H-0° and H-90°, corresponding, respectively, to the case where the proximal edge of the adherent cell is firmly attached onto the substrate or free standing. The standoff distance (S_d) between the leading edge of the cell and the center of the closer gold dot is varied from 10 to 40 µm in different units of the gold-dots/fibronectin island distributed inside the microfluidic channel for high-throughput experiments.

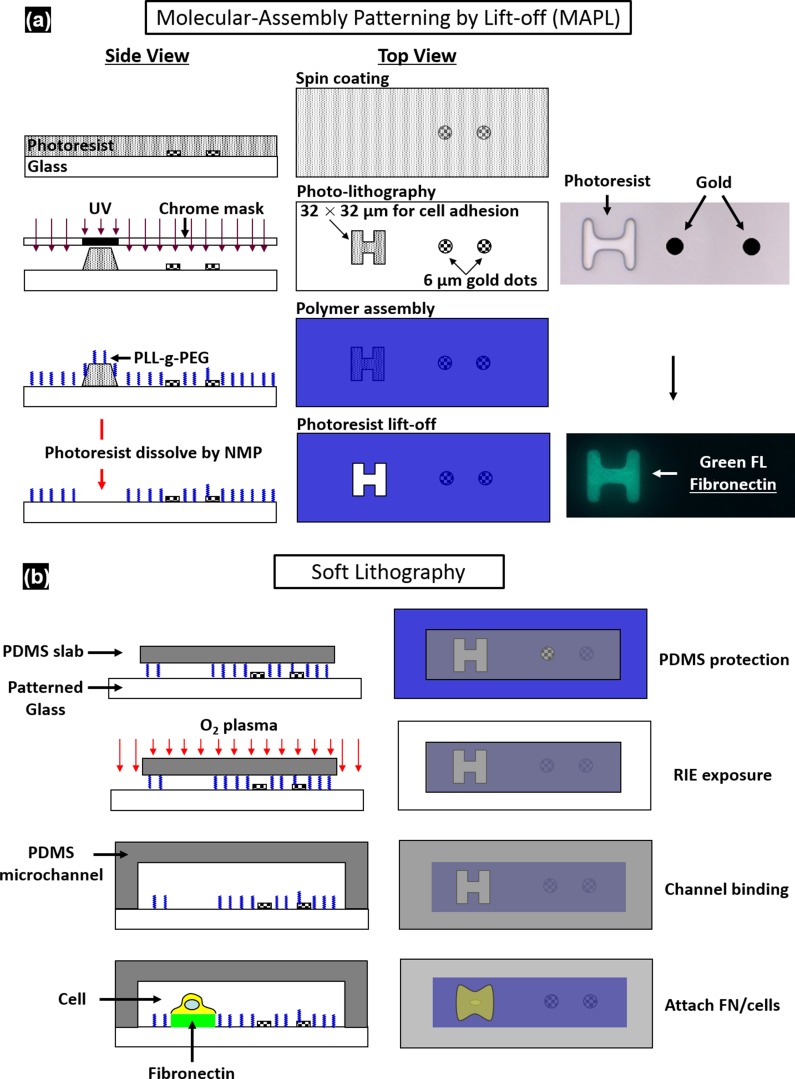
Fig. S1.

Fabrication of the microfluidic chip. (A) Preparation of the patterned glass substrate via MAPL. (B) Assembly of the microfluidic channel with plasma bonding.

By triggering the two lasers with a time delay about 2 μs, TBs of anti-phase oscillation can be produced, leading to the formation of a high-speed microjet toward the target cell. One significant advantage of the microfluidic chip design is that multiple gold dots/fibronectin islands with different combinations of S_d and adhesion patterns can be fabricated in separated channels on the same chip, allowing for high-throughput experiments under nearly identical conditions. Furthermore, by reducing the cavitation bubble(s)–cell interaction domain from 3D to a quasi-2D space (microfluidic channel height = 25 μm), the microfluidic chip design makes it possible to combine high-speed imaging of bubble dynamics with subsequent microscopy of cell deformation and bioeffect assays, as described below.

Characterization of the TB Dynamics and Resultant Jetting Flow Field.

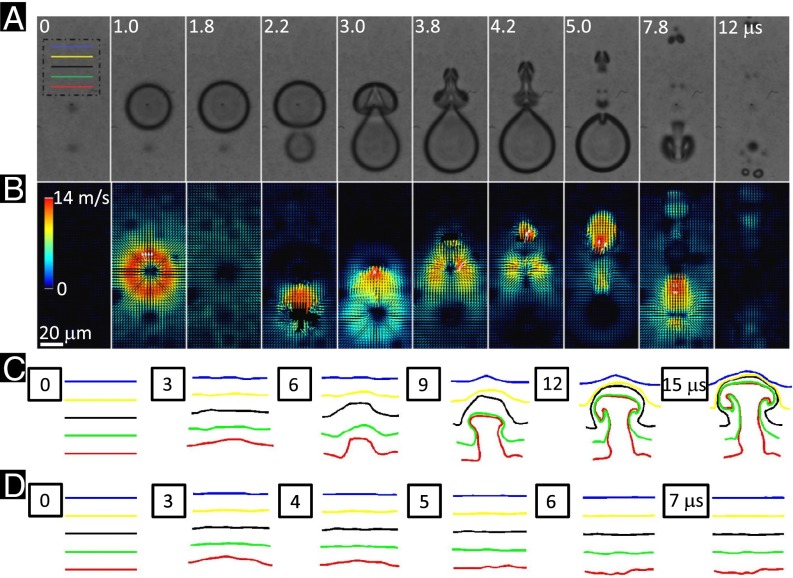
Fig. 2 shows an example of the dynamics of TB interaction and characteristics of the associated flow field. Because of phase difference, the two bubbles repel each other due to the secondary Bjerknes forces (31), leading to jetting away from the center of the TBs (Fig. 2A). The resultant flow field captured by particle image velocimetry (PIV) reveals an inward collapse of the fluid between the two bubbles, followed by an “upward” thrust leading to the jet formation from 3.0 to 5.0 μs in Fig. 2B. This directional jetting flow is concentrated in a width on the order of 10 μm, therefore imposing a highly localized shear stress and stress gradient onto the target cell grown nearby. In contrast, cells in previous studies were stretched globally by cavitation-induced shear flow on a scale of hundreds of microns either in suspension (10) or on a monolayer (14, 32). It is also worth noting that the dynamics of TB interaction are highly reproducible even in the presence of the target cell and the jet speed at touchdown on the opposite bubble wall is about 50 m/s (Fig. S2). The time-lapsed deformation of several parallel material lines in the range of S_d = 20 ∼ 60 μm (Fig. 2C) further illustrates the characteristics of TB-produced jetting flow with vortex formation in a proximity-dependent manner. In this setup, a maximum vorticity of ∼2,800 s⁻¹ could be produced in about 100 ∼ 150 μs following the TB interaction, and the vortical flow will drift along the jetting direction and gradually decay in strength within several hundred microseconds (31). In comparison, the deformation of the same parallel material lines by single bubble oscillation is much smaller both in the axial and radial directions with virtually no vortical flow formation (Fig. 2D).

Fig. 2.

Dynamics of tandem bubble interaction, jet formation, and resultant flow motion. (A) High-speed imaging of tandem bubble interaction captured by a Shimadzu HPV-X camera at a frame rate of 5 × 10⁶ frames per second. Two bubbles of 50 µm in maximum diameter were produced by two pulsed Nd:YAG lasers with about 2-µs interpulse delay. (B) Flow field around the tandem bubble was characterized by using 1-µm polystyrene beads as flow tracers and PIV with 16 × 16 µm interrogation windows and 75% overlap. (C–D) The time histories of five material lines of 40 µm in initial length at different standoff distances (S_d = 20 ∼ 60 μm) from the (C) tandem and (D) single bubble were constructed based on velocity field obtained by PIV. The image plane was 3 µm above the glass substrate of the microfluidic channel.

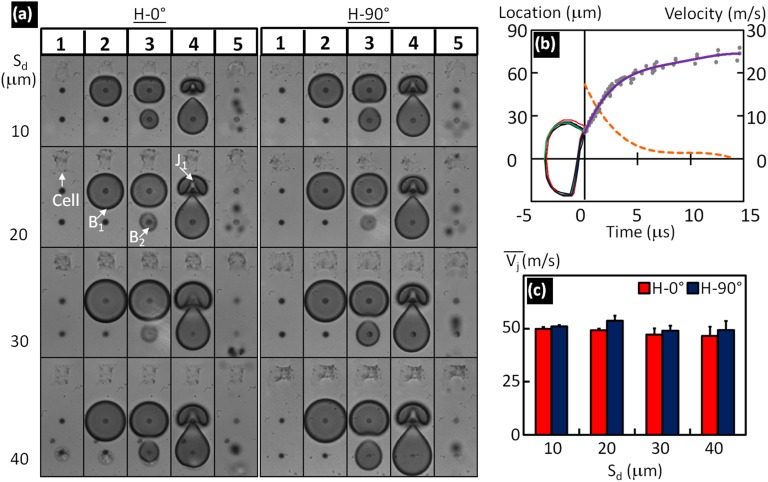
Fig. S2.

Tandem bubble–cell interaction at different standoff distances (S_d) and adhesion patterns. (A) Representative high-speed images of tandem bubble–cell interaction at S_d = 10, 20, 30, and 40 µm for individual cells grown on H-0° and H-90° patterns. Five representative time points marked on top of the images are: before experiment, first bubble at maximum diameter (∼50 µm), initial expansion of the second bubble, touchdown of the first jet on the distal wall of the first bubble, and target cell at maximum deformation. (B) Temporal development of the top and bottom poles of the first bubble, constructed using data from all eight different cases shown in A, before the first jet touchdown at time 0; scattered dots indicate the positions of the daughter bubbles after the first bubble collapse, and the solid line is a polynomial fit from which the average drifting velocity of the daughter bubbles over time is plotted in the dashed line. (C) The average velocity of the first jet before touchdown at time 0. Data at each S_d and adhesive pattern corresponds to the mean and SD from at least six measurements.

Analysis of Cell Membrane Deformation.

Cell membrane deformation caused by external stress is closely associated with intracellular responses, such as signal transduction, cytoskeleton reorganization, changes in gene expression and protein synthesis (33, 34). To quantify deformation, 1-μm polystyrene (PS) beads were attached to the cell membrane through the Arg-Gly-Asp (RGD) integrin binding (35). Fig. 3A shows an example of the cell membrane deformation (grown on the H-0° pattern) produced by the TB at S_d = 40 μm. Because of the depth of field of the imaging system, only PS beads in the peripheral region of the cell that remained within the imaging plane (z = 3 ± 1 μm above the glass surface) during and after the TB interaction were clearly visible and analyzed. In contrast, PS beads attached to the cell membrane in the nucleus region, which is often near the center of the cell with a height about 7 μm, were not captured. The temporal trajectories of 14 individual beads (Fig. 3B) revealed that the TB-induced membrane deformation is highly heterogeneous. The displacement of an individual bead (e.g., bead 6 at the leading edge of the cell, i.e., cell boundary closest to the TB) was found to correlates well with TB-induced flow motion. Specifically, along the jetting direction (x axis), the bead showed an initial stretch-to-recoil oscillation in less than 8 μs (Fig. 3D, Top), corresponding to the expansion and collapse of the first bubble (B₁). This was followed by a secondary stretch of comparable magnitude yet much longer duration (FWHM) of more than 200 μs (Fig. 3D, Lower), propelled by the jetting flow from the asymmetric collapse of B₁ with concomitant elongated expansion of the second bubble (B₂), see Fig. 3A from 2.7 to 4.3 μs. In comparison, the bead’s displacement in the direction transverse to the jetting flow (y axis) was much smaller, and hence the displacement amplitude (i.e.,$\sqrt{x^2+y^2}$) essentially overlapped with the bead’s trajectory in the flow direction. After the second stretch, the bead recovered gradually toward its original position in about 1 ms (Fig. 3D, Lower). Similar pattern of displacement could be seen from other beads with differences mainly manifested in the stretch and recoil magnitudes. It should be noted that the prolonged secondary stretch with slower recovery was sustained by the vortical flow of the jet (Fig. 2C). This feature, characteristic of TB interaction, was not seen in cell membrane deformation produced by a single bubble (e.g., B₁ in Fig. S3).

Fig. 3.

Analysis of cell membrane deformation. (A) Tandem bubble–cell interaction at S_d = 40 µm. First Row, taken at 5.0 × 10⁶ frames/s using the HPV-X camera, shows the tandem bubble dynamics with jetting toward the target cell in the initial 21 µs; Second Row, taken at 3.3 × 10⁴ frames/s using the Phantom 7.3 camera, show the deformation and recovery of the cell beyond 27 µs after the first bubble generation. A dotted line in red highlights the movement of a PS bead attached to the leading edge of the cell membrane, corresponding to the local membrane deformation. (B) Trajectory of 14 individual beads (1 µm) identified on the membrane of the target cell in A within 1 ms after tandem bubble–cell interaction. (C) Peak area strains at different locations of the cell surface calculated from multiple sets of triads of adjacent beads in B. The circle filled with green indicates primary tension and those filled with red indicate primary compression, with the circle size corresponding to the relative magnitude of the area strain. (D) Displacement of bead 6 in B over time along x (red dotted line) and y axis (blue dotted line), and its absolute deviation from the initial position (black solid line). (E) The area strains, calculated based on principal strain derived from the deformation of the triad (in red color) or the geometric area change of the triad (in blue color) defined by beads 4, 5, and 6. (F–H) Close up view of the deformation of three individual cells in response to tandem bubble-induced jetting flow (direction indicated by arrows) in which conjugated PS beads (2 µm) were attached to cell membranes (images recorded by using the Phantom 7.3 camera). Heterogeneous strain distribution along (F) or perpendicular (G) to the leading edge of the target cell can be seen by tracing the length changes of the line segments between adjacent PS beads indicated by red circles. (H) An example of membrane stretching demonstrated by the expansion of a triad area defined by three PS beads before and shortly after tandem bubble interaction (Movie S1).

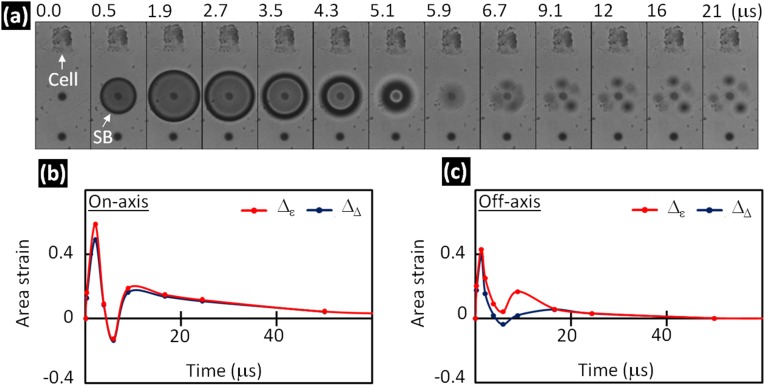
Fig. S3.

SB–cell interaction and changes in area strain of cell membrane with time. (A) SB–cell interaction at S_d = 40 µm. The image sequence, taken at 5.0 × 10⁶ frames/s, shows the characteristic single bubble dynamics with axisymmetric expansion and collapse within 6 µs. (B–C) The area strain, calculated based on principal strains (in red) or the geometric area change of the triad (in blue) for three beads on axis (B) and off axis (C). The recovery of the cell membrane deformation takes about 50 µs.

Using a triad of beads in close proximity, the local nominal area strain of the membrane deformation could be calculated based on either the principal strains or trigonometry of the triad, which represent the upper- and lower-bound values of each parameter (Materials and Methods). The maximum area change shown in Fig. 3C indicates that although the leading edge was primarily stretched (or under tension), the trailing edge or lateral sides of the cell were compressed, demonstrating again the heterogeneity in cell deformation produced by TB-induced jetting flow. Similar to the pattern observed in displacement, the temporal variation of the membrane area strain at the leading edge (Fig. 3E) showed a few initial rapid oscillations followed by a large and sustained stretch for about 100 μs (FWHM), and thereafter, a gradual recovery in a time scale on the order of 1 ms. Both methods of area strain calculation reveal a similar temporal profile in cell membrane deformation. Additional examples are shown in Fig. 3 F and G, illustrating clearly that the leading edge of the cell could be transiently stretched under biaxial tension from TB-induced jetting flow, leading to a large area strain in excess of 100% at S_d ≤ 20 μm (Movie S1). This unique feature may be responsible for TB-induced pinpoint membrane poration reported previously (13).

Assays of Bioeffects Produced by TB-Induced Jetting Flow.

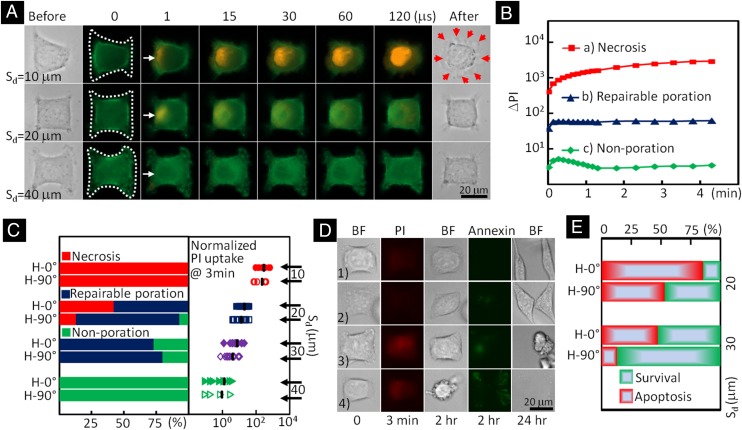
We first evaluated the S_d dependency of membrane poration using individual HeLa cells that had been transfected by LifeAct-GFP so that changes in their actin structure could be observed in real time (Fig. 4A and Movie S2). Poration was monitored by membrane impermeant propidium iodide (PI) uptake from the culture medium (16). During each experiment, a sequence of bright field and fluorescent images of the target cell before and shortly after the TB treatment were taken to capture the morphological and PI intensity changes inside the cell. Three distinctly different responses were observed based on S_d (Fig. 4A). At short S_d (i.e., 10 μm or in some case 20 μm), a local disruption in the actin structure at the leading edge of the cell facing the jetting flow could be observed in 1 s after the TB treatment. This was accompanied by a pinpoint entrance of extracellular PI into the cytosol through the rupture site with a subsequent progressive diffusion of the fluorescent PI-DNA or PI-RNA complexes inside the cytoplasm (7). The PI intensity change (ΔPI) inside the cell increased monotonically with time without saturation (red line in Fig. 4B) and the cell nucleus was stained, indicating necrosis. Previously, swelling has been reported for cells in suspension subjected to shear flow (10) or microjet impact from the asymmetric collapse of an inertial cavitation bubble near a cell trap (36). In this study, we observed predominately necrotic blebs (37) around the target cell with slightly noticeable swelling after the TB treatment at short S_d (see bright field image of the cell in the first row after treatment in Fig. 4A). At intermedium S_d (i.e., majority of 20 ∼ 30 μm), a pinpoint entry of PI at the leading edge of the cell was also observed even though the actin structure change could not be resolved at the optical resolution (∼0.4 μm) of our experimental system. In comparison, the ΔPI inside the cell was an order of magnitude lower and reached a plateau within 10 s following the TB treatment (blue line in Fig. 4B), suggesting repairable poration and likely cell survival. At long S_d (i.e., 40 μm), small but detectable membrane deformation (Fig. 3) with negligible PI uptake (green line in Fig. 4B) or nonporation was observed following TB treatment, and the cell survived with regular growth and proliferation.

Fig. 4.

Bioeffects produced in individual cells exposed to tandem bubble-induced jetting flow at different standoff distances. (A) Time-elapse fluorescence imaging of PI uptake (shown in red) after the treatment in three representative individual cells whose actins were labeled by GFP. The jetting flow comes from the left, indicated by white arrows. The necrotic blebs after the treatment are indicated by red arrows. (B) The average PI intensity change inside the cells treated at S_d = 10 (red), 20 (blue), and 40 µm (green), respectively. (C, Left) The percentage of cells undergoing necrosis (red), repairable poration (blue), negligible or nonporation (green) in groups of individual cells at different standoff distances and adhesion patterns; (Right) the average PI intensity change in the treated cells after 3 min, with all of the results normalized by the mean value of the cells grown on H-90° pattern (shown in groups of open symbols) and treated at S_d = 40 µm. (D) Viability and apoptosis assays applied to four porated cells after tandem bubble treatment. (Left to Right) The five frames show the morphology of the target cell in bright field (BF) before experiment; the PI uptake into the target cell 3 min after tandem bubble–cell interaction; the morphology of the target cell after 2 h; the Annexin V staining outcome after 2 h; and the morphology of the target cell after overnight culture. (E) Summary of the subpopulations of the cells considered being reparably porated based on PI uptake test. The survival ones are shown in green and apoptotic ones are shown in red.

Based on the characteristics of PI uptake, we further categorized the responses of individual cells treated at different S_d for two adhesion patterns (Fig. 4C). Overall, as the S_d increases from 10 to 40 µm, there is a significant shift in cell response from necrosis to repairable membrane poration to nonporation after the TB treatment. The transition is in the intermedium region of S_d = 20 ∼ 30 μm, in which the cells grown on the H-90° pattern showed a higher percentage of repairable membrane poration than their counterparts grown on the H-0° pattern (Fig. 4C, Left). This difference may be attributed to the lower area strain induced in the cells grown on the H-90° pattern because of their weak adhesion to the substrate at the leading edge facing the jetting flow. The ΔPI in 3 min after the treatment, normalized by the background intensity, also shows significant variations among individual cells in each group (Fig. 4C, Right), indicating heterogeneity in single cell response despite otherwise nearly identical experimental conditions. As a group, however, the mean of the normalized ΔPI change (in log scale) clearly showed separations between groups at different S_d. Altogether, these results indicate that distinctly different bioeffects could be produced by adjusting S_d or modulating the strength of the jetting flow applied to the cell. It is important to note that no detectable membrane poration or cell lysis could be produced by a single bubble (SB) under the same experimental condition (13).

We next investigated the subtle differences in cell apoptosis and survival in the repairable regime (i.e., S_d = 20 ∼ 30 μm). Several representative examples are shown in Fig. 4D, in which cells 1 and 2 were found to spread out with limited and discrete Annexin-V staining in 2 h after the treatment, and subsequently divided into two daughter cells within 24 h. In contrast, cells 3 and 4 were apoptotic and started to round up with dispersed Annexin-V staining at 2 h, and eventually disintegrated into small fragments within 24 h. The long-term survival and apoptotic outcome of the cells with repairable poration also shows a clear S_d and adhesion pattern dependency (Fig. 4E). In particular, cells grown on the H-0° pattern and treated at S_d = 20 μm were found to have the highest apoptotic and the lowest survival rate, which is consistent with their higher PI uptake (or likely larger pore size) among the cohort. This finding implies that a large pore size produced by cavitation during sonoporation, for example, although beneficial for drug delivery, may concomitantly increase the risk for apoptosis that will not be desirable in applications such as gene delivery.

Correlation Between Cell Membrane Deformation and Viability.

The jetting flow produced by the TB interaction imposes a transient shear stress on the cell surface, leading to membrane deformation with possible poration that may eventually affect cell survival. To explore this causal relationship, we examined the correlation between the maximum (ε_A,M) or peak area strain (PAS) produced at the leading edge of a cell and the probability of cell viability after the TB treatment. For this analysis, only data from the H-0⁰ group at the leading edge region of the cell were used in which the entire deformation process of the cell membrane (aided by the PS beads) could be clearly visualized by high-speed imaging. Furthermore, considering the impulsive nature of the jetting flow–cell interaction, we calculated the area strain integral (ASI) that incorporates the contribution of both the amplitude and duration of the area strain by:

$$ASI=\underset{t_1}{\overset{t_2}{{\displaystyle \int }}}{\epsilon }_A^{\beta }dt\text{,}$$ [1]

where ${\epsilon }_A$ (= A/A₀ − 1, where A and A₀ are the deformed and original areas of the triad) is the area strain, β is a positive constant or area strain power index, t is time, and t₁ and t₂ delineate the lower and upper integration limits where ${\epsilon }_A$ is 10% of the maximum area strain. Previous studies on RBC damage in ventricular assist device have indicated that area strain (or stress) integral may be appropriate for gauging the membrane rupture under dynamic shear stress with a value of β ∼ 2 (38, 39).

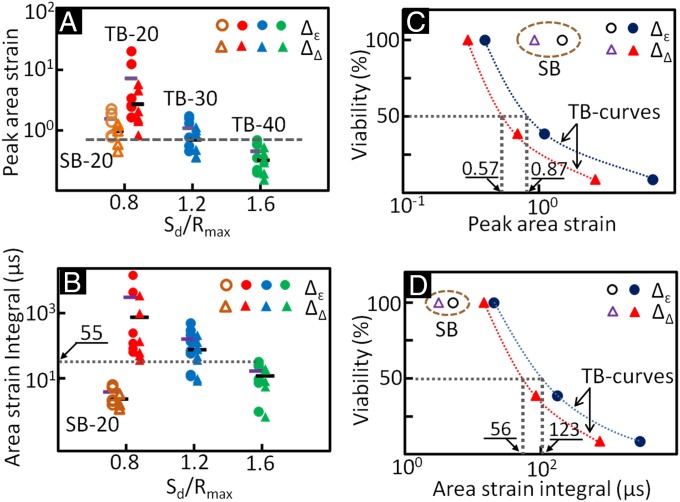
In Fig. 5, the PAS and ASI were calculated based on either trigonometry (denoted by symbol Δ) or principal strains (denoted by symbol $\epsilon$). As S_d (or S_d/R_max) increased, the PAS and ASI produced by the TBs were found to decrease significantly (Fig. 5 A and B), corresponding to reduced membrane deformations and lower propensity for membrane poration and cell injury. Overall, significant variations in individual cells at each S_d were observed. As a group, however, the average values of PAS and ASI, for example, at S_d = 20 μm were found to be significantly higher than their counterparts at S_d = 40 μm (P < 0.05, based on Student’s t test). It is also interesting to note that PAS produced by SB at S_d = 20 μm varied in a wide range overlapping with the cohorts produced by the TBs from S_d = 20 ∼ 40 μm. In contrast, ASI produced by SB at S_d = 20 μm was confined within the range produced by the TBs at S_d = 40 μm. These results suggest that a threshold of ASI may exist that correlates with the minimal high strain-rate mechanical deformation required for producing cell killing in an inertial cavitation field. The correlation between cell viability and PAS (Fig. 5C) or ASI (Fig. 5D) further confirms that ASI is a better predictor of cell viability than PAS under such dynamic impulsive loadings. Specifically, the value of ASI for the SBs falls to the left side of the viability curves for the TBs, which is consistent with the fact that no cell killing is produced by the SBs. In comparison, the value of PAS for the SBs falls to the right side of the viability curves for the TBs, which would suggest cell killing. For 50% of the cells to survive after the TB treatment, the ASI was estimated to be in the range of 56 ∼ 123 μs with a corresponding PAS in the range of 57 ∼ 87%.

Fig. 5.

Membrane deformation assessed at the leading edge of individual cells grown in the H-0° adhesion pattern at different standoff distances, and the correlation between cell viability and peak area strain or area strain integral. Relation between normalized standoff distance S_d/R_max and (A) peak area strain or (B) area strain integral; and correlation between cell viability and (C) peak area strain or (D) area strain integral. Individual cells are treated either with single bubble (open symbol) or tandem bubble (solid symbol). The area strains were calculated based on either the principal strains (Δ_ε, circle) or triad geometry (Δ_Δ, triangle). A lateral bar is used to indicate the average value in each group. The abbreviations are, for example, TB-20 denoting tandem bubble at S_d = 20 µm and SB-20 denotes a single bubble at S_d = 20 µm.

Discussion

We have shown that the pinpoint poration of an adherent cell by TB in close proximity is caused by the localized membrane deformation at the leading edge of the cell, driven by the transient shear stress associated with TB-induced jetting flow. The membrane deformation is impulsive and oscillatory, in accordance with the dynamics of TB interaction. Moreover, the membrane deformation is influenced by adhesion strength, but more predominantly, by the standoff distance of the cell to the TB. With cell shape and adhesion condition standardized by surface patterning, distinctly different outcomes in cell membrane poration, macromolecule uptake, and resultant bioeffects can be produced at various standoff distances within the maximum diameter of the bubble.

Previously, others have investigated single bubble interaction with cell(s) for membrane poration using ultrasound contrast agents (7, 15, 18, 40) or laser-generated single bubbles (14, 41). However, cell membrane deformation was not characterized, and cell shape, orientation, and adhesion conditions were not carefully controlled, which could all substantially influence the cell response and bioeffects produced under mechanical stresses (29). Further, bubble–bubble interaction, a prevalent feature in shock wave lithotripsy (SWL), high-intensity focused ultrasound (HIFU), and sonoporation, were either neglected (14, 41) or difficult to control (15, 32, 42). In comparison, the microfluidic system and methodology developed in this work allow us to simulate reliably bubble–bubble interaction, and analyze resultant jetting flow and cell deformation in sequence with improved precision. As a result, the bioeffects produced in the target cell can be correlated with the characteristics of membrane deformation under well-controlled experimental conditions. With further improvements, such a system has great potential to be used to gain mechanistic insights into bubble(s)–cell interaction and the bioeffects produced by inertial cavitation bubbles.

The bioeffects produced in a monolayer of adherent cells by a laser-generated single bubble with a maximum diameter in the range of 200 ∼ 2,000 μm have been examined rigorously (14, 41, 43). It was shown that cell detachment associated with necrosis, membrane compromise with apoptosis, repairable poration with macromolecule uptake, and cell survival could be produced progressively with an increasing radial distance from the bubble center. These varying bioeffects have been attributed to the exponentially decayed impulsive shear stress produced by either the rapid expansion of the bubble (when it is produced at 10 μm above the cell substrate) or the splashing radial outflow generated by a jet upon asymmetric collapse of the bubble (generated in this case at least 400 μm above the cell substrate). The wall shear stress estimated using a hydrodynamic model or the Glauert solution for a steady and laminar wall jet without the presence of cells is on the order of 10 kPa for membrane poration (41, 43), which is similar to the value reported for our TB system (13). It should be noted that the complexity of TB interaction in a microfluidic channel presents significant challenges in numerical modeling of bubble dynamics (44, 45). Further work is needed to fully characterize the flow field produced by TBs and the associated shear stress applied to the target cell. Despite this, the most salient features observed in the previous studies have been recapitulated in this study with distinct bioeffects produced at the single cell level using the TB system.

The jetting flow generated by the TB interaction (with maximum diameter of ∼50 μm) provides a dexterous means to concentrate cavitation energy on a small region of the cell so that highly localized shear stress and strain can be applied, leading to pinpoint membrane deformation or poration. This unique feature may be explored to probe the regional differences in cell mechanics (46), cytoskeleton rearrangement, and mechanotransduction (25) at micrometer scale. In contrast, the radial flow produced by the expansion or collapse of an SB (often with a much larger size) covers a large area occupied by multiple cells and thus exerts a shear stress globally over an individual cell surface, leading to presumably a more uniform membrane deformation and often multiple pores formed randomly in different regions of the cell (see, for example, figure 5 in ref. 32).

More importantly, the vortices generated by the TB interaction can substantially prolong the duration of jetting flow-induced impulsive stretch of the cell membrane compared with its counterpart produced by SBs of equivalent size by more than an order of magnitude (Fig. 3E and Fig. S3). This important distinction and the associated differences in membrane poration and bioeffects produced by TB vs. SB at comparable peak area strains clearly indicate the importance of loading duration on cavitation-induced membrane poration. This observation is in agreement with the characteristics of cell damage under dynamic loading, i.e., the critical stress (or strain) required to produce cell lysis increases dramatically when the loading duration is decreased by an order of magnitude in the range from seconds to milliseconds to microseconds (47, 48). The effect of loading duration on cavitation-induced bioeffects has been assessed previously by stress impulse (43, 49). Our results suggest that the area strain integral, which scales with strain energy density impulse, represents a better parameter to gauge the propensity of bioeffects produced by inertial cavitation bubbles. This observation (based on the minimal energy required to create a new surface) is consistent with the theory of membrane pore formation under dynamic surface tension (50, 51).

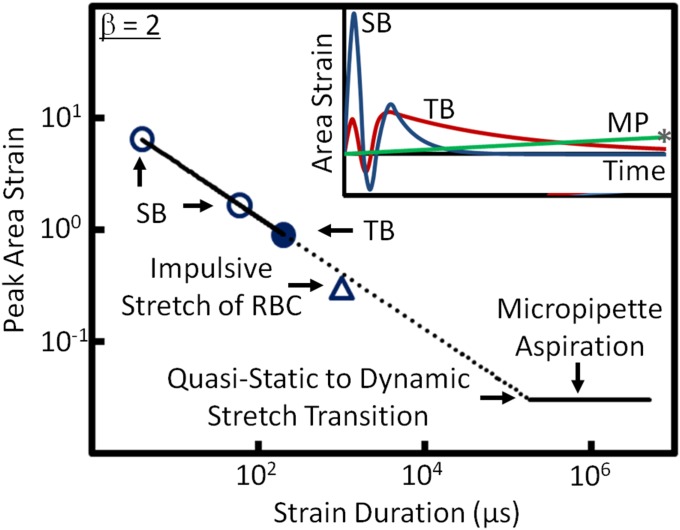
The effect of loading duration on cell membrane damage from an impulsive stretch can be further illustrated by the correlation between PAS and strain duration for different cavitation exposure scenarios (Fig. 6). Here, we assume that the threshold of ASI for membrane portion is constant, for example, a nominal value of 55 μs for HeLa cells treated by TBs (Fig. 5B). Using this criterion, and by further assuming that the strain profile induced by an SB in a cell (Fig. 6, Inset) can be approximated by a triangle, we can estimate the PAS threshold required to produce membrane poration using the following equation:

$$PAS={\left[\left(\beta +1\right)\hspace{0.17em}\cdot \hspace{0.17em}\frac{ASI}{t_s}\right]}^{\frac{1}{\beta }}\text{,}$$ [2]

where t_s is the duration of the tensile strain. As shown in Fig. S3, the membrane strain produced by an SB has two characteristic peaks, corresponding to the initial expansion and subsequent collapse of the bubble. The strain durations of the first and second stretches are about 4 and 60 μs, respectively, corresponding to 640% and 170% in PAS threshold for SB-induced membrane poration. Extrapolation of a line fitting through the PAS thresholds for SB and TB predicts a PAS threshold about 40% at 1-ms strain duration, which is similar to the area strain produced in RBCs by the impulsive stretch of a large cavitation bubble (10, 24). Furthermore, a PAS threshold of about 4% can be predicted at 100-ms strain duration, which is within the range reported for cell membrane damage measured by micropipette (MP) aspiration of RBCs under quasi-static loading rates (20, 22). Overall, the ASI threshold criterion appears to predict a general trend in impulsive stretch-induced membrane poration, which suggests that the critical PAS for membrane poration could be increased from 3% ∼6% at a loading rate about or less than 1/10 of a second, which is in the transition region, to a value greater than 100% when subjected to a loading rate of a few hundred microseconds or shorter under high strain-rate dynamic loadings.

Fig. 6.

A general relationship between peak area strain threshold that can be tolerated by individual cells under mechanical stretches of different strain rates and strain duration. Inset shows a sketch of representative strain histories produced by different loading methods: TB, SB, and MP aspiration. The peak area strain threshold at different strain duration is estimated based on Eq. 2 using a nominal area strain integral threshold of 55 µs for HeLa cells.

Even with surface patterning and precise control of standoff distance, we still observed significant variations in the membrane deformation and resultant bioeffects from individual cells in each group (Figs. 3–5). This heterogeneity in cell response may be influenced by the subtle differences in the cytoskeleton structure of individual cells (52), which needs further investigation. But more importantly, this finding is consistent with the emerging understanding that cellular heterogeneity (or diversity) that arises from stochastic processes in gene expression, protein, and metabolite synthesis is a fundamental principle of biology that ensures evolutionary advantages of the population (30). Because of cellular heterogeneity, population-based bulk measurements are often inaccurate and unreliable for understanding the functions of individual cells and their interaction. As a result, there is a growing interest in developing new technologies for single cell analysis to better understand, for example, the key signaling pathways and processes in cancer and stem cell biology (53–55). The TB system described in this work provides a versatile and noncontact tool for analyzing the mechanical deformation and bioeffects in single cells under high strain-rate load conditions, which warrant in depth studies in the future.

In conclusion, we have developed a microfluidic system to control precisely the bubble(s)–cell interaction, and demonstrated the correlation between area strain integral and cell membrane poration under dynamic shear stresses with extremely high strain rates (>10⁴ s⁻¹). With the experimental system and knowledge acquired in this work, we shall be able to explore systematically the mechanotransduction at single cell level produced by high strain-rate shear flows associated with inertial cavitation and dynamic bubble–bubble interactions that are prevalent in therapeutic ultrasound applications. The mechanistic insights and precise control in microfluidic systems will also offer us ample opportunities in single cell analysis for disease diagnosis and treatment monitoring based on mechanical characterization of the cell.

Materials and Methods

Fabrication of Microfluidic Chip.

The microfluidic chip was assembled from a polydimethylsiloxane (PDMS; Sylgard 184; Dow Corning) microchannel mold (40 × 25 × 5 mm) and a patterned glass substrate (50 × 37.5 × 1 mm). The PDMS microchannel, having a cross-section of 800 × 25 µm, was produced from a silicon master using soft lithography. AutoCAD was used to design hundreds of repeating units on the glass substrate with each unit consisting of a pair of gold dots and a square island with a H-shaped region (Fig. 1) to be covered by fibronectin while the surrounding background was passivated with PLL-g-PEG to prevent cell adhesion (56). The main variations in different repeating units are S_d and the orientation of the H-shaped region. During the fabrication, the arrays of gold dots were first patterned on the glass substrate by means of metal lift-off (57). Using molecular assembly by patterned lift-off (MAPL) technique (58), PLL-g-PEG was coated on the surface except for the H region, which was subsequently covered by fibronectin. The patterned glass substrate and the PDMS microchannel were treated by O₂ plasma separately before they were permanently bonded together. The PDMS mold was aligned to the patterned glass under a stereomicroscope aided by alignment marks. Detailed preparation protocol can be found in Supporting Information.

Cell Culture and Handling.

HeLa cells were routinely maintained in DMEM supplemented with 10% FBS and 1% antibiotic/antimycotic solution in a cell culture incubator. On the day of experiment, cells were trypsinized and resuspended in culture medium to a density of ∼5 × 10⁶ cells/mL before introduced into the microfluidic chip. The injected cells were allowed to settle down and initiated adhesion onto the fibronectin covered H regions for 30 min. Nonattached cells were flushed out, and the chip was subsequently placed back in the incubator for 1.5 h under continuous perfusion of culture medium at a flow rate of 0.2 µL/min. Using this protocol, individual cells could fully spread out and grown on the fibronectin-covered patterns (H-0° or H-90°).

To facilitate membrane deformation analysis, 1 µm carboxyl functionalized PS beads were attached to the cell membrane, serving as displacement tracers. A seeding density of 1 × 10⁹ beads/mL was used, corresponding to about 60 beads per cell on the apical membrane surface. To ensure persistent binding, the PS beads (1% wt/vol, activated with water soluble carbodiimide) were coated with RGD-containing peptide (Peptite-2000; 100 µg/mL in PBS) before attachment (59).

Before experiment, the regular DMEM was replaced by propidium iodide (PI) solution (100 µg/mL in DMEM) in the microchannel to trace in real-time macromolecular uptake after membrane poration (7). A constant flow rate of 0.5 mL/min was used throughout the experiment. For early-stage apoptosis assay, FITC Annexin V (20× dilution in PBS from stock; Life Technologies) solution was perfused for 15 min before epifluorescence microscopy imaging. Thereafter the chip was perfused with regular DMEM and returned to the incubator for culture overnight. The phenotype morphology changes of the treated cells were recorded next day.

TB Treatment and Image Acquisition.

The microfluidic chip with cells was placed on the stage of a motorized inverted microscope (Axio Observer Z1; Zeiss). Two Q-switched Nd:YAG lasers (New Wave Research) were focused through a 63× objective (LD Plan Neofluar; Zeiss) and projected on a pair of gold dots to generate tandem bubble next to a target cell. Before treatment the original intracellular PI intensity and morphology of the cell were recorded by a CCD camera (AxioCam MRc; Zeiss) using fluorescence and bright field (BF) imaging, respectively. Zeiss AxioVision software was used to control illumination shutter, dichroic mirror, and switching between two adjacent alternative positions in the rotating turret (within 200 ms). Transistor–transistor logic (TTL) trigger signals from a delay generator (565-8c; Berkeley Nucleonics Corporation) were used to synchronize lasers and cameras for TB generation and image acquisition.

Bubble oscillation, jet formation, and resultant cell deformation were captured by a high-speed video camera (HPV-X; Shimadzu) operated at 200-ns interframe time (IFT) or 5 M fps with 100-ns exposure time for 25 µs following the trigger of the first laser. Immediately after the TB–cell interaction, the recovery of the target cell membrane deformation was recorded for 1 ms using a second high-speed video camera (Phantom V7.3; Vision Research) operated at 20-µs IFT with 1-µs exposure time. Thereafter, the AxioCam camera, operated at 2–10 s IFT, was used to record PI diffusion from the poration site into the target cell for 300 s; or in other experiments, Annexin V and PI staining performed at 2 and 24 h after the TB treatment.

Characterization of TB-Generated Flow Field.

PS beads (1 µm, 2.6% wt/vol in culture medium) were used as tracers to map the flow field produced by TBs. High-speed image sequences of TB interaction recorded by the Shimadzu camera were analyzed offline using a commercial PIV software (DaVis 7.2; LaVision). The image field (100 × 200 µm) was divided into multiple interrogation windows of 16 × 16 µm each with 75% overlap, and multipass iterations and regional filters were applied to reduce the error in velocity field computation (see details in Supporting Information). To improve the accuracy of velocity field calculation, each flow field was recorded up to 3 times under the same experimental condition and the resultant images were superimposed before PIV analysis.

To further illustrate the characteristics of the flow motion produced by the TBs, the deformation of five parallel imaginary material lines, each 40 µm in length and initially placed at S_d = 20, 30, 40, 50, 60 µm, respectively, were traced. Each material line consisted of 1,000 individual material points the incremental displacements of which at consecutive time points were calculated based on the local velocity interpolated from the PIV results. By interconnecting these material points at different time steps, the evolution of the material lines in TB-induced flow field could be visualized (Fig. 2C).

Calculation of Cell Membrane Deformation.

A triangulation scheme was adapted to analyze the local membrane strain (60). The triangular areas selected for strain calculation were in the peripheral region of the cell away from the nucleus, and therefore the beads’ displacement was confined within the focal plane of the objective lens. The beads were traced over time and their coordinates were recorded from the high-speed images. Area strain calculations were carried out based on principal strains (see details in Supporting Information) determined by using a custom code written in Matlab (The MathWorks) following established protocols (61, 62). For comparison, the area strain was also calculated based on trigonometry to determine the change of the triangular area encompassed by the triad of beads.

SI Materials and Methods

Fabrication of Microfluidic Chips.

A multistep protocol was developed to pattern gold dots (for bubble generation) and fibronectin covered regions (for cell adhesion) on the same glass substrate of the microfluidic chip. First, the glass substrate was deposited with an array of paired gold dots having an interbubble distance (D_IB) of 40 μm using metal lift-off technique (57). To control the locations of cell deposition on the glass substrate, multiple sets of H (H-0° or H-90°) shaped patterns (32 × 32 μm in size) that define the regions for individual cell adhesion were produced by MAPL method (58). As shown schematically in Fig. S1A, a layer of 2-μm-thick positive photoresist (S1813, positive; Shipley, MA) was spin coated on the glass substrate already decorated with gold dots. Alignment of the H-shaped regions with the gold dots was carried out by using a chrome master photomask under a lithography mask aligner (MJB3; Suss MicroTec). After UV illumination and subsequent development, H-shaped photoresist patterns were produced next to each pair of gold dots at different standoff distance (S_d) specified in the mask design. PLL-g-PEG (0.5 mg/mL) solution was prepared in Hepes buffer [10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid, pH adjusted to 7.4 with 0.1 M NaOH solution], and a 120-μL solution drop was placed on a paraffin film. The glass substrate with hybrid gold dots/H patterns was facing down and plated onto the liquid drop, leading to an anti-biofouling layer formed electrostatically on the surface in 45 min (63). Thereafter, the glass substrate was soaked in N-Methyl-2-pyrrolidone with ultrasonic agitation to remove the H-shaped photoresist pattern, and thus exposing the underneath surface. As a result, the gold-dot patterned glass surface was coated with PLL-g-PEG everywhere to prevent cell adhesion except in the individual H-shaped regions.

Next, the microfluidic chip was formed by plasma bonding of the patterned glass substrate with a preformed PDMS microchannel (40 × 25 × 5 mm) (Fig. S1B). The PDMS microchannel and a small PDMS slab (800-μm-wide groove structure) designed to shield the patterned area of the glass substrate during plasma etching were prepared in advance using soft lithography. Oxygen reactive ion etching (RIE; 100 W, 500 mTorr, 60 s) was applied to remove PLL-g-PEG from the peripheral area of the glass substrate not covered by the PDMS slab. The PDMS microchannel with preprepared fluid access ports (ɸ = 0.64 mm) was treated under reduced dose of oxygen plasma (RIE; 25 W, 500 mTorr, 25 s), aligned to the patterned glass substrate (with the small PDMS slab removed) and brought in conformal contact under a stereoscope. After bonding, the microchannel was primed with PBS for 30 min at 1 μL/min, followed by 30 min perfusion treatment of fibronectin solution (50 μg/ml in PBS, 1 μL/min) to cover the H-shaped patterns with fibronectin. Excessive fibronectin solution in the microchannel was flushed out by injection of PBS at 30 μL/min for 5 min. Thereafter the microchannel was immediately infused with cell suspension to initiate cell attachment in a sterile biohood.

Characterization of TB Interaction with Jet Formation in the Presence of Individual Cells Nearby.

The influence of individual cells grown at S_d = 10 ∼ 40 µm on TB interaction and jet formation was evaluated. Eight representative examples were compiled in Fig. S2A, in which half of the cells were grown on H-0° (column 1) and the other half on H-90° (column 2) patterns. Overall no significant differences in bubble dynamics, TB interaction, or jet development could be observed. Only at short S_d = 10 µm (and occasionally at 20 µm), the flattening of the upper pole of the first bubble (B₁) near its maximum expansion (frames 2 and 3) due to interaction with the neighboring cell was noticed. Jet formation (J₁) driven by the collapse of B₁ with simultaneous expansion of the second bubble (B₂) led to deformation of the target cell. The severity of cell deformation increased with reduced S_d and from H-90° to H-0° patterns (see cell shape changes from frame 1 to frame 5). The temporal variations in the locations of the top and bottom poles of B₁ before touchdown, denoted by time 0 in the plot, overlapped with each other closely in all eight cases, demonstrating again the consistency in bubble expansion and collapse (Fig. S2B). The average velocity of J₁ during the asymmetric collapse of B₁ before touchdown was about 50 m/s, independent of S_d and orientation of the target cell (Fig. S2C). After the touchdown, B₁ broke down into several smaller daughter bubbles (Figs. 2A and 3A) in which some of them often traveled along the J₁ direction for about 50 µm with gradually reduced speed (see Fig. S2B for t > 0). A polynomial fit was used to illustrate the overall trend in the displacement of these daughter bubbles (solid line), from which the drifting velocity of the daughter bubbles over time was calculated (dashed line). It was noted that substantial deviation from the fitted curve starts at a distance around 50 µm above the center of the TB where the leading edge of the cell was located. Thereafter the velocity of the daughter bubbles was gradually reduced to 0 within 15 µs.

PIV analysis of Flow Field.

The optimal size and concentration of flow tracer beads were used to meet the criteria that each bead occupies between 2∼4 pixels (px) in diameter and there are ∼10 beads in each interrogation window (i.e., 16 × 16 px) (64). Based on the objective lens (63X) and the high-speed camera (400 × 250 px) used, we estimated a spatial resolution of about 0.4 µm in the focal imaging plane. The flow velocity field in the region of interest was calculated by applying cross-correlation to each interrogation window at two consecutive time points. A large interrogation window size (e.g., 32 × 32 px) was initially used to avoid beads escaping from or jumping into the final interrogation area (65). In postprocessing, regional median filter was further applied to remove spurious vectors, which may be caused by nonuniform beads distribution or out-of-plane displacement. In such cases, the affected vector was replaced by the median value interpolated from its neighbor vectors (66).

Methodology of Area Strain Calculation.

Assumption and algorithm.

The peripheral regions of the cell away from the nucleus were selected for strain calculation, and the displacements of beads chosen were confined in the focal plane of the objective lens. Under 2D plane strain assumption, the principal strains (ε₁ and ε₂) of the cell membrane in the region enclosed by a triad of beads were determined following an established method (62), from which the local area strain was calculated by:

$${\epsilon }_A=(A/A_0-1)=(1+{\epsilon }_1)(1+{\epsilon }_2)-1={\epsilon }_1+{\epsilon }_2+{\epsilon }_1{\epsilon }_2.$$ [S1]

Alternatively, the area of a planar triangle specified by its three vertices (x₁, y₁), (x₂, y₂), (x₃, y₃) can be calculated by the Heron’s formula:

$$A=\sqrt{s(s-l_1)(s-l_2)(s-l_3)}=\frac{1}{2}\left|(-x_2{y}_1+x_3{y}_1+x_1{y}_2-x_3{y}_2-x_1{y}_3+x_2{y}_3)\right|,$$ [S2]

where s = (l₁ + l₂ + l₃)/2 is the semiperimeter of the triangle and l₁, l₂, and l₃ are the lengths of the three sides, respectively.

Uncertainty analysis for area strain calculation.

The reading error in measuring the bead position (e_bp) is determined by the resolution of our imaging system and also related to the percent uncertainty ($u_{x_i}$ and$u_{y_i}$) in measuring the coordinates of vertices of the triangle (x_i and y_i) through:

$$e_{bp}=x_i\cdot u_{x_i}=y_i\cdot u_{y_i}(i=\mathrm{1,2,3}).$$ [S3]

Further, the percent uncertainty in area calculation of a triangle is given by:

$$u_A=\sqrt{{\displaystyle \sum _{i=1}^3\left({\left(\frac{x_i}{A}\cdot \frac{\partial A}{\partial x_i}\cdot u_{x_i}\right)}^2+{\left(\frac{y_i}{A}\cdot \frac{\partial A}{\partial y_i}\cdot u_{y_i}\right)}^2\right)}},$$ [S4]

in combination with Eq. S3 it can be further simplified to be:

$$u_A=\frac{e_{bp}}{2A}\sqrt{l_1^2+l_2^2+l_3^2}.$$ [S5]

Similarly, the percent uncertainty in calculating the area strain can be derived as:

$$u_{{\epsilon }_A}=\frac{A}{{\epsilon }_A{A}_0}\sqrt{{\left(u_{A_0}\right)}^2+{\left(u_A\right)}^2}=\frac{1}{\left(1-\raisebox{1ex}{$A_0$}\!\left/ \!\raisebox{-1ex}{$A$}\right.\right)}\sqrt{{\left(u_{A_0}\right)}^2+{\left(u_A\right)}^2}.$$ [S6]

From Eqs. S5 and S6, it can be seen that the uncertainty in area strain calculation is small for cell with large deformation and from triad of equal sides. Based on the experimental data collected from the images by the Phantom camera, the average uncertainties in the maximum area strain calculation were estimated to be 32%, 53%, and 63% at S_d = 20, 30, and 40 µm, respectively.

Actin Change and Rearrangement in Individual Target Cells After TB Treatment.

Cytoskeleton change and remodeling were monitored in real time for a subgroup of the cells starting at 1 s after the TB treatment. For live cell imaging, the actin filaments of the HeLa cells were prelabeled with LifeAct-GFP DNA plasmid (67). In brief, HeLa cells were grown to above 90% confluence in a 60-mm cell culture Petri dish for transfection. One day before the experiment, 6 µL DNA (1 µg/µL) and 12 µL Lipofectamine 2000 (Lifetechnologies) were diluted in 600 µL Opti-MEM reduced serum medium, respectively, for 5 min. Thereafter, two diluted solutions were mixed together and incubated at room temperature for another 5 min to allow DNA–lipid complex formation. The solution was then added into the Petri dish with cell monolayer and cocultured with cells for 24 h for gene transfection. The transfection medium was replaced with regular culture medium before trypsinization for cell seeding in the microfluidic chip. After the TB–cell interaction, the actin structure was recorded every 5 s for a total duration of 5 min.