pH-responsive self-assembly of polysaccharide through a rugged energy landscape

Abstract

Self-assembling polysaccharides can form complex networks with structures and properties highly dependent on the sequence of triggering cues. Controlling the emergence of such networks provides an opportunity to create soft matter with unique features; however, it requires a detailed understanding of the subtle balance between the attractive and repulsive forces that drives the stimuli-induced self-assembly. Here we employ all-atom molecular dynamics simulations on the order of 100 ns to study the mechanisms of the pH-responsive gelation of the weakly basic aminopolysaccharide chitosan. We find that low pH induces a sharp transition from gel to soluble state, analogous to pH-dependent folding of proteins, while at neutral and high pH self-assembly occurs via a rugged energy landscape, reminiscent of RNA folding. A surprising role of salt is to lubricate conformational search for the thermodynamically stable states. Although our simulations represent the early events in the self-assembly process of chitosan, which may take seconds or minutes to complete, the atomically-detailed insights are consistent with recent experimental observations and provide a basis for understanding how environmental conditions modulate the structure and mechanical properties of the self-assembled polysaccharide systems. The ability to control structure and properties via modification of process conditions will aid in the technological efforts to create complex soft matter with applications ranging from bioelectronics to regenerative medicine.

Introduction

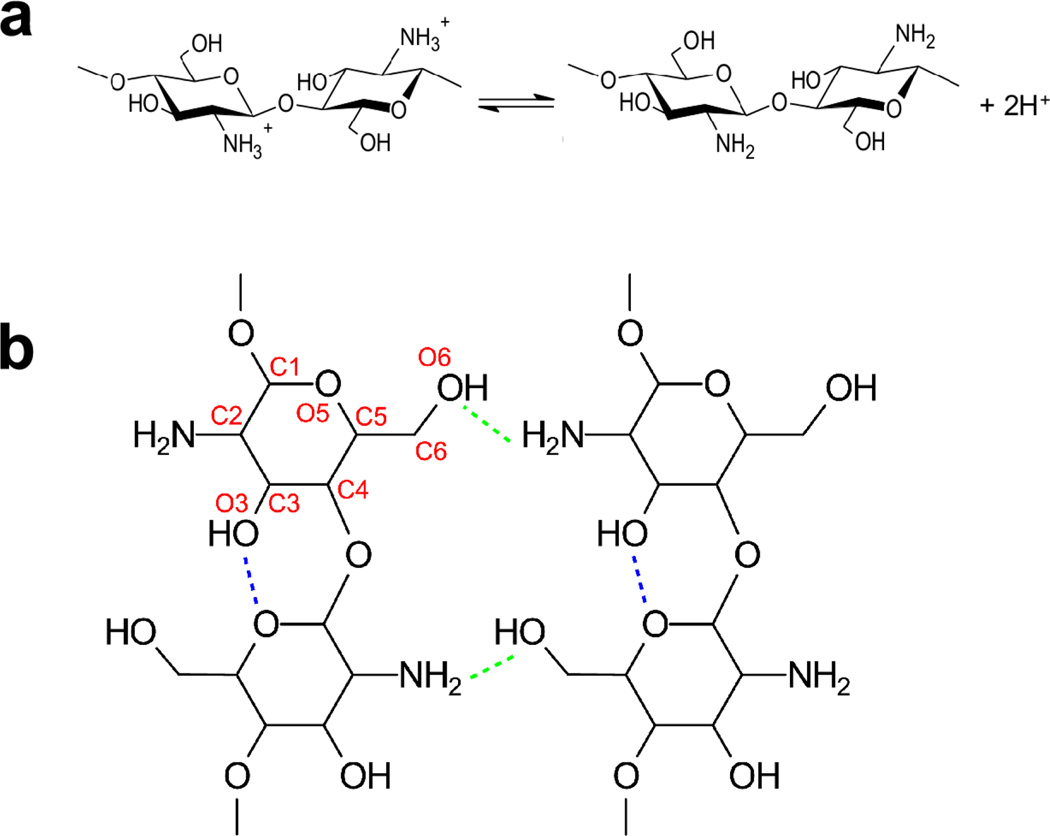
Chitosan is a pH-responsive self-assembling polysaccharide that possesses a unique combination of properties¹ useful for applications in medicine,^2,3 pharmacy,^4,5 and bioelectronics.^6,7 Formally, chitosan is a copolymer of glucosamine and N-acetylglucosamine with the pH-responsiveness conferred by the primary amine of glucosamine (1a). At low pH these amines are protonated, making chitosan a cationic polyelectrolyte. Intramolecular hydrogen bonding between the hydroxyl O3 and ring O5 atoms confers rigidity to a single chitosan chain, while intermolecular hydrogen bonding between the amine N and hydroxyl O3 as well as O6 atoms is responsible for the self-assembly and the anti-parallel packing of the chains in the crystalline domains^8,9 (1b).

Most investigations of the pH-responsive self-assembling properties of chitosan have focused on its “primary” structure. Extensive studies have evaluated how molecular weight, degree of acetylation, and sequence affect the properties of chitosan^10,11 and especially the pH-responsiveness (e.g., pK_a).¹² However, recent work suggests that the pathway of assembly may significantly impact the network structure and properties of chitosan.^13–15 For instance, it is well-known that a neutralization mechanism allows chitosan hydrogels to be electro-deposited in response to cathodic inputs, but recent experiments showed that a sequence of cathodic inputs can organize the hydrogels into complex multilayers.¹⁶ Recent work also showed that salt concentration dramatically influences the morphology and mechanical strength of the electro-deposited layers¹⁷ (2a). However, the molecular details and mechanisms of the pH-triggered formation of complex structures are currently not understood. This lack of understanding limits technological efforts to access the broad design space available for the creation of chitosan-based soft matter with unique features.

Typically, the self-assembly of chitosan is triggered by an imposed increase in solution pH that leads to the deprotonation of amines. The pH-dependent behavior of weak polyelectrolytes is traditionally characterized by an experimentally-accessible apparent pK_a value. Until now, modeling efforts to describe ionization of chitosan^18,19 and other weak polyelectrolytes^20,21 have been restricted to the mean-field approaches, i.e., solving the Poisson-Boltzmann equation for electrostatic potential based on simplified geometric models of the assembly or snapshots from molecular dynamics simulations. However, the mean-field approaches neglect the spatial variability of the dielectric environment, and most importantly they can not describe microscopic mechanisms involving coupled proton titration and conformational dynamics, which underlies the pH-controlled self-assembly processes of weak polyelectrolytes.

Here we apply traditional all-atom molecular dynamics (MD)²² and the all-atom version^23–25 of continuous constant pH molecular dynamics (CpHMD)^26,27 with the pH replica exchange (pH-REX) protocol²⁸ to elucidate the pH-controlled self-assembly of chitosan, We use 100% de-acetylated chitosan (i.e., poly-glucosamine) as a model system for simplicity. Acetylated glucosamine residues are left out in our simulations because they would not affect pH dependence²⁹ but would add significant complexity. The unique and important feature of CpHMD is that it allows simultaneous titration of all ionizable groups in response to conformational dynamics at a specific pH condition, thus enabling the mutual effect of protonation/deprotonation (behavior of polyelectrolyte) and chain dynamics including dissociation/association. The simulations show that an increase in pH leads to the deprotonation of amine groups, resulting in the formation of intermolecular hydrogen bonds and a cooperative transition from soluble chains to a crystalline-like state. Consistent with experiment but contrary to intuition, the presence of salt leads to a more ordered aggregate, revealing a rugged energy landscape in which intermediate states can be populated dependent on environmental conditions.

Results and Discussion

The self-assembly simulations were initiated from 24 unprotonated (neutral) chitosan chains comprised of 10 glucosamine units each, randomly distributed in a cubic water box of 83.5 Å in edge length, with and without 0.5 M NaCl. Due to the time scale of self-assembly, the conventional molecular dynamics was employed, with all of the glucosamines fixed in the unprotonated state. For each condition (with and without salt), three independent 300-ns trajectories were run starting from different random configurations, resulting in an aggregate sampling time of 1.8 µs. In all of the simulations a single aggregate was formed and the total number of inter-chain hydrogen bonds (2b) and the total solvent-accessible surface area (SASA) reached a plateau by ~200 ns. See Supporting Information (SI), Figure S1. We note that, the higher weight percent of chitosan in the simulation (11%), roughly seven times the experimental condition (1.5% as reported in Ref¹⁷), may accelerate the rate of self-assembly. However, we do not expect it to affect the difference in the free energy landscape, e.g., thermodynamic pathway, between the salt and no-salt conditions at the same concentration, which is the focus of the current work. While it is desirable to match the experimental concentrations, such simulations would be computationally prohibitive. That being said, we acknowledge that due to the limited number of chitosan chains, the simulations can only explore the early steps of the self-assembly process.

Significant qualitative differences are seen between the different salt conditions (2b–e). Without salt, the average number of intermolecular hydrogen bonds per glucosamine unit (H-bonds per unit) increases to one in the first 100 ns and remains nearly constant over the final 200 ns of the simulation (2b). With salt, however, the formation of hydrogen bonds continues past 100 ns, ultimately reaching about two per unit (2b). Without salt, the hydrogen bonds that form initially are somewhat stable with lifetimes that remains nearly constant over time (2b). By contrast, with salt, the initially-formed hydrogen bonds are destabilized, i.e., have a shorter lifetime, consistent with the expectation that small alkali ions break hydrogen bonds.³⁰ After 100 ns, however, as more hydrogen bonds are formed in the presence of salt (2b), their lifetime increases substantially. Dramatic differences in the network generated are seen in the final self-assembled structures. Without salt, the network shows volume-spanning inter-chain connectivity, while with salt, the more abundant intermolecular hydrogen bonds result in a more compact aggregate (2c and d). The salt-induced differences in SASA and hydrogen bonds were consistent for all 3 sets of simulations (Figure S1).

The presence of salt also results in more ordered aggregates. The distribution of the angle between pairs of chains shows a bimodal distribution with peaks near 0 and 180°, indicating that the chains adopt a parallel or anti-parallel orientation (2e). In the absence of salt this ordering is not seen, and the angle distribution has a single broad peak. These results are reminiscent of previous simulations of fatty acids aggregates, which showed that in bilayers the angles between fatty acid tails had a bimodal angle distribution, while in micelles, where there is no preferential orientation between tails, the angle distribution is a single broad peak centered at 90°.³¹ The salt-induced chain ordering was consistent for all 3 sets of simulations, although the ordering in the last run was less pronounced (Figures S2).

These data are consistent with the experimental observations (2a).¹⁷ In the absence of salt, chitosan forms a hydrogel network with a featureless morphology and high mechanical strength (high elastic modulus). However, with added salt, chitosan forms a network with an aggregated morphology and limited mechanical strength, as indicated by an elastic modulus that is three orders-of-magnitude lower with a salt concentration of 0.25 M or higher, compared to the value with no salt. More importantly, the simulation data offer a microscopic explanation for the dramatic differences. In the absence of salt, the initially formed intermolecular hydrogen bonds are relatively strong, resulting in a meta-stable network that is volume-spanning and offers mechanical strength. By contrast, in the presence of salt, the initially formed intermolecular hydrogen bonds are destabilized and their short lifetime allows the chains to rearrange and search conformational space for thermodynamically more stable states, which have a larger number of intermolecular hydrogen bonds and therefore a more compact structure.

To elucidate the pH-controlled mechanism, we employed all-atom pH-REX CpHMD simulations starting from a pre-assembled crystalline domain (referred to as model crystallite) comprised of 16 neutral 10-unit chitosan chains arranged in a 4×4 pattern (3a, and Figure S3). This particular model was chosen, as test simulations using various chain lengths and arrangements showed that it is the smallest aggregate that remained stable over the course of a 50-ns molecular dynamics simulation. Note, longer chains would form stable aggregates, however, simulations of larger aggregates are computationally more demanding. Shorter chains may also form stable aggregates with larger number of chains, however, related test runs were not performed. The final configuration was used as the starting structure for the pH-REX CpHMD simulation, where all 160 amine groups simultaneously titrate. The pH-REX protocol subjects the model crystallite to parallel molecular dynamics at 19 pH conditions, allowing the amine groups to go from the fully protonated to the fully deprotonated state and vice versa. Based on the Metropolis criterion, the replicas are allowed to swap pH conditions periodically, resulting in an accelerated convergence in both protonation and conformational space.²⁸ The simulation length was 17 ns per replica, for an aggregated simulation time of 323 ns. More details see Methods and Protocols in SI.

We monitored the pH-induced dissociation of the model crystallite by calculating the number of H-bonds per unit at different pH (3b). At pH 4, the dissociation was rapid and completed by 9 ns, while at pH 5, the process was slower and completed by 13 ns. As pH was increased to 6.5 and above, the model crystallite became only partially dissociated at the end of 15 ns (3a and b). Finally, at pH 8 and above, the model crystallite remained stable with the number of inter-chain hydrogen bonds fluctuating around 2 per residue throughout the simulation. These data are in agreement with the observation that chitosan is soluble at pH below ~6.5.¹ Convergence of the chain-chain dissociation at different pH was verified by plotting the probability distributions of the number of H-bonds per unit obtained from different time windows (Figure S4). Since the chitosan concentration in the CpHMD simulation (6% by weight) is higher than in experiment (1.5% by weight), we verified that the fully-protonated chains do not experience significant electrostatic repulsion by examining the minimum interchain N-N distances at low pH condition. We found that the probability of distances less than 12 Å was only ~5% (Figure S9). Thus, the concentration used in the CpHMD simulation should not cause anti-cooperative effect due to charge repulsion.

The simulations revealed a considerable local variation in the degree of hydration and protonation within the assembled crystallite. Consider the pH 7 condition as an example (3c). The external regions of the crystallite show high levels of hydration and the amines are readily protonated (ionized), while in the internal regions, the water-chitosan hydrogen bonds are replaced by inter-chain hydrogen bonds and the amines remain deprotonated (neutral). Thus, there is a significant spatial variation in the dielectric environment of the chitosan assembly, which influences the local degree of ionization. This demonstrates that a detailed understanding of the self-assembly behavior of weak polyelectrolytes necessitates microscopic models beyond the mean-field approaches. Importantly, the spatial variation in hydration and ionization is due to the chain-chain association and is not the result of intra-chain interactions. The latter is supported by the CpHMD simulation of a single chitosan chain in solution showing that all glucosamine residues are fully hydrated and there is little variation in the degree of protonation (3d). The spatially varying degree of ionization can also be characterized by the microscopic pK_a’s of the amines, which span a range of 6 to 7.8 for the model crystallite but 7.3 to 7.8 for a single chain (Figure S5).

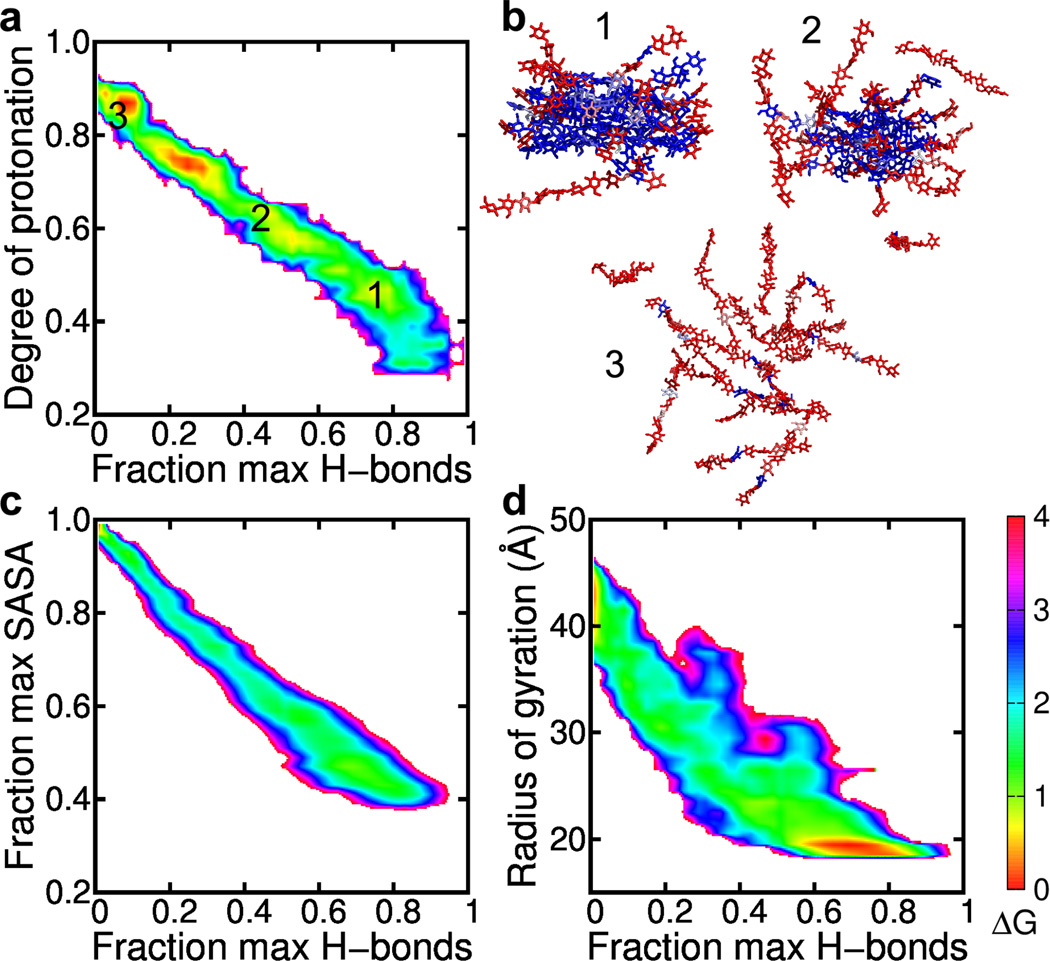
To further explore the coupling between the polyelectrolyte behavior (ionization) and chain-chain dissociation, we plotted the overall degree of protonation of the amine groups vs. the number of inter-chain hydrogen bonds per glucosamine unit (4a). The plot reveals a negative correlation, i.e., the number of hydrogen bonds decreases with increasing degree of protonation, indicating that as the chains become protonated, electrostatic repulsion leads to the disruption of the hydrogen bonds and dissociation of the crystallite. To illustrate the spatial-temporal progression of the chain-chain dissociation process and its coupling to the ionization of the amines, 4b displays three representative snapshots. In the early stage, the amine groups in the interior are deprotonated, while those at the solute-solvent interface are protonated (4b, snapshot 1). As the chain “peels away” from the hydrogen-bonded network, more amine groups become solvent exposed and protonated (4b, snapshot 2). Upon complete loss of the hydrogen-bonded network, all the amine groups are solvent exposed, and ~90% are protonated (4b, snapshot 3). These data are consistent with the spatial variation of the protonation degree of the chitosan assembly (3c), thus strengthening the view of the mutual effect between ionization and dissociation.

To characterize the disassembly pathway of chitosan, we computed the free energy surface (FES) along two progress variables, fraction of the maximum solvent accessible surface area (SASA), representing the degree of solvent exposure of the chains, and fraction of the maximum number of H-bonds, representing the degree of chain-chain association. A diagonal pathway can be seen from the fully associated state with the maximum number of H-bonds and minimum solvent exposure (4c, lower right) to the fully dissociated state with no hydrogen bonds and complete exposure to solvent (4c, upper left). Thus, the disassembly follows a pathway in which the chain-chain dissociation occurs concomitantly with the uptake of water molecules to hydrate the chains. We note that 4c is based on the data from all pH conditions, however, the shape of the pathway is independent of pH (Figure S6). As we are not modeling an equilibrium between associated and dissociated states, the values of free energies reported here (i.e. the depth of the minima) are likely not converged. However, extending the simulation would only result in addition sampling of the endpoints, changing the free energy surfaces in a quantitative manner but not qualitatively affecting the pathway we have discussed.

In analogy to the analysis of protein folding, we can also investigate the dissociation pathway of chitosan using the FES in terms of the radius of gyration representing the degree of expansion of the model crystallite and the fractional number of H-bonds representing the degree of departure from the “native state” (opposite to the degree of nativeness in protein folding³²). Consistent with the FES using the fractional SASA as one of the progress variables, a diagonal shape is seen, indicating a concomitant expansion of the crystallite and loss of intermolecular hydrogen bonds (4d). The lower right corner of the map shows a broad free energy minimum, reflecting the fact that the model crystallite is very flexible, with the fractional number of hydrogen bonds fluctuating between 0.6 and 0.9. This large fluctuation, which can be seen at other pH conditions (Figure S7), is likely due to the small size of the model crystallite.

Consistent with the dissociation of chitosan, the FES for self-assembly also shows a diagonal path, with a concurrent decrease in fractional SASA and increase in the number of hydrogen bonds in the presence and absence of salt (5), suggesting a mechanism of concomitant formation of intermolecular hydrogen bonds and expulsion of water molecules from the interior region. We note that the radius of gyration is not used here as it is not well defined for the self-assembling systems. The final states of the self-assembly simulations have larger fractional SASA and smaller number of of hydrogen bonds due to the limited simulation time. Simulations with orders of magnitude longer time may be required to reach the fully ordered crystalline-like state.

A major difference can be seen between the FES’s with (5 right) and without salt (5 left). The free energy minima for the simulations without salt are located towards the upper left corner (larger SASA and less hydrogen bonds), indicating that the self-assembly process becomes trapped in an intermediate state with less than 40% of the hydrogen bonds formed. This is consistent with the earlier data showing that the simulations without salt resulted in a less ordered aggregate (2e). Closer examination of the FES’s in the presence of salt reveals a shallow minimum in a similar location as the major minimum in the no-salt FES. Thus, these data suggest that the self-assembly of chitosan occurs on a rugged energy landscape, with multiple minima along the pathways to the final ordered state, a scenario reminiscent of RNA folding.^33,34 Salt appears to destabilize the intermediate states, enabling the formation of the thermodynamically more stable states with larger number of hydrogen bonds and more compact structure.

The pH-responsive predictions from the simulations are summarized in 6. At low pH, chitosan exists as individual, fully protonated chains, while at high pH chitosan is assembled into structures with largely unprotonated amines (6a). The transition between the two regimes occurs between pH 6.25 and 6.75 (6a). These predictions are consistent with the experimentally observed pH-dependent solubility of chitosan.¹ We compare the simulated macroscopic (bulk) titration curves of an isolated glucosamine residue, a single chitosan chain and the model crystallite (6b). The former two were obtained via additional CpHMD simulations (see SI). The simulated titration of the monomer unit (red curve) reproduces the experimental pK_a of 7.7.^29,35 Simulation of a single chain shows a small down-shift of the apparent (residue-averaged) pK_a to 7.4 (green curve), which is due to a small degree of intra-chain electrostatic repulsion. Simulation of the model crystallite shows a larger pK_a down-shift to 6.8 (black curve), in quantitative agreement with experiment (blue curve).²⁹ Thus, the 0.9-unit shift in pK^a relative to the glucosamine monomer is mainly due to the desolvation and inter-chain electrostatic repulsion and the related anti-cooperativity (Hill coefficient of 0.87) between the amines on the nearby chains. Convergence of the pK^a was verified by examining the titration curves of the model crystallite over multiple time windows (Figure S8).

Finally, the CpHMD simulations offer an estimate of the pH-dependent change in the free energy of dissociation (stability) for the model crystallite. The stability at pH 8.5 was used as a reference (since the crystallite is most stable at this pH). A negative value represents destabilization, i.e., unfavorable for self-assembly. Shown in Fig. 6c, the self-assembly becomes unfavorable by about 60 kcal/mol as pH decreases to below pH 6.25. This large free-energy change indicates the remarkable stability of the chitosan assembly. It also suggests that chitosan can self-assemble into metastable states that can persist indefinitely, reinforcing the previous conclusion of a rugged energy landscape, consistent with experimental observations that dramatic structural differences can be generated depending on how the triggering stimuli for self-assembly are imposed.^13–16

Figure 6. pH-responsive predictions from the CpHMD simulations.

a, Intermolecular hydrogen bonds per glucosamine residue at different pH. Data points are the averages over the final 3 ns of each pH condition. Error bars represent the standard deviation. Inset are final snapshots at pH 4 and 8.5, with neutral and charged residues colored blue and red, respectively. b, The fraction of unprotonated amines at different pH conditions for a single glucosamine monomer, a single 5-residue chain, and the model crystallite. The solid lines are the best fits to the Hill equation (single chain and crystallite) or Henderson-Hasselbalch equation (monomer). Unprotonated fractions were averaged over the final 5 ns of the simulations for the monomer and single chain, and over the final 3 ns of the simulation for the model crystallite. Experimental data are adapted from Ref.²⁹ c, pH-dependent free energy of dissociation of the model crystallite. The free energy of dissociation at pH 8.5 was used as a reference.

Conclusion

We applied the state-of-the-art molecular dynamics simulations to elucidate the mechanisms and pathway of the pH-triggered self-assembly of chitosan. The study demonstrates the unique capability of CpHMD as a materials science tool for investigating dynamical, pH-responsive systems and unveils several novel features of the aminopolysaccharides. At neutral and high pH, deprotonation of amine groups enables the formation of intermolecular hydrogen bonds and concomitant dehydration of the internal region of the associated chains leading to gelation. The pH-dependent transition from the soluble to gel state is analogous to the pH-dependent folding of proteins³⁶ and the morphological transition of ionizable surfactants such as fatty acids.³¹ However, unlike small natural proteins that fold on a smooth funnel-like landscape with minimum frustration,³⁷ the self-assembly pathway of chitosan follows a rugged energy landscape where intermediate states can be destabilized by the presence of salt, reminiscent of RNA folding.^33,34 Interestingly, salt disrupts weak hydrogen bonds, lubricating conformational search for maximized hydrogen-bonding network and the thermodynamically more stable states. Although our simulations represent the very early events in the electrodeposition process of chitosan films, which may take seconds or minutes to complete, these insights shed light on how processing conditions influence the structure and properties of self-assembled polysaccharide systems. The ability to form persistent meta-stable states provides a rich design space for creating soft matter with unique structures and functions; however, robust predictive tools will be needed to access this design space.

Materials and Methods

The self-assembly simulations were initialized by randomly placing 24 chitosan chains, each consisting of 10 glucosamine units, in a cubic box of 83.5 Å in length. The systems were solvated with about 17,600 CHARMM-style TIP3P water molecules. In the system with 0.5 M NaCl, 175 NaCl pairs were added via random replacement of solvent molecules. Simulations were performed in the NPT ensemble, at a constant temperature of 300 K and pressure of 1 bar, using GROMACS 4.5.5.²² Each simulation (salt and no-salt) lasted 300 ns. To ensure statistical significance, each simulation was performed three times starting from slightly different configurations.

The CpHMD simulations of model chitosan crystallite were performed using an in-house modified version of CHARMM c37b,³⁸ where the all-atom CpHMD method is implemented.²³ The crystallite contained 16 chains each consisting of 10 glucosamines. The final configuration from the 50-ns conventional MD simulation of the neutral crystallite was placed in a 90.45 Å cubic box with about 22,000 CHARMM-style TIP3P water and 160 randomly distributed titratable water (hydroniums) and chloride counter-ions. No additional salt ions were added. Titratable water was used to maintain constant charge throughout the simulations for all pH conditions.^24,25 Recent work from other groups showed that the number of counter-ions required to neutralize a simulation box may result in an artificially high concentration of ions near a charged solute,³⁹ and that high ion concentrations can possibly lead to artifacts.⁴⁰ However, since the potential artifacts affect the morphology of lipid and surfactant assemblies, which is not the topic of this work, we feel that the charge neutralization scheme used here is appropriate, especially given that our recent work showed that enforcing charge neutrality in the simulation box significantly improves the accuracy of all-atom constant pH MD simulations.²⁵ The pH-based replica-exchange protocol was applied²⁸ with 19 pH conditions, from pH 4 to 8.5 in 0.25-unit intervals. The CHARMM36 carbohydrate force field was used to represent the chitosan.⁴¹ Each pH replica was run for 17 ns at a constant temperature of 300 K and pressure of 1 atm. The aggregated simulation time was 323 ns. More details of Methods and Protocols are given in SI.

Figure 1.

a, Acid-base equilibrium of chitosan. b, Chitosan structure with intra- and intermolecular hydrogen bonds indicated by blue and green dashed lines, respectively. Atom names are given in red.

Figure 2. Self-assembly of chitosan chains in the presence and absence of salt.

a, Experimental results for chitosan films electrodeposited by a neutralization mechanism in the presence of varying levels of salt (reproduced with permission from Soft Matter¹⁷). b, The number of intermolecular hydrogen bonds per glucosamine residue as a function of simulation time in the presence of 0.0 and 0.5 M NaCl (top), and average lifetime of intermolecular hydrogen bonds as a function of simulation time at salt and no-salt conditions (bottom). c,d, Snapshots of the self-assembled structures at 300 ns in the presence of 0.0 and 0.5 M NaCl. Multiple periodic images are shown, with the primary simulation box outlined in black. Hydrogen, water, and ions are hidden for clarity. e, Distribution of angles between chitosan chains, averaged over the final 100 ns of the 3 independent runs. Angles are between the vectors joining the first and last glucosamine units of each chain.

Figure 3. pH-dependent dissociation of a model crystallite.

a, Initial structure, consisting of 16 10-unit chains in a 4×4 arrangement (top), and the final snapshot at pH 7 (bottom). b, Average inter-chain hydrogen bonds per glucosamine residue as a function of simulation time at several pH conditions. c, Hydration number and degree of protonation of individual amine groups mapped onto the final snapshot at pH 7. The hydration number (0–4) is indicated by a color scale from green to magenta. The degree of protonation (0–1) is indicated by a color scale from blue to red. Hydration number is defined as the number of water oxygens within 3.5 Å of the amine nitrogen, while the degree of protonation of an amine group is between 0 (always deprotonated) and 1 (always protonated). Both quantities are the averages over the last 0.5-ns of the pH 7 replica. d, Hydration number and degree of protonation of individual amine groups of an isolated chitosan chain in water at pH 7. Data taken from the CpHMD simulation of a single 5-unit chitosan.

Figure 4. Mechanism and pathway of the pH-induced dissociation of the chitosan crystallite.

a, Correlation between the fraction of the maximum number of H-bonds per unit and the overall degree of protonation for the model crystallite at pH 6. Color indicates the free energy (kcal/mol) relative to that of the most probable state. Calculations based on the CpHMD simulation at pH 6, with bin widths of 0.02 for the degree of protonation and fraction of maximal number of hydrogen bonds. b, Snapshots taken from the CpHMD simulation at pH 6. Neutral and charged residues are colored blue and red, respectively. Numbers correspond to the labeled states in a. c, Free energy surface in terms of the fraction of the maximum solvent-accessible surface area (SASA) and the maximum number of H-bonds per unit in the model crystallite. Calculations were based on all pH replicas. SASA was calculated using a probe radius of 1.4 Å. d, Same as c, except that the y axis is the radius of gyration of the model crystallite. A bin width of 1 Å was used for radius of gyration.

Figure 5. Salt dependence of the self-assembly pathway of chitosan.

Free energy surface in terms of the fraction of maximum SASA and maximum number of H-bonds without salt (left) and with salt (right). The maximum number of H-bonds is taken from that in the model crystallite. Each panel uses the entire 300-ns trajectory of the self-assembly simulation. Free energy is given in kcal/mol.