Abstract
Purpose:
Magnetic particle imaging (MPI) is a new imaging technology that directly detects superparamagnetic iron oxide nanoparticles. The technique has potential medical applications in angiography, cell tracking, and cancer detection. In this paper, the authors explore how nanoparticle relaxation affects image resolution. Historically, researchers have analyzed nanoparticle behavior by studying the time constant of the nanoparticle physical rotation. In contrast, in this paper, the authors focus instead on how the time constant of nanoparticle rotation affects the final image resolution, and this reveals nonobvious conclusions for tailoring MPI imaging parameters for optimal spatial resolution.
Methods:
The authors first extend x-space systems theory to include nanoparticle relaxation. The authors then measure the spatial resolution and relative signal levels in an MPI relaxometer and a 3D MPI imager at multiple drive field amplitudes and frequencies. Finally, these image measurements are used to estimate relaxation times and nanoparticle phase lags.
Results:
The authors demonstrate that spatial resolution, as measured by full-width at half-maximum, improves at lower drive field amplitudes. The authors further determine that relaxation in MPI can be approximated as a frequency-independent phase lag. These results enable the authors to accurately predict MPI resolution and sensitivity across a wide range of drive field amplitudes and frequencies.
Conclusions:
To balance resolution, signal-to-noise ratio, specific absorption rate, and magnetostimulation requirements, the drive field can be a low amplitude and high frequency. Continued research into how the MPI drive field affects relaxation and its adverse effects will be crucial for developing new nanoparticles tailored to the unique physics of MPI. Moreover, this theory informs researchers how to design scanning sequences to minimize relaxation-induced blurring for better spatial resolution or to exploit relaxation-induced blurring for MPI with molecular contrast.
Keywords: magnetic particle imaging, magnetic nanoparticles, ferrofluid relaxation, relaxation, drive field, phase lag
1. INTRODUCTION
Magnetic particle imaging (MPI) is an emerging molecular imaging technique that directly detects a safe iron oxide nanoparticle tracer. MPI is the first molecular imaging technique simultaneously capable of: nanomolar sensitivity, absolute linear quantitation of a tracer, zero attenuation with depth, depth-independent resolution, and monitoring of a safe, stable tracer for weeks to months. The images produced by MPI fundamentally differ from images produced by x-ray/CT, MRI, and ultrasound, which are inherently anatomical imaging techniques. Instead, MPI sees only a tracer and, like nuclear medicine, does not see tissue. The intense magnetic moment of superparamagnetic iron oxide (SPIO) tracers coupled with the fact that MPI does not see tissue provides unparalleled contrast and sensitivity. MPI’s technical capabilities make it complementary to existing molecular and anatomical imaging techniques, giving scientists a versatile new tool when working with angiography, cancer imaging, and cell tracking.
Because of its excellent contrast, penetration, and sensitivity, MPI is particularly well suited for safe angiography (see Fig. 1) in patients with chronic kidney disease (CKD).1–4 Twenty-five percent of patients that present to the angiography suite have CKD, and their weak kidneys cannot safely process the iodine or gadolinium contrast agents used in x-ray, x-ray/CT, and MRI angiography.5–7 In contrast, MPI uses a SPIO nanoparticle tracer, which is safe for use in the CKD population because SPIOs are cleared by the liver and not the kidneys.8,9 Indeed, one SPIO tracer (Ferumoxytol, AMAG Pharmaceuticals, Lexington, MA) is approved by the FDA as a treatment for anemia in CKD patients.10
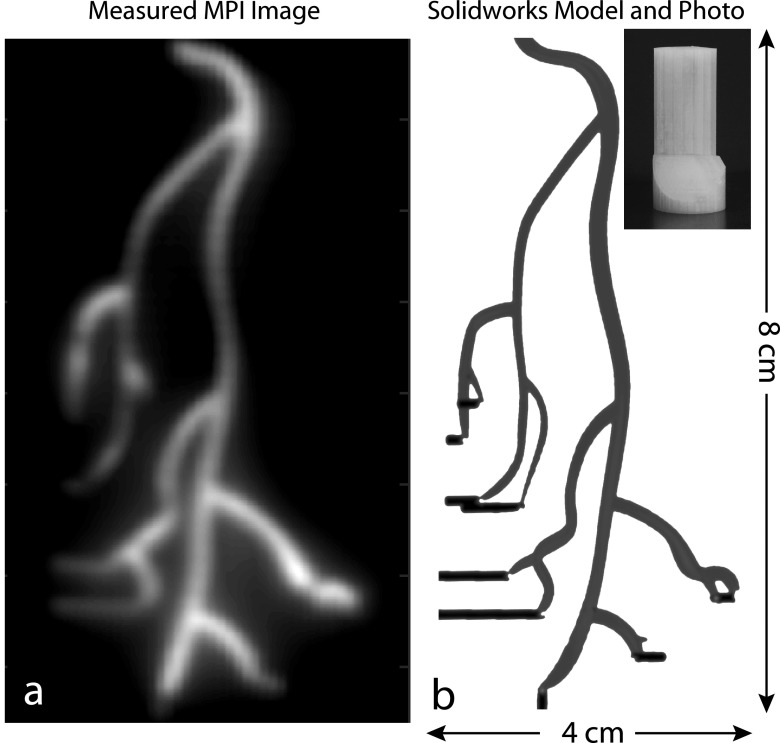
FIG. 1.
As a tracer imaging technique, MPI has applications in molecular imaging and angiography. (a) Experimental MPI image of (b) 3D printed coronary artery model. The modeled arteries (1.8–2.3 mm diameter) formed cavities within the cylindrical 3D ABS plastic model with injection holes illustrated in black and are filled with one part SPIO tracer (Nanomag-MIP) and four parts DI water. The maximum intensity projection image was acquired in the Berkeley 3D MPI scanner with a 10 min total imaging time and a 4.5 × 3.5 × 9.5 cm field-of-view. No deconvolution was performed. A threshold at 10% of the maximum signal was applied to remove noise.
The MPI imaging process is straightforward and can be described classically as a consequence of Langevin physics.1,3 MPI uses a strong magnetic gradient field known as the selection field to saturate all SPIOs outside a central field-free region, which in the scanner shown in Fig. 3(a) is a “field-free point,” or FFP, but can also be a line.1,11–13 To produce an image, the FFP is rapidly rastered over an imaging volume by a time-varying “drive field.” As the FFP traverses a SPIO nanoparticle’s location, the SPIO’s magnetization flips 180° to follow the magnetic field. The time-varying magnetization induces a voltage in the receiver coil, which can be assigned to the instantaneous FFP location to produce a MPI image.14 The intense electronic magnetization of the SPIO particles is 22 × 106 times stronger than the nuclear paramagnetism imaged in MRI at 7.0 T, which allows for MPI even at very low tracer concentrations.3 The voltages induced are linearly proportional to the number of SPIOs at the instantaneous FFP location, enabling quantification of SPIO quantity. Importantly, biological tissue does not attenuate the low-frequency magnetic fields used in MPI, making the technique independent of source depth. This makes MPI ideal for high-contrast, high-sensitivity, quantitative stem cell tracking and angiography.
FIG. 3.
(a) The Berkeley 3D MPI scanner acquires 3D images using a 7 T/m selection field. A drive coil scans the FFP of the scanner at 23.2 kHz up to 30 mT peak amplitude. The Berkeley relaxometer, shown with (b) side and (c) top views, measures the PSFs of SPIO nanoparticles. A sinusoidal magnetic field is generated in the drive coil at frequencies of 1.5–25 kHz and of 5–100 mT drive field peak amplitude, and a bias coil of ±160 mT. The MPI signal is detected using a gradiometrically decoupled receive coil and digitized at 10 MSPS.
The spatial resolution of today’s prototype MPI scanners is not yet competitive with MRI or CT. It is, therefore, of utmost importance that we explore techniques to improve the MPI resolution achieved before deconvolution or postprocessing techniques are applied. MPI spatial resolution is primarily governed by the SPIO saturation field, the strength of the selection field gradient, and the magnetic relaxation properties of the SPIO. It is well understood that we can improve MPI’s spatial resolution by increasing the selection field strength (typically 2–7 T/m with current technology). Doubling the gradient field strength will improve image resolution twofold. Synthesizing a SPIO with half the saturation field will also improve image resolution twofold. The design principle for MPI-tailored SPIOs is the theoretical cubic dependence of spatial resolution on the SPIO core size.14,15 Hence, Langevin theory posits that doubling the diameter of a SPIO from 12 to 24 nm ought to improve MPI linear resolution eightfold. Indeed, larger SPIOs specifically tailored to the unique physics of MPI have recently been synthesized and have experimentally demonstrated spatial resolution improvements.16 Research efforts to optimize SPIO core size have already reduced the full-width at half-maximum (FWHM) resolution of single-core nanoparticles by a factor of 2.17,18
Experimental results with larger diameter SPIOs (Refs. 16 and 17) suggest that there is a practical limit to the theoretical improvements implied from the Langevin model, where increasing the size of the SPIO core produces cubic gains in linear resolution. In particular, relaxation effects often become more pronounced with larger SPIOs. Relaxation effects delay the ability of a SPIO’s magnetization to flip in response to the applied field, leading to image blurring3,4,16,19,20 and reduced signal-to-noise ratio (SNR).19,21,22 Hence, we see a practical experimental limit to the improvement in spatial resolution by increasing core size.
Hence, we believe that improving MPI spatial resolution by employing larger diameter SPIOs could fail unless great care is taken to tailor the MPI imaging sequence to minimize relaxation effects. The key goal of this paper is to establish design principles for optimized scanning sequences that minimize total image blur. Indeed, in this paper, we experimentally demonstrate, for the first time, that drive field sequence optimization can improve MPI spatial resolution by as much as 40%. This goal differs considerably from that of prior work in MPI relaxation that measured and modeled relaxation times with particle size and sequence parameters.21,22 For example, we show that despite an increased relaxation time constant, image blur is actually minimized by smaller drive field amplitudes. We also show that relaxation in MPI can be approximated as a frequency-independent phase lag. These results enable us to accurately predict MPI resolution and sensitivity across a wide range of drive field amplitudes and frequencies for both a nonimaging MPI relaxometer and a 3D MPI imager. We believe that knowledge of nanoparticle behavior across a wide range of drive field frequencies and amplitudes is essential as we begin to design scanning sequences to minimize the deleterious effects of relaxation or to exaggerate regions of differing relaxation properties.
2. SPIO RELAXATION PHYSICS
Before we explore how relaxation affects the imaging process, let us first review Néel and Brownian relaxation physics. The Néel and Brownian relaxation time constants, first derived in the early 20th century,23–25 predict the time it takes for thermal fluctuations to reorient the net magnetization to zero following the removal of an applied magnetic field.23–29 Néel relaxation describes when the magnetic moment reorients within the magnetic core, and Brownian relaxation describes physical rotation of the nanoparticle. All nanoparticles simultaneously experience both Néel and Brownian relaxation, and which relaxation mechanism dominates and depends on nanoparticle characteristics and environmental parameters (e.g., temperature, magnetic core diameter, and hydrodynamic diameter of the nanoparticles). These time constants have been extensively studied in ferrofluids.26–28
Néel and Brownian formulations that neglect the presence of a strong (>10 mT), time-varying magnetic drive field have only limited application for modeling MPI. Indeed, theoretical models of SPIO behavior indicate that the rotational time constant should change as a function of the applied field,27,30–36 and the Néel time constant can be written in a more complete form that includes a dependence on applied field.23,25,28,34,37 In this regime of larger applied fields, numerical solutions to the Fokker–Planck equations describing the rotational motion of SPIOs further indicate that external magnetic field terms dominate over thermal terms.38–41 These predictions are borne out experimentally,16,31,34 confirming that the applied field can and does change the relaxation time constant of SPIO nanoparticles in a ferrofluid.
Continued exploration of these physics from first principles will no doubt benefit MPI. We have found that we can accurately model MPI image data by incorporating a first-order Debye relaxation term.4,19,20 This provides powerful intuition and accurately predictive experimental MPI imaging results.
3. MPI RELAXATION LINEAR SYSTEMS THEORY
In this section, we explore how nanoparticle relaxation affects the image formation process. First, we review the noninstantaneous x-space theory for MPI,19 which extended x-space MPI theory to include a Debye model for relaxation in order to more accurately predict measured point spread functions (PSFs). We then derive the relationship between the nanoparticle relaxation kernel and resulting image blur.
3.A. Nonadiabatic x-space systems theory for MPI
X-space MPI systems theory was originally derived assuming an “adiabatic” assumption that nanoparticles instantaneously follow the applied magnetic field.14 Experimentally, we found that the adiabatic PSF did not fully describe the measured point spread function. To better model the nanoparticle behavior, we modeled relaxation using a Debye (exponential) relaxation kernel.16,19,20,24,27 Mathematically, the signal equation including relaxation can be expressed as a convolution of the adiabatic signal sadiab(t) with a relaxation kernel r(t),
| (1) |
| (2) |
where
| (3) |
Here, (m) is the instantaneous FFP position, (m/s) is the FFP velocity, ρ(x) (nanoparticles/m) is the 1D SPIO density, and h(x) is the PSF. The signal equation is scaled by γ = B1mG/Hsat, which includes the sensitivity of the receive coil B1 (T/A), the magnetic dipole moment m (A m2), the selection field strength G [(T/m)/μ0], and the nanoparticle saturation magnetization Hsat (T/μ0). The PSF of the system is the derivative of the Langevin function of paramagnetism .14,15 In Eq. (2) the units are overloaded and the convolution inside the parentheses is a spatial convolution, and the outer convolution is a temporal convolution.
We can use the signal equation to predict the MPI image, , by gridding the signal equation [Eq. (2)] to the instantaneous spatial location of the FFP. The resulting image equation shows that the image is a convolution of the adiabatic image with the relaxation kernel r(t),
| (4) |
| (5) |
To convert the time integral in Eq. (4) to an integral in space, we assume that the FFP is scanned linearly across the field-of-view (FOV) with constant scanning rate, vs (see Appendix A). This approximation gives a linearly varying FFP position (m), which we substitute into Eq. (4) to yield the MPI image equation with relaxation
| (6) |
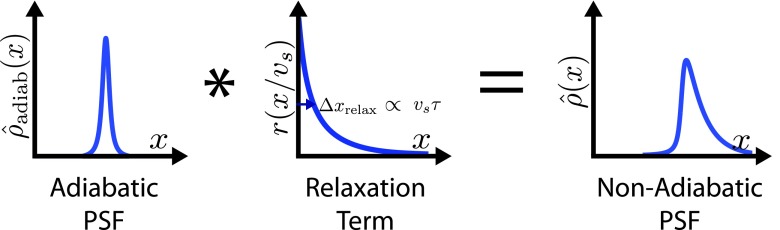
The MPI image equation with relaxation is a powerful result. The equation enables us to express the inherently temporal scanning process as a spatial convolution with a spatial relaxation kernel with unit area: . This means that relaxation causes an additional blur beyond the point spread function determined by the particle’s Langevin physics. For high-resolution MPI, it is important then to minimize the image blur due to relaxation. We will verify this model experimentally below and show that it can be misleading to only model relaxation in the temporal domain. This relationship between the temporal domain and the spatial domain is shown graphically in Fig. 2.
FIG. 2.
The adiabatic PSF is spatially convolved with a relaxation kernel r. The relaxation kernel blurs the image in the scanning direction.
3.B. Debye relaxation
So far, we have not made any assumptions for the shape of the relaxation kernel. Fortunately, in our earlier work,19 we found that Debye relaxation, which describes relaxation that follows a first-order differential equation,16,19,20,24,27 models the experimental behavior of nanoparticles accurately. The Debye exponential relaxation kernel is
| (7) |
where u(t) is the Heaviside step function and τ(s) is the relaxation time constant.
Our experimental findings indicate that the Debye time constant is a function of drive field amplitude and frequency, i.e., . Rewriting Eq. (7) in the spatial domain, we obtain the Debye relaxation kernel
| (8) |
Combining Eqs. (6) and (8), we obtain the MPI image equation with Debye relaxation,
| (9) |
3.C. Phase lag
Relaxation can also be expressed as a phase lag, ϕ (rad). That is, for a sinusoidal drive field, the phase lag describes how far the nanoparticle’s moment lags behind the drive field (in rad),
| (10) |
for small values of ϕ. From Appendix A, we see that the peak velocity can be written as vs = 2πf0Hamp/G. Substituting, we can then recast term as a function of phase lag, ϕ,
| (11) |
Combining Eqs. (6) and (11), we obtain the MPI image equation with Debye relaxation as a function of phase lag,
| (12) |
Equation (12) describes how the relaxation term blurs the image as a function of the phase lag ϕ and the drive field amplitude Hamp. Here, the division by the magnetic field gradient G translates this term from units of magnetic field (T/μ0) to units of space (m). Note that in the case where ϕ is independent of frequency, relaxation blur would only depend on the amplitude of the drive field. Later in Sec. 5, we will use phase lag to compare measured relaxation times at multiple drive field frequencies and show that ϕ is approximately frequency-independent in the investigated range of 4–25 kHz.
In this section, we derived the nonadiabatic signal and image equations for a generalized relaxation kernel and a Debye relaxation kernel. In Secs. 4–7, we use this mathematical foundation to experimentally investigate relaxation on imaging and nonimaging MPI systems in order to understand how spatial resolution changes with drive field amplitude and frequency.
4. METHODS
4.A. Berkeley 3D MPI scanner
The MPI scanner [Fig. 3(a)] acquires 3D images with a drive field coil that scans the FFP in the z direction (down the bore of the scanner) at 23.2 kHz with field strength of up to 30 mT-peak. Electromagnetic shift coils in the x, y, and z directions add a uniform magnetic field with slowly varying amplitude to raster the FFP scans throughout the sample volume. The frequency of the MPI scanner is fixed, so only the drive field amplitude was varied to examine the effects of scanning rate on relaxation-induced blurring. The magnetic field gradient is 7 T/m in the x-axis, and 3.5 T/m in the y- and z-axes. This system has been previously discussed in Refs. 3, 42, and 43.
We characterized the spatial resolution of Resovist particles in the scanner by imaging a point source containing 2 μl undiluted Resovist (Bayer-Schering) shown in Fig. 6(d). Relaxation effects blur the image in the scanning direction, producing different images for the positive-velocity scan and the negative-velocity scan.19 The spatial resolution measurements, then, are for an average of the resolutions (FWHM) of the positive- and negative-velocity scans. The phantom measured 1.0 mm in the z direction and 0.9 mm in the x direction. Scan time was 2 min 52 s for a 2 × 2 × 4.8 cm FOV.
FIG. 6.
(a) Measured FWHM spatial resolution of an undiluted Resovist point source (2 μl) in the imager drops with increasing drive field amplitude. The resolution measured in the imager is comparable to measured resolution in the relaxometer at a similar frequency (23.2 kHz for the MPI scanner vs 25 kHz for the relaxometer). (b) A typical image of a point source. (c) 1D profile through the center of the image. (d) Experimental point source. Scan time: 2 min 52 s, FOV: 2 × 2 × 4.8 cm.
4.B. Berkeley relaxometer
The Berkeley relaxometer [Figs. 3(b) and 3(c)] measures a PSF characteristic of the entire volume of a SPIO sample, from which we can measure relaxation time constant, signal strength, and spatial resolution. Unlike a MPI scanner, it has no selection field, and as a result the PSF is reported in the magnetic field domain. The relaxometer is similar in concept to a MPI spectrometer,44,45 but data analysis does not involve a Fourier transform since x-space systems theory and reconstruction do not use harmonics.1,3,14,15 During operation, the relaxometer produces a sinusoidal magnetic drive field at frequencies between 1.5 and 25 kHz with a 5–100 mT peak amplitude using a multituned resonant transmit coil driven by a voltage controlled amplifier (Crown MA-5002VZ, Elkhart, IN, USA). The SPIO response is received using an inductive gradiometric receive coil, which is digitized at 10 MSPS by a 12-bit ADC (National Instruments PCI-6115, Austin, TX, USA). In order to acquire a larger field-of-view, a bias coil surrounding the transmit and receive coils [Fig. 3(b)] produces up to ±160 mT when driven by a current-controlled amplifier (AE Techron LVC5050, Elkhart, IN, USA). The system is controlled using custom software written in matlab (The Mathworks, Natick, MA, USA). A single frequency version of this relaxometer with no bias coil is described in Ref. 16.
4.C. Partial FOV scanning to measure spatial resolution
To acquire a PSF, we acquire multiple partial FOVs in the magnetic field domain that are stitched together to compose a full FOV (Fig. 4).19,43,46–48 A large full FOV ensures that the sample reaches full saturation at the edges of the FOV. The partial FOVs are similar in concept to imaging stations described elsewhere.49–51 The relaxometer pulse sequence applies a drive field signal while simultaneously linearly ramping the bias field from −75 to +75 mT. The received signal is then divided into 1 × 103 partial FOVs. Since the linear approximation of the drive field is only valid about the zero-crossings of the drive field (see Appendix A), only the center 20% of each partial FOV was used in the computation of the PSF. The partial FOVs are velocity compensated, DC offset corrected, and then stitched to form the full FOV.43 Positive- and negative-velocity scans are reconstructed separately.
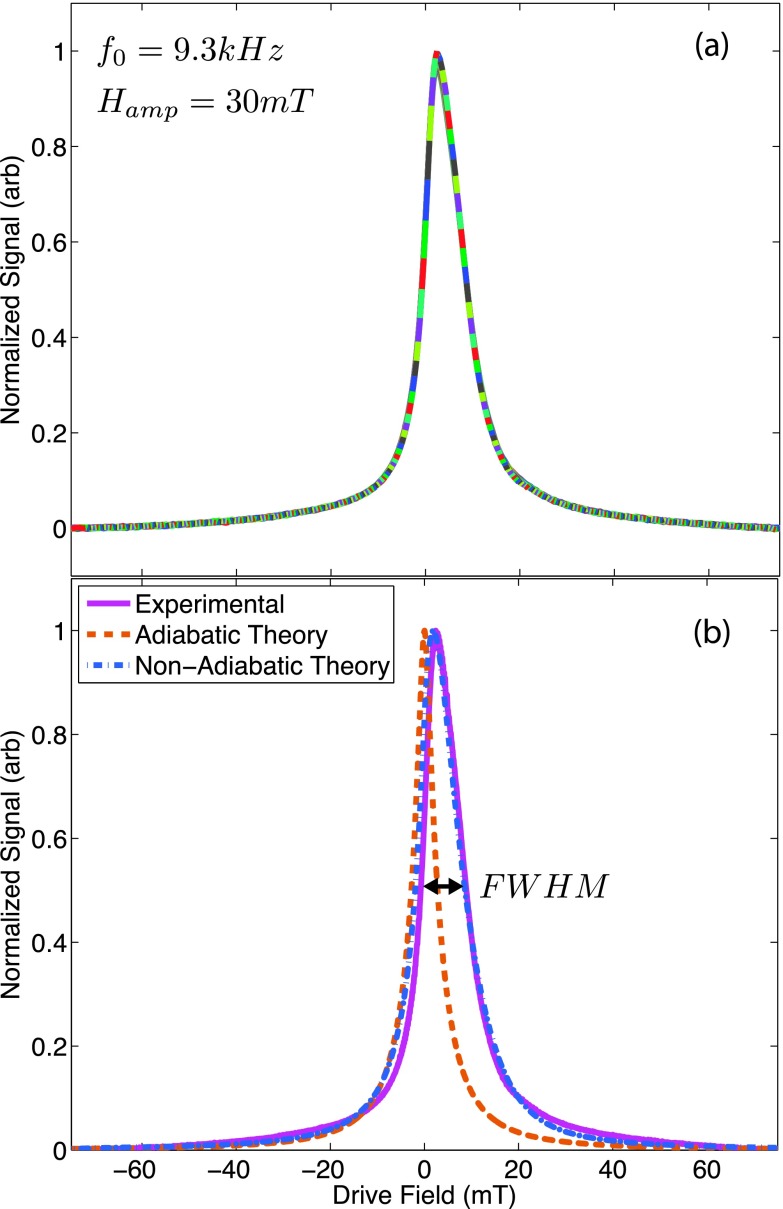
FIG. 4.
A typical PSF of Resovist measured in the relaxometer using x-space reconstruction. The drive frequency was applied at 30 mT and 9.3 kHz while a bias coil applied a linear ramp from −75 to +75 mT. The partial FOVs, each shown as a different color in (a), were merged to form the unstitched PSF. Next, the partial FOVs were averaged to form (b) the stitched PSF, which compares well to the nonadiabatic theoretical PSF (2.3 μs relaxation time). The adiabatic theory predicts a symmetric PSF with less blur, which does not capture the effects of relaxation. Only the positive scanning direction is shown.
4.D. FWHM analysis
In this paper, we use the Houston resolution criterion, which estimates that a system’s resolution is approximately the FWHM of the PSF.52 In the imager, the FWHM is measured in millimeter. In the relaxometer, the FWHM is measured in millitesla, which can be converted to spatial resolution by dividing the FWHM by a magnetic field gradient (3.5 T/m in the 3D scanner shown in this paper).
Prediction of the nonadiabatic spatial resolution (FWHM) Δx (m) of the MPI image given an adiabatic PSF and a relaxation kernel is problematic, since there is no closed form solution for the convolution of the adiabatic PSF (approximately a Lorentzian) and the relaxation kernel (an exponential), as given in Eq. (9). We have found that we can reasonably approximate the nonadiabatic FWHM as a weighted sum of the adiabatic resolution Δxadiab (m) and the blur from relaxation Δxrelax (m), i.e.,
| (13) |
where
| (14) |
See Appendix B for a derivation of Eq. (14). Combining Eqs. (10) and (14), we can express relaxation blur as a function of phase lag,
| (15) |
We estimated the weightings α and β using a nonlinear least-squares regression to the measured resolution. For a reasonable range of SPIO diameters (15–23 nm) and phase lags (0.05–0.25 rad), best fit weightings were α = 0.96 and β = 1.38.
4.E. Fitting algorithm to measure relaxation times
Relaxation times were estimated from PSFs measured in the relaxometer through least-squares fitting with one free parameter, relaxation time constant. The fitting process matched the measured PSF to a theoretical PSF relaxation time calculated using Eq. (9) for a precharacterized nanoparticle core diameter and distribution. The magnetic core diameter distribution of Resovist was chosen as 17 ± 4 nm (mean ± standard deviation) based on the previous studies.16,46,47,53 The magnetic core diameter distribution of UW33 was measured using transmission electron microscopy (TEM) and ImageJ software (National Institutes of Health) as 20 ± 2 nm. All computations were performed in matlab (The Mathworks, Natick, MA, USA).
4.F. Nanoparticle characterization
We characterized two samples in the relaxometer: undiluted Resovist particles (0.5 mM Fe, Bayer-Schering, Berlin, Germany), a commercially manufactured SPIO tracer originally developed for MRI,54 and UW33, a sample synthesized at the University of Washington.17,22,29 Our study aimed to represent the two main types of SPIOs: multicore particles and single-core particles. Resovist is the SPIO most commonly used in the MPI literature, so we chose it as the most relevant multicore nanoparticle in the MPI field. We included the UW33 particles as a sample of single-core particles that was specifically developed by our collaborators at the University of Washington for use in MPI. For a typical relaxometer data point, the peak signal was measured as the maximum value of the filtered signal in the time domain. Peak signal was measured for varying magnetic slew rates, Gvs = 2πHampf0 [(A/m)/s], instead of varying scanning rates, vs, since the relaxometer lacks a magnetic gradient field, G.13 Spatial resolution and relaxation time were measured from the PSFs reconstructed using the partial FOV method. Peak signal, spatial resolution, and relaxation time were all measured from the same data.
5. RESULTS
In Fig. 4, we demonstrate how PSF measurements are acquired as well as FWHM measurements. In Fig. 4(a), we see the overlapped partial FOVs for a 9.3 kHz drive field frequency with a 30 mT amplitude. Figure 4(b) shows that the stitched signal matches the predicted signal when using Debye relaxation.
In Fig. 5, we see TEM images (FEI Tecnai 12) show that Resovist particles contain clusters of small iron oxide cores immobilized in a carboxydextran composite [Fig. 5(a)],55,56 whereas UW33 contains a single iron oxide core [Fig. 5(b)].
FIG. 5.
TEM images of two classes of SPIO nanoparticle tracers: (a) Resovist (Bayer-Schering, Berlin, Germany), which is a conglomerate of 5 nm iron oxide cores in a dextran composite and (b) UW33, a single-core iron oxide nanocrystal that was synthesized at the University of Washington.
In Fig. 6, we see that the FWHM measured in both the MPI scanner and relaxometer improves by approximately 33% with a 60% reduction in drive field amplitude from 30 to 10 mT. The measured values of FWHM differ less than 15% between the two very different instruments. We believe the modest difference in measured FWHM between the imager and the relaxometer is due to the finite size of the point source.
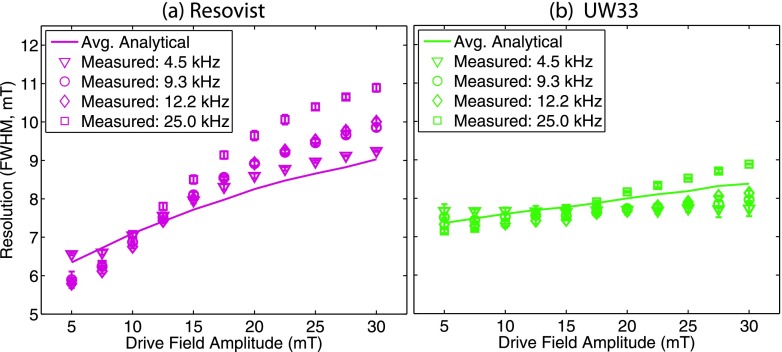
In Fig. 7, we see the measured FWHM measured using the relaxometer for a range of drive field frequencies and strengths for Resovist and UW33. The theoretical predictions of resolution using Eq. (14) are comparable to the measured resolution.
FIG. 7.
Relaxometer-measured resolution for (a) Resovist and (b) UW33 widened with increasing drive field amplitude, with only modest changes with drive field frequency. Theoretical predictions of resolution (solid lines) calculated from average phase lags showed comparable values to measured resolution (shapes). Error bars show standard deviation.
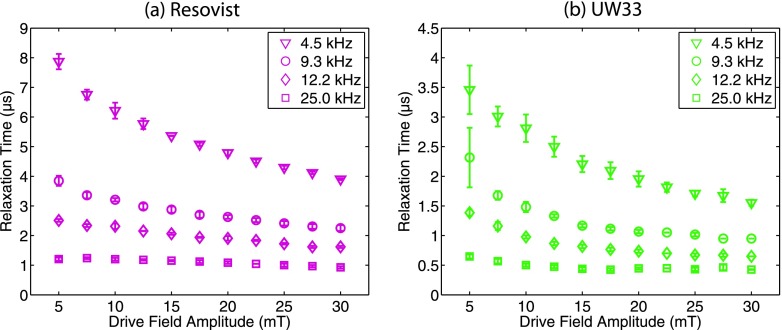
In Fig. 8, we calculate the relaxation times of Resovist and UW33 at four frequencies (4.5, 9.3, 12.2, and 25 kHz) and drive field strengths from 5 to 30 mT. As expected, the relaxation times decrease for increasing drive field strength and increasing drive field frequency.
FIG. 8.
Relaxometer-measured relaxation times of (a) Resovist and (b) UW33 decreased with increasing magnetic slew rate. This trend is shown as a function of drive field amplitude (5–30 mT) and for multiple frequencies (4.5, 9.3, 12.2, and 25 kHz). Error bars show standard deviation.
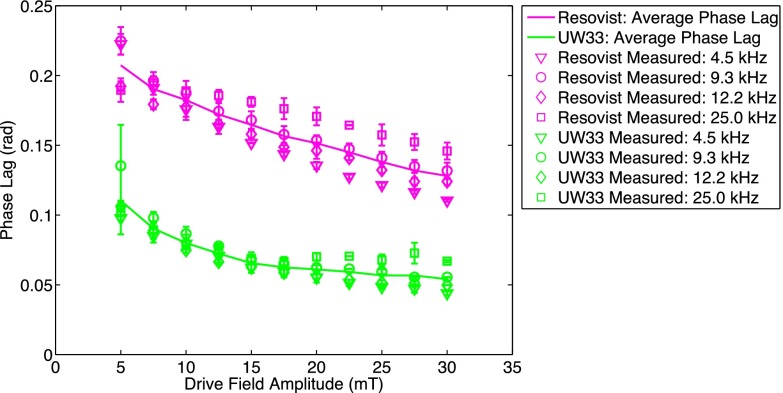
In Fig. 9, we show that the phase lag calculated using Eq. (10) is approximately constant for a given drive field strength, independent of frequency. Further, the phase lag is unique to each nanoparticle type.
FIG. 9.
Phase lag is approximately independent across a range of drive field frequencies (4.5, 9.3, 12.2, and 25 kHz) representing a fivefold range of drive field frequency. Average phase lag is displayed as a solid line.
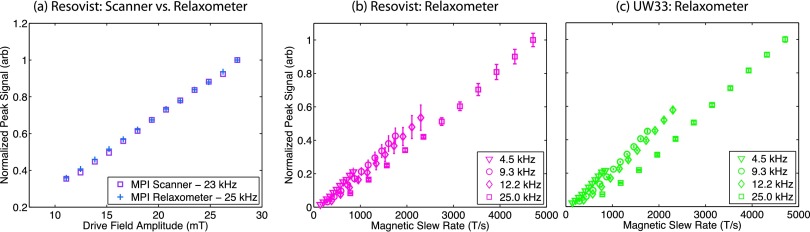
In Fig. 10, we show that the peak signal increases with magnetic field slew rate in the scanner and in the relaxometer. The increase in signal is not monotonic with magnetic field slew rate at different frequencies because of the drive field strength dependence of the signal.
FIG. 10.
Peak signal increases with the increasing magnetic field slew rate. (a) Peak signal in the imager increased approximately linearly for Resovist with increasing drive field amplitude. [(b) and (c)] Peak signal in the relaxometer increased linearly with magnetic slew rate, for Resovist and UW33 at four frequencies (4.5, 9.3, 12.2, and 25 kHz) across a range of drive field amplitudes (5–30 mT).
6. DISCUSSION
The goal of this study was to develop a phenomenological (i.e., observation-based) understanding of effects of nanoparticle relaxation in MPI. With standard x-space image reconstruction (Fig. 4), we find that image resolution improves with lower drive field strength. This improvement in resolution must be due to reduced relaxation blurring, since the Langevin model blurring is invariant to scanning parameters. If we do assume a relaxation kernel, we find that relaxation can be accurately modeled using a Debye relaxation model that assumes magnetic nanoparticle reorientation is governed by a first-order differential equation. Surprisingly, the value of the relaxation time constant can be misleading, and if we instead consider the relaxation time as a phase lag, we see that relaxation is a function of drive field strength and approximately frequency-independent. Surprisingly, all these properties (resolution, phase lag) remain consistent for two different nanoparticle types that include nanoparticle clusters and single-core nanoparticles. This finding will be powerful for future MPI pulse sequence optimization.
6.A. Resolution improvement with lower drive field strengths and implications for imaging
Scanning amplitude and frequency must be chosen to stay within the safety envelope defined by peripheral nerve stimulation (PNS) and specific absorption rate (SAR).57,58 As we develop scanners with larger diameter bores, peripheral nerve stimulation plays an increasing role and requires lower drive field amplitudes. It is estimated that the maximum drive field amplitude is 8 mT in the torso,57,58 which is far lower than the 20 mT used in early preclinical imagers. The effect of this reduction in drive field amplitude on the image quality has not been thoroughly explored.
Fortunately, this study finds that the system resolution improves with lower drive field strengths. These findings are consistent with the previously presented experimental data using x-space reconstruction methods59 and simulation data of system matrix reconstruction images,60 which both demonstrated resolution improvement with decreasing drive field amplitude. This property holds in both the imager and the relaxometer and shows that the relaxometer accurately predicts results in the imager (Fig. 6). Further investigation of FWHM as a function of drive field strength using the relaxometer (Fig. 7) shows that FWHM improves almost 40% on average as we decrease drive field strength from 30 to 5 mT when using the Resovist tracer. A solid core nanoparticle, UW33, also showed resolution improvement with lower drive field strengths, although the effect was not as pronounced. This trend was consistent at four different drive field frequencies (4.5, 9.3, 12.2, and 25 kHz).
The reduction of drive field amplitude does not come without cost as reduced drive field amplitude is accompanied by a concomitant reduction in received signal. Fortunately, the reduction in signal from lower drive field amplitude can be partially compensated through the use of higher drive field frequencies. For example, as shown in Fig. 10, the received signal is approximately proportional to magnetic field slew rate. This holds for increases in slew rate through increased drive field frequency and increased drive field amplitude. It remains to be seen if these trends continue to even higher frequencies as recent work indicates that drive fields of frequencies up to >100 kHz may be necessary in a human scanner to reach SAR limits.57,58 Additionally, some degree of resolution loss at higher drive field amplitudes may be offset using deconvolution techniques that trade-off the improvement in received signal to recover resolution, as described in the previous works.61,62
6.B. Accuracy of the MPI image equation with Debye relaxation
Figure 4 shows that a typical measured PSF reconstructed using x-space theory is accurately modeled by nonadiabatic x-space theory when assuming Debye relaxation [Eq. (9)]. The relaxation time constant (2.3 μs) used to calculate the nonadiabatic x-space theoretical PSF was estimated from the experimentally measured PSF using the fitting algorithm described in Sec. 4.D. This correspondence has very low error (<1% of the peak value) across the full field-of-view. Compared to the experimental resolution (9.7 mT), the nonadiabatic theoretical PSF gave a more accurate prediction of resolution (10.6 mT) than the adiabatic theoretical PSF (4.1 mT). We have also experimentally seen that the Debye model accurately predicts images in the imager19 and the experimentally measured PSFs of other groups.20
6.C. Phase lag, not relaxation time constant, predicts nanoparticle behavior
For ferrofluids, the speed at which a nanoparticle responds to a change in magnetic field is characterized by the nanoparticle’s relaxation time constant.23–28 In MPI, we find that phase lag can be a more powerful method to characterize the spatial blur due to relaxation. This is seen dramatically in Fig. 8, which shows how the nanoparticle’s relaxation time constant changes across a large range for different drive field amplitudes and frequencies. Figure 9 shows that, if we instead consider that the relaxation time constant is actually a phase lag in sinusoidal steady-state, we see that the phase lag is approximately independent of frequency with only modest amplitude dependence. A frequency-independent phase lag also helps to explain why measured FWHM resolution (Fig. 7) shows only modest changes with drive field frequency. Phase lags have been used in the past to describe nanoparticle behavior, but typically this is seen for rotating magnetic fields31 or with a constant low excitation field.28
Even though phase lag decreases as drive field amplitude increases, the FWHM resolution increases. This is not a contradictory result because, while phase lag may decrease with increasing drive field amplitude, the partial FOV size increases faster than the phase lag drops. This dependence is captured in Eq. (12), which calculates that the spatial convolution kernel due to relaxation has an exponential decay constant of ϕHamp.
6.D. Consistency across nanoparticle types
The two types of nanoparticles tested in this paper, UW33 and Resovist, represent two very different classes of nanoparticles, multicore conglomerates of small nanoparticle cores [e.g., Resovist, Nanomag-MIP (Refs. 54 and 63], and single-core iron oxide nanoparticles.4,17,22,29 We have found that the behavior of these two classes is consistent across many nanoparticle manufacturers, and that single-core particles with minimal aggregation tend to show minor resolution change with drive field parameters, while multicore particles show more dramatic resolution improvement with decreasing drive field amplitude. This suggests that these two different families of particles relax via different physical mechanisms. Further, magnetic core size, anisotropic characteristics, and polymer coating characteristics may all play a role in a nanoparticle’s relaxation from physical rotation, akin to Brownian relaxation, or from magnetic reversals within the iron oxide, akin to Néel relaxation.17,21,22,29 It is expected that exploring the various types of relaxation mechanisms, and tailoring particle design to MPI, will be an important area of continuing research for both SPIO optimization and MPI sequence design to minimize blurs.
7. CONCLUSIONS
In this study, we explored the blur of MPI image formation including both the adiabatic MPI magnetization theory as well as the dynamic blur due to relaxation of SPIOs during scanning. We began by building a systems theory model to describe relaxation in the spatial domain. We then carefully characterized two representative nanoparticles from distinct classes of magnetic nanoparticles at multiple drive field frequencies and amplitudes. At each of these data points, we looked at the PSF, FWHM resolution, and signal. We then estimated the nanoparticle relaxation time constant from the measured PSF.
We found that FWHM resolution improves with lower drive field amplitudes. Paradoxically, this spatial resolution improves despite longer relaxation time constants at lower drive field amplitudes. Indeed, we found that longer nanoparticle relaxation times may provide superior spatial resolution if the scanning parameters are chosen carefully. Hence, relaxation time by itself may be a misleading method to characterize a nanoparticle’s relaxation performance in MPI. Instead, relaxation can be more completely approximated as a frequency-independent phase lag that is a function of drive field amplitude. The reason that FWHM continues to increase for increasing drive field amplitudes despite smaller phase lags is that the drive field amplitude increases faster than the phase lag drops.
This study has crucial implications as we design future MPI hardware and future MPI-tailored SPIOs. While designing these systems, it is important to consider the effects of scanning amplitude and frequency when designing new scanning sequences that minimize or exploit relaxation-induced blurring. For example, while increasing drive field amplitude deteriorates resolution, faster slew rates give almost linear SNR gains. This in turn creates a trade-off between relaxation-induced blurring and SNR for drive field at a fixed frequency.
ACKNOWLEDGMENTS
The authors would like to thank the following funding sources: CIRM Tools and Technology Grant (No. RT2-01893), National Institutes of Health Grant (Nos. 1R01EB013689, 1R41EB013520, 1R24MH106053-01, and 1R01EB019458-01), Keck Foundation (No. 034717), ACTG (No. 037829), UC Discovery Grant, National Science Foundation Graduate Research Fellowship, Berkeley Fellowship for Graduate Study, and the Siebel Scholars Foundation. The authors would like to acknowledge their collaborators at the University of Washington, Dr. R. Matthew Ferguson, Amit Khandar, and Dr. Kannan Krishnan, for supplying them with high-performance, MPI-tailored nanoparticles. The authors would also like to express their appreciation to Bo Zheng for hardware assistance, and Daniel Hensley and Kuan Lu for their excellent discussions.
APPENDIX A: LINEAR APPROXIMATION FOR SINUSOIDAL DRIVE FIELDS
MPI scans the FFP using a sinusoidal drive field, , which is approximately linear about H(t) = 0,
| (A1) |
where Hamp (T/μ0) is the peak amplitude and f0 (Hz) is the frequency of the drive field. The derivative of the FFP position, or scanning rate vs (m/s), is equal to the derivative of H(t) divided by the gradient strength G,
| (A2) |
APPENDIX B: RESOLUTION OF RELAXATION BLUR
As described in Eq. (7), we model relaxation in MPI as a Debye exponential relaxation function. The FWHM, or half-life, of an exponential decay function, f(t) = e−t/τ, is defined as τln2. Using this definition to calculate the resolution, as defined by FWHM, of the exponential function in Eq. (9), we obtain
| (B1) |
Substituting in Eq. (A2) for scanning rate, we obtain
| (B2) |
REFERENCES
- 1.Gleich B. and Weizenecker J., “Tomographic imaging using the nonlinear response of magnetic particles,” Nature 435, 1214–1217 (2005). 10.1038/nature03808 [DOI] [PubMed] [Google Scholar]
- 2.Weizenecker J., Gleich B., Rahmer J., Dahnke H., and Borgert J., “Three-dimensional real-time in vivo magnetic particle imaging,” Phys. Med. Biol. 54, L1–L10 (2009). 10.1088/0031-9155/54/5/L01 [DOI] [PubMed] [Google Scholar]
- 3.Saritas E. U., Goodwill P. W., Croft L. R., Konkle J. J., Lu K., Zheng B., and Conolly S. M., “Magnetic particle imaging (MPI) for NMR and MRI researchers,” J. Magn. Reson. 229, 116–126 (2013). 10.1016/j.jmr.2012.11.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goodwill P. W., Saritas E. U., Croft L. R., Kim T. N., Krishnan K. M., Schaffer D. V., and Conolly S. M., “X-space MPI: Magnetic nanoparticles for safe medical imaging,” Adv. Mater. 24, 3870–3877 (2012). 10.1002/adma.201200221 [DOI] [PubMed] [Google Scholar]
- 5.Ix J. H., Mercado N., Shlipak M. G., Lemos P., Boersma E., Lindeboom W., O’Neill W. W., Wijns W., and Serruys P. W., “Association of chronic kidney disease with clinical outcomes after coronary revascularization: The arterial revascularization therapies study (ARTS),” Am. Heart J. 149, 512–519 (2005). 10.1016/j.ahj.2004.10.010 [DOI] [PubMed] [Google Scholar]
- 6.Reddan D. N., “Chronic kidney disease, mortality, and treatment strategies among patients with clinically significant coronary artery disease,” J. Am. Soc. Nephrol. 14, 2373–2380 (2003). 10.1097/01.ASN.0000083900.92829.F5 [DOI] [PubMed] [Google Scholar]
- 7.Coresh J., Selvin E., Stevens L. A., Manzi J., Kusek J. W., Eggers P., Van Lente F., and Levey A. S., “Prevalence of chronic kidney disease in the United States,” JAMA, J. Am. Med. Assoc. 298, 2038–2047 (2007). 10.1001/jama.298.17.2038 [DOI] [PubMed] [Google Scholar]
- 8.Ferrucci J. T. and Stark D. D., “Iron oxide-enhanced MR imaging of the liver and spleen: Review of the first 5 years,” Am. J. Roentgenol. 155, 943–950 (1990). 10.2214/ajr.155.5.2120963 [DOI] [PubMed] [Google Scholar]
- 9.Weissleder R., Stark D. D., Engelstad B. L., Bacon B. R., Compton C. C., White D. L., Jacobs P., and Lewis J., “Superparamagnetic iron oxide: Pharmacokinetics and toxicity,” Am. J. Roentgenol. 152, 167–173 (1989). 10.2214/ajr.152.1.167 [DOI] [PubMed] [Google Scholar]
- 10.Lu M., Cohen M. H., Rieves S., and Pazdur R., “FDA report: Ferumoxytol for intravenous iron therapy in adult patients with chronic kidney disease,” Am. J. Hematol. 85, 315–319 (2010). 10.1002/ajh.21656 [DOI] [PubMed] [Google Scholar]
- 11.Weizenecker J., Gleich B., and Borgert J., “Magnetic particle imaging using a field free line,” J. Phys. D: Appl. Phys. 41, 105009 (2008). 10.1088/0022-3727/41/10/105009 [DOI] [Google Scholar]
- 12.Goodwill P. W., Konkle J. J., Zheng B., Saritas E. U., and Conolly S. M., “Projection x-space magnetic particle imaging,” IEEE Trans. Med. Imaging 31, 1076–1085 (2012). 10.1109/TMI.2012.2185247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Konkle J. J., Goodwill P. W., Carrasco-Zevallos O. M., and Conolly S. M., “Projection reconstruction magnetic particle imaging,” IEEE Trans. Med. Imaging 32, 338–347 (2013). 10.1109/TMI.2012.2227121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Goodwill P. W. and Conolly S. M., “The x-space formulation of the magnetic particle imaging process: 1-D signal, resolution, bandwidth, SNR, SAR, and magnetostimulation,” IEEE Trans. Med. Imaging 29, 1851–1859 (2010). 10.1109/TMI.2010.2052284 [DOI] [PubMed] [Google Scholar]
- 15.Rahmer J., Weizenecker J., Gleich B., and Borgert J., “Signal encoding in magnetic particle imaging: Properties of the system function,” BMC Med. Imaging 9, 4 (2009). 10.1186/1471-2342-9-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Goodwill P. W., Tamrazian A., Croft L. R., Lu C. D., Johnson E. M., Pidaparthi R., Ferguson R. M., Khandhar A. P., Krishnan K. M., and Conolly S. M., “Ferrohydrodynamic relaxometry for magnetic particle imaging,” Appl. Phys. Lett. 98, 262502 (2011). 10.1063/1.3604009 [DOI] [Google Scholar]
- 17.Arami H., Ferguson R. M., Khandhar A. P., and Krishnan K. M., “Size-dependent ferrohydrodynamic relaxometry of magnetic particle imaging tracers in different environments,” Med. Phys. 40, 071904 (14pp.) (2013). 10.1118/1.4810962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ferguson R. M., Khandhar A. P., Kemp S. J., Arami H., Saritas E. U., Croft L. R., Konkle J., Goodwill P. W., Halkola A., Rahmer J., Borgert J., Conolly S. M., and Krishnan K. M., “Magnetic particle imaging with tailored iron oxide nanoparticle tracers,” IEEE Trans. Med. Imaging 34, 1077–1084 (2015). 10.1109/TMI.2014.2375065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Croft L. R., Goodwill P. W., and Conolly S. M., “Relaxation in x-space magnetic particle imaging,” IEEE Trans. Med. Imaging 31, 2335–2342 (2012). 10.1109/TMI.2012.2217979 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bente K., Weber M., Graeser M., Sattel T. F., Erbe M., and Buzug T. M., “Electronic field free line rotation and relaxation deconvolution in magnetic particle image,” IEEE Trans. Med. Imaging 34, 644–651 (2015). 10.1109/tmi.2014.2364891 [DOI] [PubMed] [Google Scholar]
- 21.Ferguson R. M., Minard K. R., and Krishnan K. M., “Optimization of nanoparticle core size for magnetic particle imaging,” J. Magn. Magn. Mater. 321, 1548–1551 (2009). 10.1016/j.jmmm.2009.02.083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ferguson R. M., Minard K. R., Khandhar A. P., and Krishnan K. M., “Optimizing magnetite nanoparticles for mass sensitivity in magnetic particle imaging,” Med. Phys. 38, 1619 (2011). 10.1118/1.3554646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brown W. F., “Thermal fluctuations of a single-domain particle,” Phys. Rev. 130, 1677–1686 (1963). 10.1103/PhysRev.130.1677 [DOI] [Google Scholar]
- 24.Debye P., Polar Molecules (The Chemical Catalog Company, New York, NY, 1929). [Google Scholar]
- 25.Néel L., “Théorie du traînage magnétique des ferromagnétiques en grains fins avec applications aux terres cuites,” Ann. Geophys. 5, 99–136 (1949). [Google Scholar]
- 26.Rosensweig R. E., “Magnetic fluids,” Annu. Rev. Fluid Mech. 19, 437–461 (1987). 10.1146/annurev.fl.19.010187.002253 [DOI] [Google Scholar]
- 27.Shliomis M. I., “Magnetic fluids,” Sov. Phys.-Usp. 17, 153–169 (1974). 10.1070/PU1974v017n02ABEH004332 [DOI] [Google Scholar]
- 28.Kötitz R., Fannin P. C., and Trahms L., “Time domain study of Brownian and Néel relaxation in ferrofluids,” J. Magn. Magn. Mater. 149, 42–46 (1995). 10.1016/0304-8853(95)00333-9 [DOI] [Google Scholar]
- 29.Krishnan K. M., “Biomedical nanomagnetics: A spin through possibilities in imaging, diagnostics, and therapy,” IEEE Trans. Magn. 46, 2523–2558 (2010). 10.1109/TMAG.2010.2046907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shliomis M. I., “Nonlinear effects in suspension of ferromagnetic particles under action of a rotating magnetic field,” Sov. Phys.-Dokl. 19, 686–687 (1975). [Google Scholar]
- 31.Dieckhoff J., Schilling M., and Ludwig F., “Fluxgate based detection of magnetic nanoparticle dynamics in a rotating magnetic field,” Appl. Phys. Lett. 99, 112501 (2011). 10.1063/1.3639276 [DOI] [Google Scholar]
- 32.Yoshida T. and Enpuku K., “Simulation and quantitative clarification of AC susceptibility of magnetic fluid in nonlinear Brownian relaxation region,” Jpn. J. Appl. Phys., Part 1 48, 127002 (2009). 10.1143/JJAP.48.127002 [DOI] [Google Scholar]
- 33.Caizer C., “The effect of the external magnetic field on the thermal relaxation of magnetization in systems of aligned nanoparticles,” J. Phys.: Condens. Matter 17, 2019–2034 (2005). 10.1088/0953-8984/17/12/023 [DOI] [Google Scholar]
- 34.Neveu-Prin S., Tourinho F. A., Bacri J. C., and Perzynski R., “Magnetic birefringence of cobalt ferrite ferrofluids,” Colloids Surf., A 80, 1–10 (1993). 10.1016/0927-7757(93)80218-4 [DOI] [Google Scholar]
- 35.Coffey W. T., Cregg P. J., and Kalmykov Y. P., “On the theory of Debye and Néel relaxation of single domain ferromagnetic particles,” Adv. Chem. Phys. 83, 263–464 (1993). 10.1002/9780470141410.ch5 [DOI] [PubMed] [Google Scholar]
- 36.Ilg P. and Kröger M., “Magnetization dynamics, rheology, and an effective description of ferromagnetic units in dilute suspension,” Phys. Rev. E 66, 021501 (2002). 10.1103/PhysRevE.66.021501 [DOI] [PubMed] [Google Scholar]
- 37.Moller W., Takenaka S., Buske N., Felten K., and Heyder J., “Relaxation of ferromagnetic nanoparticles in macrophages: In vitro and in vivo studies,” J. Magn. Magn. Mater. 293, 245–251 (2005). 10.1016/j.jmmm.2005.02.017 [DOI] [Google Scholar]
- 38.Engel A. and Reimann P., “Thermal ratchet effects in ferrofluids,” Phys. Rev. E 70, 051107 (2004). 10.1103/PhysRevE.70.051107 [DOI] [PubMed] [Google Scholar]
- 39.Raible M. and Engel A., “Langevin equation for the rotation of a magnetic particle,” Appl. Organomet. Chem. 18, 536–541 (2004). 10.1002/aoc.757 [DOI] [Google Scholar]
- 40.Weizenecker J., Gleich B., Rahmer J., and Borgert J., “Magnetic nanoparticles: Particle science, imaging technology, and clinical applications,” in Proceedings of the First International Workshop on Magnetic Particle Imaging (World Scientific Publishing Co Pte Ltd, Singapore, 2010), pp. 3–15. [Google Scholar]
- 41.Sanchez J. H. and Rinaldi C., “Rotational Brownian dynamics simulations of non-interacting magnetized ellipsoidal particles in DC and AC magnetic fields,” J. Magn. Magn. Mater. 321, 2985–2991 (2009). 10.1016/j.jmmm.2009.04.066 [DOI] [Google Scholar]
- 42.Goodwill P., Croft L. R., Konkle J., Lu K., Saritas E., Zheng B., and Conolly S., “Third generation x-space MPI mouse and rat scanner,” in Magnetic Particle Imaging, edited byBuzug T. M. and Borgert J. (Springer Proceedings in Physics, Lübeck, Germany, 2012). [Google Scholar]
- 43.Lu K., Goodwill P. W., Saritas E. U., Zheng B., and Conolly S. M., “Linearity and shift-invariance for quantitative magnetic particle imaging,” IEEE Trans. Med. Imaging 32, 1565–1575 (2013). 10.1109/TMI.2012.2236349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Biederer S., Sattel T. F., Knopp T., LaConte L., Gleich B., Weizenecker J., Borgert J., and Buzug T. M., “A spectrometer for magnetic particle imaging,” in 4th European Conference of the International Federation for Medical and Biological Engineering (Springer, New York, NY, 2009), pp. 2313–2316. [Google Scholar]
- 45.Biederer S., Knopp T., Sattel T. F., Lüdtke-Buzug K., Gleich B., Weizenecker J., Borgert J., and Buzug T. M., “Magnetization response spectroscopy of superparamagnetic nanoparticles for magnetic particle imaging,” J. Phys. D: Appl. Phys. 42, 205007 (2009). 10.1088/0022-3727/42/20/205007 [DOI] [Google Scholar]
- 46.Goodwill P. W. and Conolly S. M., “Multidimensional x-space magnetic particle imaging,” IEEE Trans. Med. Imaging 30, 1581–1590 (2011). 10.1109/TMI.2011.2125982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Goodwill P. W., Lu K., Zheng B., and Conolly S. M., “An x-space magnetic particle imaging scanner,” Rev. Sci. Instrum. 83, 033708 (2012). 10.1063/1.3694534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lu K., Goodwill P., Zheng B., and Conolly S., “The impact of filtering direct-feedthrough on the x-space theory of magnetic particle imaging,” Proc. SPIE 7965, 79652I (2011). 10.1117/12.878446 [DOI] [Google Scholar]
- 49.Gleich B., Weizenecker J., Timminger H., Bontus C., Schmale I., Rahmer J., Schmidt J., Kanzenbach J., and Borgert J., “Fast MPI demonstrator with enlarged field of view,” in Proceedings of the International Society for Magnetic Resonance in Medicine, Stockholm, Sweden (2010), Vol. 18, p. 218, see http://cds.ismrm.org/protected/10MProceedings/files/218_2116.pdf. [Google Scholar]
- 50.Rahmer J., Gleich B., Bontus C., Schmale I., Schmidt J., Kanzenbach J., Woywode O., Weizenecker J., and Borgert J., “Rapid 3D in vivo magnetic particle imaging with a large field of view,” in Proceedings of the International Society for Magnetic Resonance in Medicine, Montreal, Canada (2011), Vol.19, p. 3285, http://cds.ismrm.org/protected/11MProceedings/files/3285.pdf. [Google Scholar]
- 51.Schmale I., Rahmer J., Gleich B., Kanzenbach J., Schmidt J. D., Bontus C., Borgert J., and Woywode O., “First phantom and in vivo MPI images with an extended field of view,” Proc. SPIE 7965, 796510 (2011). 10.1117/12.877339 [DOI] [Google Scholar]
- 52.Houston W., “A compound interferometer for fine structure work,” Phys. Rev. 29, 478–484 (1927). 10.1103/PhysRev.29.478 [DOI] [Google Scholar]
- 53.Rahmer J., Weizenecker J., Gleich B., and Borgert J., “Analysis of a 3D system function measured for magnetic particle imaging,” IEEE Trans. Med. Imaging 31, 1289–1299 (2012). 10.1109/TMI.2012.2188639 [DOI] [PubMed] [Google Scholar]
- 54.Reimer P., “Ferucarbotran (Resovist): A new clinically approved RES-specific contrast agent for contrast-enhanced MRI of the liver: Properties, clinical development, and applications,” Eur. Radiol. 13, 1266–1276 (2003). 10.1007/s00330-002-1721-7 [DOI] [PubMed] [Google Scholar]
- 55.Thünemann A. F., Rolf S., Knappe P., and Weidner S., “In situ analysis of a bimodal size distribution of superparamagnetic nanoparticles,” Anal. Chem. 81, 296–301 (2009). 10.1021/ac802009q [DOI] [PubMed] [Google Scholar]
- 56.Yoshida T., Enpuku K., Ludwig F., Dieckhoff J., Wawrzik T., Lak A., and Schilling M., “Characterization of Resovist® nanoparticles for magnetic particle imaging,” in Magnetic Particle Imaging, edited byBuzug T. M. and Borgert J.,. Springer Proceedings in Physics (Lübeck, Germany, 2012). [Google Scholar]
- 57.Saritas E. U., Goodwill P. W., Zhang G. Z., and Conolly S. M., “Magnetostimulation limits in magnetic particle imaging,” IEEE Trans. Med. Imaging 32, 1600–1610 (2013). 10.1109/TMI.2013.2260764 [DOI] [PubMed] [Google Scholar]
- 58.Schmale I., Gleich B., Schmidt J., Bontus C., Eckart R., David B., Heinrich M., Mende O., Woywode O., Jokram J., and Borgert J., “Human PNS and SAR study in the frequency range from 24 to 162 kHz,” in Proceedings of the 2013 International Workshop on Magnetic Particle Imaging (IWMPI) (2013). [Google Scholar]
- 59.Croft L. R., Goodwill P. W., Price D. A., Saritas E. U., Li A. X., and Conolly S. M., “Effects of scanning rate on relaxation-induced blurring in magnetic particle image,” in Proceedings of the 2013 International Workshop on Magnetic Particle Imaging (IWMPI) (2013). [Google Scholar]
- 60.Weber A., Weizenecker J., Rahmer J., Franke J., Heinen U., and Buzug T., “Resolution improvement by decreasing the drive field amplitude,” in Proceedings of the 2015 International Workshop on Magnetic Particle Imaging (IWMPI) (2015). [Google Scholar]
- 61.Knopp T., Biederer S., Sattel T. F., Erbe M., and Buzug T. M., “Prediction of the spatial resolution of magnetic particle imaging using the modulation transfer function of the imaging process,” IEEE Trans. Med. Imaging 30, 1284–1292 (2011). 10.1109/TMI.2011.2113188 [DOI] [PubMed] [Google Scholar]
- 62.Weizenecker J., Borgert J., and Gleich B., “A simulation study on the resolution and sensitivity of magnetic particle imaging,” Phys. Med. Biol. 52, 6363–6374 (2007). 10.1088/0031-9155/52/21/001 [DOI] [PubMed] [Google Scholar]
- 63.Eberbeck D., Dennis C. L., Huls N. F., Krycka K. L., Grüttner C., and Westphal F., “Multicore magnetic nanoparticles for magnetic particle imaging,” IEEE Trans. Magn. 49, 269–274 (2013). 10.1109/TMAG.2012.2226438 [DOI] [Google Scholar]