Nonlinear elastic properties of polyacrylamide gels: Implications for quantification of cellular forces

Abstract

Because of their tunable mechanical properties, polyacrylamide gels (PAG) are frequently used for studying cell adhesion and migratory responses to extracellular substrate stiffness. Since these responses are known to heavily depend on the tensional balance between cell contractility and substrate mechanical resistance, a precise knowledge of PAG’s mechanical properties becomes quite crucial. Using the micropipette aspiration technique, we first exhibited the nonlinear elastic behavior of PAG and then successfully modeled it by an original strain-energy function. This function depends on the Poisson’s ratio and on two material parameters, which have been explicitly related to acrylamide and bis-acrylamide concentrations. Implications of these results have been highlighted with regard to traction force microscopy experiments where cellular force quantification is derived from displacements of beads embedded in PAG. We found that considering PAG as a linear elastic medium tends to significantly underestimate traction forces for substrate displacements larger than 2 μm. Interestingly, we also showed that in the range of cellular force amplitude and PAG stiffness currently used in cell traction force experiments, finite size effects become critical for PAG substrate thickness below 60 μm. Thus, our improved characterization of PAG nonlinear mechanical properties through a new constitutive law could have significant impact onto biological experimentations where such extracellular substrates experience large strains.

1. Introduction

An increasing number of experimental data shows that many cellular processes heavily depend on extracellular matrix rigidity [21,22,33]. Moreover, these data are mostly interpreted and discussed within a tensional homeostasis or mechanoreciprocity [6] conceptual framework, according to which a mechanical balance sets up between active cellular forces generated by actomyosin contractility and passive resistance of the extracellular matrix applied through cell–matrix contacts [3,25]. This mechanical balance triggers cell signaling pathways and dynamical response. Deregulation of these mechanotransduction processes contributes to the pathogenesis of several human diseases [6,17,19].

In this context, extracellular substrates with tunable mechanical properties are relevant tools for analyzing cell response to mechanical cues provided by their environment. Polyacrylamide gels (PAG) have been frequently used to analyze and quantify cell spreading [15], cell motility [22,27], cell differentiation [14], focal adhesion assembly [10,13,26,35], cell traction forces [2,7,12,29,34] and cell mechanical properties [31], mainly because PAG’s elasticity can be easily and reproducibly tuned by adjusting the ratio of acrylamide [Acry] and bis-acrylamide [Bis] [5,13,26,35]. However, precise interpretation and quantification of data obtained in these cell biology experiments clearly require an accurate characterization of PAG’s mechanical properties.

To the best of our knowledge, all quantitative studies on cell properties performed with PAG assumed that these extracellular substrates behave as linear elastic media. Such assumption could not be valid in the context of cell traction force quantification [23,30], since cellular forces may be high enough to generate large strains on the surrounding PAG. In such condition, it is necessary to quantify the cellular traction forces by considering explicitly the nonlinear elastic behavior of PAG.

By combining experimental and computational approaches, this work aims at improving the benefit of using PAG in cell biology experiments. In a first step, we extended previous studies on the characterization of PAG’s elastic moduli performed on the small strains domain [4,5]. Based on displacement measurements obtained with the micropipette aspiration technique, we proposed an original formulation of the nonlinear elastic behavior of PAG using a strain-energy function that depends on three parameters, namely two material constants and the Poisson’s ratio. We then developed a finite element analysis of sample PAG aspiration into the micropipette and successfully identified the unknown material constants from the nonlinear experimental response of PAG made with 10% of acrylamide, while bis-acrylamide concentrations vary from 0.03% to 0.10%.

The nonlinear elastic properties having been assessed, we then investigated in a second part of our study the extent to which such behavior might significantly impair the accuracy of cellular force quantification conducted in traction force microscopy experiments. For illustration, we focused on the elegant work performed by Dembo et al. [12] on the characterization of the extracellular displacement fields generated by fibroblasts migrating on PAG substrates. Starting from the substrate displacement fields reported in their paper, we compared the associated stress fields computed when PAG behave either as linear elastic or nonlinear hyperelastic media. This comparison allowed us to quantify the bias on cell traction force induced by inappropriate consideration of linear PAG elastic response.

Additionally, we investigated the influence of PAG’s finite thickness effects, using an approach similar to the one recently proposed by Merkel et al. [23] for linear elastic substrates. We demonstrated that finite size effects are critical for thin PAG substrates and quantified the range of PAG thickness values where the half-space approximation of the substrate geometry does not affect cellular force evaluation.

Our results highlight how the nonlinear elastic PAG response may help to improve the accuracy of data derived from traction force microscopy experiments and more generally from cell biology experiments conducted with these extracellular deformable substrates.

2. Materials and methods

2.1. Mechanical characterization of polyacrylamide gels

2.1.1. Preparation of PAG

Gels were processed and attached on glass cover slips according to the method described by Pelham and Wang [26]. We characterized 20 adherent PAGs containing 10% acrylamide, with concentrations of the bis-acrylamide crosslinker varying from 0.03% to 0.10%. Gel thickness h lies between 58.1 and 177.0 μm.

2.1.2. Micromanipulation and digital image processing

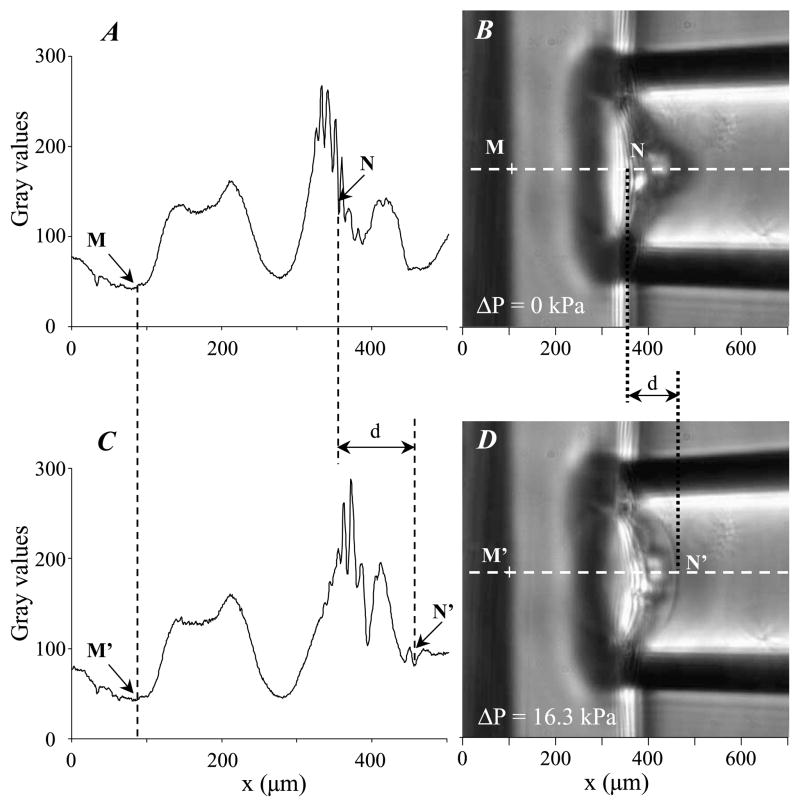
Micropipettes were first pulled from borosilicate glass capillaries (Narishige, Japan) to a fine point with a pipette-puller (model 97, Sutter Instrument, USA), then fractured with a microforge (Narishige, Japan) to get an inner micropipette radius R_i ranging from 25.6 to 160.0 μm. The shape of the tip hole was carefully checked to ensure that the condition of tip roundness has been satisfied. The water pre-filled micropipettes were connected to a homemade manometer with pressure transducer (DP103, Validyne, USA). A homemade plexiglas holder was designed to maintain the PAG coated glass slide vertically. Applied pressures have been varied between 0.3 and 16 kPa. A micromanipulator (Narishige, Japan) was used to setup the micropipette position. The micromanipulation chamber consists in a Lab-Tek chamber slide (NalgeNunc International, USA) with a side-window to provide room for pipette micromanipulation. The chamber was placed on an inverted light microscope (ZeissAxiovert S100, Germany) equipped with a ×63 oil objective (Zeiss Plan Apochromat, Germany), connected to a computer-controlled video camera (Coolsnap CS, Roper Scientific, USA). For each ratio of acrylamide/bis-acrylamide concentration, measurements were made five times on five gel samples. The images were analyzed with ImageJ software (US National Institutes of Health, USA). The gel thickness and aspirated length were determined from the axial intensity profiles extracted from the recorded images, according to the technique described in Boudou et al. [5]. Briefly, the diffraction patterns of the gel/glass interface and gel surface (labeled by arrows in Fig. 1(A, C)) generate some specific profiles that are used to accurately measure the aspirated length of the gel into the pipette (Fig. 1(B, D)).

Fig. 1.

Micropipette aspiration of polyacrylamide gels. Left part of the figure shows the two axial intensity curves (A, C) obtained along the line corresponding to the pipette axis for two video snapshots recorded during the gel aspiration (B, D). The right images (B) and (D) were taken for aspiration pressure ΔP = 0 kPa and ΔP = 16.3 kPa, respectively. The distances MN and M′N′ between the gel/glass interface and the free gel surface were precisely measured from these intensity curves, and further used to derive the aspiration length d.

2.1.3. Finite element simulation of PAG aspiration

Geometry

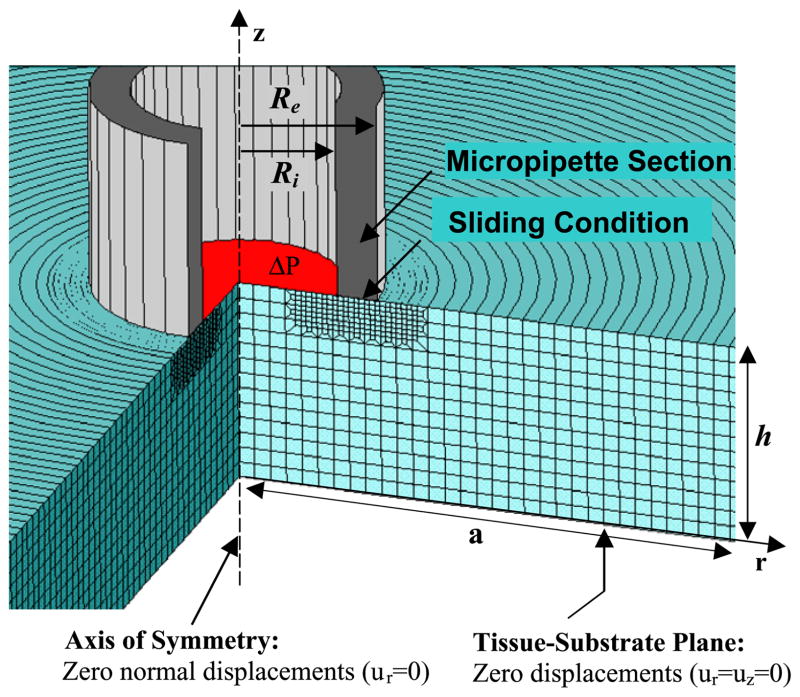
The PAG sample is represented by a thick circular slice of radius a and thickness h. The micropipette has been modeled as a rigid hollow cylinder with internal and external radii R_i and R_e, respectively. Taking advantage of the axi-symmetric conditions of our problem, we reduced this mechanical study to a two-dimensional structural analysis (Fig. 2).

Fig. 2.

Finite element mesh of a circular PAG sample with radius a and thickness h. Free boundary conditions are considered, except for displacement conditions explicitly indicated in the figure. R_i and R_e are the inner and outer radius of the micropipette, respectively, and ΔP is the applied suction pressure.

Hyperelastic model of PAG mechanical behavior

In the light of the nonlinear stress–strain responses given by micropipette measurements, the PAG was modeled as a homogeneous nonlinear hyperelastic medium. To characterize the mechanical properties of the PAG, a stress–strain relationship derived from the Yeoh’s strain energy density function [18] was used:

$$W=a_1(J^{-2/3}{I}_1-3)+a_3{(J^{-2/3}{I}_1-3)}^3+\frac{2a_1(1+\nu )}{3(1-2\nu )}{(J-1)}^2,$$ (1)

where a₁ and a₃ are two material constants (in kPa), I₁ is the first strain invariant, J is the volume ratio, and ν is the Poisson’s ratio [18]. Let us remark that, in a previous study demonstrating the quasi-incompressibility of PAG, we quantified a Poisson ratio ν = 0.48 ± 0.01 [5].

The physical interpretation of the two material constants a₁ and a₃ may be obtained by considering the PAG response to uniaxial extension in the Ox direction. The slope of this stress–strain mechanical response E_tan = ∂σ_xx/∂E_xx (where σ_xx and E_xx are the Cauchy stress and the Green–Lagrange strain components in the Ox direction, respectively) I₁ is the tangent elastic modulus (E_tan). For such uniaxial mechanical solicitation of an incompressible PAG, E_tan can be expressed as a function of the extension ratio λ = (2E_xx + 1)^1/2 in Ox direction and of the two material constants a₁ and a₃ according to the relationship [14]:

$$E_{tan}(a_1,a_3,\lambda )=2a_1\left(2+\frac{1}{{\lambda }^3}\right)+a_3\left(36{\lambda }^4-144{\lambda }^2+54\lambda +108-\frac{36}{\lambda }+\frac{54}{{\lambda }^3}-\frac{144}{{\lambda }^4}+\frac{72}{{\lambda }^5}\right).$$ (2)

Notice that, for small extension ratio (λ ~ 1), the expression of the tangent modulus reduces to:

$$E_{tan}~6a_1.$$ (3)

Thus, the material constant a₁ expresses the linear behavior of the PAG, whereas the material constant a₃ characterizes its nonlinear elastic response.

Mathematical formulation, finite element implementation and boundary conditions

In our formulation of the static problem under finite deformations, we neglected the body forces in the PAG sample. Upon total Lagrangian formulation, the local static equilibrium equation then reads [18]:

$$\text{div}\sigma =0.$$ (4)

In the above equation, the Cauchy stress tensor σ – describing the hyperelastic stress response of PAG samples – may be derived from the strain energy function W characterizing the PAG media (Eq. (1)):

$$\sigma =J^{-1}F·\frac{\partial W}{\partial E_L}·F^{\mathrm{T}},$$ (5)

where E_L and F are the Green–Lagrange strain tensor and the deformation gradient tensor, respectively [18].

The local equilibrium equation (Eq. (4)) has been solved using finite element (FE) method (Ansys software, version 11, Ansys Inc., USA). The PAG sample was meshed with approximately 4000 structural 8-nodes axisymmetric solid elements (Plane183). The interfacial area between the micropipette and the sample was specifically meshed with contact elements (conta172 and targe169) in order to insure that the aspirated medium slides without friction over the tip of the micropipette. The following additional conditions were imposed on the other sample boundaries: (i) a controlled suction pressure ΔP was applied on the sample section inside the pipette, (ii) zero normal displacement conditions were imposed along the sample section belonging to the axis of symmetry, (iii) zero displacement conditions were considered at the sample/rigid interface, and (iv) free boundary conditions were assumed for all other sample surfaces (Fig. 2).

2.1.4. Identification of PAG nonlinear material constants

Considering a small strain linear domain of deformations, we proposed in a previous work [5] an analytical relationship relating the PAG Young’s modulus of PAG to the amounts of acrylamide and bis-acrylamide that reads:

$$E([\mathit{Acry}],[\mathit{Bis}])=(m_1[\mathit{Acry}]+m_2{[\mathit{Acry}]}^2+m_3{[\mathit{Acry}]}^3)[\mathit{Bis}]$$ (6)

with m₁ = 12.839, m₂ = −4.487 and m₃ = 0.564 and where the PAG Young’s modulus E is expressed in kilopascal (kPa), while the acrylamide ([Acry]) and bis-acrylamide ([Bis]) concentrations are given in %.

We used Eqs (3) and (6) to get an initial guess of the material constant a₁ for each concentration ratio [Acry]/[Bis] we considered, the [Acry] value been kept to 10%. Then, by minimizing the least-squared error between measured and simulated sample aspirated lengths for successively imposed aspiration pressure, we precisely identified optimum values of the two material constant a₁ and a₃ for each value of [Bis]. Minimization was conducted using an advanced zero-order method, which uses only the values of the dependent variables, and doest require evaluation of their derivatives (OptypeSubp routine, Ansys).

2.2. Simulation of PAG deformation under cell traction forces

As stated in the introduction section, most of the micromanipulation techniques developed for measuring forces generated by living cells make use of the measurement of microprobes displacements at the substrate surface [1,2,7,11,12,15,22,29,34]. In this study, we paid special attention to the work of Dembo and Wang [12], who quantified cellular stresses developed by migrating fibroblasts from the tracking of fluorescent, 2 μm diameter latex beads embedded in 70 μm thick PAG composed of 10% [Acry] and 0.03% [Bis]. They first measured the beads displacements induced by fibroblasts adhesion, spreading and migration on the PAG substrate. Then, assuming a linear elastic behavior for the PAG substrate, they computed the local cellular traction stresses distribution which satisfies and fits their observed experimental displacement field. We used the study of Dembo and Wang [12] as a reference framework and reproduced one of their experiments (Fig. 1 in Dembo and Wang [12]) by digitalizing and importing in our FE model a typical cell shape, together with the associated displacement field they observed when the cell actuates the PAG substrate.

2.2.1. Finite element modeling of PAG deformations

The elastic substrate was modeled as a 70 μm thick layer of surface 600 × 600 μm. This surface has been chosen large enough – with regard to the cell size – to avoid the influence of boundary effects on the computation of substrate displacements generated by cellular forces. Zero displacement condition was applied at the basal PAG surface to model perfect gel adhesion onto the substrate. Free boundary conditions were assumed for all other sample surfaces.

Two distinct computational analyses were performed to quantify the influence of PAG nonlinearity on cellular traction forces quantification in large strains regime observed experimentally, both knowing that PAG substrates are quasi-incompressible and assuming that there are homogeneous.

In the first analysis, a linear stress–strain relationship was implemented to describe the PAG mechanical behavior. PAG was considered as a linear elastic medium and its mechanical response to cell traction was computed using the St. Venant-Kirchhoff’s strain-energy function [18]:

$$W=\frac{E}{2(1+\nu )}\text{trace}{E}_L^2+\frac{E\nu }{2(1+\nu )(1-2\nu )}{(\text{trace}{E}_L)}^2.$$ (7)

In the second analysis, the nonlinear elastic behavior of the PAG substrate was explicitly considered by using Eq. (1) to compute the stress distribution and amplitude generated on the substrate by the cellular force.

2.2.2. Reconstruction of microbeads displacement field from experimental data

In order to investigate how large strains of PAG extracellular substrate might affect the accuracy of cellular traction forces quantification, we generate a set of benchmark data from the displacements observed and measured in Dembo and Wang experiments [12]. Thus, we did not solve the associated inverse problem, but rather computed the displacement field by assuming a continuous linear distribution of normal traction forces along the cell’s periphery [12,32]. An optimal traction field was obtained by minimizing the difference between observed and computed microbeads displacements, computation being performed with the FE software Ansys (OptypeSubp routine, Ansys).

2.3. Analysis of finite thickness effect on cell forces evaluation

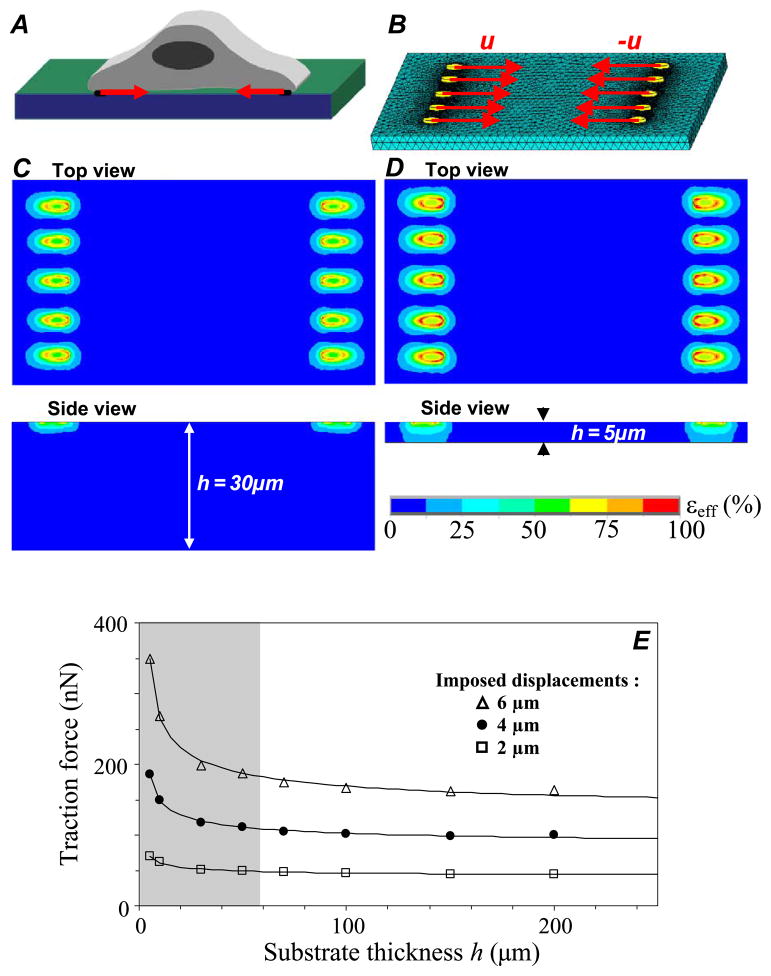
Quantification of cellular forces does not only depend on intrinsic PAG nonlinear mechanical behavior, but also possibly on geometrical parameter such as PAG thickness. Such nonlinear geometrical effects have been clearly evidenced for linear elastic material by the recent work of Merkel et al. [23]. In order to shed light on the influence of PAG finite thickness effects on force evaluation when using nonlinear elastic substrates such as PAG, we followed the approach proposed by Merkel et al. [23] and assumed that cellular forces are transmitted through spatially distributed focal adhesions at the cell/substrate interface. These mature focal adhesions were modeled by a set of ten small rigid ellipses (5 μm long axis and 2 μm small axis), equally and symmetrically distributed over the two opposite sides of a 70 × 35 μm sized rectangle (Fig. 6). In agreement with the range of PAG thickness values considered in cell biology experiments, the thickness h was varied between 5 and 200 μm. Displacements were applied uniformly at focal adhesion sites with amplitude of 2, 4 or 6 μm, and FE computation of reaction forces was conducted at the same nodes.

Fig. 6.

Influence of PAG thickness on cellular force estimation, analyzed by considering an adherent cell (A) transmitting intracellular forces to underlying substrate through 10 focal adhesions sites. The PAG is made of 0.03% of bis-acrylamide and follows a nonlinear elastic constitutive law with a₁ = 1.13 kPa, a₃ = 0.10 kPa and ν = 0.48. Its surface is 800 × 800 μm, with a thickness h varying from 5 to 200 μm. Focal adhesions sites are modeled by elliptic surfaces with 5 μm length and 2 μm width, and are equally distributed over the short sides of a 70 by 35 μm sized cell-rectangle (B). Displacements with magnitude in the range 2–6 μm are imposed on the ten focal adhesion sites, and the corresponding PAG stress and strain fields are computed using the finite element method. (C, D) Top and side view color maps showing the spatial distribution of the effective strain for a PAG substrate with thickness h = 30 μm (C) and with thickness h = 5 μm (D). (E) Influence of the substrate thickness h on the force F_NL at the centre of the focal adhesion site, where F_NL is the mean of the values computed for each of the ten elliptical focal adhesions. Imposed displacements are of 2 μm (square), 4 μm (circle) and 6 μm (triangle). The shaded area represents the domain where considering the underlying PAG as a semi-infinite medium would lead to biased quantification of forces.

3. Results

3.1. Characterization of PAG nonlinear mechanical properties

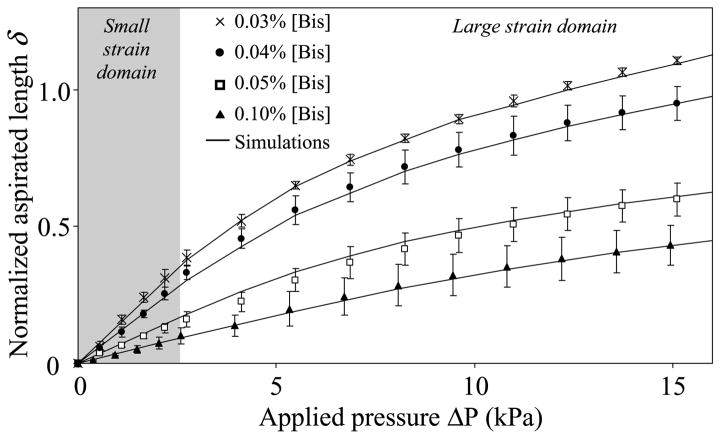
Aspirations of PAG were performed by increasing the absolute value of the internal micropipette pressure ΔP from 0.3 to 16 kPa in order to get PAG deformations in the large strains domain. As shown in Fig. 3, the mechanical response of PAG is highly nonlinear, exhibiting only a limited region of linear behavior. Computations using the constitutive linear law (Eq. (7)) failed to satisfactorily reproduce the experimental data, i.e. the geometrical nonlinearity cannot explain the observed nonlinear PAG elastic response. In contrast, we found that the adopted Yeoh’s strain energy function was highly relevant to model the nonlinear mechanical response of the PAG. Interestingly, for 10% of [Acry] and for [Bis] in the range 0.03% ≤ [Bis] ≤ 0.1%, the PAG hyperelastic material constants a₁ and a₃ (in kPa) vary almost linearly with the [Bis] concentration (%) (correlation coefficients r² = 0.981 and 0.940, for a₁ and a₃, respectively), with the two material parameters being defined through the relationships:

$$a_1=\alpha [\mathit{Bis}],$$ (8)

$$a_3=\beta [\mathit{Bis}]-\gamma .$$ (9)

Fig. 3.

Identification of the two material constants a₁ and a₃ appearing in the hyperelastic two-parameter Yeoh’s strain energy function (Eq. (1)). The two material constants a₁ and a₃ were estimated by fitting the measured normalized aspirated length δ = d/R_i (where d and R_i are the aspirated length and the inner radius of the micropipette, respectively) against the applied pressure (ΔP) for each considered bis-acrylamide concentration [Bis] ranging from 0.03% to 0.10%. Each experimental point represents the mean of n = 5 measurements with its standard deviation. The figure highlights the goodness of fit we obtained, with the continuous lines corresponding to the normalized aspirated lengths simulated for the optimal mean values of material parameters a₁ and a₃ indicated in Table 1.

For [Acry] = 10% and 0.03% ≤ [Bis] ≤ 0.1%, we get the following optimal values of the parameter set [α, β, γ] as α = 45.43, β = 77.33 and γ = 2.19. The corresponding values of material parameters a₁ and a₃ are summarized in Table 1 for the different values of [Bis] we considered. Thus, an original constitutive relationship for the nonlinear mechanical characterization of PAG can be proposed through the strain energy function:

$$W=\alpha [\mathit{Bis}](J^{-2/3}{I}_1-3)+(\beta [\mathit{Bis}]-\gamma ){(J^{-2/3}{I}_1-3)}^3+\alpha [\mathit{Bis}]\frac{2(1+\nu )}{3(1-2\nu )}{(J-1)}^2.$$ (10)

Table 1.

Means and standard deviations (n = 5) of the optimal values of material constants a₁ and a₃ identified when fitting measurements on polyacrylamide gels (PAG) made with 10% of acrylamide and varying concentrations of bis-acrylamide [Bis]. A hyperelastic Yeoh’s strain energy function (given by Eq. (1)) involving these two material constants and a Poisson’s ratio equal to 0.48, was used to model the nonlinear response of these gels

[Bis] (%)	a1 (kPa)	a3 (kPa)
0.10	4.66 ± 0.88	5.40 ± 4.80
0.05	2.48 ± 0.28	2.50 ± 1.10
0.04	1.46 ± 0.27	0.25 ± 0.10
0.03	1.13 ± 0.12	0.10 ± 0.03

3.2. Influence of PAG nonlinear behavior on of quantification cell traction forces

In the cell traction simulations, PAG nonlinear mechanical properties were derived from Eq. (1) for [Bis] = 0.03%, i.e. with the parameter set a₁ = 1.13 kPa and a₃ = 0.10 kPa. Quasi-incompressibility of PAG is considered, with a Poisson’s ratio ν = 0.48 previously estimated from our experimental data [5]. For small strains, one gets according to Eq. (3) a tangent elastic modulus E_tan = 6a₁ = 6.78 ± 0.72 kPa. These material constant values are quite similar to those considered by Dembo et al. [12] who reported a Young’s modulus of 6.2 ± 1 kPa and a Poisson’s ratio close to 0.5.

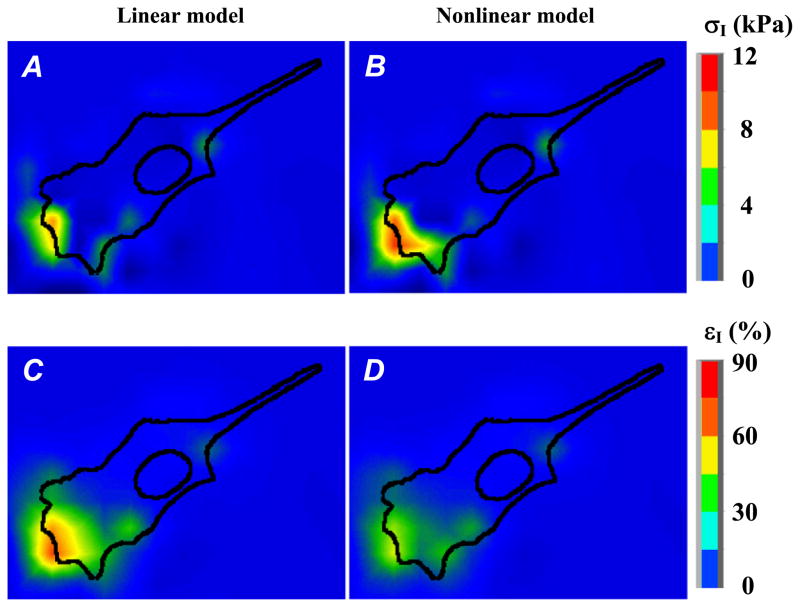
Starting from this agreement on substrate elasticity moduli, we then simulated the observed beads displacement field (Fig. 4(A, B)) when considering first a linear elastic response for the PAG substrate, with ν = 0.48 and E = 6.78 kPa. The so-computed maximum value of the first principal stress σ₁ is 6.2 kPa (Fig. 5A), which agrees quite well with the maximum value of ~7.6 kPa reported by Dembo et al. [12]. Notice that in this linear case, the computed maximum value of the first principal strain ε₁ reaches 65% (Fig. 5C).

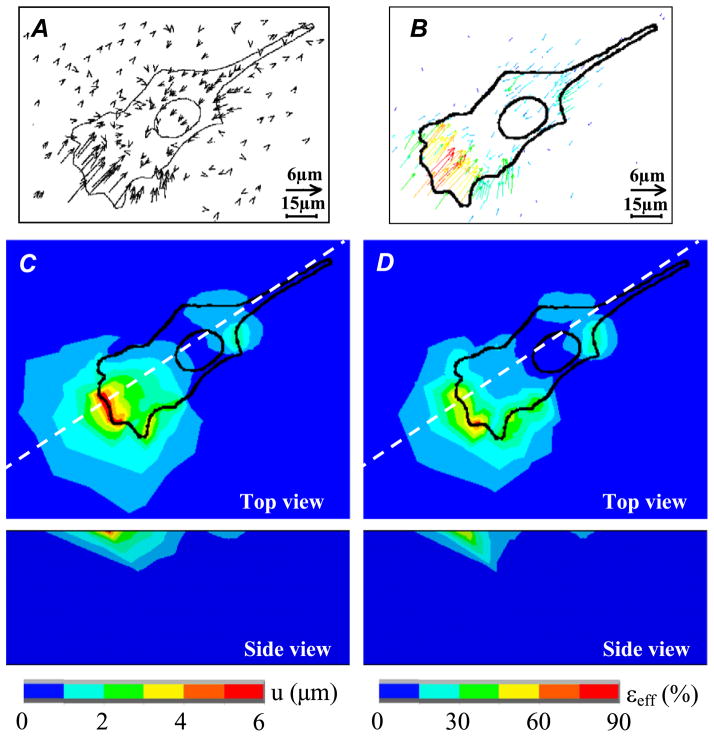
Fig. 4.

Finite element simulations of the cellular traction force experiments conducted using the measurements and observations of Dembo et al. [12]. Computations were performed assuming a linear elastic response for the PAG substrate, with Poisson ratio and Young’s modulus equal to 0.48 and 6.78 kPa, respectively. (A) Displacement vectors of latex beads during fibroblast locomotion as reported in Dembo et al. [10]. (Reprinted with permission ©1999, Biophysical Society.) (B) Computed displacements of the PAG substrate. (C and D) Top and side views color maps showing the computed displacement field (C) and effective strains field ε_eff (D). The effective strain is defined as: ε_eff = (2e_ij e_ji/3)^1/2, where e_ij are the deviatoric components of the strain tensor. Side views of the displacement and strain fields are given along the section plane defined by the dashed lines on (C) and (D).

Fig. 5.

Finite element computations of the PAG stress and strain fields induced by cellular forces considering successively a linear then a nonlinear elastic response of the gel. Considering a PAG made with 10% acrylamide and 0.03% of bis-acrylamide, the gel mechanical properties are characterized by – (i) a Young’s modulus E = 6.78 kPa and Poisson ratio ν = 0.48 (linear behavior, Eq. (7), figures (A) and (C)) or – (ii) two material constants a₁ = 1.13 kPa, a₃ = 0.10 kPa and Poisson ratio ν = 0.48 (nonlinear behavior, Eq. (1), figures (B) and (D)). Figures (A, B) and (C, D) represent the color maps of the first principal stress (σ_I) and principal strain (ε_I) distributions at the cell/PAG interface, respectively.

We then considered the nonlinear elastic response of the PAG evidenced from our experiments. In this case, the maximum value of the first principal strain ε₁ decreases to 49% (Fig. 5D), while the computed stress σ₁ peaks at 12.0 kPa (Fig. 5B), a value which is roughly two times higher than the one computed under the linear elasticity assumption.

3.3. Influence of substrate thickness on estimation of cell traction forces

The influence of PAG thickness on cell traction force evaluation was investigated as described in Section 2.3, by applying uniformly known displacements over the small ellipses modeling focal adhesion at the PAG upper surface (Fig. 6(A, B)). Substrate thickness h was varied from 5 to 200 μm. The finite element simulation of the nonlinear PAG response was conducted with the strain energy function W given in Eq. (1) for [Bis] = 0.03%, which corresponds to material constant values a₁ = 1.13 kPa, a₃ = 0.10 kPa, with Poisson’s ratio ν = 0.48.

In these conditions, the maximum effective strains ε_eff we computed spanned from 60% to 120% for the imposed displacement range of 2–6 μm (Fig. 6(C, D)). We also found that, in the displacement range considered, the relative error between the reaction forces computed for finite substrate thickness and for semi-infinite medium remains acceptable and lower than 10% if PAG thickness is larger than 60 μm (nonshaded area, Fig. 6E). However, if one keeps using this semi-infinite approximation, the cell traction force amplitude may be largely overestimated for experiments performed with PAG thickness below 20 μm.

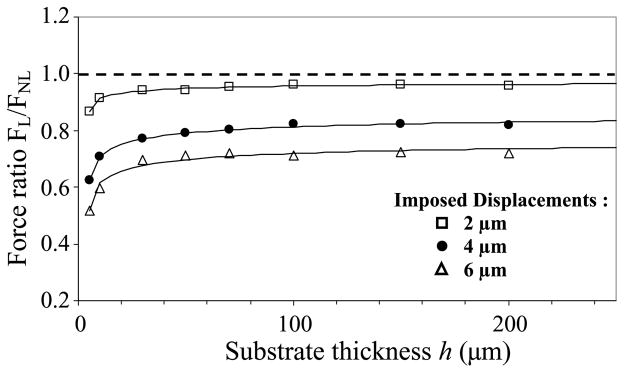
Focusing now on differences linked to the nonlinear versus linear PAG mechanical response (Fig. 7), we found that the imposed displacement amplitude may have a drastic effect on the accuracy of force evaluation. With a 2 μm displacement, assuming a linear elastic response of PAG substrate only leads to a slight underestimation of the force amplitude (F_L/F_NL ≈ 1). But this underestimation reaches 20% and 30% of relative error for imposed displacements increasing from 4 to 6 μm, respectively (Fig. 7). A threshold thickness of about 60 μm is again noticeable from the curve profile. More precisely, assuming a linear elastic response of PAG leads to a force underestimation by a factor of 2 if very thin PAG substrates have to be used in cell traction force experiments (Fig. 7).

Fig. 7.

Influence of PAG thickness h on the traction force ratio F_L/F_NL, where F_L is the mean force at the centre of the focal adhesion site obtained when assuming that the PAG considered in previous Fig. 6 rather exhibits a linear elastic response with material properties defined by E = 6.78 kPa and ν = 0.48. For small displacements (2 μm, square), the ratio is close to the theoretical limit F_L/F_NL = 1 (dashed line), i.e. the real nonlinear behavior of PAG appears reasonably approached with the linear elastic response assumption except for very thin substrate. This is no longer the case when larger displacements of 4 μm (circles) and 6 μm (triangles) are imposed, as discussed in the text.

Our results highlight that both finite size thickness and nonlinear material properties have very significant effects on cellular force quantification when PAG thickness falls below 60 μm.

4. Discussion

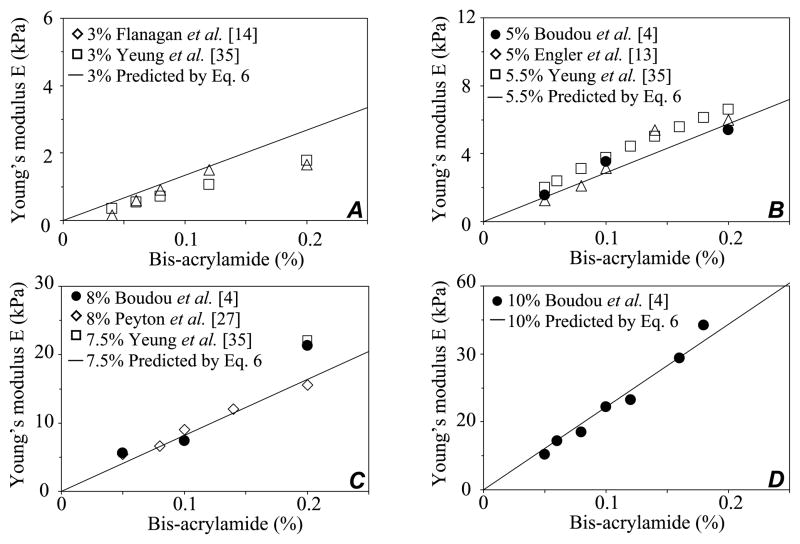
In a previous work, we showed that the micropipette aspiration technique is a valuable tool for the characterization of Young’s modulus and Poisson’s ratio of tunable polyacrylamide gels [4,5]. Notably, an analytical expression (Eq. (6)) was proposed to compute PAG Young’s modulus for bis-acrylamide and acrylamide concentrations in the ranges 0.02% ≤ [Bis] ≤ 0.20% and 3% ≤ [Acry] ≤ 10%, respectively. Interestingly, this analytical expression gathers very satisfactorily a rather large set of experimental data on PAG reported previously by other groups, as shown by the compilation of results given in Fig. 8.

Fig. 8.

Compilation of measured and predicted values of PAG Young’s modulus in the small strain domain. The solid lines correspond to the predicted modulus values given by the multi-parametric relationship (Eq. (6)) we established for varying acrylamide and bis-acrylamide concentrations. The experimental reported values are those found in the literature, including ours, with acrylamide concentrations of 3% (A), ~5% (B), ~8% (C), 10% (D), and bis-acrylamide in the range 0.02–0.2%.

In this paper, we first extended these previous studies, conducted in the small strains domain, by proposing an original constitutive law describing the nonlinear elastic behavior of PAG. Considering the experimental data we obtained with the micropipette aspiration technique, we proposed and validated an original characterization of PAG nonlinear elastic properties by a strain-energy function which depends on three parameters: the Poisson’s ratio ν and two material moduli a₁ and a₃. Moreover, we were able to establish an analytical expression of these two material moduli as functions of acrylamide and bis-acrylamide fractions for 10% [Acry] and [Bis] in the range 0.03–0.10%.

In a second part, implication of these results have been analyzed in the field of traction force microscopy which progressively sets up as a standard assay for reconstructing cellular traction forces from deformation of elastic substrates. Indeed, these experiments mainly use PAG as elastic extracellular substrates with controllable stiffness. Thus, advances on traction force reconstruction and resolution rely not only on improvements of theoretical and computational methods, as discussed recently [23,30], but also on a more precise characterization of PAG properties. In this context, recent papers focus on improvements in reliability and accuracy of traction force microscopy under the assumption of a linear elastic response of PAG. While this assumption may be justified for experiments conducted in small strains domain [11], it may induce significant bias when cellular forces exert large strains on PAG [8,9,16,20].

Taking advantage of our original description of PAG as hyperelastic media, we analyzed different aspects of this key methodological issue by investigating to which extent a linear elastic response of PAG might bias cellular force quantification when PAG experience large strains. We show that the linear elastic assumption tends to significantly underestimate traction forces for imposed displacements larger than 2 μm. For displacements up to 6 μm, which is a typical experimental value recorded during deformation of PAG by fibroblasts [12], the underestimation of the force may be 30% for gel with thickness larger than ~50 μm (Fig. 7). For thinner gels, the underestimation rises exponentially up to ~50%.

In addition, finite thickness effects may influence the apparent response of elastic media [23,24]. Such influence of substrate finite size on cellular force evaluation has been recently investigated by Merkel et al. [23] in the case of a linear elastic medium. Their study showed that force reconstruction from the displacement field of fiducial markers under the assumption of a semi-infinite elastic substrate is no longer valid when the substrate thickness is less than 60 μm, and thus the strain field of point force acting on the substrate does not follow the Boussinesq’s theory.

Following a similar computational approach, we investigated the effects of PAG’s finite thickness on force evaluation when the nonlinear elastic behavior of PAG is considered. Imposing uniformly displacements in the range 2–6 μm on opposite ellipsoidal adhesion plates, we computed the associated resistive substrate forces for PAG thickness ranging from 5 to 200 μm. In the range of PAG’s stiffness that we considered, finite size effects appear to be nonsignificant for PAG thickness above approximately 60 μm (Fig. 6). Interestingly, this threshold was found close to the half-space limit found by Merkel et al. [23] assuming linear elasticity of PAG substrates.

Our results highlight that the nonlinear elastic behavior of PAG has to be considered in cell biology experiments conducted with cells exhibiting large traction stress (up to ~10 kPa) reported in the case of fibroblast migration [15,22], endothelial cell spreading [29] or even cardiomyocyte contraction [28]. Such nonlinearity might notably be considered in traction force experiments, since still larger differences between the linear and nonlinear results may thus be expected. Moreover, considering that cells cultured on substrate containing a gradient of stiffness have been found to move preferentially toward the more rigid side [22]. The intrinsic increase of substrate rigidity in the large strains regime may have profound implications in our understanding of the manner in which cells regulate focal adhesion assembly and control the production and transduction of contractile forces by actively probing the mechanical properties of their microenvironment.