Impact of an equality constraint on the class-specific residual variances in regression mixtures: A Monte Carlo simulation study

Abstract

Regression mixture models are a novel approach for modeling heterogeneous effects of predictors on an outcome. In the model building process residual variances are often disregarded and simplifying assumptions made without thorough examination of the consequences. This simulation study investigated the impact of an equality constraint on the residual variances across latent classes. We examine the consequence of constraining the residual variances on class enumeration (finding the true number of latent classes) and parameter estimates under a number of different simulation conditions meant to reflect the type of heterogeneity likely to exist in applied analyses. Results showed that bias in class enumeration increased as the difference in residual variances between the classes increased. Also, an inappropriate equality constraint on the residual variances greatly impacted estimated class sizes and showed the potential to greatly impact parameter estimates in each class. Results suggest that it is important to make assumptions about residual variances with care and to carefully report what assumptions were made.

Introduction

An important problem in behavioral research is understanding heterogeneity in the effects of a predictor on an outcome. Traditionally the primary method for assessing this type of differential effect has been the use of interactions. A new approach for assessing effect heterogeneity is regression mixture models which allow for different patterns in the effects of a predictor on an outcome to be identified empirically without regard to a particular explaining variable.

Regression mixture models have been increasingly applied to different research areas, including marketing (Wedel & Desarbo, 1994, 1995), health (Lanza, Cooper, & Bray, 2013; Yau, Lee, & Ng, 2003), psychology (Van Horn et al., 2009; Wong, Owen, & Shea, 2012) and education (Ding, 2006; Silinskas et al., 2013). While traditional regression analyses model a single average effect of a predictor on an outcome for all subjects, regression mixtures model heterogeneous effects by empirically identifying two or more subpopulations present in the data where each subpopulation differs in the effects of a predictor or predictors on the outcome(s). Three types of parameters are estimated in regression mixture models: latent class proportions (probability of class membership), class specific regression coefficients (intercepts and slopes), and residual structures. Although all these elements are crucial to establish a regression mixture model, most methodological research in the area of mixture modeling have focused on detection of the true number of latent classes (Nylund, Asparauhov, & Muthen, 2007; Tofighi & Enders, 2008) or recovering the true effects of covariates on latent classes and outcome variables (Bolck, Croon, & Hagenaars, 2004; Vermunt, 2010). Residual variance components are often simplified without thorough examination of the consequences.

This study aims to evaluate the effects of ignoring differences in residual variances across latent classes in regression mixture models. Before examining our research question, we briefly review regression mixture models in the framework of finite mixture modeling.

Regression mixture models

Regression mixture models (Desarbo, Jedidi, & Sinha, 2001; Wedel & Desarbo, 1995) allow researchers to investigate unobserved heterogeneity in the effects of predictors on outcomes. Regression mixture models are part of the broader family of finite mixture models which also include latent class analyses, latent profile analyses, and growth mixture models (see McLachlan and Peel (2000) for a review of finite mixture modeling). In regression mixture models, subpopulations are identified by class specific differences in the regression weights, which characterize class means on the outcomes (intercepts) and the relationship between predictors and outcomes (slopes). Thus, subjects identified to be in the same latent class share a common regression line, while those in another latent class have a different regression line. The overall distribution of the outcome variable(s) is conceived as a weighted sum of the distribution of outcome(s) within each class.

Take a sample of N subjects drawn from a population with K classes. The general regression mixture model within class k for a single continuous outcome can be written as:

$$\begin{array}{l}{y}_{i\mid \mathbf{x},k}={\beta }_{\mathit{0}k}+\sum _{p=1}^P{\beta }_{pk}{x}_{ip}+{\epsilon }_{ik},\\ {\epsilon }_{ik}~N(0,{\sigma }_k^2),\end{array}$$ (1)

where y_i represents the observed value of y for subject i, k denotes the group or class index, β_0k is the class-specific intercept coefficient, p is the number of predictors, β_pk is the class-specific slope coefficient for the corresponding predictor, x_ip is the observed value of predictor x for subject i, and ε_ik denotes the class-specific residual error which may be allowed to follow a class specific variance, ${\sigma }_k^2$. The value of K is specified in advance but the class-specific regression coefficients and the proportion of class membership are estimated. Hence, regression mixture models formulated in this way allow that each subgroup in the population has a set of unique regression coefficients and potentially unique residual variances, which represent the differential effect of the predictor on outcome.

The between class portion of the model specifies the probability that an individual is a member of a given class. This model may include covariates to predict class membership and can be specified as:

$$Pr(c_i=k\mid {\mathbf{z}}_i)=\frac{exp({\alpha }_k+{\displaystyle \sum _{q=1}^Q}{\gamma }_{qk}{z}_{iq})}{{\displaystyle \sum _{s=1}^K}exp({\alpha }_s+{\displaystyle \sum _{q=1}^Q}{\gamma }_{qs}{z}_{iq})}$$ (2)

where c_i is the class membership for subject i, k is the given class, z_i is the observed value of predictor z of latent class k for subject i, α_k denotes the class-specific intercept, γ_k is the class-specific effect of z, which explains the heterogeneity captured by latent classes. In this study, we are not considering the effect of z, so the equation can be simplified to:

$$Pr(c_i=k)=\frac{exp({\alpha }_k)}{{\displaystyle \sum _{s=1}^K}exp({\alpha }_s)}.$$

Since there are many parameters to be estimated, model convergence can sometimes be a problem and, even when models do converge, they may not converge to a stable solution. To simplify model estimation, the class-specific residual variances are often constrained to be equal across classes. Referring to multilevel regression mixtures, Muthén and Asparouhov (2009) stated that, “For parsimony, the residual variance θc is often held class invariant.” (p. 640). This can be suitable in some cases, such as when the residual variances are very similar for all latent classes. However, the effects of this constraint on latent class enumeration and model results when there are differences in residual variances between classes has not been thoroughly examined.

We know of no existing research examining the effects of misspecifying the residual variances in regression mixture models and of little research examining these effects with mixture models in general. McLachlan and Peel (2000) demonstrated the impact of specifying the common covariance matrix between two clusters in multivariate normal mixtures. They found that class proportions (and consequently assignment of individuals to a class) were poorly estimated under this condition and they cautioned against the use of homoscedastic variance components. On the basis of this initial attempt, Enders and Tofighi (2008) investigated the impact of misspecifying the within-individual (level-1) residual variances in the context of growth mixture modeling of longitudinal data. In their study, the class-varying within-individual residual variances were constrained to be equal across classes and the impact on latent class enumeration and parameter estimates were assessed. They found some bias in the within-class growth trajectories and variance components when the residual variances were misspecified. In growth mixtures, intercepts and slopes are directly estimable for every individual and the value of the model is to classify individuals who are similar in patterns of these growth parameters. In regression mixture models, however, individual slopes are not directly estimable and the mixture is used to allow us to estimate variability in regression slopes which cannot otherwise be estimated. Thus, we expect that the impact of misspecifying the error variance structure on the parameter estimates to be more severe in regression mixture models than growth mixture models.

Unlike growth mixture models in which means (intercepts), slopes over time, and variances are the main focus, regression mixture models focus on the regression weights characterizing the association between the predictors and outcomes. In this case, we see clear reason to expect differences in residual variances between classes: if regression weights are larger there should be less residual variance, given the larger explained variance. Thus, even though residual variances are not the substantive focus when estimating these models, because differences between classes in residual variances are expected, it is especially important to understand the effects of misspecifying this portion of the model.

A review of the literature in which regression mixtures are used showed a lack of consensus in the specification of residual variances; some authors freely estimated the class-specific residual variance (Daeppen et al., 2013; Ding, 2006; Lee, 2013), while others constrained them to be equal across classes (Muthén & Asparouhov, 2009). Interestingly, the majority of the studies employing regression mixtures gave no information about residual variance specifications whether the equality constraint has been imposed or not (Lanza et al., 2013; Lanza, Kugler, & Mathur, 2011; Liu & Lu, 2011; Schmeige, Levin, & Bryan, 2009; Wong & Maffini, 2011; Wong et al., 2012). The contribution of this paper is to examine the degree to which this is a consequential decision that should be thoughtfully made and clearly reported, so that readers can understand regression mixture results, and so results may be replicated in the future. In the current study, we are focusing on the specification of ${\sigma }_{\mathrm{k}}^2$ which is the variance of the residual error, ε_ik, and represents the unexplained variance after taking into account the effect of all predictors in the model. We assume that the residual variances are normally distributed in this study to avoid the complex issue of non-normal errors in the regression mixture models (George et al., 2013; Van Horn et al., 2012).

Study Aims

The objective of this study is to examine the consequences of constraining class-specific residual variances to be equal in regression mixture models under conditions that approximate those likely in applied research. It is reasonable to expect that the unexplained/residual variances of the outcomes differ across the classes between which the effect size of the predictor on the outcome varies. However, in practice, residual variances are of little interest substantively, and it has been recommended that they can be constrained to be equal across the latent classes for the sake of the model parsimony. In this study, we used Monte Carlo simulations to investigate the impact of this equality constraint.

Our first aim is to investigate whether imposing equality constraints on the residual variances across classes affects the result of class enumeration. We generated data from a population with two classes. The size of the residual variances differed across simulation conditions; however, we kept the differences in effect sizes between the classes the same across conditions. We examined how often the true two classes were detected when the residual variances were constrained to be equal for ten scenarios that differ in the number of predictors, the correlation between the predictors, and whether there is a difference in intercepts between the classes. As class enumeration is mainly determined by the degree of separation between classes, we hypothesize that the equality constraints for small differences in variance will have minimal impact on selecting the correct number of latent classes. We also hypothesize that when models are misspecified by constraining variances to be equal, additional classes will be increasingly found as class separation and power increases.

The second aim is to examine parameter bias in regression coefficients, variance estimates, and class proportions that results from constraining the residual variances to be equal across classes. We hypothesize that the scenario with a large difference in residual variances between the classes will result in the regression coefficients with substantial bias because we force the two very different values to be the same. With an additional class varying predictor in the model, although the total residual variances are reduced for each latent class, the differences in the residual variances across latent classes will increase because the difference in total effect size is greater. Thus, we expect that there will be greater bias when there is an additional predictor in the regression mixture models. We expect no bias when the true model contains two classes with equal variances.

The outcome of the first aim is the proportion of simulations that select the true population model over a comparison model using the BIC and ABIC as criteria. Although AIC is also frequently used for model selection in finite mixture models, previous research have shown that AIC has no advantage for latent class enumeration and tends to overestimate the number of latent classes in regression mixtures (Nylund et al., 2007; Van Horn et al., 2009). Therefore, we do not further discuss about the AIC in this study. For the second aim, the accuracy of the parameter estimates of intercepts, regression coefficients of the predictors, residual variances, and percentages of subjects in each class are examined.

Methods

Data generation

Data were generated using R (R Development Core Team, 2010) with 1000 replications for each condition with a sample size of 3000 in each dataset. Because regression mixtures rely on the shape of residual distributions for identification, this is seen as a large sample method (Fagan, Van Horn, Hawkins, & Jaki, 2012; Liu & Lin, 2014; Van Horn et al., 2009). We choose a sample size of 3000 to be consistent with other research in the field (Smith, Van Horn, & Zhang, 2012, April) and because samples of this size are available in many publicly available datasets in behavioral research. Our starting point for finding differential effects is a population comprised of two populations (which should be identified as classes) with a small effect size for the relationship between a single predictor and an outcome (r =.20) in one and a large effect size for this relationship in the other (r =.70). The rationale for this condition is that we believe that a difference in correlations between subpopulations of .20 and .70 is the minimum needed for regression mixture models to be useful in capturing heterogeneity in the effect of X on Y. This corresponds to a small effect in one group and a large effect in the other, which can be found in some applied research employing the regression mixture models (Lee, 2013; Silinskas et al., 2013). If the method cannot find a difference between a small and large effect with a sample size of 3000, then we argue that it has limited practical value for detecting differential effects. If it meets this minimum criterion then it has application at least in some situations. This condition is therefore chosen because it represents a threshold for the practical use of the method and is a good starting point for evaluating other features of the regression mixtures.

In this study, because we focused on the effect of misspecified residual variances, we held constant class membership probabilities (.50) and differences in effect size between classes to be equal. The challenge in this situation was to create conditions in which the difference in effect sizes between the two classes was the same, but in which residual variances differed. To achieve equal variances and have distinct regression weights, we chose the regression weights that had the same absolute value but differed in directionality, in which case the residual variances would be equal in each class. We also have a condition with a moderate difference in variances in which regression weights are scaled to be closer to zero than in the .20/.70 condition. In order to maintain the same effect size in each condition we computed a Fisher’s z-transformation¹ (Fisher, 1915) for each correlation, when r is .20 and .70, z’ is .203 and .867, which led the difference between the two classes of z’=.664. Thus, the effect size difference was fixed to be a difference of z’=.664 between the two classes for all conditions. The models can be written as,

• Large difference condition:

  $$\begin{array}{ll}{Y}_{i\backslash c=\mathit{1}}=\mathit{0}+\mathit{.200}{X}_i+{\epsilon }_i,\hfill & {\epsilon }_i~N(\mathit{0},\mathit{.96})\hfill \\ Y_{i\backslash c=\mathit{2}}=\mathit{0}+\mathit{.700}{X}_i+{\epsilon }_i,\hfill & {\epsilon }_i~N(\mathit{0},\mathit{.51})\hfill \end{array}$$
• Moderate difference condition:

  $$\begin{array}{ll}{Y}_{i\backslash c=\mathit{1}}=\mathit{0}+-\mathit{.126}{X}_i+{\epsilon }_i,\hfill & {\epsilon }_i~N(\mathit{0},\mathit{.984})\hfill \\ Y_{i\backslash c=\mathit{2}}=\mathit{0}+\mathit{.491}{X}_i+{\epsilon }_i,\hfill & {\epsilon }_i~N(\mathit{0},\mathit{.759})\hfill \end{array}$$
• No difference condition:

  $$\begin{array}{ll}{Y}_{i\backslash c=\mathit{1}}=\mathit{0}+-\mathit{.321}{X}_i+{\epsilon }_i,\hfill & {\epsilon }_i~N(\mathit{0},\mathit{.897})\hfill \\ Y_{i\backslash c=\mathit{2}}=\mathit{0}+\mathit{.321}{X}_i+{\epsilon }_i,\hfill & {\epsilon }_i~N(\mathit{0},\mathit{.897})\hfill \end{array}$$

  where X was generated from a standard normal distribution with a mean of 0 and standard deviation of 1. The differences in variances are set to be .45 for large difference, .225 for moderate difference, and zero for no difference condition, while the total variance of Y is set to be 1 within each class across all conditions.

In order to assess the effects of variance constraints in situations more likely to mirror those observed in applied applications of regression mixtures, the simulations were expanded to include two predictors, the effects of which both differed between classes. This resulted in nine additional simulation conditions which differed in the correlations between these predictors as well as in the means of the outcome (intercepts) within each class. The general model for the multivariate conditions can be written as,

$$\begin{array}{ll}{Y}_{i\backslash c=\mathit{1}}={\beta }_{\mathit{01}}+{\beta }_{\mathit{11}}X\mathit{1}i+{\beta }_{\mathit{21}}X{\mathit{2}}_i+{\epsilon }_{i\mathit{1}},\hfill & {\epsilon }_{i\mathit{1}}~N(\mathit{0},{{\sigma }^{\mathit{2}}}_{\mathit{1}})\hfill \\ Y_{i\backslash c=\mathit{2}}={\beta }_{\mathit{02}}+{\beta }_{\mathit{12}}X\mathit{1}i+{\beta }_{\mathit{22}}X{\mathit{2}}_i+{\epsilon }_{i\mathit{2}},\hfill & {\epsilon }_{i\mathit{2}}~N(\mathit{0},{{\sigma }^{\mathit{2}}}_{\mathit{2}}).\hfill \end{array}$$

Because predictors in a multivariate model (especially where the predictors are operating in the same way) are typically correlated, we varied the relationship between X1 and X2 to range from having no relationship (Pearson correlation coefficient r = 0), moderate relationship (r = 0.5), and a strong relationship (r = 0.7). The population regression weights for the multivariate conditions were calculated to maintain the univariate relationships in light of the correlation between the predictors². Additionally, the intercept values for the larger effect class (β₀₂) were varied to be zero, 0.5, and 1 for the condition with two predictors in the model, while the intercepts for the smaller effect size class (β₀₁) were always zero. Therefore, we generated a total of 30 sets of simulations including three variance-difference (large, moderate, and no) conditions for the univariate model and 27 conditions (3 variance-difference x 3 correlations of predictors x 3 intercept-difference) for the multivariate model. Larger intercept differences result in greater class separation and should increase power to find 2 classes when the model is correctly specified, and to find more than 2 classes when the model is misspecified. The point of these analyses is to examine the effects of constraining class variances to be equal as class separation increases. We note that with two predictors the effect size when the predictors are both included in the model is not the same across conditions, specifically, there is less residual variance when the predictors are less correlated.

Data analysis

Mplus 7.1 (Muthén & Muthén, 1998–2012) employing the maximum likelihood estimator with robust standard errors (MLR) was used for estimating regression mixture models. We first fit the relaxed model (defined as the true model for the cases with a large and moderate difference in variances between classes) by allowing the class-varying residual variances. This serves two purposes: first, it validated the data-generating process by showing that the parameter estimates from the true model were as expected; second, this demonstrated that when there is no difference in variances between classes (i.e. for the no difference condition) it is still possible to estimate class-specific variances.

Then we examined the impact of constraining the residual variances to be the same between the classes on class enumeration. One-class, 2-class, and 3-class models were run for each of the 30 simulation conditions. The outcome is the percentage of simulations in which the true number of classes (2) is selected using the Bayesian Information Criterion (BIC; (Schwarz, 1978)) and sample-size adjusted BIC (ABIC; Sclove, 1987). Both BIC and ABIC have been shown to be effective for latent class enumeration in regression mixture models (Van Horn et al., 2009).

Next, we compared the 2-class constrained model with class-invariant residual variances to the 2-class relaxed model with residual variances freely estimated in each class. A null hypothesis test was conducted to examine whether the restricted model fit worse than the relaxed model by using the Satorra-Bentler log-likelihood ratio test (SB LRT; Satorra & Bentler, 2001). The adequacy of parameter estimates is formally assessed using the root mean squared error (RMSE) and the coverage rate for the true population value for each parameter. RMSE is a function of both bias and variability in the estimated parameter and it is computed as the rooted square value of the difference between the true population value and the estimated parameter (i.e., $\text{RMSE}=\sqrt{{(\mathit{True}-\mathit{Estimated})}^2}$). We also reported the average parameter estimates, standard errors, standard deviations, maximum and minimum values, and the coverage rates. The coverage rate is the proportion of the 1000 simulations in which the true parameter values fall in the 95% confidence interval for each model parameter. If the parameter estimates and standard errors are unbiased coverage should be 95%. It shows the accuracy of statistical inference for each parameter in each condition.

Results

Class enumeration

All models converged properly across all simulation conditions. Before examining the impact of the equality constraints on the residual variances, we analyzed the regression mixtures with freely estimating the residual variances for both classes. The percentage selecting the true 2-class model is presented in Table 1. For the single predictor model, the 2-class model was selected in 86.2% and 87.2% of the simulations using the BIC and ABIC, respectively, when the difference in variances was large. Under the moderate variance-difference condition (.225 difference), the true 2-class model was selected in 52.3% and 86.7% of the simulations, respectively. Under the no variance difference condition when freely estimating the variance within class, the 2-class model was selected only in 46.7% using the BIC, while they were correctly selected using the ABIC in 84.1% of the simulations. The simulations which include two predictors suggest that the failure to select the 2-class model is a function of power related to relatively low class separation. When there is greater class separation – larger differences between classes in variance and intercepts, and additional predictors with weak correlations – the two class model is selected nearly all of the time using penalized information criteria.³

Table 1.

Class enumeration results when the residual variances are freely estimated

Correlation	Difference in Intercept	Difference in variance	%BIC			%ABIC
			2 vs. 1	3 vs. 1&2	2 vs. 1&3	2 vs. 1	3 vs. 1&2	2 vs. 1&3
Single predictor
		Large	86.40%	0.20%	86.20%	98.40%	11.20%	87.20%
		Moderate	52.30%	0.00%	52.30%	91.40%	4.70%	86.70%
		No	46.70%	0.00%	46.70%	88.30%	4.20%	84.10%
Two predictors
Zero	No	Large	100.00%	0.10%	99.89%	100.00%	5.81%	94.19%
		Moderate	83.58%	0.00%	83.58%	86.99%	6.71%	80.28%
		No	100.00%	0.10%	99.90%	100.00%	8.20%	91.80%
	0.5	Large	100.00%	0.30%	99.70%	100.00%	7.70%	92.30%
		Moderate	92.28%	0.20%	92.08%	93.99%	6.41%	87.58%
		No	100.00%	0.00%	100.00%	100.00%	7.71%	92.29%
	1	Large	100.00%	0.40%	99.60%	100.00%	7.60%	92.40%
		Moderate	99.50%	0.30%	99.20%	99.70%	9.60%	90.10%
		No	100.00%	0.10%	99.90%	100.00%	7.90%	92.10%
0.5	No	Large	99.40%	0.20%	99.20%	100.00%	7.61%	92.39%
		Moderate	49.15%	0.10%	49.05%	55.35%	3.90%	51.45%
		No	46.55%	0.00%	46.55%	91.69%	7.81%	83.88%
	0.5	Large	100.00%	0.00%	100.00%	100.00%	6.90%	93.10%
		Moderate	63.30%	0.00%	63.30%	69.00%	4.60%	64.40%
		No	97.00%	0.10%	96.90%	100.00%	6.90%	93.10%
	1	Large	100.00%	0.20%	99.80%	100.00%	7.90%	92.10%
		Moderate	84.10%	0.30%	83.80%	87.40%	4.70%	82.70%
		No	100.00%	0.30%	99.70%	100.00%	6.90%	93.10%
0.7	No	Large	89.60%	0.20%	89.40%	99.50%	7.00%	92.50%
		Moderate	51.50%	0.00%	51.50%	57.10%	4.50%	52.60%
		No	51.95%	0.10%	51.85%	93.49%	6.11%	87.39%
	0.5	Large	99.90%	0.10%	99.80%	100.00%	7.11%	92.89%
		Moderate	60.60%	0.10%	60.50%	65.90%	3.10%	62.80%
		No	97.30%	0.00%	97.30%	100.00%	5.10%	94.90%
	1	Large	100.00%	0.20%	99.80%	100.00%	6.60%	93.40%
		Moderate	84.18%	0.00%	84.18%	87.79%	6.11%	81.68%
		No	100.00%	0.00%	100.00%	100.00%	4.90%	95.10%

The primary research questions for this paper were assessed using 1- through 3-class regression mixture models with the variance constrained to be equal between classes under all conditions. We first examined whether the true 2-class model was selected over the 1-class and 3-class models in each simulation using the BIC and ABIC. The results in Table 2 show that, as expected, the equality constraint does not impact class enumeration if the residual variances are actually the same. Under the equal variance condition for the single predictor model, the true 2-class model is usually selected by the BIC (70.4%) and the ABIC (94.4%). These detection rates for finding two classes are generally lower than those seen in previous research, possibly because differences in variance help to increase class separation. That this is due to decreased power due to less class separation is supported by because the detection rate is increased in the multivariate model where the residual variances are smaller; when the two predictors are not correlated, the 2-class model is selected in almost all simulations by the BIC (100.0%) and the ABIC (99.7%); when the two predictors are related, which decreases class separation, the detection rate for 2-classes goes down to 70.1% with the BIC, while it is quite high with the ABIC (>95.1%).

Table 2.

Class enumeration results when the residual variances are constrained to be equal across classes

Correlation	Difference in Intercept	Difference in variance	%BIC			%ABIC			%relaxed model favored
			2c vs. 1	3c vs. 1&2c	2c vs. 1&3c	2c vs. 1	3c vs. 1&2c	2c vs. 1&3c	%BIC	%ABIC	SB LRT
Single predictor
		Large	71.50%	3.50%	68.00%	94.30%	38.70%	55.60%	80.70%	92.10%	69.40%
		Moderate	68.00%	0.00%	68.00%	94.20%	1.70%	92.50%	11.60%	26.40%	33.90%
		No	70.40%	0.00%	70.40%	94.90%	0.50%	94.40%	0.90%	6.80%	9.20%
Two predictors
Zero	No	Large	100.00%	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%	100.00%	100.00%
		Moderate	78.60%	9.90%	68.70%	81.50%	52.80%	28.70%	97.70%	99.40%	99.60%
		No	100.00%	0.00%	100.00%	100.00%	0.30%	99.70%	0.60%	4.00%	6.00%
	0.5	Large	100.00%	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%	100.00%	100.00%
		Moderate	89.40%	24.60%	64.80%	91.10%	72.90%	18.20%	99.40%	99.80%	99.80%
		No	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%	0.40%	3.20%	5.20%
	1	Large	100.00%	100.00%	0.00%	100.00%	100.00%	0.00%	100.00%	100.00%	100.00%
		Moderate	99.10%	56.80%	42.30%	99.30%	91.00%	8.30%	99.90%	100.00%	100.00%
		No	100.00%	0.00%	100.00%	100.00%	0.30%	99.70%	0.70%	3.20%	5.30%
0.5	No	Large	90.50%	7.30%	83.20%	99.20%	50.50%	48.70%	97.00%	98.80%	99.30%
		Moderate	50.30%	0.00%	50.30%	55.30%	1.00%	54.30%	16.80%	36.20%	45.30%
		No	70.10%	0.00%	70.10%	95.30%	0.20%	95.10%	1.10%	4.60%	7.40%
	0.5	Large	100.00%	19.80%	80.20%	100.00%	71.00%	29.00%	98.80%	99.80%	99.80%
		Moderate	63.90%	0.10%	63.80%	68.50%	2.40%	66.10%	21.20%	43.20%	53.40%
		No	99.30%	0.00%	99.30%	100.00%	0.00%	100.00%	0.00%	2.60%	5.50%
	1	Large	100.00%	40.30%	59.70%	100.00%	86.00%	14.00%	99.50%	99.80%	99.90%
		Moderate	84.30%	0.10%	84.20%	86.80%	5.30%	81.50%	33.30%	55.70%	63.50%
		No	100.00%	0.00%	100.00%	100.00%	0.30%	99.70%	0.30%	2.80%	5.30%
0.7	No	Large	69.90%	1.00%	68.90%	95.90%	27.20%	68.70%	89.60%	95.60%	97.30%
		Moderate	52.70%	0.00%	52.70%	57.40%	0.70%	56.70%	14.10%	33.30%	42.10%
		No	72.20%	0.00%	72.20%	97.10%	0.00%	97.10%	1.30%	5.70%	8.80%
	0.5	Large	99.90%	6.90%	93.00%	100.00%	43.10%	56.90%	92.80%	97.00%	98.10%
		Moderate	61.70%	0.00%	61.70%	66.70%	1.30%	65.40%	17.80%	37.60%	45.40%
		No	99.30%	0.00%	99.30%	100.00%	0.10%	99.90%	1.00%	3.30%	5.30%
	1	Large	100.00%	17.70%	82.30%	100.00%	66.40%	33.60%	95.70%	98.60%	99.10%
		Moderate	84.80%	0.10%	84.70%	87.90%	3.80%	84.10%	25.80%	48.70%	58.00%
		No	100.00%	0.00%	100.00%	100.00%	0.20%	99.80%	0.50%	3.50%	5.90%

Note. 2c = 2-class constrained, 3c = 3-class constrained.

For simulation conditions where the constraint on the variance was inappropriate (i.e., a difference in variances existed, but was constrained to be equal; see Table 3), we hypothesized that the 3-class result would be found. The results were more nuanced than this, when class separation is high, the BIC and ABIC both select the 3-class model over the 1-class and 2-class results in every simulation. However, when class separation decreases (there is no difference between classes in the intercept and there is a higher correlation between predictors or the predictors are more correlated) the models tend to select the 1 or 2-class solutions. In fact, the misspecified model sometimes performs better than the correctly specified model because the misspecification increases the probability of selecting the 2 over the 1-class result. The detection rate for selecting the correct number of classes is slightly decreased (BIC=68.0%; ABIC=92.5%) when the actual residual variances are moderately different (.225 difference) in the univariate model. Under the large variance-difference condition (.45 difference), the detection rate is noticeably down to 55.6% using the ABIC, while the BIC was relatively stable (68.0%). When there are two uncorrelated predictors in the model, which has the biggest differences in residual variances between the two latent classes, 3-class model is selected in all simulations (100.0%) by BIC as well as ABIC, showing that the equality constraint leads us to select additional latent class. On the other hand, when there is some relationship (r = 0.5 and 0.7) between the two predictors and no intercept differences between the two classes, the power to detect the additional latent class capturing the effect heterogeneity decreases.

Table 3.

Parameter estimates from the single predictor model with equality constraints on the residual variances

Difference in Variance	Parameters	True	Estimated
			Mean (SD1)	MSE2	Min	Max	RMSE3	Coverage4 (%)
Large	Class mean5	.000	−1.755 (.57)	.481	−4.994	.315	1.76	6.4
	Intercept for Class-1 (β01)	.000	.00 (.22)	.157	−1.940	1.495	.13	94.5
	Slope for Class-1 (β11)	.200	−.219 (.20)	.147	−2.226	.311	.42	18.3
	Residual variance for Class-1 (σ21)	.960	.717 (.02)	.025	.642	.799	.24	0.0
	Intercept for Class-2 (β02)	.000	.00 (.03)	.027	−.112	.141	.02	94.5
	Slope for Class-2 (β12)	.700	.569 (.04)	.038	.428	.693	.13	10.0
	Residual variance for Class-2 (σ22)	.510	.717 (.02)	.025	.642	.799	.21	0.0
Moderate	Class mean	.000	−.777 (.52)	.519	−3.933	1.036	.80	63.2
	Intercept for Class-1 (β01)	.000	.00 (.08)	.083	−.623	.387	.06	97.3
	Slope for Class-1 (β11)	−.126	−.290 (.12)	.120	−1.248	.019	.17	70.4
	Residual variance for Class-1 (σ21)	.984	.866 (.03)	.029	.768	.943	.12	1.7
	Intercept for Class-2 (β02)	.000	.00 (.04)	.038	−.146	.157	.03	95.9
	Slope for Class-2 (β12)	.491	.401 (.06)	.065	.223	.682	.10	64.7
	Residual variance for Class-2 (σ22)	.759	.866 (.03)	.029	.768	.943	.11	2.7
No	Class mean	.000	−.011 (.51)	.505	−1.776	2.836	.39	91.2
	Intercept for Class-1 (β01)	.000	.00 (.05)	.053	−.202	.195	.04	96.7
	Slope for Class-1 (β11)	−.320	−.334 (.09)	.088	−.758	−.081	.07	91.8
	Residual variance for Class-1 (σ21)	.897	.892 (.03)	.030	.802	1.000	.02	94.0
	Intercept for Class-2 (β02)	.000	.00 (.05)	.053	−.195	.150	.04	96.0
	Slope for Class-2 (β12)	.320	.329 (.09)	.089	.082	.930	.07	92.1
	Residual variance for Class-2 (σ22)	.897	.892 (.03)	.030	.802	1.000	.02	94.0

Note.

¹Standard deviation of all replications,

²Mean of the estimated standard error,

³RMSE=Root Mean Squared Error,

⁴Coverage=Coverage of true population value across 1000 replications,

⁵class mean: small effect-size class is the reference group.

Model comparisons between the relaxed and restricted models

Next, we compared the restricted 2-class models with the equality constraint to the relaxed 2-class model with class-specific residual variances. The last three columns in Table 2 show the results of the model comparisons based on the BIC, ABIC, and SB LRT. Overall, the relaxed models were favored over the restricted models when there were large variance-differences between the classes, whereas the restricted models were favored when the equal variances were present. When there is a moderate difference in residual variances between the classes for the univariate model, all criteria tended to favor the restricted model. On the other hand, when the two predictors are not correlated, relaxed models are favored in most cases by all three criteria. Small differences were observed among the three model fit indices with the BIC always selecting the restricted model more often while ABIC selecting the relaxed model more. The SB LRT was best at choosing the relaxed model when the difference in variances was small.

Parameter estimates

We next examined the accuracy of parameter estimates from the 2-class regression mixture models when constraining the residual variances to be equal across classes. Given that we aim to know the consequence of constraining the variance for the parameter estimates and we know that the population has two classes, we included all 1000 replications in the assessment of estimation quality, rather than just the simulations in which the two class model was selected using fit indices. Table 3 presents the results of parameter estimates from the restricted 2-class model with a single predictor. The true population values for generating the simulated data are given in the table. Next to the true value, the mean of each parameter estimate across 1000 replications, standard deviation of the estimated coefficients across replications (empirical estimate of the standard error), mean of the estimated standard error across all simulations, minimum, maximum, RMSE, and coverage rates are presented.

Because they are constrained to be equal across classes, bias in the residual variances (σ²) between the classes is assured and the observed estimates are between the two true population values. The primary purpose of this aim was to assess the consequence of residual variance constraints on the other model parameter estimates. First, the class mean (i.e., log-odds of being in class-1 versus class-2) is severely biased when the large variance difference is constrained to be equal across classes. The true value of class mean is 0.00, which is the equal proportion (0.50) for the two classes. Under the large variance-difference condition, the average across simulations of the log-odds of being in class-1 is −1.755, which corresponds to a probability of .147. In other words, when variances are constrained to be equal on average, 14.7% of the 3000 subjects were estimated as being in the small effect-size class. The mean of the log-odds of class membership increased to −.777 (i.e., 31.5% of subjects are estimated as being in class-1) under the moderate variance-difference condition, which is still considerably under the true value of 0. When the actual variance is equal between the classes (no variance-difference condition), the estimated class mean is unbiased (−.011).

The regression coefficients of the predictor (i.e., slopes of regression lines) for both classes are severely biased when there is a large difference in residual variances which are constrained to be equal in estimating the model. In this case the true regression coefficient of .20 for class-1 is on average estimated to be −.22, which now is in the wrong direction (negative) from the true population model (positive). The average estimate of the slopes for class-2 is also downward biased from .70 to .57. On the other hand, the mean of the outcome variable (i.e., intercepts of regression lines) is correctly estimated to be zero for both classes. Because the average parameter estimates show substantial bias, the estimated standard errors are of little importance. However, we note that the standard deviation and minimum and maximum value of parameter estimates across simulations provide the evidence of large variation and in some cases of extreme solutions especially for the parameters estimates for class-1.

RMSEs increase as the magnitude of the variance-difference increased (see Table 3) and are especially large for the slope coefficients in the large variance-difference condition (RMSE for β₁₁ = .42; RMSE for β₁₂ = .24) indicating that these parameters are severely biased when misspecifying the residual variances to be equal across classes. The RMSE for class means indicates the extreme bias in this parameter when variances are incorrectly constrained to be equal. RMSEs for the model parameters under the equal-variance condition are small (range of .02 to .07) as they should be given that the data were generated such that the classes have equal variance in this condition.

The coverage rate for the equal variance condition is above 90% for all the parameters, which indicates that the 95% confidence interval for each parameter in the restricted model contains the true population value more than 90% of the time. The coverage rates became worse as the difference between the two residual variances increased. When the variance-difference is large, the coverage rates for the class mean, slope coefficients, and residual variances are very low, in this situation it is unlikely that the correct inference would be made.

Table 4 presents the parameter estimates from the restricted 2-class model with two strongly correlated (r = 0.7) predictors and no intercept differences between the two classes. This is one scenario of 9 total simulation scenarios of the multivariate model. All other result tables are available from the first author upon request given the limited space in the paper. Although the results are not directly comparable to the univariate model because of differences in total effect size and the size of the residual variances, the overall results are similar. When the residual variances which large differences are constrained to be the same across classes, regression weights for both classes are downward biased, causing the slope of the smaller effect to switch direction. The class mean is again downward biased indicating that more number of observations are incorrectly assigned to be in class-2 (larger effect class). As expected, there is a lack of bias in parameter estimates when the equality constraint is held for the equal variance conditions.

Table 4.

Parameter estimates from the two predictor model of 0.7 correlation and no intercept differences with equality constraint

Difference in Variance	Parameters	True	Estimated
			Mean (SD1)	MSE2	Min	Max	RMSE3	Coverage4 (%)
Large	Class mean5	.000	−1.562 (.59)	.452	−4.158	2.651	1.562	.074
	Intercept for Class-1 (β01)	.000	−.002 (.14)	.131	−.779	.728	.002	.960
	Slope 1 for Class-1 (β11)	.118	−.093 (.18)	.178	−1.482	.316	.211	.741
	Slope 2 for Class-1 (β21)	.118	−.087 (.18)	.177	−.853	.885	.205	.720
	Residual variance for Class-1 (σ21)	.959	.708 (.02)	.025	.625	.780	.251	.000
	Intercept for Class-2 (β02)	.000	.002 (.04)	.029	−.135	.769	.002	.954
	Slope 1 for Class-2 (β12)	.412	.339 (.04)	.043	.225	.487	.073	.525
	Slope 2 for Class-2 (β22)	.412	.327 (.10)	.043	−.833	.467	.085	.513
	Residual variance for Class-1 (σ22)	.495	.708 (.02)	.025	.625	.780	.213	.000
Moderate	Class mean	.000	−.704 (.42)	.421	−2.888	.601	.704	.579
	Intercept for Class-1 (β01)	.000	−.004 (.07)	.073	−.266	.300	.004	.966
	Slope 1 for Class-1 (β11)	−.074	−.162 (.11)	.109	−.814	.128	.088	.889
	Slope 2 for Class-1 (β21)	−.074	−.155 (.11)	.110	−.802	.224	.081	.892
	Residual variance for Class-1 (σ21)	.984	.860 (.03)	.029	.760	.950	.124	.012
	Intercept for Class-2 (β02)	.000	.001 (.04)	.037	−.126	.143	.001	.970
	Slope 1 for Class-2 (β12)	.289	.239 (.06)	.058	.091	.475	.050	.820
	Slope 2 for Class-2 (β22)	.289	.242 (.06)	.057	−.004	.483	.047	.830
	Residual variance for Class-1 (σ22)	.751	.860 (.03)	.029	.760	.950	.109	.021
No	Class mean	.000	.020 (.43)	.426	−2.178	1.373	.020	.932
	Intercept for Class-1 (β01)	.000	.00 (.05)	.049	−.204	.153	.000	.952
	Slope 1 for Class-1 (β11)	−.188	−.189 (.07)	.077	−.436	.031	.001	.951
	Slope 2 for Class-1 (β21)	−.188	−.191 (.08)	.077	−.621	.444	.003	.938
	Residual variance for Class-1 (σ21)	.894	.887 (.03)	.029	.790	1.003	.007	.937
	Intercept for Class-2 (β02)	.000	.00 (.05)	.051	−.368	.178	.001	.963
	Slope 1 for Class-2 (β12)	.188	.188 (.08)	.079	−.004	.573	.005	.954
	Slope 2 for Class-2 (β22)	.188	.188 (.08)	.079	−.509	.499	.006	.949
	Residual variance for Class-1 (σ22)	.894	.894 (.03)	.029	.790	1.003	.007	.937

Note.

¹Standard deviation of all replications,

²Mean of the estimated standard error,

³RMSE=Root Mean Squared Error,

⁴Coverage=Coverage of true population value across 1000 replications,

⁵class mean: small effect-size class is the reference group.

Post hoc analyses for class identification

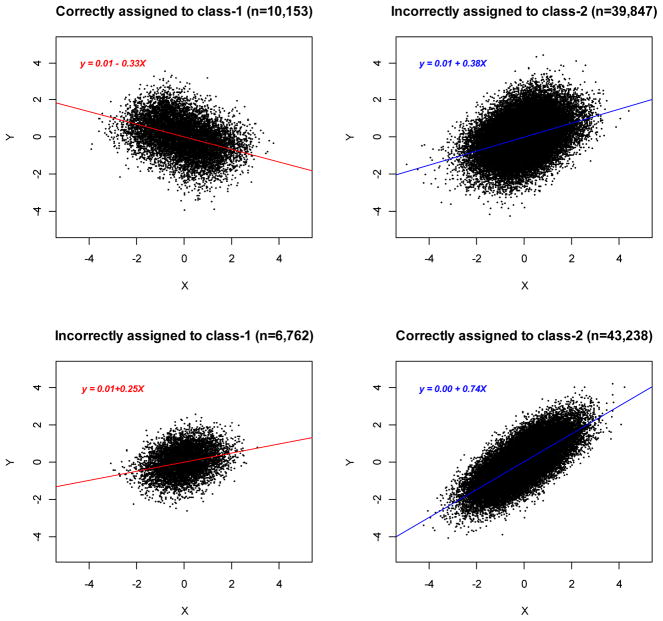
Previous analyses found that inappropriate equality constraint on the residual variances greatly impacted estimated class sizes and caused regression weights to switch direction. To better understand how this constraint impacts model results, we examined individuals who are misclassified as a result of the constraint. This analysis used a single simulated dataset of 100,000 subjects to fit the 2-class restricted mixture model where data was generated under the large-variance difference condition. We then assigned individuals to latent classes using a pseudo class draw (Bandeen-Roche, Miglioretti, Zeger, & Rathoutz, 1997) in which individuals are assigned to each class with probability equal to the model estimated posterior probability of being in that class. Because the data were simulated, we also know the true class assignment for each individual. We then examined which individuals are correctly versus incorrectly assigned as a result of constraining residual variances. Figure 1 presents the scatter plot with a regression line for each of the four groups defined by true and estimated class membership. As seen in the figure, a considerable number of class-1 subjects (about 80%) are incorrectly assigned to class-2, while most of the subjects in class-2 (above 86%) remained in the same class. The relationship between the predictor and outcome in class-1 is now changed from positive (β₁₁=.20) to negative direction (β₁₁= −.18).

Figure 1.

Assignment of individual observations when holding an equality constraint on the residual variances under the large variance-difference condition

This reassignment of individuals helps to explain the mechanism through which constraining residual variances leads to bias. Because the effect size is stronger in class-2, class-2 dominates the estimation. Extreme values from class-1, which show the strong positive relationship between X and Y, are moved to class-2 because the variance in class-2 is forced to be increased. At the same time, the residual variance of class-1 is reduced by allocating those extreme cases to class-2. Because those who followed an upward slope in class-1 have now been moved to class-2, the remaining individuals follow a downward slope (seen in the first two scatter plots of Figure 1) and the effect of X on Y in class-1 has now effectively changed direction. Individuals who are incorrectly assigned to class-1 have low variance because the variability in class-1 must be decreased and the variability in class-2 must increase. This demonstrates how a simple misspecification of residual variances can cause estimates of regression weights to switch signs.

Discussion

Regression mixture models allow investigation of differential effects of predictors on outcomes. Although they have recently been applied to a range of research, the effect of misspecifying the class-specific residual variances has remained unknown. This study examined the impact of constraining the residual variances on the latent class enumeration and on the accuracy of parameter estimates and found effects on both class enumeration and class-specific regression estimates.

Class enumeration was not affected by the equality constraint when the residual variances were truly the same. As differences in the residual variances across classes increased, detection rate for selecting the correct number of classes decreased. The ABIC seemed to be more sensitive to the misspecification of the residual variances, which was similar to the findings of Enders and Tofighi (2008) when looking at growth mixture models. However, differences in information criteria between the competing models were very small in many cases. In practice, an investigator who finds a very small difference in penalized information criterion will need to use other methods to determine the correct number of classes, in this case if the two class model shows two large classes with meaningfully different regression weights between the classes then they would be correct to choose the 2-class solution even if the BIC and ABIC slightly favored the 1-class result.

These results for latent class enumeration help to put previous research comparing indices for class enumeration into perspective. Previous research with regression mixtures has found that in situations where there is a large difference in variances between classes (as used in this paper) and large sample size (6000) the BIC performed very well and the ABIC showed no advantages (George et al., 2013). This study found that none of these indices perform as well when sample size is somewhat lower: with large differences in residual variances and the correct model specification the 2-class model was supported less than 90% of the time; when the differences in residual variances are moderate or zero the 2-class model is supported using the ABIC and support for 2-classes is strongest when residuals are constrained to be equal. Thus, we do not recommend using either the BIC or the ABIC as the sole criterion to decide the number of classes. Along with the information criteria, class proportion, regression weights for each latent class, and previous research should be taken into account when deciding the number of latent classes.

Results for parameter estimates were clearer than for latent class enumeration: parameter estimates show substantial bias in both class proportions and in regression weights when class specific variances are inappropriately constrained. This is consistent with previous research evaluating the effects of misspecification of variance parameters in other types of mixture models (Enders & Tofighi, 2008; McLachlan & Peel, 2000). Moreover, we hypothesized that the impact of misspecifying the error variance structure on the parameter estimates will be much more severe in regression mixture models than growth mixture models. As expected, while there was relatively minor bias in parameter estimates in growth mixture models (Enders & Tofighi, 2008), we found substantial bias in regression weights for both latent classes in regression mixture models. In light of these results a reasonable recommendation is that in regression mixture models residual variances should be freely estimated in each class by default unless models with constrained variances fit equally as well and there are no substantive differences in parameter estimates.

While these simulations showed no problems with estimating class specific variances, in practice there will be situations with estimation problems when class specific variances are specified. One option is to compare models in which variances are constrained to be equal to those in which they are constrained to be unequal (such as the variance of class 1 equals ½ the variance of class 2). If no model clearly fits the data better and when other model parameters change substantially, then any results should be treated with great caution.

As with most simulation studies, this study is limited to examining only a small number of conditions. Specifically, we limited the study to a 2-class model with 50/50 split in the proportion of subjects in each class, a sample size of 3000, and constant effect size differences between the two classes. The main design factor for this study is the amount of difference in residual variances and intercepts between the two classes as well as the degree of relationship between the two predictor variables. When class separation is stronger than in our simulation conditions (as indicated by larger class differences in regression weights or intercepts or more outcome variables) the models should perform better. The purpose of this study was to demonstrate the potential effects of inappropriate constraints on residual variances, the actual effects in any one condition may differ substantially from those found here, however, this illustrates the potentially strong impact of misspecification of residual variances in regression mixtures. Users of regression mixture models should be aware of the potential for finding effects that are opposite of the true effects when residuals, which are of little importance to most users, are misspecified.

Appendix

A. Parameter values for generating the multivariate population model

rx1x2	Difference in variance	β11	β21	σ21	β11	β21	σ22
0	Large	0.2	0.2	0.92	0.7	0.7	0.02
	Moderate	−.126	−.126	.968	.491	.491	.518
	No	−.32	−.32	.795	.32	.32	.795
0.5	Large	.133	.133	.956	.467	.467	.456
	Moderate	−.084	−.084	.982	.327	.327	.732
	No	−.213	−.213	.886	.213	.213	.886
0.7	Large	.118	.118	.959	.412	.412	.495
	Moderate	−.074	−.074	.984	.289	.289	.751
	No	−.188	−.188	.894	.188	.188	.894

B. R code for generating data

# Single predictor with large variance-difference condition #
dat<-matrix(NA,ncol=3,nrow=3000)
dat[1:1500,3]<-1
dat[1501:3000,3]<-2
for(i in 1:1000){
 dat[,1]<-rnorm(3000)
 dat[1:1500,2]<-dat[1:1500,1]*(-0.32)+rnorm(1500,sd=sqrt(0.898))
 dat[1501:3000,2]<-dat[1501:3000,1]*0.32+rnorm(1500,sd=sqrt(0.898))
write.table(dat,paste(C:/Temp/data',i,'.dat',sep=''),col.names=FALSE,row.names=FALSE)
}
Mplus code for analyzing regression mixture model with equality constraint
#constraining the residual variances (by default)#
Title: 2-class model with an equality constraint;
 data: file = C:/Temp/data1.dat;
 variable:
 NAMES = X Y Group;
 USEVARIABLES = X Y;
 CLASSES = c(2);
 analysis:
      type=mixture;
      starts=100 20;
 model:
 %overall%
 Y on X;
 Y;
 %c#2%
 Y on X;
 ! Y;           !constraining the variance by not writing out this statement (by default)
 Output:
    TECH14;