Phase synchrony reveals organization in human atrial fibrillation

We present a novel analysis technique to quantify the synchrony between regions of tissue during human atrial fibrillation (AF). The analysis reveals localized pockets of synchrony during AF, arguing against multiwavelet reentry and suggesting that instead AF involves spatially contiguous regions of coherence surrounded by disorganized activation.

Abstract

It remains unclear if human atrial fibrillation (AF) is spatially nonhierarchical or exhibits a hierarchy of organization sustained by sources. We utilize activation times obtained at discrete locations during AF to compute the phase synchrony between tissue regions, to examine underlying spatial dynamics throughout both atria. We construct a binary synchronization network and show that this network can accurately define regions of coherence in coarse-grained in silico data. Specifically, domains controlled by spiral waves exhibit regions of high phase synchrony. We then apply this analysis to clinical data from patients experiencing cardiac arrhythmias using multielectrode catheters to simultaneously record from a majority of both atria. We show that pharmaceutical intervention with ibutilide organizes activation by increasing the size of the synchronized domain in AF and quantify the increase in temporal organization when arrhythmia changes from fibrillation to tachycardia. Finally, in recordings from 24 patients in AF we show that the level of synchrony is spatially broad with some patients showing large spatially contiguous regions of synchronization, while in others synchrony is localized to small pockets. Using computer simulations, we show that this distribution is inconsistent with distributions obtained from simulations that mimic multiwavelet reentry but is consistent with mechanisms in which one or more spatially conserved spiral waves is surrounded by tissue in which activation is disorganized.

NEW & NOTEWORTHY

We present a novel analysis technique to quantify the synchrony between regions of tissue during human atrial fibrillation (AF). The analysis reveals localized pockets of synchrony during AF, arguing against multiwavelet reentry and suggesting that instead AF involves spatially contiguous regions of coherence surrounded by disorganized activation.

atrial fibrillation (AF) is a serious health condition, affecting over 30 million people worldwide (3) and resulting in an increased risk of stroke, heart failure, and mortality (6). During AF the organization of electrical activity in the atria no longer consists of a wave that propagates from the sino-atrial node to the atrioventricular node in an organized fashion (25, 31). Instead, tissue excitation is irregular resulting in a reduced ability to pump and a reduced blood flow (6).

While understanding the specific mechanisms that drive and sustain AF is of key importance in selecting effective treatments for the disease, many of its underlying dynamical features and initiation mechanisms remain poorly understood. Triggers from the pulmonary veins, in the form of ectopic beats, have been demonstrated to participate in the initiation of AF (11), and traditional ablation techniques attempt to isolate these veins. Unfortunately, these procedures have limited long-term success (32). Recent advances in mapping have revealed that spiral waves of excitation may play a key role in AF in some patients (7, 15, 24). Recordings from 64-pole basket electrodes demonstrate that spiral waves may be spatially conserved in patients, with tip locations that can remain in reproducible atrial regions for months at a time until eliminated (23, 24). External noninvasive mapping has also demonstrated that the location of reentries recurred repetitively in the same region (10). The importance of spiral waves in the maintenance of AF (24) is supported by reports from several groups showing that limited ablation at localized spiral waves or focal sources may improve long-term outcome compared with traditional ablation techniques (18, 24, 29).

Nevertheless, mechanisms for the maintenance of AF in general, and spiral wave dynamics in particular, are still under debate. There are two competing paradigms: multiwavelet reentry (MWR) and stable spiral wave induced breakup (SSWIB). The multiwavelet hypothesis posits that the complex activation patterns observed during AF are caused by a multitude of short-lived spiral waves with limited spatial extent (wavelets) (33). Crucial in this scenario is that these wavelets are unstable and continuously fragment and generate offspring wavelets, resulting in a stochastic pattern of activation. MWR was first described in the modeling work of Moe et al. (19) and was studied in further detail in both computer models and in animal models (1, 2, 14). Notably, MWR depends solely on the instability of the spiral wave and can thus occur in homogeneous as well as heterogeneous tissue.

During SSWIB, activation from one or more spatially conserved spiral waves breaks down away from the tip, a process know as fibrillatory conduction (12). In this scenario, the stable spiral waves, or mother rotors, are the driving sources of fibrillation and complex activation patterns arise from breakup distant to the stable spiral cores. In contrast to MWR, this scenario requires tissue heterogeneity, either in the form of conduction anisotropy, cellular heterogeneity, or tissue geometry. This is because in completely homogeneous tissue the driving spirals would either destabilize, resulting in MWR, or would control the entire domain, leading to regular activation consistent with atrial flutter or organized tachychardia (AT). This scenario also implies that not all regions contribute equally to the maintenance of fibrillation and that the regions harboring spirals are the most important. This is in sharp contrast to MWR where there are no privileged regions and the fragmentation is self-sustaining and the result of inherent tissue instability.

It is challenging to distinguish between the two hypothesized fibrillatory mechanisms. Although the spatial resolution of techniques such as focal impulse and rotor mapping (FIRM) have been shown to be able to map human spiral waves (26), spatial mapping of multiple meandering spiral waves is laborious. First, it requires specialized software to construct these maps. Second, and perhaps more importantly, it necessitates careful interpretation of these maps to identify wave tips and track their trajectory until they annihilate. Thus a simpler methodology for the interpretation of high-resolution mapping would be advantageous.

In this study, we present a methodology that focuses on the spatial distribution of temporal information obtained by the electrode recordings. Specifically, we examine the degree of phase synchronization between electrodes, a method widely used in biology, including information processing in the brain (9), in circadian rhythms (8), and the cardiorespiratory system (17). Analyzing this synchronization in clinical data provides a simple and quantitative look into underlying conduction dynamics during AF and relies only on the marking of activation times from recorded electrograms. We will show that this method is able to determine regions of synchronization in both in silico and clinical data. Furthermore, we will present results that imply that MWR is incompatible with our clinical results, suggesting that AF is maintained by SSWIB.

METHODS

In silico studies.

Activation times in square sheets of two-dimensional (2D) tissue were generated by simulating a standard model for cardiac wave propagation:

$${\partial }_{t}V=D{\nabla }^{2}V-I_{\text{ion}}/C_{\text{m}}$$ (1)

where V is the transmembrane potential, C_m (μF/cm²) is the membrane capacitance, and D∇² expresses the intercellular coupling via gap junctions. The membrane currents I_ion are described by nonlinear evolution equations coupled to V. Details of the model for these currents are not critical to our study, and we present results obtained using the Fenton-Karma model (4, 5). We coarse grained the computational domain to a similar discrete grid as in the clinical basket electrodes (i.e., an 8 × 8 grid) and recorded the activation times at the location of the resulting M = 64 nodes.

Clinical mapping studies.

Our clinical mapping methodology has been described in detail elsewhere (22–24). In brief, it consists of 64 electrode basket catheters that are inserted into both atria, either simultaneously or into the left (LA) or right atrium (RA) sequentially. Unipolar electrograms at each electrode are recorded with a temporal resolution of 1 ms. The basket covers the majority of the atrial tissue and this, combined with a spatial resolution of ∼5 mm, allows the determination of reentry waves during AF (26). In this study, we utilize data taken from patients using recording intervals of 2.8 s, unless otherwise noted. The fraction of electrodes that contains viable data ranged from 70 to 100%. All patients provided informed consent under Institutional Review Board-approved protocol of the University of California, San Diego.

Synchronization index.

To compute the level of phase synchrony between electrodes, we first converted the activation times from either the in silico data or from the clinical recordings into phase-time information. This is achieved by taking the data of an electrode or, in the case of a simulation, a virtual electrode located within the computational domain, as a periodic event, whereby the activation times mark the beginning of each new cycle. The activation time is then chosen as the time point where the phase has increased by 2π. Between activations, the phase keeps track of how far along a cycle each electrode is in time and is obtained using linear interpolation.

In particular, let the activation times for the i^th electrode be given by {t_i^k: k = 1, 2, . . ., N}, where N is the total number of activation times. Then, the phase of electrode i between the k-th and k + 1-th activation time is defined as:

$${\varphi }_i\left(t\right)=2\pi \frac{t-t_i^k}{t_i^{k+1}-t_i^k}+2\pi \left(k-1\right),\hspace{0.17em}{t}_i^k\le t<t_i^{k+1}$$ (2)

Thus the phase starts at 0 and is advanced by 2π every time the electrode records an activation event. To determine phase synchrony, we are not concerned with a single electrode's phase but instead with the time evolution of the phase difference between two electrodes. We can therefore define the time-dependent relative phase between the i^th and j^th electrode as ψ_ij = nϕ_i − mϕ_j, where n and m are integers. This gives us information about the extent to which two separate electrodes' activation dynamics tend to proceed together in time. If the relative phase between electrodes remains constant over a given time period, those electrodes are phase locked and can be said to be synchronized. Note that we are only concerned with how constant the phase difference is with time, and therefore, any global offset in either phase will not affect our results.

If the signal is purely periodic then this synchronization corresponds quantitatively to the phase locking condition |nϕ_i − mϕ_j − δ| < const, where δ is an average (constant) phase shift. Because our system is inherently noisy, however, ψ_ij fluctuates, resulting in a statistical distribution of the cyclic relative phase

$${\Psi }_{ij}={\psi }_{ij}\hspace{0.17em}\hspace{0.17em}\mathrm{mod}\hspace{0.17em}\hspace{0.17em}2\pi .$$

Synchronization corresponds to a peak in this distribution while asynchronous signals result in a uniform distribution (27). For this paper we will only consider 1:1 phase locking, thus taking n = m = 1.

A useful way to quantify the extent of phase locking in noisy biological systems is to find the synchronization number γ of the phases in question. This is defined as the amplitude of the first Fourier mode of the cyclic relative phase distribution (27)

$${\gamma }_{i,j}^2={\langle \cos \Psi {\left(t\right)}_{i,j}\rangle }_t^2+{\langle \sin \Psi {\left(t\right)}_{i,j}\rangle }_t^2,$$ (3)

where the brackets denote an average over time. Note that γ = 1 if the two signals are phase locked (corresponding to a single-peaked distribution of the cyclic relative phase) and γ = 0 if the two signals are completely asynchronous (corresponding to a uniform distribution of Ψ_ij).

Binary synchronization network.

The interelectrode synchrony between all M recording electrodes can be quantified using a network where the nodes correspond to the electrodes and where the connections represent the level of synchrony. To simplify this analysis we will assume a binary network such that the entries a_ij of the M × M adjacency matrix are either 1 (implying synchronization between electrodes i and j) or 0 (corresponding to asynchrony). The values of a_ij are determined using a threshold value, κ, of the corresponding synchronization number γ_i;j, with a_ij = 1 for γ_i;j ≥ κ. The synchronization index (SI) for electrode i is then defined as its normalized degree, namely the fraction of synchronized connections between that electrode and all other electrodes:

$${\text{SI}}_i=\frac{1}{M-1}{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^M{a}_{ij.}}$$ (4)

In other words, the SI of electrode i quantifies the fraction of electrodes with which i remains synchronized with over an extended period of time. Therefore, it encodes information about the spatiotemporal interconnectedness of activations during AF and can be used to quantify regions of tissue that activate together synchronously. In particular, we can easily compute the SI for all electrodes and make a spatially distributed SI map for a given window of time. Spatially contiguous regions with high values of SI then imply a region of spatially extended synchrony.

Note that SI takes on values between 0 and 1 and depends on both the number of synchronized electrodes and the total number of electrodes. For example, if there is a group of $\tilde{m}$ electrodes synchronized with each other, then each electrode within this group will have $\tilde{m}$ − 1 synchronized connections and a SI value of ($\tilde{m}$ − 1)/(M − 1). Similarly, if we have global synchrony over all electrodes we get SI = 1 for every electrode.

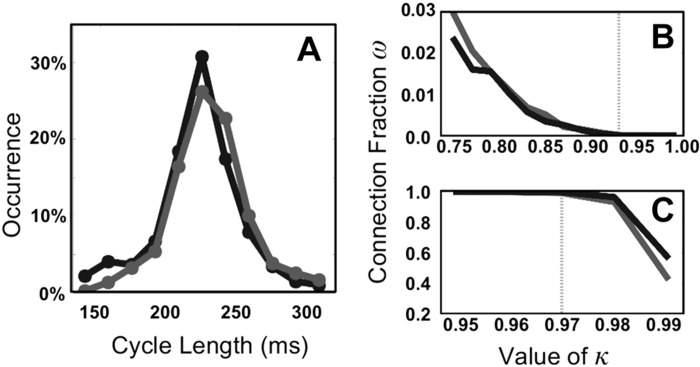
Obviously, the threshold κ will affect the quantitative outcome and needs to be chosen carefully. Choosing κ too small will create “false-positive” synchronizations and will result in an overestimation of SI. On the other hand, since our clinical data are noisy there is also an upper bound on κ. To determine the lower bound of κ we examined typical distributions of cycle lengths in patients recorded during FIRM. Two typical examples are shown in Fig. 1A, which show that the cycle lengths lie primarily between 150 and 300 ms and are roughly normally distributed.

Fig. 1.

A: distribution of cycle lengths for 2 representative patients shown in black and dark gray. B: fraction of synchronized connections, ω, as a function of the threshold κ. The activation times of the electrodes are randomly taken from the 2 distributions shown in A. Demanding that the percentage approaches 0 establishes the lower bound κ ≥ 0.92, shown by the dotted light gray line. C: as in B but now for a grid in which each electrode, taken from the 2 distributions in A, has identical activation times plus a normally distributed noise term. An upper bound on the threshold can be established by requiring that the percentage remains high despite the presence of noise: κ ≥ 0.97 (dotted light gray line).

To determine the effect of κ on the quantification of the interelectrode synchronization we created artificial timing files with a length of 2.8 s by adding together cycle lengths in a random fashion from the two distributions shown in Fig. 1A. This “scrambled data” has no spatial information and should be completely asynchronous: the only synchronizations that can occur are by chance. For each value of our synchronization threshold we created 20 artificial timing files and found the average fraction of synchronized connections, defined as $\omega =\frac{1}{M}\hspace{0.17em}{\displaystyle {\sum }_{i=1}^{M}S{I}_i}$ (Fig. 1B). From the results we can conclude that a threshold value of at least κ ≥ 0.92, shown as a dotted light gray line, results in a negligible fraction of synchronized electrodes. We have checked that introducing spatial heterogeneity in the mean of the distribution, by shifting the distribution to lower or higher cycle lengths in different regions of the domain, results in a lower bound value that is smaller than 0.92, further justifying the choice of the threshold.

To establish an upper bound on κ we populated each node of the grid with the data from a single electrode taken at random from one of the clinical distributions. Obviously, without any noise added to this data the synchronization between these nodes would be perfect, even for a threshold value of κ = 1. We next added a normally distributed noise term to these activation times with a standard deviation of 5 ms, corresponding to measurement uncertainty in timing data, and computed the synchronization values of this network. The value of ω as a function of the threshold value is shown in Fig. 1C for the two distributions shown in Fig. 1A. We see that for κ ≤ 0.97, again indicated by a gray line, the synchronization remains high, even in the presence of clinically realistic noise. We have verified that the same upper bound is valid for all patients considered in this study (Table 1). Combining these results, we have chosen our threshold value to be κ = 0.95.

Table 1.

Characteristics of patient population

Patient Characteristics
General characteristics
Number of cases	24
Age, yr	63.2 ± 9.7
Atrial fibrillation type
Paroxysmal	7
Persistent	17
Left atrial diameter, mm	48 ± 6
Left ventricular ejection, %	51 ± 15
CHADS2 score	2.0 ± 1.2
Comorbid conditions
Hypertension	16
Diabetes	9
Body mass index, kg/m2	30.7 ± 4.5
Congestive heart failure	10
Glomerular filtration rate, ml/min	75.7 ± 17.2
Magnesium, mg/dl	1.9 ± 0.1

Values are means ± SE.

RESULTS

In silico timing files.

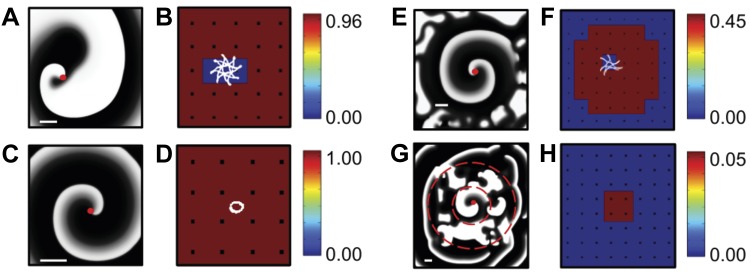
Before applying our synchronization analysis to clinical data we examined several activation time series generated using computational modeling. In a first example, we created a single dominant spiral wave in a homogeneous domain with no-flux boundary conditions. A snapshot of this simulation, focusing on the region that contains the spiral tip, is shown in Fig. 2A, where the activation is shown in a gray scale with white corresponding to depolarized (active) and black corresponding to repolarized (inactive) tissue. In Fig. 2B we plot the corresponding SI map for the coarse-grained network, which reveals a high value for the synchronization index everywhere except at the location of the spiral wave tip. This is due to the tip meander, shown in white in Fig. 2B, which has a spatial scale that is larger than the interelectrode spacing. As a consequence, the SI value for the electrodes that include the meander domain is reduced, demonstrating how our analysis can potentially determine the location of a spiral tip.

Fig. 2.

A: snapshot of a simulation with a single stable spiral wave. Membrane potential is shown using a grayscale. Parameters taken from set 1 in Ref. 5, modified to create stable spirals (τ_v2⁻ = 10 and τ_v2⁺ = 220). The location of the spiral wave tip is indicated by a red dot. B: synchronization index (SI) color map corresponding to A, with red corresponding to highly synchronized electrodes and blue corresponding to asynchronous electrodes. The tip trajectory is indicated in white. C: snapshot of a simulation containing a spatially conserved spiral wave with only a small meander, obtained using the Modified Beeler-Reuter parameter set from Ref. 4. D: SI color map corresponding to C with the tip trajectory in white. E: snapshot of a simulation in a domain consisting of a central region, harboring a single stable spiral, surrounded by a region in which this spiral breaks down into irregular, stochastic dynamics. Parameter values were taken from parameter set 3 in Ref. 5 with τ_r = 40 in the inner and τ_r = 27 in the outer domain. F: SI color map corresponding to E, which displays a synchronized central region and an asynchronous outer region. The tip trajectory of the spiral wave is shown in white. The snapshots and corresponding SI color maps have been scaled to emphasize tip meander, with scale bar = 1 cm shown in white. G: snapshot of a simulation in which a central region (within the smaller dashed circle), containing a stable nonmeandering spiral as in A with decreased diffusion constant, is surrounded by a region of spiral-wave breakdown which, in turn, is surrounded by a slow-conducting region with planar propagation (outside the larger dashed circle). Activation in the outer region occurs at irregular times and locations, resulting in a corresponding SI map (H), which shows that only the spiral wave region is synchronized.

In a second simulation we generated timing data for a spiral wave with limited meander (Fig. 2C). As can be seen in Fig. 2D, the tip trajectory remains within a domain bordered by neighboring electrodes. As a result, the SI map (Fig. 2D) displays a uniformly high value of synchrony. Thus these simulations show that the synchronization index is able to identify coherent domains associated with spatially conserved spiral waves and can locate the spiral tip only if its meandering path exceeds a minimum spatial scale.

In a third simulation, we simulated a spatially stable spiral wave in a 15 × 15 cm tissue (Fig. 2E) that contains two regions with different values of one of the model parameters (see Ref. 26). The parameter value within a circular coherent domain, with a radius of 6 cm and centered in the computational domain, was chosen such that a spiral wave remains spatially stable. Outside this coherent domain, the parameter value was taken such that a spiral wave inherently breaks down as can be seen in the screenshot of the simulation (Fig. 2E). The corresponding SI map is plotted in Fig. 2F and shows a clearly synchronized domain, surrounded by asynchronous tissue. Importantly, the size of the synchronous region corresponds to the coherent domain of the spiral wave.

We should note that it is possible that a less organized region functions as a driver for a more organized region (13). An example of this is shown in Fig. 2G, which shows a snapshot of a simulation in which a stable nonmeandering spiral (region within the smaller dashed circle) is surrounded by an asynchronous region, which, in turn, is surrounded by a slow-conducting region which exhibits planar activation (outside the larger dashed circle). The corresponding SI map (Fig. 2H) shows low synchronization values in all regions except the one controlled by the spiral wave. This can be understood by the fact that the activation of the outer region occurs at irregular locations and times, resulting in irregular propagation patterns, nonconstant phase differences between electrodes, and SI values that are below the threshold. In contrast, the SI analysis is able to identify the central domain that is controlled by the spiral wave.

We should also point out that restricting the extent of the spatial coupling between the spiral-wave breakdown domain and the slow conducting domain in our simulations might result in more regular activation of the outer domain. For example, electrically isolating the domain outside the larger dashed circle, except for a single small isthmus, will restrict the initiation site for the planar waves. This might lead to spatiotemporally regular wave activation in the outer domain, resulting in high SI values. Whether this scenario is relevant for interatrial activation during human AF requires simulations that incorporate anatomically realistic coupling between the two atria, clearly beyond the scope of our current study. However, it is unlikely that within the same atrium there will be a region that, when activated by a region of spiral wave breakdown, exhibits high SI even if it has planar propagation.

We next applied our synchronization analysis to modeling results that simulate different types of spiral wave breakup and dynamics. In particular, we used computational modeling to generate data that are consistent with either MWR or SSWIB in a 12.6 × 12.6 cm domain with biperiodic boundary conditions. To simulate MWR we performed simulations using all parameter sets reported by Fenton et al. (5) that result in spiral wave breakup in homogeneous computational domains (i.e., parameter sets 3–6, 8, and 9 in Ref. 5). To get the desired fibrillatory dynamics for the spiral breakup data, we first initiated a single spiral and then applied random pulsing of stimuli. After the transient behavior ceased, we stored 2.8 s of data for analysis. This is repeated five times for each parameter set, making sure that the episode did not experience spontaneous termination.

We can quantify the level of synchrony within the domain by examining the number of electrodes with nonzero SI, namely the fraction of synchronized electrodes. This is defined as the fraction of electrodes with a synchronization index larger than zero: Ω ≡ ∑_isgn(SI_i)/M. For the simulated MWR we find that almost all nodes are asynchronous. This can be seen from the histogram of Ω (Fig. 3), which is clearly peaked for low values of Ω. This implies that during our simulated MWR tissue activation is highly irregular throughout the entire domain.

Fig. 3.

A: representative snapshot of a simulation exhibiting MWR. B: SI colormap corresponding to A. C: corresponding distribution of W for all MWR simulations. D: representative snapshot of a simulation exhibiting SSWIB. Parameters taken from set 1 in Ref. 5, modified to create stable spirals (=10–90 and =220). The tissue was homogeneous within the dashed quadrant and heterogenous outside, as described in the text. A spatially stable spiral is present within the homogeneous quadrant. E: SI colormap corresponding to C, highlighting the stable spiral seen in the snapshot. F: distribution of W for 60 SSWIB simulations.

Data consistent with SSWIB can be created in at least two different ways. One way is to carry out simulations corresponding to Fig. 2, E and G. In these simulations, a stable localized spiral drives the surrounding fibrillatory activation and, as shown in Fig. 2, F and H, the tissue in which the breakdown occurs is asynchronous while the size of the synchronized region will be roughly equal to the size of the stable domain. In these simulations, Ω will depend on the amount of tissue controlled by the stable spiral and will roughly equal to the ratio of the stable domain size and the total domain size. Thus the distribution of Ω obtained from multiple simulations will reflect the distribution of chosen stable domain sizes. In particular, choosing a uniform distribution of stable domain sizes will result in a broad distribution of Ω, in sharp contrast to the distribution during simulated MWR. Of note, this argument is not restricted to simulations of a single stable spiral but will hold for multiple stable spiral waves as well.

An alternative way of simulating SSWIB, one that highlights potential dynamical features, introduces smooth spatial heterogeneities in part of the computational domain. Here, we varied one of the parameters controlling the time scale in parameter set 1 of the Fenton-Karma model (τ_v2⁻) across three quadrants of the computational domain in a random fashion. Specifically, we first divided the heterogeneous domain into discrete squares with a width and height of 0.2 cm. The parameter value in each of these squares was modified with a probability of p = 0.20, where a modification consisted of τ_v2⁻ being multiplied by a random integer between 1 and 9, resulting in values that range from 10 to 90. We have verified that spiral waves in homogeneous tissue with these values of τ_v2⁻ are stable, ensuring that breakup in our simulations is induced by the heterogeneity. We then smoothed the spatial parameter variation by convolving the squares with an isotropic 2D Gaussian with a standard deviation of 0.1 cm.

As before, simulations were started with an induced spiral wave combined with random stimulations. Following a transient period of 5 s, we examined 2.8 s of activation data. A snapshot of one of our 60 simulations is shown in Fig. 3C with its corresponding SI map plotted in Fig. 3D. Here, the homogeneous region consists of the lower left quadrant and is indicated by the dashed red line. Simulations revealed that the ensuing dynamical state depends critically on the initial conditions. In some simulations, a localized stable spiral was unable to form in the homogeneous tissue and the ensuing activity resembled MWR. In others, a stable spiral was formed in the lower left quadrant, which was surrounded by breakup in the heterogeneous regions. The extent of this stable spiral's control on the tissue is itself dependent on the dynamical state of the system and the surrounding breakup. The distribution of Ω, computed from 60 simulations, is shown in Fig. 3F and is almost uniform, consistent with the distribution one would obtain using the first method of simulating SSWIB with varying stable domain sizes. Importantly, this distribution is distinct from the one obtained simulating MWR, which exhibits a peak for small values of Ω.

Clinical data.

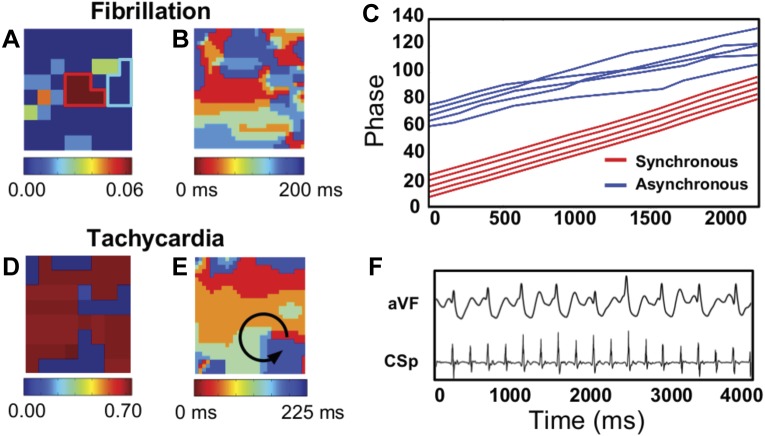
To demonstrate the application of our synchronization analysis to clinical data, we begin by examining the transition between AF and AT in a patient. In Fig. 4A we plot the SI map of the LA of a 65-yr-old patient for an episode corresponding to AF of duration 2.2 s. A small region in the center of the field of view displays localized synchrony and is surrounded by asynchronous tissue. The phase as a function of time for the five electrodes within this synchronized region is shown in Fig. 4C, along with five other nearby electrodes within the asynchronous domain, as indicated by the light blue border in Fig. 4A. For visualization purposes, each phase was phase shifted. Clearly, the phases within the synchronous region display 1:1 phase locking such that their phase difference remains roughly constant. The other phases, in contrast, show multiple crossings, demonstrating that their phase differences vary significantly, resulting in low values of γ_i,j and a_ij = 0. Interestingly, an isochronal map obtained within the same time frame shows significant variability throughout the domain, as shown in Fig. 4B.

Fig. 4.

Human atrial fibrillation (AF) data, showing that synchronization increases during the transition from AF to atrial tachychardia (AT). A: SI map from a patient during AF displays a synchronized region in the posterior wall of the left atrium (LA). B: corresponding isochronal map of this patient, with red (blue) corresponding to earliest (latest) activation, shows a complex activation pattern. C: phase as a function of time for 5 electrodes within the organized domain of A (red lines) and 5 electrodes outside this domain (blue lines). For visualization purposes, a constant offset is added to each phase. D: SI map of the same patient after AF converted to AT. The organization has increased, with most of the LA now displaying high levels of synchrony. E: corresponding isochronal map shows a counterclockwise rotating spiral wave in the posterior wall of the LA, indicated by the arrow. F: electrogram recordings during AT, showing a highly regular signal with a cycle length of 220 ms. aVF, arteriovenous fistula; CSp, carotid sinus pressure.

Later during mapping, AF in this patient converted to AT, as can be seen from the electrograms (Fig. 4F), which are highly regular and have a high signal-noise ratio. The SI map for this episode is shown in Fig. 4D and reveals an almost completely synchronous LA. The isochronal map corresponding to the AT episode shows a spatially conserved spiral wave (Fig. 4E). Thus both the synchronization maps and the activation maps reveal the spatiotemporal organization underlying the transition from AF to AT. The advantage of the SI maps, however, is their potential for quantitative characterization of organization during human AF.

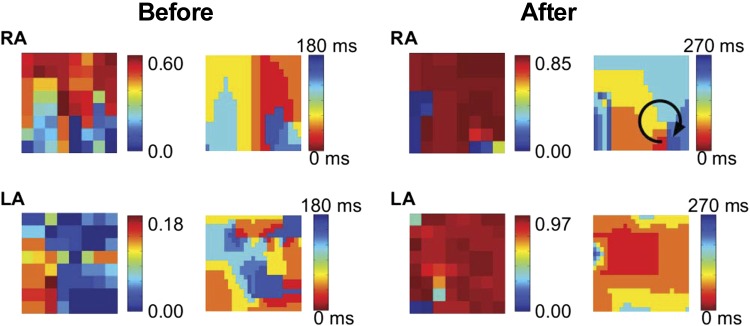
A second clinical example is shown in Fig. 5 where we show the SI maps before and after the administration of ibutilide, with recording intervals of 1.6 s. Ibutilide is a class III anti-arrhythmic agent that prolongs action potential duration and flattens its rate-response (restitution) curve by blocking the rapid component of the delayed rectifier potassium current, I_Kr (16, 20, 30). It can rapidly terminate AF or flutter in 30–50% of cases and may organize AF in remaining patients (16, 30). However, it is uncertain if ibutilide acts by reducing the probability for reentry, via collision of leading and trailing edges of a spiral wave, by reducing the number of sources, or by preventing spiral wave breakdown.

Fig. 5.

Ibutilide organizes human AF. Plotted are the SI map and the isochronal map during AF in a 66-yr-old patient before and after the administration of ibutilide. The maps for both the LA and the right atrium (RA) are shown and reveal that AF organizes after ibutilide was introduced, with a clockwise rotating spiral in the RA (arrow).

Figure 5 (before) shows the SI map of AF in a 66-yr-old patient revealing a synchronous region in the RA. The corresponding isochronal map reveals the existence of a spiral wave in the lower RA. From the SI map, then, we can conclude that roughly half the field of view is controlled by this spiral wave. Ibutilide (1 mg) was administered intravenously and the resulting SI map was computed. Notably, the spatial extent of this domain in Fig. 5 (after) spans nearly the entire field of view, demonstrating that in this patient ibutilide increased the spatial organization of the reentry underlying AF.

In addition to slowing and increasing organization of the spiral wave in the primary AF-sustaining chamber (in this case, the RA), ibutilide also profoundly altered spatiotemporal organization at remote sites (here, the LA). The patient's LA initially displayed only a small region of synchrony (Fig. 5). After ibutilide, LA activation is synchronized within almost the entire LA, likely reflecting activation from RA to LA over Bachmann's bundle and illustrating reduced complexity in activation. As expected, this increase organization is also evident from the isochronal maps of the LA.

A third clinical example is provided in Fig. 6 where we plot the SI map for different time intervals during a FIRM ablation procedure. Figure 6A corresponds to the SI map obtained at the start of the procedure and shows a synchronized region in the posterior LA. Figure 6B shows a SI map from data obtained 46 min later. Between these intervals the synchronized region remains conserved but has increased in size.

Fig. 6.

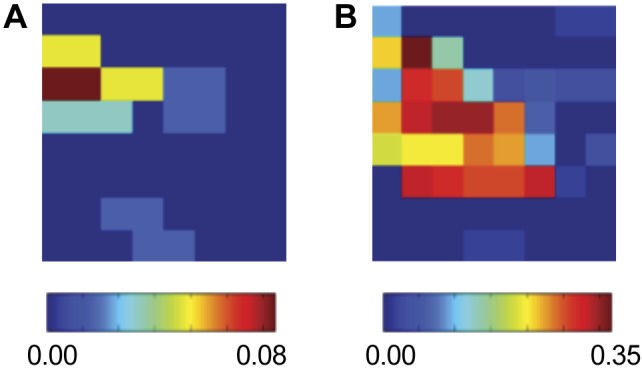
Human AF analyses, showing SI maps for the LA of a 65-yr-old patient. A and B: show this map at different stages of targeted ablation: at onset (A) and after 46 min (B). The synchronized region in the posterior LA remains conserved but has increased in size.

A fourth clinical example is shown in Fig. 7 where we plot the SI map and corresponding isochronal map of a focal source present in the LA of a 75-yr-old patient. In the atrium controlled by the focal source, we expect a clear synchronized region extending across the domain signifying activation by this source. This is confirmed in the SI map, demonstrating that focal sources manifest as synchronized regions.

Fig. 7.

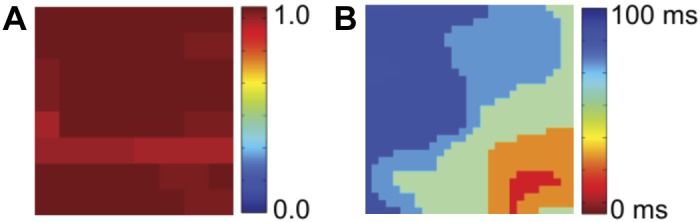
Analysis of a focal source in the LA of a 75-yr-old-patient during AF. A: SI map of the LA shows synchrony across the entire domain. B: corresponding isochronal map shows organized activation from the focal source, located in the inferolateral LA. The mechanistic role of the focal source was proven clinically when targeted ablation at this site alone in this patient terminated persistent AF to sinus rhythm.

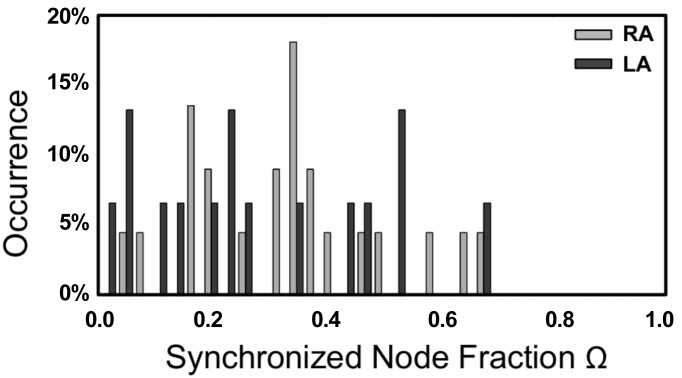
As a final application of our method, we computed the distribution of the fraction of synchronized electrodes, Ω, in patients before ablation. To this end, we examined the synchronization network in 24 patients for who bi-atrial electrode recordings were available. We computed these over a time period of 2.8 s, resulting in 22 RA and 15 LA recordings of sufficient length. The result of our analysis is shown in Fig. 8 and shows that this distribution is broad, containing patients with only a few synchronized electrodes and patients for which most electrodes are synchronized. This distribution is inconsistent with the distribution generated by simulating MWR, which was strongly peaked at small Ω, while it is compatible with the results obtained from simulated SSWIB data (see Fig. 3). The details of the patient population are described in Table 1.

Fig. 8.

Distribution of the fraction of synchronized electrodes, Ω, for 24 patients during AF. Shown are the distributions of both the LA and RA before any ablation has occurred.

DISCUSSION

We have outlined here an analysis method based on phase synchronization of the activation times of a coarse electrode grid. We have used it to demonstrate that AF in humans is consistent with SSWIB and that organization by clinically applied drugs may operate by increasing the spatial domain of a dominant mother rotor. The method employed here is not specific to the details of the electrode array used. Here, we applied the methodology to recordings from the basket electrodes we have described earlier (22, 24). Furthermore, the method quantifies the level of synchrony within the tissue covered by the basket and is independent of the exact coverage.

Our method has several advantages. First, it directly describes dynamical interconnectedness, rather than other methods that describe only single-site organization and therefore require inferring dynamical connections (21, 28). Also, it only relies on activation time information and a single parameter (κ). This is in contrast to other methods, including the use of complex fractionated atrial electrograms (CFAE) to determine AF organization (21), that sensitively depend on both the signal and how this signal is processed and analyzed. Furthermore, it does not require the creation and visual interpretation of spatiotemporal maps as is the case for isochronal maps or phase maps. These advantages make our methodology uniquely able to quantify the spatiotemporal activation of human AF.

We first tested our method on in silico data and demonstrated that spatially conserved spiral waves will manifest themselves as synchronized domains within the synchronization map. We have verified that focal sources will also manifest themselves as synchronized domains. Furthermore, the size of the synchronized regions corresponds to the domain that is controlled by the local, stable source. Thus our measure offers a way to estimate the coherent domains during cardiac arrhythmias.

Our analysis of the clinical data shows that this coherent domain increases when AF converts to AT. While this may be expected, since AT corresponds to activation that is more organized, the congruent localization of synchronized regions between AF and AT argues in favor of shared mechanisms between these arrhythmias. The analysis following a pharmaceutical intervention, ibutilide, demonstrates how our methodology can be used to gain insight into organization during drug delivery. In the analyzed patient, the administration of ibutilide clearly organizes the activation. Clearly, results of more patients are required before we can draw general conclusions about the effects of ibutilide on AF organization. Furthermore, we also show that regions of synchrony can be conserved during an ablation procedure. These localized regions of sustained synchrony may play an important role in the underlying fibrillatory dynamics, regardless of the precise dynamics of the activation. It also is possible that these are regions that correlate to more homogeneous tissue and therefore exhibit more synchronous activation times when activated by a distant source. Further insight into the role of these regions might be possible using a combination of synchrony analysis and isochronal mapping.

We have also shown that our technique can afford us more general insight into the underlying dynamics inherent to AF. The synchronization distribution, as computed for 24 patients that experience AF, is broad. In other words, the number of synchronized electrodes in these patients varies from small to large and spans most of the possible range. We have shown that this result cannot be reconciled with MWR as the primary source of AF. This is clear from our simulation data that show that MWR leads to activation that is asynchronous over the entire domain, resulting in very few synchronized electrodes. In contrast, the synchronization distribution obtained from simulations mimicking SSWIB is similar to the clinical one, suggesting that AF consists of regions of coherence and synchrony surrounded by domains in which the activation is irregular and asynchronous. In our simulations, we modeled this scenario by introducing spatially varying heterogeneities in part of the computational domain. For appropriate tissue characteristics, the homogeneous domain admits a spatially conserved spiral wave while the heterogeneities result in spiral wave breakup.

We should note that the broad synchronization distribution we observe in the clinical data does not indicate that SSWIB is the exclusive source of AF in every patient. It is possible that during AF both mechanisms are present at the same time. For example, one atrium might exhibit MWR while the dynamics of the other is consistent with SSWIB. Also, it is also possible that tissue heterogeneity results in large-scale domains in which one of the two mechanisms is present. However, the presence of large fractions of synchronized electrodes implies that MWR cannot be the sole AF mechanism. Furthermore, we should also point out that focal sources might play a role in the maintenance of AF, as also observed in our mapping studies (24). If these sources occur randomly in both place and time, then the resulting tissue would be asynchronous. The interaction between the multiple activation fronts, however, is likely to result in multiple reentry events, resulting in a dynamical state that is similar to MWR.

Future work should include the investigation of synchrony over prolonged and continuous intervals. This is challenging using spatiotemporal maps but is relatively straightforward using phase synchrony. Examining the SI maps as a function of time will allow us to determine whether all localized sources are stable or whether some exhibit transient dynamics during which a spiral wave or focal source “comes-and-goes.” These studies might enable us to determine if some sources are more important in the maintenance of AF than others, should lead to a deeper understanding of cardiac arrhythmias, and could help and guide future treatment options.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grants R01-HL-122384 (to W.-J. Rappel) and R01-HL-83359 and K24-HL-103800 (to S. M. Narayan).

DISCLOSURES

Dr. W.-J. Rappel reports being coinventor on intellectual property owned by the University of California and licensed to Topera Medical, Dr. S. M. Narayan reports being coinventor on intellectual property owned by the University of California and licensed to Topera Medical, and Dr. S. M. Narayan reports having received consulting fees from Medtronic, UpToDate, and the American College of Cardiology.

AUTHOR CONTRIBUTIONS

Author contributions: D.V. and W.-J.R. conception and design of research; D.V. and W.-J.R. analyzed data; D.V., S.M.N., and W.-J.R. interpreted results of experiments; D.V. prepared figures; D.V. and W.-J.R. drafted manuscript; D.V., S.M.N., and W.-J.R. edited and revised manuscript; D.V., S.M.N., and W.-J.R. approved final version of manuscript; S.M.N. performed experiments.