The Prediction of the Expected Current Selection Coefficient of Single Nucleotide Polymorphism Associated with Holstein Milk Yield, Fat and Protein Contents

Abstract

Milk-related traits (milk yield, fat and protein) have been crucial to selection of Holstein. It is essential to find the current selection trends of Holstein. Despite this, uncovering the current trends of selection have been ignored in previous studies. We suggest a new formula to detect the current selection trends based on single nucleotide polymorphisms (SNP). This suggestion is based on the best linear unbiased prediction (BLUP) and the Fisher’s fundamental theorem of natural selection both of which are trait-dependent. Fisher’s theorem links the additive genetic variance to the selection coefficient. For Holstein milk production traits, we estimated the additive genetic variance using SNP effect from BLUP and selection coefficients based on genetic variance to search highly selective SNPs. Through these processes, we identified significantly selective SNPs. The number of genes containing highly selective SNPs with p-value <0.01 (nearly top 1% SNPs) in all traits and p-value <0.001 (nearly top 0.1%) in any traits was 14. They are phosphodiesterase 4B (PDE4B), serine/threonine kinase 40 (STK40), collagen, type XI, alpha 1 (COL11A1), ephrin-A1 (EFNA1), netrin 4 (NTN4), neuron specific gene family member 1 (NSG1), estrogen receptor 1 (ESR1), neurexin 3 (NRXN3), spectrin, beta, non-erythrocytic 1 (SPTBN1), ADP-ribosylation factor interacting protein 1 (ARFIP1), mutL homolog 1 (MLH1), transmembrane channel-like 7 (TMC7), carboxypeptidase X, member 2 (CPXM2) and ADAM metallopeptidase domain 12 (ADAM12). These genes may be important for future artificial selection trends. Also, we found that the SNP effect predicted from BLUP was the key factor to determine the expected current selection coefficient of SNP. Under Hardy-Weinberg equilibrium of SNP markers in current generation, the selection coefficient is equivalent to 2*SNP effect.

INTRODUCTION

Holstein-Friesian cattle have been selected intensively during the last millennia, especially in the last five decades after the breeding programs were started in the 1960s (Skjervold and Langholz, 1964; Mwai et al., 2015). Holsteins have been selected for milk yield and milk composition, which was progressed through the development of reproductive technologies like pedigree evaluation of bulls, artificial insemination, embryo transfer and the like. Recently, genomic selection have accelerated the selection process (Catillo et al., 2001; Goddard and Hayes, 2007). This selection has resulted in an increase in the frequency of favorable alleles affecting selected traits. The selection will have also increased the frequency of alleles of neutral markers in linkage disequilibrium with the favorable alleles (Smith and Haigh, 1974). In addition, identifying genomic regions subject to selection could reveal the mutations responsible for improved production (Boitard and Rocha, 2013). However, the current selection trends have been ignored. Thus, we focused on the current selection trends and selection coefficient based on single nucleotide polymorphisms (SNPs).

To predict each SNP’s selection coefficient associated with Holstein milk-related traits, we used Fisher’s fundamental theorem of natural selection, which states that the rate of increase in fitness of any organism at any time is equal to its genetic variance in fitness at that time (Hartl, 1988). We can calculate the relative selection coefficient based upon this theorem and the linear additive model. The model is the best linear unbiased prediction (BLUP). BLUP was originally proposed by Henderson (Henderson, 1975). The predicted SNP effects from BLUP were used to calculate the additive genetic variances of the SNPs. Fisher’s theorem links the additive genetic variance to the selection coefficient (Hartl, 1988). The selection coefficient is dependent on the phenotypes and their units. So it can be called “expected relative current selection coefficient”. “Expected” implies that the selection coefficient is the expected value in the F₁ generation. “Relative” means that it is dependent on the unit of phenotypes. Thus, it was recalibrated by the maximum value. The predicted value of the selection coefficient could be the actual value if selection were performed only using breeding values of a given trait and selection followed Fisher’s theorem.

The genes containing highly significant SNPs were obtained using Ensembl website (Flicek et al., 2011). The BLUP-based relative selection coefficient has the current selection information. We analyzed the ontology of the genes containing the highly significant SNPs (top 1% or p-value <0.01). The P-values were obtained under the normal assumption of selection coefficient.

MATERIALS AND METHODS

Materials

Female Holsteins were randomly collected in Korea. The phenotypes were milk yield, fat and protein contents with parity 1 and the number of Holstein with phenotypic values in the data was 462. Genomic DNAs from Holstein cows were genotyped using Illumina 50K SNP Beadchip (Illumina, San Diego, CA, USA) following the standard protocol. A total number of 41,099 genotyped SNPs were imputed using BEAGLE version 4.0 (Browning and Browning, 2009) and filtered using minor allele frequency (MAF<0.05), Hardy-Weinberg equilibrium (HWE p<0.001), missing genotype data (>0.1) and we excluded the SNPs on the sex chromosome. After these quality controls, there remained 37,854 autosomal SNPs. Individual animals with missing phenotypic values were excluded before filtering, e.g., filtering by MAF.

Prediction of SNP effects for milk production traits

The BLUP model is the following formula:

$$\text{y}=\text{Xb}+\text{Zu}+\text{e}$$ (1)

Where y was the vector of phenotypic values, X and Z were the incidence matrices, b and u were vectors of fixed and random effects, respectively. Random effects and residual errors were assumed to be normally distributed. These multivariate normal distributions is usually notated as u~MVN(0,Gu) and e~MVN(0,R) where MVN are denoted as multivariate normal distribution. The SNP effects were calculated using single nucleotide polymorphism-genomic best linear unbiased prediction (SNP-GBLUP) using the SNP-SNP relationship matrix (Lee et al., 2014). This SNP-SNP relationship matrix (SSRM) is based on the genomic relationship matrix (GRM) (Goddard et al., 2011). SSRM was denoted as G_u and GRM as G. The SSRM (G_u) can be calculated using the relationship, G_u = (Z^TG⁻¹Z)⁻¹ (Lee et al., 2014). The fixed effect was season. The R package, “rrBLUP” was used for the analysis (Endelman, 2011).

Estimation of expected current relative selection coefficient

Fisher’s fundamental theorem of natural selection states that fitness change of any organism per unit time is equal to its genetic variance in fitness at that time. In the linear additive model, therefore, we can easily calculate the additive genetic variance and selection coefficient based on this theorem (Price, 1972; Hartl, 1988; Ewens, 1989). The relative selection coefficient was calculated using the following formula:

$$\begin{array}{l}{\sigma }_a^2=\frac{dw}{dt}=2pq{[p(w_{AA}-w_{A{A}^{\prime }})+q(w_{A{A}^{\prime }}-w_{A^{\prime }{A}^{\prime }})]}^2\\ =2pq{[p\times (-\frac{s}{2})+q\times (-\frac{s}{2})]}^2=\frac{pq{s}^2}{2}\end{array}$$ (2)

Where fitness per genotype is (w_AA, w_AA′, w_A′A′) = (1-s, 1-s/2, 1) and s is the selection coefficient symbol.

$$\begin{array}{l}{s}_j^2=\frac{2{\sigma }_{a,j}^2}{p_j{q}_j}(\text{according\hspace{0.17em}to\hspace{0.17em}Fisher}’\text{s\hspace{0.17em}theorem\hspace{0.17em}}[\text{by\hspace{0.17em}Eq\hspace{0.17em}}\{2\}\hspace{0.17em}\text{and\hspace{0.17em}if\hspace{0.17em}dt}=1]\\ =\frac{2\times \text{var}(Z_{ij}\times u_j)}{p_j{q}_j}\text{according\hspace{0.17em}to\hspace{0.17em}}{\sigma }_{a,j}^2\\ =\text{var}(Z_{ij}\times u_j)\end{array}$$ (3)

Where i represents i^th individual, j represents j^th marker or SNPs, Z_ij represents the i^th individuals and j^th SNPs’ 0, 1, 2 coding. u_j represents the SNP effect. The additive genetic variance calculation is a data-driven method which uses the Z matrix, directly.

Equation (3) is based on the Fisher’s fundamental theorem of natural selection (Frank and Slatkin, 1992). The relative selection coefficient of a given locus is in the range of −1(minimum) to 1(maximum). We assumed the normality of relative selection coefficient and then set the criteria of highly selective SNPs as p-value <0.01 (nearly top 1% SNPs).

Especially, if the SNP markers are under HWE in current generation, s² = 4u² according to var(Z_i) = 2pq. If we pay heed on the expected relationship of the sign between selection coefficient s and SNP effect u, we can derive that s = 2u.

$$s_j=2u_j\hspace{0.17em}(\text{if\hspace{0.17em}HWE\hspace{0.17em}in\hspace{0.17em}current\hspace{0.17em}generation})$$ (4)

Characterization of candidate genes under selection regions

We identified the genes which contained significantly selective SNPs and performed gene ontology analysis using the ClueGo plugin of Cytoscape program (Bindea et al., 2009). The gene catalog was retrieved from Ensembl website (www.ensembl.org). In the ClueGo analysis, we used the default parameter except for setting the 2 minimum number of genes in gene ontology (GO) term/Pathway selection and then we corrected p-value through Benjamini-Hochberg method (Benjamini and Hochberg, 1995).

RESULTS AND DISCUSSION

SNP-GBLUP method results and highly selective SNPs

The mean and standard deviation of Holstein milk yield, fat and protein records for parity 1 were 8,845; 1,425, 339; 58 and 283; 44, respectively. We estimated narrow-sense heritability of the milk yield, fat and protein using results of SNP-GBLUP method which were 0.39, 0.45, and 0.40, respectively. The fixed effects (season) of milk yield, fat and protein (kilograms) were (8,655, 8,847, 8,935, 8,907), (325, 342, 344, 343) and (275, 286, 286, 283) for spring, summer, autumn, and winter, respectively. From SNP effects from SNP-GBLUP method, we estimated the selection coefficients of each SNP.

Figure 1 shows the flow chart of the analysis which is designed by theory and method. Figure 2 shows the plot of relative selection coefficient against SNP effect. It implies that the selection coefficient is mainly determined by SNP effect. The sign of relative selection coefficient was inferred from the sign of SNP effect. Figure 3 indicates the diagram of ontology of the genes which contain nearly the top 1% SNPs in the protein contents. We selected the genes containing SNPs with p-value <0.01 (nearly top 1% SNPs) and performed gene ontology. The condition was the default value except for setting 2 as the minimum number of genes in the GO Term/Pathway selection item.

Figure 1.

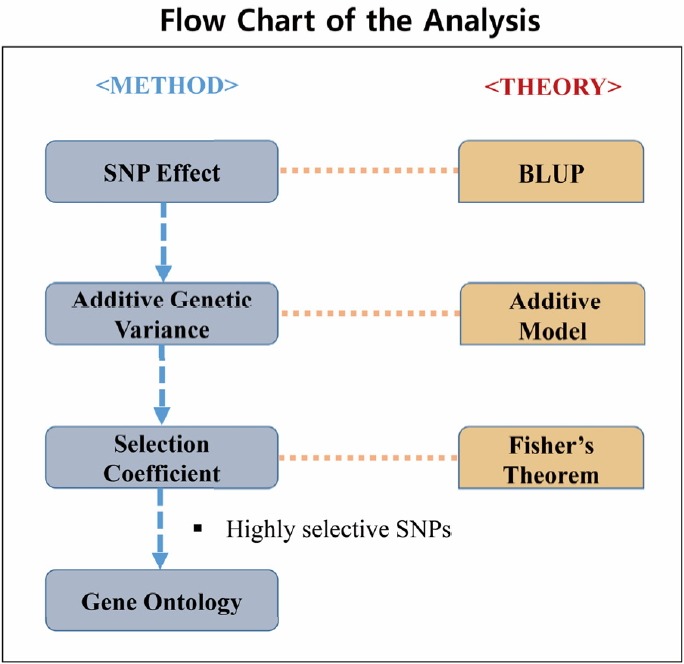
The figure shows the flow chart of our analysis which is stipulated by method and theory. The single nucleotide polymorphisms (SNP) effects, additive genetic variance and selection coefficient were sequentially calculated. The gene ontology was performed using Cytoscape program ClueGo plugin.

Figure 2.

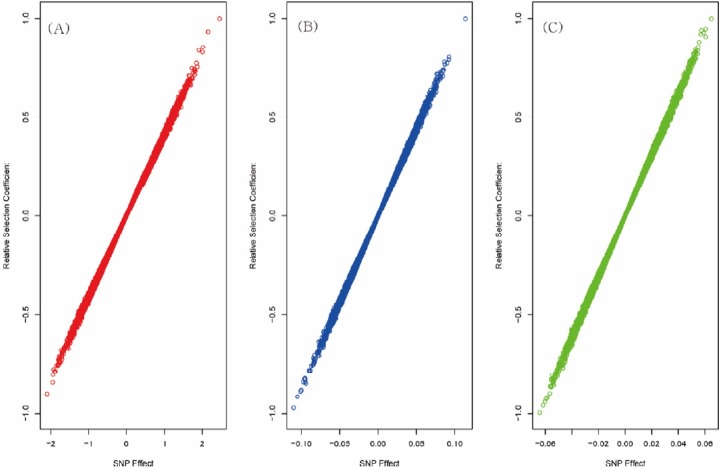
Plot of single nucleotide polymorphisms (SNP) effects and relative selection coefficients of SNPs. The phenotypes were milk yield (A panel), fat (B panel) and protein content (C panel). It was estimated using SNP-genomic best linear unbiased prediction (SNP-GBLUP) and Fisher’s fundamental theorem of natural selection. The plot shows that the SNP effect is the major factor to determine the selection coefficient.

Figure 3.

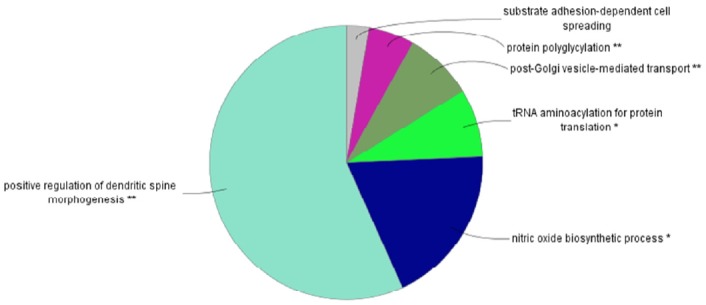
Diagram of gene ontology of the genes which contain the highly selective SNPs in the milk protein trait. We selected the genes containing single nucleotide polymorphisms (SNPs) with p-value <0.01 (nearly top 1% SNPs) and performed gene ontology. The condition was the default value except setting 2 minimum number of genes in the gene ontology (GO) Term/Pathway selection item. The positive regulation of dendritic spine morphogenesis was the most significant gene ontology. Dendritic spine morphogenesis is important in synaptic development and plasticity of the mammalian brain.

Table 1 illustrates the F₁ generation’s expected allele frequency change under linear additive model. It demonstrates that allele frequency can be predicted via the SNP effect. Table 2 shows highly selective SNPs and the genes containing them (any p-value <0.001; nearly top 0.1% SNPs). The genes containing very highly selective SNPs with p-value <0.01 (nearly top 1% SNPs) in all traits and p-value <0.001 (nearly top 0.1%) in any traits were phosphodiesterase 4B (PDE4B), serine/threonine kinase 40 (STK40), collagen, type XI, alpha 1 (COL11A1), ephrin-A1 (EFNA1), netrin 4 (NTN4), neuron specific gene family member 1 (NSG1), estrogen receptor 1 (ESR1), neurexin 3 (NRXN3), spectrin, beta, non-erythrocytic 1 (SPTBN1), ADP-ribosylation factor interacting protein 1 (ARFIP1), mutL homolog 1 (MLH1), transmembrane channel-like 7 (TMC7), carboxypeptidase X, member 2 (CPXM2), and ADAM metallopeptidase domain 12 (ADAM12). We inferred the sign of relative selection coefficient from the SNP effect information in Table 1. The positive sign of SNP effect represents that of the selection coefficient and vice versa.

Table 1.

F₁ generation’s (the next in the current generation) allele frequency change according to the single nucleotide polymorphism (SNP) effect under linear additive model¹

Allele frequency (P)	0.25 (AA)	0.5 (AA′)	0.25 (A′A′)
Fitness change	1-2u	1-u	1
SNP effect	Allele frequency change(F1)
0.5	0	0.5	0.5
0.05	0.24	0.5	0.26
0.25	0.17	0.5	0.33
0.005	Approximately HWE	Approximately HWE	Approximately HWE
0	HWE	HWE	HWE

¹We assumed the Hardy-Weinberg equilibrium (HWE) in P (Parental) generation and depicted the SNP effect as selection coefficient according to Equation (4). The allele coded as “2” assumed to be A′A′ and u denoted SNP effect*.

*Note that the SNP effect is sensitive to the unit of phenotypic values and we assumed that the SNP effect would be the selection coefficient*2

Table 2.

Highly selective SNPs with any p-value <0.001 (top 1% SNPs) in the analysis of milk yield, fat and protein phenotypes and the genes containing it¹

Chromosome	SNP	SNP position	MRSC	FRSC	PRSC	Milk2	Fat3	Protein4	GeneID5	Gene start	Gene end	Gene name
1	ARS-BFGL-NGS-29472	138,650,000	0.444	0.769	0.530	0.013455	0.000053	0.011769	ENSBTAG00000012798	138,455,304	138,676,649	KCNH8
2	ARS-BFGL-NGS-107330	116,829,914	0.653	0.305	0.783	0.000563	0.063954	0.000402	ENSBTAG00000021327	116,803,654	116,839,529	DAW1
3	BTA-99819-no-rs	79,508,402	−0.742	−0.698	−0.842	0.000098	0.000184	0.000142	ENSBTAG00000008636	79,284,893	79,734,224	PDE4B
3	BTB-01155479	79,378,528	−0.754	−0.841	−0.957	0.000078	0.000009	0.000018	ENSBTAG00000008636	79,284,893	79,734,224	PDE4B
3	ARS-BFGL-NGS-31953	79,480,234	−0.757	−0.693	−0.866	0.000073	0.000205	0.000094	ENSBTAG00000008636	79,284,893	79,734,224	PDE4B
3	Hapmap39300-BTA-99855	79,333,053	−0.803	−0.881	−0.994	0.000028	0.000004	0.000009	ENSBTAG00000008636	79,284,893	79,734,224	PDE4B
3	ARS-BFGL-NGS-102149	110,078,547	0.555	0.742	0.672	0.002813	0.000091	0.002019	ENSBTAG00000015969	110,074,348	110,109,946	STK40
3	BTB-01582389	40,625,026	0.570	0.651	0.651	0.002235	0.000524	0.002682	ENSBTAG00000021217	40,448,699	40,682,012	COL11A1
3	ARS-BFGL-NGS-112442	40,588,026	0.577	0.619	0.655	0.002023	0.000920	0.002540	ENSBTAG00000021217	40,448,699	40,682,012	COL11A1
3	ARS-BFGL-NGS-64215	15,525,599	−0.622	−0.759	−0.802	0.000899	0.000054	0.000272	ENSBTAG00000020244	15,521,494	15,528,093	EFNA1
4	BTB-00172204	31,172,819	0.326	0.690	0.524	0.052424	0.000256	0.012614	ENSBTAG00000015539	31,017,033	31,222,267	RAPGEF5
5	Hapmap53993-rs29024740	60,373,086	0.499	0.678	0.567	0.006441	0.000316	0.007694	ENSBTAG00000003183	60,372,425	60,502,966	NTN4
5	BTB-00239812	121,135,969	0.582	0.229	0.723	0.001852	0.127036	0.000990	ENSBTAG00000020341	121,099,143	121,164,873	MOV10L1
6	ARS-BFGL-NGS-4767	107,186,270	0.515	0.806	0.578	0.005127	0.000024	0.006713	ENSBTAG00000005711	106,483,716	107,356,158	NSG1
6	Hapmap38694-BTA-76566	61,591,415	0.533	0.401	0.783	0.003943	0.022142	0.000402	ENSBTAG00000027569	61,362,546	61,744,231	APBB2
9	BTB-00404639	90,037,629	1.000	0.605	0.708	0.000000	0.001172	0.001220	ENSBTAG00000007159	89,969,586	90,255,801	ESR1
9	Hapmap47116-BTA-84683	90,002,616	0.776	0.624	0.514	0.000054	0.000849	0.014135	ENSBTAG00000007159	89,969,586	90,255,801	ESR1
10	ARS-BFGL-NGS-113766	81,459,970	−0.790	0.060	−0.842	0.000037	0.389680	0.000142	ENSBTAG00000009998	81,396,104	81,494,769	GALNTL1
10	ARS-BFGL-NGS-82682	89,774,836	0.698	0.095	0.775	0.000249	0.322371	0.000452	ENSBTAG00000020480	89,756,991	89,852,261	SPTLC2
10	ARS-BFGL-NGS-110578	91,602,885	0.628	0.314	0.771	0.000863	0.058033	0.000483	ENSBTAG00000025324	91,597,994	92,223,876	NRXN3
10	ARS-BFGL-NGS-3900	89,804,719	0.689	0.087	0.759	0.000296	0.337759	0.000583	ENSBTAG00000020480	89,756,991	89,852,261	SPTLC2
11	ARS-BFGL-NGS-51235	37,228,325	0.627	0.368	0.835	0.000889	0.032657	0.000177	ENSBTAG00000006995	37,030,009	37,241,384	SPTBN1
13	ARS-BFGL-NGS-90758	35,352,877	0.201	0.630	0.212	0.159441	0.000762	0.185064	ENSBTAG00000001204	35,331,913	35,368,126	JCAD
13	Hapmap60259-rs29016362	34,887,980	0.067	0.627	0.112	0.373241	0.000804	0.319634	ENSBTAG00000027444	34,860,211	34,965,895	SVIL
13	Hapmap49926-BTA-24453	21,167,068	−0.226	−0.740	−0.349	0.126467	0.000081	0.065057	ENSBTAG00000023216	21,049,546	21,386,152
15	ARS-BFGL-NGS-107160	75,065,222	0.160	0.636	0.418	0.214312	0.000685	0.037164	ENSBTAG00000008465	75,047,569	75,068,534	ACS
17	ARS-BFGL-NGS-11818	4,393,229	0.745	0.449	0.775	0.000100	0.012179	0.000452	ENSBTAG00000008816	4,308,229	4,436,083	TRIM2
17	BTB-00668797	4,827,067	0.707	0.670	0.775	0.000210	0.000371	0.000452	ENSBTAG00000008438	4,732,242	4,868,678	ARFIP1
17	ARS-BFGL-NGS-77442	63,480,469	0.576	0.413	0.759	0.002035	0.019096	0.000576	ENSBTAG00000001806	63,474,993	63,497,850	IQCD
21	ARS-BFGL-NGS-104549	57,731,221	0.689	0.291	0.738	0.000296	0.073074	0.000794	ENSBTAG00000006620	57,596,461	57,783,306	SLC24A4
22	Hapmap38236-BTA-55228	10,502,283	0.624	0.625	0.926	0.000925	0.000826	0.000037	ENSBTAG00000016758	10,492,112	10,585,992	MLH1
23	Hapmap55007-rs29021986	13,484,531	0.361	0.617	0.380	0.036246	0.000945	0.052479	ENSBTAG00000027197	13,389,447	13,520,727	KIF6
25	ARS-BFGL-NGS-93374	17,040,004	0.602	0.654	0.906	0.001351	0.000497	0.000052	ENSBTAG00000016505	17,039,666	17,081,449	TMC7
26	ARS-BFGL-NGS-19663	43,933,332	0.931	0.691	0.919	0.000002	0.000249	0.000041	ENSBTAG00000018941	43,829,293	43,966,907	CPXM2
26	ARS-BFGL-NGS-110497	45,870,133	0.542	0.620	0.604	0.003440	0.000895	0.004904	ENSBTAG00000012444	45,848,827	46,238,138	ADAM12
26	ARS-BFGL-NGS-30392	44,539,739	−0.526	−0.750	−0.464	0.004132	0.000065	0.022510	ENSBTAG00000010957	44,431,214	44,558,731	LHPP
26	ARS-BFGL-NGS-30060	45,983,109	0.673	0.606	0.805	0.000394	0.001141	0.000282	ENSBTAG00000012444	45,848,827	46,238,138	ADAM12
28	ARS-BFGL-NGS-28818	7,138,132	0.378	0.614	0.318	0.030058	0.000997	0.087874	ENSBTAG00000020361	6,762,322	7,195,661	SLC35F3

SNP, single nucleotide polymorphism; MRSC, milkyield relative selection coefficient; FRSC, fat relative selection coefficient; PRSC, protein relative selection coefficient.

¹p-value was computed under the normality assumption of relative selection coefficient. The gene catalog was retrieved from Ensembl server.

²Milkyield p-value.

³Fat p-value.

⁴Protein p-value.

⁵Ensembl gene ID.

Gene ontology analysis of highly selective SNPs

We chose the highly selective SNPs (p-value <0.01) in milk yield, fat, protein-associated analyses and performed the gene ontology analysis with Cytoscape ClueGo plugin program (Shannon et al., 2003). For milk yield and fat cases, there were no great information about gene ontology. For proteins, significant gene ontologies were dendritic spine morphogenesis and the nitric oxide biosynthetic process with dendritic spine morphogenesis being highly significant. Dendritic spine is the major site of excitatory synaptic transmission in the mammalian brain and is very important in synaptic development and plasticity (Penzes et al., 2003; Tada and Sheng, 2006). The specific genes which produce milk protein and influence the morphogenesis of dendritic spine in the mammalian brain may be a putative and important target of future artificial selection trends in the Holstein cattle.

SNP-GBLUP and selection coefficient

The SNP-GBLUP has merits to predict the SNP effects by assigning the SNP-SNP relationship matrix (Lee et al., 2014). The accurate estimation of the sign of SNP effect as well as its value is crucial to accurately predict the selection coefficient. Thus, we used the SNP-GBLUP rather than SNP-BLUP which assumes the effect being IID (independent and identically distributed) between markers. Not only the sample size but also the accurate prediction of the SNP effect is necessary to predict the relative selection coefficient.

Fisher’s theorem and best linear unbiased prediction

One of Fisher’s contributions to population genetics is a fundamental theorem of natural selection. It elucidated selection theory and subsequently breeding science. (Frank and Slatkin, 1992). The theorem indicates that the change of average fitness can be related to genetic variance which is specific to markers like SNPs. Average fitness in the next generation can be designated through selection coefficient in the linear additive model. The fitness change in the next generation can lead to the change of selection coefficient. The linear additive model like BLUP was used to compute the genetic variance of each SNP.

Figure 2 shows that the larger SNP effects, the greater selection coefficients. This finding that the selection coefficients are proportional to the SNP effects, matches the common sense of selection. If one individual had many SNPs with large effects, it would have large breeding values and would be selected by artificial selection. Thus, it seems to be natural that genetic factors like SNPs can determine the selection. It certainly links selection in the population to the breeding programs.

The sign of relative selection coefficient of SNP

The sign of the selection coefficient of a SNP is not explicit. However, the sign of SNP effect is definite. Thus we inferred the sign of relative selection coefficient of a SNP from SNP effect. A positive sign of relative selection coefficient indicates a positive sign of the SNP effect and vice versa. If the sign of a SNP effect were positive, the frequency of the allele coded as ‘2’ would increase and the contribution to the genomic estimated breeding values (GEBVs) would increase. If sign were negative, the situation would be vice versa, i.e. the frequency of the allele coded as ‘0’ would increase by selective breeding.

The features of our study

The characteristics of our paper was: first, we found that the SNP effect in the BLUP model is equivalent to the selection coefficient and is the powerful cause of a population’s allele frequency change; second, we used Fisher’s theorem and SNP-GBLUP. We adopted Fisher’s theorem to calculate selection coefficient. SNP-GBLUP which uses the SSRM (SNP-SNP relationship matrix) via GRM to predict the SNP effects.

IMPLICATIONS

The objective of our study was to find the selection coefficient of SNP in the population and find the SNPs which are expected to be highly selective in the next generation. The sign of selection coefficient of SNP was inferred from the sign of SNP effect. The signs of highly selective SNPs (p-value <0.01 or nearly top 1% SNPs) were nearly identical in all traits’ analyses. We found that the selection coefficients of SNPs were linearly proportional to the SNP effects. Especially, selection coefficient would be 2×SNP effect under HWE in the current generation. The significant genes may be crucial in future selection trends of Korean Holsteins.