Abstract
The efficacy of ultrasound therapies such as shock wave lithotripsy and histotripsy can be compromised by residual cavitation bubble nuclei that persist following the collapse of primary cavitation. In our previous work, we have developed a unique strategy for mitigating the effects of these residual bubbles using low amplitude ultrasound pulses to stimulate their aggregation and subsequent coalescence—effectively removing them from the field. Here, we further develop this bubble removal strategy through an investigation of the effect of frequency on the consolidation process. Bubble removal pulses ranging from 0.5 – 2 MHz were used to sonicate the population of residual nuclei produced upon collapse of a histotripsy bubble cloud. For each frequency, mechanical index (MI) values ranging from 0 to approximately 1.5 were tested. Results indicated that, when evaluated as a function of bubble removal pulse MI, the efficacy of bubble removal shows markedly similar trends for all frequencies tested. This behavior divides into three distinct regimes (with provided cutoffs being approximate): (1) MI < 0.2: Minimal effect on the population of remnant cavitation nuclei; (2) 0.2 < MI < 1: Aggregation and subsequent coalescence of residual bubbles, the extent of which trends toward a maximum; (3) MI > 1: Bubble coalescence is compromised as bubble removal pulses induce high magnitude inertial cavitation of residual bubbles. The major distinction in these trends came for bubble removal pulses applied at 2 MHz, which were observed to generate the most effective bubble coalescence of all frequencies tested. We hypothesize that this is a consequence of the secondary Bjerknes force being the major facilitator of the consolidation process, the magnitude of which increases when the bubble size distribution is far from resonance such that the phase difference of oscillation of individual bubbles is minimal.
INTRODUCTION
Residual cavitation bubble nuclei produced by the collapse of primary acoustic cavitation can limit the efficacy of ultrasound therapies such as shock wave lithotripsy (SWL) [1–6] and histotripsy [7]. The collapse of a single primary bubble can generate dozens of microscopic (<10 µm [4, 8]) residual daughters [9–12], which have been observed to persist from 10s of milliseconds [13, 14] up to full seconds [11, 12, 15, 16]. If subsequent acoustic pulses arrive prior to their dissolution, these residuals can seed further cavitation activity [9, 13, 15, 17, 18]. In SWL this can manifest in compromised stone comminution at high shock rates [2, 6, 19–22], as residual nuclei that persist along the path of shock wave propagation induce a selective attenuation of the waveform’s tensile phase [1–4]. A similar rate-dependent efficacy has been documented in histotripsy treatment of soft tissue [7], in which the physical location of residual bubble nuclei persisting within the target volume causes repeated cavitation events at a discrete set of sites—i.e., a memory effect. This, in turn, produces inhomogeneous tissue fraction and requires an excess number of pulses to achieve complete homogenization of the targeted zone.
In our previous work we have explored a strategy for the active removal of these remnant nuclei following a cavitation event [23], with the ultimate goal of mitigating the ill-effects of residual bubbles in cavitation-based ultrasound therapies. It was shown that the application of appropriately designed low amplitude ultrasound pulses can stimulate the aggregation and subsequent coalescence of residual bubble nuclei, in effect removing them from the field. These acoustic sequences, which we denote as bubble removal pulses, were hypothesized to operate via a synergistic interplay between the primary and secondary Bjerknes forces. Microscopic residual bubble nuclei, being smaller than the resonant size of the 500 kHz bubble removal pulse previously utilized, tend to move up the pressure gradient and congregate at the antinode of the bubble removal field (primary Bjerknes force) [24–28]. When brought into close proximity with one another, bubbles that are of similar size experience an attractive force, further promoting their consolidation (secondary Bjerknes force) [24, 25, 28, 29]. Our previous results indicate that the secondary Bjerknes force is likely the dominant facilitator of the bubble consolidation process, with a select set of acoustic parameters producing optimal aggregation and coalescence [23].
The optimization of bubble removal pulses to manipulate residual nuclei following primary cavitation collapse could lead to a pronounced adjunct for ultrasound therapies such as SWL and histotripsy. In the present study, we further explore this phenomenon through an investigation of the effect of frequency on the bubble removal process. Our previous work considered only a single frequency (500 kHz) to sonicate remnant cavitation bubbles. Here we extend the parameter space and examine bubble removal pulses of 0.5, 1, and 2 MHz, investigating if previously observed trends hold across frequency. The acoustic implications of residual nuclei remaining in the field following bubble removal are also explored by measuring the transmission of a secondary pulse through the volume of interest.
METHODS
A. Experimental Setup
The experimental setup used to investigate the effects of bubble removal pulse frequency was the same as that described previously [23], with the addition of a needle hydrophone (Müller-Platte Needle Probe 100-100-1, Dr. Müller Instruments, Oberursel, Germany) positioned adjacent to the histotripsy transducer focus at an offset distance of 2 mm, distal relative to the bubble removal module (Fig. 1). Once again, all experiments were conducted in deionized water degased to physiologically relevant levels (dissolved oxygen content of 7.1 ± 0.1 mg/L at 21.1 ± 0.4 °C (mean ± SD), corresponding to 78 ± 1% of saturation); this mimics the dissolved gas content of human urine, for example [30–32]. Each experiment was monitored using a Photron Fastcam SA1.1 high speed camera (Photron USA Inc., San Diego, CA) at a frame rate of 20 kfps and exposure time of 49 µs. A 10× super-long working distance microscope objective (T Plan SLWD 10×/0.20, Nikon Instruments Inc., Melville, NY) coupled to a 70 mm macro lens (Sigma 70 mm 1:2:8 DG Macro, Sigma Corporation of America, Ronkonkoma, NY) provided the optical power to resolve the microscopic residual nuclei of interest in this study. The theoretical resolution limit of this optical setup is 1.3 µm, while the theoretical depth of field is 18.3 µm. A large area, high power LED light source (BXRA-50C9000, Bridgelux Inc., Livermore, CA) was used to backlight the experiments such that bubbles generated in the field were visible as dark shadows on the optical images.
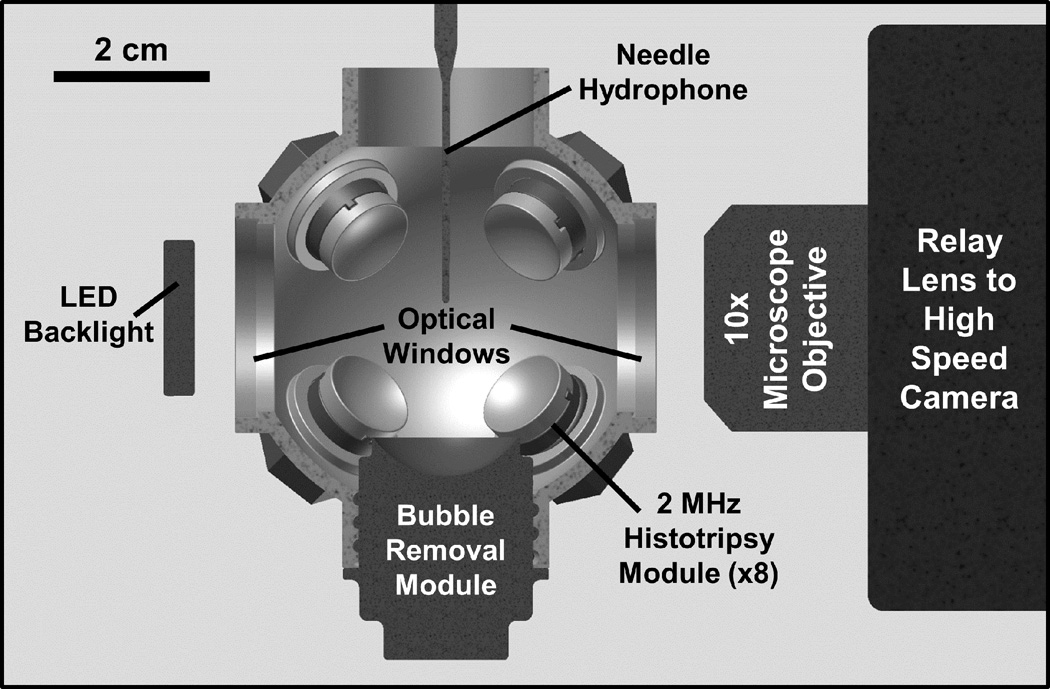
Fig. 1.
Half-section view of the experimental setup used to study effects of sonication frequency on the bubble removal process. Primary cavitation was initiated by an array of eight 2 MHz histotripsy modules arranged in a spherical pattern, while bubble removal pulses were delivered from a separate bubble removal module (0.5, 1, or 2 MHz) aligned at a predetermined offset relative to the histotripsy focus (see text). All transducer modules were held within an Accura 60 plastic scaffold that also served as the water tank for the experiments. Optical windows in the front and rear of the scaffold permitted the use of backlit high speed photography to monitor the bubble removal process. A needle hydrophone positioned adjacent to the histotripsy focus, at an offset 2 mm distal relative to the bubble removal module, was used to measure the transmission of interrogation pulses propagating through the field.
A 2 MHz histotripsy transducer constructed in-house was used to initiate primary cavitation activity (a cavitational bubble cloud). It consisted of eight PZT-4 disc elements (Steiner & Martins Inc., Miami, FL), measuring 10 mm in diameter and 1 mm in thickness. Water-tight modules designed to hold individual elements were fabricated from Accura 60 plastic (3D Systems Inc., Rock Hill, SC) using a stereolithography machine. The front face of each module contained an Accura 60 acoustic lens with a focal length of 20 mm; PZT-4 elements were matched to this lens using an epoxy (1C-LV Hysol, Loctite Corporation, Rocky Hill, CT) filled 100 mesh copper screen (McMaster-Carr, Aurora, OH) to achieve the proper thickness and impedance. The eight individual histotripsy modules were aligned confocally in a spherical arrangement using a plastic scaffold, also fabricated via stereolithography from Accura 60. This scaffold doubled as the water tank for the experiments, and had optical windows in the front and rear to permit the use of backlit high speed photography. The spherical geometry of this transducer produced a highly confined focal zone conducive to the high optical magnification required to resolve remnant bubble nuclei, with the −6-dB beamwidths measuring approximately 500 µm in both the lateral and axial dimensions. These measurements were conducted at a pressure amplitude of 6 MPa (linear regime) using a fiber optic hydrophone with a 100 µm diameter sensing tip [33]. The histotripsy transducer was driven using a pulse amplifier developed in our lab, which was designed to produce very short intense bursts. More details regarding the acoustic output generated by this setup are provided in section C of the Methods.
A separate set of transducers—which we collectively refer to as the bubble removal modules—were used to sonicate residual cavitation nuclei produced by collapse of the histotripsy bubble cloud. Similar to the histotripsy modules, these transducers were constructed in-house using a stereolithography-fabricated Accura 60 housing and acoustic lens. To test the effect of frequency on the bubble removal process, three distinct module designs were utilized, which included those with center frequencies of 0.5, 1, and 2 MHz. All bubble removal modules were constructed using Pz36 disc elements (Ferroperm Piezoceramics A/S, Kvistgaard, Denmark). For a given module, the front face of the Pz36 element was mated directly to the Accura 60 acoustic lens using epoxy adhesive (Hysol E-120 HP, Loctite Corporation, Rocky Hill, CT); a copper screen matching layer was not utilized in these cases due to the low acoustic impedance of Pz36 (specified at 14 MRayl by the manufacturer). The 0.5 MHz bubble removal module was constructed from two 1 MHz Pz36 disc elements measuring 20 mm in diameter and 1.6 mm in thickness, which were stacked and driven in unison to produce a 0.5 MHz equivalent source. The 1 MHz bubble removal module was constructed from a single 1 MHz Pz36 disc element, also measuring 20 mm in diameter and 1.6 mm in thickness. Lastly, the 2 MHz bubble removal module was constructed from a single 2 MHz Pz36 disc element, measuring 10.2 mm in diameter and 0.8 mm in thickness. For a given experiment, the bubble removal module of interest was held within the same spherical scaffold used to position the histotripsy modules (Fig. 1). All bubble removal modules were driven using a sinusoid at their respective center frequency from an ENI AP400B controllable power amplifier (Electronic Navigation Industries Inc., Rochester, NY); further details on the acoustic outputs are presented in the subsequent sections.
B. Bubble Removal Module Design
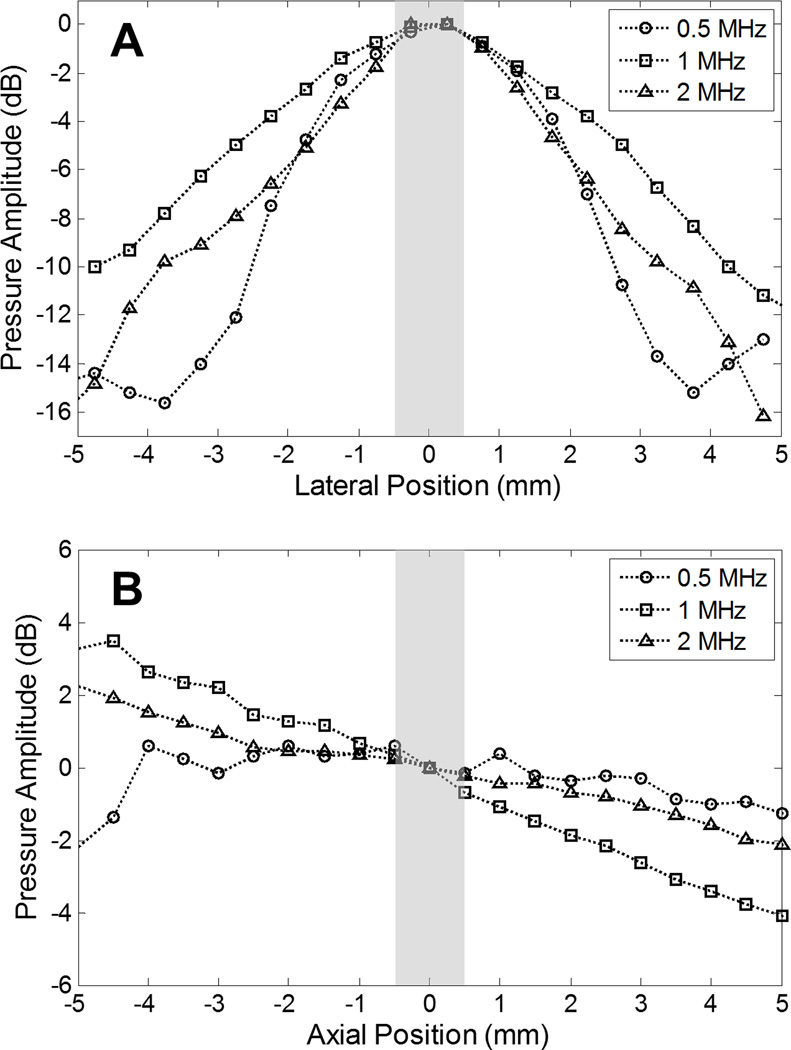
To investigate the consequences of sonication frequency on the bubble removal process, it is desirable to keep all other exposure conditions constant. This includes the dimensions of the acoustic field produced by a given bubble removal module, as the pressure gradients strongly influence the behavior of acoustically driven bubbles. For this reason we took care to ensure that the acoustic field dimensions produced by each respective bubble removal module were as similar as possible in the vicinity in which the residual bubble nuclei were produced (i.e., the histotripsy focus). This design process was conducted using a Fast Object-Oriented C++ Ultrasound Simulator (FOCUS, developed by McGough, et al. [34–37]), which is a cross-platform freeware that consists of a Matlab (MathWorks Inc., Natick, MA) user interface and object-oriented C++ computation core. Linear transient simulations were performed to predict the field dimensions generated by a particular set of module parameters. These included the source’s center frequency, size, acoustic lens power, and offset relative to the histotripsy transducer focus. The ultimate parameter sets implemented for the three bubble removal modules characterized in this study are as follows: (1) 0.5 MHz source measuring 20 mm in diameter, mated to an acoustic lens with a 25 mm focal length and offset a distance of 18 mm from the histotripsy transducer focus; (2) 1 MHz source measuring 20 mm in diameter, mated to an acoustic lens with a 25 mm focal length and offset 35 mm from the histotripsy transducer focus; (3) 2 MHz source measuring 10.2 mm in diameter, mated to an acoustic lens with a 20 mm focal length and offset 35 mm from the histotripsy transducer focus. The lateral and axial beam profiles generated by these bubble removal modules are displayed in Fig. 2, measured using an HNR-0500 needle hydrophone (Onda Corporation, Sunnyvale, CA) at a pressure amplitude of 500 kPa for each. As specified by the manufacturer, this hydrophone has a measurement uncertainty of 1.5 dB in the frequency range 0.5 – 1 MHz and 1 dB in the frequency range 1 – 15 MHz. In the lateral dimension, the −6-dB beamwidths measured on the pressure amplitude were found to be 4.1 mm, 6.2 mm, and 4.2 mm for the 0.5, 1, and 2 MHz modules, respectively. Corresponding values in the axial dimension were observed to exceed 8 mm in all cases. It should be noted, however, that the population of residual bubble nuclei generated by the histotripsy transducer was empirically observed to reside within a zone measuring approximately 1 × 1 × 1 mm centered at the histotripsy transducer focus. This region is represented by the gray bars included in Fig. 2, and it can be seen that the acoustic field dimensions produced by the three bubble removal modules used in this study are extremely similar over this zone of interest.
Fig. 2.
Bubble removal module field scans performed in the (A) lateral and (B) axial dimensions using an HNR-0500 needle hydrophone. Position 0 corresponds to the point of overlap with the histotripsy transducer focus. In all cases, the pressures are normalized to their respective values at this location. Gray bars represent the region over which residual bubble nuclei generated by the histotripsy transducer generally occur, empirically observed to be an approximate 1 × 1 × 1 mm volume centered at the histotripsy transducer focus. The field dimensions of the bubble removal modules are quite consistent over this region of interest.
C. Acoustic Pulse Sequence
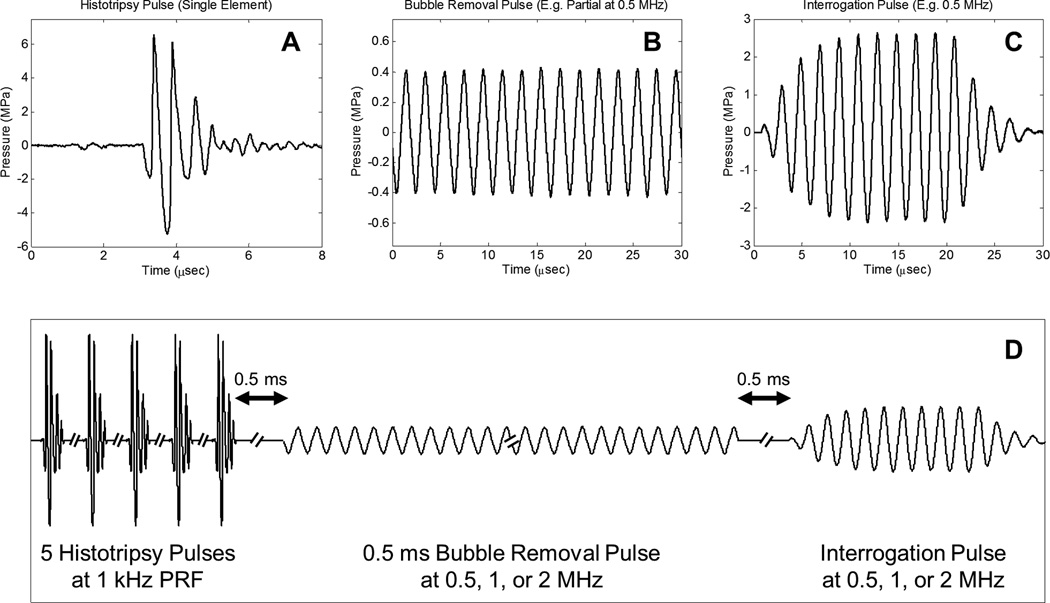
Consistent with our previous work [23], three general types of acoustic pulses were utilized in this study, as represented in Fig. 3(a) – Fig. 3(c): (1) Histotripsy pulses generated by the 2 MHz histotripsy transducer were used to initiate cavitation activity in the form of a cavitational bubble cloud; (2) Bubble removal pulses produced by the bubble removal modules (0.5, 1, or 2 MHz) were used to sonicate residual bubble nuclei following primary cavitation collapse, stimulating their coalescence and removal from the field; (3) An interrogation pulse, also delivered from the bubble removal module utilized in a given experiment, was used to probe the field for the presence of residual nuclei following bubble removal. The function of this interrogation pulse was twofold. Firstly, it caused remaining microscopic nuclei to expand and be more easily detected via high speed imaging. Secondly, it provided a measure of the acoustic ramifications of bubble nuclei remaining in the field, as its transmission was measured by the needle hydrophone positioned just distal to the histotripsy focus (Fig. 1). The overall timing of this pulse scheme is summarized in Fig. 3(d), with specifics provided henceforth.
Fig. 3.
General pulse scheme used to study the effect of sonication frequency on the bubble removal process. A. Representative waveform acquired from a single 2 MHz histotripsy module; the histotripsy pulse amplitude at the focal location can be estimated as the linear sum of the waveforms from all eight histotripsy modules, suggesting a focal peak negative pressure of approximately 40 MPa. B. Example segment of a 0.5 ms bubble removal pulse at 0.5 MHz; bubble removal pulses with center frequencies of 0.5, 1, and 2 MHz were investigated, while the amplitude was varied from 0 to approximately 2 MPa at a given frequency. C. Example interrogation pulse at 0.5 MHz; interrogation pulses were generated by the bubble removal module utilized in a given experiment and had a constant duration of 10 cycles, while the amplitude was frequency-dependent (see text). D. Overall timing of experimental pulse scheme.
The initiation of primary cavitation activity in this study was achieved using a train of five histotripsy pulses delivered at a pulse repetition frequency (PRF) of 1 kHz. Histotripsy pulses were very short (approximately 2 µs) and intense. The acoustic output from a single histotripsy module is displayed in Fig. 3(a), measured using the same fiber optic hydrophone used to perform histotripsy field scans. Due to the sparse and spherical distribution of the modules that compose the histotripsy transducer, there is minimal superposition of individual waveforms until they reach the geometric focal location; as such, we estimate the output of the histotripsy transducer as the linear sum of the outputs from the eight individual modules [38]—suggesting a peak negative pressure of approximately 40 MPa. This overall output exceeds the intrinsic cavitation threshold in water [38], permitting the histotripsy transducer to initiate a cavitational bubble cloud with each pulse. A train of five histotripsy pulses in rapid succession was utilized to maximize the extent of cavitation. Similar to the bubble proliferation phenomenon observed in SWL [11, 12], this arrangement of histotripsy pulses was empirically determined to enhance cavitation activity as residual daughter bubbles persisting between pulses seeded additional sites for cavitation inception.
Following collapse of the final histotripsy-induced bubble cloud, residual cavitation nuclei were sonicated with a 0.5 ms long bubble removal pulse at a given frequency (0.5, 1, or 2 MHz) to stimulate their removal from the field via bubble coalescence. A partial segment of a representative bubble removal pulse at 0.5 MHz is displayed in Fig. 3(b), acquired using the same HNR-0500 needle hydrophone used to perform bubble removal module field scans. All bubble removal pulses were applied at a delay of 0.5 ms following the final histotripsy pulse, which allowed the histotripsy bubble cloud to collapse and produce residual nuclei in an unimpeded manner. To investigate the influence of acoustic pulse amplitude on the bubble removal process at a given frequency, bubble removal pulses with mechanical indices (MIs) ranging from 0 to approximately 1.5 were tested. Specifically, bubble removal pulses at 0.5 MHz were applied at amplitudes of 0, 80, 150, 230, 310, 400, 570, 750, and 1100 kPa. Those at 1 MHz were applied at amplitudes of 0, 80, 210, 280, 360, 430, 660, 890, 1300, 1600, and 1900 kPa. Finally, bubble removal pulses at 2 MHz were applied at amplitudes of 0, 100, 160, 220, 290, 430, 570, 790, 1100, 1300, 1700, 2100, and 2400 kPa. As the bubble removal pulses were observed to have some amplitude variation across their 0.5 ms duration (~10%), these reported values represent the mean amplitude over all cycles composing the pulse.
The presence of residual nuclei remaining in the field following the bubble removal pulse was probed for using a second, much shorter, pulse from the bubble removal module, which we denote as the interrogation pulse. Because the microscopic remnant bubble nuclei of interest in this study are likely on the order of the of the 1.3 µm theoretical resolution limit of our optical setup, they can be difficult to detect and quantify; furthermore, they may fall out of the depth of field imaging plane (estimated at 18 µm). For these reasons the interrogation pulse was used to expand any bubble nuclei remaining in the field such that they could be more easily detected via high speed imaging. The interrogation pulse also provided a measure of the acoustic consequences of residual bubbles that persist in the field, as its transmission through the volume of interest was measured by the needle hydrophone positioned just distal to the histotripsy focus (Fig. 1). Interrogation pulses propagating through the field experienced an attenuation commensurate with the extent of residual bubble nuclei remaining, providing an acoustic metric for quantifying the effectiveness of bubble removal. Fig. 3(c) displays a representative interrogation pulse waveform generated by the 0.5 MHz bubble removal module, as calibrated by the HNR-0500 needle hydrophone. For all bubble removal frequencies, a 10 cycle pulse was used to interrogate the field at 0.5 ms following the completion of bubble removal. Interrogation pulses generated by the 0.5 MHz module had peak-positive/peak-negative (P+/P−) pressures of 2.6/2.4 MPa, those generated by the 1 MHz module had P+/P− of 2.3/1.5 MPa, and those from the 2 MHz module P+/P− of 3.0/1.5 MPa. These values were selected based on the empirical observation that they yield the same baseline level of P− attenuation across frequency, as is shown in the Results section. Interrogation pulses were found not to initiate any cavitation bubbles independently (i.e., when not preceded by the generation of a population of cavitation bubble nuclei).
D. Quantification of Bubble Removal Pulse Efficacy
Two distinct metrics were utilized to quantify the efficacy of bubble removal in this study. First, the backlit area of shadow of remnant nuclei expanded by the interrogation pulse was calculated. The entire duration of each pulse sequence was imaged using high speed photography at 20 kfps, and it was empirically determined that the 110th frame in the image sequence corresponded to the time point of maximal bubble expansion induced by the interrogation pulse. This is consistent with the interrogation pulse arrival at 5.5 ms depicted in Fig. 3. The backlit area of bubble shadow in this frame was calculated for all experiments using Matlab to sum the pixels that resided below a threshold value, nominally set to 15 standard deviations from the background mean and then scaled on a per-pixel basis to account for variations in light intensity across the field of view. Secondly, the transmission of the interrogation pulse was detected by the needle hydrophone located 2 mm distal to the histotripsy transducer focus. The degree of attenuation of this received pulse is indicative of the extent of residual nuclei remaining in the field, thus providing a practical metric for the effectiveness of the bubble removal process. Interrogation pulse transmission was quantified using the transmitted peak-negative pressure, based on the observation that this metric displays a uniform baseline attenuation across the frequency range investigated (see Results). For each frequency ten trials were performed at each bubble removal pulse amplitude in a randomized fashion, with a minimum rest time of one minute imposed between successive trials. All statistical analysis was performed using a Student’s t-Test with P < 0.05 considered significant.
E. Residual Bubble Nuclei Sizing
In a separate set of experiments, the size distribution of residual bubble nuclei generated by histotripsy bubble cloud collapse was investigated via optical imaging. The same setup described previously (Section A) was utilized for these experiments, with the exception of the camera and its associated optics. In this case images were acquired using a Point Grey Chameleon camera (Point Grey Research Inc., Richmond, BC, Canada), which was selected based on its smaller pixel size of 3.75 µm affording increased resolution relative to the Photron SA1.1 high speed camera used in the previous portion of this study (20 µm pixels). A 20× super-long working distance microscope objective (T Plan SLWD 20×/0.30, Nikon Instruments Inc., Melville, NY) coupled to a 200 mm macro lens (AF Micro-Nikkor 200mm f/4D IF-ED, Nikon Corporation, Tokyo, Japan) provided the optical power in this case. The theoretical resolution limit of this optical setup is 0.4 µm, while the theoretical depth of field is 6.7 µm. Again, the initiation of primary cavitation was generated using a train of five histotripsy pulses delivered at a PRF of 1 kHz and estimated peak negative pressure of 40 MPa. In this case no bubble removal or interrogation pulses were applied, and a single image of the remnant bubble nuclei was exposed for 2 µs at a delay of 0.5 ms following the final histotripsy pulse. This sequence was repeated 1000 times with a delay of 10 seconds imposed between successive trials to allow for complete dissolution of remnant bubbles. Resulting images were processed in Matlab using the native function ‘imfindcircles’ to detect and size bubbles that were in focus.
RESULTS
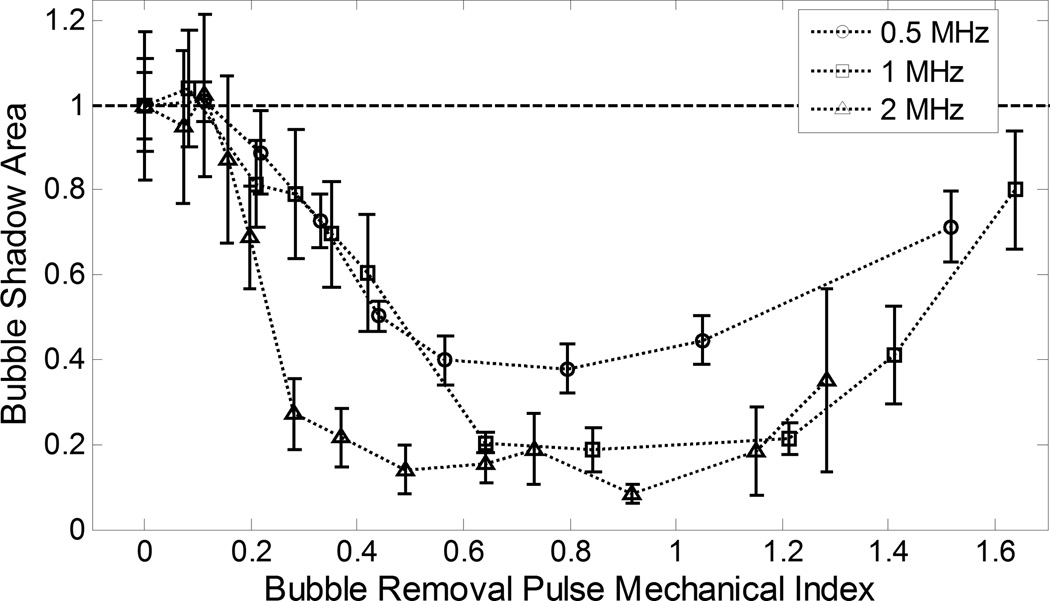
The backlit area of shadow from bubbles expanded by the interrogation pulse is displayed in Fig. 4, while transmission of interrogation pulse peak-negative pressure is shown in Fig. 5. Data in each of these plots has been normalized to its respective baseline case. For the backlit area of bubble shadow, this baseline is defined as the interrogated bubble shadow area when the bubble removal pulse amplitude is set to 0 (i.e., when no removal of residual nuclei is stimulated). For interrogation pulse transmission, the baseline is defined as the transmitted peak-negative pressure when the histotripsy pulse amplitude is set to 0 (i.e., when no cavitation bubbles are generated prior to interrogation). In this way, when bubble removal pulses eliminate residual nuclei from the field, it produces a decrease in the interrogated bubble shadow area relative to its baseline value; correspondingly, attenuation of the interrogation pulse is relieved and transmission recovers toward its respective baseline.
Fig. 4.
Backlit area of shadow (mean ± SD, n = 10) from bubbles expanded by the interrogation pulse. Data at all frequencies has been normalized to its corresponding baseline value (bubble removal pulse amplitude set to 0). When evaluated as a function of MI, three distinct regimes of behavior are apparent across all frequencies tested (with provided cutoffs being approximate values): (1) MI < 0.2: Minimal bubble coalescence is observed and bubble shadow area does not deviate significantly from its baseline value; (2) 0.2 < MI < 1: Bubble coalescence becomes more pronounced with increasing MI, and bubble shadow area decreases and trends toward a minimum; (3) MI > 1: Bubble coalescence is compromised as removal pulses incite violent cavitation and bubble shadow area increases.
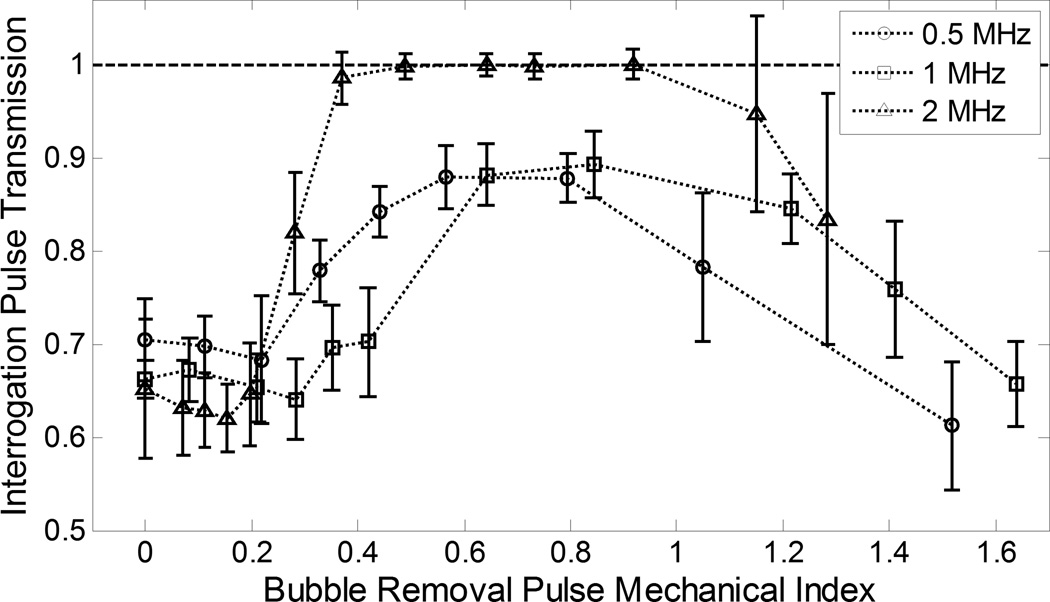
Fig. 5.
Transmission of interrogation pulse peak-negative pressure (mean ± SD, n = 10). Data at all frequencies has been normalized to its corresponding baseline value (histotripsy pulse amplitude set to 0—i.e., no cavitation bubbles generated prior to interrogation). When evaluated as a function of MI, three distinct regimes of behavior are apparent across all frequencies tested (with provided cutoffs being approximate values): (1) MI < 0.2: Minimal bubble coalescence is observed and interrogation pulse transmission does not deviate significantly from its baseline value; (2) 0.2 < MI < 1: Bubble coalescence becomes more pronounced with increasing MI, and interrogation pulse transmission increases and trends toward a maximum; (3) MI > 1: Bubble coalescence is compromised as removal pulses incite violent cavitation and interrogation pulse transmission decreases.
Collapse of the final histotripsy bubble cloud was observed to produce an extensive set of microscopic residual bubble nuclei. Based on our optical sizing experiment, bubbles in this population fell within a size distribution of 5.6 ± 1.1 µm diameter (mean ± SD). With the bubble removal pulse amplitude set to 0, these residual nuclei persisted over the entirety of the 0.5 ms bubble removal pulse duration, gradually dispersing with time within an approximate 1 × 1 × 1 mm volume centered at the histotripsy transducer focus. Propagation of the interrogation pulse through this population of residual bubbles produced pronounced attenuation of the waveform, with peak-negative pressure transmission from the 0.5, 1, and 2 MHz modules measured at 0.70 ± 0.04, 0.6µ± 0.02, and 0.65 ± 0.03 relative to their baseline values, respectively.
Increasing the bubble removal pulse amplitude from 0 resulted in three distinct regimes of residual nuclei behavior, consistent with our previous observations at the single sonication frequency of 500 kHz [23]. When evaluated as a function of bubble removal pulse mechanical index (MI), these regimes are markedly consistent across the 0.5 – 2 MHz frequency range investigated in this study. More specifically, at a given bubble removal sonication frequency the following general behavior is observed (with provided cutoffs being approximate values): (1) MI < 0.2: Minimal bubble coalescence with some dispersion of residual nuclei stimulated; (2) 0.2 < MI < 1.0: The aggregation and subsequent coalescence of residual nuclei becomes more pronounced with increasing MI, reaching an optimum in the vicinity of MI = 0.8; (3) MI > 1.0: The efficacy of bubble coalescence is compromised as bubble removal pulses induce high magnitude inertial cavitation, the collapse of which produces additional residual daughter nuclei. The results of optical high speed imaging documenting this behavior for bubble removal pulses at 500 kHz can be found in our previous publication on the topic [23]. Bubbles were not observed to translate out of the field of view under any circumstances.
At MIs of approximately 0.2 and below, minimal bubble coalescence was observed on high speed imaging; rather, these ultra-low bubble removal intensities stimulated a minimal degree of translation of the residual nuclei within the bubble removal focal volume. Correspondingly, bubble removal pulses applied at MI < 0.2 did not produce a statistically significant variation in interrogated bubble shadow area (Fig. 4) relative to the respective baseline cases in which the bubble removal amplitude was set to 0 (t-test, P > 0.16). An analogous result was observed for interrogation pulse transmission in this range (Fig. 5), with values found not to deviate from that produced with the bubble removal pulse set to 0 at each respective frequency (t-test, P > 0.13).
Bubble removal pulses with MIs ranging from approximately 0.2 to 1 stimulated the aggregation and subsequent coalescence of residual nuclei, the extent of which was observed to increase with increasing MI over this range. A corresponding decrease in interrogated bubble shadow area (Fig. 4) was generated relative to baseline for each bubble removal frequency when MI ≥ 0.2 (t-test, P < 0.02), with this decrease becoming more pronounced and trending toward a minimum value as the bubble removal pulse MI was increased. Interrogation pulse transmission (Fig. 5) showed an analogous trend, as pulse attenuation was lessened and transmission observed to increase for all frequencies relative to their respective values when bubble removal was set to 0. For 0.5, 1, and 2 MHz, statistically significant increases in transmission were observed above MIs of 0.22, 0.28, and 0.20, respectively (t-test, P < 0.04). The extent of this increase became more pronounced with increasing bubble removal pulse MI, ultimately reaching a maximum for each given frequency. The extrema observed for both the bubble shadow area and interrogation pulse transmission metrics displayed distinct characteristics based on bubble removal pulse frequency. In each case, bubble removal pulses applied at 2 MHz trended toward the extremum more rapidly in comparison to 0.5 or 1 MHz, with the value of this extremum being more pronounced. With respect to bubble shadow area, bubble removal at 2 MHz generated a rapid decrease, falling to a normalized value of 0.27 ± 0.08 by MI = 0.28. Further increases in MI within this range produced moderate reductions in bubble shadow area below this level, with the absolute minimum having a value of 0.08 ± 0.02 at an MI of 0.92. Minimums in bubble shadow area generated by 0.5 and 1 MHz bubble removal pulses had normalized values of 0.38 ± 0.06 and 0.19 ± 0.05, respectively. The minimum at 0.5 MHz fell within the range 0.57 ≤ MI ≤ 0.80 (t-test, P > 0.47), while that for 1 MHz occurred in the vicinity 0.64 ≤ MI ≤ 1.21 (t-test, P > 0.23). Interrogation pulse transmission in the 2 MHz case fully recovered to its baseline value by MI = 0.37, maintaining this level through MI = 0.92 (t-test, P > 0.12). Interrogation pulse transmissions at 0.5 and 1 MHz were never observed to fully recover to their respective baselines, reaching peak values of 0.88 ± 0.03 and 0.89 ± 0.04, respectively. At 0.5 MHz this transmission maximum was maintained over the range 0.57 ≤ MI ≤ 0.80 (t-test, P > 0.90), while the corresponding range at 1 MHz was 0.64 ≤ MI ≤ 0.84 (t-test, P > 0.49). Optical observation via high speed imaging corroborated these trends in the bubble shadow area and interrogation pulse transmission metrics, with bubble removal pulses delivered at a given intermediate MI value observed to produce more complete consolidation of residual nuclei at 2 MHz relative to that produced at 0.5 or 1 MHz
Bubble removal pulses with MIs exceeding approximately 1 showed a decrease in the efficacy of the bubble coalescence process with increasing MI. High speed imaging indicated that, while pulses in this range continued to stimulate the aggregation of nuclei, coalescence was compromised as a result of residual nuclei undergoing high magnitude inertial cavitation—the collapse of which produced additional residual daughter bubbles. Measurements of interrogated bubble shadow area (Fig. 4) show a corresponding increase in this range. At 0.5 and 2 MHz, all bubble removal pulses tested with MI > 1 produced an increase in bubble shadow area relative to the respective minimum values observed at intermediate amplitude (t-test, P < 0.02). At 1 MHz, the minimum in bubble shadow area persists to a slightly higher MI of 1.21, with bubble removal pulses applied above this value producing an increase in area consistent with the other frequencies tested (t-test, P < 0.001). Compromised bubble coalescence at high MI generated an analogous trend in interrogation pulse transmission (Fig. 5), with all bubble removal pulses of MI > 1 producing a reduction in transmission relative to their respective maximums observed at intermediate amplitudes. This reduction was statistically significant in all cases (t-test, P < 0.01), with the exception of 2 MHz bubble removal at an MI of 1.15 (t-test, P = 0.12). The large error bars in this later case are a result of the fact that residual nuclei were more prone to being displaced large distances (i.e., out of the path of attenuation measured by the hydrophone) at the high pressures required to achieve an MI > 1 at this highest frequency.
DISCUSSION
This study further develops a unique strategy for mitigating the effects of residual bubble nuclei produced by cavitation collapse, using low-amplitude acoustic bursts to stimulate their removal from the field via bubble coalescence. Expanding upon our preliminary work [23], here we investigated the implications of bubble removal pulse frequency on the nuclei consolidation process. It was found that all tested frequencies (0.5 – 2 MHz) were capable of stimulating the coalescence of remnant nuclei, with markedly similar trends emerging when the process is evaluated as a function of bubble removal pulse MI. The major distinction came for bubble removal pulses applied at the highest tested frequency of 2 MHz, which were observed to stimulate the most effective coalescence of residual nuclei. This is evidenced by both the backlit area of shadow (Fig. 4) and interrogation pulse transmission (Fig. 5) metrics, and corroborated by direct optical observation of the bubble coalescence process via high speed photography.
In our previous work we hypothesized that the primary and secondary Bjerknes forces are the major facilitators of the bubble coalescence process, with the secondary force being the dominant contributor [23]. Briefly, when a bubble is driven in an acoustic field it will experience a force generated by the field itself (the primary Bjerknes force), as well as a force generated by adjacent oscillating bubbles (the secondary Bjerknes force) [24–29, 39–41]. The magnitude and direction of the primary Bjerknes force is dependent upon the phase of oscillation of the bubble relative to that of the acoustic field—which we denote as θs—while the magnitude and direction of the secondary Bjerknes force is dependent upon the phase of oscillation of two bubbles relative to one another—denoted as θb (where θb = θs2 – θs1). When evaluated as a function of equilibrium bubble size θs displays a sigmoidal-shaped dependence, with the extreme cases of bubbles being much smaller or much larger than resonant size corresponding to phase differences θs of 0 or π, respectively. This result can be obtained from the equations of motion when a bubble is modeled as a damped forced oscillator [28, 42].
It is an informative exercise to examine the theoretical behavior of residual bubble nuclei in this study in the framework provided by Bjerknes theory. Based on the Minnaert formula [43], the 0.5, 1, and 2 MHz bubble removal pulses evaluated here correspond to resonant bubble diameters of 12, 6, and 3 µm, respectively. The equilibrium diameter of the remnant bubble nuclei produced by the histotripsy transducer was optically sized to fall within a distribution measuring 5.6 ± 1.1 µm (mean ± SD). As such, at the lowest tested bubble removal pulse frequency of 0.5 MHz (12 µm resonant diameter) we would expect the residual nuclei to be smaller than the resonant size of the sonication frequency. This manifests in a phase difference of oscillation relative to the sound field of 0 ≤ θs < π/2, inducing their migration up the pressure gradient and congregation at antinodes [28, 44]. Furthermore, because the size distribution of nuclei is relatively tight—residing entirely to one side of resonance—we expect the phase difference of oscillation between adjacent bubbles to fall within the range 0 ≤ | θb | < π/2 such that the secondary Bjerknes force is attractive [24, 28, 29]. Conversely, at the highest tested bubble removal pulse frequency of 2 MHz (3 µm resonant diameter) residual nuclei should be larger than resonant size. Thus, we expect a phase difference of oscillation relative to the sound field of π/2 < θs ≤ π, promoting their migration down the pressure gradient and congregation at nodes [28, 44]. Because the size distribution of nuclei is again relatively tight and resides to one side of resonance, we expect the phase difference of oscillation of adjacent bubbles to fall within the range 0 ≤ | θb | < π/2 such that the secondary Bjerknes force remains attractive. Lastly, at the intermediate bubble removal pulse frequency of 1 MHz the size distribution of remnant bubble nuclei is likely to be bisected by the 6 µm equilibrium diameter corresponding to resonance. As such, migration both up and down the pressure gradient could be expected as a result of the primary Bjerknes force, while all nuclei remain in a tight size distribution such that 0 ≤ | θb | < π/2 and an attractive secondary Bjerknes force develops.
The observed behavior of residual nuclei in this study gives further support to the theory that the secondary Bjerknes force is the dominant facilitator of the bubble consolidation process [23]. While the primary Bjerknes force is likely a contributor to the initial aggregation of nuclei at the lowest tested frequency of 0.5 MHz, its effect on consolidation is potentially counterproductive at the higher frequencies investigated in this study. Furthermore, as residual nuclei coalesce, the average equilibrium diameter of bubbles present in the field will increase. This is likely to further diminish any positive aggregative effects generated by the primary force, as bubbles further exceed resonant size and are subject to a force oriented down the pressure gradient away from the axis of consolidation. Nevertheless, pronounced aggregation and coalescence of residual nuclei was observed for all frequencies tested, implying that the secondary Bjerknes force is the major contributor to the process. The fact that bubble consolidation did not become pronounced until intermediate MIs is also consistent with this theory, as previous studies have demonstrated that the secondary Bjerknes force increases with intensity more significantly than the primary [45–47]. Finally, the dominance of the secondary Bjerknes force provides an explanation as to why the highest tested bubble removal frequency of 2 MHz generates the most effective nuclei coalescence. When residual bubble nuclei begin to coalesce and their average equilibrium diameter increases beyond the initial measured value, the resulting bubble size population will reside the farthest from resonance when sonicated at 2 MHz (relative to the other frequencies tested). As such, the phase difference of oscillation (θb) of bubbles within the population will be the smallest for this highest frequency, leading to a more pronounced secondary Bjerknes force (which has a dependence on cos(θb) [28]).
Our future work will include the development of a mathematical simulation to verify both the relative contributions of the Bjerknes forces and the implications of bubble removal pulse frequency. Based on the empirical results presented here, we expect higher bubble removal frequencies to generate the most effective nuclei consolidation for remnant bubbles of this size. It remains to be seen if ultrasound therapy sources of different frequencies (be it histotripsy or SWL) generate remnant cavitation nuclei of varying mean size, and this will be an important consideration in determining the optimal bubble removal frequency for a given application. Furthermore, as it will be desirable for the bubble removal sound field to encompass the entire population of residual bubble nuclei, there will be practical tradeoffs between the bubble removal sonication frequency and the resulting focal dimensions. One important point in this regard is the fact that—while this study aimed to investigate the bubble removal mechanism in a simplified environment—application of this process in-vivo is likely to be more complex with tissue structures influencing the distribution and mobility of remnant bubbles. The porosity of tissue with respect to these micron-sized bubbles is currently unknown. However, we expect this approach to translate directly to the fluid-filled space of the kidney’s collecting system in which renal stones typically reside. Our future work will aim to address these questions through the use of simulation and continued experimentation, with the end goal of producing an optimized bubble removal process that stands to augment cavitationally based ultrasound therapies such as histotripsy and SWL.
CONCLUSION
In this work we further developed a novel strategy for mitigating the effects of residual bubble nuclei produced by cavitation collapse, exploring the implications of bubble removal pulse frequency on the nuclei consolidation process. It was found that, when evaluated as a function of bubble removal pulse MI, the efficacy of bubble removal shows markedly similar trends across the frequency range tested (0.5 – 2 MHz). At low bubble removal pulse MIs (approximately MI < 0.2) minimal effect was produced, at intermediate MIs (approximately 0.2 < MI < 1) pronounced aggregation and coalescence of residual nuclei was generated, and at high MI (approximately MI > 1) residual cavitation nuclei were re-excited and the coalescence process was compromised. The main distinction in these trends was the fact that, at a given intermediate bubble removal pulse MI, the highest tested frequency of 2 MHz generated the most effective consolidation of remnant nuclei. We attribute this result to the likelihood that the secondary Bjerknes force is the major facilitator of the consolidation process, and plan to further investigate the phenomenon with the aid of mathematical simulation. It is our hope that these efforts will result in an adjunct for cavitationally based ultrasound therapies such as histotripsy and SWL, enhancing efficiencies that are currently limited by the effects of residual cavitation bubbles.
Supplementary Material
ACKNOWLEDGMENTS
Research reported in this publication was supported by The National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health under award number R01DK091267. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
DISCOLOSURE
C.A. Cain, W.W. Roberts, and T.L. Hall have financial interests and/or other relationships with HistoSonics, Inc., which has licensed intellectual property related to this manuscript.
REFERENCES
- 1.Pishchalnikov YA, Sapozhnikov OA, Bailey MR, Pishchalnikova IV, Williams JC, McAteer JA. Cavitation selectively reduces the negative-pressure phase of lithotripter shock pulses. Acoust Res Lett Online. 2005 Nov 3;6:280–286. doi: 10.1121/1.2127115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pishchalnikov YA, McAteer JA, Williams JC, Jr, Pishchalnikova IV, Vonderhaar RJ. Why stones break better at slow shockwave rates than at fast rates: in vitro study with a research electrohydraulic lithotripter. J Endourol. 2006 Aug;20:537–541. doi: 10.1089/end.2006.20.537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pishchalnikov YA, McAteer JA, Bailey MR, Pishchalnikova IV, Williams JC, Evan AP. Acoustic shielding by cavitation bubbles in shock wave lithotripsy (SWL); 17th International Symposium on Nonlinear Acoustics; 2005. pp. 319–322. [Google Scholar]
- 4.Pishchalnikov YA, McAteer JA, Williams JC., Jr Effect of firing rate on the performance of shock wave lithotriptors. BJU Int. 2008 Dec;102:1681–1686. doi: 10.1111/j.1464-410X.2008.07896.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lautz J, Sankin G, Zhong P. Turbulent water coupling in shock wave lithotripsy. Phys Med Biol. 2013 Feb 7;58:735–748. doi: 10.1088/0031-9155/58/3/735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wiksell H, Kinn AC. Implications of cavitation phenomena for shot intervals in extracorporeal shock wave lithotripsy. Br J Urol. 1995 Jun;75:720–723. doi: 10.1111/j.1464-410x.1995.tb07378.x. [DOI] [PubMed] [Google Scholar]
- 7.Wang TY, Xu Z, Hall TL, Fowlkes JB, Cain CA. An efficient treatment strategy for histotripsy by removing cavitation memory. Ultrasound Med Biol. 2012 May;38:753–766. doi: 10.1016/j.ultrasmedbio.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mettin R, Akhatov I, Parlitz U, Ohl CD, Lauterborn W. Bjerknes forces between small cavitation bubbles in a strong acoustic field. Physical Review E. 1997 Jan 09;56:2924–2931. [Google Scholar]
- 9.Flynn HG, Church CC. A mechanism for the generation of cavitation maxima by pulsed ultrasound. J Acoust Soc Am. 1984 Aug;76:505–512. doi: 10.1121/1.391592. [DOI] [PubMed] [Google Scholar]
- 10.Brennen CE. Fission of collapsing cavitation bubbles. Journal of Fluid Mechanics. 2002;472:153–166. [Google Scholar]
- 11.Pishchalnikov YA, McAteer JA, Pishchalnikova IV, Williams JC, Bailey MR, Sapozhnikov OA. Bubble proliferation in shock wave lithotripsy occurs during inertial collapse," in; 18th International Symposium on Nonlinear Acoustics; 2008. pp. 460–463. [Google Scholar]
- 12.Pishchalnikov YA, Williams JC, McAteer JA. Bubble proliferation in the cavitation field of a shock wave lithotripter. J Acoust Soc Am. 2011 Aug;130:EL87–EL93. doi: 10.1121/1.3609920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xu Z, Hall TL, Fowlkes JB, Cain CA. Optical and acoustic monitoring of bubble cloud dynamics at a tissue-fluid interface in ultrasound tissue erosion. The Journal of the Acoustical Society of America. 2007;121:2421–2430. doi: 10.1121/1.2710079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen WS, Matula TJ, Crum LA. The disappearance of ultrasound contrast bubbles: observations of bubble dissolution and cavitation nucleation. Ultrasound Med Biol. 2002 Jun;28:793–803. doi: 10.1016/s0301-5629(02)00517-3. [DOI] [PubMed] [Google Scholar]
- 15.Huber P, Jochle K, Debus J. Influence of shock wave pressure amplitude and pulse repetition frequency on the lifespan, size and number of transient cavities in the field of an electromagnetic lithotripter. Phys Med Biol. 1998 Oct;43:3113–3128. doi: 10.1088/0031-9155/43/10/029. [DOI] [PubMed] [Google Scholar]
- 16.Epstein PS, Plesset MS. On the stability of gas bubbles in liquid-gas solutions. The Journal of Chemical Physics. 1950;18:1505–1509. [Google Scholar]
- 17.Fowlkes JB, Crum LA. Cavitation threshold measurements for microsecond length pulses of ultrasound. The Journal of the Acoustical Society of America. 1988;83:2190–2201. doi: 10.1121/1.396347. [DOI] [PubMed] [Google Scholar]
- 18.Arora M, Junge L, Ohl CD. Cavitation cluster dynamics in shock-wave lithotripsy: part 1. Free field. Ultrasound Med Biol. 2005 Jun;31:827–839. doi: 10.1016/j.ultrasmedbio.2005.02.007. [DOI] [PubMed] [Google Scholar]
- 19.Vallancien G, Munoz R, Borghi M, Veillon B, Brisset JM, Daudon M. Relationship between the frequency of piezoelectric shock waves and the quality of renal stone fragmentation. In vitro study and clinical implications. Eur Urol. 1989;16:41–44. doi: 10.1159/000471527. [DOI] [PubMed] [Google Scholar]
- 20.Greenstein A, Matzkin H. Does the rate of extracorporeal shock wave delivery affect stone fragmentation? Urology. 1999;54:430–432. doi: 10.1016/s0090-4295(99)00176-4. [DOI] [PubMed] [Google Scholar]
- 21.Weir MJ, Tariq N, Honey RJ. Shockwave frequency affects fragmentation in a kidney stone model. J Endourol. 2000 Sep;14:547–550. doi: 10.1089/08927790050152113. [DOI] [PubMed] [Google Scholar]
- 22.Paterson RF, Lifshitz DA, Lingeman JE, Evan AP, Connors BA, Fineberg NS, et al. Stone fragmentation during shock wave lithotripsy is improved by slowing the shock wave rate: studies with a new animal model. J Urol. 2002 Nov;168:2211–2215. doi: 10.1016/S0022-5347(05)64357-1. [DOI] [PubMed] [Google Scholar]
- 23.Duryea AP, Cain CA, Tamaddoni HA, Roberts WW, Hall TL. Removal of Residual Nuclei Following a Cavitation Event using Low-Amplitude Ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control. 2014 Oct;61:1619–1626. doi: 10.1109/TUFFC.2014.006316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Blake FG. Bjerknes Forces in Stationary Sound Fields. The Journal of the Acoustical Society of America. 1949;21:551–551. [Google Scholar]
- 25.Neppiras EA. Subharmonic and Other Low-Frequency Emission from Bubbles in Sound-Irradiated Liquids. The Journal of the Acoustical Society of America. 1969;46:587–601. [Google Scholar]
- 26.Crum LA, Eller AI. Motion of Bubbles in a Stationary Sound Field. The Journal of the Acoustical Society of America. 1970;48:181–189. [Google Scholar]
- 27.Crum LA. The motion of bubbles in a stationary sound field. The Journal of the Acoustical Society of America. 1969;46:1411. [Google Scholar]
- 28.Leighton TG. The Acoustic Bubble. San Diego, CA: Academic Press Inc; 1997. [Google Scholar]
- 29.Crum LA. Bjerknes forces on bubbles in a stationary sound field. The Journal of the Acoustical Society of America. 1975;57:1363–1370. [Google Scholar]
- 30.Chaigneau M, Le Moan G. On the composition of gas dissolved in human urine. C R Acad Sci Hebd Seances Acad Sci D. 1968 Nov 25;267:1893–1895. [PubMed] [Google Scholar]
- 31.Fowlkes JB, Carson PL, Chiang EH, Rubin JM. Acoustic generation of bubbles in excised canine urinary bladders. J Acoust Soc Am. 1991 Jun;89:2740–2744. doi: 10.1121/1.400713. [DOI] [PubMed] [Google Scholar]
- 32.Hwang EY, Fowlkes JB, Carson PL. Variables controlling contrast generation in a urinary bladder model. J Acoust Soc Am. 1998 Jun;103:3706–3716. doi: 10.1121/1.423070. [DOI] [PubMed] [Google Scholar]
- 33.Parsons JE, Cain CA, Fowlkes JB. Cost-effective assembly of a basic fiber-optic hydrophone for measurement of high-amplitude therapeutic ultrasound fields. J Acoust Soc Am. 2006 Mar;119:1432–1440. doi: 10.1121/1.2166708. [DOI] [PubMed] [Google Scholar]
- 34.McGough RJ, Samulski TV, Kelly JF. An efficient grid sectoring method for calculations of the near-field pressure generated by a circular piston. J Acoust Soc Am. 2004 May;115:1942–1954. doi: 10.1121/1.1687835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.McGough RJ. Rapid calculations of time-harmonic nearfield pressures produced by rectangular pistons. J Acoust Soc Am. 2004 May;115:1934–1941. doi: 10.1121/1.1694991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kelly JF, McGough RJ. A time-space decomposition method for calculating the nearfield pressure generated by a pulsed circular piston. IEEE Trans Ultrason Ferroelectr Freq Control. 2006 Jun;53:1150–1159. doi: 10.1109/tuffc.2006.1642513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chen D, McGough RJ. A 2D fast near-field method for calculating near-field pressures generated by apodized rectangular pistons. J Acoust Soc Am. 2008 Sep;124:1526–1537. doi: 10.1121/1.2950081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Maxwell AD, Cain CA, Hall TL, Fowlkes JB, Xu Z. Probability of Cavitation for Single Ultrasound Pulses Applied to Tissues and Tissue-Mimicking Materials. Ultrasound in Medicine & Biology. 2013 Mar;39:449–465. doi: 10.1016/j.ultrasmedbio.2012.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bjerknes V. Fields of Force. 1906 [Google Scholar]
- 40.Bjerknes V. Die Kraftfelder. 1909 [Google Scholar]
- 41.Kornfeld M, Suvorov L. On the destructive action of cavitation. Journal of Applied Physics. 1944;15:495–506. [Google Scholar]
- 42.Morse PM. Theoretical Acoustics. Princeton University Press; 1986. [Google Scholar]
- 43.Minnaert M. XVI. On musical air-bubbles and the sounds of running water. Philosophical Magazine Series 7. 1933 Aug 01;16:235–248. 1933. [Google Scholar]
- 44.Leighton TG, Walton AJ, Pickworth MJW. Primary Bjerknes forces. European Journal of Physics. 1990;11:47. [Google Scholar]
- 45.Hatanaka S, Yasui K, Kozuka T, Tuziuti T, Mitome H. Influence of bubble clustering on multibubble sonoluminescence. Ultrasonics. 2002 May;40:655–660. doi: 10.1016/s0041-624x(02)00193-2. [DOI] [PubMed] [Google Scholar]
- 46.Lauterborn W, Kurz T, Mettin R, Ohl CD. Experimental and theoretical bubble dynamics. Adv. Chem. Phys. 1999;110:295–380. [Google Scholar]
- 47.Mettin R, Luther S, Ohl CD, Lauterborn W. Acoustic cavitation structures and simulations by a particle model. Ultrasonics Sonochemistry. 1999;6:25–29. doi: 10.1016/s1350-4177(98)00025-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.