Fast single image haze removal via local atmospheric light veil estimation

Abstract

In this study, a novel single-image based dehazing framework is proposed to remove haze artifacts from images through local atmospheric light estimation. We use a novel strategy based on a physical model where the extreme intensity of each RGB pixel is used to define an initial atmospheric veil (local atmospheric light veil). Across bilateral filter is applied to each veil to achieve both local smoothness and edge preservation. A transmission map and a reflection component of each RGB channel are constructed from the physical atmospheric scattering model. The proposed approach avoids adverse effects caused by the error in estimating the global atmospheric light. Experimental results on outdoor hazy images demonstrate that the proposed method produces image output with satisfactory visual quality and color fidelity. Our comparative study demonstrates a higher performance of our method over several state-of-the-art methods.

1. Introduction

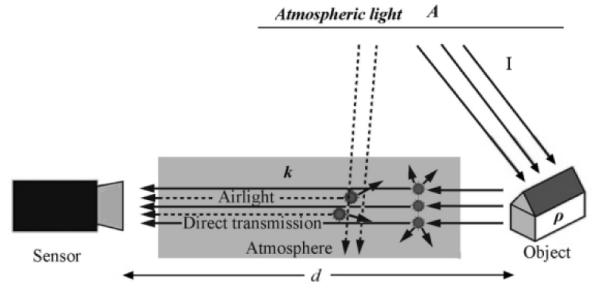
Performances of outdoor vision systems for object detection, tracking and recognition are often degraded by weather conditions, such as haze, fog or smoke. Haze is the turbid medium (e.g., particles and water droplets) in the atmosphere, which can degrade the performance of the imaging system due to atmospheric absorption and scattering. The amount of scattering depends on the depth of scene and the light irradiance received by the camera attenuated along the line of sight. As a result, the haze-related degradation is varying spatially and the incoming light is scattered in the air forming an atmospheric veil in the physical atmospheric scattering model, i.e., the ambient light is reflected into the line of sight by atmospheric particles. Consequently, the degraded image loses both contrast and color fidelity. The atmospheric scattering model is illustrated in Fig. 1.

Fig. 1.

Atmospheric scattering model.

In the past decades, research on hazy removal has received great attention. Many approaches have been proposed which have advantage of restoring a single hazy image without depending on any other source of information [1-9]. In [2], Fattal used local window-based operations and graphical models for dehazing. This method achieves reasonable results in separating uncorrelated fields, but is computationally intensive. In comparison, the method proposed by Tan in [1]does not always achieve equally good results on every saturated scene. However, this method is more generic and easier to apply to different types of images. In particular, it works on both color and grayscale images. In [31], the method of Ancuti uses a fusion-based strategy derived from two original hazy image inputs. This method first-demonstrated the utility and effectiveness of a fusion-based technique for dehazing, but the color of the restored image is often less vivid and the contrast may not be correct. Recently, an effective image prior, called the dark channel prior [4] has been proposed to remove haze from a single image. The key observation is that most local patches in outdoor haze-free images contain some pixels whose intensity are significantly lower than other pixels in at least one of the RGB color channels. The intensity of this dark channel is considered to be a rough approximation of the thickness of the haze. The algorithm proposed by Hein [4] applies a closed-form framework of matting to refine the transmission map,andthis algorithm works with color image input. Based on He’s study, the dark channel prior was employed in a number of studies for single image dehazing[14,24,26]. For example, Tripathi and Mukhopadhyay[8]proposed an efficient algorithm using anisotropic diffusion for refining transmission map based on the dark channel prior.

In [4] based on the theory of dark channel prior and atmospheric scattering model, the global atmosphere light is defined as the brightness of an infinity scene, which is an important parameter for the image restoration based on the physical atmospheric scattering model[27].The restored image is darker if the estimated global atmospheric light is stronger than it should be, and vice versa. In other words, halo or oversaturation effect will occur in the sky area if the estimated value is smaller than the true value [26]. Some experimental results with different global atmospheric light values are shown in Fig.2. Similar to [4], Xiao et al.[14] chose the brightest pixels (0.2 %) in the dark channel to improve the accuracy of the atmospheric light. However, some brightest pixels in white objects may lead to undesirable result of the global atmospheric light value. Yeh et al. [24] determined the range of atmospheric light empirically by selecting the top 0.1% brightest value in dark channel and the top 30% darkest value in the bright channel, then estimated the atmospheric light of the hazy image.

Fig. 2.

Over statured results caused by the error of global atmospheric light value.(a) Original hazy image, (b) Restored image by the method proposed in [27] with A = 162 (c) (b) Restored image with A = 152 (d) Hazy free image patches(Top: restored with global atmospheric light; Bottom: restored with proposed local atmospheric light veil).

Despite the achievements made so far, there still lacks an effective method to accurately estimate global atmospheric light[13]. To improve the efficiency of the physical model based single image restoring algorithm, and inspired by the patch-based dark channel prior, two major factors which are critical to the quality of the restored images are addressed in details in this study. Our result provides more accurate estimation of the transmission map from which color and brightness of the image can be well restored. The major contributions of this study are outlined as follows.

• 1) In order to avoid the problem caused by the error in global atmospheric light estimation, we present a strategy to define a local atmospheric light veil A(x,y) from the hazy image patches with the premise that the local illumination of the scene is the same as the local atmospheric light.

• 2) Both the local atmospheric light veil and the transmission map are calculated, and then the reflection component of the RGB channel is constructed from the atmospheric scattering model. This approach compensates the non-uniform illumination effects on images.

The rest of the paper is organized as follows: In section 2, the atmospheric scattering model, some related works and typical hazy removal algorithms are discussed in detail. Section 3 presents the proposed atmospheric scattering model based on the local atmospheric light veil. Section 4 provides a detailed description of the proposed algorithms. In Section 5, comparative experiments with both subjective and objective evaluations are described. Finally, we summarize our approach and discuss its limitations in Section6.

2. Related work and problem statement

2.1 Atmospheric scattering model

In computer vision, a widely used mathematical expression for describing the intensity L of a hazy image is established by Koschmieder[9,10,11]:

$$L(x,y)=L0(x,y)e^{-\mathit{kd}(x,y)}+A(1-e^{-\mathit{kd}(x,y)})$$ (1)

where the apparent luminance of the captured image is L(x, y), d(x, y) is the distance of the corresponding object at a scene point (x, y) from the camera, A is the global atmospheric light constant, L0(x, y) is the haze-free image, which can be defined as the scene radiance, and k denotes the extinction coefficient of the atmosphere. The relationships among these variables and parameters are shown in Fig.1.

According to the atmospheric scattering model, haze is an exponential decay, given by t(x, y) = e^{–kd(x, y)}, where t(x,y) is the transmission function. Haze reduces the visibility and contrast of the object in the scene. The second effect of haze produced by a white atmospheric veil V(x, y) = A(1–e^{–kd(x, y)}), which is an increasing function of the object distance d(x, y) .Atmospheric scattering model can be directly extended to a color image by applying the same scheme to each RGB channel, and L(x, y) can be defined as L_c(x, y), c∈[R, G, B].For the sake of conciseness, we just use L(x, y) to represent color images in this paper, and ρ(x, y) to represent the reflectance of each R,G or B channel and L₀(x, y)=I(x, y)* ρ(x, y).

In order to solve the haze-free image L0(x, y) from Eq.(1), Koschmieder’s law can be transformed as

$$L_0\phantom{)}(x,y)\phantom{(}=\frac{L(x,y)-A(1-e^{-\mathit{kd}(x,y)})}{e^{-\mathit{kd}(x,y)}}$$ (2)

According to Eq.(2), the proposed restoration algorithm contains the following steps:(1) inference of V(x) from L(x, y) based on the dark channel prior;(2)estimation of A and t(x, y) from V(x); and (3)calculation of L₀(x, y) by Eq. (2).According to the atmospheric scattering model and the dark channel prior, the lowest reflectivity in red, green or blue channel at scene point (x, y) is supposed to be close to zero, i.e. ρ(x, y)→0,then atmospheric veil V(x, y) can be constructed from Eq. (1)

$$\underset{\rho (x,y)\to 0}{L(x,y)}\to A\phantom{)}(1-e^{-\mathit{kd}(x,y)})\phantom{(}$$ (3)

Assuming d(x, y)→∞ and ρ(x, y)→0,from Eq.(3), we have

$$\underset{\rho (x,y)\to 0\&d(x,y)\to \infty }{L(x,y)}\to A$$ (4)

So, givenconstraints ρ(x, y)→0, and d(x, y)→∞, A can be estimated from Eq.(4).

Based on (3) and (4) and (1), t(x, y) and L₀(x, y) can be solved. According to the dark channel prior [4], V(x, y) can beroughly estimatedby

$$V_{\mathit{dc}}\phantom{)}(x,y)\phantom{(}=\underset{c\in \{R,G,B\}}{\min }{L}_c\phantom{)}(x,y)\phantom{(}$$ (5)

Various filtering algorithms have been developed to obtain more accurate A and V(x, y), including soft matting, cross bilateral filtering and guided filtering. The composition of the scene is usually complex, so ρ(x, y)→0 and d(x, y)→∞ cannot be both met in every point, as a result Eq.(5) only provides a severely under-constrained problem of estimation of A, and we will improve the solution based on mathematical modeling.

2.2 Problems in estimation of global atmospheric light

The global atmosphere light A is a key parameter for constructing the transmission function expressed in (3).A is a global atmosphere light value as observed in (1). If the conditions ρ(x, y)→0 and d(x, y)→∞ are both met, A can be calculated. In many single-image dehazing methods, the global atmospheric light A is usually estimated from pixels with the densest haze, for example, in[4] and [14],the brightest pixels in the dark channel were chosen, which correspond to the foggiest regions. Then A can be estimated from the brightest pixels in the chosen region as shown in Fig.2(a). However, this method depends on prerequisite d(x, y)→∞ and we are not sure whether it is true in real scenes as the patches shown in Fig.2(a).The area in the top red box is obviously the haziest area for calculating A, while the area in the bottom red box is less hazy and does not satisfy all the requirements for applying(4). To show how the value of A affects the restored image, examples of restored results are given in Fig.2(b) and Fig.2(c) by the method proposed in [27] with A = 162 and A=152. It can be seen that there are some halo effects in Fig.2(c) as discussed in Section 1.So, global atmospheric light A is a critical factor for haze removal algorithms and a small error will lead to disastrous consequences.

For the bottom patch in Fig.2(a), two restored images are shown. Top image given in Fig.2(d) is the restored image by the method proposed in [27] and it gets halo effect because the conditions in Eq.(4) cannot be met in this hazy patch. With the proposed method, we get a better restored image as the bottom one given in Fig.2(d).

Inspired by a recent research on global atmospheric light A [24], we focus on how to explain and choose A from the hazy images. In [24], Yeh et al. proposed that the density of haze in different regions of an image is different, and the value of atmospheric light for each pixel should be different accordingly. Based on the pixel-based dark channel prior and bright channel prior, they determined the pixel value $A_{\text{highest}}^c$ of the color channel C with the highest haze density in the image by selecting the pixel value corresponding to the top 0.1% brightest value in dark channel J^dark_pixel, while determining the pixel value $A_{\text{lowest}}^c$ of the color channel C with the lowest haze density in the image by selecting the pixel value corresponding to the top 30% darkest value in bright channel J^bright_pixel. In this way, the atmospheric light A(x) for the image I(x) and the transmission map can be estimated via haze density analysis and bilateral filter respectively. However, it should be noticed that the color cast effect emerges in the restored image as shown in Fig.3 (l).There are three possible reasons for the color cast. Firstly, some researchers have demonstrated that treating the atmospheric light as a constant in a given image works well as we have given in Eq.(4), and some theoretical analysis should be made to support the transform of atmospheric light from a constant to a variable. Secondly, selections of thresholds in dark and bright channels are purely empirical which cannot be fully justified theoretically, which makes the method less convincing. After all, bilateral filter may not be the best choice for refining the transmission map, which has been shown in several reports [4,14,25].

Fig. 3.

Hazy image restoration using proposed and comparative methods.

(a) Input hazy color image; (b)Preliminary atmosphere veil; (c) Opening operation on (b); (d) Cross bilateral filtering on (b)&(c); (e) Preliminary local atmosphere light veil; (f) Closing operation on (e); (g) Cross bilateral filtering on (e)&(f); (h) Transmission function; (i)Restored scene radiance by the proposed method; (j) Restored scene reflectance by the proposed method; (k) Restored result by He[4]; (l)Restored result by Yeh[24].

3. Proposed atmospheric scattering model based on local atmospheric light

As discussed in section 2, it is sometimes severely under-constrained to solve the scene radiance from the physical model given in (1).In this section, we analyze the reflectance of the scene point, and a new concept named local atmospheric light will be proposed to obtain more constraints in local regions.

The proposed method attempts to estimate the reflectance of RGB components of each point, which is determined by both the illumination and the perceived image. Illumination of one patch can be estimated as the maximum values among RGB channels (max-RGB), and then the maximal reflectance of RGB channel in this patch will be normalized to1, which is a very important hypothesis inspired by [29].The perceived color of one point is determined by the ratio of RGB reflection coefficients, so this hypothesis does not change the tone of the scene, but saturation will be increased because of the normalization. Due to the nonlinearity of the nature scene illumination, it is almost impossible to determine its reflectance for every pixel, but the max-RGB method often gives a good approximation of the reflectance characteristics of the natural scene [18,19].

In this paper, we will estimate the atmospheric light value in local patches of the image, and this process will be derived form a new point of view. As stated before, the global atmospheric light in the hazy image can be solved analytically from (3) and (4), provided that the assumptions of zero reflectivity and infinite distance are satisfied. But the major problem is that these conditions are difficult to be met, as a result, new methods with relaxed constraints are needed.

According to (1), one effect of the fog is an exponential decay of the scene radiance. Another effect is the addition of an atmospheric veil which is a function of the atmospheric light. We thus assume that the haze is uniform and heavy so that there is no direct sunlight in the scene. In this case, the global atmospheric light is equal to the illumination of the scene, and the uniform illumination of the scene at any point will be A.

With the imaging model L₀(x, y)=A_ρ(x, y),Eq.(1) can be rewritten as follows:

$$L(x,y)=A\rho (x,y)e^{-\mathit{kd}(x,y)}+A(1-e^{-\mathit{kd}(x,y)})$$ (6)

As discussed previously, the highest reflectivity among RGB components of one pixel can be approximated as ρ(x, y)→1. For the patches in a hazy image, if any high reflectivity pixel exists, the atmospheric light of patch P_i can be solved from(6)with ρ(x, y)→1.Thus, atmospheric light A of patch P_i can be estimated by

$$A_{P_i}=\underset{(x,y)\in P_i,c\in [R,G,B]}{\max }\phantom{)}(L_c\phantom{)}(x,y)\phantom{(})\phantom{(}$$ (7)

According to Eq. (7), if the hazy image is divided into small patches, then the global atmospheric light should be changed into a local property which we define as the local atmospheric light veil. The constant global atmospheric light A transforms into variable A(x, y) ,and a new physical atmospheric scattering model can be established by

$$L(x,y)=A(x,y)\rho (x,y)e^{-\mathit{kd}(x,y)}+A(x,y)(1-e^{-\mathit{kd}(x,y)})$$ (8)

The same procedures as those for Eq. (1) can used to estimate the parameters in (8).

For Eq.(6), the hypothesis is that the sky is cloudy and there is no direct sunlight on the scene, and the unfavorable factors of reflectance of each RGB channel can be confined in a small area by advanced filtering algorithms. Compared with haze removal with the global atmospheric light, the method based on local patches atmospheric light can reduce the risk of influence of errors, and a comparison of restored images with local atmospheric light veil and global atmospheric light are given in Fig.2 (d).Obviously, with the global atmospheric light, some pixels in the patch are oversaturated. This problem can be solved using the proposed local atmospheric light veil.

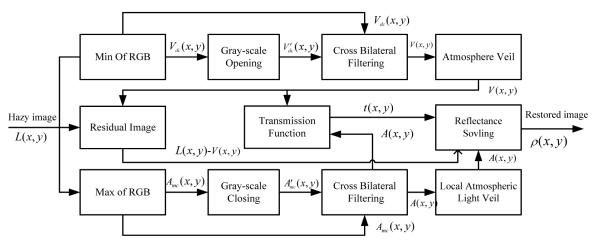
4.Proposed solution for hazy removal and scene reflectance calculation

According to(8), we can calculate atmospheric veil V_dc(x, y), local atmospheric light veil A(x, y) using Eqs (5) and (7), respectively. Reflectivity ρ(x, y) can be restored from the hazy image.

4.1Atmosphericveil inference

We expect V(x, y) to produce a relatively smooth output image and maintain the edge details of the target. From (5), we can roughly estimate V_dc(x, y) by the dark channel prior. After grayscale opening operation on V_dc(x, y), we get an estimated value of $V_{\mathit{dc}}^{\prime }(x,y)$. Let E=V_dc(x, y) and $D=V_{\mathit{dc}}^{\prime }(x,y)$ be the input images as shown in Fig.3 (b) and (c).The filtered image, V(x, y), in the joint spatial-range domain is given by

$$V\phantom{)}(x,y)\phantom{(}=\sum _{j\in \mathit{pw}}\frac{C}{h_s^2{h}_r}{k}_1\left(\Vert \frac{E-E_j}{h_r}\Vert \right)k_2\left(\Vert \frac{c-c_j}{h_s}\Vert \right){}^{\ast }D_j$$ (9)

Where p^w is the window for calculating V(x, y), C, is the spatial part, c_j is the position surrounding (x, y) within p_w. E_j is the range of the point c_j,k₁,k₂ are the common profile of the kernel used in both domains, h_s and h_r are the employed kernel bandwidths, and C is the corresponding normalization constant. Thus, the bandwidth h = (h_s,h_r) is the only parameter to control the size of the kernel. Eq. (9) is illustrated in Fig.3 (d)

We used the fast approximation algorithm for cross bilateral filtering [20]. The result is shown in Fig.3 (d), which preserves the computational simplicity while still provides near-optimal accuracy.

4.2 Atmospheric light veil

According to (7), the preliminarily local atmospheric light veil function A(x, y) can be defined as

$$A_{\mathit{mc}}\phantom{)}(x,y)\phantom{(}=\underset{c\in \{R,G,B\}}{\max }{L}_c\phantom{)}(x,y)\phantom{(}$$ (10)

An example of A_mc(x, y) is shown in Fig.3 (e). The local atmospheric light veil function must be obtained before estimating the haze-free image. As discussed above, the basic property of the atmospheric light is its smoothness in a local area, and A(x, y) should be both relatively smooth and capable of maintaining the edge details of the scene [18,19]. Therefore, the cross bilateral filter matches well with these requirements [25,28].

In order to get an accurate distribution of the local atmospheric light veil, we modify A_mc(x, y) by performing morphological closing of the A_mc(x, y) image with a structural element. The radius of the structural element, which is typically defined as r = min[w, h]/10(w, h are the width and height of input image respectively), can be dynamically adjusted. If appropriate parameters are chosen, vivid color can be preserved in the recovered images. Additionally, the output of the grayscale closing operation on image A_mc(x, y) is defined as $A_{\mathit{mc}}^{\prime }(x,y)$.By substituting E = A_mc(x, y) and $D=A_{\mathit{mc}}^{\prime }(x,y)$ into Eq.(9), A(x, y) can be obtained. The assignment specifies that the filtered data at the spatial location (x, y) have range values of $A_{\mathit{mc}}^{\prime }(x,y)$ as shown in Fig.3 (f). A(x, y) is given in Fig.3 (g).

4.3. Procedures of proposed algorithm for reflectance restoration

The procedures of proposed algorithm are given as follows and the corresponding results are given in Fig.3(a)-(i):

1. Input the hazy color image L(x, y) with RGB channels.

2. According to R, G, and B channels at each pixel location, roughly estimate atmosphere veil V_dc(x, y) by Eq. (5) (Fig.3 (b)).

3. Perform opening operation and joint bilateral filtering on V_dc(x, y) to estimate atmosphere veil V(x, y) (Fig.3(c) and Fig.3 (d)).

4. According to R, G, and B channels at each pixel location of L(x, y), roughly estimate local atmospheric light veil A_mc(x, y) by Eq. (10) (Fig.3(e)).

5. Use closing operation and joint bilateral filtering on A_mc(x, y) to estimate local atmospheric light veil A(x, y) (Fig.3(f) and Fig.3(g)).

6. Subtract V(x, y) from L(x, y) to obtain a residual image without atmosphere veil V(x, y).

7. With V(x, y) = A(x, y)(1–e^{–kd(x, y)}) and A(x, y), calculate transmission function (Fig.3(h)).

8. From Eq.(2), compute the scene radiance by L₀(x, y)=A(x, y)ρ(x, y)(Fig.3(i)). The target reflectance ρ(x, y) is obtained by L₀(x, y)/ A(x, y) according to Eq. (8). The result is truncated to the range of [0 1](Fig.3(j)).

We note that the reflectance image may or may not be the desired output of the algorithm since illumination factors such as shading could be natural components of the object appearance. Therefore, in this paper, we give two choices of outputs, e.g. scene radiance and reflectance as shown in Fig3.(i) and Fig3 (j).

As we can see, the restored images in Fig.3 (i) and Fig.3 (j) are clearer and brighter than those results given by He [4] and Yeh[24]. Especially, the central area in the restored images exhibit excellent performance and looks brighter and more vivid, while the image in Fig.3 (l) shows some color cast. The flow chart of the proposed algorithm is shown in Fig.4.

Fig. 4.

Block diagram of the proposed hazy removal algorithm for color images

5. Experiments

To demonstrate the effectiveness of the proposed algorithm, several groups of images were selected for restoration experiments. An efficient filtering procedure was used [21,22], whose complexity was linear to the image size. It took about 1.42 seconds to process a 735*492 image on a PC with a 3.0 GHz Intel Pentium 4 Processor and MATLAB7.8.0.In comparison, the methods of Tan [1], He et al. [4] and Fattal [2] needed approximately 5 minutes, 20 seconds, and35 seconds, respectively. This result shows that the proposed method is efficient in computation, which is important in case where real-time computation is required.

5.1 Subjective evaluation

The ultimate goal of the image enhancement algorithm is to increase the visibility while preserving the details in the image. Figs.5and6 show the experimental results of some outdoor hazy scenes. The details and vivid colors can be unveiled by our approach even in heavily hazy regions and the restored scenes look more natural. When checking the restored images of ‘ny1’ and ‘goose’, it should be noticed that some small structures survive in our restored results.

Fig.5.

Restoredresults of image ‘ny1’ (a) Hazy input image; (b) Restored scene radiance by the proposed method; (c) Restored scene reflectance by the proposed method;

Fig.6.

Restoredresults of image ‘goose’ (a) Hazy input image; (b) Restored scene radiance by the proposed method; (c) Restored scene reflectance by the proposed method;

In Figs.7-10, more comparable results are presented to show the performance of the proposed method. From these comparisons, some color cast can be seen in Yeh’s[24] and Fattal’s[2]methods, especially in Fig.8 and Fig.10 for Yeh’s method and Fig.9 for Fattal’s method. Although their results are generally acceptable, they look darker in a certain degree. The proposed method enhances the hazy image by haze removal and illumination elimination, and the resulting images show more layering and present improved colors and details. In the bottom left corner of Fig.9(f),we can see a red pinecone hidden in the tree. InFig.7(e),we can see the details on the mountain. In Fig.10(f), we can clearly distinguish the withered and alive stems of flowers. In contrast, the Ancuti’s method [31] shown in Fig.9(e) and Fig.10(e) produces less vivid color and the results look darker although the details are acceptable.

Fig.7.

Comparable results of image ‘mountain’ (a) Hazy input image (b) Restored by Fattal’s method; (c) Restored by He’s method; (d) Restored by Yeh’s method; (e) Restored by proposed method;

Fig.10.

Comparable results of image ‘pumpkin’(a) Hazy input image (b) Restored by Fattal’s method; (c) Restored by He’s method; (d) Restored by Yeh’s method; (e) Restored by Ancuti’s method (f)Restored by proposed method;

Fig. 8.

Comparable results of image ‘house’ (a) Hazy input image (b) Restored by Fattal’s method; (c) Restored by He’s method; (d) Restored by Yeh’s method; (e) Restored by proposed method;

Fig. 9.

Comparable results of image ‘forest’ (a) Hazy input image (b) Restored by Fattal’s method; (c) Restored by He’s method; (d) Restored by Yeh’s method; (e) Restored by Ancuti’s method;(f)Restored by proposed method;

Mean Opinion Score (MOS) of the automatic visual quality assessment are shown in Table 1 for Figs.7-10 by classifying them into one of the following five classes: bad, poor, fair, good and excellent. The MOS is calculated with a range from 1(worst) to 5 (best). From Table 1, we conclude that the proposed algorithm get the highest score in MOS for the restored images shown in Figs.7-10.

Table 1.

Mean opinion score (MOS) of different enhancement algorithms

Quality vs Algorithms	Color	Detail	Halo	Contrast	Natural	MOS	Score Class
Original	2	2	4	2	4	2.80	5Excellent
Fattal[2]	3	4	3	4	3	3.40	4 Good
He[4]	4	4	4	4	4	4.00	3 Fair
Yeh[24]	3	4	3	4	3	3.40	2 Poor
Ancuti[31]	3	4	4	3	4	4.25	1 Bad
Proposed Algorithm	5	5	4	4	4	4.50

5.2 Objective evaluation

Currently, the most widely used blind assessment method in image enhancement is the visible edge gradient method proposed by Hautiere, et al.[23]. This method defines a ratio e of the number of visible edges in the original image and the restored image, as well as the average gradient ratio $\left(\overline{r}\right)$ defined as the objective measurements of enhancement effect. Also, the percentage of pixels (∑)which becomes completely black or completely white after enhancement is calculated. In this paper, to quantitatively assess and rate algorithms, we compute three indicators, $\overline{r}$, and ∑. Experimental results of various foggy images: ‘y01’, ‘y16’, ‘ny17’ are presented in Figs. 11-13. All implementations have been done in MATLAB 7.8.0 on a PC with a 3.0 GHz Intel Pentium 4 Processor.

Fig.11.

Comparison of dehazing performances of different algorithms for hazy image ‘y01’. (a) Original hazy image. (b) Restored by Fattal et al.’s algorithm. (c) Restored by Tan et al.’s algorithm. (d) Restored by Koef et al.’s algorithm. (e) Restored by Tarel et al.’s algorithm. (f) Restored by He et al.’s algorithm. (g) Restored by A.K. et al.’ algorithm. (h) Restored by proposed algorithm.

Fig.13.

Comparison of dehazing performances of different algorithms for image ‘ny17’.(a) Original hazy image. (b) Restored by Fattal et al.’s algorithm. (c) Restored by Tan et al.’s algorithm. (d) Restored by Koef et al.’s algorithm. (e) Restored by Tarel et al.’s algorithm. (f) Restored by He et al.’s algorithm. (g) Restored by A.K. et al.’ algorithm. (h) Restored by proposed algorithm.

Results evaluated by the three indicators are shown in Table 2. The proposed algorithm performs well in terms of ∑ values. According to the gradient ratio $\overline{r}$, the proposed algorithm gives satisfactory results and shows good performance in indicator e.Compared with other algorithms; the objective indicators have been improved or maintained. But for the mist images, the restored results of He et al. appears to be more preferable, since they appear to have less whitish hazy effects.

Table 2.

Produced by proposed algorithm and competing methods

Image	Y01			Y16			Ny17
Algorithm	e	$\overline{r}$	∑	e	$\overline{r}$	∑	e	$\overline{r}$	∑
Fattal’08[2]	0.0864	1.2152	0.0012	0.0583	1.2033	0.0032	−0.1061	1.5346	0.0202
Tan’08[1]	0.1219	2.2283	0.0039	−0.0165	2.0602	0.0045	−0.0412	2.1900	0.0077
Kopf.’08[5]	0.0947	1.6362	0.0002	0.0009	1.3456	0.0028	0.0169	1.6136	0.0136
Tarel’09[3]	0.2092	1.9903	0.0000	0.2406	1.9583	0.0000	0.1104	1.7057	0.0000
He et al.’09[4]	0.1426	1.3134	0.0101	0.1314	1.3674	0.0019	0.0232	1.6297	0.0023
A.K.’12[8]	0.2532	1.4244	0.0000	0.1632	1.4937	0.0002	0.2456	2.1832	0.0036
Proposed alg.	0.1172	1.6951	0.0001	0.1292	1.9523	0.0004	0.0811	2.0216	0.0000

6. Conclusion

Dark channel prior based methods are currently popular in the field of hazy image enhancement. While these methods show acceptable results in most cases, the dark channel prior becomes invalid when the scene objects are inherently similar to the atmospheric light, which causes saturation in the restored image due to errors in estimation of the global atmospheric light. And this in turn results in information loss.

In this paper, major factors affecting the visual quality in the restored images are discussed to improve the effectiveness of single image restoring algorithms based on the use of a physical model. The proposed method removes halo effect by cross bilateral filtering and by applying a local atmospheric light veil, through which undesirable illumination is eliminated and the “true color” and reflectance of a specific object is obtained. Using the cross bilateral filtering, a scene restoration scheme was proposed that produced good color rendition even in the presence of severe gray-world violations. Our technique has been tested on a large data set of natural hazy images. Experimental results demonstrated that the proposed algorithm is capable of removing haze effectively and restoring images faithfully. It yields a reasonable result even the condition d(x, y)→∞ is not satisfied. Also, the proposed method is faster than most existing single image dehazing methods.

• A novel strategy is proposed based on the minimum and maximum of each RGB pixel.

• The concept of local atmosphere light veil is defined in this study.

• The reflection component of the scene is calculated accurately with imaging physical model.

• The proposed method yields even better results than the state-of-the-art techniques.

Fig.12.

Comparison of dehazing performances of different algorithms for image ‘y16’.(a) Original hazy image. (b) Restored by Fattal et al.’s algorithm. (c) Restored by Tan et al.’s algorithm. (d) Restored by Koef et al.’s algorithm. (e) Restored by Tarel et al.’s algorithm. (f) Restored by He et al.’s algorithm. (g) Restored by A.K. et al.’ algorithm. (h) Restored by proposed algorithm.

Biography

Wei Sun, he was born in 1980, Anhui province, China. He received his Bachelor degree in Measuring & Control Technology and Instrumentations, Master and Ph.D. degrees in Circuit and System from Xidian University, Xi’an, China, in 2002, 2005 and 2009, respectively. Since 2012, he has been an associate Professor in School of Aerospace Science and Technology at Xidian University, Xi’an, China. His research interests include visual information perception, pattern recognition, and embedded video systems.

Changhao Sun, He is a PhD candidate in School of Automation Science and Electrical Engineering, Beihang University.

Baolong Guo, he was born in 1962. He received the B. S. degree in 1984, the M. S. degree in 1988 and the Ph.D. degree in 1995, all in Communication and Electronic System from Xidian University, Xi’an, China. From 1998 to 1999.Now ,he is a professor in Xidian University.

Hao Wang, He is a PhD candidate in department of Electrical& Computer Engineering in University of Pittsburgh.

Wenyan Jia, PhD, she received her PhD in biomedical engineering from Tsinghua University, China, in 2005 before joining the University of Pittsburgh as a postdoctoral scholar. In 2009, she was promoted to research assistant professor in the Department of Neurological Surgery.

Mingui Sun, PhD, he received his MS degree in electrical engineering in 1986 from the University of Pittsburgh, where he also earned a PhD degree in electrical engineering in 1989. He is a professor in the Department of Neurological Surgery now.His research interests include neurophysiological signals and systems, biosensor designs, brain-computer interface, bioelectronics and bioinformatics. He has more than 360 publications.