Rare variant testing across methods and thresholds using the multi-kernel sequence kernel association test (MK-SKAT)

Abstract

Analysis of rare genetic variants has focused on region-based analysis wherein a subset of the variants within a genomic region is tested for association with a complex trait. Two important practical challenges have emerged. First, it is difficult to choose which test to use. Second, it is unclear which group of variants within a region should be tested. Both depend on the unknown true state of nature. Therefore, we develop the Multi-Kernel SKAT (MK-SKAT) which tests across a range of rare variant tests and groupings. Specifically, we demonstrate that several popular rare variant tests are special cases of the sequence kernel association test which compares pair-wise similarity in trait value to similarity in the rare variant genotypes between subjects as measured through a kernel function. Choosing a particular test is equivalent to choosing a kernel. Similarly, choosing which group of variants to test also reduces to choosing a kernel. Thus, MK-SKAT uses perturbation to test across a range of kernels. Simulations and real data analyses show that our framework controls type I error while maintaining high power across settings: MK-SKAT loses power when compared to the kernel for a particular scenario but has much greater power than poor choices.

1. INTRODUCTION

Identification of genetic variants influencing complex phenotypes and disease is a major goal of modern human genetics research. So far, despite the success of genome wide association studies (GWAS) [9], newly discovered trait-associated genetic variants still fail to explain a large proportion of the heritability of complex traits [6]. It is hoped that with the advent of accessible DNA sequencing technology [18, 17, 2], investigators can uncover more of the socalled missing heritability. Some of the added information contained in sequencing data includes rare variants, that is variants with minor alleles whose population frequency is low. This contrasts with microarray technology which typically focuses on common variants that have relatively high minor allele frequency (MAF). Rare variants associated with disease have already been reported [4, 25, 22]. However, important distinctions between the analysis of common variants and rare variants must be made [3]. Most importantly, the standard analysis of common variants focuses on analysis of each individual variant, one-by-one. Yet, power decreases with lower MAF such that standard approaches for common variants are vastly underpowered for analysis of rare variants. Also, multiple comparison corrections are a concern since the number of variants is dramatically larger.

To address the limitations of using standard analytical approaches for variants, investigators have turned to region based approaches for rare variant association testing. In this class of approaches, multiple genetic variants within a region, typically a biologically meaningful unit such as a single gene or an exon, are simultaneously considered together. The cumulative effect of the entire group of variants, or more often a subgroup of the variants (e.g. those with MAF <1%), is assessed for association with the phenotype. Grouping the variants and testing only the cumulative effect allows aggregation of effects across several variants. It also addresses the multiple comparison correction concern by substantially decreasing the number of tests performed. A wide range of methods have been developed with varying characteristics and underlying principles [19, 13, 20, 16, 21, 27].

Despite the success of current approaches for rare variant testing [4, 25, 22], a number of practical concerns have arisen. In particular, given the wide range of testing approaches which are optimized toward different scenarios, it is unclear which method to use for any particular data set. Furthermore, it is unclear which strategy to use for grouping variants, e.g. grouping variants with MAF <3% vs <1%, within a region. Unfortunately, the answer to both questions depends on the underlying true state of nature which is unknown prior to analysis. Knowledge on this would preclude need for analysis. Selecting the “best” (often most significant) result after conducting analyses using multiple methods or multiple group strategies would lead to severely inflated type I error and increased false positives. Although some recent work has been done on omnibus testing across different grouping strategies [23, 14] or across different testing approaches [12], few methods consider both the testing approach and the grouping strategy simultaneously.

To address this problem, we propose the multi-kernel sequence kernel association test (MK-SKAT). In this article, we show that many commonly used testing approaches are equivalent to particular cases of the sequence kernel association test (SKAT). SKAT is a similiarity based analysis approach for rare variant testing wherein pair-wise similarity between individuals based on their rare variant profiles is measured via a kernel function and then compared to pairwise similarity in phenotype. Specifically, the currently used methods are equivalent to versions of SKAT using different kernel functions. We further show that different choices of grouping strategies are also equivalent to using the SKAT with different kernel functions. Consequently, the question of selecting a test to use as well as selecting a grouping strategy reduces to the problem of selecting an appropriate kernel function. This equivalence then leads us to exploit perturbation based procedures for omnibus testing across multiple kernels (and accordingly multiple grouping and rare variant testing approaches) [26]. We conduct simulations and a real data application to validate our approach and show that our proposed method loses a small amount of power when compared to the optimal grouping and testing approach, but offers considerably more power over poor choices.

Broadly speaking, the main contribution of this work is to address a practical problem faced by applied statistical researchers interested in analyzing sequencing association studies. In addition, we explicitly draw the connections between SKAT and several other rare variant tests and grouping strategies which then enables utility of our previously developed perturbation testing framework [26]. Although the perturbation framework underlies the statistical mechanisms for generating a p-value, we emphasize that the current project differs significantly from our previous work in terms of the overall objective and the application to rare variants. Furthermore, to accommodate features specific to rare variant sequencing studies, i.e. larger number of kernels (corresponding to different tests and grouping strategies) as well as the larger number of variants which are not highly correlated, we also make some technical modifications to the perturbation procedure to improve computation.

The remainder of this paper is organized as follows. In the next section, we first review the generic SKAT method and describe how different testing approaches and different groupings all correspond to SKAT under different kernels. We then present the proposed MK-SKAT approach for testing across different tests and groupings. We show results from some representative simulation studies and from real data to illustrate our approach. We conclude with a brief discussion.

2. METHODS

Within this article, we describe our methodology within the context of analyzing a single gene region. However, the approach can be applied to multiple regions separately, with appropriate control for multiple comparisons. We let y_i denote the phenotype for the i^th individual in the study (i = 1, …, n), and X_i be a vector of environmental or demographic variables for which we would like to adjust. For dichotomous phenotypes we let y_i = 0 or 1 for controls and cases, respectively. For each given region, we let Z_i be the vector of genetic variants within the region coded under the additive model. The objective is to test for an association between y and all the variants in Z or a subset of the variants in Z while adjusting for X. We let 𝒢 denote the indices of the variants within Z that we would like to test. For instance 𝒢 may be the indices of the variants with MAF < 1% or the nonsynonymous variants. In doing so, one may select a subset of the variants in the region to test or one may test all of the variants within the region. Clearly, restricting attention to the truly causal variants would result in the highest power; however, which variants are causal is unknown. At the same time, there are a range of tests to choose from. Determining which group of variants to test and which test to use poses a grand challenge for geneticists.

In this section, we first review the SKAT method and draw connections between SKAT and several other important tests. We describe how the questions of which test to use and which variants to test can be recast as a question of kernel choice. We then develop the MK-SKAT to construct an omnibus test that simultaneously considers multiple tests and grouping strategies.

2.1 Connections between SKAT and other methods

2.1.1 SKAT

SKAT is a similarity based test that operates by comparing pair-wise genotypic similarity between individuals to pair-wise phenotypic similarity, with correlation suggestive of association. Mathematically, SKAT uses the linear model for quantitative traits

$$y_i={\alpha }_0+{\mathbf{X}}_i^{\prime }\mathit{\alpha }+h({\mathbf{Z}}_{{\mathcal{G}}_i})+{\epsilon }_i$$

and the logistic model for case/control studies

$$\text{logit}P(y_i=1)={\alpha }_0+{\mathbf{X}}_i^{\prime }\mathit{\alpha }+h({\mathbf{Z}}_{{\mathcal{G}}_i})$$

where α₀ is an intercept term, α is the vector of regression coefficients for the covariates, and ε_i has mean zero and variance σ². The variants of interest Z_𝒢i for the i-th individual are related to the outcome only through the function h(·) which is a general function lying in a functional space generated by a positive definite kernel function K(·, ·). Intuitively, K(Z_𝒢i, Z_𝒢i′) measures similarity between i-th and i′-th individuals in the study based on Z_𝒢, the variants of interest. This function fully specifies the relationship between the variants and the outcome. If one sets $K({\mathbf{Z}}_{{\mathcal{G}}_i},{\mathbf{Z}}_{{\mathcal{G}}_{i^{\prime }}})={\mathbf{Z}}_{{\mathcal{G}}_i}^{\prime }{\mathbf{Z}}_{{\mathcal{G}}_{i^{\prime }}}$, which is the linear kernel, then this implies that the function h(Z_𝒢i) = Σ_j∈𝒢 β_jZ_ij, i.e. h(·) is linear and the outcome depends on the variants in a linear manner. By specifying a different kernel, one may specify an alternative model. Under the default SKAT parameters, $K({\mathbf{Z}}_{{\mathcal{G}}_i},{\mathbf{Z}}_{{\mathcal{G}}_{i^{\prime }}})={\sum }_{j\in \mathcal{G}}{w}_j^2{Z}_{ij}{Z}_{i^{\prime }j}$ where w_j is equal to the beta probability density function with parameters 1 and 25 evaluated at the MAF for the j-th variant. Also by default, 𝒢 is set to be the entire group of both common and rare variants within a region. This corresponds to a linear model but with additional up-weighting for the effect of rarer variants.

To test the effect of the rare variants under SKAT corresponds to testing H₀ : h(Z_𝒢) = 0. Defining the kernel matrix, K, to be the n-by-n matrix with i, i′-th term equal to K(Z_𝒢i, Z_𝒢i′), for quantitative traits, we construct the variance component score statistic

$$Q=\frac{{(\mathbf{y}-\widehat{\mathbf{y}})}^{\prime }\mathbf{K}(\mathbf{y}-\widehat{\mathbf{y}})}{{\widehat{\sigma }}^2}$$

where ŷ = α̂₀ + Xα̂ with α̂₀, α̂, and σ̂ estimated under H₀. For dichotomous traits, we can construct a similar score statistic

$$Q={(\mathbf{y}-\widehat{\mathbf{y}})}^{\prime }\mathbf{K}(\mathbf{y}-\widehat{\mathbf{y}})$$

where ŷ = logit⁻¹(α̂₀ +Xα̂) and α̂₀, α̂ are again estimated under H₀. To obtain a p-value for significance, asymptotically, $Q~\sum {\lambda }_j{\chi }_1^2$ is a mixture of chi-squared distributions, with weights λ_j equal to the eigenvalues of ${\mathbf{P}}_0^{1/2}{\mathbf{KP}}_0^{1/2}$ where P₀ = D − DX(X′DX)⁻¹X′D with D = I for quantitative traits and D = diag{ŷ_i(1 − ŷ_i)} for dichotomous traits. This null distribution can be approximated using moment matching approaches [15] or exact methods [5].

2.1.2 Existing methods and grouping strategies as special cases of the SKAT

A wide range of region-based analysis approaches of rare variants have been proposed. Generally, however, they tend to fall within two classes: burden-based approaches and similarity-based approaches. Burden-based tests generally operate by collapsing the rare variants within a region into a single value using (possibly weighted) averaging and then testing for association by regressing the phenotype on the collapsed variable or applying appropriate permutation-based approaches. Letting 𝒢 denote the indices of the rare variants over which we would like to collapse, then the cohort allelic sum test (CAST) and combined multivariate collapsing (CMC) collapses the genetic variants within a region to a single binary variable

$$C_i=I\left(\sum _{j\in \mathcal{G}}{Z}_{ij}>0\right)$$

which is an indicator for whether the i^th individual has any rare variants within the region. In a slight variation, the count-based collapsing method computes the collapsed variable as

$$C_i=\sum _{j\in \mathcal{G}}{Z}_{ij}$$

which is the total number of rare variants within the region. To place a higher weight on variants which are rarer, the weighted count collapsing method collapses the variants in 𝒢 into

$$C_i=\sum _{j\in \mathcal{G}}{w}_j{Z}_{ij}$$

where w_j is a weight for the j^th variant which is inversely related to the MAF for the j^th variant. To test whether the rare variants are related to the phenotype, the outcome is regressed on the collapsed variable and possible covariates using the models

$$y_i={\alpha }_0+{\mathbf{X}}_i^{\prime }\mathit{\alpha }+{\beta }_C{C}_i+{\epsilon }_i$$

or

$$\text{logit}P(y_i=1)={\alpha }_0+{\mathbf{X}}_i^{\prime }\mathit{\alpha }+{\beta }_C{C}_i$$

for quantitative and dichotomous traits, respectively. Testing for the rare variant effect then corresponds to testing H₀ : β_C = 0 which can be done using a standard 1-df test. The burden-based rare variant association tests are similar in that they sum over all of the rare variant genetic information. Thus, they are most powerful when the effects of the variants are truly associated with the outcome and with common direction of effect, that is, all variants are deleterious or all variants are protective. Power is lost when effects are opposite in directions or non-causal variants are included in 𝒢.

Similarity-based tests were proposed to address the power loss due to variants with opposing effects. This class includes SKAT, and compares pair-wise similarity between individuals in terms of their genotype values to pair-wise similarity in phenotype, with correlation suggestive of association. Also included within this class is the C-alpha test which tests for an over-dispersion of the variance resulting from a rare variant effect rather than a change in the mean effect. By testing variance rather than net effect, the test is powerful to detect genetic association when the effects of the variants are not all in the same direction.

It has been previously noted that individual tests are equivalent to SKAT under particular kernel functions [27, 12]. For example, the C-alpha test is equivalent to SKAT using the kernel function K(Z_𝒢i, Z_𝒢i′) = Σ_j∈𝒢 Z_ijZ_i′j. Further, each of the burden based methods operate by using a univariable summary of the rare variants in 𝒢 such that the outcome is a simple linear function of the collapsed variable C_i. Therefore, each of the CAST/CMC, count-based collapsing, and weighted count-based collapsing can be viewed as SKAT with a linear kernel constructed based on the collapsed variable. Thus we have the following tests and corresponding kernels:

• (Default) SKAT: K(Z_𝒢i, Z_𝒢i′) = Σ_j∈𝒢 w_jZ_ijZ_i′j

• C-alpha: K(Z_𝒢i, Z_𝒢i′) = Σ_j∈𝒢 Z_ijZ_i′j

• CAST (Binary Collapsing): K(Z_𝒢i, Z_𝒢i′) = I(Σ_j∈𝒢 Z_ij > 0)I(Σ_j∈𝒢 Z_i′j > 0)

• Count-Based Collapsing: K(Z_𝒢i, Z_𝒢i′) = {Σ_j∈𝒢 Z_ij}{Σ_j∈𝒢 Z_i′j}

• Weighted Count-Based Collapsing: K(Z_𝒢i, Z_𝒢i′) = {Σ_j∈𝒢 w_jZ_ij}{Σ_j∈𝒢 w_jZ_i′j}

Given that many individual tests reduce to SKAT under different kernel, then the problem of choosing a particular test reduces to the problem of choosing a particular kernel.

We have, thus far, focused on testing the variants in a particular group, 𝒢. In practice however, one must also choose, a priori, a group of variants to test. For example, one may apply each of the tests to all of the variants in the region or one could restrict the variants of interest to just the variants with <3% MAF, < 1% MAF, or <0.5% MAF, depending on how one wishes to define “rare”. Additionally the investigator may want to restrict to a set of only non-synonymous variants or those that are predicted to be “harmful” by Polyphen-2 [1] or other software for predicting function. Use of different choices of variants can easily be translated into a problem of kernel choice by simply restricting 𝒢 to be different sets of variants. For example, we can define 𝒢^3% to be the variants with MAF < 3% and 𝒢^0.5% to be the variants with MAF < 0.5%. Then if we are interested in the C-alpha test, we can apply it to the variants with MAF < 3% or < 0.5% by constructing the kernels $K({\mathbf{Z}}_{{\mathcal{G}}_i^{3\%}},{\mathbf{Z}}_{{\mathcal{G}}_{i^{\prime }}^{3\%}})={\sum }_{j\in {\mathcal{G}}^{3\%}}{Z}_{ij}{Z}_{i^{\prime }j}$ and $K({\mathbf{Z}}_{{\mathcal{G}}_i^{0.5\%}},{\mathbf{Z}}_{{\mathcal{G}}_{i^{\prime }}^{0.5\%}})={\sum }_{j\in {\mathcal{G}}^{0.5\%}}{Z}_{ij}{Z}_{i^{\prime }j}$, respectively and test using the usual SKAT procedure. Therefore, it follows that the problem of choosing which group of variants to test also reduces to the problem of choosing a particular kernel.

2.2 Multi-kernel sequence kernel association test

The questions facing researchers interested in rare variant analysis are first, which is the most powerful test to use for a given data set, and second, which is the best group of variants to test within a particular region? As noted earlier, these questions can be reduced to a question of kernel choice: which kernel, from among a group of candidates, will yield highest power? Despite transforming the problem, the answer to this question requires prior knowledge of which variants are causal and what is their effect size and direction, knowledge which is rarely available (since this would preclude the need for analysis). As a solution, one may choose to test under all candidate kernels and report the best p-value, but this clearly leads to inflated type I error. However, by exploiting the connections between SKAT and other tests, we can utilize a perturbation strategy, related to the approach of Wu et al. [26], to incorporate many tests and groupings while conserving type I error.

Our proposed unifying method, the multi-kernel SKAT (MK-SKAT), simultaneously considers several test and variant grouping choices at once and constructs an omnibus test. The idea behind the approach is that it constructs kernels based on each candidate test and grouping approach. For example, one may test using CAST, count-based collapsing, C-alpha, and the default SKAT with 3 grouping strategies per test (MAF <3%, <1%, or <0.5%) for a total of 12 combinations corresponding then to 12 candidate kernels. MK-SKAT then conducts an omnibus test using a modified version of the perturbation approach of Wu et al. [26] to test across all of the candidate kernels. Operationally, the strategy applies SKAT with each of the kernels, takes the minimum p-value, and then uses perturbation based techniques to correct for having taking the minimum p-value. A single p-value is reported.

The intuition behind the procedure is that asymptotically σ̂⁻¹(y_i − ŷ_i) will be approximately normal such that we can replace it with a simulated normal random variable. Using the same simulated normals for each candidate kernel allows for capture of the correlation between tests. The full MK-SKAT procedure is as follows:

1. For each combination of candidate testing procedure and each candidate grouping procedure, construct a corresponding kernel matrix, K_ℓ, to obtain a total of L candidate kernels.

2. Using each candidate kernel, K_ℓ, obtain a corresponding score statistic as Q_ℓ and p-value for significance p_ℓ.

3. Find the minimum p-value: p_min = min_1≤ℓ≤L p_ℓ

4. For ℓ ∈ 1, …, L, compute Λ_ℓ = diag(λ_ℓ,1, …, λ_ℓ,mℓ), and V_ℓ = [v_ℓ,1, v_ℓ,2, …, v_ℓ,mℓ] where λ_ℓ,1 ≥ λ_ℓ,2 ≥ … ≥ λ_ℓ,mℓ are the m_ℓ positive eigenvalues of ${\mathbf{P}}_0^{1/2}{\mathbf{K}}_{\ell }{\mathbf{P}}_0^{1/2}$ with corresponding eigenvectors v_ℓ,1, v_ℓ,2, …, v_ℓ,mℓ

5. Generate ${\mathbf{r}}^{\ast }={[r_1^{\ast },r_2^{\ast },\dots ,r_n^{\ast }]}^{\prime }$ with each $r_j^{\ast }~N(0,1)$.

6. For each ℓ ∈ 1, …, L, rotate r^* using the eigenvectors to generate ${\mathbf{r}}_{\ell }^{\ast }={\mathbf{V}}_{\ell }^{\prime }{\mathbf{r}}^{\ast }$.

7. Compute $Q_{\ell }^{\ast }={\mathbf{r}}_{\ell }^{\ast \prime }{\mathbf{\Lambda }}_{\ell }{\mathbf{r}}_{\ell }^{\ast }$ for each ℓ and obtain a corresponding p-value, $p_{\ell }^{\ast }$, by comparing $Q_{\ell }^{\ast }$ to the distribution function estimated for Q_ℓ and obtain the upper tail probability exceeding $Q_{\ell }^{\ast }$. We set $p^{\ast }={min}_{1\le \ell \le L}{p}_{\ell }^{\ast }$.

8. Repeat (5)–(7) B times to obtain $p_{(1)}^{\ast },p_{(2)}^{\ast },\dots ,p_{(B)}^{\ast }$ for some large number B.

9. The final p-value for significance is estimated as

   $$p=B^{-1}\sum _{b=1}^{B}I(p_{(b)}^{\ast }\le p_{\mathit{min}})$$

   It is important to note that direct use of the p-value is necessary rather than using the maximum score statistic since the raw score statistics have different degrees of freedom.

As noted earlier, this procedure is closely related to the general perturbation procedure previously used for testing across multiple kernels [26]. However, some technical modifications have been made to tailor the procedure towards the current application. In particular, the previous procedure required generation of a large augmented matrix with dimensionality equal to the sum of the number of nonzero eigenvalues from all of the kernels under consideration followed by eigen decomposition of the augmented matrix. This can be slow if the rank of the individual kernels is high (i.e. many variants with low correlation) and if many kernels are under consideration (i.e. many combinations of groupings and possible tests); both of these can be true in rare variant studies. In contrast, the present strategy requires simulation of more normal random variables but bypasses the need for working with a large, augmented matrix.

Two key features of our test ensure that type I error is conserved despite the application of multiple tests and grouping. First, our test requires uninformed selection of tests and variant groupings. In contrast, using the data to select a single optimal test would not conserve type I error. Second, while it is true that the p-values of the test/grouping combinations are correlated, as some tests are in fact nested, our perturbation method properly captures the correlation and thus retains type I error control.

By capturing the correlation, our approach can accommodate a large number of tests and groups as a long as they are highly correlated. Perfect correlation across tests would be equivalent to conducting just a single test. Thus, under such scenarios, the increase in cost is primarily computational. If the correlation between kernels is low, there is the potential for larger power loss, though this is counterbalanced by the fact that one of the competing kernels may have much higher power. Therefore, we generally recommend inclusion of a broad range of tests and grouping strategies.

Although this strategy also generates a monte carlo p-value, there are two advantages in comparison to permutation. First, covariates and variants can be correlated. In contrast, in order for permutation to be valid, the variants must be uncorrelated with the covariates. Second, the MK-SKAT procedure is more computationally efficient since the computation now relies only on generating and then rotating n normal random variables while all other parameters remain the same. In contrast, permutation requires complete re-estimation of the kernel matrices, P₀ matrices, eigen-decompositions, and distribution parameters.

2.3 Simulations

We conducted a series of simulations to verify that the proposed MK-SKAT procedure is valid in terms of controlling type I error and has reasonable power compared to the individual tests across which the MK-SKAT is combining.

2.3.1 Type I error

To demonstrate that the proposed methods are valid tests, in terms of protecting type I error, we conducted a series of simulations under null models for both continuous and dichotomous traits. We used a coalescent model to simulate a region with 100 variants in 10⁴ haplotypes with LD structure representative of a European population [24]. Eighty-five of the simulated variants had a true MAF less than 3% and 80 had a MAF less than 1%. We then paired haplotypes to simulate n = 1,000 or 2,000 diploid individuals. For type I error simulations, we simulated quantitative outcomes for each individual without regard to the genotype values under the null model:

$$y_i=0.5X_{i1}+0.03X_{i2}+{\epsilon }_i$$

where X_i1 ~ ber(0.506), X_i2 ~ N(29.2, 21.1), and ε_i ~ N(0, 1). For dichotomous outcomes, we simulated n/2 cases and n/2 controls from the null logistic model:

$$\text{logit}P(y_i=1)=-4.2+0.5X_{i1}+0.03X_{i2}$$

where X_i1 ~ ber(0.506) but X_i2 ~ N(0, 1).

In total, we simulated 10⁵ data sets as described. We applied the MK-SKAT testing procedure to each data set. Specifically, we considered four different testing procedures: CAST, count-based collapsing, the C-alpha, and SKAT tests. We also considered three different grouping strategies: we set the rare variant grouping, 𝒢, equal to the variants with MAF < 0.5%, variants with MAF < 1%, and variants with MAF < 3%. Under the equivalence with SKAT, this yielded a total of 12 different candidate kernels. We estimated the type I error rate at the 0.05 level of 1) SKAT with each individual kernel, 2) MK-SKAT conditional on a particular testing procedure (i.e. we assumed a fixed test while considering multiple groupings), 3) MK-SKAT conditional on a particular grouping strategy (i.e. we assumed a fixed grouping while considering multiple tests), and 4) MK-SKAT testing across all twelve candidate kernels.

2.3.2 Power

We also assessed the power of the MK-SKAT procedure under three different simulation settings. For each setting, we again simulated haplotypes for a region containing 100 variants as in the type I error simulations. These were then paired to generate n = 1,000 individuals. Then we simulated outcomes under the alternative model for quantitative traits:

$$y_i=0.5X_{i1}+0.03X_{i2}+{\mathit{\beta }}^{\prime }{\mathbf{Z}}_i^c+{\epsilon }_i$$

and for dichotomous traits:

$$\text{logit}P(y_i=1)=-4.2+0.5X_{i1}+0.03X_{i2}+{\mathit{\beta }}^{\prime }{\mathbf{Z}}_i^c$$

X_i1, X_i2 and ε_i were as before, but ${\mathbf{Z}}_i^c$ were the genotypes of the causal variants and β were the corresponding regression coefficients which varied across simulation settings. For dichotomous outcomes n/2 subjects were sampled as cases with the remaining n/2 set as controls.

Under Setting 1, we considered a quantitative outcome with 50% of the variants with true population MAF < 1% randomly selected to be causal. All causal variants were given the same effect with β = 0.5. Since a large proportion of the variants were causal and they all had the same effect, this scenario favored the burden approaches and particularly count based collapsing.

Setting 2 again examined quantitative traits and was identical to Setting 1 except the effects of the causal variants were equal to −0.5 and 0.5 with equal probability. Since the causal variants had opposing effects, this scenario favored the similarity based tests.

Setting 3 differed from Settings 1 and 2 in that it examined the case where the outcome was dichotomous. Of the variants with true MAF < 3%, 20% were randomly selected to be causal. All causal variants were again given equal effect size of β = 0.5.

We emphasize that these simulations were not intended to serve as a comprehensive comparison of the methods across scenarios nor to understand when individual tests and grouping strategies are optimal (since this depends on the true state of nature, which is unknown in any real data). Instead, these simulations serve to understand how MK-SKAT behaves relative to the best method and grouping strategy.

3. RESULTS

3.1 Type I error and power

Type I error simulation results for quantitative traits and dichotomous traits are shown in Table 1 and Table 2, respectively. For quantitative traits, individual methods as well as MK-SKAT appropriately controlled the type I error at the α = 0.05 level. However, for dichotomous traits, the C-alpha test and SKAT test tended to be conservative, reflecting previous results [27]. Thus, MK-SKAT tests were conservative as well.

Table 1.

Type I error simulation results for quantitative traits. Each cell in the table corresponds to the type I error of SKAT using a kernel constructed based on the testing procedure at the top of the table and the grouping strategy at the left of the table. Rows and columns labeled MK-SKAT correspond to the omnibus tests across tests (with fixed group) and across groupings (with fixed test). The cells with both rows and columns labeled MK-SKAT correspond to the omnibus test across all test and groupings

	C-alpha	SKAT	CAST	Count	MK-SKAT
n=1000
0.5%	0.048	0.047	0.050	0.049	0.048
1%	0.048	0.049	0.049	0.050	0.050
3%	0.048	0.049	0.051	0.051	0.051
MK-SKAT	0.050	0.051	0.051	0.051	0.051
n=2000
0.5%	0.049	0.049	0.050	0.050	0.052
1%	0.047	0.047	0.050	0.050	0.051
3%	0.047	0.047	0.050	0.049	0.051
MK-SKAT	0.052	0.051	0.052	0.051	0.050

Table 2.

Type I error simulation results for dichotomous traits. Each cell in the table corresponds to the type I error of SKAT using a kernel constructed based on the testing procedure at the top of the table and the grouping strategy at the left of the table. Rows and columns labeled MK-SKAT correspond to the omnibus tests across tests (with fixed group) and across groupings (with fixed test). The cells with both rows and columns labeled MK-SKAT correspond to the omnibus test across all test and groupings

	C-alpha	SKAT	CAST	Count	MK-SKAT
n=1000
0.5%	0.033	0.032	0.051	0.050	0.042
1%	0.042	0.040	0.050	0.049	0.045
3%	0.046	0.044	0.050	0.050	0.046
MK-SKAT	0.039	0.037	0.052	0.051	0.044
n=2000
0.5%	0.041	0.041	0.050	0.050	0.047
1%	0.046	0.046	0.050	0.050	0.049
3%	0.047	0.047	0.050	0.050	0.050
MK-SKAT	0.047	0.045	0.051	0.051	0.047

Results of the power analysis for the 3 settings are shown in Tables 3 through 5. In Setting 1 (Table 3), the count kernel applied to the variants with MAF <1% performed the best, followed closely by the CAST kernel applied to the same grouping. This was not surprising considering they were best adapted to the true model in which all effects have the same size and direction, and only rare variants with MAF <1% are sampled to be causative. The MK-SKAT which tested over all 12 kernels had a power slightly less than the most powerful single kernel. The results of the MK-SKAT testing across all 4 tests at the 1% MAF threshold group showed power would be nearly equivalent to the most powerful single kernel as well. Also, if one tested the count kernel over the 3 groupings, power would be conserved.

Table 3.

Power results for Setting 1. Each cell in the table corresponds to the power of SKAT using a kernel constructed based on the testing procedure at the top of the table and the grouping strategy at the left of the table. Rows and columns labeled MK-SKAT correspond to the omnibus tests across tests (with fixed group) and across groupings (with fixed test). The cells with both rows and columns labeled MK-SKAT correspond to the omnibus test across all test and groupings

	C-alpha	SKAT	CAST	Count	MK-SKAT
n=1,000
0.5%	0.43	0.43	0.64	0.66	0.64
1%	0.74	0.76	0.84	0.85	0.86
3%	0.47	0.64	0.63	0.63	0.71
MK-SKAT	0.69	0.72	0.81	0.85	0.84
n=2,000
0.5%	0.70	0.71	0.85	0.87	0.87
1%	0.92	0.93	0.98	0.98	0.98
3%	0.76	0.89	0.88	0.88	0.92
MK-SKAT	0.92	0.93	0.97	0.98	0.97

Table 5.

Power results for Setting 3. Each cell in the table corresponds to the power of SKAT using a kernel constructed based on the testing procedure at the top of the table and the grouping strategy at the left of the table. Rows and columns labeled MK-SKAT correspond to the omnibus tests across tests (with fixed group) and across groupings (with fixed test). The cells with both rows and columns labeled MK-SKAT correspond to the omnibus test across all test and groupings

	C-alpha	SKAT	CAST	Count	MK-SKAT
n=1000
0.5%	0.26	0.26	0.31	0.32	0.33
1%	0.53	0.55	0.52	0.50	0.59
3%	0.73	0.78	0.69	0.69	0.78
MK-SKAT	0.77	0.79	0.72	0.73	0.80
n=2000
0.5%	0.52	0.53	0.47	0.48	0.57
1%	0.75	0.77	0.70	0.69	0.78
3%	0.84	0.88	0.82	0.80	0.88
MK-SKAT	0.90	0.91	0.85	0.86	0.91

In Setting 2, power was dramatically decreased for the count and CAST kernels compared to Setting 1 (Table 4). This was due to the true model having bidirectional genetic effect on the outcome. Some rare variants increased the outcome, while some decreased the outcome. Compared to Setting 1, power was reduced for C-alpha and linear weighted kernels, but not to the same extent as count and CAST. C-alpha and linear weighted kernels applied to the variants with MAF <1% performed the best in Setting 2. MK-SKAT testing over all 12 kernels displayed power somewhat less than the most powerful single kernel, but much greater than any of the CAST or count kernels. If one applied MK-SKAT over the three groupings of the linear weighted kernel, power would be nearly equivalent to the most powerful single kernel. This setting clearly showed the adaptability of the MK-SKAT method under variation in the genotype/phenotype structure.

Table 4.

Power results for Setting 2. Each cell in the table corresponds to the power of SKAT using a kernel constructed based on the testing procedure at the top of the table and the grouping strategy at the left of the table. Rows and columns labeled MK-SKAT correspond to the omnibus tests across tests (with fixed group) and across groupings (with fixed test). The cells with both rows and columns labeled MK-SKAT correspond to the omnibus test across all test and groupings

	C-alpha	SKAT	CAST	Count	MK-SKAT
n=1000
0.5%	0.37	0.37	0.10	0.12	0.32
1%	0.63	0.65	0.17	0.23	0.57
3%	0.39	0.54	0.13	0.16	0.46
MK-SKAT	0.60	0.63	0.16	0.23	0.55
n=2000
0.5%	0.68	0.69	0.15	0.17	0.61
1%	0.87	0.88	0.26	0.36	0.84
3%	0.63	0.80	0.17	0.23	0.72
MK-SKAT	0.87	0.89	0.27	0.36	0.83

Setting 3 compared power between methods for a dichotomous outcome (Table 5). The linear weighted kernel applied to the variants with MAF <3% performed the best. They were best adapted to the true model where only 20% of the variants were truly causal, and rare variants with MAF <3% were sampled as causative. MK-SKAT testing over all 12 kernels had power slightly greater than the most powerful single kernel, though this is likely to be within the range of monte carlo error. If one applied MK-SKAT to the three groupings using either the linear weighted or C-alpha kernel, power would nearly equivalent to the most powerful single kernel.

Overall, results show that while protecting type I error, the MK-SKAT can achieve power close to using the optimal test and grouping strategy. While there is generally some modest loss in power relative to the best choice, the proposed omnibus tests offer considerably better power than poor choices and represent a reasonable compromise. If one is able to restrict attention to a particular group of variants based on prior information or to a particular testing procedure based on hypotheses of the underlying model, then power can be further increased by restricting the MK-SKAT to fewer tests or fewer groupings.

3.2 Data analysis

We examined the performance of our proposed method on a high-depth sequence data set with 2,000 subjects from the CoLaus population-based collection [7]. Briefly, we examined a single candidate gene containing 86 variants of which the majority had allele frequency less than 3%. Eight variants were non-synomymous and two were predicted to be harmful. This gene is a drug target which has been shown to be associated with obesity and cardiovascular related outcomes. In addition to genotype information, we had 42 separate traits, most of which are related to obesity and cardiovascular measures, and additional demographic covariates including age, gender and the top five eigenvalues of genetic variability derived from the GWAS data. We illustrate the MK-SKAT procedure by applying it to identify which of the 42 outcome traits are associated with the rare variants within this candidate gene.

We specifically considered testing using CAST, count based collapsing, weighted count based collapsing, the C-alpha, and the default SKAT. For groupings, we considered using all of the variants in the region, the variants with MAF <3%, variants with MAF <1%, variants with MAF <0.5%, nonsynonymous variants, and variants predicted to be harmful. In total we considered 27 different kernels based on combinations of the test choice and grouping choice — the CAST, count based collapsing, and weighted count based collapsing were not applied to all of the variants. In addition to applying SKAT with each of the candidate kernels, we also applied the MK-SKAT testing across all 27 kernels.

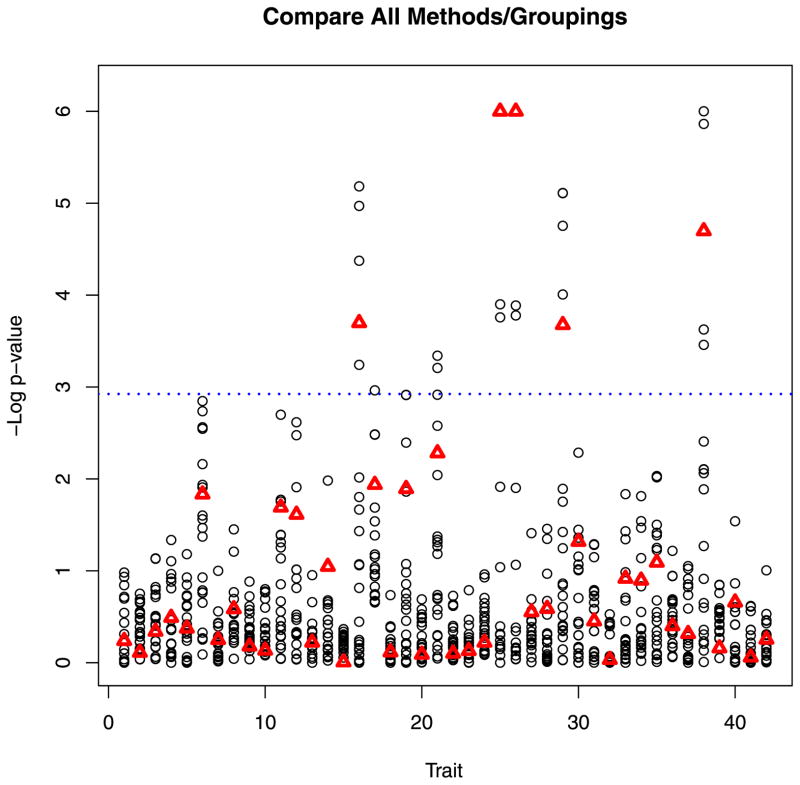
Analysis results are presented in Figure 1, with p-values truncated at 10⁻⁶. Several p-values would have met the threshold for significance and will be presented elsewhere. Given that the candidate gene was selected as a positive control and that many of the outcome measures are closely related, these results are in line with what we would anticipate. However, for the purposes of illustrating our methodology, the individual p-values are not particularly interesting. The key result is that for many traits, using different methods and different groupings resulted in very different results in terms of significance. MK-SKAT did not tend to have the smallest p-values. In general, MK-SKAT tended to yield results slightly less significant than those using the best kernel (choice of test and grouping strategy). However, MK-SKAT still performed considerably better than poor choices of kernels.

Figure 1.

Real data analysis results. Each column of circles corresponds to the p-values from analyzing a different trait while each circle represents the p-value from a different kernel. The triangle indicates the p-value from applying MK-SKAT to all of the kernels. p-values have been truncated at 10⁻⁶. The dashed line indicates the bonferroni significance level.

3.3 Computational run time

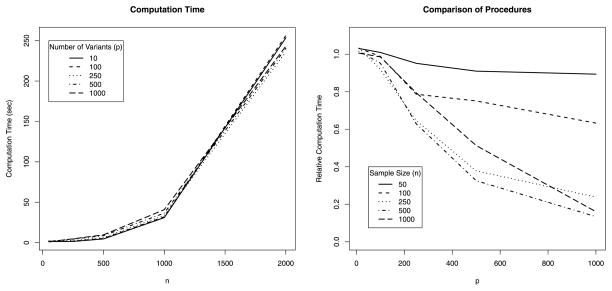
We examined the computational efficiency of the MK-SKAT procedure. Specifically, we considered the run time associated with running MK-SKAT to analyze a region with p observed variants in n individuals assuming that we would like to consider 12 kernels constructed by considering count based collapsing, weighted count based collapsing, SKAT and C-alpha tests with grouping thresholds of 1%, 3% and 5%. This differs slightly from the earlier simulations and was adjusted in order to accommodate the wider range of sample sizes and observed variants under consideration. However, the computational results should not change as the kernels and relative complexity are still the same. Results are presented in the left panel of Figure 2 and show that the run time increases with sample size. Although there are some differences in the computation time for situations with different numbers of variants, such were small compared to differences in run time from increased sample size. This is in part because the kernel machine framework requires working with n×n kernel matrices, irrespective of the dimensionality.

Figure 2.

Computational runtime as a function of sample size for the proposed algorithm (left panel) and the relative computational cost of the current procedure relative to a previous procedure for multi-kernel testing [26] (current/previous) as a function of the number of variants and sample size (right panel).

As noted earlier, the testing procedure developed in this project is based on our previous work [26]. However, technical adjustments were made due to improve computation within the context of rare variant analysis with many possible kernels. To illustrate the improvement in computation, we further compared the relative computational expense of the current MK-SKAT procedure to our previous procedure. The results are presented in the right panel of Figure 2 with the relative run times (run time of our current procedure divided by run time of the previous procedure) as a function of sample size and number of observed variants. When the sample size is large and when the number of variants under consideration increases, our current procedure can be considerably faster. On the other hand, when the number of variants is modest, then the previous procedure can be slightly faster though the difference is small.

4. DISCUSSION

In analysis of genetic rare variants, given the difficulties associated with selecting a test and selecting a particular group of variants to test, MK-SKAT allows investigators to agnostically consider several different, popular, testing approaches as well as several different ways of thresholding the variants. Although there is some loss of power compared to the best single test and best grouping, the power is still considerably higher than when using a poor choice of test or a poor choice of grouping strategy while still conserving type I error.

Restriction of the MK-SKAT to a smaller set of possible kernels (i.e. smaller set of tests or groupings) can yield higher power if the considered kernels are closer to the best test and grouping strategy. If such information is available, such as through previous studies of common variants within the region or through bioinformatics knowledge, we strongly encourage investigators to directly restrict interest to a smaller group of candidate kernels. On the other hand, in the absence of reliable prior knowledge, we recommend consideration of a wide range of kernels. Importantly, if kernels are very similar to one another, then the perturbation procedure will accommodate the correlation and will not penalize the significance as much as if the considered kernels are more different.

We acknowledge that the computational expense of MK-SKAT can be high with larger sample size, making it difficult to analyze large, genome-wide sequencing studies, but a simple approach to decrease this burden would be to first screen using each of the candidate kernels individually. If none of the individual kernels are close to significance, then MK-SKAT is unlikely to yield a significant result. Since the majority of genetic regions are not related to outcomes, applying MK-SKAT to only the promising genetic regions can considerably reduce the overall computational expense of analyzing any real experiment. Further computational improvements may be possible using powerful, new (i.e., parallel or grid) computing technologies and represent an area of future research.

Interestingly, while several methods are special cases of SKAT, some other methods are special cases of the MK-SKAT. The variable threshold test [23] is equivalent to MK-SKAT when the kernels under consideration are based on a single testing approach with only the variable grouping being varied. However, we note that use of perturbation still offers computational advantage over the threshold test. Similarly, the SKAT-O method [12] is equivalent to MK-SKAT in which the variable grouping is fixed but one is considering a range of linear combinations of SKAT and collapsing kernels. Thus, in comparison to SKAT-O, MK-SKAT would tend to excel when the ideal variable grouping is not chosen for SKAT-O. MK-SKAT buffers against a broad range of variable groupings since many can be tested simultaneously.

Further methods may also fall within the MK-SKAT framework, but although many popular tests can be considered using MK-SKAT, there are certainly many useful tests that fall outside. For example, tests that use the outcome information in order to estimate weights for variants [11, 10, 8, 14] cannot be applied. While these tests still can be considered special cases of SKAT, the kernel is now estimated using the outcome such that standard asymptotics for SKAT and the perturbation based techniques for MK-SKAT cannot be used to obtain p-values. Further statistical work is needed in order to allow the MK-SKAT procedure to encompass these methods.