Dissociation between location and shape in visual space

Abstract

There are often large perceptual distortions of shapes lying on the ground plane, even in well-lit environments. These distortions occur under conditions for which the perception of location is accurate. Four hypotheses are considered for reconciling these seemingly paradoxical results, after which 2 experiments are reported that lend further support to one of them–that perception of shape and perception of location are sometimes dissociable. The 2 experiments show that whereas perception of location does not depend on whether viewing is monocular or binocular (when other distance cues are abundant), perception of shape becomes more veridical when viewing is binocular. This means that perception of shape is not fully constrained by the perceived locations of the vertices that define the shape.

Dissociation between location and shape in visual space

Striking failures of shape constancy are commonplace in natural environments viewed under full cues. As an example, Figure 1 shows two views of a portion of a popular walkway in Barcelona, Spain. The gray and white tiles define a sinusoidal profile of constant modulation depth (in the direction of the walkway) and constant wavelength (in the orthogonal direction). Conflicting sharply with the constant physical depth modulation is the strong impression of a decreasing modulation with distance that disappears within just a few meters; this impression holds whether viewing the figure or binocularly viewing the walkway in person. The variation in apparent depth modulation (upper panel) is a striking failure of shape constancy in the presence of abundant distance cues. Similarly, when one looks sideways at the walkway (bottom panel), the undulation appears to exaggerate with increasing distance—another striking failure of shape constancy.¹

Figure 1.

Two views of Las Ramblas walkway in Barcelona, Spain. The gray and white tiles define sinusoidal stripes extending from one edge of the walkway to the other, stripes that are uniform in modulation depth along the length of the walkway. Contrasting with the uniform stimulus, visual perception exhibits a dramatic failure of shape constancy, even when one views the walkway binocularly under good lighting conditions. Specifically, when one looks down the length of the walkway, the depth modulation appears to decrease with distance, as is apparent in the top panel of the figure. Conversely, when one looks to the side, the curvature of the sinusoidal modulation appears to increases with distance, as is apparent in the bottom panel of the figure.

A number of experiments have confirmed that failures of shape constancy in the natural world are robust and commonplace. In many of these experiments, perceived shape is assessed by having observers match a width extent (in a frontoparallel plane) by an adjoining depth extent (in the median sagittal plane). In one such experiment (Loomis, Da Silva, Fujita, & Fukusima, 1992), observers adjusted depth extents defined by targets on the ground to be physically equal to width extents, also defined by targets on the ground. Even under these "objective instructions", depth extents positioned from 3 to 12 m away had to be made 1.5 to 1.9 times as large as the width extents in order to be judged as equal. In a related experiment, Beusmans (1998) obtained evidence of even greater distortion, again using objective instructions. In his experiment, observers adjusted the width extents to match the depth extents. For small extents positioned more than 15 m away, observers judged width extents to be equal to depth extents that were 2.5 to 5 times larger! Other evidence of systematic perceptual distortion of shape has been obtained using slightly different procedures and stimuli (Baird & Biersdorf, 1967; Levin & Haber, 1993; Loomis & Philbeck, 1999; Norman, Todd, Perotti, & Tittle, 1996; Philbeck, 2000; Ribeiro, Fukusima, & Da Silva, 1995; Tittle, Todd, Perotti, & Norman, 1995; Todd, Tittle, & Norman, 1995; Toye, 1986; Wagner, 1985). Perceptual distortions of related origin have also been reported in connection with the judgment of the slants of hills (Bhalla & Proffitt, 1999; Proffitt, Bhalla, Gossweiler, & Midgett, 1995) and of the angles of corners of buildings (Hecht, van Doorn, & Koenderink, 1999). Also, in the above cited article (Beusmans, 1998), a second experiment was reported that involved the matching of two depth extents within the median sagittal plane, one more distant than the other. Here too, evidence of large perceptual distortion was obtained, with the farther extent being nearly twice as large as the nearer one in order for them to be judged as equal. All of these experiments indicate large distortions of shape and relative extent under full-cue viewing.

These failures of shape constancy under full cue viewing are not unexpected when one considers the enormous challenge that the visual system must confront when processing shapes that vary greatly in perspective. For example, a little appreciated fact, even among vision researchers, is the degree of anisotropy in the perspective of patterns viewed at a slant (see Gillam, 1981). As a square pattern moves along the ground away from a viewing point, its angular width is approximately inversely proportionally to its distance; meanwhile, its angular height (corresponding to depth in the ground plane) is approximately inversely proportional to the square of its distance (Gillam, 1981; Purdy, 1960). The ratio of angular height to angular width is equal to the cosine of the optical slant, which is the angle between the normal to a surface patch and the line of sight to that patch (Gibson & Cornsweet, 1952; Joynson, & Newson, 1962; Kaiser, 1967; Purdy, 1960, Sedgwick, 1983; Wallach & Moore, 1962); for a person of average height, the “aspect ratio” of a small square texture element 10 m away is only 0.17.

Despite the large changes in perspective of a target as it varies in distance, there is by no means a complete absence of shape constancy. Humans are able to compensate partially for the retinal perspective and consequently perceive shapes closer to the distal (e.g., Beck & Gibson, 1955; Joynson & Newson, 1962; Pizlo, 1994; Pizlo & Stevenson, 1999; Sedgwick, 1986; Thouless, 1931). Loomis and Philbeck (1999) found that judgments of the aspect ratios of L-shaped objects on the surface plane were roughly midway between the distal and retinal values.

Another result obtained by Loomis and Philbeck (1999) is that the degree of perceptual distortion increased slightly with egocentric distance of the L-shaped objects, a result also apparent in the extent matching results of Beusmans (1998) and Loomis et al. (1992). At first glance, it might appear that the increasing perceptual shape distortion with distance is the consequence of diminishing effectiveness of distance cues, such as accommodation, convergence, and binocular disparity. However, by using projectively equivalent L-shaped figures at two scales differing by a factor of 3, Loomis and Philbeck (1999) found that the degree of distortion was independent of scale for monocular viewing and nearly so for binocular viewing; their finding suggests that the perceptual shape distortion is much more dependent on the optical slant of the 2-D pattern being judged than on its egocentric distance, whether physical or perceived.

Given the above mentioned misperceptions of shape and extent, one might expect that perception of egocentric distance under the same conditions would also exhibit substantial error, possibly in the form of a compressively nonlinearity between physical and perceived distance (e.g., Gilinsky, 1951). Yet a number of recent studies using "visually directed action", such as blind walking toward a previewed target, have demonstrated that perception of egocentric distance under similar conditions is both linear in physical distance and accurate out to at least 20 m (Elliott, 1986, 1987; Fukusima, Loomis, & DaSilva, 1997; Loomis et al., 1992; Loomis, Klatzky, Philbeck, & Golledge, 1998; Philbeck & Loomis, 1997; Philbeck, Loomis, & Beall, 1997; Rieser, Ashmead, Talor, & Youngquist, 1990; Sinai, Ooi, & He, 1998; Steenhuis & Goodale, 1988; Thomson, 1983; for a summary see Loomis and Knapp [in press]). The accuracy with which egocentric distance is perceived appears to conflict with the systematic misperception of shape and extent under similar conditions.

Four Hypotheses

Loomis et al. (1992) and Philbeck (2000) have presented three hypotheses that might potentially reconcile the accurate egocentric responding with the systematic distortion of shape and of perceived extents. Here we add a fourth. The four hypotheses need not be exclusive.

Before presenting the hypotheses, we define some terms. "Egocentric distance" is the distance between a target location and the observer. Strictly speaking, egocentric distance is measured only along a radial direction from the observer (a line of sight), but occasionally we use it to refer to distance along a horizontal plane (e.g., the ground) in those cases where the primary variation is in a radial direction. "Perceived egocentric distance" is the corresponding perceived distance. "Perceived location" is given by the perceived egocentric distance of a target and its perceived direction, which is generally considered to be accurate (for clear evidence, see Ooi, Wu, & He, 2001). "Exocentric distance" is the distance (extent) between two target locations, neither of which coincides with the observer. (In the vision literature, exocentric distance often has meant the separation between two locations in a radial direction, but we do not so restrict the meaning here). "Perceived exocentric distance" is the perceived extent between two locations. "Perceived shape" of a two-dimensional figure in 3-D space is assumed to be determined by the perceived exocentric distances between its various vertices; for example, the perceived shape of a rectangle lying on the ground and oriented toward the observer is determined by the ratio of its perceived width (in a frontoparallel plane) and its perceived depth (in the median sagittal plane). A "depth extent", strictly speaking, is an exocentric distance lying in a radial direction. In the presentation of the empirical findings above, what were referred to as depth extents (those lying in both the ground plane and the median sagittal plane) were not depth extents in the strict sense, for they did not lie along lines of sight; still, most of their variation was in a radial direction. For ease of exposition, we will continue to use the less strict meaning. The definition of a "width extent" is even more problematic, for points along any straight line necessarily vary in distance from the observer. However, line segments that subtend only a few degrees and which are both symmetric about and perpendicular to a line of sight are prototypical of what we mean by width extents.

Hypothesis 1: Accurate Perception of Location and Dissociation of Location and Shape

This is the hypothesis first put forth by Loomis et al. (1992) and later elaborated by Loomis, DaSilva, Philbeck, and Fukusima (1996). It assumes that location is perceived accurately (i.e., without systematic error) out to at least 20 m under full cue conditions. Because perceived shapes under the same conditions are perceived with large systematic error, the hypothesis further assumes that the perception of extent and of shape is based on neural computations different from those involved in the perception of location. In particular, it assumes that the perception of extent and of shape is not fully constrained by the perceived locations of the vertices defining the extent/shape (see also Baird & Biersdorf, 1967). This means that the perception of extent/shape can vary even when the perceived locations of the vertices defining the extent/shape remain constant. Strong support for this idea in the context of reaching and grasping has been provided in recent experiments by Bingham (2001) and by Crowell, Todd, & Bingham (2001). A similar idea has been proposed in connection with 2-D shapes viewed in a frontoparallel plane (Abrams & Landgraf, 1990; Gillam, 1998; Gillam & Chambers, 1985; Mack, Heuer, Villardi, & Chambers, 1985; MacLeod & Willen, 1995; Post & Welch, 1996).

Hypothesis 2: Accurate Perception of Location and Anisotropy of Perceived Extent

According to this hypothesis, based in part on a model originally posed by Foley (1991) and subsequently revised by Foley, Ribeiro-Filho, and DaSilva (2001), a unified visual space exists in which perceived locations fully constrain the perceived extents. However, the model further predicts that perceived depth extents differ from perceived width extents–the metric for perceived extent is computed in terms of the polar coordinates (direction and egocentric distance) of perceived locations and gives greater weight to directional change than to change in egocentric distance. Hypothesis 2 goes beyond the model of Foley et al. (2001) in assuming that locations on the ground plane are accurately perceived in both visual direction and egocentric distance when distance cues are abundant. Thus, this hypothesis can explain both the accurate perception of location and the perceptual inequality of depth and width extents and thus distortion of 2-D shape. Unlike Hypothesis 1, Hypothesis 2 predicts that there cannot be changes in perceived extent/shape without there being accompanying changes in the perceived locations defining the extent/shape.

Hypothesis 3: Correction of Misperceived Distance

This hypothesis consists of two assumptions: (1) perceived egocentric distance is a compressively nonlinear function of physical distance and (2) through experience, calibration of the output transform between perceived distance and the observer’s response can compensate for the nonlinearity between physical distance and perceived distance, enabling accurate responding to physical distance. For example, suppose a target 20 m away consistently appears to be 15 m away. Through experience, an observer could learn that he/she needs to walk 20 m to arrive at a target that appears 15 m away. In using it to reconcile shape distortion with accurate egocentric responding, one would further assume that perceived extents correspond to a metric computed on the perceived locations in this distorted space. Because a compressive nonlinearity between physical and perceived egocentric distance (e.g., a power function with exponent less than one) would result in greater foreshortening of depth extents than width extents (for a wide range of metrics), perceived depth extents are smaller than perceived width extents of equal physical length. Thus, shape matching and shape judgment tasks ought to reflect the perceived distortion because both tasks involve a direct perceptual comparison of the two extents prior to any output transform that results in some form of judgment.

Hypothesis 4: Two Visual Systems

According to this hypothesis, visually-based action is controlled by a visuomotor system distinct from that underlying conscious visual experience, the latter of which is the basis for the visual matching task. Considerable support for two functionally distinct visual systems, the parietofrontal system and the occipitotemporal system, has accrued over the years from research with both brain damaged patients (e.g, Marotta, Behrmann, & Goodale, 1997; Milner & Goodale, 1995; Weiskrantz, 1986, 1990) and neurologically intact observers (e.g, Aglioti, DeSouza, & Goodale, 1995; Bhalla & Proffitt, 1999; Bridgeman, 1999; Bridgeman, Peery, & Anand, 1997; Creem & Proffitt, 1998; Haffenden & Goodale, 1998; Proffitt et al., 1995; Servos, 2000; Servos & Goodale, 1994).

As stated above, the four hypotheses are not mutually exclusive. It is likely that understanding the accurate perception of location under visual conditions where shape constancy fails will ultimately require two or more of the hypotheses. In what follows, we note some of the weaknesses of the various hypotheses.

A weakness of Hypothesis 4 (Two Visual Systems) is that non-motoric measures of perceived egocentric distance (e.g. verbal report of distance and measures based on judgments of perceived size) are often in close agreement with those based on visually directed action; in particular, reducing the availability of distance cues has very similar effects on both measures (large scale: Loomis et al., 1998; Loomis & Knapp, in press; Philbeck & Loomis, 1997; small scale: Foley 1977, 1985). These results indicate that open-loop visually directed action is controlled by the same internal variable, perceived target location, that underlies the non-motoric measures. (In contrast, closed-loop visually guided action, action that is guided by continuously available visual information, might be controlled in an altogether different way).

There are at least two weaknesses associated with a Hypothesis 3 (Correction of Misperceived Distance). First, few if any observers ever walk blindly to previewed targets more than 3 m away, so there should be little opportunity for the hypothesized correction of the perceptual errors associated with distances beyond 3 m. Second, the first author and his colleagues have conducted a number of experiments involving variants of visually directed action, the results of which are inconsistent with the idea of a nonlinearity in the walking response that compensates for the presumed nonlinearity of visually perceived distance. In “triangulation by pointing”, the observer views a target and then walks blindly along an oblique path, while attempting to continue pointing in the direction of the previously viewed target (Fukusima et al., 1997; Loomis et al., 1992). In “triangulation by walking”, the observer views a target and then walks blindly along an oblique path; at some unexpected location, the observer is instructed to turn and begin walking toward the target (Fukusima et al., 1997). In still another variant, the observer walks blindly along an oblique path, turns when instructed, and then attempts to walk the full distance to the target (Loomis et al., 1998; Philbeck et al., 1997). When distance cues are abundant, observers walked without systematic error, whether they walked along a direct or indirect path (Loomis et al., 1998; Philbeck et al., 1997); however, when distance cues were sparse, observers made the expected errors of overwalking to near targets and underwalking to far targets (Philbeck et al., 1997). In both full-cue and reduced-cue conditions, the mean responses (centroid of stopping points) for the direct path were very close to those for the indirect path. This pattern of results refutes the idea of a nonlinearity in the response process that compensates for the presumed nonlinearity of visually perceived egocentric distance. Although Hypothesis 3, as stated, appears untenable, it is possible that a more general interpretation of Hypothesis 3 is tenable, one which does not involve calibration through experience and which involves a compensating nonlinearity in a general response process rather than in one tied to a specific motor response (e.g., walking along a direct path).

The two remaining hypotheses are not contradicted by existing evidence but they do suffer from a vagueness about the underlying computational mechanisms. Still, the two hypotheses separately or in combination seem promising for explaining the paradoxical result of accurate perception of location under conditions where shape distortion also occurs.

The two experiments reported here lend further support to Hypothesis 1 in showing that perceived shape can vary even though the perceived locations of the vertices defining the shape do not. We report two experiments which complement each other. The results of Experiment 1 are more robust but were obtained with methods that leave some ambiguity about the interpretation. The results of Experiment 2 are less striking but are more definitive in their interpretation.

Experiment 1

Method

Observers

Sixteen observers (10 male, 6 female) from the University of California at Santa Barbara (UCSB) community were paid for their participation. Their ages ranged from 20 to 29 years (M = 24), and all were naive about the purposes of the experiment. Their visual acuity was at least 20/20 (corrected if necessary), as measured by Keystone Orthoscope. All observers were within normal limits of lateral phoria and had good stereoacuity (25 s of arc or better). The observers were randomly assigned to participate in either the monocular-viewing group or the binocular-viewing group, with 8 observers in each group.

Stimuli, apparatus and design

An original aim of this study was to create two viewing configurations that were nearly projectively equivalent but differed in scale by a ratio of approximately 8:1. The stimuli were two sets of white spheres, 9.8 cm and 1.2 cm in diameter. The precise scale ratio (8.2) we used was determined by the sizes of these spheres. The large scale stimuli were seen resting on the floor of a carpeted indoor laboratory (7.3 m × 4.3 m). Each observer viewed these stimuli from an eye height of 150 cm; eye height was controlled by means of a chinrest. This standing chinrest apparatus has been described elsewhere (Philbeck & Loomis, 1997), and could be easily swung out of the way to permit the observer to walk toward the stimulus after viewing it. The small-scale stimuli were positioned on a rectangular board (89 cm × 53 cm), painted with a speckled texture that closely resembled the laboratory carpeting. The height of this horizontal surface was adjusted for each observer to yield an eye height of 18.3 cm when the observer’s head was held in a nearby chinrest. The viewing distances also varied by the same 8:1 factor across the two scales (large scale: 200, 300, and 400 cm; small scale: 24.4, 36.6, and 48.8 cm). These distances were measured along the horizontal viewing surface from a point directly below the observer's eyes to the stimulus sphere (or to the nearest sphere in trials presenting several spheres in combination). The stimuli at the nearest locations of the two scales were viewed at the same optical slant so that the spheres and their immediate backgrounds were virtually identical in monocular perspective; the same was also true for the intermediate and farthest distances.

Other than the between-groups monocular/binocular manipulation, all other factors were varied within observers. Each observer performed two perceptual tasks, Location judgments and extent matches. (1) Location responses: Observers indicated the location of a single sphere without visual guidance, either by attempting to walk to it (large scale) or by attempting to place the tip of the index finger there (small scale). (2) Extent matches: Observers attempted to adjust the depth extent between two spheres to match the width extent of two spheres. These extents were specified by a total of three spheres, presented in an L-shaped configuration. The depth extent was specified by two spheres lying on the ground in the observer’s median sagittal plane; the nearest sphere of this pair, together with a third sphere displaced to the observer’s right in a frontoparallel plane, specified the width extent. The lateral displacement of the third sphere was 50 cm and 6.1 cm for the large and small scales, respectively.

The scale manipulation was blocked and counterbalanced, with four observers in each group seeing the small scale stimuli first and the rest, the large scale stimuli first. Within each scale block, location responses were made first and then extent matches. On each trial, the stimuli appeared at one of the three possible distances listed above.

On match trials, perceptual matches were created using both ascending and descending series, with two measurements collected apiece. Three measurements per condition per observer were collected on location trials. Within blocks, the presentation order was completely randomized.

Procedure

The observers wore hearing protectors (noise reduction rating: 25 dB) to minimize auditory localization information. Monaural sound was presented via a wireless microphone system (Telex AAR-1 and TW-6); the observer carried an FM receiver/amplifier and wore small headphones underneath the hearing protectors, and the experimenter wore a microphone and transmitter (for more details, see Philbeck et al., 1997). The observers began each trial with his or her head immobilized in a chinrest. For the monocular group, the lateral position of the chinrest was adjusted so that the observer’s uncovered dominant eye was in the same sagittal plane as an imaginary line that connected the three possible egocentric stimulus distances. For the binocular group, the chinrest was positioned so that the midpoint between the eyes lay in this plane. The markers used to position the stimuli at both scales were invisible to the observer. No error feedback was provided in any of the following four trial types.

Large Scale, Location Responses

The observer viewed the single stimulus sphere for approximately 5 sec. Afterwards, the observer lowered a blindfold, swung the chinrest to the side, and attempted to walk to the stimulus location. The stimulus was removed from the observer’s path before walking began. The experimenter recorded the walked distance as the straight-line distance from the observer’s starting position to the terminal position. After recording the walked distance, the experimenter guided the observer (still blindfolded) back to the starting location.

Small Scale, Location Responses

The observer viewed the stimulus sphere for approximately 5 sec, then closed the eyes, and, using the dominant hand, attempted to place the tip of the index finger at the stimulus location. The stimulus was removed before the observer began to move. The observer was instructed to first raise his/her hand above the horizontal board and then lower the finger to the stimulus location. This instruction prevented the observer from moving his or her hand along a line of sight until the index finger met the table, a response that could yield accurate performance without relying upon distance perception.

Extent Matches (large and small scales)

The observer viewed the configuration of 3 spheres. On ascending trials, the far sphere of the depth pair was initially placed just behind the near sphere; on descending trials, the far sphere was initially placed approximately 2.5 to 3 times farther behind the near sphere than the lateral separation between the width pair of spheres. The observer then directed the experimenter to move the far sphere closer or farther until the separation between the depth pair matched the separation between the width pair (objective instructions). To prevent the observer from being able to scale the distance relations by relying upon motion parallax during the adjustment, the observer closed his or her eyes after each directional instruction (“closer” or “farther”). The experimenter then moved the sphere by some small amount in the indicated direction while the observer’s eyes were closed.

Results

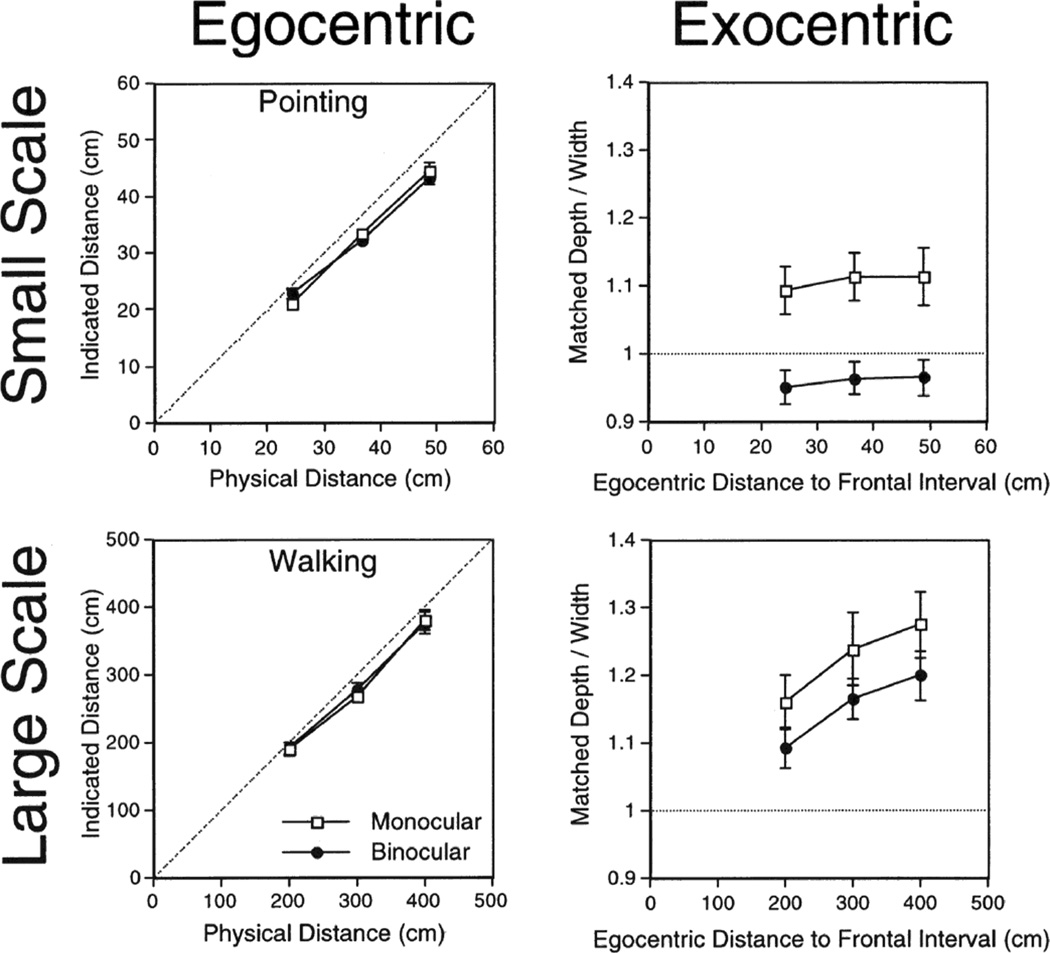
Figure 2 gives the results of Experiment 1. Because response to visual direction is usually without systematic error in such a task, we measured only distance responses. The left-hand panels clearly show that location responses were unaffected by the monocular/binocular manipulation, at both the small and large scales. In striking contrast, the upper right-hand panel shows that this manipulation had a large effect upon the small-scale matching of extent. On average, extent matches made under monocular vision were nearly 15% larger than those made under binocular vision, even though judgments of location made under the same viewing conditions showed no hint of this effect. At the larger scale, where the monocular and binocular views were much more similar, this effect was attenuated.

Figure 2.

Results of Experiment 1. The left panels give the results for the distance responses for monocular and binocular viewing. The error bars, where visible, represent ± 1 SE of the individual observer means. The right panels give the results for the extent matches for monocular and binocular viewing. The error bars represent ± 1 SE of the individual observer means.

To make the indications of distance comparable across scale, the walking and pointing responses were converted to a signed percentage of the target distance before analysis. An analysis of variance (ANOVA) confirmed that the distance judgments were not statistically different between the monocular and binocular groups (F(1, 14) = .09; p > .05); both groups showed a slight underestimation of about 8% of the target distance. The responses also did not differ across scale (F(1, 14) = 1.63; p > .05), even though different motor effectors were used to produce the responses, and there was no Group × Scale interaction (F(1, 14) = .013; p > .05). In fact, none of the main factors and none of their interactions reached significance.

Each matching response was converted to a ratio between the depth extent set by the observer and the width extent. A separate ANOVA performed on these ratios revealed a main effect of the monocular/binocular manipulation (F(1, 14) = 6.12; p = .026), but this was qualified by a significant interaction with scale (F(1, 14) = 5.33; p = .037). Matching ratios were generally smaller for the binocular group, but this difference was most pronounced at the small scale. The matching ratios of both groups tended to increase with the egocentric distance of the stimulus configuration within each scale (F(2, 28) = 8.71; p < .01), but this effect was significant only at the large scale (F(2, 28) = 9.08; p < .001). Matches made under ascending and descending series did not differ significantly (F(1, 14) = 1.66; p > .05). There were no other significant effects.

Immediately following the experimental trials, two observers in the monocular group switched to binocular viewing for a second half of the experiment, and two from the binocular group switched to monocular viewing. We suspected that any effects of viewing condition on extent matches would be observable within observers and wanted to verify this. However, preliminary data from these four observers showed that there were strong carry-over effects between the viewing condition blocks. After viewing stimuli monocularly, observers continued to exhibit a “monocular” pattern of responses under binocular viewing (see Figure 2). Similarly, observers who initially viewed stimuli binocularly continued to produce a “binocular” pattern of responses under monocular viewing. It is possible that these carry-over effects are due to perseveration in response strategies and not perseveration in perceived locations and/or perceived shape. However, rather than investigating this issue, which was tangential to our primary goal, we elected to present only the data obtained in the first block for these four observers.

Discussion

The major result of the experiment² is that, for large and small scales, the monocular/binocular manipulation had a large effect on perceived shape, as measured by the extent matching task, but absolutely no effect on perceived location, as measured by the walking and pointing tasks. This is consistent with a dissociation between the perception of shape and the perception of location.

As mentioned in the introduction, there is accumulating evidence of a dissociation between conscious visual perception and visually-guided action even among neurologically intact observers. Because the egocentric distance judgments in Experiment 1 were action-based while the shape judgments were not, there is the possibility that the results of these experiments simply reflect the operation of two visual pathways, one concerned with conscious visual awareness and the other with visuomotor control (Hypothesis 4). Indeed, other research has shown, in the context of reaching and grasping, that the binocular/monocular manipulation has an influence on visuomotor responses but none at all on location-based responses associated with conscious perception (Marotta et al., 1997; Servos, 2000; Servos & Goodale, 1994). In addition, because of the different types of responses, there is the possibility that the results might be interpretable under Hypothesis 3 (Correction of Misperceived Distance). To discriminate between Hypothesis 1 and these two alternatives (Hypotheses 3 and 4), we conducted Experiment 2 using verbal reports for both judgments of stimulus distance and stimulus shape.

Experiment 2

Method

Observers

Eight UCSB undergraduates (5 male and 3 female) participated as observers. Their ages ranged from 16 to 24 years, with a median age of 21. Each was paid for participation in the two 1-hour experimental sessions. Visual acuity was verified to be at least 20/30 (corrected if necessary) for all observers. Stereoacuity was also verified to be 25 s of arc or better for all observers, measured with a Keystone (Meadville, PA) orthoscope.

Stimulus Configuration

Ten L-shaped stimuli were constructed of black-painted cylindrical steel rods, approximately 2 mm in diameter. Sizes and aspect ratios of the stimuli are shown in Table 2. The stimuli were presented to the observer on a 3 m × 0.4 m surface, with a random textured, light-colored surface shading. The observer's eye height was set to a fixed position 40.6 cm above the surface using a chin-rest apparatus. Eight potential stimulus distances from the observer were chosen, ranging from 0.75 m to 2.5 m in steps of 0.25 m. It was also possible to rotate the entire experimental apparatus 180 degrees in the room in which the experiment was conducted. This rotation afforded changing the viewed background of the room between experimental sessions.

Table 1.

L-shaped figure aspect ratios used in Experiment 2 as a function of the base width of the stimulus.

Values marked with an asterisk are 'test’ values.

Design and Procedure

A total of 54 trials were presented to the observer over the course of an experimental session. Half of the trials were considered "dummy" trials and half "test" trials. We included the dummy trials because we wanted to collect extensive data on just one aspect ratio but wished the observers to be exposed to a wider range of aspect ratios. The test trials consisted of the following stimulus/distance combinations: all L-shapes with aspect ratio 2.0, and distances of 1.0, 1.5, and 2.0 m. Each possible stimulus/distance combination from this subset was presented 3 times, for a total of 27 trials. The remaining 27 trials consisted of a random selection of stimuli/distance combinations. The presentation order of all trials was randomized, such that the presentation of "dummy" or "test" trial on any given trial was equally probable. The largest stimulus, a "dummy" of aspect ratio 3.0 and base width of 20 cm, was never presented from the 2.5 m distance, however, since at this position, the top of this stimulus exceeded the length of the presentation surface.

Observers made two types of verbally-based judgments on every trial: an aspect ratio judgment (relating to perceived shape) followed by a distance judgment (relating to perceived location). The aspect ratio judgments were verbal reports of the depth to width ratio of the L-shape, expressed as a percentage under objective instructions. The distance judgments were verbal reports of the stimulus distance (i.e., horizontal distance from the observer to the intersection of the two line-segments forming the L-figure), expressed in feet and inches.

Each observer completed two experimental sessions, one performed under binocular viewing conditions, and another under monocular conditions. Experimental sessions were conducted on separate days, with the orientation of the stimulus presentation apparatus rotated 180 degrees between sessions (to reduce memory carryover). The session order was determined at random, with half of the observers having received binocular conditions followed by monocular, and half having received monocular conditions followed by binocular.

Results

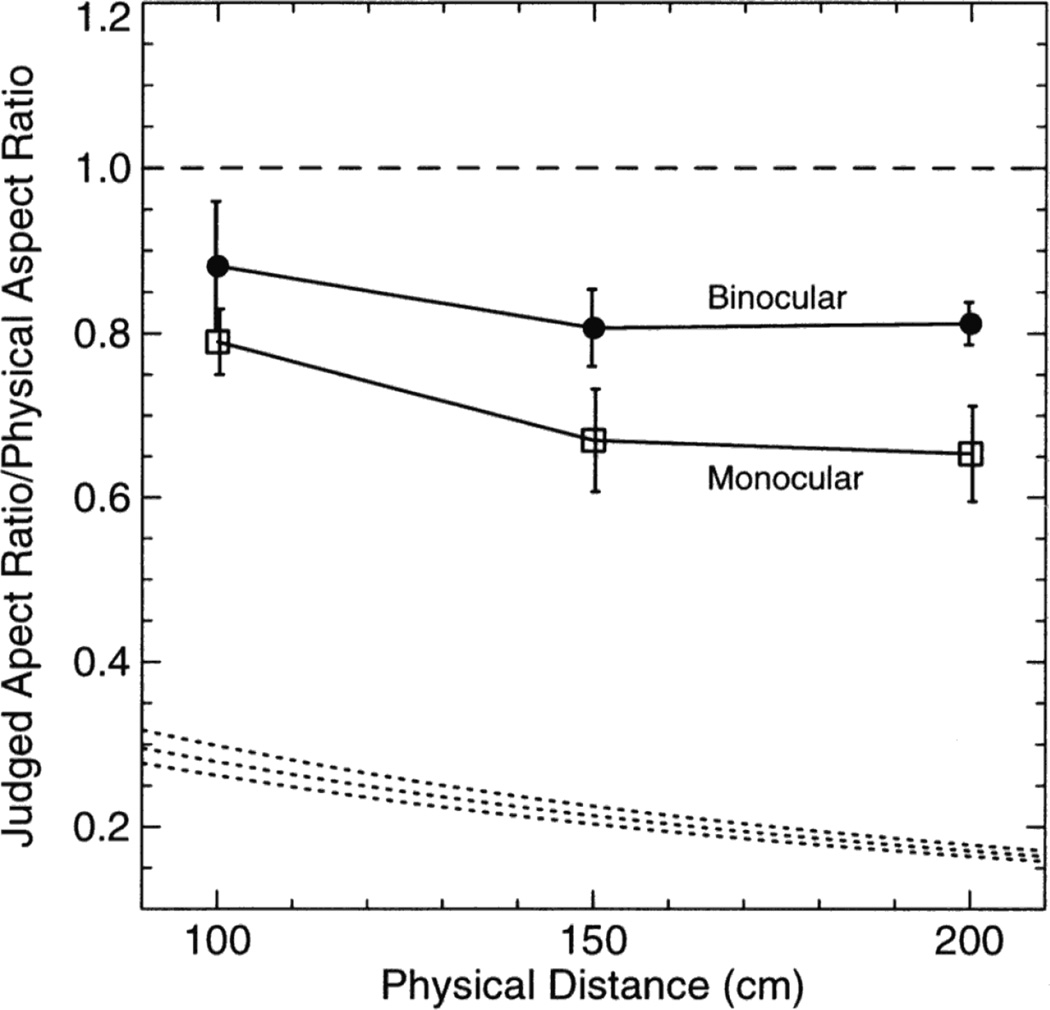
The data from one observer were excluded from all analyses, due to this observer's expressed confusion about the experimental task. Aspect ratio judgments were normalized by the stimulus aspect ratio for all subsequent analyses. A 4-factor mixed design ANOVA was used to analyze this response measure, with viewing condition order treated as a between-observers variable, and distance, size, and view conditions treated as within-observer variables. This analysis revealed a significant interaction between viewing condition and viewing order, F(1,22) = 5.859, p = .024. As such, a greater difference between monocular and binocular viewing conditions was observed in first session data than in second session data. In light of these carryover effects, we will restrict further discussion to data collected in the first experimental session. Because this restriction does not allow for within-observer evaluations of the viewing condition variable, a modified analysis was applied to the data using a 3-factor mixed design ANOVA which treated distance and size as within-observer variables, and viewing condition as a between observer variable. As expected, significant main effects were observed for both the distance, F(2,44) = 8.287, p = .001, and viewing condition variables, F(1,22) = 11.548, p = .003. Tests of the size variable main effect and all other interactions proved to be non-significant. Figure 3 gives the first session shape judgment results collapsed across stimulus size. The effects of viewing condition are readily apparent. Note that there is considerable shape distortion in both viewing conditions, as indicated by the normalized aspect ratio values being less than unity.

Figure 3.

Results of shape judgment task in Experiment 2. Mean normalized aspect ratio judgments (first session only) as a function of target distance and viewing condition. Filled symbols represent data from the binocular condition, and open symbols represent data from the monocular condition. Error bars denote. The dashed line gives the predicted response for veridical shape perception. The three dotted lines (corresponding to the 3 stimulus sizes) give the predicted responses if perceived shape were equal to retinal shape.

The distance data were analyzed in a similar fashion as the shape judgment data. A 3-factor mixed design ANOVA was conducted on data from the first experimental session only. As before, this analysis treated distance and size as within-observer variables, and viewing condition as a between observer variable. Only the main effect of stimulus distance yielded significant results, F(2,44) = 610.702, p < .001. A summary of these results is shown in Figure 4 for the first session data collapsed across stimulus size. The most pertinent result is the non-significant difference between binocular and monocular viewing conditions, F(1,22) = 0.001, p = .971, with both conditions leading to quite accurate performance.

Figure 4.

Results of distance judgment task in Experiment 2. Mean verbal reports of distance (first session only) as a function of target distance. Filled symbols represent the data for binocular viewing, and open symbols represent the data for monocular viewing. Error bars denote ± 1 SE of the individual observer means. The dashed line represents perfect responding.

Discussion

Like the results of Experiment 1, the results here demonstrate that the monocular/binocular manipulation had a sizeable effect on the perception of shape, as indicated by the aspect ratio judgment, but no influence on the judgment of perceived location, as indicated by the distance judgment. Whereas the results of Experiment 1 might possibly be explained in terms of Hypotheses 3 or 4, the use here of a common response, verbal report, rules out this possibility. Thus, this experiment provides the strongest evidence of a dissociation between perceived location and perceived shape in visual space.

General Discussion

The two experiments reported here, along with previous research, show that visually perceived location, as measured by visually directed walking and verbal report, is accurate for binocular and monocular viewing of targets on a horizontal plane. In contrast, the same research shows that the perception of 2-D shapes viewed under the same conditions exhibits large systematic distortion. As discussed in the introduction, four hypotheses have been proposed as possible ways of reconciling these two findings. The present research provides support for Hypothesis 1, Accurate Perception of Location and Dissociation of Location and Shape. If perceived shape were linked to the perceived locations of the vertices defining the shape, any manipulation that changes perceived shape would necessarily involve changes in the perceived locations of these vertices. Experiments 1 and 2 show that the distortion observed with monocular viewing decreases significantly with binocular viewing; whereas, the monocular/binocular manipulation has no discernible effect on perceived location. This is strong evidence for a dissociation within perception. However, we note that the dissociation occurs under special circumstances where perspective cues associated with a ground plane provide reliable information about location. In the absence of such cues, such as when points of light are viewed without obvious attachment to surfaces, oculomotor cues, binocular cues, and optic flow must determine perception. Under these conditions, a much tighter coupling between perceived location and perceived shape/extent seems to be the case (see Foley, 1980, 1991 in connection with oculomotor and binocular cues).

Given the large distortions of perceived shape on the surface plane, it may seem paradoxical that perceived egocentric distance along the surface plane can be perceived accurately. The fallacy in thinking that perceived distance must be inaccurate may lie in the implicit belief that perceived egocentric distance to a target on the surface plane should be equal to the sum of successive perceived depth extents defined by visually distinct points lying between the observer and the target. The idea that globally perceived egocentric distance might be the sum of local depth extents along the ground plane is a special case of the Fechnerian assumption that one can integrate successive just-noticeable-differences along some perceptual dimension to obtain the overall perceptual difference between the two endpoints. Using just such an assumption, Gilinsky (1951) attempted to derive a scale of perceived egocentric distance based on a task in which observers constructed a sequence of equal-appearing physical extents. Given that her observers adjusted more distant extents as larger in order to appear equal to nearer extents, the use of the Fechnerian assumption led to a scale of perceived egocentric distance that was a compressively nonlinear function of physical distance, specifically a hyperbolic function. Because this result is so completely at odds with the results obtained with visually directed action and other methods (Da Silva, 1985), we conclude that the Fechnerian assumption is false in this application.

Having supported the hypothesis of a functional dissociation between perceived location and perceived shape, do we have any way of explaining it in terms of visual processing? We consider three mechanistic hypotheses.

The first of these was proposed by Walter Gogel (personal communication, 1996) and is predicated on changes in perception from fixation to fixation. When we look at a pattern, we successively fixate different parts of the figure. Gogel (1965, 1990) has argued that for a given fixation, nonfixated visual targets lying closer or farther than the fixated target are attracted toward the perceived location of the latter in accord with the “equidistance tendency”. The degree of perceptual flattening of the 3-D configuration is the result of a compromise between the equidistance tendency and the strength of the relative distance cues; thus, for near stimulus configurations, strong binocular disparity cues reduce the degree of flattening in comparison with more distant configurations, for which binocular disparity is less effective. As applied to the current findings, Gogel’s hypothesis is that when one fixates a target under full-cue conditions, the location of the target is perceived correctly, but nonfixated targets move perceptually toward the fixated target. Thus, judgments of shapes lying in depth exhibit the distortion produced by the equidistance tendency, but egocentric responses to fixated targets are accurate.

Philbeck (2000) has tested and rejected this hypothesis. In his experiment, observers fixated one of two visible targets lying in depth on the floor of a well lit room. Fixation of the target was controlled by very brief stimulus presentations of the room visible through a large liquid-crystal shutter and by a just visible fixation point appearing at the same 3-D location as one of the targets. After the stimulus configuration and the fixation point were blanked, one of the two targets was specified as the destination and the observer attempted to walk to its location without vision. Walked distance, the indicator of perceived distance, showed accurate responding to all targets, with no tendency whatsoever for nonfixated targets to move perceptually toward the fixated target.

The second mechanistic hypothesis supposes that the perception of location on the ground plane is based on visual processing that is quite different from that underlying the perception of shape. We believe, like many others (e.g., Gibson 1950a, 1950b; Ooi et al., 2001; Sinai et al., 1998; Sedgwick, 1983), that perceived egocentric distance to a target on the surface plane depends strongly on the perspective cues of texture gradient, linear perspective, and height in the field (angular elevation, angular declination). Texture gradient and linear perspective are likely to be the primary basis for the global organization of the ground plane and its apparent recession in distance. Any particular point on this perceived ground plane is specified by its height in the field so that its perceived egocentric distance is determined by its height in the field acting in concert with the cues of texture gradient and linear perspective. Because the perspective cues are sufficient for localizing a point on the ground plane, binocular information is superfluous. Now in the case of shape perception, it is reasonable to suppose that surface texture is involved in monocularly perceiving the relative sizes of local extents on the ground plane; if so, the anisotropy of texture density might explain the distortion of perceived shape, like that apparent in Figure 1. When viewing switches from monocular to binocular, the addition of binocular disparity leads to more accurate perception of depth extents and thus reduces the shape distortion.

The third and related hypothesis hinges on the distinction between central tendency and dispersion. It begins with the assumption that each location in physical space is represented by an ensemble of graded activity within a population of neurons with overlapping place fields in 3-D (analogous to the idea of receptive fields in 2-D), with one neuron near the center of the population typically giving a maximal response. This profile of graded activity can be characterized by its centroid and one or more parameters reflecting its dispersion; the dispersion reflects both the intrinsic connectivity of the visual pathway and internal noise relating to the quality of the stimulus information about the target location. According to the second assumption of this hypothesis, perceived 3-D location corresponds to the centroid of this profile of graded activity. The degree of dispersion corresponds to the precision with which the location is specified. Thus, even though two different combinations of distance cues might determine the same centroid (thus specifying the same location), they could determine different levels of precision. The third assumption is that perceived separation between two targets is analogous to the d’ measure of signal detection theory. Thus, the perceived separation between two physical locations is equal to the distance between the two centroids, divided by the dispersion parameter. This hypothesis predicts that distance cues which increase the precision of the representation (decrease its spread) will increase the perceived separation between two targets without modifying the perceived locations of the points. Thus, adding binocular disparity to monocular perspective cues might increase the perceived separation between two points in depth without modifying their perceived locations, as specified by other cues such as height in the field.

Finally, we note that direct estimates of extent seem to be subject to less distortion than simultaneous comparison of two extents. In one of their experiments, Loomis et al. (1992) had observers walk without vision to two previewed targets on the ground defining either a width extent or a depth extent. For equal size depth and width extents, observers walked the same distances. Loomis et al. (1992) speculated that the isotropic walking response could be explained by observers walking in succession to two locations stored in memory. However, Philbeck (1997) has found that even when observers view two targets and the extent between them and then estimate the extent using a number of different responses (e.g., verbal estimate, pacing out a distance from the viewing position), there is only a slight anisotropy for width and depth extents; a similar result has been reported by Wender (1999). It appears that when subjects abstract the length of an extent in order to perform some response other than walking to its endpoints, their response does not reflect the perceived extent but is corrected to some degree. In contrast, when depth and width extents are simultaneously visible and must be directly compared, either through an extent matching task (Beusmans, 1998; Loomis et al., 1992) or through a judgment of aspect ratio, observers do perceive a big difference in length. This interpretation is supported by an experiment by Amorim, Loomis, & Fukusima (1998), which showed that observers were more accurate in reproducing an L-shaped stimulus from memory (after viewing it under perspective) than when reproducing the same shape while viewing it concurrently. Similarly, Vishton, Rea, Cutting, and Nuñez (1999) found the observers showed a much greater vertical/horizontal illusion when responding simultaneously to the vertical and horizontal extents of the illusion figure (e.g., when shaping the hand to respond to both extents) than when responding serially to each extent. They interpret their results in terms of a distinction between the judgment of relative extent (shape) and the judgment of absolute extent. Without further research, it is unclear whether this distinction is useful in understanding the present dissociation. Regardless, the present results indicate that perceived shape does depend upon whether viewing is` monocular or binocular, whereas, perceived location does not.